Abstract
Path-integral Monte Carlo methods were applied to calculate the second, B(T), and the third, C(T), virial coefficients for water. A fully quantum approach and state-of-the-art flexible-monomer pair and three-body potentials were used. Flexible-monomer potentials allow calculations for any isotopologue; we performed calculations for both H2O and D2O. For B(T) of H2O, the quantum effect contributes 25% of the value at 300 K and is not entirely negligible even at 1000 K, in accordance with recent literature findings. The effect of monomer flexibility, while not as large as some claims in the literature, is significant compared to the experimental uncertainty. It is of opposite sign to the quantum effect, smaller in magnitude than the latter below 500 K, and varying from 1% at 300 K to 10% at 700 K. When monomer flexibility is accounted for, results from the CCpol-8sf pair potential are in excellent agreement with the available experimental data and provide reliable B(T) at temperatures outside the range of experimental data. The flexiblemonomer MB-pol pair potential yields B(T) that are slightly too high compared to experiment. For C(T), our calculations confirm earlier findings that the use of three-body potential is necessary for meaningful predictions. However, due to various uncertainties of the potentials used, especially the three-body ones, we were not able to establish benchmark values of C(T), although our results are in qualitative agreement with available experimental data. The quantum effect, never before included for water, reduces the magnitude of the classical value for H2O by a factor of 2.5 at 300 K and is not entirely negligible even at 1000 K.
1. Introduction
While the electronic structure of molecules can be described only using quantum mechanics, the motions of molecular nuclei can often be approximated well enough using equations of classical mechanics. Of course, in all such cases, one has to switch to quantum treatment of these motions at some threshold of accuracy required for description of a phenomenon. However, there are many systems for which only a quantum treatment of nuclear motions gives reasonable predictions. One group of such systems are atomic and molecular clusters.
An extreme example is the helium dimer, one of the weakest interatomic interactions in nature. This dimer has only one bound state, some time ago considered to be nonexistent. Now reliable experimental1–6 and theoretical7–11 information on properties of this state is available. This state is an important example of a halo state, i.e., it is a state with the property that the particles are mostly found in the classically forbidden region,11,12 an extreme example of quantum effects. The properties of this state depend in a measurable way on physical phenomena not often considered for molecular systems. One has in particular go beyond Schrödinger’s quantum mechanics and include relativistic and quantum electrodynamics effects,11,12 as these effects significantly impact the halo character of this state. At the required level of accuracy, one also has to include the nonadiabatic effects in an essentially exact way.11 At this advanced level, theoretical predictions of the size and binding energy of the bound state are significantly more accurate than experimental results. In particular, a recent measurement of the latter property6 resulted in experiment becoming compatible with theory,9 but the theoretical uncertainties are much smaller than the experimental ones. It is also worth mentioning that theoretical properties of helium gas are now being used in upcoming metrology standards.13,14 One element of theoretical input are virial coefficients, which are calculated from quantum scattering cross-sections10 (classical calculations are far from achieving the required accuracy).
The next example is a dimer of diatomic molecules, H2–CO. The rovibrational motions in this floppy dimer are extremely anharmonic, leading to complicated spectra where many measured lines are resonances.15 Full quantum treatment is needed to describe such motions, and the same is true for description of scattering of H2 on CO.16 The mixed second virial coefficient was calculated for this system using the path-integral Monte Carlo (PIMC) method.17 The quantum approach has to be used for essentially all temperatures of interest; only above 1000 K can one rely on the classical values.
Nuclear motions in water clusters and in liquid water are much less quantum than in the two dimers discussed above, and in fact classical molecular dynamics describes liquid water reasonably well.18,19 Nevertheless, with recently improved potential energy surfaces,20–23 the quantum effects, if neglected, are becoming the largest source of uncertainties in theoretical predictions of water properties. In particular, quantum corrections are substantial for virial coefficients, the subject of the present work.
Advances in computational quantum mechanics have enabled creation of increasingly realistic models for water. While simple empirical rigid-monomer pair models like SPC/E24 or TIP4P25 are still useful in simulations of condensed phases of water, they give huge discrepancies with experiment if used in calculations of virial coefficients (see Fig. 4 in Ref. 26). This is because such potentials effectively incorporate three- and higher-body effects in the pair potentials, while the virials are defined in terms of exact K-body potentials. More sophisticated empirical potentials that incorporate polarization effects do provide somewhat better second virial coefficients.27 Still, most rigid-monomer water dimer potentials fitted to ab initio interaction energies in the past 20 years gave second virial coefficients that agreed with experiment significantly better, see, e.g., Refs. 18, 26, 28, and 19. In fact, theoretical data became so accurate, that, in their correlation of experimental data for B(T) of H2O, Harvey and Lemmon29 included for T > 700 K values calculated from the SAPT-5s potential of Ref. 28. The first accurate flexible-monomer pair potentials were developed in 2006.30,31 The most accurate current potentials of this type are those of Refs. 22 and 21. The number of three-body potentials for water is much smaller, and reliable potentials of this type were created only in the past decade32–34 (note that by three-body interaction energy we mean the trimer interaction energy minus the sum of all dimer interaction energies, with all vertical interaction energies, i.e., all the total energies are computed with monomers in the same geometries as in the trimer35,36). The currently best three-body potentials of this type are those from Refs. 23 and 20; the former is a flexible- and the latter a rigid-monomer potential. The development of high-quality potential functions for water has been reviewed by Szalewicz et al.37 and by Cisneros et al.38
Fig. 4.
Importance of quantum effects in water’s B(T). The virial coefficients computed classically and semiclassically are shown relative to the PIMC values for the same rigid-monomer potentials.
While a fair number of third virial, C(T), calculations have been published for rare-gas atoms,39–44 there are only a few calculations of C(T) for water. The first calculation with realistic potentials was performed by Kusalik et al.,27 but the three-body potential was represented only by a simple point-charge polarization model. The most recent calculation of C(T) was published by Schultz et al.45
Virial coefficients appear in the expansion describing deviation from ideal-gas behavior as a series in powers of density
| (1) |
where p is the pressure, ρ the molar density, R the molar gas constant, and T the absolute temperature. The second virial coefficient B(T) is rigorously defined by the pair potential only, the third virial coefficient C(T) depends on both the two-body and three-body potentials, etc. The virial expansion is useful for describing thermodynamic properties of water vapor in a variety of contexts, including steam turbines and atmospheric science. The third virial coefficient is expected to be important for water as three-body effects account for at least 15% of the values of properties of liquid water.18,19,33,35
For ordinary water (H2O), B(T) is well known from experiment above approximately 320 K,29 while there is much less knowledge of C(T). For heavy water (D2O), B(T) is known over a more narrow range of temperature,46 and C(T) is known only for a few values of T from a single study. Calculating virial coefficients from potentials can therefore serve two functions. First, comparing calculated B and C at temperatures where reliable experimental data exist serves as a test of the accuracy of the potentials and of the methods used to compute the virials. Second, for potentials that are shown to be sufficiently accurate, the calculated B and C at temperatures where no (accurate) data exist provide much needed estimates of these important thermodynamic functions.
The simplest to calculate are classical virial coefficients, as these are straightforward multidimensional integrals. However, because of the small moments of inertia of the water molecule, quantum effects on the virial coefficients are expected to be larger than in most molecules. Indeed, for the second virial coefficients, this has been known for long time, for example, calculations of Ref. 26 found that quantum effects reduce the the magnitude of classical B(T) by 14% at 298 K (however, no quantum calculations are available for C(T)). Note that such large quantum effects may seem to be in contradiction to the fact that these effects, as mentioned earlier, make in general fairly small contributions in simulations of liquid water; see a discussion of this issue in Sec. 5. The most often used expression for quantum effects is the leading term, proportional to the square of the reduced Planck constant, ℏ2, in the Wigner–Kirkwood expansion.47 Various other semiclassical approximations have been developed,48–51 but the errors of these approximations are difficult to estimate. We therefore employ the PIMC approach, which converges to the full quantum solution if sufficient computer resources are used.50,52,53
The PIMC calculations will be performed with full-dimensional potentials. Apart from this being the only way to get near-exact values, the ability to obtain the virials at this level is important for at least two other reasons. First, by performing PIMC calculations also with rigid-monomer potentials, we can determine the relative importance of monomer-flexibility effects on virials. One wants to know these contributions since for systems larger than water calculations of such corrections are beyond capabilities of present methods. The current information on monomer-flexibility effects is limited. For the second virial coefficient of H2, Garberoglio et al.54 found that a rigid-monomer model with the bond length at its vibrationally averaged ground-state value gives results nearly identical to the fully flexiblemonomer calculation, and later effects of similar size (0.8% effect at 300 K and 0.09% at 1000 K) were found for H2-CO.17 On the other hand, for H2O, it has been claimed that monomer flexibility has a large effect on B(T). Refson et al.55 computed this effect as 10% in the range 373–673 K, while Donchev et al.56 computed it as 20–40% for T ∊ 300 − 800 K, with 40% effect at 300 K. In contrast, recent calculations by Jankowski et al.21 gave much smaller monomer flexibility effects. In particular, near the edges of the investigated range of temperatures the effect was 2.4% (at 298 K) and −9% (at 3000 K). The percentage effect does become large at temperatures around 1500 K, but this is not meaningful since B(T) crosses zero there. Jankowski et al. also found that these effects are an order of magnitude smaller than quantum effects at low T, but become larger in magnitude for T larger than about 600 K. However, the quantum effects were computed only at the Takahashi–Imada level49 and only for rigid monomers. Our ability to calculate virial coefficients at exact quantum level from a flexible-monomer potential will allow us to definitely evaluate whether the literature claims of large flexibility effects are correct.
Second, the knowledge of the full-dimensional quantum results will allow evaluation of various approximate methods of including monomer-flexibility effects. While the virial coefficients for fully flexible monomers are uniquely defined, derivations of approximate methods have to employ somewhat arbitrary procedures of averaging over intramolecular coordinates and therefore it is difficult to compare such methods based on the derivations. These issues have recently been extensively discussed in Refs. 54 and 21.
One more advantage of performing flexible-monomer calculations is that such calculations can be done for all isotopologues, such as D2O, using a single potential. This is because the clamped-nuclei (Born–Oppenheimer) potential does not depend on nuclear masses. Rigid-monomer water models typically use the angle and bond length of H2O, while D2O has a slightly different geometry.57 Thus, either a separate potential has to be developed for D2O or some error is introduced by using the H2O geometry. This problem has been very recently partly overcome in Ref. 58 by using the atom-following method of Refs.59 and 60. However, with a flexible-monomer model, we can compute virial coefficients for D2O with full consideration of its (flexible-monomer) geometry, or we can “freeze” the flexiblemonomer model at the vibrationally averaged ground-state D2O geometry in order to perform simpler rigid-rotor calculations. The virial coefficients of D2O are of particular interest for a current effort to produce a new international standard reference equation of state for the thermodynamic properties of heavy water.61
In this work, we use the PIMC method to calculate B(T) for H2O and D2O at a fully quantum level from two high-accuracy flexible-monomer pair potentials. We also examine the effect of flexibility by performing PIMC calculations on rigid-monomer versions of those models, and examine the importance of quantum effects by performing classical and semiclassical calculations. We use the same pair potentials, in combination with one flexible-monomer and one rigid-monomer three-body potential, to calculate C(T) for H2O and D2O.
2. Theory
The path-integral calculations of virial coefficients from ab-initio potentials reported in this paper are largely based on the theory we developed in Ref. 54. Since in that paper we dealt specifically with linear molecules (H2 isotopologues), we now briefly describe how the results can be extended to deal with the general case.
2.1. Quantum exchange effects in an isolated water molecule
Let us denote by X = [xH1,xH2,xO] a point in 9-dimensional vector space of Cartesian coordinates of the atoms in a water molecule and let |X〉 be the quantum mechanical state of a molecule where the atomic positions have definite values described by the coordinates X. If the two hydrogens are treated as indistinguishable particles (that is, in the case of H2O or D2O), then the single-molecule partition function at temperature T is given by
| (2) |
where β = (kBT)−1 , kB is the Boltzmann constant, H1 is the single-molecule Hamiltonian, and the operator χ exchanges the coordinates of the two hydrogens, that is χ|X〉 = χ|xH1,xH2,xO〉 = |xH2,xH1,xO〉. The Hamiltonian is of the form H1 = t +u(X), where t is the kinetic energy operator for the three atoms and u(X) the potential energy of the system. As usual, we evaluate the right-hand side of Eq. (2) using the Trotter theorem
truncated at a large but finite value of P, and inserting completeness relations of the form
(with k = 2,…,P) between the appropriate exponential operators. The space of states |Xk〉 is identical to the space of states |X〉, and we will from now on denote the latter states as |X1〉. In this way we arrive at the usual path-integral representation of quantum statistical mechanics:54,62 the first term in Eq. (2) (called the Boltzmann term) is equivalent to the partition function of a system of distinguishable particles where each of the initial atoms is replaced by a ring polymer with P beads. The beads having the same index k interact via the potential u(Xk)/P and the subsequent beads corresponding to the same atom a interact via a harmonic potential with the harmonic constant Ka = MaP(βℏ)−2, where Ma is the mass of atom a. Hence, the potential energy of a ring-polymer molecular configuration is
| (3) |
where denotes the position of atom a (a = 1,…,N, where N is the number of atoms within the considered molecule) in the i-th bead. Notice that due to the condition of closed ring polymers, one has XP+1 = X1.
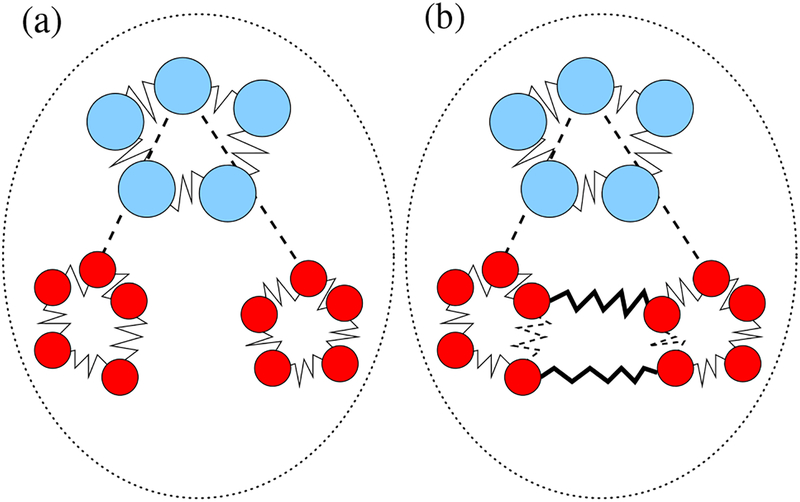
The second term in Eq. (2) (called the exchange term) corresponds to a classical system where the ring polymers of the two hydrogen atoms within the same molecule are coalesced into a single ring polymer of 2P beads. A pictorial representation of these two cases is presented in Fig. 1. When considering exchanged configurations, we will denote the ring-polymer potential energy as . Notice that the only difference between and is in the harmonic contribution of Eq. (3), and it corresponds to the variation in energy obtained by cutting the dashed bonds between hydrogen atoms in Fig. 1(b) and adding the bold ones.
Fig. 1.
Water molecules in the ring-polymer representation; the blue ring polymer corresponds to the oxygen atom, the red ring polymers to the two hydrogens. (a) Example of a Boltzmann configuration. (b) Example of an exchanged configuration, obtained from (a) by cutting the dashed bonds between hydrogen atoms and creating the bold ones.
As shown in Ref. 54, the relative importance of the Boltzmann versus exchanged configurations depends on the temperature. In the limit of high temperatures, only the Boltzmann configurations contribute to sampling. At finite temperatures, the relative probability Ξ(T) of the appearance of exchanged configurations vs. Boltzmann ones can be obtained via thermodynamic integration
| (4) |
where denotes an average of the potential energy difference
(independent of λ) performed by sampling molecular configurations where ring-polymer potential is given by
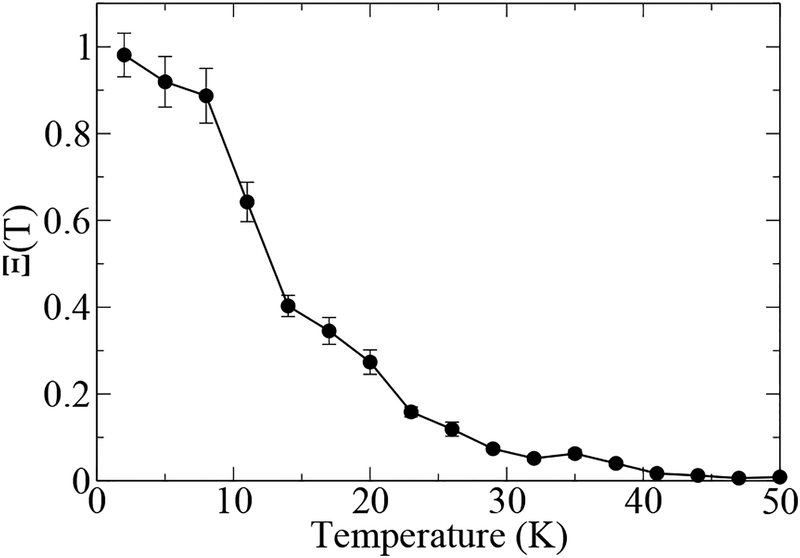
As discussed above, depends only on the difference in the harmonic energy between the exchange and Boltzmann configuration (see Fig. 1). The relative probabilities Ξ(T) for a single H2O molecule in vacuum are plotted in Fig. 2. This figure shows that the exchange effects are completely negligible above T = 40 K. Since in the following we will be interested in temperatures T ≥ 200 K, this result implies that only Boltzmann polymers will contribute to the calculation. Thus, we will neglect the exchange term in Eq. (2), resulting in a considerable simplification of the sampling procedure.
Fig. 2.
The relative importance of exchange versus Boltzmann polymers – the quantity Ξ in Eq. (4) – in the case of a single H2O molecule in vacuum.
2.2. PIMC virial coefficients
The virial coefficients discussed here are determined in terms of partition functions Qi, i = 1,2,3: the monomer partition function Q1, defined in Eq. (2), the dimer one Q2, and the trimer one Q3. The definitions of Q2 and Q3 are completely analogous to the definition of Q1: neglecting exchange effects, and denoting by qN all the coordinates necessary to describe N molecules, one has
| (5) |
where HN is the quantum mechanical Hamiltonian of an N-molecule system. Introducing the auxiliary variables
| (6) |
where V is the volume containing the system under consideration, we can write the second virial coefficient as63,64
| (7) |
and the third one as
| (8) |
The derivation of the PIMC expression for the second virial coefficient from Eq. (7) is analogous to that described in Ref. 54, starting from the expression
with
where ti is the kinetic energy operator for all the atoms in molecule i, Xi is the variable X of Sec. 2.1 with the subscript distinguishing the two molecules, and U2 is the flexible-monomer intermolecular potential which, in this notation, depends on 18 variables. Since the intermolecular potential is invariant by an overall translation or rotation of the coordinate system, U2 actually depends on 12 independent variables. In PIMC with P beads, the evaluation of the partition function Q2 results in a 18P-dimensional integral. In this integral, the potential U2 enters as the sum
| (9) |
where Xc,i denotes the positions of the atoms of monomer c in the ith bead and . Thus, is a function of 18P variables. Since the integral is invariant to translations of the whole dimer, one can integrate three of the 18P coordinates, which we choose as the position of the first bead of the oxygen of molecule a. This results in the appearance of a factor V, and, in the remaining integrand, this bead can be considered fixed at the origin of the coordinate system. Further simplifications of Eq. (7) can be achieved by realizing that among the remaining 18P − 3 coordinates one describes the relative position of the two molecules: we use the first bead of the oxygen in molecule b and denote its value by x. The remaining 18P−6 coordinates describe the internal configurations of the two ring polymers. We note that the expression of B(T) includes two single-molecule partition functions Q1 in the denominator, which are both proportional to V due to translational invariance, resulting in a cancellation of the volume factors in Eq. (7). Furthermore, one can interpret the integration in the 18P−6 internal coordinates in Q2 as an average over two single-molecule ring polymers, whose oxygens in the first bead are separated by x. Using these considerations, one can then show54 that the formula for the second virial coefficient can be written as
| (10) |
where z2(x) is defined by
| (11) |
with the average 〈⋯〉 performed over ring-polymer configurations of isolated water molecules whose oxygen atoms in the first bead are separated by x. In our computer code, these ring-polymer configurations are generated using a hybrid Monte Carlo procedure.65,66 Equation (10) is also valid in the case of rigid molecules. In this case, the center of mass of the molecule in the first bead is fixed at the origin of the coordinate system, and x denotes the position of the center of mass of the first bead of the second molecule. The average is then performed over ring-polymer configurations corresponding to free rigid-water molecules that have been sampled using the straightforward Metropolis Monte Carlo.
Starting from Eq. (8), the third virial coefficient can be written as
| (12) |
| (13) |
where is the total three-body potential averaged over the P beads, with a definition analogous to in Eq. (9), in the configuration where the first bead of the oxygen atom of molecule a is fixed at the origin of the coordinate system, and the first beads of the oxygen atoms of the other two molecules (b and c) are in positions x and y, respectively. As in the case of z2(x), the average leading to z3(x, y) is performed over the configurations of three free-molecule ring polymers. In actual calculations averages such as that of Eq. (11) are performed on the fly while integrating over x (and y in the case of the third virial), using at least 12 independent pairs (or triplets) of ring polymers. When calculating B(T), invariance under rotation implies that the integrand is a function only of |x|, whereas in the case of C(T), the integrand is a function only of |x|, |y|, and the angle between x and y. Integrations over these independent coordinates are performed using the VEGAS algorithm, sampling 5000 points for B(T) and 105 points for C(T).
The Trotter index P was fixed at P = 64 for the flexiblemonomer models (both H2O and D2O), because we found convergence at this value for B(T) even at the lowest investigated temperature. In the case of rigid molecules, we used a temperature-dependent value given by P = 2500 K/T +4 for both isotopologues. In this case, this value was fixed by checking the convergence of B(T) at the temperatures of 200 K, 300 K, 500 K, and 1000 K. The statistical uncertainties on the calculations are reported as the variance of the mean taken on 16 independent runs.
2.3. Kinetic energy transition matrix for rigid monomers
For rigid monomers, the variables describing the state of a single molecule in a cluster are the molecular center-of-mass coordinates, RC, and the set of three Euler angles, Ω, describing its orientation. In this case, the most time-consuming step of a PIMC simulation is the calculation of the transition matrix for the rotational kinetic energy operator trot
| (14) |
which is a function of the Euler angles ΔΩ describing the rotation from the configuration described by the Euler angles Ω0 to the configuration described by the Euler angles Ω1. This quantity has been studied by Noya et al.,67,68 and can be expressed in the form of nested loops, as shown in Eq. (15) of Ref. 68. We precalculate ρrot(ΔΩ) on a three-dimensional grid with an angular resolution of 2°, and use cubic spline interpolation to obtain its value during the path-integral simulation. This approach resulted in a significant speedup of calculations with a negligible impact on the accuracy.
2.4. Semiclassical virial coefficients
By expanding Eq. (7) in powers of ℏ, it turns out that the fully quantum second virial coefficient can be approximated by a classical calculation with a modified potential.50 One common form of this semiclassical potential is the one proposed by Feynman and Hibbs62,69 (FH) which – in the case of two interacting rigid rotors whose centers-of-mass separation is denoted by R and whose orientations are given by the Euler angles Ω1 and Ω2, respectively – has the form
| (15) |
where μ is the reduced mass of the two interacting molecules and θni denotes a rotation around the principal axis i of molecule n, with Ii being the corresponding moment of inertia. However, we used the Takahashi–Imada (TI)49 form of the effective potential, which involves only the first order derivatives and is given by
| (16) |
where F is the force between the centers of mass of the two molecules and τni is the i-th component of the torque acting on molecule n. The classical and semiclassical virial coefficients for rigid monomers are usually written as 9-dimensional integrals over (R,Ω1,Ω2), but can be reduced to 6-dimensional integrals due to isotropy of the potential. In our calculations, integrations were performed in 7 dimensions, i.e., all the 6 Euler angles and the radial separation, as it was easier to sample such subspace uniformly.
In the case of the third virial coefficient, we are not aware of any semiclassical formula for rigid or flexible molecules. In this case, we followed Ref. 45, and used the TI potential for the two-body interaction, while keeping the regular potential for the three-body interaction.
2.5. Intermolecular potentials
Given the importance of water in many physical and chemical processes, a large number of intermolecular potentials have been developed and optimized for specific applications (e.g., simulation of the liquid and solid phase). In this work, we will consider only potentials that have been developed using ab-initio electronic structure calculations performed on water dimers and trimers.
In the case of two-body interaction, we will consider the CCpol-8sf21,30,70 and MB-pol23 potentials, which explicitly consider flexible molecules, as well as their rigid-molecule approximations, obtained by fixing the O–H distance and the H–O–H angle at their average values in the ground rovibrational state, rOH = 0.9716257 Å and HOH= 104.69°, respectively.71 In this case, the CCpol-8sf potential reduces to the rigid-monomer CCpol-8s potential of Ref. 72 (which is an improved version of the CCpol-5s potential of Ref. 73). The CCpol2 potential20 is very similar to CCpol-8s, but represents a small improvement over it (mainly by using additional grid points at small intermonomer separations from Ref. 74). To take advantage of this improvement, we used CCpol2 in rigid-monomer calculations (note that there are some mistakes in the Supplementary Information of Ref. 20, which are corrected in an erratum75). The same approach has been applied to generate rigid-monomer heavy-water potentials; in this case we have used rOD = 0.97077 Å and DOD= 104.408°.57
Few three-body potentials are available for water. Two full-dimensional potentials exist: the surface of Ref. 76 (an improved version of the surface from Ref. 34) and the three-body part of MB-pol.23 CCpol320 is a recent three-body potential developed using highly-accurate quantum mechanical calculations and a much denser grid than in Refs. 76 and 23, but it was developed only in rigid-monomer form. Despite this, we will use it also for flexible-monomer simulations in the following way: when the PIMC program requires a value of three-body potential at some deformed monomer geometry, this geometry is projected onto the closest rigid-monomer configuration obtained using the bisector-axis embedding described in the Supplementary Information of Ref. 21 and such rigid-monomer value of the three-body potential is used. Since CCpol3 is in site-site form, another option would be to use the atom-following scheme.59,60
As a general remark, we note that all of these potentials have been obtained by fitting a given functional form using a large number (from several thousands to hundreds of thousands) of water dimer or trimer configurations. The resulting functions reproduce with high fidelity the ab-initio energies of configurations close to the training set. However, in performing the integrals leading to the virial coefficients, one often needs the value of the potential for molecular configurations very dissimilar from those used in the fitting procedure, and the resulting extrapolation might lead to unphysical values of the potential which, in turn, results in inaccurate virial coefficients. In general, we identified two cases in which this extrapolation is particularly inaccurate: short intermonomer distances and large monomer deformations.
To deal with the first case, we introduced a short-range cutoff, setting the potential to a very high value (105 K) whenever two molecules are closer than a specific distance. The details of this procedure depend on the specific potential: in the case of MB-pol we used a criterion based on the center-of-mass distance d, assuming strong repulsion as soon as d < 1.8 Å. In the case of CCpol-8sf, we used a more complicated criterion based on the distances dab between atoms a and b on different molecules; we assumed strong repulsion as soon as at least one of the following conditions were met: dOO < 1.8 Å, dHH < 1.3 Å, dOH < 1.3 Å.
The case of large molecular deformations, which appear quite frequently in the path-integral sampling, was particularly problematic for CCpol-8sf. We noticed that intermolecular energies resulted in unphysical values when extrapolating beyond the range of OH bond-lengths [0.8639–1.0778] Å and HOH angles [76.68 –137.27°] used in the training set. In that case, we adjusted the problematic monomer to a geometry corresponding to the nearest endpoint of the appropriate range. In the case of MB-pol, this problem did not appear, possibly due to the fact that there was no range of separations and angles used for selecting grid points, but rather such points were extracted from molecular simulations.
Another unphysical behavior exists in the case of the published version of the CCpol3 potential.75 This fit produces unphysical values at configurations with at least one intermonomer distances larger than about 25 Å, and insufficiently accurate values in the range 10 Å to 25 Å. The problem is related exclusively to the exchange terms proportional to the third power of orbital overlap integrals. However, the exchange terms should be completely negligible for distances larger than 10 Å. Thus, a simple solution is to set the exchange terms to zero at such distances, which then gives a well-behaved function without any loss of accuracy (see Ref. 75 for more details). To be on the safe side, we decided to truncate the exponential part for separations larger than 7 Å. The induction part of the potential, which dominates three-body interactions at large separations, does not exhibit any problems and was kept in our calculations. The same approach was taken by Schultz et al.45
All the calculations used the PJT2 potential by Polyansky et al.77 to represent the intramonomer energy u(X).
3. Results for B(T)
Table 1 shows the calculated second virial coefficients B(T) for H2O for the full-dimensional potentials (CCpol-8sf and MB-pol) and for various approximations (PIMC for a rigid-monomer potential at the vibrationally averaged ground-state geometry, semiclassical rigid, classical rigid). For conciseness, we do not tabulate semiclassical and classical results for the rigid MB-pol pair potential; deviations of these approximations from the PIMC calculation are nearly identical for CCpol2 and MB-pol.
Table 1.
Values of B(T) in cm3/mol for H2O for various approximations and potentials. The uncertainties are the statistical uncertainties of the calculation. All results were obtained using PIMC unless noted otherwise.
| Temperature (K) | Harvey-Lemmon | CCpol-8sf (flexible) |
MB-pol (flexible) |
CCpol2 (rigid) |
CCpol2 (rigid, semiclassical) |
CCpol2 (rigid, classical) |
MB-pol (rigid) |
|---|---|---|---|---|---|---|---|
| 200 | −15190 | −12451.(19) | −12694.(44) | −12887.(22) | −13010.(32) | −23825.(58) | −12291.(21) |
| 225 | −6516 | −5362.(8) | −5386.(13) | −5445.(11) | −5381.(10) | −8620.(16) | −5330.(11) |
| 250 | −3252 | −2789.8(26) | −2786.(6) | −2813.(4) | −2744.(5) | −3985.(7) | −2678.(5) |
| 273.15 | −1916.9 | −1716.3(20) | −1703.(4) | −1694.(3) | −1661.(3) | −2259.(5) | −1634.(3) |
| 300 | −1163.0 | −1085.6(10) | −1070.6(27) | −1061.2(11) | −1042.2(22) | −1330.1(20) | −1034.5(15) |
| 325 | −795.9 | −763.1(9) | −748.4(9) | −742.2(10) | −727.4(14) | −893.5(15) | −730.1(11) |
| 350 | −580.1 | −566.4(7) | −555.4(11) | −547.4(11) | −536.4(10) | −636.5(9) | −537.7(7) |
| 375 | −443.3 | −437.7(5) | −426.7(8) | −417.6(7) | −411.7(7) | −478.4(7) | −413.0(6) |
| 400 | −351.1 | −348.6(5) | −340.4(7) | −330.8(5) | −326.2(5) | −372.4(6) | −329.1(5) |
| 450 | −237.5 | −236.5(4) | −229.8(6) | −221.2(3) | −220.0(4) | −244.8(5) | −222.4(2) |
| 500 | −171.97 | −171.4(3) | −166.7(3) | −160.4(3) | −158.3(4) | −172.4(4) | −161.6(3) |
| 550 | −130.18 | −130.28(28) | −125.5(4) | −119.81(15) | −118.97(25) | −128.3(3) | −121.94(19) |
| 600 | −101.66 | −102.02(22) | −98.2(4) | −93.15(21) | −92.36(25) | −98.70(24) | −94.61(20) |
| 700 | −65.94 | −66.05(22) | −63.41(23) | −59.29(16) | −58.88(19) | −62.46(21) | −61.08(15) |
| 800 | −45.00 | −44.60(16) | −43.19(20) | −39.52(13) | −38.93(19) | −41.28(18) | −40.93(14) |
| 900 | −31.51 | −31.74(21) | −30.38(22) | −26.48(17) | −26.50(17) | −27.58(13) | −28.24(13) |
| 1000 | −22.22 | −22.40(19) | −20.90(21) | −17.79(17) | −17.54(14) | −18.55(12) | −19.28(11) |
| 1250 | −8.35 | −8.66(18) | −7.26(13) | −4.90(8) | −4.58(8) | −5.04(10) | −6.02(9) |
| 1500 | −0.84 | −1.00(16) | 0.10(14) | 2.28(6) | 2.33(9) | 2.08(8) | 1.06(7) |
| 1750 | 3.78 | 3.80(19) | 4.36(10) | 6.40(7) | 6.36(7) | 6.20(6) | 5.39(5) |
| 2000 | 6.85 | 5.79(21) | 7.23(9) | 9.09(4) | 9.19(4) | 8.88(6) | 8.16(5) |
The experimental B(T) data for H2O were reviewed by Harvey and Lemmon.29 For comparison purposes, in this paper we discuss only the sources they found to be reliable; many older data are inaccurate due to adsorption effects. Kell et al.78 extracted B(T) from volumetric measurements between 423 K and 773 K. Eubank et al.79 used the Burnett expansion method to derive B(T) from 348 K to 623 K. Both the Kell and Eubank studies made corrections for adsorption, which are essential below roughly 500 K. Abdulagatov et al.80 reported B(T) from volumetric data from 523 K to 653 K, and Vukalovich et al.81 used previously measured high-temperature volumetric data from his laboratory to derive B(T) from 773 K to 1173 K. Finally, Harvey and Lemmon29 derived B(T) from the vaporization data of Osborne et al.82,83 This procedure only works in a limited temperature range; Harvey and Lemmon report values from 323 K to 473 K.
Harvey and Lemmon (HL)29 represented the experimental B(T) (and some theoretical values as mentioned earlier), along with some data related to dB/dT, with a correlation function that was stated to be valid, i.e., reproduce data within their uncertainty, between 310 K and 1170 K. We will use the HL correlation as the baseline for examining how well our calculated
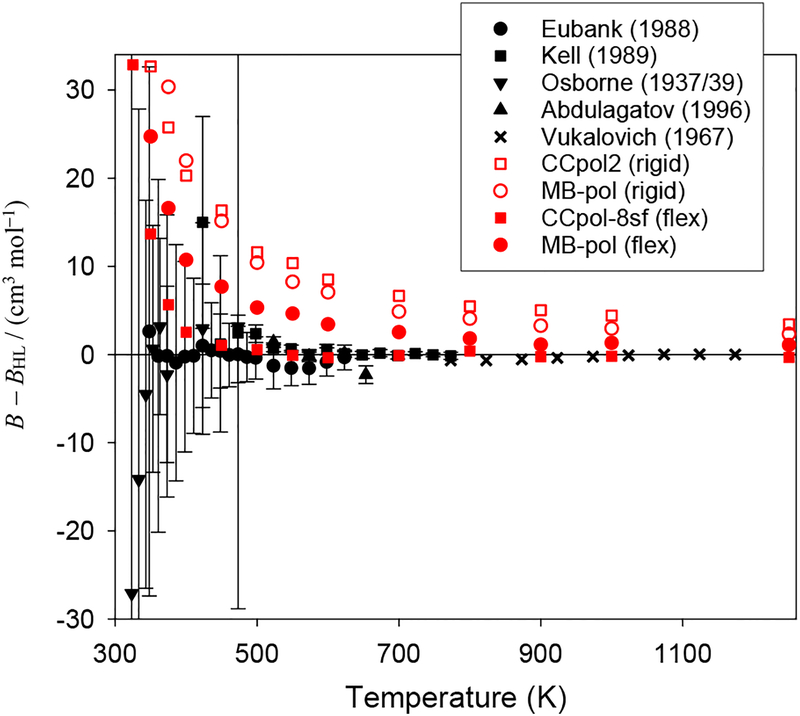
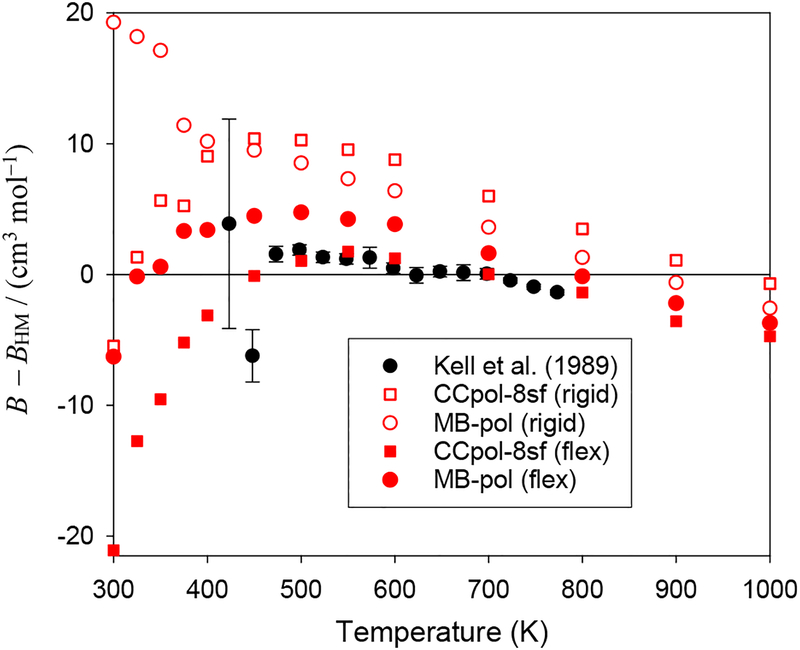
Figure 3 shows the calculated B(T) for H2O from both pair potentials, with and without monomer-flexibility contributions, as the difference from the HL correlation. The selected experimental data are also plotted, along with their uncertainties (expanded uncertainties with coverage factor 2, roughly corresponding to a 95% confidence interval) where available. The results from the flexible-monomer CCpol-8sf potential are in excellent agreement with the HL correlation and with the experimental data. The differences are large only relative to the data of Osborne et al.83 in the range 325 K – 350 K, but these data have uncertainties so large that theoretical and experimental values are still consistent. In the same range, the discrepancies with the HL correlation are also fairly large (although smaller than with Ref. 83), but note that this region is close to the validity limit. As seen in Table 1, below this limit the relative discrepancies become still larger. While the flexible-monomer MB-pol potential yields results that are near the experimental data, they are clearly not consistent with experiment, yielding B(T) slightly too high over the entire range.
Fig. 3.
The second virial coefficient of H2O compared with experimental data, all relative to the HL correlation values.
Table 1 and Fig. 3 show that the effect of monomer flexibility for both pair potentials is to lower B(T) for T > 250 K. This effect is several times larger than the uncertainties of the experimental data, showing that accounting for flexibility is necessary for quantitative agreement with experiment at the current level of experimental accuracy. As a percentage of the total B(T), the monomer-flexibility effect varies from 1% at 273 K to 10% at 700 K (for higher temperatures the relative contribution becomes very large, but this is mainly due to the fact that the function B(T) crosses zero near 1500 K). This shows that the effect calculated by Refson et al.,55 close to 10% in the whole range investigated by them, was too large in magnitude, except at their highest value of T, whereas the 20–40% contribution obtained by Donchev et al.56 was much too large. On the other hand, the agreement with monomer-flexibility effects computed by Jankowski et al.21 in the range 273 K – 1000 K is excellent, to within about 1%. Although the virial coefficients from all-dimensional CCpol-8sf and MB-pol potentials are fairly close to each other, Fig. 3 shows that the monomer-flexibility corrections are about twice as large for CCpol-8sf as for MB-pol in the range of T displayed.
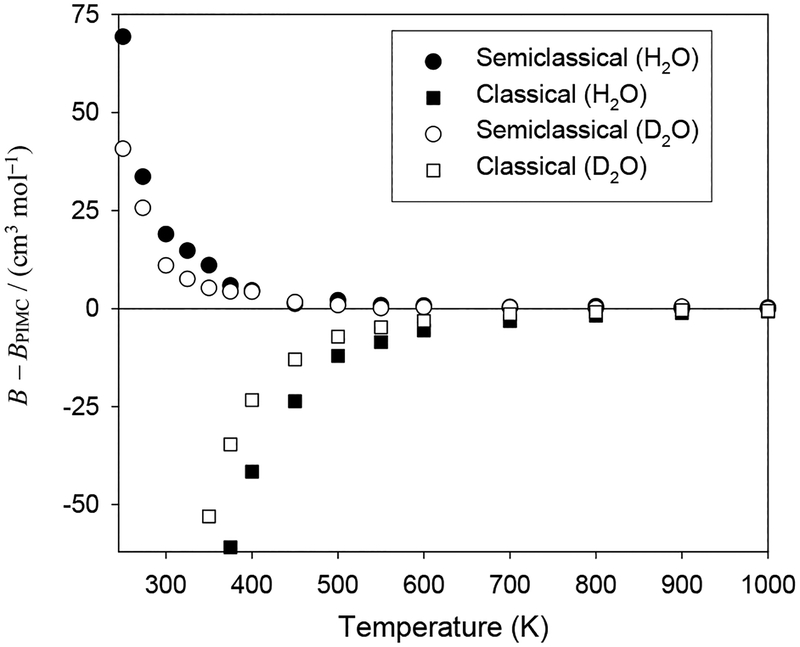
In Fig. 4, we show the effect of approximating the quantum nature of the B(T) calculations. Only results from the CCpol2 potential for H2O and the rigid-monomer version of the CCpol-8sf potential for D2O are shown; the results for the rigid-monomer versions of MB-pol are similar. The vertical axis on Fig. 4 is the difference between the approximately calculated B(T) and that obtained from a full PIMC calculation (in rigid-monomer approximation). As expected for a molecule with a small moment of inertia and strongly anisotropic intermolecular forces, quantum effects are significant even at high temperatures, amounting to 4% at 1000 K (the larger relative contribution for some higher temperatures is again related to the crossing of zero). As temperature decreases, the percentage increases to reach 25% at 300 K. The quantum effects move the B(T) curve up, acting opposite to monomer-flexibility effects. However, a significant cancellation between the two effects takes place only in a relatively narrow range of T: from about 450 K to 600 K (as the former effects decrease with T, while the latter increase). The semiclassical approximation works well over virtually the whole range of temperatures, as it recovers PIMC results to within about 2% (except near the crossing of zero). The absolute discrepancies may seem large below roughly 400 K, but even at 300 K the error is only 1.8%, very small compared to experimental uncertainties in this region. This is a positive finding for future work on larger molecules, since the TI calculations are much less expensive than the PIMC ones.
The second virial coefficients can be compared with those computed by Jankowski et al.21 Both calculations used the same CCpol-8sf potential, but different methods of computing B(T). The authors of Ref. 21 calculated the monomer-flexibility correction by subtracting the values computed with the potential averaged over the monomer ground-state vibration, 〈U2〉0, from values computed with the potential taken at the vibrationally averaged geometry, U2(〈r〉0). As discussed above, this correction is in excellent agreement with our results. The correction was then added to the quantum virial coefficients computed in TI approximation from the U2(〈r〉0) potential. Since Jankowski et al. performed calculations for temperatures used in experiments, only a few of these coincide with those used by us. At 273 K and 450 K, the differences are 6% and 2% (after an interpolation from 448 K), respectively. At 1000 K, 1500 K, and 2000 K, the differences are below 1.8 cm3/mol. Thus, the agreement is very good. At the lowest T, the discrepancy is mainly due to an incomplete account of quantum effects. When these effects become less important, the agreement improves at 450 K. At high T, the discrepancies are due to the different treatments of monomer-flexibility effects.
Table 2 shows results of PIMC calculations for D2O. For this isotopologue, the only reliable experimental B(T) are from Kell et al.,78 extending from 423 K to 773 K. Hill and MacMillan46 (HM) used those data and the behavior of H2O to derive a correlation for B(T) of D2O; we use the HM correlation as a baseline for plotting our calculated D2O results.
Table 2.
PIMC values of B(T) in cm3/mol for D2O for various approximations and potentials. The uncertainties are the statistical uncertainties of the calculation. All rigid-monomer calculations used the appropriate D2O geometry.
| Temperature (K) | Hill-MacMillan | CCpol-8sf (flexible) |
MB-pol (flexible) |
CCpol-8sf (rigid) |
MB-pol (rigid) |
|---|---|---|---|---|---|
| 200 | −13406 | −15675.(23) | −15832.(38) | −16267.(38) | −15397.(23) |
| 225 | −5890 | −6369.(9) | −6396.(15) | −6591.(12) | −6177.(15) |
| 250 | −3052 | −3171.(4) | −3161.(8) | −3210.(5) | −3075.(5) |
| 273.15 | −1855.1 | −1901.8(22) | −1887.(4) | −1899.(4) | −1846.(4) |
| 300 | −1153.2 | −1174.3(17) | −1159.4(18) | −1158.6(20) | −1133.9(13) |
| 325 | −799.1 | −811.9(13) | −799.3(18) | −797.8(12) | −781.0(9) |
| 350 | −585.9 | −595.4(5) | −585.3(10) | −580.2(7) | −568.8(6) |
| 375 | −448.8 | −453.9(6) | −445.4(7) | −441.2(7) | −437.4(10) |
| 400 | −355.7 | −358.8(9) | −352.3(9) | −346.6(6) | −345.5(4) |
| 450 | −240.8 | −240.9(3) | −236.3(6) | −230.4(4) | −231.3(3) |
| 500 | −174.61 | −173.6(4) | −169.9(3) | −164.33(23) | −166.08(21) |
| 550 | −132.31 | −130.6(5) | −128.1(3) | −122.8(4) | −125.00(24) |
| 600 | −103.21 | −102.0(4) | −99.4(3) | −94.43(21) | −96.81(16) |
| 700 | −65.97 | −65.9(3) | −64.35(24) | −59.97(18) | −62.36(17) |
| 800 | −43.25 | −44.6(3) | −43.39(21) | −39.75(14) | −41.95(14) |
| 900 | −27.95 | −31.5(3) | −30.14(20) | −26.86(14) | −28.57(16) |
| 1000 | −16.93 | −21.7(3) | −20.64(19) | −17.63(11) | −19.51(12) |
| 1250 | 0.72 | −8.0(2) | −7.14(13) | −4.48(8) | −6.16(6) |
| 1500 | 11.40 | −1.0(2) | 0.13(13) | 2.42(9) | 0.97(8) |
| 1750 | 18.79 | 3.7(3) | 4.51(12) | 6.61(6) | 5.25(5) |
| 2000 | 24.41 | 6.6(3) | 7.31(12) | 9.38(6) | 8.20(6) |
In Fig. 5, we show B(T) as differences from the HM correlation, along with the experimental data. Once again, we find quantitative agreement between our calculations with CCpol-8sf and the experimental data in the range 450 K to 800 K, with the MB-pol pair potential yielding B(T) somewhat too high. As was the case for H2O, quantitative agreement with the experimental data requires accounting for monomer flexibility. Figure 5 and Table 2 also show that, unlike the HL correlation for H2O which is accurate at high temperatures (since it was fitted to theory there), high-temperature extrapolation of the HM correlation for D2O overestimates B(T) and the present theoretical data should be used in this region. Similarly as for H2O, the agreement becomes poor for T’s below the range covered by experiments, and theory is likely more reliable in this region.
Fig. 5.
The second virial coefficient of D2O compared with experimental data. The baseline is the HM correlation.
As expected from its larger moment of inertia, the quantum effects on B(T) are smaller for D2O than for H2O. Figure 4 shows the error introduced by the classical and semiclassical approximations. The size of the error for D2O in the classical approximation is slightly more than half of the error for H2O at the same temperature. The semiclassical approximation also yields somewhat smaller errors than for H2O, maintaining quantitative accuracy in absolute terms to near 300 K (the relative accuracy is good throughout).
4. Results for C(T)
The calculation of C(T) requires substantial computer time (roughly 1500 hours per temperature on a single core of a 2.5 GHz machine for the full-dimensional case), but is tractable with the methods described in Sec. 2.2. Such calculations, if sufficient accuracy can be achieved, would be valuable since the few available experimental data sources for H2O78–81,84 are not fully mutually consistent and there is only one experimental source for D2O.78 We report C(T) at only five temperatures (300 K, 500 K, 600 K, 700 K, and 1000 K) in order to discuss qualitative trends and the size of various effects. Except for 300 K, these temperatures overlap available experimental data. The point at 300 K allows us to examine quantum effects which should be relatively large at that low temperature. We could have performed calculations for more points, but as discussed below, the present three-body potentials need more work to yield results with better quantitative accuracy.
In Table 3, we present C(T) calculated for H2O using several different methods, along with the values interpolated (to the T values used in the table) from available experimental sources. To see the influence of three-body effects, we perform fully quantum PIMC calculations with only the CCpol2 rigid-monomer pair potential, and then with the addition of the rigid-monomer CCpol3 three-body potential. We also test the MB-pol potential in a rigid-monomer three-body calculation. To evaluate the magnitude of nuclear-motion quantum effects, we perform the rigid-monomer CCpol2 + CCpol3 calculation in the classical and semiclassical approximations. Finally, we perform three calculations with the molecules treated as flexible. We use the flexible-monomer CCpol-8sf pair potential, with the three-body energies mapped onto the rigid-monomer CCpol3 three-body energies as discussed in Sec. 2.5. For MB-pol, C(T) is calculated with both two-body and three-body potentials in flexible-monomer form. Lastly, since the CCpol-8sf pair potential performed better than MB-pol for B(T), we combine it with the flexible three-body contribution from MB-pol.
Table 3.
Values of C(T) in cm6/mol2 for H2O using various approximations and potentials and interpolated from experimental sources. The uncertainties are statistical uncertainties of the calculation. All calculations use PIMC unless otherwise noted.
| Temperature (K) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 300 | 500 | 600 | 700 | 1000 | ||||||
| value | unc | value | unc | value | unc | value | unc | value | unc | |
| CCpol2 | −2.17×106 | 2×104 | 8837 | 62 | 5083 | 16 | 2888 | 6 | 863 | 2 |
| CCpol2+CCpol3 (rigid, classical) | −2.15×107 | 4×105 | −14957 | 339 | −335 | 81 | 903 | 34 | 592 | 8 |
| CCpol2+CCpol3 (rigid, semiclassical) | −7.90 ×106 | 2×105 | −9631 | 315 | 41 | 80 | 887 | 47 | 579 | 9 |
| CCpol2+CCpol3 (rigid) | −8.67×106 | 1×105 | −9160 | 251 | 162 | 71 | 923 | 37 | 576 | 8 |
| CCpol−8sf + CCpol3 (flex) | −8.02 ×106 | 2×105 | −11171 | 554 | 0 | 119 | 1008 | 72 | 655 | 15 |
| MB−pol (rigid) | −8.97 ×106 | 2×105 | −13274 | 478 | −1368 | 128 | 257 | 46 | 379 | 12 |
| MB−pol (flexible) | −1.37×107 | 6×105 | −17878 | 642 | −2310 | 146 | −117 | 69 | 350 | 16 |
| CCpol−8sf + MB−pol3 (flex) | −1.20×107 | 2×105 | −18999 | 241 | −2189 | 73 | 6 | 23 | 377 | 3 |
| Kell78 | −17000 | 490 | 1335 | |||||||
| Eubank79 | −14000 | 580 | ||||||||
| Abdulagatov80 | 100 | |||||||||
| Vukalovich81 | 655 | |||||||||
The first thing we can see in Table 3 is the crucial role of three-body forces. Comparing the fully quantum results with only the CCpol2 pair potential (first line in the table) with those including the three-body CCpol3 contribution (fourth line), we see that omitting the three-body forces gives the wrong sign of C at some temperatures, and that in general the three-body contribution is similar in magnitude to the value of C itself. It is clear that approximating C(T) with only two-body forces, while often done in the literature, is seriously in error for water.
Second, we examine the quantum effects on C(T) by comparing the values calculated with the full PIMC method for the rigid CCpol2+CCpol3 case (fourth line in Table 3) with the classical and semiclassical approximations (second and third lines). The classical calculation is consistent with the fully quantum results at 700 K and 1000 K, but not below. In fact, the performance of the classical approximation deteriorates dramatically at lower temperatures, and at 300 K the classical value is 2.5 times larger in magnitude than the quantum one. The semiclassical approximation retains accuracy at 600 K, and marginally so at 500 K. These ranges of validity for the classical and semiclassical approximations are similar to the corresponding ranges for B(T). As with B(T), the classical calculation produces C(T) that are too negative.
The effect of monomer flexibility is smaller than that of three-body forces, but it is significant compared to the experimental and theoretical uncertainties. This can most easily be seen by comparing the rigid-monomer MB-pol results (sixth line in Table 3) with those computed with full pair and three-body flexibility in MB-pol (seventh line). Monomer flexibility makes C(T) more negative (as was the case for B(T)), and at the two temperatures where multiple data sources exist this effect is somewhat larger than the magnitude of the scatter among data sources.
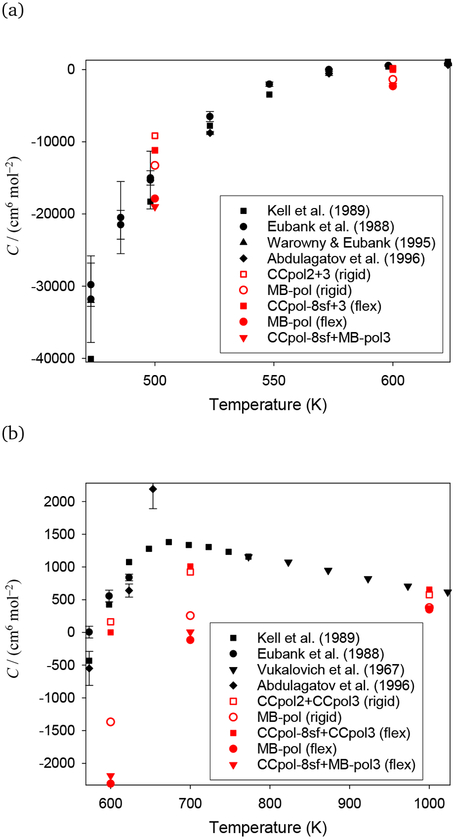
In Fig. 6, we compare the performance of different approaches to experimental data. For clarity, we omit the pair-only calculations and the classical and semiclassical approximations. The MB-pol flexible-monomer model gives C(T) distinctly lower than experiment at all temperatures but 500 K, where it is consistent with the experimental data. The situation with the CCpol family of potentials is better; CCpol-8sf+ CCpol3 (flex) yields C(T) reasonably close to experiment at 500 K (the value is above most experimental data, but consistent within mutual uncertainties with one of the data sources79). The agreement is excellent at 1000 K (to three significant digits which is certainly fortuitous). At 600 K, the theoretical result lies somewhat below the two higher experimental values,78,79 but agrees well with the interpolated value of Ref. 80. At 700 K there is a discrepancy with the single experimental data source,78 but since Kell et al. did not report uncertainties in C(T) it is difficult to say whether the difference is significant. If (as the MB-pol results suggest) incorporation of flexibility in the three-body potential adds a negative contribution to C(T), adding such flexibility to the CCpol3 potential would worsen agreement with experiment except at 500 K.
Fig. 6.
The third virial coefficient of H2O for several potentials and water models, together with experimental results. Panel (a): temperature range 470–625 K. Panel (b) temperature range 570–1025 K. CCpol-8sf+3 (flex) denotes the use of a flexible-monomer approach for the two-body part and a mapping for the three-body potential, see text.
We note that the low-temperature experimental C(T) values are not beyond question; absorption of water on the surfaces of apparatus makes deriving virial coefficients from experiment, especially coefficients beyond the second, very difficult at roughly 500 K and below. This difficulty is apparent in comparing the data of Kell et al.78 and Eubank et al.79 for H2O. The two sets already differ significantly at 500 K (visible in Fig. 6a and in Table 3), and the disagreement increases at lower temperatures, reaching a factor of three at their lowest common temperature of 423 K (not shown).
Finally, we consider the combination of the CCpol-8sf two-body potential with the MB-pol three-body potential. We might expect this to be the best performer, since it combines the flexible-monomer pair potential that almost perfectly reproduces experimental B(T) with a three-body potential that includes flexibility. However, as is apparent in Fig. 6, this combination does not improve matters, producing C(T) values similar to those from MB-pol and similarly inconsistent with experiment above 500 K. The fact that both high-quality flexible-monomer pair potentials (CCpol-8sf and MB-pol2) yield almost identical C(T) when combined with the same three-body potential (MB-pol3) suggests that the two-body potentials are adequate for use in C(T) calculations, and that the need for improvement lies in the three-body potentials.
One more way to analyse the results is to realize that the values of C(T) obtained with the CCpol2+3 rigid-monomer potential are likely very close to the limit values for the rigid-monomer approximation. This is because both the two- and three-body parts of this potential were fitted to highly-accurate ab initio data computed for a very large number of grid points (more than 70 thousand for the three-body part in 12 dimensions). Thus, if the monomer-flexibility effects lower the value of C(T), as MB-pol calculations imply, C(T) computed with CCpol2+3 provides an upper bound for this quantity. If this were true, it would suggest that the Kell et al. results in the range 600 K – 750 K may be systematically high. However, we cannot be certain about the sign of the monomer-flexibility effect. The three-body part of MB-pol was fitted to about 10 thousand grid points in 21 dimensions, which gives a much less dense grid than in the case of CCpol3. Thus, the rigid-monomer part of MB-pol3 is quite different from CCpol3, which is seen from MB-pol rigid-monomer results being significantly different from CCpol2+3. We have no way to determine how accurate the monomer-flexibility correction given by MB-pol is. If experiments are right, even the sign of the true correction would be different from what MB-pol gives.
Table 4 and Fig. 7 present analogous results for D2O. We note that the calculations with rigid-monomer pair potentials are performed not at the H2O geometry but rather with the flexiblemonomer potentials (CCpol-8sf and MB-pol) “frozen” at the D2O geometry as described in Sec. 2.5. Some error is introduced by the use of the CCpol3 three-body potential for D2O since it was developed for the H2O geometry and we have kept the monomers in this geometry. We expect this error to be small, since the averaged geometries of the H2O and D2O monomers are not very different.
Table 4.
Values of C(T) in cm6/mol2 for D2O using various approximations and potentials and interpolated from experimental sources. The rigid-monomer calculations used potentials evaluated at the average ground rovibrational state geometry of D2O. The uncertainties are the statistical uncertainties of the calculation.
| Temperature (K) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 300 | 500 | 600 | 700 | 1000 | ||||||
| value | unc | value | unc | value | unc | value | unc | value | unc | |
| CCpol−8sf (rigid) | −2.53 ×106 | 4×104 | 9158 | 125 | 5277 | 50 | 2970 | 12 | 871 | 3 |
| CCpol−8sf+CCpol3 (rigid, classical) | −1.97 ×107 | 4×105 | −13291 | 453 | −197 | 140 | 878 | 63 | 605 | 12 |
| CCpol−8sf+CCpol3 (rigid, semiclassical) | −1.14×107 | 3×105 | −10431 | 423 | 129 | 110 | 1031 | 40 | 592 | 14 |
| CCpol−8sf+CCpol3 (rigid) | −1.18×107 | 3×105 | −10937 | 445 | −85 | 144 | 1042 | 56 | 582 | 11 |
| CCpol−8sf + CCpol3 (flexible) | −1.07 ×107 | 3×105 | −11966 | 499 | 103 | 193 | 1057 | 62 | 683 | 17 |
| MB−pol (rigid) | −1.34×107 | 4×105 | −14751 | 406 | −1664 | 134 | 144 | 49 | 385 | 12 |
| MB−pol (flexible) | −1.61×107 | 5×105 | −19018 | 513 | −1987 | 131 | −15 | 58 | 351 | 15 |
| Kell78 | −17500 | 790 | 1320 | |||||||
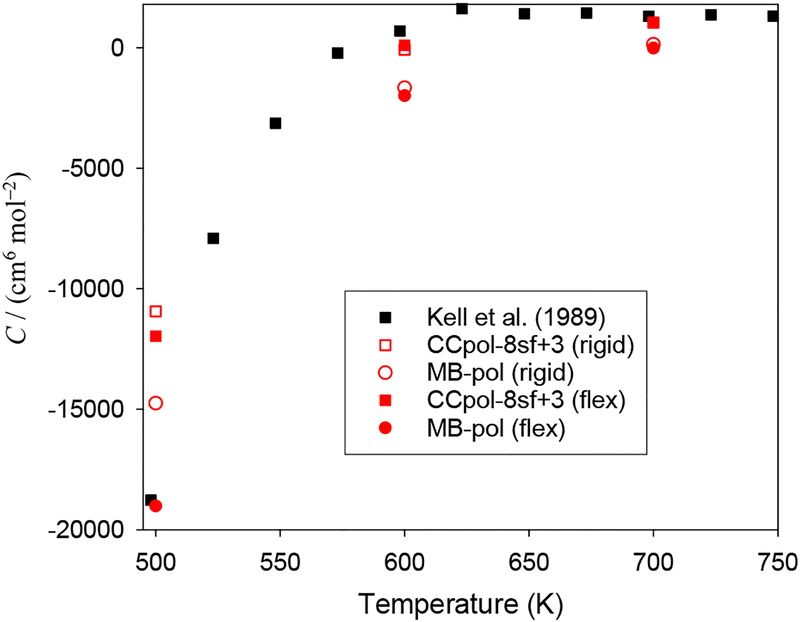
Fig. 7.
The third virial coefficient of D2O for several potentials and water models, together with experimental results. CCpol-8sf+3 (flex) denotes the use of a flexible-monomer approach for the two-body part and a mapping for the three-body potential, see text.
For D2O, the situation is similar to that for H2O, although there is only one experimental data source.78 Three-body effects are essential for even qualitative accuracy. The quantum effects are, as expected, somewhat smaller than for H2O. Flexibility makes C(T) more negative by an amount similar to that found for H2O. Results from the CCpol models are only slightly below the experimental data at 600 K and 700 K, but lie above the data near 500 K. The C(T) from the MB-pol model are clearly too low at the higher temperatures, but (if flexibility is included) agrees with the lone data source near 500 K.
5. Discussion and Conclusions
With the path-integral methods developed in this and earlier work,54 and with the existing state-of-the-art pair and three-body potentials, we have calculated from first principles the second and third virial coefficients for H2O and D2O with full account of both quantum nuclear motion effects and monomer-flexibility effects. The only previous calculations of this type for B(T) were by Babin et al.22 In the case of C(T), our work represents the first calculations at this level for water. The method is general, and could be applied to other isotopologues such as HDO or for unlike interactions such as H2O–HDO.
For the second virial coefficient B(T), rigid-molecule quantum calculations are inconsistent with the experimental data, giving B(T) higher than experiment. The monomer-flexibility correction is negative for T larger than 250 K. For H2O, the percentage values of this correction vary from 1% at 273 K to 10% at 700 K. While this is significant compared to experimental uncertainties, it is smaller than some earlier values reported in the literature, but agrees very well with recent calculations of Jankowski et al.21
The nuclear-motion quantum effects in water are very significant and at 300 K amount to 25% of B(T). These effects, always positive, decrease with increasing T, but still amount to 4% at 1000 K (although this large relative value is partly due to T approaching the value where B(T) crosses zero). The quantum effects are recovered well by the semiclassical approximation which for most points differs from the fully quantum values by less than 2%. We note, however, that there is no algorithm for using a semiclassical approximation with flexible-monomer potentials. The method proposed in Ref. 21 partly avoids this problem by constructing potentials averaged over the ground-state rovibrational motion in monomers. In fact, our current PIMC approach is similar in spirit. Due to the opposite behavior as functions of T, at very large T the monomer-flexibility effects are much larger in magnitude than quantum effects, becoming about the same in magnitude near T = 500 K, which results in near cancellations over a narrow range of T. As expected, the quantum effects are smaller for D2O than for H2O.
For the second virial coefficient, theory has reached a level where first-principles calculations can match experiment and yield reliable values at temperatures where no reliable data exist (or for isotopologues where reliable data are lacking). With monomer-flexibility and quantum effects included, B(T) from CCpol-8sf are fully consistent with the experimental data, except perhaps at the lowest temperatures where the experimental values are highly uncertain. The corresponding MB-pol B(T) values are somewhat too high compared to experiment. The present results agree well with those of Jankowski et al.,21 since both the semiclassical model and the approximate account for monomer flexibility used in that work turned out to perform quite well. However, the more advanced methods used here resulted in an improvements of the agreement with experiment. For temperatures outside the range of experimental data, especially for D2O where the experimental data are more sparse, we believe the present full-dimensional results with the CCpol-8sf pair potential provide the best available values of B(T). These values have already been used as input for a new reference equation of state for heavy water.61
Ideally, we would assign uncertainties to our values of B(T), as we have done in some previous work.43,54 This would require knowledge of the uncertainty of the pair potential, including uncertainty for configurations when the monomers are deformed. Calculations with “plus” and “minus” potentials displaced by the uncertainty would then provide uncertainty bounds on B(T). In addition, further uncertainty is introduced for the CCpol-8sf potential by the need to restrict the range of molecular deformations allowed in the path-integral sampling. Work is ongoing to develop a pair potential that remains valid for the complete range of deformations encountered in PIMC simulations.
For the third virial coefficient C(T), theory is not as reliable as for B(T), and we cannot claim to be able to calculate C(T) for H2O and D2O with accuracy challenging experiments. Our results show that three-body interactions are critical in determining C(T) and incorporation of monomer flexibility appears to be necessary for quantitative accuracy. The CCpol3 potential is close to the exact rigid-monomer potential, but by definition gives no information about monomer-flexibility contributions. The flexible-monomer MB-pol three-body potential, while producing qualitatively correct behavior, does not yield C(T) consistent with available experimental data: C(T)’s are clearly too low in comparison with experiment at all but the lowest temperatures (see Figs. 6 and 7). The CCpol potential gives C(T) values that agree with experiment much better than those from MB-pol, except at the lowest temperature (see Fig. 6a) where it is nevertheless compatible with one experimental source (and we have less confidence in the experimental results at those temperatures). However, since the three-body part of CCpol is in rigid-monomer form, if the corresponding monomerflexibility correction is added, the agreement with experiment may deteriorate. Addressing this situation will require the development of three-body potentials that are accurate both for configurations with the monomers at their vibrationally-averaged geometries (here the rigid-monomer CCpol3 potential might provide a reference point) and also over the entire range of intramolecular deformations sampled in PIMC calculations.
The large nuclear quantum effects on the virial coefficients of H2O (at 300 K, roughly 25% for B(T) and a factor of 2.5 for C(T)) may seem surprising. Classical simulations of liquid water near 300 K with high-quality polarizable potentials can typically produce agreement with experiment to within a few percent for properties such as neutron scattering cross sections, heat of vaporization, diffusion coefficients, density, etc.18,19,74 While the cited work used rigid monomers, a cancellation of large quantum and monomer-flexibility effects is unlikely. Two exceptions are recent flexible-monomer MB-pol classical calculations for H2O by Reddy et al.85 of the isobaric heat capacity which gave values of this quantity 56% larger than experiment and of the dielectric constant which was 13% smaller than the experimental value. By performing both quantum and classical simulations with the flexible-monomer MB-pol potential for liquid water at ambient conditions, Medders et al.86 found that quantum effects were very small for some properties, such as the density, neutron scattering cross-sections, and the self-diffusion coefficient (note that Ref. 85 corrected an erroneous self-diffusion coefficient reported in Ref. 86). Quantum effects were found to be more significant, 8%, for the enthalpy of vaporization, however, note that the joint statistical uncertainty of the two calculations amounts to 6%. Medders et al.86 also found a very large quantum effect in the orientational relaxation time: the quantum value of this quantity is 2.3 times smaller than the classical one. One can conclude from this survey that the quantum effects in liquid water are at most a few percent for many properties, but that a few properties show larger effects of similar magnitude to those we found for the virial coefficients. It is worth noting that, because the virial coefficients provide only corrections to ideal-gas values, cf. Eq. (1), these effects do not have a large impact on measurable properties such as pressure; for the saturated vapor the virial coefficients reduce the pressure by approximately 0.2% at 300 K (where the saturation pressure is so low that the vapor is nearly ideal) and 3% at 400 K.
The fact that virial coefficients include large quantum contributions can be rationalized by realizing that these coefficients reflect directly the strength of intermolecular interactions. Assuming that this strength can be measured by the dissociation energy of the water dimer and considering the values for (H2O)2: 1105 ± 10 cm−1 (Ref. 87) and for (D2O)2: 1244 ± 10 cm−1 (Ref. 88), we can conclude that quantum effects make the interaction weaker (physically, this is largely due to a greater delocalization of the H atom relative to the D atom, weakening the hydrogen bonds more in ordinary water), and then extrapolate to the classical case (a hypothetical high-mass H atom) as resulting in the strongest interactions. This quantum weakening of the intermolecular interactions is consistent with quantum effects making B(T) less negative. If the weakening of the interactions is the major factor impacting quantum effects in properties of liquid water, one can understand why these effects are of different size for different properties. For example, one can expect that properties depending more directly on strength of interactions, like enthalpy of vaporization or heat capacity, will be affected more, while a quantity like liquid density that depends mainly on molecular size will be affected less, which indeed seems to be the case. Some information about the expected size of nuclear-motion quantum effects can be inferred from accurately known data on D2O vs. H2O at 300 K: molar density of liquid D2O is 0.3% smaller,61,89 dielectric constant of liquid is 0.5% smaller,90,91 molar heat capacity of liquid is 11% larger,61,89 enthalpy of vaporization is 3.3% larger,61,89 and second virial coefficient is 8% larger in magnitude (Tables 1 and 2). All these trends are in line with the expected effects on various properties due to quantum weakening of intermolecular interactions. Using these results, one can also comment on the few published large values of quantum effects in liquid water that were listed above. For example, the 8% quantum effect for the enthalpy of vaporization86 and the 56% effect on heat capacity85 could be expected based on experimental data, whereas the 13% effect on the dielectric constant appears too large.
Acknowledgements
Preliminary computer simulations were performed on the KORE computing system at Fondazione Bruno Kessler. For the development of the massively parallel code used to calculate C(T), we acknowledge PRACE for awarding us access to MARCONI at CINECA in Casalecchio di Reno (Italy), SuperMUC at Leibniz-Rechenzentrum in Garching (Germany), and Hazel Hen at High Performance Computing Center in Stuttgart (Germany) as part of PRACE Preparatory Access Type A during May and June 2017. We acknowledge the CINECA award under the ISCRA initiative, for the availability of high performance computing resources and support. This work was also supported by the National Science Foundation Grant CHE-1566036.
We thank Andrew Schultz for discussions on the use of CCpol3. Partial contribution of the National Institute of Standards and Technology, not subject to copyright in the U.S.
Footnotes
Conflicts of interest
There are no conflicts to declare.
Notes and references
- 1.Luo F, McBane GC, Kim G, Giese CF and Gentry WR, J. Chem. Phys, 1993, 98, 3564–3567. [Google Scholar]
- 2.Luo F, Giese CF and Gentry WR, J. Chem. Phys, 1996, 104, 1151–1154. [Google Scholar]
- 3.Schollkopf W and Toennies JP, Science, 1994, 266, 1345– 1348. [DOI] [PubMed] [Google Scholar]
- 4.Schollkopf W and Toennies JP, J. Chem. Phys, 1996, 104, 1155–1158. [Google Scholar]
- 5.Grisenti RE, Schollkopf W, Toennies JP, Hegerfeldt GC, Kohler T and Stoll M, Phys. Rev. Lett, 2000, 85, 2284–2287. [DOI] [PubMed] [Google Scholar]
- 6.Zeller S, Kunitski M, Voigtsberger J, Kalinin A, Schottelius A, Schober C, Waitz M, Sann H, Hartung A, Bauer T, Pitzer M, Trinter F, Goihl C, Janke C, Richter M, Kastirke G, Czasch MWA, Kitzler M, Braune M, Grisenti RE, Schollkopf W, Schmidt LPH, Schoffler M, Williams JB, Jahnke T and Dorner R, Proc. Nat. Acad. Sci. USA, 2016, 113, 14651–14655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Korona T, Williams HL, Bukowski R, Jeziorski B and Szalewicz K, J. Chem. Phys, 1997, 106, 5109–5122. [Google Scholar]
- 8.Jeziorska M, Cencek W, Patkowski K, Jeziorski B and Szalewicz K, J. Chem. Phys, 2007, 127, 124303. [DOI] [PubMed] [Google Scholar]
- 9.Przybytek M, Cencek W, Komasa J, Łach G, Jeziorski B and Szalewicz K, Phys. Rev. Lett, 2010, 104, 183003. [DOI] [PubMed] [Google Scholar]
- 10.Cencek W, Przybytek M, Komasa J, Mehl JB, Jeziorski B and Szalewicz K, J. Chem. Phys, 2012, 136, 224303. [DOI] [PubMed] [Google Scholar]
- 11.Przybytek M, Cencek W, Jeziorski B and Szalewicz K, Phys. Rev. Lett, 2017, 119, 123401. [DOI] [PubMed] [Google Scholar]
- 12.Przybytek M, Jeziorski B, Cencek W, Komasa J, Mehl JB and Szalewicz K, Phys. Rev. Lett, 2012, 108, 183201. [DOI] [PubMed] [Google Scholar]
- 13.Fischer J and Ulrich J, Nature Phys, 2016, 12, 4–7. [Google Scholar]
- 14.Moldover MR, Tew WL and Yoon HW, Nature Phys, 2016, 12, 7–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jankowski P, McKellar ARW and Szalewicz K, Science, 2012, 336, 1147–1150. [DOI] [PubMed] [Google Scholar]
- 16.Faure A, Jankowski P, Stoecklin T and Szalewicz K, Nature Sci. Rep, 2016, 6, 28449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Garberoglio G, Jankowski P, Szalewicz K and Harvey AH, J. Chem. Phys, 2017, 146, 054304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bukowski R, Szalewicz K, Groenenboom GC and van der Avoird A, Science, 2007, 315, 1249–1252. [DOI] [PubMed] [Google Scholar]
- 19.Bukowski R, Szalewicz K, Groenenboom GC and van der Avoird A, J. Chem. Phys, 2008, 128, 094314. [DOI] [PubMed] [Google Scholar]
- 20.Góra U, Cencek W, Podeszwa R, van der Avoid A and Szalewicz K, J. Chem. Phys, 2014, 140, 194101. [DOI] [PubMed] [Google Scholar]
- 21.Jankowski P, Murdachaew G, Bukowski R, Akin-Ojo O, Leforestier C and Szalewicz K, J. Phys. Chem. A, 2015, 119, 2940–2964. [DOI] [PubMed] [Google Scholar]
- 22.Babin V, Leforestier C and Paesani F, J. Chem. Theory Comput, 2013, 9, 5395–5403. [DOI] [PubMed] [Google Scholar]
- 23.Babin V, Medders GR and Paesani F, J. Chem. Theory Comput, 2014, 10, 1599–1607. [DOI] [PubMed] [Google Scholar]
- 24.Berendsen HJC, Grigera JR and Straatsma TP, J. Phys. Chem, 1987, 91, 6269–6271. [Google Scholar]
- 25.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW and Klein ML, J. Chem. Phys, 1983, 79, 926–935. [Google Scholar]
- 26.Mas EM, Szalewicz K, Bukowski R and Jeziorski B, J. Chem. Phys, 1997, 107, 4207–4218. [Google Scholar]
- 27.Kusalik PG, Liden F and Svishchev IM, J. Chem. Phys, 1995, 103, 10169–10175. [Google Scholar]
- 28.Mas EM, Bukowski R, Szalewicz K, Groenenboom GC, Wormer PES and van der Avoird A, J. Chem. Phys, 2000, 113, 6687–6701. [DOI] [PubMed] [Google Scholar]
- 29.Harvey AH and Lemmon EW, J. Phys. Chem. Ref. Data, 2004, 33, 369–376. [Google Scholar]
- 30.Szalewicz K, Murdachaew G, Bukowski R, Akin-Ojo O and Leforestier C, in Lecture Series on Computer and Computational Science: International Conference of Computational Methods in Science and Engineering (ICCMSE 2006), ed. Maroulis G and Simos T, Brill Academic Publishers, Leiden, 2006, vol. 6, pp. 482–491. [Google Scholar]
- 31.Huang X, Braams BJ and Bowman JM, J. Phys. Chem. A, 2006, 110, 445–451. [DOI] [PubMed] [Google Scholar]
- 32.Mas EM, Bukowski R and Szalewicz K, J. Chem. Phys, 2003, 118, 4386–4403. [Google Scholar]
- 33.Mas EM, Bukowski R and Szalewicz K, J. Chem. Phys, 2003, 118, 4404–4413. [Google Scholar]
- 34.Wang Y, Carter S, Braams BJ and Bowman JM, J. Chem. Phys, 2008, 128, 071101. [DOI] [PubMed] [Google Scholar]
- 35.Szalewicz K, Bukowski R and Jeziorski B, in Theory and Applications of Computational Chemistry: The First Fourty Years, ed. Dykstra CE, Frenking G, Kim KS and Scuseria GE, Elsevier, Amsterdam, 2005, ch. 33, pp. 919–962. [Google Scholar]
- 36.Gora U, Podeszwa R, Cencek W and Szalewicz K, J. Chem. Phys, 2011, 135, 224102. [DOI] [PubMed] [Google Scholar]
- 37.Szalewicz K, Leforestier C and van der Avoird A, Chem. Phys. Lett, 2009, 482, 1–14. [DOI] [PubMed] [Google Scholar]
- 38.Cisneros GA, Wikfeldt KT, Ojamäe L, Lu J, Xu Y, Torabifard H, Bartók AP, Csányi G, Molinero V and Paesani F, Chem. Rev, 2016, 116, 7501–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mas EM, Lotrich VF and Szalewicz K, J. Chem. Phys, 1999, 110, 6694–6701. [Google Scholar]
- 40.Bich E, Hellmann R and Vogel E, Mol. Phys, 2007, 105, 3035–3049. [Google Scholar]
- 41.Malijevsky A, Karlicky F, Kalus R and Malijevsky A, J. Phys. Chem. C, 2007, 111, 15565–15568. [Google Scholar]
- 42.Jäger B, Hellmann R, Bich E and Vogel E, J. Chem. Phys, 2011, 135, 084308. [DOI] [PubMed] [Google Scholar]
- 43.Garberoglio G, Moldover MR and Harvey AH, J. Res. Natl. Inst. Stand. Technol, 2011, 116, 729–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cencek W, Garberoglio G, Harvey AH, McLinden MO and Szalewicz K, J. Phys. Chem. A, 2013, 117, 7542–7552. [DOI] [PubMed] [Google Scholar]
- 45.Schultz AJ, Kofke DA and Harvey AH, AIChE J, 2015, 61, 3029–3037. [Google Scholar]
- 46.Hill PG and MacMillan RDC, Ind. Eng. Chem. Res, 1988, 27, 874–882. [Google Scholar]
- 47.Gray CG and Gubbins KE, Theory of Molecular Fluids Volume 1: Fundamentals, Clarendon Press, Oxford, 1984. [Google Scholar]
- 48.Powles JG and Rickayzen G, Mol. Phys, 1979, 38, 1875– 1892. [Google Scholar]
- 49.Takahashi M and Imada M, J. Phys. Soc. Jpn, 1984, 53, 3765–3769. [Google Scholar]
- 50.Schenter GK, J. Chem. Phys, 2002, 117, 6573–6581. [Google Scholar]
- 51.Wormer PES, J. Chem. Phys, 2005, 122, 184301. [DOI] [PubMed] [Google Scholar]
- 52.Fosdick LD and Jordan HF, Phys. Rev, 1966, 143, 58–66. [Google Scholar]
- 53.Garberoglio G and Harvey AH, J. Res. Nat. Inst. Stand. Tech, 2009, 114, 249–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Garberoglio G, Jankowski P, Szalewicz K and Harvey AH, J. Chem. Phys, 2014, 141, 044119. [DOI] [PubMed] [Google Scholar]
- 55.Refson K, Lie GC and Clementi E, J. Chem. Phys, 1987, 87, 3634–3638. [Google Scholar]
- 56.Donchev AG, Galkin NG and Tarasov VI, Phys. Rev. Lett, 2006, 97, 220401. [DOI] [PubMed] [Google Scholar]
- 57.Czakó G, Mátyus E and Császár AG, J. Phys. Chem. A, 2009, 113, 11665–11678. [DOI] [PubMed] [Google Scholar]
- 58.Metz MP, Szalewicz K, Sarka J, Császár AG and Mátyus E, J. Chem. Theory Comput, 2018. [Google Scholar]
- 59.Murdachaew G and Szalewicz K, Faraday Discuss, 2001, 118, 121–142. [DOI] [PubMed] [Google Scholar]
- 60.Murdachaew G, Bukowski R and Szalewicz K, Phys. Rev. Lett, 2002, 88, 123202. [DOI] [PubMed] [Google Scholar]
- 61.Herrig S, Thol M, Span R, Harvey AH and Lemmon EW, J. Phys. Chem. Ref. Data, 2018. [Google Scholar]
- 62.Feynman RP and Hibbs A, Quantum Mechanics and Path Integrals, Dover, New York, 2010. [Google Scholar]
- 63.Hirschfelder JO, Curtiss CF and Bird RB, Molecular theory of gases and liquids, John Wiley & Sons, 1954. [Google Scholar]
- 64.Hill TL, An Introduction to Statistical Thermodynamics, Dover, 1987. [Google Scholar]
- 65.Duane S, Kennedy AD, Pendleton BJ and Roweth D, Phys. Lett. B, 1987, 195, 216–222. [Google Scholar]
- 66.Tuckerman ME, Berne BJ, Martyna GJ and Klein ML, J. Chem. Phys, 1993, 99, 2796–2808. [Google Scholar]
- 67.Noya EG, Sesé LM, Ramírez R, McBride C, Conde MM and Vega C, Mol. Phys, 2011, 109, 149–168. [Google Scholar]
- 68.Noya EG, Vega C and McBride C, J. Chem. Phys, 2011, 134, 054117. [DOI] [PubMed] [Google Scholar]
- 69.Hellmann R, Bich E and Vesovic V, J. Chem. Thermodyn, 2016, 102, 429–441. [Google Scholar]
- 70.Leforestier C, Szalewicz K and van der Avoird A, J. Phys. Chem, 2012, 137, 014305. [DOI] [PubMed] [Google Scholar]
- 71.Mas EM and Szalewicz K, J. Chem. Phys, 1996, 104, 7606– 7614. [Google Scholar]
- 72.Cencek W, Szalewicz K, Leforestier C, van Harrevelt R and van der Avoird A, Phys. Chem. Chem. Phys, 2008, 10, 4716– 4731. [DOI] [PubMed] [Google Scholar]
- 73.Bukowski R, Szalewicz K, Groenenboom GC and van der Avoird A, J. Chem. Phys, 2008, 128, 094313. [DOI] [PubMed] [Google Scholar]
- 74.Akin-Ojo O and Szalewicz K, J. Chem. Phys, 2013, 138, 024316. [DOI] [PubMed] [Google Scholar]
- 75.Some mistakes in the Supplementary Information of Ref. 20 are corrected at. http://www.physics.udel.edu/~szalewic/ccpol23/.
- 76.Wang Y, Hunag X, Shepler BC, Braams BJ and Bowman JM, J. Chem. Phys, 2011, 134, 094509. [DOI] [PubMed] [Google Scholar]
- 77.Polyansky OL, Jensen P and Tennyson J, J. Chem. Phys, 1996, 105, 6490–6497. [Google Scholar]
- 78.Kell GS, McLaurin GE and Whalley E, Proc. R. Soc. Lond. A, 1989, 425, 49–71. [Google Scholar]
- 79.Eubank PT, Joffrion LL, Patel MR and Warowny W, J. Chem. Thermodyn, 1988, 20, 1009–1034. [Google Scholar]
- 80.Abdulagatov IM, Bazaev AR, Gasanov RK and Ramazanova AE, J. Chem. Thermodyn, 1996, 28, 1037–1057. [Google Scholar]
- 81.Vukalovich MP, Trakhtengerts MS and Spiridonov GA, Therm. Eng, 1967, 14, 86–93. [Google Scholar]
- 82.Osborne NS, Stimson HF and Ginnings DC, J. Res. Nat. Bur. Stand, 1937, 18, 389–447. [Google Scholar]
- 83.Osborne NS, Stimson HF and Ginnings DC, J. Res. Nat. Bur. Stand, 1939, 23, 197–260. [Google Scholar]
- 84.Warowny W and Eubank PT, Fluid Phase Equilib, 1995, 103, 77–95. [Google Scholar]
- 85.Reddy SK, Straight SC, Bajaj P, Pham CH, Riera M, Moberg DR, Morales MA, Knight C, Gotz AW and Paesani F, J. Chem. Phys, 2016, 145, 194504. [DOI] [PubMed] [Google Scholar]
- 86.Medders GR, Babin V and Paesani F, J. Chem. Theory Comput, 2014, 9, 2906–2910. [DOI] [PubMed] [Google Scholar]
- 87.Rocher-Casterline BE, Ch’ng LC, Mollner AK and Reisler H, J. Chem. Phys, 2011, 134, 211101. [DOI] [PubMed] [Google Scholar]
- 88.Ch’ng LC, Samanta AK, Czako G, Bowman JM and Reisler H, J. Am. Chem. Soc, 2012, 134, 15430–15435. [DOI] [PubMed] [Google Scholar]
- 89.Wagner W and Pruß A, J. Phys. Chem. Ref. Data, 2002, 31, 387–535. [Google Scholar]
- 90.Malmberg CG, J. Res. Nat. Bur. Stand, 1958, 60, 609–612. [Google Scholar]
- 91.Hamelin J, Mehl JB and Moldover MR, Int. J. Thermophys, 1998, 19, 1359–1380. [Google Scholar]