Abstract
Constitutive models for biological tissue are typically formulated as a mixture of constituents and the overall response is then assembled by superposition or compatibility. This ensures the stress response of the biological tissue to be in the range of a given constitutive relationship, guaranteeing that at least one parameter combination exists so that an experimental response can be sufficiently well captured. Another, perhaps more challenging, problem is to use constitutive models as a proxy to infer the structure/function of a biological tissue from experiments. In other words, we determine the optimal set of parameters by solving an inverse problem and use these parameters to infer the integrity of the tissue constituents. In previous studies, we focused on the mechanical stress-stretch response of the murine patellar tendon at various age and healing timepoints and solved the inverse problem using three constitutive models, i.e., the Freed-Rajagopal, Gasser-Ogden-Holzapfel and Shearer in order of increasing microstructural detail. Herein, we extend this work by adopting a Bayesian perspective on parameter estimation and implement the constitutive relations in the tulip library for uncertainty analysis, critically analyzing parameter marginals, correlations, identifiability and sensitivity. Our results show the importance of investigating the variability of parameter estimates and that results from optimization may be misleading, particularly for models with many parameters inferred from limited experimental evidence. In our study, we show that different age and healing conditions do not correspond to statistically significant separation among the Gasser-Ogden-Holzapfel and Shearer model parameters, while the phenomenological Freed-Rajagopal model is instead characterized by better indentifiability and parameter learning. Use of the complete experimental observations rather than averaged stress-stretch responses appears to positively constrain inference and results appear to be invariant with respect to the scaling of the experimental uncertainty.
Keywords: Uncertainty quantification, Bayesian inference, Constitutive models for murine patellar tendons, Parameter sensitivity and identifiability
1. Introduction
Mechanical tests, reproducing relevant physiologic loading conditions are commonly employed to understand structure-function relationships in soft tissues. In this context, some commonly used testing methods are compression, shear, uniaxial and biaxial tensile tests. However, experimental data from these tests is invariably collected with some degree of uncertainty stemming from various sources, e.g., error in estimating the unloaded or reference configuration of the tissue, accuracy of the chosen deformation tracking method (i.e. optical vs. grip-to-grip tracking), the precision level of the load cell as well as biological variability. Constitutive models describe the response of materials to loads under specific conditions [1], and include parameters that are trained from experimental data, in order to investigate structure-function relationships in the tissue of interest. These models are then used in mathematical modeling and computational simulations of growth and remodeling [2], material failure phenomena [3] and for patient-specific simulations with the aim of guiding clinical decisions [4].
Often, particularly for complex constitutive models, parameter training is achieved through optimization, i.e., without explicitly characterizing the variability associated with parameter estimates, and also a thorough study of the parameter identifiability and sensitivity is not performed, limiting the translational relevance of these approaches and delaying their clinical adoption. In this context, transition to robust approaches for parameter estimation under uncertainty will lead to more dependable analyses and simulations, thereby enhancing clinical relevance. Recent studies in the literature have also used robust Bayesian approaches to increase physiological and clinical relevance of soft tissue models [4, 5, 6, 7, 8, 9].
In this study, we discuss the problem of identifying the parameters for constitutive models of the murine patellar tendon, under uncertainty due to random experimental and modeling errors [7]. In prior work, three constitutive models with varied levels of microstructural detail and a varying number of parameters were considered [10]. Herein, we extend this work using a statistical model with Gaussian additive errors, thus leveraging adaptive Markov chain Monte Carlo [11] to sample from the posterior distribution of the constitutive parameters for each model. We investigate the conditions facilitating learning for these parameters, examine how age and injury affect their distributions, inspect their correlations and study their identifiability and sensitivities.
It may be argued that an additional form of uncertainty relates to partial information provided by the nature of the collected experimental data. In other words, the availability of a complete set of multiaxial experiments would significantly improve the identifiability of even very complex microstructurally motivated constitutive models. On the other hand, we don’t have data other than experimental results from uniaxial tests (as typically the case), and therefore we ask ourselves about the best parameter estimates we can provide under these specific settings. Thus, the conclusions we draw from our study are to be understood in light of the constitutive models we selected and experimental evidence discussed in Section 2.1.
For patient-agnostic applications, it is of interest to determine some sort of average behavior of the soft tissues. However, the wide inter-specimen variability commonly observed leads to a lack of consensus on the optimal approach to use for computing this average and a debate exists between fitting model to each data sample and then computing average of the model parameters versus fitting model to the average experimental data [7, 12, 13, 14]. In our study, we address this issue and compare model training by assembling all experimental data in the likelihood or just the average stress levels.
The paper is organized as follows. Section 2.1 discusses the experimental dataset, while the mathematical formulation of the three constitutive models selected for this study is explained in Section 2.2. The prior ranges for each parameter are justified in Section 2.3. Section 2.4 explains how the parameter estimation problem is formulated based on a Bayesian paradigm, while Sections 2.5 and 2.6 focus on the parameter identifiability and global sensitivity, respectively. Inference results are presented in Section 3 and critically analyzed in Section 4.
2. Materials and Methods
2.1. Experimental data
Stress-stretch data for murine patellar tendon at various aging and healing timepoints before and following injury are gathered from studies in the literature [15, 16, 17, 18]. These studies followed an established excisional injury model to the mid-substance of the tendon [19, 20], with their experimental protocols approved by the University of Pennsylvania Institutional Animal Care and Use Committee. Pre-(0 week) and post-(3 and 6 weeks) injury, real-time load-displacement and the undeformed cross-sectional area data were obtained from three age groups of female C57BL/6 mice: 120, 270, and 540 day-olds which were considered as mature, aging and aged, respectively (Table 1). The nominal stress is computed from the load and undeformed cross-sectional area and converted to the true stress via push forward [21, 22]. A quasi-static (strain rate = 0.1%/sec) uniaxial ramp-to-failure test was performed with a 10% stretch cutoff [23, 24], justified considering 1–4% elongation experienced by healthy tendons under normal physiologic loading, and up to 8% under acute stress.
Table 1:
Number of uniaxial experiments repetitions by age group and injury time points.
| Age | |||
|---|---|---|---|
| Mature (120 days) | Aging (270 days) | Aged (540 days) | |
| 0 week (uninjured) | 5 | 14 | 20 |
| 3 weeks | 17 | 15 | 9 |
| 6 weeks | 14 | 15 | 11 |
2.2. Constitutive Models
Collagen in tendons has a unique hierarchical arrangement [24]. Intact tendons mostly consist of uniaxially organized collagen fascicles, i.e., bundles of collagen fibers formed by aggregation of wavy collagen fibrils [25]. Historically, most models employed to characterize the response of tendons and ligaments to mechanical loading are phenomenological, i.e., providing a purely mathematical description of the nonlinear stress-stretch response [26, 27], but offering little to no insight on tissue level mechanisms governing the response to external loads. In addition, the parameters of such models vary widely, and are therefore prone to a subjective interpretation.
In our prior work, three constitutive models with varied level of microstructural motivation were selected for study [10]. The Shearer (SHR) constitutive model has the greatest microstructural detail, describing tendons at both the fibrillar and fascicular levels [28]. The Gasser-Ogden-Holzapfel (GOH) model contains some phenomenological parameters, but uniquely captures the dispersion of collagen fibers and their alignment about an identified direction [29]. Finally, the simplest model is the Freed-Rajagopal (FR) model for tissue fibers, which contains three interpretable parameters [30].
2.2.1. Hyperelastic formulation for the SHR and GOH models
The patellar tendon was assumed to be incompressible and with transversely isotropic solid cylindrical geometry [31, 32]. Hence, for uniaxial tensile test, the deformation gradient tensor F and corresponding right Cauchy-Green tensor C are:
| (1) |
where λ is the stretch measured along the z axis of the tendon during the uniaxial extension test. The first and fourth strain invariants are I1 = tr(C) = 2 λ−1 + λ2 and . The forth invariant is also expressed as and , for the SHR and GOH models, respectively. The vector represents the preferred collagen fascicle/fiber direction in the reference configuration, measured from the z axis. In cylindrical coordinates this is and , where ψ is the fascicle alignment angle, similar to ξ in the GOH model, i.e., the fiber alignment angle, both measured from z and determined through imaging, if available. The hyperelastic framework for transverse isotropy [33] is employed, with the Cauchy stress tensor obtained as a function of the strain energy-density function (SEF), W = W(I1, I4):
| (2) |
where b is the left Cauchy-Green strain tensor. The SHR SEF yields the following expression for the axial Cauchy stress, after the Lagrange multiplier (p) is found by applying a no-traction boundary condition at the tendon’s outer radial surface within the equilibrium equation ,
| (3) |
where
| (4) |
where ϕ ∈ (0,1] is the collagen fiber volume fraction, μ is the shear modulus of the ground matrix which consists of non-collagenous substances such as elastin, glycosamino-glycans, and proteoglycans, E is the fibril Young’s modulus, θ0 is the crimp angle of the outermost fibrils and is the stretch along the fascicle direction that straightens the outer fibrils, i.e., the critical or transition stretch. Note also how the expression (4) assumes a zero fibril helix angle α for the murine patellar tendon, as justified by preliminary computational studies on the same experimental dataset, and also alluded to by Shearer for the patellar tendon in humans [28].
Likewise, for the GOH model, the following is obtained for the axial Cauchy stress
| (5) |
where
In (5), κ ϵ [0, 1/3] quantifies the collagen fiber dispersion about . It is zero when the fibers are perfectly aligned and 1/3 for an isotropic distribution. The quantity c1 > 0 is a modulus-like parameter, while c2 > 0 is a dimensionless parameter. These two parameters provide a phenomenological description of the structural response of the collagen fibers, but their physical significance is unclear and subject to personal interpretation as neither parameter can be measured experimentally.
Remark (Fascicle and fibril alignment angle parameters ψ and ξ). The formulation discussed in this section was derived for direction vectors , not necessarily aligned with the longitudinal tendon axis z. The alignment angle parameters thus introduced interact with the other model parameters, for example in quantifying the transition between an elastin-dominated low-stretch response and the collagen-dominated linear response. To see this, we consider the relation between the transition stretch λ* = 1/cos θ0 in the SHR model and the beginning of the linear response region evaluated through the change in the stress-stretch curve derivative. This is shown in Figure 1. For small alignment angles, the transition stretch λ* fully correlates with the beginning of the linear region, as expected. For increasingly large alignment angles, the linear region appears to be confined close to the 10% stretch limit and to be independent from the crimp angle parameter θ0. This demonstrates how the crimp and alignment angles interact in determining the transition stretch λ*, and how the identifiability of (say) θ0 is progressively reduced for an increasing alignment angle ψ. This also motivates an investigation on how the alignment angles affect the inferred GOH and SHR model parameters. As discussed in Section 3.1.2, we repeated Bayesian inference by including and excluding ξ and ψ.
Figure 1:
Relation between the Shearer transition stretch λ* and a transition stretch based on the stress-stretch curve derivative. For an increasing alignment angle ψ, the large transition stretch affects the extension of the linear portion of the stress-stretch curve.
2.2.2. The Freed-Rajagopal (FR) model
The FR model splits the total tissue strain in the contribution of the elastic filament network and collagen fibers, respectively. While the collagen fibers are treated as neo-Hookean, the elastin filament network serves as strain limiter, with mechanical response obtained from an implicit SEF [30]. The three-parameter stretch as a function of stress FR model is
| (6) |
where Ee (> 0) and Ec (> Ee) are the elastic moduli of the toe and linear regions - dominated by elastin (e) and collagen fibers (c), respectively and (> 1) is the inverse of the true strain at which the linear region starts, and the collagen fibers are straight.
2.3. Parameter Bounds
To ensure physical validity and motivate physiologic relevance, bounds were placed on all model parameters (Table 2). For structural model parameters, all angles were constrained between 0 and π/2 and collagen dispersion parameter κ from Q to 1/3. Material parameters that cannot be measured experimentally were simply required to be positive. The collagen fibril elastic modulus was constrained based on available experimental data. A detailed discussion on the chosen bounds can be found in [10]. Additionally, uninformative uniform priors are assumed for all parameters, with ranges also reported in Table 2.
Table 2:
Theoretically and experimentally motivated bounds on GOH, SHR and FR model parameters and associated priors. Adapted from Table 1 in [10].
| Model | Parameter | Constraint | References | Prior range | |
|---|---|---|---|---|---|
| Material | GOH & SHR | (1 – ϕ)μ | > 0 | [0, 108] | |
| GOH | c1 | > 0 | [0,108] | ||
| GOH | c2 | >0 | [0,103] | ||
| SHR | ϕ E | 0 – 14 GPa | [34] | [0, 108] | |
| FR | Ec | >0 | [10−3, 108] | ||
| FR | Ee | > 0 | [10−3, 108] | ||
| Structural | GOH | k | 0 – 1/3 | [29] | [0, 1/3] |
| GOH | ξ | 0 – π/2 | [0, π/2] | ||
| SHR | θ0 | 0 – π/2 | [28] | [10−3, π/2] | |
| SHR | ψ | 0 – π/2 | [0, π/2] | ||
| FR | β | 10 – 1000 | [101, 103] |
2.4. Bayesian Parameter Estimation
We denote all model parameters with the vector and embrace a Bayesian perspective on parameter estimation, treating θ as a vector of random variables. Specifically, we consider a complete probability triplet (Ω, , P) equipped with a space of elementary events ω ∈ Ω, a Borel σ-algebra of events defined over 2Ω and a probability measure P assigning values in [0,1] to elements in . The arbitrarily distributed and correlated parameters , i = 1,…,d are characterized in probability through their joint distribution ρ(θ).
2.4.1. Statistical model for uniaxial stress and stretch
The experimental uniaxial stress (stretch) in the z-direction for the GOH, SHR and FR material models is considered as a random variable with distribution induced by the following statistical model
| (7) |
where M = {GOH, SHR, FR} and is an error term assumed Gaussian, with variance and standard deviation σϵ. The model (7) suggests with likelihood function expressed as
| (8) |
where represents the i-th experimental result available under the j-th measured axial stretch λj for a single age/healing group (see Table 1), S is the total number of samples per group and N is the total number of stretch levels. For convenience, the vector λ = [λ1, λ2,…, λN] will contain all experimental stretch levels, while the tensor σzz(λ) denotes all experimental stresses at all stretch levels within a single age-healing group. Note how the additive nature of the noise term in the statistical models (7) essentially determines the expression (8) for the likelihood. While we do not consider here alternative likelihood formulations, the results in Section 3.2 suggest σϵ to be an unimportant parameter that does not affect significantly the inference process. The effect of systematic errors and more complicated error distributions can be taken into account through the selection of an appropriate likelihood function.
2.4.2. Adaptive Markov Chain Monte Carlo
The joint posterior distribution for θ is obtained through Bayesian conjunction of likelihood and prior (see, e.g., [35]) as:
| (9) |
and, in practice we use Markov chain Monte Carlo (MCMC) [36, 37] to generate independent samples from (9). Complex constitutive models with many parameters, inferred from limited experimental evidence (e.g., uniaxial stress-stretch tests for a multiaxial constitutive model) may present significant negative correlations among parameters or, in other words, a lack of identifiability, meaning that multiple combinations of parameters could generate outputs matching the experimental data equally well. We will see in the result sections how the GOH and SHR models are affected by this phenomenon, particularly when the alignment angles ξ and ψ are included in estimation. Specification of a prior for the parameters can substantially improve parameter learning and identifiability [38] and justifies our adoption of a Bayesian approach to inference.
Due to the non linearity of the three constitutive models in θ, the likelihood (8) is generally not normally distributed, and generation of samples from the stationary posterior (9) through random walk Metropolis may require a very large number of forward evaluation of the selected constitutive models. Differential evolution adaptive Metropolis (DREAM) [11, 39] combines differential evolution [40] and self adaptive randomized subspace sampling, leveraging parallel Markov chains to automatically adapt the scaling and orientation of the trial distribution. It also shows a substantial improvement with respect to other adaptive MCMC schemes when sampling from heavy tailed or multi-modal posteriors.
2.4.3. Convergence Assessment
Convergence, i.e., the ability of the adaptive Markov chain to generate samples from the desired posterior distribution is assessed, in this study, through the Gelman-Rubin diagnostic metric (RGR) [41], but several other approaches are available through the literature. GR evaluates the similarity of m parallel chains with n sample each based on an analysis of variance. Consider the j-th sample from the i-th parameter generated from the k-th Markov chain , and the quantities
| (10) |
The inter-chain and intra-chain variance for parameter θi are expressed as
| (11) |
Based on (10) and (11), an estimate of the parameter marginal posterior variance and a convergence indicator RGR can be computed as
| (12) |
2.4.4. MAP Estimate
A maximum a posteriori (MAP) estimate of the model parameters θ is determined by optimization. Specifically, we employ a restarted Nelder-Mead (NM) algorithm [42] and set the initial guess equal to the parameter realization associated with the maximum posterior distribution during MCMC. Additionally, we restart the NM iteration several times, according to references in the literature showing how this consistently improves convergence [43].
2.5. Local Parameter Identifiability
In an identifiable system, the parameters can be uniquely determined from the available observations. If this happens in a neighborhood of a specific location θ the system is locally identifiable and globally identifiable if this happens over the whole parameter space Θ. A review of identifiability for nonlinear ODE models in viral dynamics is provided, for example, in [44]. In this study, we use several metrics to detect non identifiable combinations of parameters using both a frequentist and Bayesian perspectives. First, we investigate local identifiability using the rank of the Fisher information matrix (see, e.g., [45]). As a direct result of assuming the likelihood in equation (8), we have:
| (13) |
Note that Equation (13) is easily obtained by combining the matrix of local derivatives (e.g., computed through finite differences) with the diagonal precision matrix of the experimental stress (GOH, SHR) or stretch (FR). As discussed in the literature [45], rank deficiency in reveals the presence of non-identifiable combinations of parameters, and null eigenvectors can be computed to identify such combinations. In practice, the numerical eigenvalues could be small but not negligible and therefore it may be difficult to identify parameter combinations lacking identifiability, particularly if these involve a large number of parameters. On the other hand, it is rather easy to identify locally unimportant parameters, where the eigenvalue is very small (e.g., < 10−10) and the eigenvector is dominated by a single component. Also, changes in the rank deficiency of as a result of applying different scaling factors to the experimental precision matrix is useful to recognize true singularities.
Other identifiability metrics are obtained as a byproduct of Bayesian inference, for example, the parameter correlations identified from the MCMC stationary posterior samples. Large negative correlations between two parameters may by indicative of unidentifiability, i.e., stress changes compensate in the model response. The shape of the marginal posterior distribution may also be indicative of the importance of a given parameter. Specifically, a flat posterior distribution typically indicates negligible importance. Finally, reduction in marginal variance from prior to posterior is an indication of how much a certain parameter was learned upon conditioning on the available data. In this context, a learning factor γj for the j-th parameter was introduced in [4] as
| (14) |
where denotes the marginal posterior variance for parameter θj while denotes its prior marginal variance.
2.6. Variance Based Global Sensitivity Analysis
Consider the stress , i.e., the stress response of a generic constitutive model M at a given stretch level λj (the dependence on λj will be omitted below for simplicity) as a function of rescaled inputs defined over the hypercube [0,1]d. Under these circumstances, the stress response can be decomposed as
| (15) |
where is a constant and , and are function of one, two and d parameter respectively, subject to the condition
| (16) |
or, in other words, is decomposed into zero-mean contributions of increasing dimensionality [46], and, as a consequence . If we elevate (15) to the second power and integrate over the d-dimensional hypercube, we obtain
| (17) |
suggesting how the variance can be decomposed as a sum of contributions with increasing dimensionality, i·e
| (18) |
Following this approach, direct, first order global sensitivity indices (i.e., effect of single random inputs) can be determined as
| (19) |
quantifying the contribution to the variance of the i-th random input alone. Similarly, total sensitivity indices can be computed as
| (20) |
summing in all contributions to the variance of terms having at least one index equal to i.
Note how, in our case, the parameter realizations are available through arbitrary correlated and distributed samples from MCMC. Computation of the sensitivity indices is accomplished by first creating a polynomial chaos surrogate of the quantity of interest using regression. Second, the direct and total sensitivities are determined through Monte Carlo estimates. Consider a sample matrix of size N × 2d, where each row is a sample of dimension 2d, generated from the probability distributions of the random inputs. Denote with A the first d columns of this sample matrix, and the remaining d columns as . This effectively gives two independent samples of the d-dimensional random inputs at N locations. Consider d additional N × d matrices ABi, i = 1,2,…, d, such that the i-th column of ABi is equal to the i-th column of B, and the remaining columns are from A. Now, each constitutive model is evaluated at the N ·(d + 2) parameter realizations stored in the matrices A, B, and ABi, i = 1,…, d and the sensitivity indices (direct and total, respectively) are computed from the estimators
| (21) |
The interested reader is referred to the discussions in [47, 48, 49] for further details on Monte Carlo estimators for Sobol’ sensitivity indices.
2.7. The tulip software library
All computations discussed in the previous sections are carried out using the tulip library for uncertainty analysis. Tulip is a C++ library that provides a Python API layer and implements a complete separation between models, actions and data. Models are generic black box relations between inputs and outputs and can be used to wrap the evaluation of constitutive models, physics-based solver, particularly lumped parameter representations of circulation networks. Actions are generic steps in uncertainty quantification, such as forward propagation with Monte Carlo simulation or stochastic spectral expansion, optimization, local and global sensitivity analysis, local identifiability analysis, adaptive Markov chain Monte Carlo sampling and others. Finally, likelihood or cost functions can be evaluated by combining model outputs with data from various sources, e.g., CSV files, XML files or remote repositories. The library is designed to be extensible and new models, actions or data sources can be added by implementation of virtual functions.
3. Results
3.1. Bayesian inference
Results obtained from Bayesian estimation through adaptive MCMC are presented next. We investigate the convergence of the parallel chains, the marginal distribution of each θi, i = 1,…, d, the uncertainty in the identified stress-stretch constitutive relations, the correlations among parameters.
3.1.1. Convergence from parallel inference
We look at the convergence diagnostic discussed in Section 2.4.3 for all parameters, all models and all aging-healing groups. The number of parallel Markov chains was selected equal to the number of parameters and 30,000 generations (i.e., model evaluations) were performed for each chain. Figure 2 shows how the 5–95% percentiles for the Gelman-Rubin statistic (RGR) fall below an acceptance threshold of 1.1 in all cases. Moreover, the model complexity (i.e., the number of constitutive parameters) clearly affects how many posterior evaluations are needed for convergence, with the FR model showing the best convergence followed by SHR and GOH. Similar convergence plots (not shown) are obtained by introducing the alignment angles ξ and ψ in the GOH and SHR model, respectively.
Figure 2:
Mean value and 5–95% percentiles for Gelman-Rubin diagnostic across all parameters and age-healing groups.
3.1.2. Marginal parameter learning and distributions
To investigate the ability to identify constitutive model parameters from experimental data with a suffi ciently large confidence, we evaluated the learning factors (14) for all models and parameters. We also differentiate cases where the complete experimental dataset was included in the likelihood (denoted by ALL in Figure 3 and 10) rather than just average stress levels (denoted by AVG).
Figure 3:
Learning factors for GOH, SHR (arbitrary and zero alignment angles) and FR.
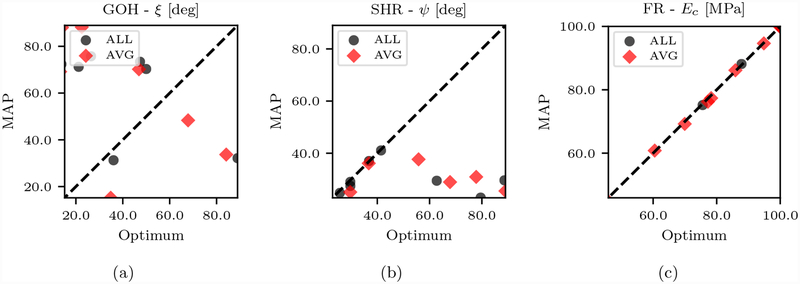
Figure 10:
GOH, SHR and FR representative model parameters computed through optimization and maximum a posteriori estimates from MCMC.
For the GOH model, the only parameter showing satisfactory variance reduction relates to the ground matrix response parameter (1 - ϕ) μ, which is the only load-carrying mechanism occurring at a sufficiently low stretch, i.e., before full engagement of collagen fibers. The maximum learning factors for parameters associated with the collagen fiber response remain instead limited to approximately 0.2, indicating correlation among parameters and a reduced identifiability. Additionally, larger learning factors are obtained for the GOH model when the complete experimental dataset is included. Finally, a zero alignment angle ξ significantly improves learning of the fiber dispersion parameter κ.
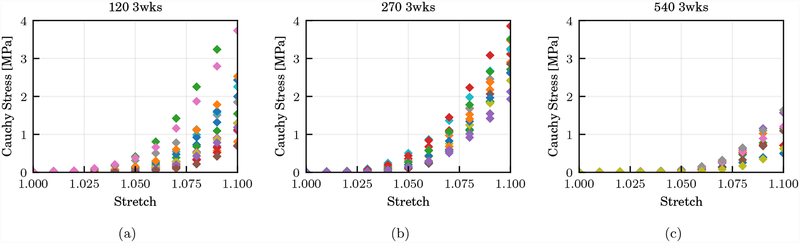
The SHR model shows improved learning factors in all parameters due to a reduced model complexity, but also highlights the benefits of including the complete set of experimental stresses. The learning factor at 540 days age and 3 weeks healing appears associated with a particularly small learning factor even after including the complete experimental dataset during training (not shown). This can be attributed to two factors, first a relatively small number of experimental data points for this specific age-healing group (see Table 1) and second to the larger impact of injury for this age group. For the same stretch range, the stresses are lower but also the variability in the stress response is reduced as shown in Figure 4. Therefore, for this experimental group there is little difference between training using average stresses or the complete experimental dataset. Finally, the parameters of the FR constitutive model appear to be equally well learned in all cases, with a slightly reduced learning of the collagen elastic modulus Ec from all stress values.
Figure 4:
Number of experimental data points at various stretch levels, for the same healing group (3 weeks) at age 120 days (a), 270 days (b) and 540 days (c).
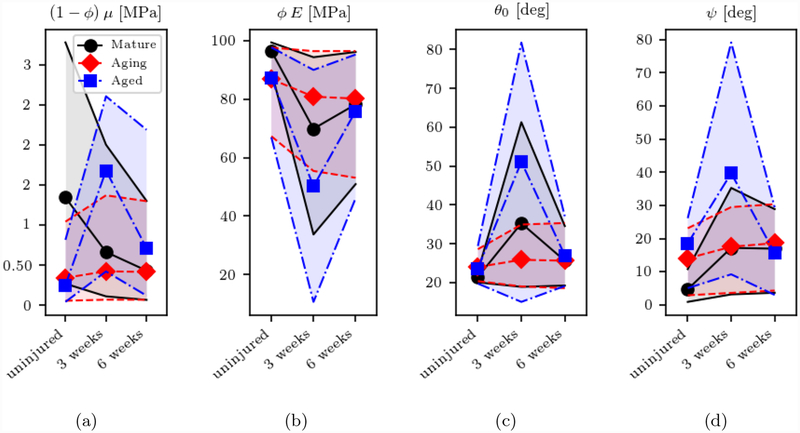
Next, we look at the changes in the parameter marginal median for each model, following injury in various age groups. To better understand the variability associated to the parameter estimates, we report the marginal posterior median together with the 10–90% confidence intervals. Due to the higher learning ratios consistently provided, Figures 5, 6, 7, 8, 9 were produced by training the models using the complete stress dataset for each age-injury group. They show how evaluation of parametric uncertainty from Bayesian estimation is essential to be able to identify changes in the tendon ligament microstructure from the uniaxial stress-stretch response. In this regard, the GOH and SHR models do provide a more complete description of the microstructure but at the expense of large uncertainties in the estimated parameters. Conversely, the FR model is characterized by only three parameters each associated to a well defined stretch range (i.e. low-stretch elastin response modulus Ee, transition parameter β and collagen response parameter Ec) and considerably smaller uncertainties, as shown in Figure 9.
Figure 5:
Changes in the parameter median value and 10–90% percentile due to injury and age for the GOH model with ξ ≠ 0.
Figure 6:
Changes in the parameter median value and 10–90% percentile due to injury and age for the GOH model with ξ = 0.
Figure 7:
Changes in the parameter median value and 10–90% percentile due to injury and age for the SHR model with ψ ≠ 0.
Figure 8:
Changes in the parameter median value and 10–90% percentile due to injury and age for the SHR model with ψ = 0.
Figure 9:
Changes in the parameter median value and 10–90% percentile due to injury and age for the FR model.
Figures 5 to 9 confirm that microstructural parameters, whose median estimate may look different for various age/healing groups, cannot be distinguished under uncertainty. Note how classical parameter fitting through optimization might have led to the opposite conclusion, as a results of the inability to quantify the confidence in these estimates. This suggests how measures of confidence are essential for the interpretability of the results, e.g., when it is of interest to quantify function from the identified microstructural model parameters. This also shows how the complexity of the underlying constitutive model should play a role in the interpretation of the results, where the presence of non identifiable parameter combinations may contribute substantially to the marginal parameter variance.
For the GOH and SHR models, several factors contribute to the parameter marginal variance for each age/healing group. First, the aged group appears to be associated with the largest variability in the parameter estimates. This is expected due to the increasing difficulties to produce experimental data at 540 days. Additionally, the marginal variance appears to change for the same age groups and across healing conditions. As reported in Table 1, the number of uniaxial experiment repetitions may vary sensibly with the healing condition and surely affects the marginal variance. Finally, a significant contribution to the parameter marginal variance is due to non-identifability, as confirmed by the large negative correlations from MCMC, shown in Section 3.1.4.
We conclude this section by reporting the MAP parameter estimates for the three models in Tables 3, 4 and 5. The most interesting behavior relates to the GOH and SHR models, specifically how the MAP estimate changes by setting the alignment angle to zero. While the estimates for the (1 − ϕ) μ, ϕc1, c2 and ϕ E parameters seem to be consistent, more noticeable changes are observed in κ and θ0. In the GOH model, the estimated ξ angle is considerable (33.7–49.3 degrees). When ξ = 0 the fiber dispersion (κ) become more isotropic to reduce the stress response that has increased due to a perfect alignment of the fibers. A similar trend is observed for the SHR model between the two parameters θ0 and ψ, but with smaller estimated fascicle alignment angle.
Table 3:
Parameter estimates for the GOH constitutive model
| Parameter | Units | Age | Healing - ξ ≠ 0 | Healing - ξ = 0 | ||||
|---|---|---|---|---|---|---|---|---|
| Uninjured | 3 Weeks | 6 Weeks | Uninjured | 3 Weeks | 6 Weeks | |||
| Mature | 2.0(±1.7) | 0.7(±0.7) | 0.8(±1.7) | 1.5(±1.3) | 0.6(±0.5) | 0.8(±0.7) | ||
| (1 – ϕ) μ | MPa | Aging | 0.8(±0.7) | 0.8(±0.7) | 0.8(±0.7) | 0.8(±0.7) | 0.8(±0.7) | 0.7(±0.6) |
| Aged | 0.7(±0.7) | 1.4(±0.8) | 0.9(±0.8) | 0.6(±0.6) | 1.0(±0.7) | 0.9(±0.8) | ||
| Mature | 53.8(±28.0) | 35.6(±32.0) | 26.4(±23.5) | 57.6(±23.9) | 29.3(±28.7) | 24.4(±22.6) | ||
| ϕ c1 | MPa | Aging | 37.4(±23.2) | 31.2(±25.9) | 22.9(±23.6) | 32.1(±20.8) | 27.7(±23.0) | 19.8(±17.5) |
| Aged | 27.0(±20.5) | 45.5(±29.9) | 34.1(±26.8) | 25.6(±19.7) | 39.1(±29.2) | 37.5(±30.0) | ||
| Mature | 647.3(±213.4) | 649.1(±244.0) | 699.3(±220.6) | 614.3(±208.7) | 605.6(±263.5) | 670.1(±229.0) | ||
| c2 | - | Aging | 748.1(±187.0) | 750.5(±190.4) | 700.9(±234.6) | 670.0(±215.5) | 720.2(±203.8) | 680.6(±231.1) |
| Aged | 724.9(±224.8) | 505.8(±287.4) | 681.3(±218.5) | 671.0(±238.6) | 501.7(±288.6) | 655.8(±239.3) | ||
| Mature | 0.18(±0.09) | 0.20(±0.09) | 0.19(±0.09) | 0.28(±0.02) | 0.27(±0.06) | 0.27(±0.03) | ||
| k | - | Aging | 0.20(±0.08) | 0.20(±0.08) | 0.17(±0.09) | 0.28(±0.02) | 0.28(±0.03) | 0.27(±0.03) |
| Aged | 0.20(±0.08) | 0.24(±0.09) | 0.21(±0.09) | 0.27(±0.02) | 0.31(±0.03) | 0.28(±0.03) | ||
| Mature | 37.4(±20.4) | 37.1(±18.4) | 33.7(±19.3) | |||||
| ξ | degrees | Aging | 34.0(±16.8) | 36.9(±21.0) | 37.2(±22.0) | - | - | - |
| Aged | 33.9(±22.4) | 49.3(±19.3) | 35.0(±20.4) | |||||
Table 4:
Parameter estimates for the SHR constitutive model
| Parameter | Units | Age | Healing - ψ ≠ 0 | Healing - ψ ≠ 0 | ||||
|---|---|---|---|---|---|---|---|---|
| Uninjured | 3 Weeks | 6 Weeks | Uninjured | 3 Weeks | 6 Weeks | |||
| Mature | 1.6(±1.3) | 0.9(±0.8) | 0.6(±0.6) | 1.4(±1.14) | 0.8(±0.66) | 0.6(±0.55) | ||
| (1 – ϕ) μ | MPa | Aging | 0.5(±0.5) | 0.6(±0.6) | 0.6(±0.6) | 0.4(±0.51) | 0.6(±0.55) | 0.6(±0.55) |
| Aged | 0.4(±0.4) | 1.6(±0.8) | 1.0(±0.9) | 0.3(±0.36) | 0.9(±0.68) | 0.9(±0.86) | ||
| Mature | 95.3(±4.4) | 66.9(±22.3) | 75.8(±16.8) | 95.1(±4.53) | 66.6(±23.56) | 71.5(±18.55) | ||
| ϕ E | MPa | Aging | 84.5(±11.5) | 78.0(±15.8) | 77.1(±16.4) | 79.3(±13.06) | 71.2(±18.41) | 70.9(±19.03) |
| Aged | 84.6(±11.8) | 50.2(±28.6) | 73.0(±18.5) | 76.7(±14.46) | 43.9(±26.18) | 39.6(±19.69) | ||
| Mature | 21.5(±1.4) | 37.9(±16.8) | 26.4(±5.9) | 21.9(±1.14) | 50.9(±15.76) | 32.3(±5.53) | ||
| θ0 | degrees | Aging | 24.3(±3.4) | 26.6(±6.3) | 26.4(±6.5) | 27.3(±2.89) | 32.2(±5.50) | 33.1(±5.96) |
| Aged | 24.14(±3.7) | 49.64(±24.2) | 27.88(±7.9) | 28.6(±3.28) | 62.3(±18.85) | 34.2(±8.21) | ||
| Mature | 5.4(±4.0) | 18.5(±12.8) | 16.6(±9.3) | |||||
| ψ | degrees | Aging | 13.6(±7.4) | 17.1(±9.4) | 18.0(±9.6) | - | - | - |
| Aged | 17.1(±7.7) | 42.1(±25.2) | 16.1(±10.0) | |||||
Table 5:
Parameter estimates for the FR constitutive model
| Parameter | Units | Age | Healing | ||
|---|---|---|---|---|---|
| Uninjured | Healing 3 Weeks | 6 Weeks | |||
| Mature | 99.3(±0.7) | 96.2(±3.3) | 98.0(±1.8) | ||
| Ec | MPa | Aging | 99.3(±0.7) | 87.4(±7.0) | 96.2(±3.4) |
| Aged | 99.5(±1.2) | 75.9(±13.6) | 98.3(±1.6) | ||
| Mature | 0.9(±0.9) | 0.6(±0.6) | 0.8(±0.6) | ||
| Ee | MPa | Aging | 0.5(±0.8) | 0.9(±1.0) | 0.7(±0.6) |
| Aged | 0.6(±1.4) | 0.5(±0.5) | 0.4(±0.2) | ||
| Mature | 30.4(±4.0) | 14.1(±2.3) | 16.2(±3.9) | ||
| β | - | Aging | 19.0(±2.6) | 16.6(±3.6) | 16.0(±2.9) |
| Aged | 17.8(±3.1) | 13.0(±2.2) | 16.9(±1.4) | ||
3.1.3. Optimal and MAP parameter estimates and stress-stretch response
Lack of identifiability has also a deleterious effects on the ability to gather microstructurally relevant parameters from experiments through optimization. To show this, we have determined the parameters using both the Nelder-Mead optimization algorithm (see, e.g., [42]) and by identifying the maximum of the posterior distribution from the MCMC samples. The results in Figure 10 show how the parameters are inconsistent in the GOH and SHR models while perfect agreement is observed for FR. This suggests a lack of convexity in the posterior distribution, where either the selection of different initial guesses leads to convergence to a different local maxima or the optimizer encounters a region of flat posterior. This is indeed a manifestation of the lack of identifiability.
After verifying the agreement between estimated parameters, we checked the uncertainty in the stress-stretch response. To do so, we have separated the stress-stretch curves based on age and showed how the response changes with the healing conditions. We also superimposed on the same figure the experimental data, the stress-stretch response corresponding to the MAP parameter estimate, the associated 5–95% percentile variation and the results obtained by straight optimization without taking experimental uncertainty into consideration. The experimental stresses are characterized by significant overlap following 6 weeks injury recovery, as shown in Figures 11, 12 and 13, leading to very similar constitutive responses. Stress response remain similar after setting the alignment angles ξ and ψ to zero.
Figure 11:
Assimilated and experimental stress-stretch response for the GOH model. The experimental stress at various ages has been slightly shifted on the stretch axis to improve clarity.
Figure 12:
Assimilated and experimental stress-stretch response for the SHR model. The experimental stress at various ages has been slightly shifted on the stretch axis to improve clarity.
Figure 13:
Assimilated and experimental stress-stretch response for the FR model. The experimental stress at various ages has been slightly shifted on the stretch axis to improve clarity.
3.1.4. Parameter Correlations
The average parameter correlations over all age-healing groups are shown in Figure 14, from models trained using both the complete set of experimental stresses or only their average levels. It appears clear from this plots how the availability of complete experimental information accentuates the negative correlations for the GOH and SHR models, while confirming the lack of correlation among FR constitutive parameters. The strong negative correlation between the fiber dispersion parameter κ and the alignment parameter ξ is particularly evident. This simply suggests that unaltered experimental stresses can be obtained, for example, increasing the degree of random orientation of the fibers and reducing the alignment angle, and confirms the difficulty in discerning between these two phenomena from uniaxial experiments. Finally, we observe a recurrent block structure in the correlation matrix for the GOH and SHR models, where the two blocks correspond to the low and high-stretch response, dominated by the ground matrix and collagen fibers, respectively.
Figure 14:
GOH parameter correlations from MCMC under average (a) and complete (d) experimental data. The parameter correlations for the SHR (b, e) and FR (c, f) models are also shown.
3.2. Including data variability in inference
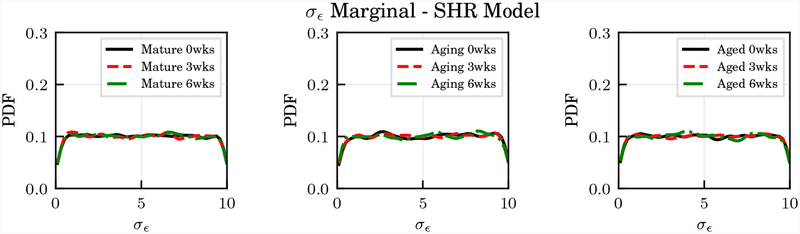
Instead of just assuming a deterministic value for σϵ, we performed numerical tests to understand how specification of this quantity affects the results from parameter estimation. Specifically, we assumed an experimental uncertainty in the GOH and SHR models equal to 106 σϵ (i.e., the experimental uncertainty is expressed in MPa). Stresses for these two models are measured in Pa and therefore the final uncertainty is assumed uniform over the whole stretch range and equal to 0.1 to 10.0 MPa. Since the FR model has stretch outputs, the uncertainty was assumed instead as 0.01 σϵ. The marginal posterior of these parameters was found completely flat as shown for the SHR model in Figure 16, suggesting how this parameter can be set to any reasonable value and it does not affect parameter identification. The parameter correlations in Figure 14 also show how the experimental uncertainty is completely uncorrelated with respect to all other parameters for the three models.
Figure 16:
Representative marginal distributions for the standard deviation of the experimental stress σϵ in the SHR model.
3.3. Local Identifiability
The identifiability of the three models has been formally analyzed using the Fisher information matrix rank discussed in Section 2.5. Local identifiability was determined for parameter configurations in a neighborhood of the realizations associated with maximum posterior distribution from MCMC, and using all experimental data rather than just the average experimental stresses at each stretch level.
Due to the scaling provided by the inverse variance from the experiments in (13), definition of a sharp cutoff for zero eigenvalues may result in variability in the identifiability results. To overcome this difficulty, we amplified the experimental precisions with factors in the range [10−2,103] and observed the corresponding change in the FIM eigenvalues. For the GOH and SHR models with zero alignment angle and FR, all eigenvalues are affected by the scaling suggesting these models to be locally identifiable (i.e. associated with a non singular FIM around the MAP parameter estimates), while zero eigenvalues remain for the GOH and SHR models with non-zero alignment angles. We then set a cutoff equal to 10−10 allowing for the selection of eigenvalues remaining small even after significantly amplifying the experimental precisions.
As expected, Figure 17a suggests a sensible increase in the eigenvalues as a result of setting the alignment angles ξ and ψ to zero. Additionally, the analysis confirms how the standard deviation parameter is locally unimportant as suggested by the dominant null-eigenvectors in Figures 17b and 17c. Figure 17b suggests instead how the GOH parameters ϕc1 and (1 − ϕ) μ form an unidentifiable combination. This is consistent with the large negative correlation shown by these two parameters in Figure 14 and Figure 15, with two possible constituents able to withstand the low stretch response, i.e., elastin matrix or collagen fibers. Finally, Figure 17c suggests the fibril elastic modulus ϕ E to be unimportant for the SHR model with non-zero alignment angles. This can be explained by looking at Figure 1 and the relatively large MAP estimates for ψ. For large alignment angles the transition to the linear region of the stretch-stress curve occurs at very large stretches and therefore the importance of the collagen modulus ϕ E remains limited.
Figure 17:
Fisher Information matrix eigenvalues for GOH and SHR models. Models with zero and nozero alignment angles are compared in (a) to emphasize the change in local identifiability promoted by suppressing the alignment angles. The null eigenvectors are also illustrated in (b, c) for the GOH and SHR models, respectively.
Figure 15:
Parameter correlations under zero alignment angle. GOH parameter correlations from MCMC under average (a) and complete (b) experimental data. The parameter correlations for the SHR (c, d) are also shown.
3.4. Local and Global Sensitivity Analysis
The next sections report the global and local sensitivity indices for the three models. We have plotted the direct and total sensitivity indices (SI) using the Monte Carlo estimates mentioned in Section 2.6 using 50, 000 samples from the posterior distribution, thus accounting for the correlations between model parameters from MCMC. For comparison, we have also computed the direct sensitivities from the polynomial chaos (PC) expansion coefficients. Specifically, independent model parameters were assumed with uniform marginal distribution in the interval , where is the average value of the i-th parameter computed from the MCMC traces, while σ[θi] is its standard deviation. We also have determined the polynomial chaos coefficients using numerical integration on a third-order Smolyak sparse grid and the Gauss-Legendre integration rule. We remark how the polynomial chaos-based sensitivity indices do not account for the correlations among parameters, assumed independent. The average sensitivity indices are computed together with their 10%−90% confidence intervals over age/healing conditions, where the likelihood in MCMC is assembled from the complete set of experimental stretch-stress data, and we have also compared non-zero and zero alignment angles for the GOH and SHR models. Local sensitivity indices (LSI) are instead computed using normalized derivatives from central finite differences (FD). Common to all models, the sensitivity indices at zero stretch are zero as expected, as a zero stress is obtained irrespective of the selected realization in parameter space.
3.4.1. GOH Model
For non-zero helix angles, the stress response of the GOH model is dominated by the fiber dispersion and alignment angle parameters κ and ξ, respectively and this is captured both using polynomial chaos expansion and from the local sensitivities. The contribution of these two parameters to the total stress variance is observed to vary significantly at larger stretches across age-healing groups.
When ξ = 0, the MC based sensitivities seem to capture a different trend than polynomial chaos or local sensitivity indices. Specifically, local sensitivities assign a greater importance to the fiber response through the orientation parameter κ and, in second instance, to the ϕ c1 and c2 parameters both at small and large strain regimes. Conversely, the Monte Carlo estimates for the global sensitivities appear to assign a greater importance to the stiffness contribution of the elastin matrix rather than collagen fibers. Finally, the Monte Carlo estimates for the direct and total sensitivity indices appear to be very similar, with limited resulting interactions among the parameters. Note how the importance of parameters for the GOH model is significantly altered by setting ξ = 0, consistent with the large values of the alignment angle estimates in Table 3.
3.4.2. SHR Model
The modulus of the elastin matrix appears to be an important parameter for the SHR model with no-zero alignment angle ψ, particularly in the small stretch regime, as expected. Additionally, the large sensitivities of the stress response to the alignment angle ψ and transition parameter θ0 appear to be consistent across global and local sensitivities, while the collagen elastic modulus shows an increasing effect on the stress response for increasing stretch levels. The large correlation from MCMC occurring between the helix angle ψ and the parameter θ0, justifies the difference between the Monte Carlo and polynomial chaos sensitivity estimates for these two parameters. By setting ψ = 0, the importance of the elastin modulus is amplified in the MC estimates, particularly when the underlying correlation of elastic modulus and collagen fiber modulus is considered (i.e., sensitivities from MCMC). Increased importance of the elastin modulus for zero alignment angles is also a feature observed in the GOH model sensitivities. In a neighborhood of the MAP parameter estimate, the response is predominantly affected by the collagen modulus and transition parameter θ0, as confirmed through the local sensitivities. Finally, setting the alignment angle to zero seems to affect the SHR model less than the GOH model.
3.4.3. FR Model
The most important parameters are the elastin modulus Ee and the transition parameter β. This latter parameter affects how much of the stress-stretch response relates to a linear regime and so it is expected for β to have larger sensitivity than Ec. Additionally, the importance of the elastin modulus descreases for an increasing stretch, while the importance of the transition parameter increases, as expected. Finally, the importance of the collagen modulus Ec seem to increase with the stretch level, as expected.
4. Discussion
Micro-structurally motivated constitutive models may be formulated as a superposition of the response provided by various constituents, possibly operating at overlapping stretch regimes. This approach is typically verified in terms of forward model evaluations and the ability to have a certain number of experimental results in the range of the model, i.e., the set of representable stress-stretch responses. A different but perhaps more important problem relates to identify the parameters of the models from uncertain experimental data and infer structure and function from these parameters. In this context, i.e., inverse problems, superposition of stress generated by different microstructural mechanisms typically reduces the identifiability of the model parameters from experiments, phenomenon that is even more apparent under limited experimental evidence. In this study, we employ Bayesian inference to compare three constitutive models for the murine patellar tendon representing three degrees of microstructural complexity and investigate how their parameters may be inferred from uncertain uniaxial stress-stretch experimental data. The experimental data was collected on mice under various conditions related to age and degree of injury [15, 16, 17, 18]. For two of these models, i.e., GOH and SHR, an additional parameter for the fiber and fascicle alignment angle, respectively was added as a free parameter, and the effects on the MAP parameter estimates, identifiability and sensitivity observed.
We report the following findings. First, from numerical experiments comparing inference with complete and average stress responses, we conclude that use of all available data has a positive effect on constraining inference and leads to highest learning factors, i.e., reduces the variability in the estimated parameters. Second, changes in the data standard deviation σϵ do not seems to affect the estimates of the parameters, as confirmed by a flat marginal posterior if this parameter is added to the inference. Third, we observe a trade-off between the complexity of the underlying microstructural constitutive model and effective inference of tendon structure-function from the data. Supporting our prior work, the FR phenomenological model was the only model for which changes in function caused by age/healing could be directly observable from the model parameters [10]. This model is however not perfect as the transition parameter determines the extent of the linear response region, and therefore inference of β interacts with inference of Ec. Fourth, this study highlights the importance of investigating the amount of variability of the parameter estimates, particularly in case of point estimates obtained through optimization. While MAP and optimal parameter estimates may be possibly close in simpler phenomenological models, the same does not seem to occur with models that include a more complex microstructure. Fifth, introduction of structural parameters such as the fiber and fascicle alignment angle reduces the identifiability of the other model parameters due to a non trivial interaction, for example, with the transition parameter as shown in Figure 1 for the SHR model. Finally, this paper demonstrates how Bayesian inference and the analysis of parameter sensitivity and identifiability are essential complements to the knowledge of the underlying microstructural mechanics to provide constitutive models that are informative on the structure-function of a certain biological tissue and, in particular, able to distill the information obtained from experimental testing. We also showed how all analysis tasks in uncertainty quantification can be delegated to a library able to include a constitutive model as an black box and presented result using the tulip library.
We hope this study may provide guidance to other researchers in the solution of inverse problems under uncertainty, for applications in bio-mechanics. In this spirit, we have organized the inference tasks in this study following a rational order, starting with the specification of a simple statistical model (which can be further refined based on a more detailed analysis of the source of experimental errors and their correlation) and by entering the prior distribution for each parameter (based on histological and biomechanical admissibility). We have generated parameter samples from the joint posterior distribution through MCMC with a large number of model solutions, examined distributions of model results, parameter correlations and performed an analysis of the parameter sensitivity and identifiability.
It is evident how this process requires more work than classical parameter fitting, particularly due to the large volume of generated results, and the additional time required to verify their consistency, where the comparisons need to be performed between distributions rather than point values. Acceptable results are evaluated based on various metrics. Essential is to verify the convergence of the MCMC sampler, which may be far from trivial for non-identifiable and overparameterized models. Additionally, results are not set in stone and maybe refined taking advantage of additional structure by specifying, e.g., a different prior thus leading to improved estimators characterized by reduced variance (see, e.g., the multi-level estimator discussed in [4]). As discussed in the introduction, additional experimental evidence (e.g., multi-axial testing) might also be provided to further reduce the variance of the estimates. Thus, parameter estimation under uncertainty is more a dynamic process subject to iterative refinements than a static, certain but possibly myopic answer.
This work investigates the difficulties in inferring structural or functional changes from the solution of an inverse problem starting from uniaxial stress-stretch experimental data for various age/healing groups in the murine patellar tendon. Future work will instead be devoted to the development of improved Bayesian approaches for estimating the contribution of multiple constituents. Future research will also be devoted to drive data collection in order to estimate specific parameters.
Figure 18:
Average global and local sensitivity indices for the GOH model and associated 10%−90% percentile confidence across age-healing groups. Model parameters are identified using the complete dataset of uniaxial tests.
Figure 19:
Average global and local sensitivity indices for the GOH model and associated 10%−90% percentile confidence across age-healing groups. Model parameters are identified using the complete dataset of uniaxial tests and with zero alignment angle ξ.
Figure 20:
Average global and local sensitivity indices for the SHR model and associated 10%−90% percentile confidence. Model parameter are identified using the complete dataset of uniaxial tests.
Figure 21:
Average global and local sensitivity indices for the SHR model and associated 10%−90% percentile confidence. Model parameter are identified using the complete dataset of uniaxial tests and with zero helix angle.
Figure 22:
Average global and local sensitivity indices for the FR model and associated 10%−90% percentile confidence across age-healing groups. Model parameter are identified using the complete dataset of uniaxial tests.
Acknowledgements and Disclosures
This work was supported by NIH through the awards P20GM103629 (KSM) and RÜ1-EB018302 (PI Alison Marsden, subcontractor DES) and by a DARPA Young Faculty Award (DES). We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome. This research used computational resources provided through the Center for Research Computing at the University of Notre Dame and high performance computing resources at Tulane University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Humphrey JD and DeLange S. An introduction to biomechanics: solids and fluids, analysis and design. Springer Science & Business Media, 2013. [Google Scholar]
- [2].Miller KS, Lee YU, Naito Y, Breuer CK, and Humphrey JD. Computational model of the in vivo development of a tissue engineered vein from an implanted polymeric construct. Journal of biomechanics, 47(9):2080–2087, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Ionescu I, Guilkey J, Berzins M, Kirby RM, and Weiss J. Computational simulation of penetrating trauma in biological soft tissues using the material point method. Studies in health technology and informatics, 111:213–218, 2005. [PubMed] [Google Scholar]
- [4].Schiavazzi DE, Baretta A, Pennati G, Hsia TY, and Marsden AL. Patient-specific parameter estimation in single-ventricle lumped circulation models under uncertainty. International journal for numerical methods in biomedical engineering, 33(3), 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Seyedsalehi S, Zhang L, Choi J, and Baek S. Prior distributions of material parameters for bayesian calibration of growth and remodeling computational model of abdominal aortic wall. Journal of biomechanical engineering, 137(10):101001, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Sankaran S, Humphrey JD, and Marsden AL. An efficient framework for optimization and parameter sensitivity analysis in arterial growth and remodeling computations. Computer methods in applied mechanics and engineering, 256:200–210, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Madireddy S, Sista B, and Vemaganti K. Bayesian calibration of hyperelastic constitutive models of soft tissue. Journal of the mechanical behavior of biomedical materials, 59:108–127, 2016. [DOI] [PubMed] [Google Scholar]
- [8].Doraiswamy S and Srinivasa AR. A Bayesian approach to accounting for variability in mechanical properties in biomaterials. arXiv preprint arXiv:13122856, 2013. [Google Scholar]
- [9].Ritto TG and Nunes LCS. Bayesian model selection of hyperelastic models for simple and pure shear at large deformations. Computers & Structures, 156:101–109, 2015. [Google Scholar]
- [10].Akintunde AR and Miller KS. Evaluation of microstructurally motivated constitutive models to describe age-dependent tendon healing. Biomechanics and modeling in mechanobiology, 17(3):793–814, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Vrugt JA, Ter Braak CJF, Diks CGH, Robinson BA, Hyman JM, and Higdon D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. International Journal of Nonlinear Sciences and Numerical Simulation, 10(3):273–290, 2009. [Google Scholar]
- [12].Bellini C and Di Martino ES. A mechanical characterization of the porcine atria at the healthy stage and after ventricular tachypacing. Journal of biomechanical engineering, 134(2):021008, 2012. [DOI] [PubMed] [Google Scholar]
- [13].Ferruzzi J, Bersi MR, and Humphrey JD. Biomechanical phenotyping of central arteries in health and disease: advantages of and methods for murine models. Annals of biomedical engineering, 41(7):1311–1330, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Robertson D and Cook D. Unrealistic statistics: how average constitutive coefficients can produce non-physical results. Journal of the mechanical behavior of biomedical materials, 40:234–239, 2014. [DOI] [PubMed] [Google Scholar]
- [15].Dunkman AA, Buckley MR, Mienaltowski MJ, Adams SM, Thomas SJ, Satchell L, Kumar A, Pathmanathan L, Beason DP, Iozzo RV, et al. Decorin expression is important for age-related changes in tendon structure and mechanical properties. Matrix Biology, 32(1):3–13, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Dunkman AA, Buckley MR, Mienaltowski MJ, Adams SM, Thomas SJ, Kumar A, Beason DP, Iozzo RV, Birk DE, and Soslowsky LJ. The injury response of aged tendons in the absence of biglycan and decorin. Matrix Biology, 35:232–238, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Dunkman AA, Buckley MR, Mienaltowski MJ, Adams SM, Thomas SJ, Satchell L, Kumar A, Pathmanathan L, Beason DP, Iozzo RV, et al. The tendon injury response is influenced by decorin and biglycan. Annals of biomedical engineering, 42(3):619–630, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mienaltowski MJ, Dunkman AA, Buckley MR, Beason DP, Adams SM, Birk DE, and Soslowsky LJ. Injury response of geriatric mouse patellar tendons. Journal of Orthopaedic Research, 34(7):1256–1263, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Beason DP, Kuntz AF, Hsu JE, Miller KS, and Soslowsky LJ. Development and evaluation of multiple tendon injury models in the mouse. Journal of biomechanics, 45(8):1550–1553, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Lin TW, Cardenas L, Glaser DL, and Soslowsky LJ. Tendon healing in interleukin-4 and interleukin-6 knockout mice. Journal of biomechanics, 39(1):61–69, 2006. [DOI] [PubMed] [Google Scholar]
- [21].Taber LA. Nonlinear theory of elasticity: applications in biomechanics. World Scientific, 2004. [Google Scholar]
- [22].Humphrey JD. Cardiovascular solid mechanics: cells, tissues, and organs. Springer Science & Business Media, 2013. [Google Scholar]
- [23].Józsa LG. Human tendons. Anatomy, physiology and pathology, 1997. [Google Scholar]
- [24].Kannus P. Structure of the tendon connective tissue. Scandinavian journal of medicine & science in sports, 10(6):312–320, 2000. [DOI] [PubMed] [Google Scholar]
- [25].Fratzl P. Collagen: structure and mechanics, an introduction In Collagen, pages 1–13. Springer, 2008. [Google Scholar]
- [26].Holzapfel GA, Gasser TC, and Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of elasticity and the physical science of solids, 61(1–3):1–48, 2000. [Google Scholar]
- [27].Weiss JA, Maker BN, and Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Computer methods in applied mechanics and engineering, 135(1–2):107–128, 1996. [Google Scholar]
- [28].Shearer T. A new strain energy function for modelling ligaments and tendons whose fascicles have a helical arrangement of fibrils. Journal of biomechanics, 48(12):3017–3025, 2015. [DOI] [PubMed] [Google Scholar]
- [29].Gasser TC, Ogden RW, and Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the royal society interface, 3(6):15–35, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Freed AD and Rajagopal KR. A promising approach for modeling biological fibers. Acta Mechanica, 227(6):1609–1619, 2016. [Google Scholar]
- [31].Vergari C, Pourcelot P, Holden L, Ravary-Plumioen B, Gerard G, Laugier P, Mitton D, and Crevier-Denoix N. True stress and Poisson’s ratio of tendons during loading. Journal of biomechanics, 44(4):719–724, 2011. [DOI] [PubMed] [Google Scholar]
- [32].Dourte LM, Pathmanathan L, Mienaltowski MJ, Jawad AF, Birk DE, and Soslowsky LJ. Mechanical, compositional, and structural properties of the mouse patellar tendon with changes in biglycan gene expression. Journal of Orthopaedic Research, 31(9):1430–1437, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Ogden RW. Nonlinear elasticity, anisotropy, material stability and residual stresses in soft tissue In Biomechanics of soft tissue in cardiovascular systems, pages 65–108. Springer, 2003. [Google Scholar]
- [34].Andriotis OG, Chang SW, Vanleene M, Howarth PH, Davies DE, Shefelbine SJ, Buehler MJ, and Thurner PJ. Structure-mechanics relationships of collagen fibrils in the osteogenesis imperfecta mouse model. Journal of The Royal Society Interface, 12(111):20150701, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Tarantola A. Inverse problem theory and methods for model parameter estimation, volume 89 SIAM, 2005. [Google Scholar]
- [36].Gilks WR and Roberts GO. Strategies for improving MCMC In Markov chain Monte Carlo in practice, pages 89–114. Springer, 1996. [Google Scholar]
- [37].Jackman S. Estimation and inference via Bayesian simulation: An introduction to Markov chain Monte Carlo. American Journal of Political Science, pages 375–404, 2000. [Google Scholar]
- [38].Gustafson P, Gelfand AE, Sahu SK, Johnson WO, Hanson TE, Joseph L, and Lee J. On model expansion, model contraction, identifiability and prior information: Two illustrative scenarios involving mismeasured variables. Statistical Science, pages 111–140, 2005. [Google Scholar]
- [39].Vrugt JA. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environmental Modelling & Software, 75:273–316, 2016. [Google Scholar]
- [40].Storn R and Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4):341–359, 1997. [Google Scholar]
- [41].Gelman A and Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science, pages 457–472, 1992. [Google Scholar]
- [42].Nelder JA and Mead R. A simplex method for function minimization. The computer journal, 7(4):308–313, 1965. [Google Scholar]
- [43].McKinnon KIM. Convergence of the Nelder-Mead simplex method to a nonstationary point. SIAM Journal on Optimization, 9(1):148–158, 1998. [Google Scholar]
- [44].Miao H, Xia X, Perelson AS, and Wu H. On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM review, 53(1):3–39, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Rothenberg TJ. Identification in parametric models. Econometrica: Journal of the Econometric Society, pages 577–591, 1971. [Google Scholar]
- [46].Sobol IM. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Mathematics and computers in simulation, 55(1–3):271–280, 2001. [Google Scholar]
- [47].Saltelli A. Making best use of model evaluations to compute sensitivity indices. Computer physics communications, 145(2):280–297, 2002. [Google Scholar]
- [48].Owen AB. Variance components and generalized Sobol’ indices. SIAM/ASA Journal on Uncertainty Quantification, 1(1):19–41, 2013. [Google Scholar]
- [49].Janon A, Klein T, Lagnoux A, Nodet M, and Prieur C. Asymptotic normality and efficiency of two Sobol index estimators. ESAIM: Probability and Statistics, 18:342–364, 2014. [Google Scholar]