Comment on “Short-lived pause in Central California subsidence after heavy winter precipitation of 2017” by K. D. Murray and R. B. Lohman

Does a wet winter recharge deep aquifers in California?

Abstract

In a study by Murray and Lohman (M&L), the authors suggest that remote sensing data are useful for monitoring land subsidence due to aquifer system compaction. We agree. To infer aquifer dynamics, we provide a more detailed and joint analysis of deformation and groundwater data. Investigating well data in the Tulare Basin, we find that groundwater levels stabilized before 2015 and show that M&L’s observed continued subsidence through July 2016 is likely caused by the delayed compaction of the aquitard. Our analysis suggests the observed 2017 transient uplift is not due to recharge of the aquifer system after heavy winter rainfall because it requires an unrealistic vertical hydraulic gradient nearly five orders of magnitude larger than that typical of Tulare Basin. We find that, regardless of the amount of rainfall, transient annual uplifts of ~3 cm occur in May to June. Using an elastic skeletal storage coefficient of 5 × 10⁻³, we link this ground uplift to annual groundwater level changes.

In their recent work, Murray and Lohman (1) investigate a set of 69 C-band synthetic aperture radar (SAR) images acquired by Sentinel-1A/B satellites over the Tulare Basin, southern Central Valley, California. The dataset spans from November 2014 to October 2017 with a temporal sampling rate of 6 to 12 days. The maps of final line-of-sight (LOS) deformation velocity have a spatial resolution of 60 m. They find a LOS subsidence rate of up to 30 cm/year affecting parts of the basin [figure 1 in (1) ]. The LOS time series also show long-term subsidence with occasional deviations [figure 2 in (1)]. In early 2017, LOS subsidence time series show an apparent deviation from the multiyear subsidence trend, followed by a slight uplift signal, which correlates with the time of an “anomalously heavy winter precipitation,” inferred from the Deer Creek discharge data [figure 4 in (1)]. M&L (1) state that observed land subsidence “illuminates secular and seasonal trends modulated by changes in withdrawal rates and the magnitude of winter precipitation,” suggesting a direct recharge of the aquifer system and/or reduced groundwater pumping due to the abundance of surface water, which causes the occasional deviation from multiyear subsidence. Note that due to low permeability of the sands in the southern and western unconfined aquifers and highly mineralized water in the upper parts of the aquifer system in the west (2), most of the freshwater reservoirs in the San Joaquin Valley are deep, with some wells pumping at ~1000-m depth. Although M&L (1) quote general values of groundwater level data, they do not explicitly investigate these datasets. We additionally examine groundwater data to improve our understanding of the underlying processes driving surface deformation and suggest an alternative interpretation of the deformation data presented by M&L (1).

Deformation of an aquifer system is governed by effective stress σ′, which is the normal stress σ minus pore pressure p. Assuming a constant overburden load, change in effective stress is given by: Δσ′ = −Δp = −Δhρ_wg, where Δh is the change in groundwater level (3). An increase in effective stress beyond preconsolidation stress level results in a permanent loss of aquifer system storage capacity through inelastic deformation (4, 3). If groundwater pumping were to end, then a delayed compaction may occur during the time τ due to a lagged equilibration between aquitard and neighboring aquifer head levels. τ is a function of thickness, vertical hydraulic conductivity, and specific storage of the equilibrated layer (5). In theory, by knowing the compaction of a single interbed following a step change in groundwater level, τ can be estimated (Eq. 1) (6). Moreover, Miller et al. (4) show that τ is equal to the interval between when the groundwater level stabilizes and when land subsidence stops. Furthermore, Burbey (7) links Biot’s three-dimensional (3D) consolidation theory to the groundwater flow equations through

$$K\bullet \mathrm{\partial }h/\mathrm{\partial }z=\mathrm{\partial }{u}_z/\mathrm{\partial }t$$ (1)

Equation 1 assumes a no-flow condition at the bottom of the aquifer system, ∂h/∂z is the vertical hydraulic gradient, ∂u_z/∂t is the vertical displacement gradient, and K is the vertical hydraulic conductivity. The value of K for the San Joaquin Valley is, on average, 1.23 × 10⁻⁸ m/day (5).

Here, we use the same SAR interferometric dataset presented by M&L (1) and perform a multitemporal interferometric analysis to obtain time series of LOS displacement over the Tulare Basin. Our method is described and validated by Shirzaei et al. (8), and the velocity map and example time series are shown in Fig. 1 (A and B), which are consistent with that presented by M&L (1). We find a fast subsidence rate of >30 cm/year, occurring between January 2015 and July 2016. Then, the subsidence nearly stops, and a moderate uplift of ~3 cm is observed between April and August 2017. We next detrend the LOS time series using a principal components analysis (Fig. 1B, magenta curve) (9). We find that uplift signals occur annually around summer with amplitudes similar to or larger than that of 2017. These transient signals are not readily detectable before July 2016 because they are overprinted by the rapid subsidence signal.

Fig. 1. Synergy between surface deformation, groundwater level, and precipitation data.

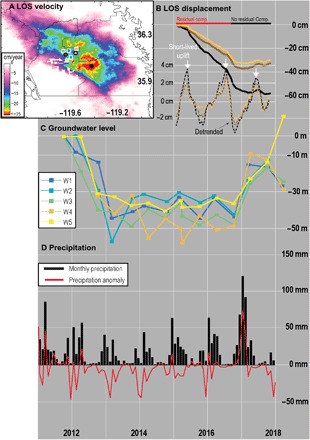
(A) Our LOS velocity obtained from interferometric processing of the 69 C-band SAR images acquired by Sentinel-1 satellite during November 2014 through October 2017. (B) Time series of LOS deformation at three locations marked in (A) with color-coded circles. Detrended time series are also provided (dashed lines). Arrows show timing of annual transient uplifts. The horizontal red line marks the period that aquitard undergoes residual compaction (residual comp.), while the black line shows the period that residual compaction nearly halts (no residual comp.). (C) Time series of groundwater level change measured at five wells, whose locations are marked in (A) with color-coded squares (source: water.ca.gov). For comparison purpose, the time series are shifted to start at zero level at the beginning of the time. Site codes are W1: 361753N1196460W001 (longitude, −119.6460; latitude, 36.1753), W2: 361158N1196258W001 (longitude, −119.6258; latitude, 36.1158), W3: 361700N1196900W001 (longitude, −119.6900; latitude, 36.1700), W4: 361900N1195800W001 (longitude, −119.5800; latitude, 36.1900), and W5: 360900N1196600W001 (longitude, −119.6600; latitude, 36.0900). (D) Monthly precipitation (black bars) and monthly anomalies compared with 18-year average (red curve) for Tulare Basin (source: pmm.nasa.gov/trmm).

We also compile the groundwater level data from five available wells with a depth of >200 m, a minimum of two samples per year, and observation during 2011–2018 (source: water.ca.gov). These wells measure groundwater level in the confined aquifers that are usually exploited (10). Well locations are shown in Fig. 1A, and groundwater time series are presented in Fig. 1C. For better comparison, these time series are shifted so that water levels are zero at the beginning; thus, values show relative changes in water level. We find that some levels decline ~50 m between the end of 2011 and middle of 2013. However, groundwater levels at all wells (including W5) stabilize before 2015. Following 2015, water levels only show oscillations. These patterns are also consistent with daily observation at U.S. Geological Survey well 361334N1200351W01 located at latitude 36°13′34.7″ and longitude 120°03'54.6". We conclude that for most of the period covered by the Sentinel-1 dataset (November 2014 to October 2017), recharge and pumping are on average balanced and that residual compaction of the aquitard likely caused the continued subsidence due to a delayed equilibration of hydraulic head levels between aquifer and aquitard units. Similar behavior is observed in the Tucson Valley, where Miller et al. (4) report 6.6 years of residual compaction following groundwater level recovery due to the implementation of artificial recharge efforts in the early 2000s. Comparing the groundwater level and land subsidence time series, we infer a time lag of τ ≈ 2 years consistent with that estimated for San Joaquin Valley during the 2007–2010 drought by Smith et al. (5). Note that although the subsidence continues, the groundwater level does not decline during 2013–2016; thus, effective stress remains nearly constant, and no inelastic deformation is occurring in the aquifer unit.

To further investigate whether the observed uplift in 2017 can be related to groundwater recharge following the heavy winter rainfall, we apply Eq. 1 with ∂u_z/∂t ≈ 3 cm/180 days and K =1.23 × 10⁻⁸ m/day, which results in an unrealistically large vertical hydraulic gradient ∂h/∂z = 1.35 × 10⁺⁴. Given the observations at nearby wells W1 and W3 (Fig. 1, A and C) with well depths of ~200 and ~500 m, respectively, the estimated vertical hydraulic gradient is ~0.1. Thus, a deep aquifer system recharge following the winter rainfall is unlikely to be the driver of observed subsidence rate change and transient uplift. This conclusion is consistent with the estimated rate of recharge to unconfined aquifers in Central Valley [~600 mm/year after (11)] and the rate of focused recharge (i.e., rainfall transformed to stream flow in the Deer Creek) to (semi-)confined aquifers [up to 80 mm/year after (12)], which indicates that rain water may only reach shallow unconfined layers on monthly time scales. To quantify the contribution of shallow aquifers to the uplift signal, we use a 1D consolidation model that relates change in effective stress to deformation of soil (13). Assuming a maximum depth of 10 m for the shallow aquifer, Biot-Willis coefficient of 0.2 [after (14)], and static bulk modulus of 150 MPa [after (3)], we find that the uplift signal due to recharge of shallow aquifers is ~1 mm, which is negligible given the observation errors.

We further compile ~18 years of precipitation data taken every 3 hours on a 0.25° by 0.25° grid over the Tulare Basin, provided by the Tropical Rainfall Measuring Mission’s multisatellite product (source: pmm.nasa.gov/trmm). The data are aggregated to obtain a monthly estimate of precipitation (Fig. 1D, black bars). We derive precipitation anomalies as the difference between each month’s precipitation and its ~18-year average (Fig. 1D, red curve). We find that despite the winter rains and except for a few months, the precipitation anomaly is mostly negative compared with the 18-year average and, thus, there is a deficit in supply of precipitation. This conclusion holds if we estimate the precipitation anomaly given a 100-year average obtained from the Global Precipitation Climatology Centre (source: gpcc.dwd.de).

The transient uplifts in 2015–2017 (Fig. 1B) and associated annual groundwater level change (Fig. 1C) occur around summer (May and June) in the growing season, when crops are heavily irrigated. This is likely related to the vertical return flow through >100,000 pumped and nonpumped wells, which substantially enhances the vertical hydraulic conductivity across the Corcoran Clay (10). Given an upper bound of 5 × 10⁻³ for the elastic skeletal storage coefficient in the San Joaquin Valley (3), an annual groundwater level change observed in Fig. 1C is sufficient to produce a transient uplift of ~3 cm observed in Fig. 1B. The seasonal uplift signals before August 2016 are overprinted by a larger subsidence signal due to residual compaction (Fig. 1B). After the aquitard begins to equilibrate with the neighboring aquifer and residual compaction nearly halts, the uplift signal becomes more evident.

In summary, geodesy provides valuable tools to monitor aquifer system compaction. It can improve our understanding of underlying processes, particularly when supplemented with hydrogeological data, such as groundwater levels.