PREDICTION ALGORITHM OF THE CAT SPINAL SEGMENTS LENGTHS AND POSITIONS IN RELATION TO THE VERTEBRAE

Abstract

Detailed knowledge of the topographic organization and precise access to the spinal cord segments is crucial for the neurosurgical manipulations as well as in vivo neurophysiological investigations of the spinal networks involved in sensorimotor and visceral functions. Because of high individual variability, accurate identification of particular portion of the lumbosacral enlargement is normally possible only during postmortem dissection. Yet, it is often necessary to determine the precise location of spinal segments prior to in vivo investigation, targeting spinal cord manipulations, neurointerface implantations, and neuronal activity recordings. To solve this problem, we have developed an algorithm to predict spinal segments locations based on their relation to vertebral reference points. The lengths and relative positions of the spinal cord segments (T13-S3) and the vertebrae (VT13-VL7) were measured in 17 adult cats. On the basis of these measurements, we elaborated the estimation procedure: the cubic regression of the ratio of the segment’s length to the lengths of the VL2 vertebra was used for the determination of segment’s length; and the quadratic regression of the ratio of their positions in relation to the VL2 rostral part was used to determine the position of the segments. The coefficients of these regressions were calculated at the training sample (9 cats) and were then confirmed at the testing sample (8 cats). Although the quality of the prediction is decreased in the caudal direction, we found high correlations between the regressions and real data. The proposed algorithm can be further translated to other species including human.

INTRODUCTION

The spinal cord of mammals as well as some other vertebrates (tailless amphibians) occupies only a portion of the length of the spinal canal (Nieuwenhuys, 1964) due to the faster growth of the vertebral column in relation to the spinal cord (Streeter, 1919; Sakla, 1969; Ghazi and Gholami, 1994). This causes a significant discrepancy between vertebrae and the spinal cord segments position, where the spinal segments are shifted rostrally in relation to the corresponding vertebrae. In early publications (Nieuwenhuys, 1964) this phenomenon is called “spinal segments ascent” and it is mostly prominent for lower subdivisions of spinal cord (lumbar and sacral segments).

Numerous studies have described the measurements of the spinal cord and vertebral segments in various mammals including cat (Thomas and Combs, 1962; Mellström and Skoglund, 1969; Eldridge, 1984; Maierl and Liebich, 1998), rabbit (Pisaleva and Fasahutdinova, 2008; Farag et al., 2012), dog (Pisaleva and Fasahutdinova, 2008), rat (Gelderd and Chopin, 1977; Radmanabhan, Singh, 1979; Gilerovich et al. 2008), mouse (Harrison et al., 2013), mongoose (Rasouli et al. 2015), horse (Selcuk and Bahar, 2014), sheep (Ghazi and Gholami, 1994), monkey (Thomas and Combs, 1965) and human (Ko et al., 2004; Canbay et al., 2014). However, the majority of these studies assessed the spinal cord and vertebral column separately, without considering any inter-relations between the positions of spinal cord segments and vertebrae. To our knowledge, the rare exceptions were studies of Radmanabhan and Singh (1979) and Gilerovich et al. (2008), which proposed the scheme of rat’s spinal cord (without subdivision to inter-rootless and rootless areas) and vertebra; Harrison et al. (2013) which described segment’s positions inside the vertebral column in mouse; report of Maierl and Liebich (1998) which established relations between the basic subdivisions of cat’s spinal cord (cervical, thoracic etc.) and vertebrae, and work of Eldridge (1984) which described the mean locations and boundaries of the rootlet parts of the spinal segments inside the vertebral column and proposed to predict the positions of S1-S2 segments based on positions of the L4-L5 spinal segment boundaries.

The size and neuroanatomical organization of cat make it suitable as an experimental model to study sensorimotor and visceral functions in normal and pathological conditions. During the past three decades, spinal cord injury models performed in cats have pioneered the development of treadmill-based rehabilitation therapies (de Leon et al., 1998), pharmacological interventions (Rossignol et al., 2001), and electrical spinal cord stimulation (Gerasimenko et al., 2005). Cats present several advantages for the translation of therapies to humans. First, their locomotor system is more developed compared to rodents. Second, the size of their spinal cord is more comparable to that of humans. Third, contrary to monkeys, spinal cord injured cats can be maintained in good health and trained for extensive period of time. These factors stress the importance of obtaining accurate neuroanatomical data of cat spinal cord topography.

It has been shown recently in various experimental models, including decerebrated and spinalized cats, that spinal networks underlying locomotor and postural control can be triggered by electrical stimulation of lumbosacral cord (Gerasimenko et al., 2002; Musienko et al., 2005, 2010). The features of locomotor pattern, level of body weight support during stepping and standing (Musienko et al., 2013), degree of the flexors and extensors motoneuronal pools activation (Musienko et al., 2009), and even direction of locomotion all are dependent on the stimulation of specific spinal segments (Musienko et al., 2012). Although such evidences open clear opportunities to artificially control and modulate the spinal cord circuitry in a task-dependent manner, the development of these techniques in vivo requires detailed knowledge of the topographic organization of the spinal cord segments in order to target particular portions of lumbosacral enlargement based on their relation to vertebral reference points.

We should underline that all mentioned above experimental models use the dorsal roots as landmarks for spinal cord segmentation. So we found useful to follow the same approach at this work (see Discussion for other approaches for spinal cord subdivision).

The aims of this study were (i) to identify patterns of mutual spatial organization of lumbosacral spinal segments and the lumbar vertebrae in adult cat, (ii) to describe the individual differences in spinal segments and vertebrae topography, and (iii) to develop the algorithm allowing prediction of the spinal segments size and their positions in relation to the vertebrae.

MATERIAL AND METHODS

Experimental animals

Seventeen outbred domestic adult cats of both sexes (10 males and 7 females) weighing 2.3 to 4 kg were used for this study. All animals had no signs of neurological disorders and any obvious abnormalities of spinal cord and musculoskeletal system. Experiments were carried out in accordance with the Directive of the European Parliament and of the Council on the protection of animals used for scientific purposes (2010/63EU) and with the approval of Ethics Commission of the Pavlov Institute of Physiology. All animals were also used for additional neurophysiological and neuromorphological experiments.

Perfusion and anatomical dissection

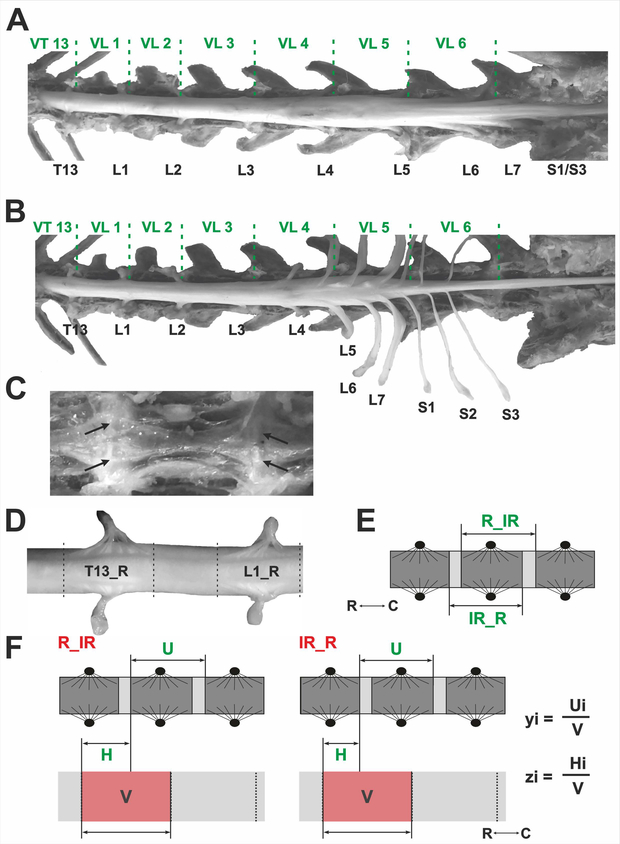
Under deep anesthesia (isoflurane, 5% mixed with oxygen 1%) animals were perfused transcardially with 2 liters of 0.9% sodium chloride followed by 2 liters of 4% buffered paraformaldehyde solution (Immunofix, BioOptika, pH = 7.6). The fixed spinal columns were dissected: soft tissues and T12-VL7 vertebral laminae were removed (Fig. 1A). The dura mater was cut and removed from the dorsal surface of the spinal cord to provide access to the dorsal roots and dorsal root ganglia (DRGs); then DRGs were dissected out, removed from the vertebral canal and gently pulled to visualize the entrance of the dorsal roots to the spinal cord (Fig. 1B). After removal of the spinal cord from the vertebral canal, the body lengths of the VT13-VL7 vertebrae were measured together with adjacent caudal and rostral halves of the intervertebral cartilage (Fig. 1C). The length of the entrance areas of dorsal roots (rootlet areas) of the T13-S3 segments as well as inter-rootlet areas (if any) were measured. Interrootlet areas were defined as space of the cord surface between two successive spinal nerve roots and devoid of any rootlets. Rootlet areas as well as interrootlet areas can be clearly seen in Fig. 1D. The positions of rootlet and interrootlet areas in relation to the vertebral bodies were also registered when the spinal cord was in the vertebral canal. All measurements were performed using a caliper (1 mm division value).

Fig. 1.

Anatomical dissection and measurements of spinal segments and vertebrae. (A) The spinal cord inside the vertebral canal after removal the vertebral laminae. Dura matter is not removed. (B) Dura matter is removed, DRGs are dissected and removed from the vertebral canal. The borders between the vertebrae is marked with green dashed lines. VT13, VL1–7 – thoracic and lumbar vertebrae, T13, L1–7, S 1–3 – thoracic, lumbar, and sacral DRGs. (C) View of the vertebral bodies from inside the vertebral canal (white arrows indicate vertebrae junctions). (D) Enlarged part of T13 and L1 rootlet areas (T13_R and L1_R) and interrootlet area between them. (E) Two ways of spinal cord segments subdivisions (R_IR and IR_R): dark-gray – rootlet areas and light-gray - interrootlet areas of the segments. C and R – caudal and rostral poles. (F) Definition of the ratios used for prediction algorithm, V – corpus vertebri, U – the length of individual spinal cord segment, H – the length from the rostral part of V to the spinal cord segment. y_i – the ratio of the segment’s length to the length of one the lumbar vertebra. z_i – the ratio of the segment’s position to the length of the vertebra.

Different systems of measurement of spinal segments sizes exist in literature. Some authors define a segment as a rostral rootlet area and the adjacent caudal interrootlet area (Thomas and Combs, 1962, 1965; Farag, 2012; Canbay, 2014). This variant is referred to as R_IR in the present work (Fig. 1E). Other authors propose that a segment consists of caudal rootlet area and rostral interrootlet area (Ko et al. 2004; variant IR_R; Fig. 1E). Alternatively, interrootlet areas may be divided in halves, and each half attributed to the neighboring segment (Maierl and Liebich, 1998).

Prediction algorithm

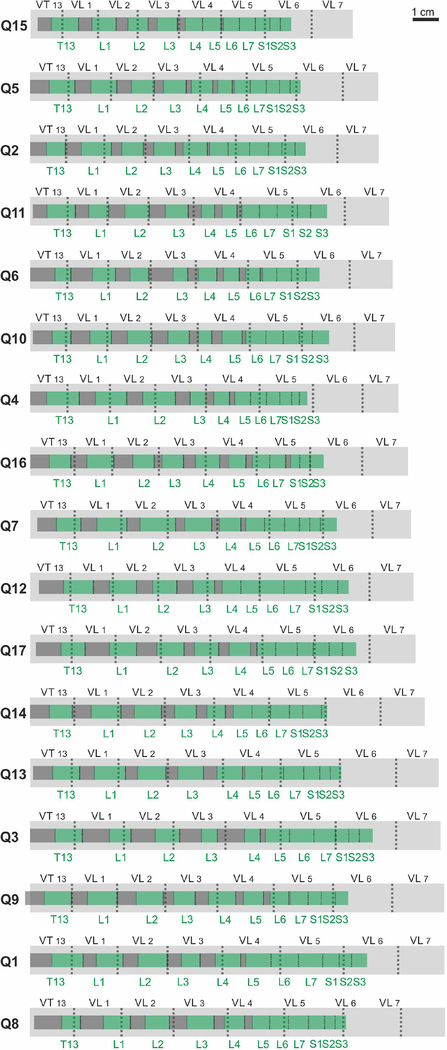
The aim of the present algorithm is to express the length of spinal segments and to determine their position based on the length of the most easily accessible vertebrae. The total sample of 17 cats was divided randomly into 2 groups. One group (9 cats, Q1-Q9 in Fig.2) was used as a training sample to compute the regression coefficients, and the second group (8 cats, Q10-Q17 in Fig.2) was used as a testing sample to evaluate the quality of the regression.

Fig. 2.

The positions of the segments in relation to the vertebrae in individual cats. Light grey – the vertebrae VT13-VL7, green – the rootlet areas of the spinal cord segments T13-S3, dark-grey – the interrootlet areas of the spinal cord segments.

The dependence of the lengths of segments T13-S3 on the size of the animal’s trunk was estimated as a ratio of the segment’s length to the length of one of the lumbar vertebrae (VT13-VL5) (Fig.1F, y_i ratio). For each vertebrae of each cat of the training sample, we defined y_i = U_i/V as the ratio of each spinal segment length (U_i, with i=0, 1, …, 10 corresponding to spinal segments T13, L1, …, S3) to the length of the vertebrae, V, and fitted y_i with different regression models: linear, y_i= ai + b, quadratic, y_i=ai² + bi + c, and cubic, y_i=ai³ + bi² + ci + d. A separate regression was performed for each vertebra; except for VL6 and VL7 because only minor part of the spinal cord was presented in these vertebrae. These regressions were fitted based on the testing sample, and used to predict the lengths of the segments in cats of both training and testing samples. The approximation quality was checked by comparison of the predicted and real lengths values: for each cat and each segment, we computed |U^e_i-U_i|/ U_i (where U^e_i = y^e_i V, y^e_i and U^e_i are the estimated values of y_i and U_i), i.e. the relative value of the absolute difference between predicted and real length of each segment. Then these relative values were averaged across the cats of training and testing samples.

The dependence of the position of segments T13-S3 on the position of rostral part of one of the vertebrae VT13-VL5 was estimated as a ratio of the segment’s position to the length of this vertebra (Fig.1F, z_i ratio). For each vertebrae of each cat of the training sample, we defined z_i = H_i/V as the ratio of each spinal segment rostral part position (H_i, with i=0, 1, …, 10 corresponding to spinal segments T13, L1, …, S3) to the length of the vertebrae, V, and fitted z_i with different regression models: linear, z_i= ai + b, quadratic, z_i=ai² + bi + c, and cubic, z_i=ai³ + bi² + ci + d. A separate regression was performed for each vertebra; except for VL6 and VL7 because only minor part of the spinal cord was presented in these vertebrae. These regressions were fitted based on the testing sample, and used to predict the positions of the segments in cats of both training and testing samples. The approximation quality was checked by comparison of the predicted and real lengths values: for each cat and each segment, we computed |H^e_i-H_i|/ U_i (where H^e_i = z^e_i V, y^e_i and H^e_i are the estimated values of z_i and H_i), i.e. the relative value of the absolute difference between predicted and real position of each segment. Then these relative values were averaged across the cats of training and testing samples.

The quantitative characteristics (mean ± standard error of the regression coefficients) were calculated using standard statistical software (Microsoft Excel 2010, Matlab 2010b).

RESULTS

The general spatial characteristics of the spinal cord segments and the vertebrae

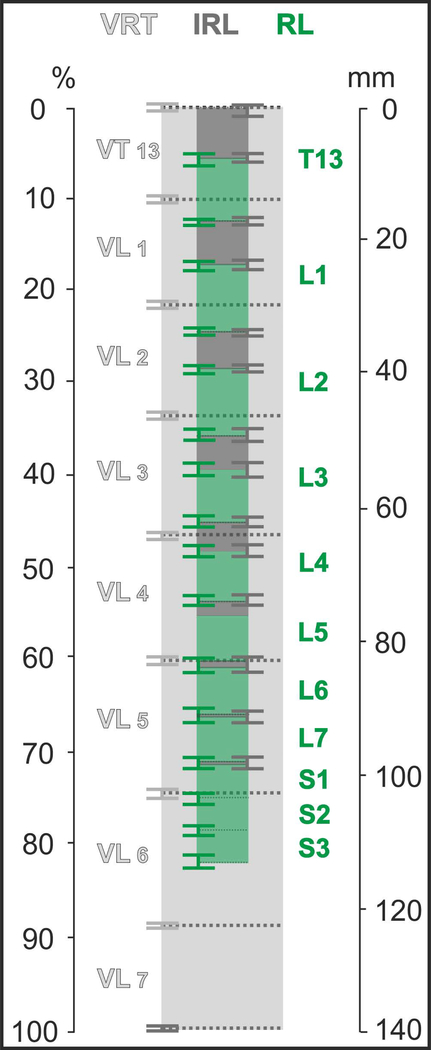
The positions of the segments in relation to the vertebrae in individual cats are presented in Fig. 2, the average positions are shown in Fig.3. Because the length of the spines in different animals varied, the lengths of spinal segments and vertebrae in Fig. 3 were expressed not only in mm but also as a percentage of the total length of vertebrae VT13-VL7.

Fig.3.

The averaged positions of the segments in relation to the vertebrae (Mean ± SE, n=17 cats). Light grey – the vertebrae VT13-VL7, green – the rootlet areas of the spinal cord segments T13-S3 (dark green – their SE-whiskers), dark-grey – the interrootlet areas of the spinal cord segments (grey – their SE-whiskers).

As shown in Fig. 3 the vertebrae length increases from VT13 (10.40%±0.12% of total length) to VL5 (14.19%±0.11%) and VL6 (14.05%±0.13%), and thereafter decreases down to 11.29%±0.22%, in vertebrae VL7. The length of the rootlet area of the segments increases from T13 (6.66%±0.31%) to L1 (7.14%±0.22%), and then decreases until segment S3 (3.27%±0.20%). The percentage length of the interrootlet area of the segments decreases from the interrootlet area adjacent rostrally to T13 (5.30%±0.21%) until the interrootlet area adjacent caudally to L7 (0.09%±0.09%). Segments S2 and S3 are composed of rootlet areas only. The “spinal segments ascent” phenomenon, where caudal spinal segments are located in comparatively rostral vertebrae, is clearly seen in Fig. 2 and Fig. 3: typically, the rootlet area of the segment L5 is located within or below the body of the vertebra VL4, the rootlet areas of segments L6, L7 and S1 are located within or below the body of the vertebra VL5, and the segments S2 and S3 are located within or below the body of vertebrae VL6.

Variability of the size of the spinal segments and of their positions in relation to the vertebrae

The mean values of the total vertebrae length (VT13-VL7) and the total spinal cord length (T13-S3) are shown at Fig. 4A. It is important to note that the size of the vertebrae and the segments, as well as the position of the segments in relation to the vertebrae have individual variability. For instance, both vertebrae and spinal segments were longest in cat Q1 (151 mm, identical to Q8, and 125 mm respectively), and shortest in cat Q15 (117.5 mm and 95 mm respectively). It can be seen (Fig.4B) that there is significant correlation (r²=0.78) between the total lumbar vertebrae length (VT13-VL7) and total lumbosacral spinal cord (T13-S3) length. The longer is vertebrae the longer is spinal cord. The slope of the linear regression between these lengths is approximately equal to 1 so their interdependence is very simple: the total length of the vertebrae is approximately 21 mm higher than the total length of the spinal cord.

Fig.4.

The interrelations between vertebrae and spinal cord segments. (A) The mean values of total length of vertebrae (VT13-VL7) and spinal cord segments (T13-S3). (B) The relations between total length of spinal cord segments and vertebrae.

Though the rootlet areas of the rostral segments (T13-L3) are typically located in the vertebra of corresponding number, the boundaries of these segments don’t correspond to the borders of the vertebrae (this discrepancy is more pronounced when using the IR_R convention). Moreover, the rootlet area of the most rostral segment considered in this paper, the T13, may be located in the body of the corresponding vertebra, VT13, or may almost entirely shift in the body of the vertebra VL1 (cat Q12). Even when the total length of the vertebrae is constant, the caudal spinal segments may be located within the different vertebral bodies. For example, the length of the lumbosacral vertebrae in cats Q8 and Q1 is identical, 151 mm, segments S2-S3 are located in VL6 in Q1 and VL5 in Q8. Despite these considerable inter-individual variations, the morphologies of the vertebrae and of the spinal cord are correlated; for instance there was a clear linear relationship (Fig. 4B) between the total length of the vertebrae and of the spinal cord. This indicates that measurements of the vertebrae may be used to predict the position of spinal segments, as shown next.

The prediction of the length of the segments

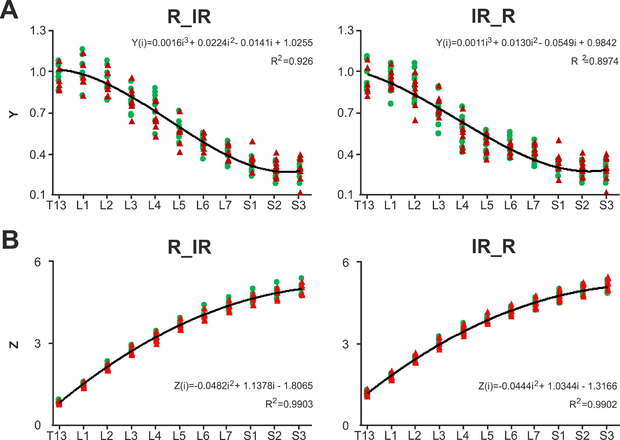
The best fit for both variants of the spinal cord segmentation were obtained for the ratio of the length of segments to the length of vertebra VL2. The coefficients of determination for linear and quadratic regression are high: for linear regression r²=0.90 for variant R_IR and r²=0.87 for variant IR_R, for quadratic regression r²=0.91 for variant R_IR and r²=0.89 for variant IR_R. Yet the cubic regression has the maximal coefficient of determination (Fig. 5A) (r²=0.93 for variant R_IR, r²=0.90 for variant IR_R) in relation to them. The coefficients of cubic regression are

$${\mathrm{Y}}_{\mathrm{R}\_\mathrm{I}\mathrm{R}}\left(\mathrm{i}\right)=0.0016{\mathrm{i}}^3-0.0224{\mathrm{i}}^2-0.0141\mathrm{i}+1.0255$$ (1)

$${\mathrm{Y}}_{\mathrm{I}\mathrm{R}\_\mathrm{R}}\left(\mathrm{i}\right)=0.0011{\mathrm{i}}^3-0.013{\mathrm{i}}^2-0.0549\mathrm{i}+0.9842$$ (2)

where i=0 for the segment T13, i=1 for the segment L1, …, i=10 for the segment S3.

Fig. 5.

Prediction of spinal segments length and size. (A) The ratios y_i of training (green dots) and test (red dots) samples. Approximation of the ratios y_i (based on VL2) for segments T13-S3 in training sample with cubic regression. (B) The ratios z_i of training (green dots) and test (red dots) samples. Approximation of the ratios z_i (VL2) for segments T13-S3 in training sample with quadratic regression. Negative and positive values correspond to segments located rostrally or caudally than VL2 consequently. IR_R and R_IR – two variants of the subdivision of spinal cord segments.

These coefficients obtained with the training sample are also suitable for the testing sample – the coefficient of determination is r²=0.92 for variant R_IR, r²=0.89 for variant IR_R. The average differences between the real and the calculated lengths of the segments (as a percentage of its length) at this approximation are presented in Table 1. The average differences for training and testing samples do not differ significantly from each other (12.05%±2.64% vs 13.79%±3.87% for variant R_IR, 13.34%±3.38% vs 15.82%±4.05% for variant IR_R), indirectly indicating the homogeneity of the samples. Because absolute difference between the predicted and the actual length of each segment is approximately constant, while the length of the segments decreases in the caudal direction, the relative error increases in the caudal direction (see Table 1).

Table 1.

The average differences between the real and the calculated lengths of the segments (as a percentage of each spinal segment’s length) at approximation of cubic regression.

Segment	Variant R_IR		Variant IR_R
	Training sample, %	Testing sample, %	Training sample, %	Testing sample, %
T13	6.58±1.61	8.51±2.24	9.27±1.17	9.76±1.91
L1	7.29±2.31	7.48±2.07	7.92±2.00	5.14±1.43
L2	8.99±1.83	6.82±1.60	10.87±2.16	10.36±3.18
L3	10.59±2.29	9.75±2.82	11.97±3.68	6.47±2.16
L4	13.40±2.86	12.69±3.45	17.53±6.29	18.37±5.87
L5	11.73±2.67	14.58±5.22	14.46±4.74	15.07±5.32
L6	10.58±2.94	8.30±2.41	12.07±2.50	8.07±1.45
L7	15.96±2.39	10.65±2.25	15.77±3.29	19.41±2.56
S1	12.71±2.47	18.64±3.54	12.79±2.89	25.47±4.01
S2	17.49±4.14	20.07±3.95	17.19±4.45	21.46±4.80
S3	17.26±3.55	34.15±12.97	16.86±3.98	34.49±11.85
Mean±SE	12.05±2.64	13.79±3.87	13.34±3.38	15.82±4.05

The prediction of the positions of the segments

The rostral part of the same vertebra VL2 was used for the prediction of the relative positions of the segments. The coefficient of determination of the quadratic regression (Fig. 5B) was higher (r²=0.99 for both variants) than the coefficient of determination of the linear regression (r²=0.95 for both variants) and was equal to the coefficient of determination of the cubic regression. The coefficients of quadratic regression are

$${\mathrm{Z}}_{\mathrm{R}\_\mathrm{I}\mathrm{R}}\left(\mathrm{i}\right)=-0.0482{\mathrm{i}}^2+1.1378\mathrm{i}-1.8065$$ (3)

$${\mathrm{Z}}_{\mathrm{I}\mathrm{R}\_\mathrm{R}}\left(\mathrm{i}\right)=-0.0444{\mathrm{i}}^2+1.0344\mathrm{i}-1.3166$$ (4)

where i=0 for the segment T13, i=1 for the segment L1, …, i=10 for the segment S3.

Using equations (1) and (3) or (2) and (4) for variants R_IR and IR_R respectively it is possible to predict the lengths and the positions of spinal segments by multiplying the Y(i) by the length of the VL2 where i is the number of given segment. E.g., if the length of VL2 is 18 mm then at variant IR_R for the length of the L6 segment following the equation (2) we receive Y_{IR_R}(6) * 18 mm ≈ 0.4244*18 mm ≈7.6 mm, and for the position of the same segment following the equation (4) we receive Z_{IR_R}(6) * 18 mm = 3.2194*18 mm ≈ 59.2 mm from the rostral part of the VL2.

The coefficients obtained at training sample are also suitable for the testing sample – the coefficient of determination is also equal to 0.99 for both variants. The average differences between the real and the calculated positions of the segments (as a percentage of its length) at this approximation are presented in Table 2. The Table 2 shows that the prediction accuracy decreases in the caudal direction for both training sample (from 7% to 102% of the segment length for variant R_IR, from 10% to 103% of the segment length for variant IR_R), and testing sample (from 7% to 115% of the segment length for variant R_IR, from 13% to 102% of the length of the segment for variant IR_R). In absolute terms, the error of the prediction of the positions of segments increases in caudal direction from 2.05±0.05 mm to 4.50±0.26 mm.

Table 2.

The average differences between the real and the calculated positions of the segments (as a percentage of each spinal segment’s length) at approximation of quadratic regression.

Segment	Variant R_IR		Variant IR_R
	Training sample, %	Testing sample, %	Training sample, %	Testing sample, %
T13	7.35±2.37	7.29±1.88	10.18±3.25	12.63±2.84
L1	8.48±2.12	11.76±2.51	9.62±2.98	18.54±2.28
L2	13.24±3.14	18.09±1.50	11.90±2.67	24.17±3.03
L3	16.50±4.85	24.65±4.25	22.74±7.21	26.78±7.18
L4	18.75±5.83	30.25±5.68	27.19±9.30	38.69±9.30
L5	21.89±5.28	37.49±7.43	22.87±5.29	36.09±11.62
L6	33.60±10.88	47.00±11.84	30.75±9.14	38.24±10.38
L7	44.71±11.62	60.80±15.30	42.05±10.19	48.33±12.75
S1	71.14±17.26	74.97±19.62	67.64±12.94	59.33±13.03
S2	102.05±29.29	94.07±19.99	90.78±18.74	86.65±13.57
S3	99.14±25.66	115.87±22.55	103.51±18.57	101.71±15.18

DISCUSSION

Detailed knowledge of the topographic organization and accurate access to the spinal cord segments is primordial for in vivo studies of the spinal networks involved in sensorimotor and visceral functions. Because of high individual variability, the accurate identification of particular portions of the lumbosacral enlargement is normally possible only though postmortem anatomical dissection. Yet, it is often necessary to locate specific spinal segments before the invasive surgery. To solve this problem we have developed a unique algorithm to predict the spinal segments positions based on their relation to vertebral reference points. One notable characteristic of this algorithm is that it predicts the length and position of each spinal segment relative to the unique vertebra, VL2. We found that other schemes based on the average values (Fig.3) where each spinal segment’s spatial characteristics are predicted relative to the nearest vertebra didn’t yield better accuracy. Therefore, the algorithm proposed here represents an efficient and practical solution, where an experimenter may measure the position of a single vertebra (VL2) to predict the length and position of all spinal segments in the same experiment.

There are different methodological approaches to divide the spinal cord into subregions. One possible approach is to compare the shape of the gray matter in spinal cord transverse sections with existing atlases (e.g. Harrison et al., 2016). Because the shape of the gray matter mainly depends on the location of motor neuron pools, this approach is in a good agreement with a recently developed six-region schema of spinal cord organization (Mitchelle and Watson, 2016) based on expression of hox-genes (Philppidou and Dasen, 2013). Other popular way is to choose a macroanatomical segmental approach with dorsal roots as landmarks for segmentation. According to the literature and our own experience (Minev et al., 2015; Wenger et al., 2016), this is the most effective practical approach. The dorsal roots contain the proprioceptive afferent fibers so they are the appropriate target for the electrical stimulation (Capogrosso et al., 2013).

There are possible variants in attribution of interrootlet areas. The most commonly used approach is considering the segment as a sum of the rootlet area and the caudally attached interrootlet area (Thomas and Combs, 1962, 1965; Farag, 2012; Canbay, 2014). But another approach, considering the segment as the sum of the interrootlet area and the caudally attached rootlet area, was also described (Maierl and Liebich, 1998; Ko et al., 2004). These discrepancies perhaps led to the mismatch of the data obtained about segments positions in relation to the vertebral bodies, across different studies. There is no doubt about the assignment of the rootlet area of the segment, because dorsal roots emerge from the ganglion, which is located in the vertebra of the corresponding number. In contrast, it is rather subjective to assign the interrootlet area to rostral or caudal segment and both approaches seem acceptable. To date, it is assumed based on anatomical and functional data that there are no precise natural boundaries between spinal segments (Sengul et al., 2011, Leijnse and D’Herde, 2016), hence the segmentation of the spinal cord mainly has topographic sense. Yet, it is very important for physiologists and surgeons to have precise landmarks for targeting spinal cord manipulations, neurointerfaces implantations, and neuronal activity recordings.

To provide more comprehensive approach we have considered 2 variants of dividing the spinal segments based on inputs of dorsal roots to the spinal cord differing in assignment of the interrootlets areas. The length and positions of the vertebrae and the spinal cord segments obtained in the present work are in a good agreement with the literature. Thus, L1 is the longest segment of the cat’s lumbar spinal cord as in other mammals: horses, donkeys, monkeys and humans (Thomas and Combs, 1965; Ko et al., 2004; Selcuk and Bahar, 2014). Maierl and Liebich (1998) showed that the length of the vertebra increases from VT13 to VL5, and then decreases from VL5 to VL7, while the length of the spinal cord segments (variant of segmentation IR_R) decreases from T13 to S3. However, in the works mentioned above (Maierl and Liebich, 1998; Eldridge, 1984) only the absolute average values of the lengths and positions of the segments and vertebrae were assessed, whereas the present work provides a prediction algorithm based on the relative values.

Eldridge (1984) has proposed the way of determining the position of sacral segments S1-S3 based on the positions of the mid-lumbar segments (L4 and L5). However, this approach requires a laminectomy that is invasive and often impossible for ongoing neurophysiological experiments. Our prediction algorithm allows estimating the lengths and the positions of the spinal cord segments in relation to the vertebrae based on the vertebrae length, which can be determined without invasive spinal injury. Consequently, this prediction can be made using non-invasive techniques (e.g., X-ray or tomographic examination of vertebrae). Furthermore, a similar approach may be developed and translated to human clinical practice in future. Such non-invasive method of the spinal cord topography measurement would be essential in spinal neurosurgery clinics for the express diagnostics, and defining the extent of surgical treatment of vertebral and spinal disorders.

The best quality of the approximation for both variants of segmentation has been obtained using the length of VL2. This may be due to the fact that upper lumbar vertebrae need longer time to grow (Maierl and Liebich, 1998), and therefore, their length is more related to the size of the animal. Similar to study by Eldridge (1984), the variability of the predictions increased in caudal direction (Table 1, 2). The quality of the segment length prediction was higher than its position prediction. Despite the extremely high quality of the approximation (r² = 0.99), based on the characteristics of the vertebra VL2, it is possible to predict more confidently the positions of lumbar than the sacral spinal cord segments because they are much smaller.

Among the limitations of the algorithm at present stage we should mention first the inability to use it directly onto other regions of the spinal cord because this requires the anatomical measurments of the segments and vertebrae and the recalculation of specific parameters of abovementioned equations. The same procedure should be done for translation it to other vertebrate species and even for those cat breeds, which have a genetic abnormality in spine structure (Manx and Japanese Bobtail) (DeForest and Basrur, 1979, Pollard et al., 2014). Another limitation of the algorithm is inability to predict lengths and positions separately for the interrootlet and rootlet parts of the spinal segments.

CONCLUSION

The individual differences in spinal segments and vertebrae topography were described. Taking them into account the patterns of mutual spatial organization of lumbosacral spinal segments and the lumbar vertebrae in adult cat were identified. It allowed to elaborate an algorithm of the non-invasive prediction of lengths and positions of spinal cord segments based on vertebrae characteristics. The proposed approach of establishing co-relations between spinal cord segments and vertebrae can be further translated to other species including primates.