Abstract
Understanding the nature of the genetic regulation of gene expression promises to advance our understanding of the genetic basis of disease. However, the methodological impact of the use of local ancestry on high-dimensional omics analyses, including, most prominently, expression quantitative trait loci (eQTL) mapping and trait heritability estimation, in admixed populations remains critically underexplored. Here, we develop a statistical framework that characterizes the relationships among the determinants of the genetic architecture of an important class of molecular traits. We provide a computationally efficient approach to local ancestry analysis in eQTL mapping while increasing control of type I and type II error over traditional approaches. Applying our method to National Institute of General Medical Sciences (NIGMS) and Genotype-Tissue Expression (GTEx) datasets, we show that the use of local ancestry can improve eQTL mapping in admixed and multiethnic populations, respectively. We estimate the trait variance explained by ancestry by using local admixture relatedness between individuals. By using simulations of diverse genetic architectures and degrees of confounding, we show improved accuracy in estimating heritability when accounting for local ancestry similarity. Furthermore, we characterize the sparse versus polygenic components of gene expression in admixed individuals. Our study has important methodological implications for genetic analysis of omics traits across a range of genomic contexts, from a single variant to a prioritized region to the entire genome. Our findings highlight the importance of using local ancestry to better characterize the heritability of complex traits and to more accurately map genetic associations.
Keywords: admixture, eQTL, local ancestry, transcriptome, mixed models, heritability, omics, population structure
Introduction
Greater understanding, which can be derived from, for example, the prominent method of eQTL mapping, of the genetic determinants of high-dimensional molecular traits promises to advance our understanding of the genetic architecture of complex traits.1, 2 Because the majority of trait-associated variants identified by genome-wide association studies (GWASs) reside in non-coding regions,3 eQTL data provide an important resource for elucidating the underlying mechanisms of these non-coding variants by linking them to gene expression.1 In addition, heritability estimation, i.e., determining the trait variance explained by regulatory variants, might provide important insights into the genetic architecture of gene expression traits. However, to date, eQTL mapping and heritability analysis have been conducted primarily in populations of European ancestry, and omics data in recently admixed populations, such as African Americans (AAs), that are disproportionately affected by a variety of complex diseases, are lacking;4, 5, 6, 7 this limits our understanding of the genetic basis of trait variance in human populations. Populations of African descent have greater genetic variation and less extensive linkage disequilibrium (LD), and these traits might restrict the generalizability of genetic associations identified in non-African populations to AAs.8, 9 Importantly, the impact of the admixed genome structure on eQTL mapping and heritability estimation has not been adequately studied.
The eQTL (regulatory) effect on gene expression is typically modeled (via linear regression) assuming an additive effect of genetic variation on gene expression.10 The resulting association analysis tests only the correlation between genotype and phenotype instead of testing for causal effects and is easily subject to confounding from population structure. The chromosomes of AAs comprise mosaic regions of different ancestral origins, resulting in two types of population structure that might be present in genetic association analyses.11 One arises from global ancestry, which reflects the admixture proportions of the (previously isolated) ancestral populations (primarily African and European, though a relatively small proportion of Native American ancestry12 might also be present) and is typically estimated with the first principal component (PC), which is derived from genome-wide genotype data and separates the European and African ancestral populations.13 (The assumption of a small number of ancestral populations is often made for methodological and computational convenience.) The PCs have been shown to have a geographic interpretation, and their use has been widely adopted due to computational efficiency.14, 15 Mixed models incorporate the pairwise genetic similarity between every pair of individuals in the association mapping and have been effectively deployed to correct for population structure, family structure, and cryptic relatedness,16, 17 but until recently, mixed-model approaches have been too computationally intensive for eQTL mapping.
Population structure in association studies of an admixed population might also arise from local ancestry, which is the number of inherited alleles (0, 1, or 2) from each ancestral population at a particular locus.18 Local ancestry might vary across the genome, as well as across individuals, even those of similar global ancestry,13 at any given locus. Because a large proportion of gene-expression phenotypes have been found to be differentially expressed between Africans and Europeans,4 increased spurious eQTL associations (false positives) could arise, leading to pseudo-associations that are not driven by the genetic variants being tested but, instead, by their local ancestral backgrounds. Studies that explore the methodological importance of local ancestry in genetic-association analyses have been limited to a small number of highly polygenic traits.19, 20 Incorporating local ancestry into eQTL mapping, which tests associations between millions of SNPs and thousands of genes, has been too computationally intensive.
Heritability estimation is usually performed with linear mixed models (LMMs) but has been conducted primarily in ancestrally homogeneous populations. LD score regression (LDSR) is a summary-statistics-based approach to estimating heritability and confounding,21 but its applicability to studies involving admixed individuals has not been investigated. Heritability of gene expression traits has been characterized by a more sparse genetic architecture22 and by an a priori, functionally relevant (cis) region, in contrast to polygenic complex traits, suggesting a greater role for local ancestry than global ancestry. Local ancestry might be determined by a range of factors, including population demographic history (e.g., migration, population bottleneck, etc.), and these factors can shape complex admixture dynamics (e.g., as trans-Atlantic migration has impacted the local ancestry of African Americans). The impact of the use of local ancestry on estimating the heritability of gene expression traits is thus a critical gap in our understanding of their genetic architecture. Furthermore, high-dimensional omics studies provide an opportunity to assess, more comprehensively, the contribution of local ancestry to human phenotypic variation through joint analysis of thousands of molecular traits.
Here, we provide a statistical framework for analyzing the relationships among the proportion of variance explained (PVE) by genetic variation , PVE by local ancestry , global ancestry, and degree of population differentiation at causal regulatory variants for gene-expression traits in admixed populations. We performed a comprehensive analysis of the variation explained by local ancestry versus global ancestry in gene expression. We analyzed the impact of the use of local ancestry on eQTL mapping and heritability estimation through extensive simulations and the application of our approach to a transcriptome dataset in an admixed population, as well as to GTEx project data2 consisting of samples from multiethnic individuals. We develop an efficient approach to eQTL mapping in an admixed population, demonstrating that the use of local ancestry can substantially improve mapping of genetic associations. We demonstrate that our approach shows improved control of the type I error rate, as well as increased statistical power compared with a global-ancestry adjustment approach in eQTL mapping, and we find a greater replication rate for eQTLs specific to our approach. Finally, we propose a method for heritability estimation in admixed populations, opening avenues for research into the genetic architecture of complex traits.
Material and Methods
Genotype Data
We downloaded GTEx v7 genotype data (from 635 individuals) from the database of Genotypes and Phenotypes (dbGaP) (dbGaP study accession: phs000424.v7.p2). The genotype dataset contains data from individuals with recent admixture (e.g., African Americans)2 and individuals of more homogeneous (European) ancestry, the latter comprising the majority of the samples (∼85%). We performed minor allele frequency (MAF) > 0.01 filtering following the methods previously published by GTEx2 and removed all multiallelic SNPs and SNPs on the sex chromosomes. The number of SNPs left was 9,910,646. We used GTEx data for PVE analysis and eQTL mapping in multiethnic samples.
We used three tissue types from GTEx. We used the GTEx v7 skeletal-muscle dataset (n = 491 with genotype data, of which n = 57 are AA samples) for PVE estimation (see “PVE Estimation in Real Transcriptome Data”). We used this tissue because it has the largest number of AA samples in the GTEx data. We used the GTEx whole-blood (n = 369) and cell-EBV-transformed lymphocytes (LCL, n = 117) datasets to test our eQTL mapping approach in a multiethnic population (see “Cis-eQTL Mapping in NIGMS and GTEx”). We excluded samples with East Asian ancestry, and we used 356 (EA = 308, AA = 48) and 114 (EA = 93, AA = 21) samples in these two datasets, respectively, for the cis-eQTL mapping.
We used 100 AA samples that were part of the National Institute of General Medical Sciences (NIGMS) Human Variation Panels to assess the impact of local ancestry in pure admixed populations. We downloaded the genotype intensity files from dbGaP (dbGaP study accession: phs000211.v1.p1). The genotyping had been performed on an Affymetrix Genome-Wide Human SNP Array 6.0 platform containing 908,194 SNPs. We used the Affymetrix Genotyping Console to process the genotype intensity files and to call the genotypes on the forward strand. We kept data from 83 individuals with gene-expression measurements. We merged the genotype with genotype data from 1000 Genomes phase 3 and performed the principal-component analysis (PCA) with PLINK.23 Two individuals with partial East Asian ancestry were removed from the subsequent analysis, leaving 81 samples. Quality control was performed with PLINK. We removed SNPs that are on the sex chromosomes, have duplicated positions, are multiallelic in the 1000 Genomes reference panel, are out of Hardy-Weinberg equilibrium (p values < 1 × 10−5), and who have a genotyping missing rate larger than 5% and a MAF less than 5%. The total number of SNPs remaining in the analysis after the quality control was 724,100. We used this dataset for simulations and eQTL mapping. We also used 60 CEU (U.S. residents with northern and western European ancestry) samples from Phase 2 HapMap (release 23) and kept 714,082 SNPs that were a subset of the NIGMS AA dataset. We used this dataset for the replication of eQTLs detected in the NIGMS AA dataset.
Local Ancestry Estimation
After quality control, the genotype data were phased with SHAPEIT,24 using 1000 Genomes phase 3 in build 37 coordinates as the reference genome. We utilized the YRI (Yoruba people of Ibadan, Nigeria) samples and CEU samples from the 1000 Genomes Phase 3 as the reference ancestral genomes to estimate the local ancestry (0, 1, or 2 African ancestry alleles) by using a conditional random-field based approach, RFMix.12 When performing local ancestry inference, RFMix models strand-flip errors to account for potential phase errors. The window size in RFMix was set to be 0.15 Mb for the GTEx data and 0.20 Mb for the NIGMS data because the latter have fewer SNPs. We compared the first PC with the average local ancestry across the genome; this comparison shows a high correlation in both the NIGMS and GTEx datasets (Figure S6), suggesting robust estimation of local ancestry. We used the local ancestry value, the number of African ancestry alleles (0, 1, or 2) of each SNP, as an additional covariate in the eQTL mapping and to construct the local-ancestry-based similarity matrix for PVE estimation.
Gene-Expression Data
We used the gene-expression data from the GTEx v7 skeletal-muscle dataset (n = 491 with genotype data, of which n = 57 are AA samples) for PVE estimation (see “PVE Estimation in Real Transcriptome Data”). We used this tissue because it has the largest number of AA samples in the GTEx data. The expression values have been normalized for 19,850 autosomal genes.
We used GTEx whole-blood (n = 369) and cell-EBV-transformed lymphocyte (LCL, n = 117) datasets to test our eQTL mapping approach in a multiethnic population (see “Cis-eQTL Mapping in NIGMS and GTEx”). There were 19,432 and 21,467 expressed autosomal genes in these two datasets, respectively.
We obtained gene expression data for 81 AAs (represented in the NIGMS dataset) and 60 HapMap CEU samples from the Gene Expression Omnibus (GEO); the accession number is GEO: GSE10824.25 The expression intensity for 8,793 probes was quantile normalized and corrected for background noise with the Robust Multichip Average (RMA) method. We filtered probes whose variances were less than the 0.4 quantile of variances of all genes, probes without Entrez Gene ID, duplicated probes, and probes on sex chromosomes. We performed log2 transformation on the gene-expression data. A total of 4,595 probes representing 4,595 genes were included in the analysis after the quality control. We converted the probe IDs to the gene symbols by using the HG Focus annotation file and obtained gene positions from the GENCODE release 19.
Statistical Model
Let denote the ith individual and denote a local causal genetic variant for a gene. Then gene expression can be written as follows:26
Here is the effect size of the genetic variant on gene expression trait y, is the normalized local ancestry, , is the variance of local ancestry, is the variance of genotype at SNP , and is the residual that is not dependent on local ancestry. are Bernoulli-distributed according to the allele frequency of the SNP in population 0 or 1 .
Single Causal Variant
, which is the effect explained by local ancestry at the SNP , can be estimated from We note that . If we assume a single causal eQTL variant, such as is often assumed to simplify certain types of eQTL analysis,2, 27 we obtain the following:
by using the mean of a Bernoulli random variable (i.e., ).
Because and , where is the global ancestry, we obtain:
Let
be the fixation index (Fst), which quantifies population differentiation or allele-frequency difference at the variant .28 Then the following expression, which relates the effect explained by local ancestry, global ancestry, the effect of the genetic variant, and the degree of population differentiation in a single equation, follows:
| (1) |
Multiple Causal Variants
We sought to generalize equation (1) to the case of multiple causal eQTL variants in the cis region. Here, it matters for the purpose of estimating the variance explained by local ancestry, whether there is any local ancestry transition in the region, and how many such transitions exist. (Local ancestry segments might extend over a large distance.) Suppose there are n local ancestry transitions. This implies n + 1 local ancestry classes in the region (with f∗ being the local ancestry membership of the variant f). (A stretch of the genome in between local ancestry transitions represents a local ancestry class.) Let m be the number of local causal genetic variants for the expression of the gene. (In what follows, we will assume there are no other causal [e.g., trans] eQTLs outside the region, strictly restricting our focus to cis variants.) Then we obtain, in accordance with Zaitlen et al.,26 the following:
by Cauchy-Schwarz inequality. This implies:
| (2) |
where is the total extent of population differentiation at causal eQTL variants. We confirmed this inequality by using simulations (see Table S1). This relates the trait variance explained by local ancestry, the aggregate genetic effect on phenotype, the level of population differentiation of the causal variants, and the degree of polygenicity of the trait. Equation (2∗), as the derivation shows, applies in a more restrictive setting with the dual assumptions of polygenicity and independence.
Note is the aggregate genetic effect and the total extent of population differentiation for the causal eQTLs included in the sum. Because the latter depends on the number of causal eQTLs, it might be useful to consider the mean level of population differentiation in the cis region, .
Local Ancestry, Its Aggregate Effect, and Trait Heritability Estimation
A linear mixed model (LMM) can be used to obtain an aggregate estimate of regulatory (genetic) effect on gene expression. For a given -vector of gene expression levels for individuals, the LMM approach fits the following model:
| (3) |
Here, is a matrix of covariates (of dimension ), is the -vector of effects for the covariates (including the intercept term), is an matrix, is an -vector of random effects, is the residual vector, is a genetic similarity matrix, is the variance of residual errors, and is the ratio of two variance components. The approach estimates PVE by genetic variants , defined as follows:
using restricted maximum likelihood (REML). We note that the random genetic effect is gene-specific. This simple-LMM model has been used to characterize infinitesimal genetic architectures in an ancestrally homogeneous population. However, we evaluated the concordance with results from assuming a more general genetic architecture, namely a mixture distribution for the effect sizes, by using a Bayesian sparse linear mixed model (BSLMM),29 which includes the LMM and Bayesian variable selection regression as special instances.
A revised version of the univariate LMM model (3) can be used to estimate the trait variance explained by local ancestry. Here, analogously to using the SNP data, the similarity matrix 26 is constructed from the local ancestry values (0, 1, or 2 African ancestry alleles):
| (3∗) |
Model (3∗) allows the estimation of the PVE by local ancestry :
with REML. Alternatively, the effect explained by local ancestry throughout the genome can be modeled to derive from a mixture of a normal distribution and a point mass at 0:
where is the proportion of non-zero effects in the genome. In simulations, we assessed the accuracy of the estimate of from the Gaussian approach (versus a mixture approach) for modeling the effect size explained by local ancestry. Under the same assumptions for equation (2∗), model (3∗) provides an estimate of for trait heritability, as is also previously noted in Zaitlen et al.:26
However, in contrast with Zaitlen et al.,26 this estimate is more appropriately viewed as the “expected heritability” in the presence of admixture, departure from which yields additional insights into genetic architecture (i.e., violation of the assumption of polygenicity or independence) or might indicate the presence of stratification. Notably, we also obtain a measure of departure from expectation if is substantially different from one:
Thus, can be used not only to estimate the expected heritability given the presence of admixture, as in the expression for , but also to evaluate the potential presence of population stratification due to local ancestry, as in the expression for .
We also implemented a joint model that partitions gene expression into two components, the genetic component and the local-ancestry component ():
The local-ancestry component may be written as a function of the causal variants: . A simple estimator is the first principal component derived from the (whole-genome) genotype matrix (i.e., an estimate of global ancestry). Other statistical approaches can be implemented with varying predictive and computational performance. By explicitly modeling the component that is a result of local ancestry, we might get a more accurate estimate of the overall genetic effects. However, the gain in accuracy depends on the choice for fitting the estimate . In our approach (which we term joint genetics and local ancestry [joint-GaLA]), for computational purposes and simplicity, we assume Gaussian distributions for and and restrict the model to the variants in the cis region:
Here, and are random effects with corresponding similarity matrices and generated from local genetic variation and the corresponding local ancestry, respectively. By using simulations (see “Simulation Framework for Heritability Estimation”), we assessed the accuracy of the estimate of from joint-GaLA and compared this estimate to that obtained from simple-LMM (equation [3]). Furthermore, we compared this model with the use of global ancestry to fit .
Simulation Framework for Heritability Estimation
We conducted extensive simulations, utilizing both real (from the NIGMS AA dataset up to 500 causal variants) and simulated genotype data of admixed samples, in order to (1) validate the analytically derived relationships (inequality [2] and equation [2∗]) and confirm the expression for the “expected heritability” in the presence of admixture, as well as show a departure from the expected value in the presence of local ancestry stratification; (2) evaluate the accuracy of the PVE estimation methods when assuming different levels of stratification; and (3) compare the estimate and the from global ancestry (estimated from simple linear regression).
To simulate genotype data, we tested across five input parameters: (1) number of ancestral populations (n = 2); (2) number of individuals (n = 1000); (3) number of variants (n = 1000), (4) FST values (FST = 0.16 and FST = 0.3); and (5) heritability values ( = 0.3, the observed mean in the GTEx skeletal-muscle data, and = 0.8). Global ancestry for the ith individual was drawn from a truncated normal distribution . Local ancestry at the variant was defined as the sum of two draws from the binomial distribution . The ancestral-allele frequency was assumed to be distributed as Unif(0.05, 0.95) and, along with , was used to generate the allele frequency, which was drawn from the beta distribution with parameters and . The genotype for the ith individual at the kth causal variant was then derived from a random draw from the binomial distribution and had an expected value defined by the local ancestry for the individual. We assumed one local-ancestry transition (because the local ancestry tract in AAs is usually >10 Mb). We varied the number of causal eQTLs (10, 25, 100, 200, 500, or 1000) to assess the accuracy of the method as a function of sparsity or polygenicity. The number of causal variants reflects the number of predictors in PrediXcan models30 built with GTEx v7 data and enloc results from real data.31 (We describe below the simulation framework for the case m = 1 in the simulations for genetic association [eQTL] mapping.) The effect size of the kth causal variant was simulated as , wherein is equal to the number of causal variants. As we previously noted, this assignment of effect sizes is a strong assumption (shared with the widely used genome-wide complex trait analysis [GCTA]32 or LDSR21) about how heritability is distributed among the causal eQTLs and is independent of LD.
We simulated gene expression as follows:
The first summation is the phenotype effect due to genetic variation, whereas the second is due to local ancestry. Because the local-ancestry tract typically exceeds the size of the cis region, we assumed a constant value for in the second summation. The single effect size for local ancestry was obtained from the empirical distribution (in NIGMS) at four different percentiles (the quartiles for at 0.00138, 0.005444, 0.01755, and 0.2877), representing different levels of stratification. The residual was added and assumed to be distributed as . We set when simulating gene expression without stratification.
We derived estimates from simple-LMM and joint-GaLA from 100 independent runs for each set of choices for the parameters. Estimates for were obtained, assuming model (3∗), in 100 independent runs to confirm equation (2∗).
Departure from the expected heritability was tested, assuming local ancestry stratification, in simulations with real genotype data (Mann-Whitney U test in 100 independent runs). In this case, we calculated the mean level of (equation [2∗]) for the tested causal variants by using information on allele frequency from the 1000 Genomes CEU and YRI samples for the ancestral populations.
Comparison with LD Score Regression for Estimates of Population Stratification and of Heritability
LDSR is a widely used approach for estimating confounding due to population stratification and for estimating heritability with only GWAS summary statistics. We therefore sought to investigate how LDSR performs at these tasks in 100 independent runs for each set of configurations defined above by using , , the number of transitions, and . We calculated the LD score at each variant by using the LD in the NIGMS genotype data. The use of the actual LD as observed in the dataset simulates the use of a perfectly matched population reference panel. We ran linear regression with simulated gene expression and real genotype data and with global ancestry as a covariate. We applied LDSR to the simulated GWAS datasets to estimate the heritability and the amount of confounding as quantified by the “intercept” (along with the standard error for each). We note that LDSR, by design, does not provide an estimate for .
PVE Estimation in Real Transcriptome Data
We estimated the PVE by local (defined as within 1 Mb of the gene) genetic variants for each gene in the GTEx AA skeletal-muscle samples, and we used REML, as implemented in GCTA.32 We used this tissue in order to maximize the number of AA samples (n = 57). We used only common variants (MAF > 0.10; n = 6,122,246) in this AA subset to increase the estimation accuracy. We calculated the gene-specific genetic-relatedness matrix by using local genetic variants and incorporated three PCs, ten probabilistic estimation of expression residuals (PEER) variables,33 sex, and the sequencing platform as fixed effects in the LMM. We used a non-constrained model that allows the PVE estimates to be negative or larger than 1 in order to obtain unbiased estimates, but we restricted ourselves to genes whose estimates were between 0 and 1 in the downstream analysis. We used the p value from the likelihood ratio test for the genetic-variance component to select genes with nominally significant estimates (nominal p value < 0.05) and a more stringent Benjamini and Hochberg (BH)-corrected34 false discovery rate (FDR) < 0.10.
We randomly selected 57 samples of European descent out of the 491 GTEx samples in order to compare the between two populations. The chosen sample size of European Americans (EAs) (n = 57) matches the sample size of AAs in the simulations and PVE estimation. We selected common variants in this subsect (MAF > 0.10; n = 4,946,431) and applied the LMM approach described above.
We identified differentially expressed genes between AAs and EAs in skeletal-muscle tissue with a t test (BH FDR < 0.05).
Similarly, we estimated the PVE by local ancestry at common local variants in the GTEx AA skeletal-muscle samples. We used the estimated local ancestry around each gene (within 1 Mb of the gene) to construct the relatedness matrix . The LMM was fitted to estimate for each gene-expression phenotype via the same set of fixed effects as in the analysis.
Using GTEx AA skeletal-muscle data, we applied joint-GaLA (see above). We then compared the estimated from joint-GaLA with the estimate from the simple-LMM model.
We investigated the possible reasons for any observed difference in between the populations. We performed LMM-association analysis with Genome-wide Efficient Mixed Model Association (GEMMA)29 by fitting a model of gene expression with each local SNP and the genetic-relatedness matrix constructed from local SNPs. We compared the distributions of allele frequency and of effect size for significant SNPs (nominal p value < 0.05 from the LMM association) between the populations. We also considered the variance in genetic relatedness generated from the local genetic variants for pairs of distinct individuals:
By definition, , where is the genotype at variant for individual , is the allele frequency, and is the number of local variants. Now, simplifies to the sum of LD correlations over all pairs of variants that were used in the relatedness matrix [], as has also been previously noted.35 Thus, the variance in relatedness, , can be used to evaluate the effect of differential LD patterns near the gene on the population specificity of its genetic regulation.
Sparsity or Polygenicity of Gene Expression
To systematically characterize the sparsity or polygenicity of gene expression in a recently admixed population, we applied a BSLMM29 to generate an estimate of (the proportion of variance explained by the sparse genetic effect) and (the sum of the polygenic and sparse effects) for each gene in the GTEx AA skeletal-muscle dataset. This analysis would determine genes for which gene expression is influenced by a small number of genetic variants. We calculated the Spearman correlation between from the BSLMM and . We identified genes with highly discordant estimates between the two methods; these were defined as those genes with more than two times the standard error away from ( [], for PVE estimation methods and ). We performed simulations (see above) to evaluate the accuracy of the LMM approach as a function of the number of causal variants (i.e., as a function of a sparse or polygenic architecture).
Use of Local Ancestry in eQTL Mapping (Joint-GaLA-QTLM)
The statistical approach assumes an additive effect of genotype on gene expression and adjusts for the variant-level local ancestry covariate in addition to the sample-level covariates (such as age, sex, or principal components). For each gene-variant pair, we fit the following baseline model:
| (4) |
where the-vector g is the expression measurement of a gene for the individuals; s is the genotype of a marker (typically a SNP proximal, e.g., within 1 Mb, to the gene) encoded by 0, 1, and 2 representing the number of alternative alleles with effect size on expression level; is the kth covariate (e.g., age, sex) with effect ; is the intercept; l is the local ancestry encoded by 0, 1, and 2 according to the number of African ancestry alleles at the tested variant with effect size ; and is the residual assumed to be normally distributed with mean 0 and variance . Here is a matrix of covariates, including the intercept term, with weight . The baseline model accounts for population structure by adjusting for the local ancestry, whereas in the usual model, the admixture proportions or, because of computational efficiency, the top PCs of the genotype matrix are incorporated into the model as quantitative covariates (among the ’s) and locus-specific ancestry is ignored.
Because the genotype and local ancestry at the variant might be correlated, we estimated how much the variances in the effect sizes, and , might be increased because of multicollinearity. We fit the ordinary least square regression , estimated the , and calculated the variance inflation factor .
We implemented this model, building on a widely-used eQTL mapping method, Matrix eQTL.10 Matrix eQTL speeds up the eQTL mapping process by performing billions of association tests via matrix operations. The Matrix eQTL algorithm first regresses out the covariates (age, sex, PEER variables, etc.) from each gene expression trait and each genotype and then standardizes residuals to obtain and , respectively. Then it calculates the correlation of each residual pair through matrix multiplication and transforms the correlation to a t-statistic (); here, df is the number of degrees of freedom in the linear regression model. However, incorporation of local ancestry, which varies by variant, cannot be done in the same manner as the subject-level covariates (e.g., age or sex). Our developed algorithm first regresses out the covariates from gene expression, genotype, and local ancestry to obtain standardized residuals, , and . It then regresses out from to obtain and proceeds to calculate and again via matrix operations for efficient processing. We note that equation (4) is equivalent to the following expression after regressing out the covariates:
| (4∗) |
The test for nonzero effect on residual gene expression () can be done via an F test () for the partial correlation coefficient. Equivalently, a t-statistic can be calculated with the following expression, where df is the number of degrees of freedom in the multivariate linear regression model:
Type I Error Simulations for eQTL Mapping
In the type I error simulations for eQTL mapping, we considered two scenarios: population stratification due to global ancestry and population stratification due to local ancestry. We utilized real genotype data from the NIGMS AA samples and simulated gene-expression levels with different sources of confounding. Because of the difference in variance explained by the first PC and by local ancestry, we utilized the empirical distribution of effect size for each with the scaled expression value () in the NIGMS dataset. We extracted the effect sizes at four different percentiles from the empirical effect-size distribution for local ancestry and PCs, separately analyzed, and used those in the simulations.
We randomly selected 100 out of 4,595 genes and simulated the gene expression :
where is the effect size at each percentile and is the first PC or the average local ancestry around each gene. Then we performed cis-eQTL mapping for these genes with no adjustment, global ancestry adjustment (adjustment for the first three PCs), or local ancestry adjustment. We used a range of p values from 1 × 10−6 to 1 to calculate the false positive rate. We repeated the simulation 1,000 times and averaged the false positive rate.
Type II Error Simulations for eQTL Mapping
In order to test the effects of different population structure adjustment methods on the type II error rate, we first randomly chose 1,000 SNPs from the NIGMS genotype data and simulated 500 gene expression variables with standard normal distribution. We tested two scenarios. In the first scenario, the gene expression was only associated with the genotype. We randomly selected 50 SNPs to be true eQTLs whose effect sizes of genotype are 0.9. This choice for the eQTL effect size was motivated by the median of the absolute value of the estimated effect sizes for the significant SNP associations (BH-adjusted p < 0.05) with scaled gene expression () in the NIGMS data. In the second scenario, both genotype and local ancestry contributed to the gene expression. We randomly selected 50 SNPs, and we chose an effect size of the genotype of 0.9 and an effect size of local ancestry of 0.8. Again, the effect size of local ancestry was chosen from the significant local-ancestry associations (BH-adjusted p < 0.05) with gene expression from fitting a regression , where is also the scaled gene expression, is the genotype dosage, and is the local ancestry value, in the actual NIGMS data. We performed the eQTL estimation with no adjustment, global-ancestry adjustment, or local-ancestry adjustment. We used a range of p values from the minimum to the maximum p value in each simulation to identify the number of false positives and true positives, and we calculated the area under the curve (AUC) of the receiver operating characteristic (ROC) curve to summarize the performance of each approach.36 We repeated the simulations 100 times and plotted a single ROC curve. We compared the AUC of global ancestry adjustment and local ancestry adjustment for a false positive rate in the range 0–0.2 via a paired two-sided t test.
Cis-eQTL Mapping in NIGMS and GTEx
To identify eQTLs in the NIGMS data, we tested associations between each gene and SNPs within 1 Mb upstream of the gene start site and 1 Mb downstream of the gene end site by using the local-ancestry adjustment approach joint-GaLA-QTLM. We compared the association results from the adjustment for 1, 2, or 3 PCs and gender and those from the adjustment for local ancestry and gender.
We utilized a hierarchical correction method to identify eQTLs. This method was demonstrated to produce a lower FDR and greater true positive rate than the method that applies correction over all association tests.37 We first used the Benjamini and Yekutieli (BY) procedure38 to adjust p values for all association tests by each gene. We then pooled the minimum BY-adjusted p value of every tested gene to obtain its best associations. We corrected the pooled minimum p values by the BH correction method.34 We selected significant eGenes with the threshold of 0.10 for the BY-BH-adjusted p values and used the corresponding minimum BY-adjusted p value as the threshold to select significant SNPs for these eGenes.
We utilized the eQTL mapping results in the GTEx (v7) LCLs with 117 multiethnic samples as a replication panel. We calculated the replication rate for eQTLs unique to the local ancestry adjustment approach and to the global ancestry adjustment approach.
We then applied joint-GaLA-QTLM (equation [4]) to the GTEx whole-blood and LCL datasets. We excluded samples with East Asian ancestry and used 356 and 114 samples in these two datasets, respectively, for the cis-eQTL mapping. For the global-ancestry adjustment method, we used sex, sequencing platform, three PCs, and PEER variables (35 for the whole-blood dataset, 11 for the LCL dataset, consistent with the latest GTEx analysis for the optimal number of PEER factors to avoid overfitting).2 For the local-ancestry adjustment approach, we replaced the three PCs with local ancestry. We applied the hierarchical correction method described above and used the threshold of 0.05 for the BY-BH-adjusted p values to select significant eQTLs. We also report the number of eQTLs and eGenes identified at the less stringent threshold (BY-BH p value < 0.1).
We estimated the empirical distribution of the effect size of local ancestry on expression for each gene in both the NIGMS and GTEx whole-blood datasets while adjusting for the same covariates as in the eQTL mapping.
Results
Relationship Among the Effect of Genetic Variation on Gene Expression, the Variance Explained by Local Ancestry, Population Differentiation, and Global Ancestry
Gene expression might differ in its genetic architecture from a complex disease or general quantitative trait in several crucial ways, including in the importance of the local (cis) region and the potential for a large, sparse genetic component. In the case of an admixed population, we hypothesize that the ancestry background near the gene of interest might have a primary importance, where local ancestry potentially explains a greater proportion of transcriptional variation than global ancestry. We therefore consider these key features in modeling the trait variance explained by local ancestry and genetic variation (see Material and Methods).
First, we assume the simplest case of a single causal variant, as is sometimes assumed in certain eQTL analyses (such as fine mapping and single-variant association tests). We define the population genetic parameter, , at the variant in terms of the allele frequencies and (in the ancestral populations 1 and 0) and the genotype variance as follows:
We then obtain the following (see Material and Methods for derivation):
This expression relates, for a given causal eQTL, the effect explained by local ancestry with the effect of the genetic variant on gene expression , global ancestry , and the degree of population differentiation .
We extend equation (1) to the case of multiple causal eQTL variants in the cis region of a gene, as would be relevant for heritability estimation assuming allelic heterogeneity. We obtain the following inequality (see Material and Methods):
where is the total extent of population differentiation at causal eQTL variants. This provides an upper bound on the trait variance explained by local ancestry in terms of the aggregate genetic effect , the magnitude of population differentiation of the causal regulatory variants , and the degree of polygenicity of the gene expression trait (captured by the number of causal eQTLs, ). We confirmed inequality (2) by using simulations across a range of genetic architectures (see Material and Methods and Table S1).
Implications of the Statistical Model
From equation (1), potential sources of bias in the estimate of include all the remaining parameters (, and ), the last two of which are local parameters and, indeed, dependent on . In addition to the level of admixture, uncertainty in local-ancestry estimation and the degree of population differentiation might contribute to bias. Importantly, global-ancestry adjustment ignores local heterogeneity in the LD pattern and differences in allele frequency across the genome in ancestral populations. (We investigate the single-variant case extensively below when we evaluate the use of local ancestry in mapping genetic associations.)
From inequality (2), these consequences follow:
-
1.
The parameters (a characteristic of the population) and (a population genetic parameter that measures genetic distance between the ancestral populations) are a priori unrelated to the phenotype (gene expression), whereas and the polygenicity parameter are specific to the phenotype. The population differentiation statistic used by a recent study26 assumes a highly specific genetic architecture and incorporates the trait-dependent weight at the variant , thus it varies by phenotype for each variant and is consequently not a purely population-genetic parameter. For eQTL studies involving thousands of (gene-expression) phenotypes with varying levels of polygenicity and potentially displaying a range of genetic architectures, we wanted to utilize a phenotype-independent measure of genetic distance between the ancestral populations at each variant, and this decision determined our model and led to inequality (2). Of course, summing the genetic distance over all causal eQTL variants for the specific gene expression trait introduces phenotype dependence. Nevertheless, assuming shared eQTLs across populations (though with possibly different allele frequencies), this framework would facilitate more straightforward population comparisons by disentangling the contribution of the population-genetic parameters from that of the phenotype-dependent variables.
-
2.
Because the maximum of is 0.25, the quantity in inequality (2) determines whether local ancestry (in the cis region) explains less of the transcriptional variation than genetic variation. In particular, if , local ancestry would explain less of the variation in gene expression. Now the quantity is linear in the mean level of differentiation at the gene but quadratic in the degree of polygenicity, indicating that characterization of a gene-expression trait as sparse or polygenic has important implications for assessing the variation explained by local ancestry and by genetic variation.
-
3.
If we assume (1) a highly polygenic architecture for a gene-expression trait wherein each causal variant contributes only a modest proportion that depends only on the total number of contributing variants, i.e., , and (2) the independence of the contribution of causal variants to trait variance and degree of population differentiation (i.e., independence of and ), we obtain (see Material and Methods):
| (2∗) |
where Equation (2∗) therefore provides an estimate of for , and this value can be viewed as the “expected heritability” in the presence of admixture, departure from which might yield additional insights into genetic architecture (see Material and Methods). The condition is an assumption about the causal eQTL effects being drawn from a single (Gaussian) distribution with the given expected value or mean. We note that the assumption of a single distribution of effect sizes might be a reasonable one for all cis effects, but trans effects might plausibly require a different distribution. Similarly, a single distribution of effect sizes might not hold for both common and rare regulatory variants. The condition is thus a strong assumption about how heritability is distributed across the cis region of the gene, with its assignment of causal effects from the same distribution independently of LD. Under the two assumptions of polygenicity and independence, we get from inequality (2), indicating that the variance explained by local ancestry would be less than that explained by local genetic variation. We emphasize that inequality (2) holds for a wide range of genetic architectures, but equation (2∗) assumes strict constraints on the genetic architecture.
We note that the statistical model applies more broadly to the analysis of trait variance explained by local ancestry and genetic variation in studies of the proteome, the methylome, and other types of omics data. Furthermore, inequality (2) and equation (2∗) characterize the expected in the presence of admixture, and violation of these relationships might well indicate the presence of stratification or, in the case of equation (2∗), violation of at least one of the two assumptions of polygenicity and independence (see Material and Methods).
Local Ancestry and Mapping Genetic Associations
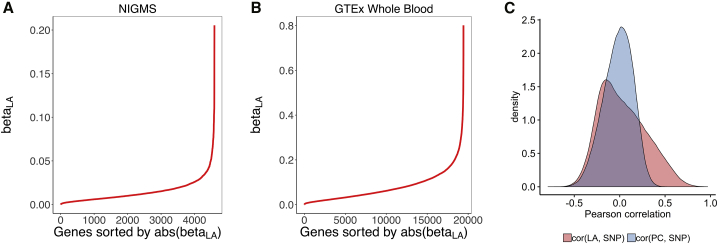
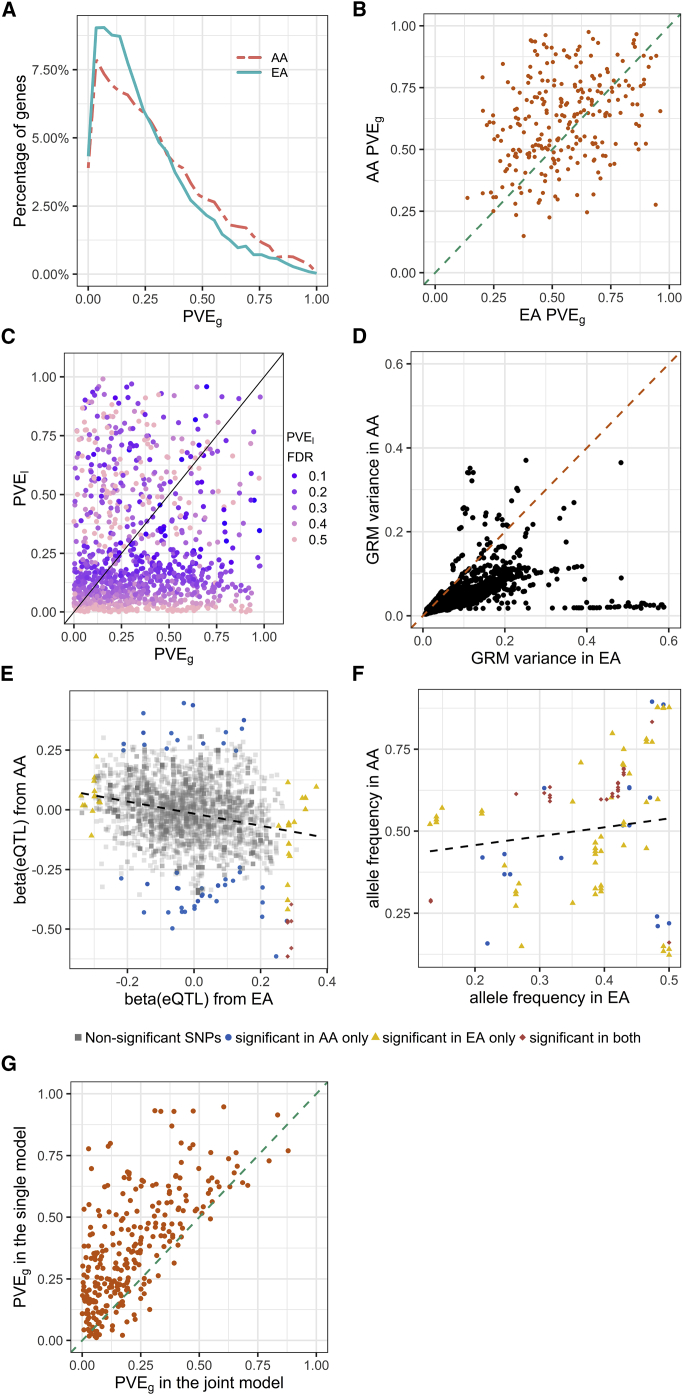
We sought to investigate the importance of the use of local ancestry for eQTL mapping in an admixed population (joint-GaLA-QTLM; see Material and Methods). We plotted the empirical distribution of the maximum absolute-effect size of local ancestry for each gene and found, for a number of genes, that a large proportion of the variance in expression can be explained by the local ancestry at a single variant in both NIGMS and GTEx (NIGMS: 36 out of 4,595 genes, FDR < 0.10, Figure 1A; GTEx whole-blood: 3,129 out of 19,432 genes, FDR < 0.10, Figure 1B), suggesting that the confounding due to local ancestry might exist not only in studies of recently admixed populations but also in studies with multiethnic samples.
Figure 1.
Effect Explained by Local Ancestry and an eQTL Association Test
We evaluated the effect explained by local ancestry and the correlation between local ancestry and genotype.
(A and B) An empirical distribution of the maximum absolute-effect size of local ancestry for each gene-expression trait (betaLA) in the NIGMS dataset (admixed samples, A) and in the GTEx whole-blood dataset (multiethnic samples, B), showing a large effect for a substantial number of genes.
(C) A comparison of the genotype-local-ancestry (LA) correlation and genotype-principal-component (PC) correlation in the NIGMS dataset. The distribution for LA is skewed to the right (or higher values of the correlation), indicating that multi-collinearity, and thus inflated variance of estimated SNP effect size on gene expression [as quantified by the variance inflation factor of the ancestry predictor, ], is a greater problem for LA than for PC.
Using the NIGMS dataset, we showed that the genotype-local-ancestry correlation was significantly higher than the genotype-PC correlation (one-sided Wilcoxon rank sum test, p value < 2.2 × 10−16, Figure 1C). This correlation can lead to inflated variance in the estimated , by the presence of the local ancestry or the global ancestry in equation (4), as quantified by . We identified three SNPs with of local ancestry larger than 10 (dbSNP: rs1314014, dbSNP: rs13313624, and dbSNP: rs186332) but no SNPs from the same threshold for PC. This suggests that multi-collinearity is a greater problem for local ancestry than for PCs, and the confounding due to local ancestry is more likely to happen.
Comparison of Type I Error Rate and Statistical Power
Here, we performed simulations to compare the effects of global-ancestry and local-ancestry adjustment for population structure on the type I error rate (Table 1). We used the actual genotypes of 81 NIGMS AAs and simulated gene expressions that we then associated with the first PC or the average local ancestry of tested genes (see Material and Methods). When the stratification is due to local ancestry (for example, effect size is the maximum of its distribution), the false positive rate is higher in the global-ancestry adjustment than in the local-ancestry adjustment (4.12 × 10−3 > 1.03 × 10−4). The inflation with no adjustment is larger when the stratification is due to local ancestry versus global ancestry (for example, effect size at the 100th percentile, 1.07 × 10−2 > 2.75 × 10−4). As expected, the inflation decreases as the effect size decreases. Importantly, adjusting for global ancestry was insufficient to remove stratification, which might vary at each marker.
Table 1.
Type I Error Rate from Analysis with No Adjustment, Global-Ancestry Adjustment, and Local-Ancestry Adjustment for Population Structure
| Effect Size Percentile | Stratification Source (Effect Size) | No Adjustment | GA Adjustment | LA Adjustment |
|---|---|---|---|---|
| (100% percentile) | GA (57.47) | 2.75 × 10−4 | 9.79 × 10−5 | 1.10 × 10−4 |
| LA (1.13) | 1.07 × 10−2 | 4.12 × 10−3 | 1.03 × 10−4 | |
| (75% percentile) | GA (22.43) | 1.20 × 10−4 | 1.02 × 10−4 | 1.00 × 10−4 |
| LA (0.27) | 2.00 × 10−4 | 1.50 × 10−4 | 1.04 × 10−4 | |
| (50% percentile) | GA (13.40) | 1.05 × 10−4 | 9.85 × 10-5 | 9.83 × 10−5 |
| LA (0.16) | 1.30 × 10−4 | 1.19 × 10−4 | 1.01 × 10−4 | |
| (25% percentile) | GA (6.71) | 1.03 × 10−4 | 9.84 × 10−5 | 1.01 × 10−4 |
| LA (0.07) | 1.07 × 10−4 | 1.03 × 10−4 | 9.84 × 10−5 |
False positives were identified by using p < 1 × 10−4. GA stands for global ancestry and LA stands for local ancestry.
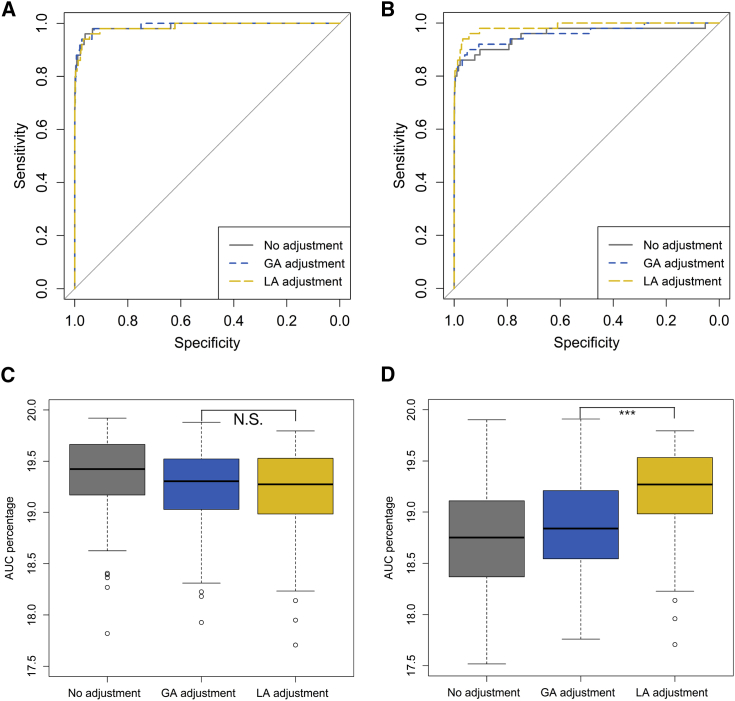
To compare the type II error rate, we again used the actual genotype data and randomly selected SNPs to be causal eQTLs for pre-specified genes. When the gene expression was associated only with the genotype, the areas under the ROC curves for the identification of true eQTLs were similar between the two adjustment methods (Figures 2A and 2C, paired t test of the AUC for a false positive rate in the range 0–0.2 over 100 simulations: Bonferroni-adjusted p value = 0.17). However, when the gene expression was associated with the SNP and its corresponding local ancestry simultaneously, the ROC curve for local-ancestry adjustment was above that for global-ancestry adjustment (Figures 2B and 2D, paired t test of AUC for a false positive rate in the range 0–0.2 over 100 simulations: Bonferroni-adjusted p value = 1.42 × 10−13). Power comparison results show that the two adjustment approaches are equally powerful for identifying true eQTLs, whereas local-ancestry adjustment can substantially increase the power when gene expression changes with local ancestry.
Figure 2.
Power Analysis for eQTL Mapping with Simulated Data Based on the NIGMS Dataset
We simulated the expression of 500 genes and calculated associations with a random sampling of 1,000 SNPs via different methods in order to control for population structure confounding. Among 500,000 associations, we selected 50 SNPs to be true eQTLs.
(A and C) A receiver operating characteristic (ROC) curve (A) and average area under the curve (AUC) for the false positive rate (1-specificity) in the range 0–0.2 (C) across 100 simulations, wherein gene expression was associated with the SNP, showing similar performance (significance was calculated from a paired two-sided t test).
(B and D) A ROC curve (B) and average AUC for the false positive rate (1-specificity) in the range 0–0.2 (D) across 100 simulations, wherein gene expression was associated with both SNP and local ancestry (LA), showing improved performance with LA adjustment.
eQTL Mapping in Admixed Samples
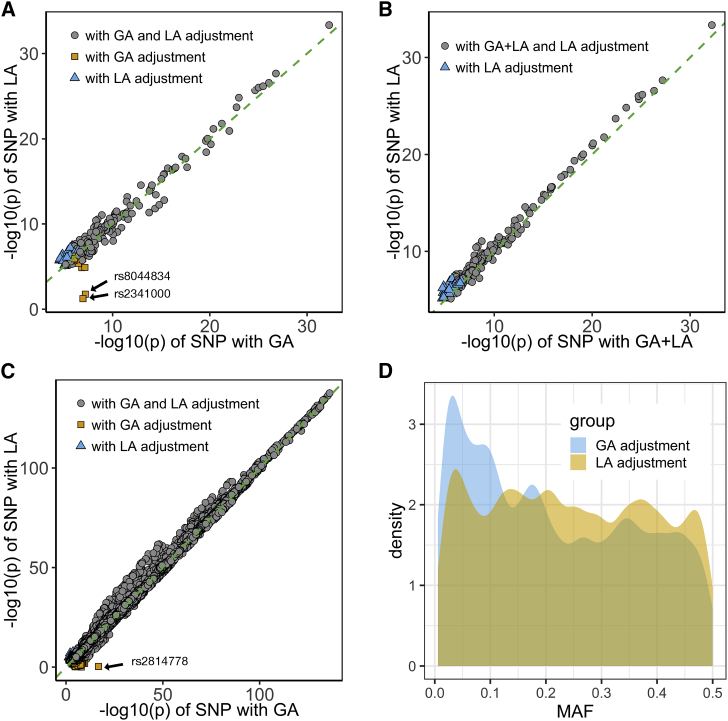
We developed an efficient approach, joint-GaLA-QTLM, to eQTL mapping with local ancestry in a recently admixed population (see Material and Methods). We applied joint-GaLA-QTLM to cis-eQTL mapping in the NIGMS dataset. We adjusted for the top three PCs in the global-ancestry adjustment method, and adjusted for the corresponding local ancestry of each tested SNP in the local-ancestry adjustment method. We used a hierarchical correction method to select significant eQTLs (see Material and Methods). We detected 270 eQTLs with the global-ancestry adjustment method and 277 eQTLs with the local-ancestry adjustment method. Among these eQTLs, 256 were shared by these two methods, whereas 21 and 14 eQTLs were detected only with the local-ancestry and global-ancestry adjustment methods, respectively. We compared the nominal (SNP association) p values from the various methods (Figure 3A). The eQTLs found by both methods were more significant than the eQTLs unique to either method alone, suggesting that both methods were sufficiently powerful to identify significant eQTLs.
Figure 3.
Comparison of eQTL Mapping Conducted with Different Ancestry Adjustment Methods
We performed eQTL mapping by using global-ancestry (GA) and local-ancestry (LA) adjustment in the NIGMS dataset of African Americans (AAs) and the GTEx whole-blood dataset (including European Americans [EAs] and AAs). The NIGMS is a recently admixed sample set, whereas GTEx is a multiethnic sample set, and we sought to compare the approaches in both scenarios. Marked dots in A and C represent eQTLs, whose effect sizes were highly inflated in the GA adjustment method and were potential false positives.
(A) eQTL nominal p values with GA adjustment or LA adjustment in the NIGMS dataset showing potential false positives (marked dots, Figure S1).
(B) eQTL nominal p values with GA + LA adjustment or LA adjustment in the NIGMS dataset, showing that LA adjustment alone (i.e., without the additional adjustment for global ancestry) might suffice.
(C) eQTL nominal p values with GA adjustment or LA adjustment in the GTEx whole-blood dataset showing a potential false positive (marked dot).
(D) A minor allele frequency (MAF) distribution of eQTLs unique to GA or LA adjustment in the GTEx whole-blood dataset showing a higher proportion of low-frequency variants unique to GA adjustment.
We further investigated the eQTLs identified only by one method. Most of these method-specific eQTLs clustered at the margin of statistical significance. However, two eQTLs (dbSNP: rs8044834 with AMFR [MIM: 604343], p value with global-ancestry adjustment: 6.35 × 10−8, p value with local-ancestry adjustment: 1.74 × 10−2; dbSNP: rs2341000 with PLA2G4C [MIM: 603602], p value with global-ancestry adjustment: 1.12 × 10−7, p value with local-ancestry adjustment: 5.81 × 10−2) were highly significant only according to the global-ancestry adjustment (Figure 3A and Table 2). Notably, local ancestry was significantly associated with gene expression at these loci (Table 2), and identified SNPs showed large differentiation in allele frequency between CEU and YRI; thus, we hypothesized that local ancestry confounded the eQTL association, resulting in false positive eQTLs. To test the hypothesis, we evaluated the association between genotype and gene expression in a subsample with two African ancestry alleles and in a HapMap CEU cohort (n = 60), and we found that the eQTL associations were no longer significant (Figure S1). These eQTLs were not significant in the GTEx (v7) LCL eQTL database as well. This highlights the possibility of spurious association between genotype and gene expression in loci where local ancestry is associated with gene expression. Among 21 eQTLs unique to local-ancestry adjustment, 9 were significant (42.86%) in the GTEx LCL eQTL database. For 14 eQTLs that were unique to global-ancestry adjustment, only 1 eQTL was significant (7.14%). The replication rate is significantly higher for eQTLs unique to local-ancestry adjustment than for eQTLs unique to global-ancestry adjustment (chi-square test p value = 2.20 × 10−2).
Table 2.
eQTLs Unique to Global Ancestry Adjustment
| SNP Ref/Alt | Gene | eQTL P Value, No Adjustment | eQTL P Value, GA Adjustment | eQTL P Value, LA Adjustment | LA Association P Value | Alt Allele Frequency in YRI | Alt Allele Frequency in CEU |
|---|---|---|---|---|---|---|---|
| dbSNP: rs8044834 C/T | AMFR | 2.26 × 10−9 | 6.35 × 10−8 | 1.74 × 10−2 | 8.80 × 10−4 | 4% | 58% |
| dbSNP: rs2341000 G/T |
PLA2G4C | 3.01 × 10−8 | 1.12 × 10−7 | 5.81 × 10−2 | 7.17 × 10−3 | 100% | 46% |
| dbSNP: rs2814778 C/T |
ACKR1 | 2.43 × 10−44 | 1.67 × 10−17 | 4.77 × 10−1 | 1.99 × 10−44 | 0% | 99% |
Two eQTLs (dbSNP: rs8044834 and dbSNP: rs2341000) were found to have highly significant associations by the global ancestry (GA) adjustment method, but were non-significant according to the local ancestry (LA) adjustment method in the NIGMS dataset (marked dots in Figure 3A); similarly, one such eQTL (dbSNP: rs2814778) was found in the GTEx whole-blood dataset (marked dot in Figure 3C).
Included in the table are the p values of allelic association tests with no correction for ancestry, with GA adjustment, with LA adjustment, and with the p value of LA in the allelic association with LA adjustment. Allele frequencies are from 1000 Genomes Phase3 data. GA stands for global ancestry and LA stands for local ancestry.
We then compared the results from local-ancestry adjustment with results from alternative methods. We tested the effects of local-ancestry plus global-ancestry adjustment on the cis-eQTL mapping (Figure 3B). Surprisingly, the p values with both adjustments were less significant than those with the local-ancestry adjustment alone for shared eQTLs (Wilcoxon signed rank test: p value = 1.29 × 10−20), suggesting that including PCs as additional adjustment for population structure to local ancestry will reduce power. By using only one or two PCs, we observed a similar pattern as the results based on three PCs (Figures S2A and S2B). We also ran the cis-eQTL analysis that used the LMM approach (implemented in GEMMA) to control for population structure and cryptic relatedness. The GEMMA approach demonstrated higher statistical power compared to local-ancestry adjustment but failed to remove the false positives (Figure S2C).
eQTL Mapping in Multiethnic Samples
Mapping eQTLs in GTEx data allowed us to evaluate the generalizability of our findings on the importance of local-ancestry adjustment in a recently admixed population to multiethnic eQTL studies consisting of both subjects of relatively homogeneous ancestry and individuals of recent admixture. We applied joint-GaLA-QTLM to the GTEx LCL (n = 114) and whole-blood (n = 356) datasets. Consistent with the results in the NIGMS dataset, more eQTLs were identified with local-ancestry adjustment than with global-ancestry adjustment (see Table S1). Nominal p values from local-ancestry adjustment were more significant than those from global-ancestry adjustment (Wilcoxon signed rank test; LCL dataset: p value < 2.2 × 10−16; whole-blood dataset: p value < 2.2 × 10−16, Figure 3C) for shared eQTLs. In the whole-blood dataset, we identified one SNP that was highly significant only according to global-ancestry adjustment (dbSNP: rs2814778 with ACKR1 [MIM: 613665], p value with global-ancestry adjustment: 1.67 × 10−17, p value with local-ancestry adjustment: 4.77 × 10−1), and we found its local ancestry and genotype had perfect correlation, again suggesting potential local ancestry confounding. Notably, eQTLs unique to global-ancestry adjustment were more likely to have a small MAF (MAF < 0.10, chi-square test: p value = 1.69 × 10−135, Figure 3D) than those unique to local ancestry adjustment. Taken together, these results demonstrate the importance of local-ancestry adjustment for cis-eQTL mapping even in samples with a relatively small proportion of admixture.
Empirical Study of PVE by Local Ancestry
We quantified the variance explained by local ancestry with a LMM model, which models a random effect according to the local admixture relatedness between individuals (see Material and Methods). We estimated the distribution of (mean = 0.30, variance = 0.08) in the GTEx AA muscle dataset samples (Figure 4A and Table S2). The range of reliably estimated (FDR < 0.10) was [0.23, 0.99]. Genes with reliable estimates were significantly enriched for differentially expressed genes (see Material and Methods) between AAs and EAs (hypergeometric test: p value = 2.21 × 10−6), suggesting that could be capturing the degree of population differentiation at causal variants, as is also implied by our statistical model. Furthermore, the proportion (0.22) of genes with nominally significant estimates (p < 0.05) was much greater than expected by chance (0.05). The greater proportion of genes with significant estimates than with significant estimates (Table S2) raises the possibility that joint analysis of local ancestry and genetic variation might improve heritability estimation in this population.
Figure 4.
Analysis in African Americans
To determine the variance explained by local ancestry, we estimated for genes in the GTEx skeletal-muscle dataset in African Americans (AAs). The of global ancestry (PC1) from simple linear regression with gene expression did not capture the variance explained by local ancestry.
(A) A distribution of (total of 1,740 genes).
(B) A comparison of and of global ancestry (PC1) from simple linear regression with gene expression.
When genes with reliable estimates were overlapped with the same number of genes selected according to the significance of the association between gene expression and the first PC, we found no shared genes, indicating the extent to which the global ancestry failed to capture the variance explained by the local admixture structure. In GTEx muscle data, from a linear regression of the global ancestry (PC1) with gene expression tended to underestimate the variance explained by local ancestry, (Figure 4B). When we used the local ancestry from the entire genome to construct the genetic relatedness matrix, we identified no genes with reliable estimates (FDR < 0.10), suggesting either that the variation in gene expression was more related to the local, instead of the global, admixture structure or that we were underpowered to obtain a precise estimate (in analogy with estimating the trans-eQTL contribution by using a trans-eQTL-based genetic relatedness matrix [GRM]).
Simulation Studies of Heritability Estimation in an Admixed Population
We designed extensive simulations, which used real and simulated (admixed) genotype data, of diverse genetic architectures (see Material and Methods) to compare three methods for estimating the heritability of gene expression in admixed populations. The first method, simple-LMM, applies restricted maximum likelihood (REML) to obtain an estimate. The second method, LDSR,21 estimates the confounding due to population stratification (from the “intercept”) and the trait heritability (from the “slope”) by regressing the GWAS test statistics on LD scores. We also applied another method, joint-GaLA, which includes a local-ancestry component when estimating the heritability and which was previously introduced in the Material and Methods. In all three methods, we control for global ancestry (PC1) to remove potential confounding due to global ancestry.
In simulations with simulated genotype data, the estimates derived from REML were in line with equation (2∗), analytically derived from the statistical model (Table S3), confirming the expression for the estimate of the expected heritability in the presence of admixture (see Material and Methods). From equation (2∗), the trait variance explained by local ancestry () might therefore be reflecting the fixation index () at causal variants and/or the “tagging” of causal variant effect () on phenotype. Furthermore, the Gaussian approach, versus the (more computationally intensive) mixture model approach, to modeling the effect explained by local ancestry (see Material and Methods) was sufficient to provide accurate estimates (Table S3) consistently across all choices for the number of causal variants.
We simulated gene expression with local ancestry effect (several percentiles chosen from real data to represent different degrees of stratification). estimates from simple-LMM and LDSR, controlling only for global ancestry, tended to suffer from upward bias (Figure 5A), whose magnitude increased with a greater degree of stratification, across the range of numbers of causal variants tested (Figure S3). In all cases, joint-GaLA was closer to the assumed heritability and significantly different from simple-LMM (median values, at 10, 25, 100, 200, and 500 causal variants, of [0.492, 0.507, 0.500, 0.508, and 0.498] versus [0.366, 0.351, 0.309, 0.335, and 0.286] for simple-LMM and joint-GaLA when = 0.2 and = 0.3, respectively; Mann-Whitney U test p < 0.002 for all comparisons between the two methods). Estimates from LDSR showed a significantly larger standard error than estimates from joint-GaLA (Mann-Whitney U test p = 0.008).
Figure 5.
Estimation in Simulations
We performed simulations with real genotype data to evaluate the accuracy of heritability estimation with simple-LMM, joint-GaLA, and LDSR. We assumed the effect of local ancestry on gene expression () was 0.2 (one of several levels of stratification tested, based on empirical data) and varied the number of causal variants.
(A) The assumed heritability was 0.30 and is shown as a dashed horizontal line. The estimates of from simple-LMM were substantially inflated in comparison with those from joint-GaLA and nearly identical to those from LDSR across the range of numbers of causal variants tested. LDSR showed the widest variation in the estimates. Joint-GaLA was closer to the expected heritability than simple-LMM and showed significantly improved estimates for all comparisons (based on number of causal variants; Mann-Whitney U test p < 0.002).
(B) The intercept estimates from LDSR, assuming the same genotype data and a fixed effect of local ancestry on phenotype, showed wide variation.
(C) The estimates for heritability were negatively correlated with the intercept estimates for the amount of stratification. Note the presence of inflated estimates of heritability observed even under low estimated levels of confounding (e.g., near 1 for the intercept).
(D) from global ancestry (PC1), estimated from linear regression, substantially underestimated the trait variance explained by local ancestry across all choices for the number of causal variants. The dashed line shows the expected trait variance explained by local ancestry.
Simple-LMM and LDSR generally gave near-equivalent estimates of heritability across the range of numbers of causal variants tested (Figure 5A), but LDSR estimates had substantially larger variability (Mann-Whitney U test p = 0.008). As an estimate of population confounding, the intercept from LDSR showed wide variation (Figure 5B), and there was a higher estimate of population confounding associated with greater uncertainty (i.e., larger standard error) in the heritability estimate (Spearman’s ρ = 0.56, p = 5.27 × 10−28). The estimates for heritability were negatively correlated (Spearman’s ρ = −0.45, p = 2.45 × 10−17) with the intercept estimates for the amount of confounding, and inflated estimates of heritability were observed even under low estimated levels of confounding (Figure 5C). Note that LDSR, by design, does not provide an estimate for , and because of the wide variation in the estimate for the intercept, we would caution against using the intercept as a proxy for population confounding due to local ancestry.
Furthermore, we found that the from global ancestry, estimated from linear regression, substantially underestimated the trait variance explained by local ancestry across all choices for the number of causal variants (Figure 5D).
Empirical Study of PVE by Genetic Variation in an Admixed Population
We utilized the GTEx skeletal-muscle data to gain further insights into (see Material and Methods) in the largest amount of RNA-seq and whole-genome sequencing data that was available to us for AAs. With simple-LMM, we estimated the distribution of in the AA samples (mean = 0.30, variance = 0.05) and in the EA samples (mean = 0.25, variance = 0.04) of the same sample size (Figure 6A). Table S2 contains summary data on the estimates in the two populations in this tissue, and Table S4 contains all estimates. We identified genes with nominally significant estimates (defined as p value < 0.05) in one population but not in the other, suggesting population-specific regulation. The comparison of for genes with nominally significant estimates in both populations showed a modest but significant correlation (Spearman’s ρ = 0.33, p value = 1.28 × 10−7; Figure 6B). At a more stringent threshold (FDR < 0.10), we continued to observe a significant correlation (Spearman’s ρ = 0.44, p value = 0.01; Figure S4). We found no significant correlation between and (Spearman’s ρ = 0.04, p value = 0.21; Figure 6C) in AA samples, suggesting the independence of these two components.
Figure 6.
Analysis in European Americans and African Americans
We estimated the for gene expression traits in the GTEx skeletal-muscle dataset for African Americans (AAs) and an equal sample size (n = 57) of European Americans (EAs) separately. Although there was a significant correlation in between the populations, many genes with nominally significant estimates (p value < 0.05) were discordant between the populations (B). We investigated the contribution of variance in genetic relatedness (D), effect size (E), and allele frequency (F) to the population specificity of . A comparison of and showed low correlation across the genes. We then fitted, for each gene, a joint model (joint-GaLA) consisting of both genetic variation and local ancestry to estimate the change in the estimate for . Most genes showed a decreased estimate for with the incorporation of local ancestry into the model, suggesting that local ancestry might explain some of the gene expression variation.
(A) A distribution of in AAs and EAs (total of 8,832 and 8,670 genes in AAs and EAs, respectively).
(B) A comparison of among genes with nominally significant estimates (p value < 0.05) in both AAs and EAs (total of 253 genes); the comparison shows a significant correlation. A similar result is observed at a false discovery rate (FDR) < 0.1 (Figure S4).
(C) A comparison of and (points are color-coded according to the FDR for ).
(D) A comparison of the variance of the local genetic relatedness between AAs and EAs for all 19,850 genes; EAs show significantly greater variance (from a one-sided Wilcoxon signed rank test, p value < 2.2 × 10−16).
(E) An example of a gene, ZCCHC24, for which local SNPs have an opposite allelic direction between EAs and AAs. (The gene is not differentially expressed between the two populations.) The black dashed line is a fitted regression line.
(F) An example of a gene, DDT, for which SNPs associated with expression level (nominal p value < 0.05 from LMM association in either population) are population differentiated in allele frequency. The black dashed line is a fitted regression line.
(G) A comparison of between simple-LMM and joint-GaLA.
We investigated the possible sources of the imperfect correlation in the estimated . The variance in genetic relatedness can be written as the sum of LD correlation over all pairs of SNPs that make up the GRM (see Material and Methods).35 The difference, estimated using the variance in the GRM (Figure 6D), between the two populations in local LD pattern near each gene can influence the estimated standard error of . We provide two examples to illustrate additional reasons for the population difference. LMM association analysis of the gene ZCCHC24 ( in AAs: 0.85, p value = 1.23 × 10−2; in EAs: 0.29, p value = 4.36 × 10−2) showed that the effect sizes of local SNPs were negatively correlated between the two populations (Spearman’s ρ = −0.23, p value = 1.52 × 10−36; Figure 6E), suggesting population-dependent regulation with an opposite allelic direction. We compared the allele frequency of SNPs associated with DDT (MIM: 602750), expression (nominal p value < 0.05 in either population) between EAs and AAs (in AAs: 0.93, p value = 2.46 × 10−4; in EAs: 0.46, p value = 7.11 × 10−3) and found no evidence for correlation (Spearman’s ρ = 0.09, p value = 0.23; Figure 6F). In both examples, although the gene had a significant in both populations, the gene was nevertheless associated with a different set of variants (which were not in LD) in the different populations, suggesting alternative genetic regulation. For example, among the 50 SNPs that were associated with ZCCHG24 expression in EAs, only 5 were in LD (LD > 0.8) with associated SNPs in AAs. Finally, the polygenicity or sparsity of gene expression, which we explore in the next section, might differ for a given gene in the two populations.
We finally applied joint-GaLA in the GTEx AA samples. Interestingly, we found that the estimates from the simple-LMM model (see Material and Methods) tended to be inflated in comparison with the estimates from the joint-GaLA model (Figure 6G). This is consistent with simulations, in which joint-GaLA outperformed simple-LMM across all choices of number of causal variants when local ancestry contributed to the variance in phenotype.
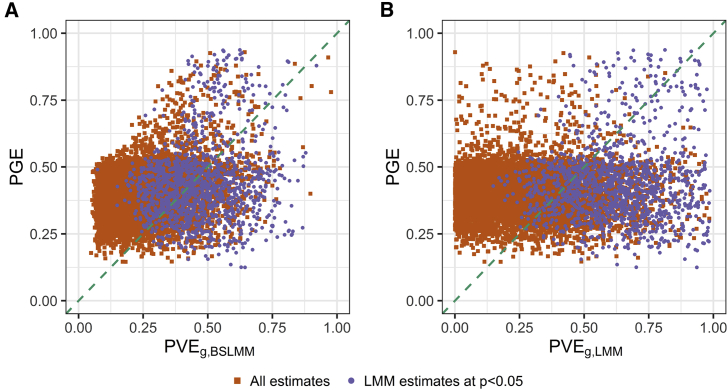
Sparsity or Polygenicity of Gene Expression in an Admixed Population
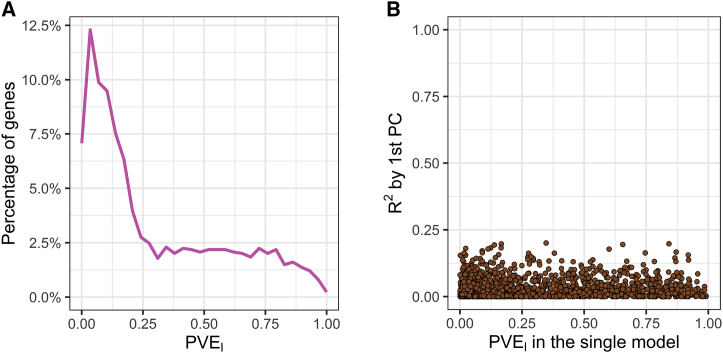
We sought to characterize the sparsity or polygenicity of gene expression traits in this admixed population and compared the results of the PVE analysis from the LMM approach (see Material and Methods), which is suitable for infinitesimal genetic architectures, and from a BSLMM (all estimates in Table S5), which assumes a mixture distribution of effect sizes. The two approaches were highly correlated in their estimate of the polygenic component (Spearman’s ρ = 0.82 between BSLMM-derived and LMM-derived , p value < 2.2 × 10−16) (Figure S5). Nevertheless, we also identified genes for which BSLMM analysis showed a highly sparse local genetic architecture, i.e., genes with high estimated PGE (the proportion of gene expression variance explained by sparse genetic effects) and also high estimated (Figure 7A). Furthermore, the estimated total sparse genetic effect PGE was largely independent of the estimated total polygenic effect across all genes tested, as well as across all genes with a nominally significant estimate of (cor = 0.076; Figure 7B).
Figure 7.
Sparsity and Polygenicity of Gene Expression in African Americans
We characterized the sparsity or polygenicity of gene expression traits by using a Bayesian sparse linear mixed model (BSLMM) analysis in the GTEx African American (AA) skeletal-muscle data. We estimated the proportion of variance in gene expression that can be explained by sparse effects () and the proportion of variance in gene expression that can be explained by sparse effects and random effects together (), the latter of which is most equivalent to our LMM-based . In the genes analyzed, estimated values that were significant at p value < 0.05 were defined as nominally significant estimates.
A. The comparison of and the estimate from the BSLMM. Genes with a large and a large estimate are likely to have highly sparse local genetic architecture.
B. The comparison of from GCTA and the estimate from the BSLMM showing the independence of the two components.
Discussion
This study evaluated the use of local ancestry in the analysis of genetic regulation of gene expression in an admixed population through simulations and in real datasets. We developed a statistical model that allowed us to analytically formulate the relationships among global ancestry, the level of population differentiation at a causal eQTL, the trait variance explained by local ancestry, and the eQTL effect size. The model provides insights into potential bias sources, including the degree of population differentiation and the uncertainty in local ancestry estimation, in the estimated regulatory effect of genetic variation on gene expression. We extended this framework to the study of multiple causal eQTL variants. As a corollary of the model, characterization of gene expression in terms of sparsity or polygenicity has important implications for estimating the phenotypic variance explained by local or global ancestry. Hence, we quantified the sparse genetic component and the polygenic component of gene expression in a recently admixed population, though this analysis was limited to a single tissue. Multi-tissue studies in a much larger sample size should facilitate additional insights into genetic architecture.
We performed a comprehensive analysis of the variance explained by local ancestry around each gene and across the genome to gene expression variation. In simulations with different degrees of stratification—informed by empirical data—due to local ancestry, an approach that incorporated local ancestry into the heritability estimation (as in joint-GaLA) provided a more accurate estimate of heritability in an admixed population than a naive approach (as in simple-LMM) that controlled only for global ancestry (e.g., as quantified by principal components). In these simulations, simple-LMM and LDSR provided near-equivalent estimates of heritability. Both methods showed upward bias when controlling only for global ancestry in the presence of local ancestry stratification, although LDSR had significantly larger standard errors. Furthermore, the LDSR intercept, a measure of population confounding, showed wide variation and a higher estimated level of confounding significantly associated with a greater degree of uncertainty in the estimate. Finally, under stratification, the estimated amount of confounding was found to be significantly (negatively) correlated with the estimated heritability in LDSR, indicating inflated estimates of heritability (slope) despite low reported levels of population confounding (intercept). As another corollary, the confounding can distort cross-population analyses of the contribution of genetic variants to variation in gene expression. In particular, studies, in which one of the populations is admixed, that investigate the population specificity or sharedness of regulatory effects without taking into account local ancestry might suffer from this confounding. Given their diminished assumed level of stratification due to local ancestry in simulated genotype data, joint-GaLA and simple-LMM approached near-identical estimates of heritability, and LDSR, given its equivalence with simple-LMM, would facilitate more reliable heritability estimation in this more controlled context.
Applying estimation to real data, we observed a modest but significant correlation in estimated overall genetic effect between the populations, suggesting the existence of “shared regulatory architecture” for a number of genes. We investigated several factors underlying the population specificity of . The standard error of the estimate is closely related to the LD structure; thus, local ancestry transitions present challenges for PVE analysis in recently admixed populations. Indeed, as our statistical model implies, local ancestry transitions can contribute to population differences in the estimated . Furthermore, our study would suggest that PVE estimation methods that explicitly incorporate LD adjustment might yield larger power.39 Given the small sample size, for nearly half of expressed genes (33.38% in AAs and 45.32% in EAs) we could not obtain estimates because the phenotypic variance-covariance matrix is not positive definite. This observation demonstrates the necessity of a large sample size for PVE analysis, even for intermediate (e.g., molecular) phenotypes.
We developed an R package, LAMatrix, which adjusts for local ancestry in eQTL mapping and implements joint-GaLA-QTLM in a computationally efficient framework. Our implementation can be exploited in studies that incorporate a SNP-level covariate (e.g., epigenetic marker or structural variant), and this might prove crucial in disentangling the influences of various factors on a cellular phenotype. We illustrated with simulations that type I and type II errors will be inflated when gene expression is associated with local ancestry; this result was observed for a substantial number of genes in both admixed samples and multiethnic samples. The application of joint-GaLA-QTLM to the NIGMS dataset (admixed) and GTEx whole-blood and LCL datasets (multiethnic) showed that our approach displayed greater power to identify eQTLs than the prevailing approach that adjusts for global ancestry. In the GTEx whole-blood study, more eQTLs unique to GA adjustment have a small MAF, which is vulnerable to false positives,33 again supporting that the proposed local-ancestry adjustment is more powerful for identifying true eQTLs. One limitation of our study is that the joint-GaLA-QTLM and joint-GaLA methods apply to an admixed population with two ancestral populations. Future studies should extend the method to more heterogeneous populations (e.g., Hispanics/Latinos).
Discovery of genomics biomarkers and causative genetic variants has been slow in admixed populations, leading to a growing disparity in genomic medicine. Some of this disparity is due to the paucity of omics data in these populations, but just as important is the lack of adequate statistical methodologies needed to account for the complexity of the genomes. We provide here a comprehensive study of the population specificity of the genetic regulation of gene expression, both in aggregate across the cis region of a gene and at a single variant within this region. We show that the use of local ancestry can improve the identification of regulatory variants (QTL mapping) and the estimation of their total effect (heritability estimation), and this has broad implications for genetic studies of complex traits. Taken together, these results extend existing approaches and provide a framework for future large-scale studies of genetic regulation of gene expression in multiethnic or admixed samples.
Declaration of Interests
The authors declare no competing interests.
Acknowledgments
We would like to thank Yuan Li and Yinan Zheng for advice on software development. We thank Tanima De, Zhou Zhang, Yiben Yang, and Jun Xiong for helpful discussion. E.R.G. benefited immensely from a fellowship at Clare Hall, University of Cambridge while holding a visiting post in the Medical Research Council (MRC) Epidemiology Unit and MRC Biostatistics Unit, Cambridge, UK. We would like to thank the Genotype-Tissue Expression (GTEx) Project, an initiative supported by the Common Fund of the Office of the Director of the National Institutes of Health (NIH), and by the National Cancer Institute (NCI), the National Human Genome Research Institute (NHGRI), the National Heart, Lung, and Blood Institute (NHLBI), the National Institute on Drug Abuse (NIDA), the National Institute of Mental Health (NIMH), and the National Institute of Neurological Disorders and Stroke (NINDS), for making the data available to the scientific community. This work was supported by National Institutes of Health (NIH)/National Institute on Minority Health and Health Disparities (NIMHD) grants R01 MD009217 and U54 MD010723. E.R.G. acknowledges support from R01 MH101820 and R01 MH090937.
Published: May 16, 2019
Footnotes
Supplemental Data can be found online at https://doi.org/10.1016/j.ajhg.2019.04.009.
Web Resources
Online Mendelian Inheritance in Man: https://www.omim.org/
Supplemental Data
References
- 1.Albert F.W., Kruglyak L. The role of regulatory variation in complex traits and disease. Nat. Rev. Genet. 2015;16:197–212. doi: 10.1038/nrg3891. [DOI] [PubMed] [Google Scholar]; Albert, F.W., and Kruglyak, L. (2015). The role of regulatory variation in complex traits and disease. Nat. Rev. Genet. 16, 197-212. [DOI] [PubMed]
- 2.Battle A., Brown C.D., Engelhardt B.E., Montgomery S.B., Getz G., Hadley K., Handsaker R.E., Huang K.H., Kashin S., Karczewski K.J., GTEx Consortium. Laboratory, Data Analysis &Coordinating Center (LDACC)—Analysis Working Group. Statistical Methods groups—Analysis Working Group. Enhancing GTEx (eGTEx) groups. NIH Common Fund. NIH/NCI. NIH/NHGRI. NIH/NIMH. NIH/NIDA. Biospecimen Collection Source Site—NDRI. Biospecimen Collection Source Site—RPCI. Biospecimen Core Resource—VARI. Brain Bank Repository—University of Miami Brain Endowment Bank. Leidos Biomedical—Project Management. ELSI Study. Genome Browser Data Integration &Visualization—EBI. Genome Browser Data Integration &Visualization—UCSC Genomics Institute, University of California Santa Cruz. Lead analysts. Laboratory, Data Analysis &Coordinating Center (LDACC) NIH program management. Biospecimen collection. Pathology. eQTL manuscript working group Genetic effects on gene expression across human tissues. Nature. 2017;550:204–213. [Google Scholar]; Battle, A., Brown, C.D., Engelhardt, B.E., Montgomery, S.B., Getz, G., Hadley, K., Handsaker, R.E., Huang, K.H., Kashin, S., and Karczewski, K.J.; GTEx Consortium; Laboratory, Data Analysis &Coordinating Center (LDACC)-Analysis Working Group; Statistical Methods groups-Analysis Working Group; Enhancing GTEx (eGTEx) groups; NIH Common Fund; NIH/NCI; NIH/NHGRI; NIH/NIMH; NIH/NIDA; Biospecimen Collection Source Site-NDRI; Biospecimen Collection Source Site-RPCI; Biospecimen Core Resource-VARI; Brain Bank Repository-University of Miami Brain Endowment Bank; Leidos Biomedical-Project Management; ELSI Study; Genome Browser Data Integration &Visualization-EBI; Genome Browser Data Integration &Visualization-UCSC Genomics Institute, University of California Santa Cruz; Lead analysts; Laboratory, Data Analysis &Coordinating Center (LDACC); NIH program management; Biospecimen collection; Pathology; eQTL manuscript working group (2017). Genetic effects on gene expression across human tissues. Nature 550, 204-213.
- 3.Hindorff L.A., Sethupathy P., Junkins H.A., Ramos E.M., Mehta J.P., Collins F.S., Manolio T.A. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. USA. 2009;106:9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]; Hindorff, L.A., Sethupathy, P., Junkins, H.A., Ramos, E.M., Mehta, J.P., Collins, F.S., and Manolio, T.A. (2009). Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. USA 106, 9362-9367. [DOI] [PMC free article] [PubMed]
- 4.Storey J.D., Madeoy J., Strout J.L., Wurfel M., Ronald J., Akey J.M. Gene-expression variation within and among human populations. Am. J. Hum. Genet. 2007;80:502–509. doi: 10.1086/512017. [DOI] [PMC free article] [PubMed] [Google Scholar]; Storey, J.D., Madeoy, J., Strout, J.L., Wurfel, M., Ronald, J., and Akey, J.M. (2007). Gene-expression variation within and among human populations. Am. J. Hum. Genet. 80, 502-509. [DOI] [PMC free article] [PubMed]
- 5.Stranger B.E., Montgomery S.B., Dimas A.S., Parts L., Stegle O., Ingle C.E., Sekowska M., Smith G.D., Evans D., Gutierrez-Arcelus M. Patterns of cis regulatory variation in diverse human populations. PLoS Genet. 2012;8:e1002639. doi: 10.1371/journal.pgen.1002639. [DOI] [PMC free article] [PubMed] [Google Scholar]; Stranger, B.E., Montgomery, S.B., Dimas, A.S., Parts, L., Stegle, O., Ingle, C.E., Sekowska, M., Smith, G.D., Evans, D., Gutierrez-Arcelus, M., et al. (2012). Patterns of cis regulatory variation in diverse human populations. PLoS Genet. 8, e1002639. [DOI] [PMC free article] [PubMed]
- 6.Zhang W., Duan S., Kistner E.O., Bleibel W.K., Huang R.S., Clark T.A., Chen T.X., Schweitzer A.C., Blume J.E., Cox N.J., Dolan M.E. Evaluation of genetic variation contributing to differences in gene expression between populations. Am. J. Hum. Genet. 2008;82:631–640. doi: 10.1016/j.ajhg.2007.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]; Zhang, W., Duan, S., Kistner, E.O., Bleibel, W.K., Huang, R.S., Clark, T.A., Chen, T.X., Schweitzer, A.C., Blume, J.E., Cox, N.J., and Dolan, M.E. (2008). Evaluation of genetic variation contributing to differences in gene expression between populations. Am. J. Hum. Genet. 82, 631-640. [DOI] [PMC free article] [PubMed]
- 7.Sajuthi S.P., Sharma N.K., Chou J.W., Palmer N.D., McWilliams D.R., Beal J., Comeau M.E., Ma L., Calles-Escandon J., Demons J. Mapping adipose and muscle tissue expression quantitative trait loci in African Americans to identify genes for type 2 diabetes and obesity. Hum. Genet. 2016;135:869–880. doi: 10.1007/s00439-016-1680-8. [DOI] [PMC free article] [PubMed] [Google Scholar]; Sajuthi, S.P., Sharma, N.K., Chou, J.W., Palmer, N.D., McWilliams, D.R., Beal, J., Comeau, M.E., Ma, L., Calles-Escandon, J., Demons, J., et al. (2016). Mapping adipose and muscle tissue expression quantitative trait loci in African Americans to identify genes for type 2 diabetes and obesity. Hum. Genet. 135, 869-880. [DOI] [PMC free article] [PubMed]
- 8.Auton A., Brooks L.D., Durbin R.M., Garrison E.P., Kang H.M., Korbel J.O., Marchini J.L., McCarthy S., McVean G.A., Abecasis G.R., 1000 Genomes Project Consortium A global reference for human genetic variation. Nature. 2015;526:68–74. doi: 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]; Auton, A., Brooks, L.D., Durbin, R.M., Garrison, E.P., Kang, H.M., Korbel, J.O., Marchini, J.L., McCarthy, S., McVean, G.A., and Abecasis, G.R.; 1000 Genomes Project Consortium (2015). A global reference for human genetic variation. Nature 526, 68-74. [DOI] [PMC free article] [PubMed]
- 9.Martin A.R., Gignoux C.R., Walters R.K., Wojcik G.L., Neale B.M., Gravel S., Daly M.J., Bustamante C.D., Kenny E.E. Human demographic history impacts genetic risk prediction across diverse populations. Am. J. Hum. Genet. 2017;100:635–649. doi: 10.1016/j.ajhg.2017.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]; Martin, A.R., Gignoux, C.R., Walters, R.K., Wojcik, G.L., Neale, B.M., Gravel, S., Daly, M.J., Bustamante, C.D., and Kenny, E.E. (2017). Human demographic history impacts genetic risk prediction across diverse populations. Am. J. Hum. Genet. 100, 635-649. [DOI] [PMC free article] [PubMed]
- 10.Shabalin A.A. Matrix eQTL: Ultra fast eQTL analysis via large matrix operations. Bioinformatics. 2012;28:1353–1358. doi: 10.1093/bioinformatics/bts163. [DOI] [PMC free article] [PubMed] [Google Scholar]; Shabalin, A.A. (2012). Matrix eQTL: Ultra fast eQTL analysis via large matrix operations. Bioinformatics 28, 1353-1358. [DOI] [PMC free article] [PubMed]
- 11.Price A.L., Tandon A., Patterson N., Barnes K.C., Rafaels N., Ruczinski I., Beaty T.H., Mathias R., Reich D., Myers S. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 2009;5:e1000519. doi: 10.1371/journal.pgen.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]; Price, A.L., Tandon, A., Patterson, N., Barnes, K.C., Rafaels, N., Ruczinski, I., Beaty, T.H., Mathias, R., Reich, D., and Myers, S. (2009). Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 5, e1000519. [DOI] [PMC free article] [PubMed]
- 12.Maples B.K., Gravel S., Kenny E.E., Bustamante C.D. RFMix: A discriminative modeling approach for rapid and robust local-ancestry inference. Am. J. Hum. Genet. 2013;93:278–288. doi: 10.1016/j.ajhg.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]; Maples, B.K., Gravel, S., Kenny, E.E., and Bustamante, C.D. (2013). RFMix: A discriminative modeling approach for rapid and robust local-ancestry inference. Am. J. Hum. Genet. 93, 278-288. [DOI] [PMC free article] [PubMed]
- 13.Patterson N., Price A.L., Reich D. Population structure and eigenanalysis. PLoS Genet. 2006;2:e190. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]; Patterson, N., Price, A.L., and Reich, D. (2006). Population structure and eigenanalysis. PLoS Genet. 2, e190. [DOI] [PMC free article] [PubMed]
- 14.Price A.L., Patterson N.J., Plenge R.M., Weinblatt M.E., Shadick N.A., Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]; Price, A.L., Patterson, N.J., Plenge, R.M., Weinblatt, M.E., Shadick, N.A., and Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38, 904-909. [DOI] [PubMed]
- 15.Novembre J., Johnson T., Bryc K., Kutalik Z., Boyko A.R., Auton A., Indap A., King K.S., Bergmann S., Nelson M.R. Genes mirror geography within Europe. Nature. 2008;456:98–101. doi: 10.1038/nature07331. [DOI] [PMC free article] [PubMed] [Google Scholar]; Novembre, J., Johnson, T., Bryc, K., Kutalik, Z., Boyko, A.R., Auton, A., Indap, A., King, K.S., Bergmann, S., Nelson, M.R., et al. (2008). Genes mirror geography within Europe. Nature 456, 98-101. [DOI] [PMC free article] [PubMed]
- 16.Yu J., Pressoir G., Briggs W.H., Vroh Bi I., Yamasaki M., Doebley J.F., McMullen M.D., Gaut B.S., Nielsen D.M., Holland J.B. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006;38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]; Yu, J., Pressoir, G., Briggs, W.H., Vroh Bi, I., Yamasaki, M., Doebley, J.F., McMullen, M.D., Gaut, B.S., Nielsen, D.M., Holland, J.B., et al. (2006). A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38, 203-208. [DOI] [PubMed]
- 17.Price A.L., Zaitlen N.A., Reich D., Patterson N. New approaches to population stratification in genome-wide association studies. Nat. Rev. Genet. 2010;11:459–463. doi: 10.1038/nrg2813. [DOI] [PMC free article] [PubMed] [Google Scholar]; Price, A.L., Zaitlen, N.A., Reich, D., and Patterson, N. (2010). New approaches to population stratification in genome-wide association studies. Nat. Rev. Genet. 11, 459-463. [DOI] [PMC free article] [PubMed]
- 18.Sankararaman S., Sridhar S., Kimmel G., Halperin E. Estimating local ancestry in admixed populations. Am. J. Hum. Genet. 2008;82:290–303. doi: 10.1016/j.ajhg.2007.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]; Sankararaman, S., Sridhar, S., Kimmel, G., and Halperin, E. (2008). Estimating local ancestry in admixed populations. Am. J. Hum. Genet. 82, 290-303. [DOI] [PMC free article] [PubMed]
- 19.Wang X., Zhu X., Qin H., Cooper R.S., Ewens W.J., Li C., Li M. Adjustment for local ancestry in genetic association analysis of admixed populations. Bioinformatics. 2011;27:670–677. doi: 10.1093/bioinformatics/btq709. [DOI] [PMC free article] [PubMed] [Google Scholar]; Wang, X., Zhu, X., Qin, H., Cooper, R.S., Ewens, W.J., Li, C., and Li, M. (2011). Adjustment for local ancestry in genetic association analysis of admixed populations. Bioinformatics 27, 670-677. [DOI] [PMC free article] [PubMed]
- 20.Qin H., Morris N., Kang S.J., Li M., Tayo B., Lyon H., Hirschhorn J., Cooper R.S., Zhu X. Interrogating local population structure for fine mapping in genome-wide association studies. Bioinformatics. 2010;26:2961–2968. doi: 10.1093/bioinformatics/btq560. [DOI] [PMC free article] [PubMed] [Google Scholar]; Qin, H., Morris, N., Kang, S.J., Li, M., Tayo, B., Lyon, H., Hirschhorn, J., Cooper, R.S., and Zhu, X. (2010). Interrogating local population structure for fine mapping in genome-wide association studies. Bioinformatics 26, 2961-2968. [DOI] [PMC free article] [PubMed]
- 21.Bulik-Sullivan B.K., Loh P.R., Finucane H.K., Ripke S., Yang J., Patterson N., Daly M.J., Price A.L., Neale B.M., Schizophrenia Working Group of the Psychiatric Genomics Consortium LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 2015;47:291–295. doi: 10.1038/ng.3211. [DOI] [PMC free article] [PubMed] [Google Scholar]; Bulik-Sullivan, B.K., Loh, P.R., Finucane, H.K., Ripke, S., Yang, J., Patterson, N., Daly, M.J., Price, A.L., and Neale, B.M.; Schizophrenia Working Group of the Psychiatric Genomics Consortium (2015). LD Score regression distinguishes confounding from polygenicity in genome-wide association studies. Nat. Genet. 47, 291-295. [DOI] [PMC free article] [PubMed]
- 22.Wheeler H.E., Shah K.P., Brenner J., Garcia T., Aquino-Michaels K., Cox N.J., Nicolae D.L., Im H.K., Im H.K., GTEx Consortium Survey of the heritability and sparse architecture of gene expression traits across human tissues. PLoS Genet. 2016;12:e1006423. doi: 10.1371/journal.pgen.1006423. [DOI] [PMC free article] [PubMed] [Google Scholar]; Wheeler, H.E., Shah, K.P., Brenner, J., Garcia, T., Aquino-Michaels, K., Cox, N.J., Nicolae, D.L., Im, H.K., and Im, H.K.; GTEx Consortium (2016). Survey of the heritability and sparse architecture of gene expression traits across human tissues. PLoS Genet. 12, e1006423. [DOI] [PMC free article] [PubMed]
- 23.Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M.A., Bender D., Maller J., Sklar P., de Bakker P.I., Daly M.J., Sham P.C. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]; Purcell, S., Neale, B., Todd-Brown, K., Thomas, L., Ferreira, M.A., Bender, D., Maller, J., Sklar, P., de Bakker, P.I., Daly, M.J., and Sham, P.C. (2007). PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559-575. [DOI] [PMC free article] [PubMed]
- 24.Delaneau O., Marchini J., Zagury J.F. A linear complexity phasing method for thousands of genomes. Nat. Methods. 2011;9:179–181. doi: 10.1038/nmeth.1785. [DOI] [PubMed] [Google Scholar]; Delaneau, O., Marchini, J., and Zagury, J.F. (2011). A linear complexity phasing method for thousands of genomes. Nat. Methods 9, 179-181. [DOI] [PubMed]
- 25.Price A.L., Patterson N., Hancks D.C., Myers S., Reich D., Cheung V.G., Spielman R.S. Effects of cis and trans genetic ancestry on gene expression in African Americans. PLoS Genet. 2008;4:e1000294. doi: 10.1371/journal.pgen.1000294. [DOI] [PMC free article] [PubMed] [Google Scholar]; Price, A.L., Patterson, N., Hancks, D.C., Myers, S., Reich, D., Cheung, V.G., and Spielman, R.S. (2008). Effects of cis and trans genetic ancestry on gene expression in African Americans. PLoS Genet. 4, e1000294. [DOI] [PMC free article] [PubMed]
- 26.Zaitlen N., Pasaniuc B., Sankararaman S., Bhatia G., Zhang J., Gusev A., Young T., Tandon A., Pollack S., Vilhjálmsson B.J. Leveraging population admixture to characterize the heritability of complex traits. Nat. Genet. 2014;46:1356–1362. doi: 10.1038/ng.3139. [DOI] [PMC free article] [PubMed] [Google Scholar]; Zaitlen, N., Pasaniuc, B., Sankararaman, S., Bhatia, G., Zhang, J., Gusev, A., Young, T., Tandon, A., Pollack, S., Vilhjalmsson, B.J., et al. (2014). Leveraging population admixture to characterize the heritability of complex traits. Nat. Genet. 46, 1356-1362. [DOI] [PMC free article] [PubMed]
- 27.GTEx Consortium Human genomics. The Genotype-Tissue Expression (GTEx) pilot analysis: Multitissue gene regulation in humans. Science. 2015;348:648–660. doi: 10.1126/science.1262110. [DOI] [PMC free article] [PubMed] [Google Scholar]; GTEx Consortium (2015). Human genomics. The Genotype-Tissue Expression (GTEx) pilot analysis: Multitissue gene regulation in humans. Science 348, 648-660. [DOI] [PMC free article] [PubMed]
- 28.Bhatia G., Patterson N., Sankararaman S., Price A.L. Estimating and interpreting FST: The impact of rare variants. Genome Res. 2013;23:1514–1521. doi: 10.1101/gr.154831.113. [DOI] [PMC free article] [PubMed] [Google Scholar]; Bhatia, G., Patterson, N., Sankararaman, S., and Price, A.L. (2013). Estimating and interpreting FST: The impact of rare variants. Genome Res. 23, 1514-1521. [DOI] [PMC free article] [PubMed]
- 29.Zhou X., Carbonetto P., Stephens M. Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet. 2013;9:e1003264. doi: 10.1371/journal.pgen.1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]; Zhou, X., Carbonetto, P., and Stephens, M. (2013). Polygenic modeling with Bayesian sparse linear mixed models. PLoS Genet. 9, e1003264. [DOI] [PMC free article] [PubMed]
- 30.Gamazon E.R., Wheeler H.E., Shah K.P., Mozaffari S.V., Aquino-Michaels K., Carroll R.J., Eyler A.E., Denny J.C., Nicolae D.L., Cox N.J., Im H.K., GTEx Consortium A gene-based association method for mapping traits using reference transcriptome data. Nat. Genet. 2015;47:1091–1098. doi: 10.1038/ng.3367. [DOI] [PMC free article] [PubMed] [Google Scholar]; Gamazon, E.R., Wheeler, H.E., Shah, K.P., Mozaffari, S.V., Aquino-Michaels, K., Carroll, R.J., Eyler, A.E., Denny, J.C., Nicolae, D.L., Cox, N.J., and Im, H.K.; GTEx Consortium (2015). A gene-based association method for mapping traits using reference transcriptome data. Nat. Genet. 47, 1091-1098. [DOI] [PMC free article] [PubMed]
- 31.Wen X., Pique-Regi R., Luca F. Integrating molecular QTL data into genome-wide genetic association analysis: Probabilistic assessment of enrichment and colocalization. PLoS Genet. 2017;13:e1006646. doi: 10.1371/journal.pgen.1006646. [DOI] [PMC free article] [PubMed] [Google Scholar]; Wen, X., Pique-Regi, R., and Luca, F. (2017). Integrating molecular QTL data into genome-wide genetic association analysis: Probabilistic assessment of enrichment and colocalization. PLoS Genet. 13, e1006646. [DOI] [PMC free article] [PubMed]
- 32.Yang J., Lee S.H., Goddard M.E., Visscher P.M. GCTA: A tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]; Yang, J., Lee, S.H., Goddard, M.E., and Visscher, P.M. (2011). GCTA: A tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88, 76-82. [DOI] [PMC free article] [PubMed]
- 33.Stegle O., Parts L., Durbin R., Winn J. A Bayesian framework to account for complex non-genetic factors in gene expression levels greatly increases power in eQTL studies. PLoS Comput. Biol. 2010;6:e1000770. doi: 10.1371/journal.pcbi.1000770. [DOI] [PMC free article] [PubMed] [Google Scholar]; Stegle, O., Parts, L., Durbin, R., and Winn, J. (2010). A Bayesian framework to account for complex non-genetic factors in gene expression levels greatly increases power in eQTL studies. PLoS Comput. Biol. 6, e1000770. [DOI] [PMC free article] [PubMed]
- 34.Benjamini Y., Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B. 1995;57:289–300. [Google Scholar]; Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289-300.
- 35.Visscher P.M., Goddard M.E. A general unified framework to assess the sampling variance of heritability estimates using pedigree or marker-based relationships. Genetics. 2015;199:223–232. doi: 10.1534/genetics.114.171017. [DOI] [PMC free article] [PubMed] [Google Scholar]; Visscher, P.M., and Goddard, M.E. (2015). A general unified framework to assess the sampling variance of heritability estimates using pedigree or marker-based relationships. Genetics 199, 223-232. [DOI] [PMC free article] [PubMed]
- 36.Robin X., Turck N., Hainard A., Tiberti N., Lisacek F., Sanchez J.-C., Müller M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [PMC free article] [PubMed] [Google Scholar]; Robin, X., Turck, N., Hainard, A., Tiberti, N., Lisacek, F., Sanchez, J.-C., and Muller, M. (2011). pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics 12, 77. [DOI] [PMC free article] [PubMed]
- 37.Huang Q.Q., Ritchie S.C., Brozynska M., Inouye M. Power, false discovery rate and Winner’s Curse in eQTL studies. Nucleic Acids Res. 2018;46:e133. doi: 10.1093/nar/gky780. [DOI] [PMC free article] [PubMed] [Google Scholar]; Huang, Q.Q., Ritchie, S.C., Brozynska, M., and Inouye, M. (2018). Power, false discovery rate and Winner’s Curse in eQTL studies. Nucleic Acids Res. 46, e133. [DOI] [PMC free article] [PubMed]
- 38.Benjamini Y., Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001;29:1165–1188. [Google Scholar]; Benjamini, Y., and Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 29, 1165-1188.
- 39.Speed D., Hemani G., Johnson M.R., Balding D.J. Improved heritability estimation from genome-wide SNPs. Am. J. Hum. Genet. 2012;91:1011–1021. doi: 10.1016/j.ajhg.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]; Speed, D., Hemani, G., Johnson, M.R., and Balding, D.J. (2012). Improved heritability estimation from genome-wide SNPs. Am. J. Hum. Genet. 91, 1011-1021. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.