Geographic Variation and Bias in the Polygenic Scores of Complex Diseases and Traits in Finland

Abstract

Polygenic scores (PSs) are becoming a useful tool to identify individuals with high genetic risk for complex diseases, and several projects are currently testing their utility for translational applications. It is also tempting to use PSs to assess whether genetic variation can explain a part of the geographic distribution of a phenotype. However, it is not well known how the population genetic properties of the training and target samples affect the geographic distribution of PSs. Here, we evaluate geographic differences, and related biases, of PSs in Finland in a geographically well-defined sample of 2,376 individuals from the National FINRISK study. First, we detect geographic differences in PSs for coronary artery disease (CAD), rheumatoid arthritis, schizophrenia, waist-hip ratio (WHR), body-mass index (BMI), and height, but not for Crohn disease or ulcerative colitis. Second, we use height as a model trait to thoroughly assess the possible population genetic biases in PSs and apply similar approaches to the other phenotypes. Most importantly, we detect suspiciously large accumulations of geographic differences for CAD, WHR, BMI, and height, suggesting bias arising from the population’s genetic structure rather than from a direct genotype-phenotype association. This work demonstrates how sensitive the geographic patterns of current PSs are for small biases even within relatively homogeneous populations and provides simple tools to identify such biases. A thorough understanding of the effects of population genetic structure on PSs is essential for translational applications of PSs.

Introduction

Understanding the causes behind geographic health differences can help to optimally apply limited healthcare resources and improve public health. Geographic health differences can be partially explained by lifestyle and environmental factors, but also by genetic differences that affect health both through population-specific genetic diseases, e.g., the Finnish Disease Heritage (see Web Resources), and through variation in the polygenic components of many complex diseases.^{1, 2, 3} In particular, recent discoveries from genome-wide association studies (GWASs)⁴ have enabled improved polygenic prediction of complex diseases and traits and raised expectations for their future translation to clinical use.^{5, 6, 7, 8} It is an open question to what extent the geographic distribution of phenotypes could be explained by their polygenic predictions.

A standard way to estimate a polygenic score (PS) of an individual is to select a set of independent variants identified by a GWAS, to weight the number of copies of each variant by its estimate of effect size from the GWAS, and to sum these quantities over the variants. PSs have turned out to be a useful tool for identifying individuals at high risk for many diseases, such as breast cancer,⁵ prostate cancer,⁹ and Alzheimer disease.⁸ As an example, a PS for coronary artery disease (CAD) can characterize individuals who have a risk that is equivalent to that of carrying a monogenic variant of familial hypercholesterolemia.⁷ At the same time, two recent studies have raised concerns about comparing PSs between populations with varying demographic histories.^{10, 11} Both studies showed that when a PS was built on a GWAS conducted in European populations and then applied to populations from Africa or East Asia, the differences in the PS were inconsistent with the actual phenotypic differences between the populations. Exact reasons for this inconsistency are unclear, but it has been speculated that a complex interplay of population genetic differences, including varying linkage-disequilibrium patterns and allele-frequency differences, between the target sample and the GWAS data can limit generalizability across populations.^{10, 11} Can similar problems appear also within a much more genetically and environmentally homogeneous setting than between populations from different continents? This is a crucial question for the public healthcare systems in countries that have the growing potential to implement PSs as part of their population-wide practice.

In this work, we evaluate the geographic distribution of the PSs of several complex diseases and traits in Finland and demonstrate how the effect of genetic population structure needs to be assessed before PSs can become a robust tool for population-wide use. The data resources available in Finland provide several favorable characteristics for this study. First, on a world-wide scale, Finland has a demographically and socially homogeneous population and a top-level public healthcare system,¹² and these together reduce many possible environmental effects contributing to geographic variation in health. Second, some notable geographic differences in phenotypes and general health still occur in Finland. A good example is the CAD incidence rate that is 1.6 times higher in eastern Finland than in western Finland (Sepelvaltimotauti-indeksi, see Web Resources) (Figure 1). In fact, even larger differences in CAD incidence were observed in the 1970s, and despite the extensive and successful public health campaign to reduce these rates through the Northern Karelia project,¹⁴ differences between east and west still remain today. Third, the genetic structure in Finland is well-characterized^{13, 15, 16, 17, 18, 19} (Figure 1), a factor that enables a detailed comparison between the geographic distribution of PSs and the overall genetic population structure within the country.

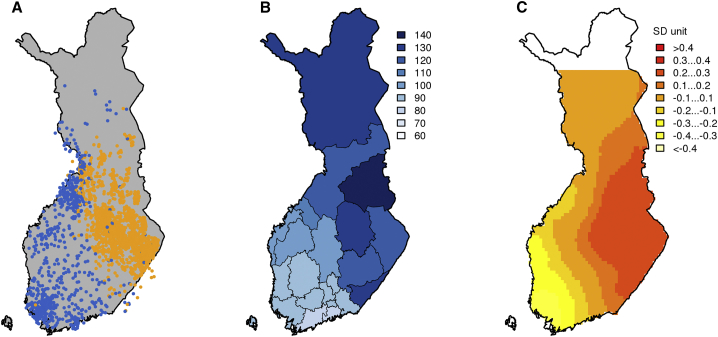
Figure 1.

A Comparison of Genetic Population Structure, Incidence Rates, and Distribution of the Polygenic Score of Coronary Artery Disease in Finland

(A–C) Main genetic population structure (A), the incidence rate for age-adjusted coronary artery disease (CAD) in 2013–2015 (Sepelvaltimotauti-indeksi, see Web Resources) (B), and the distribution of the polygenic score (PS) for CAD (C) in Finland. The population structure was estimated by clustering 2,376 samples into two groups.¹³ The incidence rate is scaled to have a mean = 100. The PS distribution is shown in units of standard deviation.

In our analyses, we observe clear geographic structure in PS distributions for most phenotypes considered. Furthermore, the spatial pattern is similar across the phenotypes and resembles the population genetic east-west division of Finland (see a comparison for CAD in Figure 1). Although a population genetic difference can well result in such patterns, a major goal of this work was to thoroughly assess whether these geographic patterns could alternatively result from some bias that emerges when the GWAS estimates of tens of thousands of variants are accumulated into PSs. We do this by generating many versions of PSs with different variant-inclusion criteria and by monitoring how the geographic structure accumulates across these PSs.

To demonstrate our approach, we consider the adult height (HG) as a model trait. In addition to HG, we apply our approach to two additional quantitative traits, body-mass index (BMI) and waist-hip ratio (WHR), in five diseases: coronary artery disease (CAD), rheumatoid arthritis (RA), schizophrenia (SCZ), Crohn disease (CD), and ulcerative colitis (UC). The results suggest that polygenic components of CAD, RA, SCZ, WHR, BMI, and HG show differences along the east-west direction, whereas only HG and WHR also show differences in the north-south direction. PSs for CD and UC do not show significant regional differences in either direction. Last, we discuss the credibility of the observed geographic differences. In particular, we report possible population-stratification-related biases in PSs for CAD, WHR, BMI, and HG. Our results raise concerns about how to reliably interpret geographic variation in PSs even within relatively homogeneous populations.

Material and Methods

Geographically Defined Target Data

We used data from the National FINRISK Study, which is a survey of the Finnish adult population (aged from 25 to 74) to estimate risk and protective factors of chronic diseases.²⁰ The FINRISK Study has collected several thousand samples every five years since 1972. We used data from the FINRISK Study survey of 1997 from 2,376 individuals in a geographically defined sample that was previously described in Kerminen et al.¹³ The two parents of each individual in this sample were both born within 80 km of each other. For the genetic analyses, we used genotypes from Illumina HumanCoreExome-12 BeadChip (see details in Kerminen et al.¹³) and imputed genotypes as described by Ripatti et al.²¹

Variant Filtering for Polygenic Scores

We derived PSs in our target data for each disease and trait on the basis of large international GWAS meta-analyses whose summary statistics were publicly available. We derived all PSs by excluding variants whose minor allele frequency (MAF) was below 1% in a meta-analysis, whose meta-analysis p value was above 0.05, or that resided in the major histocompatibility complex (chr 6: 25–34 Mb).²² In addition, where applicable, we filtered out variants whose imputation quality was below 90% or variants that had been present in less than 90% of the cohorts or samples of the meta-analysis. We also excluded all multi-allelic variants. Table 1 summarizes GWAS characteristics and variant filtering for all PSs. Finally, the PSs were built by selecting independent variants with PLINK 1.9³¹ (see Web Resources) via the clump command with a 500 kb window radius and a 0.1 threshold for r².

Table 1.

Summary of the Background GWAS and Our Polygenic Scores

Trait	Study	Method	GWAS Ancestry	GWAS N	Finnish Samples	Filtering in PS	SNPs in PS
CAD	CARDIoGRAMplusC4D (Nikpay et al., 201523)	Logistic	European + South Asian + East Asian	60,801/123,504	5,825/5,639	P value, MAF, MHC, INFO, #Cohorts	19,597
RA	Okada et al., 201424	Logistic	European	18,136/49,724	–	P value, MAF, MHC	32,736
CD	IIBDGC (Liu et al., 201525)	Logistic	European	5,956/14,927	–	P value, MAF, MHC, INFO, #Cohorts	21,771
UC	IIBDGC (Liu et al., 201525)	Logistic	European	6,968/20,464	–	P value, MAF, MHC, INFO, #Cohorts	23,513
SCZa	PGC (Ripke et al., 201426)	Logistic	European + East Asian	36,989/113,075	–a	P value, MAF, MHC, INFO, #Cohorts	30,311
WHR	GIANT (Locke et al., 201527)	Linear	European	224,459	∼16,000	P value, MAF, MHC, #Samples	13,727
	FINRISK20	Linear	Finnish	24,919	24,919	P value, MAF, MHC	43,252
BMI	GIANT (Shungin et al., 201528)	Linear	European	322,154	∼23,000	P value, MAF, MHC, #Samples	12,742
	UKBB (Neale lab29)	Linear	White British	337,199	–	P value, MAF, MHC	75,979
	FINRISK20	Linear	Finnish	24,919	24,919	P value, MAF, MHC	44,920
HG	GIANT (Wood et al., 201430)	Linear	European	253,288	∼23,000	P value, MAF, MHC, #Samples	27,066
	UKBB (Neale lab29)	Linear	White British	337,199	–	P value, MAF, MHC	113,079
	FINRISK20	Linear	Finnish	24,919	24,919	P value, MAF, MHC	50,536

For diseases, GWAS N = affected individuals/controls. The filtering column describes the thresholds used as follows: p value = p value < 0.05; MAF = Minor allele frequency > 0.01; MHC = major histocompatibility complex removed; INFO = imputation quality > 0.9; #Cohorts = exists in over 90% of GWAS cohorts; #Samples = exists in over 90% of GWAS samples. Other abbreviations are as follows: CAD = coronary artery disease; RA = rheumatoid arthritis; CD = Crohn disease; UC = ulcerative colitis; SCZ = schizophrenia; WHR = waist-hip ratio; BMI = body-mass index; and HG = height.

^aOur SCZ-PS excludes Finnish samples (546/2,011) from Ripke et al. In Figures S6 and S7 we show SCZ-PS, including these Finnish samples.

Additional GWASs for FINRISK, UK Biobank, and GIANT

FINRISK

We used Hail (see Web Resources) to run standard linear regression for HG, BMI, and WHR (adjusted for BMI) in 24,919 individuals across the National FINRISK Study collections from 1992–2012. These data excluded all 2,376 target individuals. We used sex, age, FINRISK project year, genotyping chip, and the first ten principal components of population structure as covariates in the analysis. In addition, we ran a linear mixed model for HG with BOLT-LMM v.2.3³² with the same samples and covariates.

UK Biobank

For the UK Biobank (UKBB), we performed a linear mixed model GWAS for HG with BOLT-LMM v2.3.³² For this analysis, we mimicked the linear regression analysis (round 1) of the Neale lab²⁹ and used UKBB v2 genotypes on 343,728 samples with white British ancestry. We used age, sex, and the first 20 principal components as covariates, and we used directly genotyped variants with a MAF above 1% and missingness below 10% for generating the variance component. GWAS statistics were calculated for imputed data with a MAF above 0.1% and an imputation quality above 0.7.

GIANT

We made two additional versions of the GIANT consortium meta-analysis with METAL,³³ as in Wood et al.,³⁰ except that in the first version we excluded the cohorts that included samples from the National FINRISK Study (FUSION, MIGEN, and COROGENE) and in the second version we excluded all cohorts that included any Finnish samples (DGI, FTC, FUSION, GENMETS, MIGEN, NFBC1966, COROGENE, FINGESTURE, HBCS, and YFS).

Polygenic Scores

We calculated PSs for the target set of 2,376 FINRISK individuals by using the additive model of:

$${\text{PS}}_{\text{i}}=\sum _{\text{j}=1}^{\text{M}}{\text{x}}_{\text{ij}}{\widehat{\text{β}}}_{\text{j}},$$

where PS_i is a polygenic score for individual i, M is the number of SNPs in the score (after variant filtering), x_ij is the individual’s (imputed) genotype dosage for SNP j, and $\hat{\beta }$_j is the effect size estimate of SNP j from the GWAS.

Genetic Risk Maps

To visualize the geographic distribution of PSs, we used the geographic locations of our geographically well-defined sample of 2,376 individuals and their PSs. We estimated an individual’s geographic location as the mean of his or her parents’ birthplaces. We then created risk maps in R by using a geographical centroid approach; this approach lays a grid on the map of Finland, and for each grid point p, it calculates the average of individuals’ PSs inversely weighted by their squared distance to the grid point as

$${\text{PS}}_{\text{p}}=\frac{1}{{\text{r}}_{\text{Tot}}}\sum _{\text{i}=1}^{\text{N}}\frac{{\text{PS}}_{\text{i}}}{{\text{r}}_{\text{ip}}^2},$$

where r_ip is the distance between individual i and grid point p and ${\text{r}}_{\text{Tot}}=\sum _{\text{i}}1/{\text{r}}_{\text{ip}}^2$ is the sum of the weights. We used a grid with a square size of 10 km and limited the minimum value for r_ip to be 50 km to avoid high variance in weights. In addition, to control for uncertainty in the areas that have a low sample size, we added to the calculation of PS_p one pseudo-individual whose PS is the population average PS and whose distance to the point p is the minimum of the observed distances r_ip. This modification draws the PS values of grid points toward the population average, especially in sparse areas where there are few individuals at the minimum range from the grid point. Last, the risk maps were scaled by the population average and standard deviation with a subset of 1,042 geographically evenly distributed individuals as described in Kerminen et al.¹³ The border line for the map of Finland was obtained from GADM (see Web Resources).

A Linear Model for Correlated Data for Assessing Spatial PS Differences

To quantify whether the PS has geographic differences, we performed a regression analysis with a linear model for correlated data wherein we explained PS with latitudinal or longitudinal coordinates and accounted for genetic relatedness as

$${\text{PS}}_i=\text{μ}+{\text{x}}_i\text{α}+\text{ε}\text{ε}\sim \text{N}(0,{\text{σ}}_{\text{ε}}^2\text{R}),$$

where x_i is the coordinate of individual i, μ is the intercept, and α is the effect of latitude or longitude on PS reported in Tables 2, S4, S6 and S7. For the structure of the error terms, we used the genetic relationship matrix R that was estimated with PLINK 1.9^{31, 34} (command --make-rel) with 61,598 independent variants from the Illumina HumanCoreExome chip described in Kerminen et al.¹³ Regression results from the standard linear model without accounting for genetic relatedness are shown in Table S1.

Table 2.

Results from the Linear Model for Correlated Data where Polygenic Score is Explained by Latitude or Longitude

		Latitude		Longitude
Trait	SNPs	Estimate	P value	Estimate	P value	WF-EF Difference (95% CI)
CAD	19,597	−6.3 × 10−4	0.97	0.05	1.6 × 10−4∗	−0.63 (−0.71, −0.55)
RA	32,736	0.03	0.12	0.06	5.5 × 10−5∗	−0.63 (−0.71, −0.55)
CD	21,771	0.03	0.18	−0.002	0.87	0.10 (0.01, 0.19)
UC	23,513	0.03	0.23	0.02	0.22	−0.26 (−0.35, −0.18)
SCZ	30,311	0.04	8.7 × 10−2	0.04	4.0 × 10−3∗	−0.35 (−0.43, −0.26)
BMI	12,742	0.03	9.4 × 10−2	0.04	1.8 × 10−3∗	−0.53 (−0.61, −0.44)
WHR	13,727	0.10	1.0 × 10−9∗	0.08	4.7 × 10−12∗	−1.16 (−1.23, −1.09)
HG	27,066	−0.18	1.1 × 10−40∗	−0.15	2.1 × 10−60∗	1.51 (1.45, 1.58)

SNPs = number of variants in PS. The difference in PS between Western Finland (WF) and Eastern Finland (EF) subpopulations is given in the standard deviation unit of PS. ^∗ marks a p value < 0.05. Abbreviations are as follows: CI = confidence interval, CAD = coronary artery disease; RA = rheumatoid arthritis; CD = Crohn disease; UC = ulcerative colitis; SCZ = schizophrenia; WHR = waist-hip ratio; BMI = body-mass index; and HG = height.

Polygenic and Phenotypic Differences between Subpopulations

The two main subpopulations in Finland are located in western Finland (WF) and eastern Finland (EF); they were previously described in Kerminen et al.¹³ and are shown in Figure 1A. Here, we reproduced this analysis by using CHROMOPAINTER and FineSTRUCTURE³⁵ with our current sample of 2,376 individuals to estimate both phenotypic and polygenic score differences between these two populations. The analysis divided our target sample into 1,604 EF and 772 WF individuals, and we used this division for estimating the differences between subpopulations.

PS Differences in Standard Deviation Units

We calculated the PS differences between the subpopulations by first scaling the PSs of the target sample with the subset of 1,042 geographically evenly distributed samples. We then used scaled PSs to calculate the difference between WF and EF. This strategy ensured a robust comparison between PSs on the basis of a fixed reference set. The 95% confidence intervals for the difference between two groups were given by Welch’s t test in R 3.4.1.³⁶

Phenotypic Differences Predicted by PS

For HG, BMI, and WHR, we also estimated the phenotypic difference predicted by PS between our subpopulations. First, we fitted the linear model wherein we explained the phenotype with the general covariates of sex, age (measured in 1997 and also represented by the birth year), and age² (WHR was additionally adjusted for BMI) in our target sample. Then we fitted another linear model wherein we explained the residuals with PS. On the basis of the effect estimates of the second model, we were able to estimate the predicted phenotypic effect by multiplying the PS effect estimate with the PS difference between the populations. We estimated the respective 95% credible intervals by using a simulation approach wherein we generated 100,000 sample pairs of effect estimates for PS difference, d, and PS effect on phenotype, β, from their sampling distributions, and we used the empirical distribution of d^∗β to determine the 95% credible interval. The sampling distribution of d was modeled as a normal distribution with a mean set to the observed PS difference and the standard deviation calculated from the 95% confidence interval from the Welch’s t test as $\left(\overline{x}-C{I}_{low}\right)/1.96$. The sampling distribution of β was modeled as a normal distribution with a mean set to the observed effect estimate and the standard deviation set to the corresponding standard error from the linear model.

Observed Phenotypic Differences for HG, BMI, and WHR

We estimated the observed phenotypic differences in HG, BMI, and WHR between WF and EF by adjusting the corresponding trait for sex, age, and age² (WHR was additionally adjusted for BMI) via linear regression, and then we calculated the difference of the subpopulation means on the basis of the residuals from this regression. The residuals were maintained in the units of the original phenotypes.

P Value Thresholding in PSs

We studied the effect of p value threshold for our PSs by applying seven different thresholds (p value < 1 × 10⁻², 1 × 10⁻³, 1 × 10⁻⁴, 1 × 10⁻⁵, 1 × 10⁻⁶, 1 × 10⁻⁷, and 1 × 10⁻⁸) to the variants of initial PSs (that used a threshold of 0.05) and calculated the additional PSs as described above.

Detecting Accumulation of Biases with Weakly Associated Variants (“Random PSs”)

To detect the accumulation of biases, we used an approach where we first filtered the GWAS summary statistics similarly to the original scores (as explained above), except we considered only variants with the GWAS p value > 0.5. This left us with, at most, very weakly associated variants. Among these p > 0.5 variants, we performed linkage disequilibrium (LD) clumping with the same parameters as above, except we set the p value cut-off to 1 in order to not further exclude any variant on the basis of its p value, and we permuted the p values among the p > 0.5 variants to ensure that the resulting scores are random with respect to their p value. LD clumping resulted in different numbers of variants for different traits, and from those we randomly sampled increasing numbers of variants (5,000, 10,000, 20,000, 40,000, 60,000, and 80,000). For BMI and WHR, the remaining number of variants after LD clumping was <80,000, and hence we were not able to compute a PS for 80,000 for these two traits. Finally, we calculated the PS for each individual and evaluated the difference between subpopulations in these “random PSs.” To assess uncertainty, we repeated the random PS generation ten times, and we report the mean and the range of the subpopulation difference over these ten random PSs.

To understand the expected behavior of PSs with truly zero effect sizes and to compare with our observed random PSs, we generated 1,000 simulated PSs for each observed random PS. These PSs were simulated from the variants from the random PSs but sampled their effect estimates independently from a normal distribution with a mean of zero and a standard deviation that corresponded to the standard error of the variant in GWAS. In Figure 5, we see that the 95% highest probability interval of the population difference is approximately constant across the different number of variants in the PSs and across the different GWASs. Supplemental Text S1 describes the theoretical basis for this property.

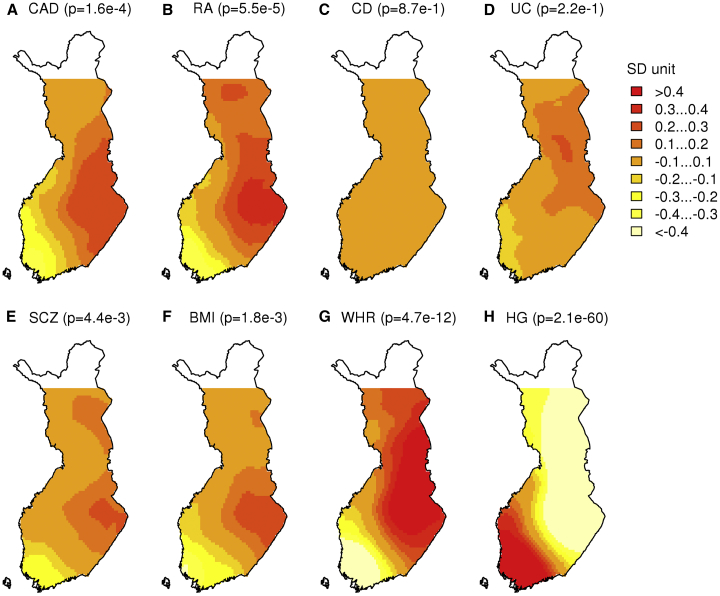
Figure 5.

Accumulation of Geographic Differences in Random Polygenic Scores

The absolute value of PS difference between western and eastern subpopulations with different numbers of independent variants (r² < 0.1) randomly chosen with GWAS p value > 0.5. For BMI and WHR, the data did not contain more than 60,000 independent variants. The solid region is the 95% probability interval under the theoretical null assumption of zero effect sizes and completely independent variants (r² = 0) (see Material and Methods). Points show the mean, and error bars show the range over ten random scores.

Our simulated 95% intervals assume completely independent variants, whereas our PS pipeline used a more liberal LD threshold of r² < 0.1. Therefore, we also compared the effects of residual LD to our random scores by performing LD clumping with r² thresholds of 0.01 and 0.001 for CAD and HG with GIANT and UKBB data. Figure S1 shows that, for GIANT-PS, the residual LD does not have an effect on the accumulation of population difference, and a similar tendency is suggested for CAD-PS even though the data are limited. For UKBB-PS, there is no accumulation of difference for any r² threshold.

The imputation-quality filter did not noticeably affect the results from either the actual PS or the random PS (Figure S2).

Results

Polygenic Scores Show Geographic Differences in Finland

We estimated PSs across Finland by using a geographically well-defined sample of 2,376 individuals from the National FINRISK Study 1997 survey.²⁰ The parents of each of these 2,376 individuals were born within 80 km of each other, and the means of the parents’ coordinates were used as the individuals’ locations. We derived PSs for the individuals with summary statistics from publicly available GWAS meta-analyses by applying LD pruning (r² < 0.1), MAF filtering (MAF > 0.01), and p value thresholding (p < 0.05) (see Material and Methods). To visualize the results on the map of Finland (Figure 2), we estimated the score at each map point by averaging individuals’ PSs inversely weighted by the individuals’ squared distance from the point (see Material and Methods).

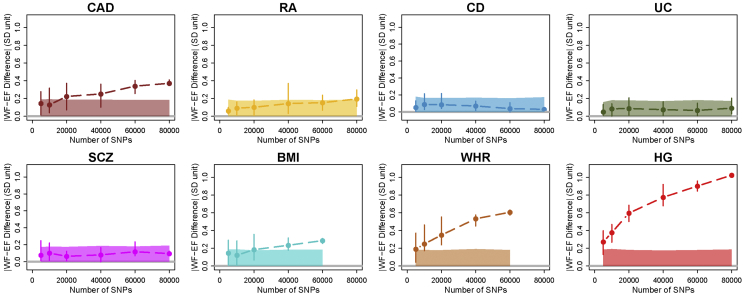
Figure 2.

Distribution of Polygenic Scores in Finland

(A–H) Distribution of polygenic scores for (A) coronary artery disease, (B) rheumatoid arthritis, (C) Crohn disease, (D) ulcerative colitis, (E) schizophrenia, (F) body-mass index, (G) waist-hip ratio adjusted for body-mass index, and (H) height. P values correspond to the association with longitude presented in Table 2.

We applied our approach to five diseases, CAD, RA, CD, UC, and SCZ, as well as to three quantitative traits, BMI, WHR adjusted for BMI, and HG. We observe that the PS patterns for CAD, RA, SCZ, BMI, HG, and WHR closely resemble the main population structure in Finland (Figure 1A). CD and UC do not show clear geographic differences between any parts of the country.

To evaluate statistically whether the PSs show geographic differences, we quantified the patterns by using a linear model for correlated data, wherein we explained individuals’ PSs with either longitude or latitude and accounted for genetic relatedness of the samples (see Material and Methods). The strongest differences were observed for HG (p = 2.1 × 10⁻⁶⁰) and WHR (p = 4.7 × 10⁻¹²) based on longitude, and lower but non-zero differences were observed for CAD, RA, SCZ, and BMI (all with p < 0.05) (Table 2, see Table S1 for results based on the standard linear model without accounting for genetic relatedness). HG and WHR showed differences also based on latitude, whereas CD and UC did not show differences based on either longitude or latitude. Table 2 also shows that the difference in PS between WF and EF subpopulations is the largest in HG (1.51 SDs) and in WHR (−1.16 SDs). In general, we observed stronger PS differences between east and west than between north and south, and this observation is in line with the main population structure in Finland.

Recently, it has been reported that PS differences between populations are prone to technical and confounding biases arising especially from population genetic differences (i.e., genetic divergence) or relatedness structure between the GWAS discovery and the target data.^{10, 11, 37, 38, 39} To assess whether some of the results in Figure 2 and Table 2 might be affected by these problems, we next concentrate on evaluating our PSs in several ways. We used HG as a model trait for developing the methodology.

Height PSs in Three Independent Cohorts

Adult height (HG) is a highly heritable and polygenic trait^{30, 40, 41} and shows clear phenotypic differences in Finland; western Finns are on average 1.6 cm taller than eastern Finns (see Material and Methods and Figure 3A). Furthermore, HG is a quantitative trait that makes it possible to compare geographic differences between the observed phenotype and the predictions based on PS. For such comparisons, we regressed out effects of sex, age, and age² from HG by using residuals from a standard linear model.

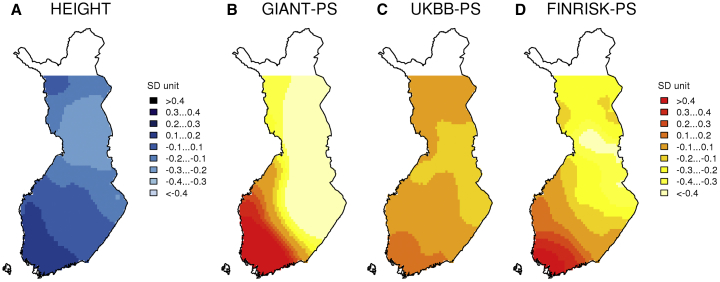
Figure 3.

Distributions of Adult Height and Three Polygenic Scores for Height

(A–D) A distribution of sex-, age-, and age²-adjusted adult height (A) and polygenic score (PS) distributions of GIANT-PS (B), UKBB-PS (C), and FINRISK-PS (D) for height in Finland. The values are presented in standard deviation units.

We calculated HG-PS by using summary statistics from three independent GWASs, including results from the GIANT consortium (a meta-analysis from a heterogeneous set of European samples),³⁰ the UK Biobank (a single cohort of uniformly genotyped and phenotyped white-British samples), and the National FINRISK study (Finnish samples genotyped with two different chips) using our standard pipeline (see Material and Methods). Table 3 summarizes the performance of these three scores.

Table 3.

Summary of the Results in the HG-PS Comparison

Source GWAS	Ancestry	GWAS N	Finnish Samples	Variants in PS	Adjusted R2	Predicted WF-EF HG Difference (cm; 95% CI)	Observed WF-EF HG-PS Difference (SD unit; 95% CI)
GIANT	European	253,288	∼23,000	27,066	14%	3.52 (3.14, 3.90)	1.51 (1.45, 1.5)
GIANT NOFINNS	European	230,794	0	25,660	17%	1.78 (1.53, 2.05)	0.70 (0.62, 0.79)
UK Biobank	British	337,199	0	113,079	22%	0.64 (0.39, 0.89)	0.23 (0.14, 0.32)
FINRISK	Finnish	24,919	24,919	50,536	15%	1.35 (1.14, 1.58)	0.59 (0.51, 0.67)

Adjusted R² is the variance explained by the PS in the target set.

The GIANT consortium height GWAS is a meta-analysis of 250,000 samples from multiple European populations, and it includes about 23,000 Finnish samples.³⁰ The GIANT-PS included 27,000 variants, explained 14% of the variance of height, and showed dramatic geographic differences in Finland (Figure 3B). The GIANT-PS was 1.5 SDs larger in WF than in EF, and we estimated, by regressing height on this PS in the target sample of 2,376 Finnish individuals, that this difference would correspond to a predicted height difference of 3.5 cm between WF and EF (see Material and Methods). This difference is over twice the observed phenotypic difference between the subpopulations. Note that even if we assumed that all variation in height was genetic, we would expect our GIANT-PS (that has R² < 15%) to explain only a part of the actual 1.6 cm WF-EF height difference. This raises concerns that in our target sample, GIANT-PS produces geographically biased results that cannot be interpreted directly on the phenotypic scale. The predicted WF-EF difference was even larger for GIANT-PS if the HG-on-PS regression was done within the WF subpopulation (4.7 cm) or within the EF subpopulation (6.4 cm) alone (Table S2), indicating challenges of interpretability for absolute differences among subpopulations.

Second, we built a PS based on over 330,000 UK Biobank British ancestry samples analyzed by the team led by Benjamin Neale.²⁹ Using the same pipeline as with GIANT-PS, this UKBB-PS contained considerably more variants and gave qualitatively similar geographic results to GIANT-PS, but quantitatively it showed much smaller WF-EF differences (Figure 3C). UKBB-PS explained 22% of the variation of height in the target sample and corresponded to a 0.6 cm predicted WF-EF difference in height.

Third, we built a PS based on the Finnish-population-specific summary statistics from the National FINRISK Study.²⁰ This FINRISK GWAS included nearly 25,000 samples and excluded all our 2,376 target individuals. This FINRISK-PS (50,000 SNPs) explained 15% of the variance of height and showed significant WF-EF differences that corresponded to a 1.4 cm difference in predicted height (Figure 3D). For FINRISK-PS and UKBB-PS, the predictions were robust to whether the regression was done in the whole target sample or in its WF or EF subset alone (Table S2).

These results show a consistent direction in predicted height differences between western and eastern Finland on the basis of three independent GWASs that have different relationships to the target sample. The predicted direction is also consistent with the observed phenotypic difference. However, the results show considerable, and concerning, variation in the predicted geographic difference of the genetic component of height.

Evaluating Possible Biases in Polygenic Score for Height

A PS from GIANT Accumulates Geographic Differences

An accumulation of small biases might be a substantial risk in the PSs of thousands of variants. These small biases can arise, for example, from unadjusted population structure in the underlying GWAS or from overlapping samples between GWAS and target data.^{42, 43} To understand whether the differences in our PS and the unrealistic predictions of geographic height differences might be due to a bias accumulation, we generated additional PSs by varying the inclusion criteria of variants.

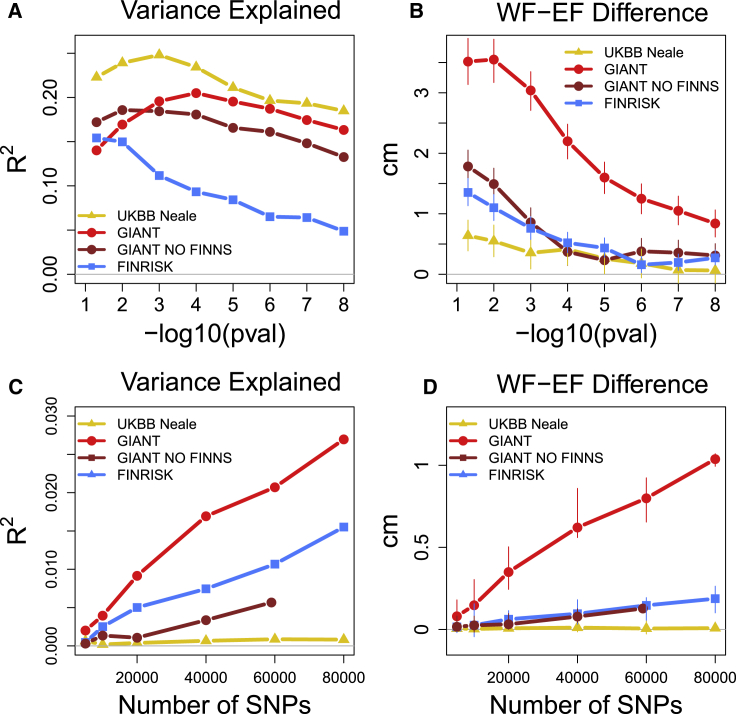
First, we used variants from the initial PS but applied different p value thresholds. Even though these scores included different numbers of variants, the variance explained did not vary strongly across the thresholds for GIANT-PS or UKBB-PS (Figure 4A), a finding that replicates the behavior of PSs reported earlier by Wood et al.³⁰ for other target populations. For FINRISK, the variance explained increased considerably with a more liberal p value threshold because of the smaller sample size of the study; specifically, the FINRISK-PS included only a handful of variants for the smallest p value thresholds, and thus had only a little predictive power there (Figure 4A). Conversely, the predicted east-west height differences in the GIANT-PS decreased considerably as more stringent p value cutoffs were used, whereas the variance in height explained by the PS increased simultaneously (Figure 4B). The decrease was much subtler for the other two PSs. To confirm the effect of the number of variants on the predicted height differences, we randomly sampled 1,000 variants from each of the different p value thresholds in GIANT-PS and calculated the corresponding scores. These PSs showed similar levels of predicted WF-EF height difference (about 1 cm) independent of the p value threshold, suggesting that the number of variants is a more important factor behind the geographic structure of GIANT-PS than the actual phenotypic variance explained by the variants (Figure S3).

Figure 4.

A Comparison of PSs Constructed from Height-Associated versus Random SNPs Demonstrates Differences in Stratification Effects by GWAS Summary Statistics

Top row: (A and B) Height variance explained by PS (A) and east-west difference in height predicted by PS (B) as a function of p value threshold in GWAS data.

Bottom row: (C and D) Height variance explained by PS (C) and east-west difference in height predicted by PS (D) as a function of the number of independent variants in PS when all variants have a p value > 0.5 in GWAS (“random scores”). Variance explained is given as adjusted R². In C and D, the values are based on ten random scores, and error bars in D show the range of those scores.

Concerned about the accumulation of WF-EF differences in GIANT-PS, we tested whether similar accumulation occurred even over random, non-associated variants. We randomly sampled different numbers of independent variants whose p values were over 0.5 in GWAS (suggesting a negligible association to height) and calculated PSs for them (we call these “random PSs”). This test showed considerable geographic differences in random PSs based on GIANT GWAS, and these differences increased with the number of variants (Figures 4C and 4D). Similar but weaker behavior was detected for FINRISK variants but not for UKBB variants.

Correlation of PS with Principal Component 1

One potential explanation for the observed behavior of GIANT-PS is that the effect-size estimates have a consistent directional bias that is aligned with the main population structure in Finland. Indeed, GIANT-PS is highly correlated with the leading principal component (PC1) of population structure in our target sample (r = 0.80), and when we removed the linear effect of PC1 from the GIANT-PS (see Material and Methods), the residuals explained more variance (19%) of height than the original GIANT-PS (14%). This suggests that in the effect-size estimates of GIANT-PS, a part of the true height association is masked by a strong component aligned with PC1 in Finland. For neither FINRISK-PS nor UKBB-PS did the removal of the linear effect of PC1 improve the variance explained in our target sample (Table S3). None of the three PSs showed WF-EF differences after the PC1 was regressed out (Table S3). By using the variants from GIANT-PS and the effect estimates from UKBB, we observed that the strong geographic differences in GIANT-PS are likely driven also by the choice of the GIANT variants and not only by a bias in the GIANT effect estimates (Supplemental Text S2).

Together, these analyses suggest that the geographic distribution of PSs based on the GIANT summary statistics consistently exaggerates height differences between the main Finnish subpopulations, whereas much less confounding from population stratification is seen in FINRISK-PS, and almost none is observed in UKBB-PS. A few possible reasons for this bias accumulation could be the inadequate adjustment for population structure in GWASs^{37, 39} or partially overlapping or related samples between GWAS samples and test data.

Effect of Sample Overlap and Population-Specific Samples

Our target data originate from the National FINRISK Study that is not reported among the GIANT cohorts (neither among cohorts in Lango et al.,⁴⁴ nor among additional cohorts in Wood et al.³⁰). However, a closer look into the cohort descriptions suggested that the COROGENE, FUSION, and MIGEN cohorts might include some FINRISK samples. This shows that it is not always straightforward to keep track of where publicly accessible samples have been used previously, and this observation would be a crucial piece of information for appropriately validating PSs. Although computational methods exist to detect sample overlaps between GWAS summary statistics,⁴⁵ their behavior in large datasets is not yet completely understood.⁴⁶

To test whether overlapping individuals affect the results of GIANT-PS, we built a new PS without any FINRISK samples (called GIANT-NOFR-PS). This GIANT-NOFR-PS explained 16% of the height variance and predicted a 3.4 cm (95% CI: 3.0–3.7) difference between WF and EF, and this difference is very similar to the result of the original GIANT-PS (14%, 3.5 cm [95% CI: 3.2–3.9]). Thus, a possible sample overlap is not causing the exaggerated WF and EF differences in GIANT-PS.

Next, we excluded the cohorts that included any Finnish samples from the meta-analysis. This GIANT-NOFINNS-PS explained 17% of the height variance and predicted a 1.7 cm (95% CI: 1.5–2.1) difference between WF and EF (Figure S4). This is a significantly smaller difference than that found by the original GIANT-PS, and a similar drop is also seen in the bias accumulation of GIANT-NOFINNS-PS (Figures 4 and S5). A similar but weaker effect was detected for SCZ when comparing PSs based on meta-analyses with and without Finnish samples (see Figures S6 and S7 and Table S4). These results suggest that although population-specific PSs have the potential to increase prediction accuracy, they might also introduce considerable bias if the population structure has not been adjusted properly.

When we ran the HG-GWAS in FINRISK and UKBB data with a linear mixed model that accounts for genetic relatedness, the resulting PSs predicted smaller geographic differences between WF and EF than our original GWAS based on linear regression with ten PCs as covariates, but the differences were not significant (Figure S8 and Table S5).

Bias Accumulation in Other Complex Diseases and Traits

After assessing multiple sources of bias accumulation in HG, we applied similar strategies to the other seven phenotypes. For each phenotype, we generated random PSs with increasing numbers of variants to detect a possible accumulation of biases. Here, we present absolute difference between western and eastern Finland using standardized PSs because we did not have a way to turn these to the phenotypic scale for the disease studies. Figure 5 shows that for RA, CD, UC, and SCZ, the absolute WF-EF PS difference of the random score is close to zero, whereas for CAD, BMI, WHR, and HG we observe a possible accumulation of bias.

Similarly to HG, we were able to compare the geographic distribution of the PSs of BMI and WHR to their phenotypic counterparts. Neither BMI nor WHR shows clear geographic patterns in our data, but the PSs of BMI and WHR largely repeat the results of the PS of HG (Figures S9, S10, S11, and S12 and Tables S6 and S7). For both BMI and WHR, GIANT-PS shows much larger differences and bias accumulation in random scores between WF-EF than FINRISK-PS (BMI and WHR) or UKBB-PS (only BMI available).

Discussion

Polygenic scores (PSs) have recently reached predictive power for some well-established monogenic risk factors for disease,⁷ and several projects are currently testing their utility in health care settings. PSs could also potentially inform us about the role of genetics in the geographic variability of traits and disease. However, a major challenge is that the geographic distribution of PSs is a complex function of population genetic differences between the GWAS data and the target samples, complicating its interpretation.^{10, 11, 47, 48} Here, we studied the geographic distribution of several PSs within Finland and assessed their robustness and possible biases in several ways.

By generating PSs for eight phenotypes in Finnish samples, we observed strong similarities between the geographic distribution of several PSs and the main Finnish population structure that runs from south-west to north-east.¹³ We further showed that even the least statistically significantly associated half of the effect sizes (with GWAS p value > 0.5) was carrying a consistent pattern of east-west difference for CAD (CARDIoGRAM data) and the three anthropometric traits from the GIANT consortium: HG, BMI, and WHR, findings that we interpret to indicate a likely bias. In theory, such a pattern could also result from extreme polygenicity. However, with the highly polygenic HG as our model trait, we showed that the random score from our largest HG GWAS based on the UK Biobank did not show any east-west variation within Finland. This suggests that the geographic difference accumulating in the random score from GIANT is rather due to bias than polygenicity. Furthermore, we observed for HG that the GIANT-PS was so strongly aligned with the first principal component of the genetic structure in our target data that this association masked some of the predictive power of the PS. This suggests that the effect estimates from GIANT contain a bias aligned with the main population structure in Finland, and this finding is in line with two recent studies that have reported related biases in the context of polygenic selection studies.^{37, 39} When we removed all Finnish samples from the GIANT meta-analysis of HG, the east-west difference in PS was halved, but still remained threefold compared to that in UKBB-PS. Also, the random scores showed that although a considerable proportion of the bias in GIANT-PS was related to the Finnish GWAS samples, a considerable bias still remained after excluding the Finnish samples.

For all three quantitative traits, PSs predicted unrealistically large geographic differences compared to the actual phenotypic differences. A theoretical but unlikely possibility remains that the geographic structure of the genetic component not explained by our current PSs could be opposite to the component that is explained by our current PSs, and this could eventually balance out the unrealistically large estimates for GIANT-PS and FINRISK-PS. However, given that the estimated difference consistently increases with the inclusion of more variants in PSs, a more plausible explanation is that we simply cannot robustly interpret the geographic differences in PSs derived from existing GWASs on the phenotypic scale via a simple regression framework. Earlier, the results of phenotypically inconsistent PS differences between continental groups have been reported.^{10, 11, 38} Here, we show that similar patterns can exist even for a relatively small geographic area and the relatively homogeneous population of Finland. We note that even if the genetic EF-WF difference in Finland might be large compared to variation within some other European countries,¹⁹ it is tiny compared to the continental differences.⁴⁹

Our results showed that the phenotypes that did not accumulate EF-WF differences were the two types of inflammatory bowel disease (CD and UC), SCZ, and RA. Of these, CD and UC did not show any geographic PS variation in Finland. To our knowledge, only two studies have studied the geographic variation in the prevalence of inflammatory bowel disease (IBD) in Finland. Lehtinen et al.⁵⁰ reported higher incidence rates of pediatric IBD in more sparsely populated areas, whereas Jussila et al.⁵¹ reported increasing prevalence rates of UC in Northern Finland but no geographic structure for CD. Our polygenic risk prediction for CD is in line with the observations in Jussila et al.,⁵¹ and even though the PS of UC did not show significant geographic differences in our statistical analysis, the genetic risk map for UC shows some increasing risk pattern in Northern Finland. SCZ showed a higher polygenic risk in EF than in WF, a finding in line with extensive geographic incidence information from several studies^{52, 53, 54, 55, 56, 57} that describe the highest SCZ prevalence and incidence rates in northern and eastern Finland and the lowest rates in the southwestern parts of the country. Also, RA showed higher polygenic risk in EF than in WF. Our limited information about the regional incidence of RA in Finland is from Kaipiainen-Seppänen et al.,⁵⁸ who reported the highest RA incidence rates for North Karelia (in EF) and the lowest for Ostrobothnia (on the west coast), but unfortunately the study did not include southwestern or northern Finland. Neither our SCZ nor our RA GWAS summary statistics included any Finnish samples. Together these two diseases exemplify the potential of PSs to explain geographic health differences.

To conclude, we recommend the following practices for geographic evaluation of PSs. (1) Check residual geographic stratification of PSs by generating random scores for non-associated variants and by testing whether PSs unrealistically strongly align with the leading PCs of genetic structure. (2) Use a linear/logistic mixed model instead of the standard linear/logistic regression model in GWAS. (3) Compare the genetically predicted phenotypic difference between populations to the observed phenotypic difference in order to detect unrealistic genetic predictions. With these tools, we showed that although PSs for several traits in Finland followed the geographic distribution of the phenotype (HG, CAD, SCZ, RA, CD, and UC), for CAD and HG, as well as for BMI and WHR, we observed in the geographic distribution of PSs suspicious behavior that could indicate a bias arising from population genetic structure rather than from a direct genotype-phenotype association. Our results emphasize that we have limited understanding of the interplay between our current PSs and genetic population structure even within one of the most thoroughly studied populations in human genetics. Therefore, we recommend refraining from using the current PSs to argue for a significant polygenic basis for geographic phenotype differences until we understand better the source and extent of the geographic bias in the current PSs.

Declaration of Interests

V.S. has participated in a conference trip sponsored by Novo Nordisk and received an honorarium from the same source for participating in an advisory board meeting. He also has an ongoing research collaboration with Bayer Ltd.

Published: May 30, 2019

Web Resources

• The Finnish Disease Heritage, http://www.findis.org/

• GADM, https://gadm.org/

• Hail, https://github.com/hail-is/hail

• PLINK 1.9., www.cog-genomics.org/plink/1.9/

• Sepelvaltimotauti-indeksi, T.H.L. Ikävakioitu (2013–2015), http://www.terveytemme.fi/sairastavuusindeksi/2015/maakunnat_html/atlas.html?select=01&indicator=i0