Abstract
In recent years, protein kinases have become some of the most significant drug targets in cancer patients. Kinases are known to regulate the activity of many human proteins, and consequently their inhibition has been used to control cancer proliferation. A significant challenge in drug discovery is the rapid and efficient identification of new small molecules. In this study, we propose a novel in silico drug discovery approach to identify kinase targets that impinge on nuclear receptor signaling with data generated using high-content analysis (HCA). A high-throughput imaging dataset was generated from an siRNA human kinome screen on engineered cells that allow direct visualization of effects on estrogen receptor-α or a chimeric progesterone receptor B binding to specific DNA. Two types of kinase descriptors are extracted from these imaging data: first, a population-median-based descriptor and second a bag-of-words (BoW) descriptor that can capture heterogeneity information in the imaging data. Using these descriptors, we provide prediction results of drug-kinase-target interactions based on single-task learning, multi-task learning, and collaborative filtering methods. The best performing model in target-based drug discovery gives an area under the receiver operating characteristic curve (AUC) of 0.86, whereas the best model in ligand-based discovery gives an AUC of 0.79. These promising results suggest that imaging-based information can be used as an additional source of information to existing virtual screening methods, thereby making the drug discovery process more time and cost efficient.
Keywords: drug discovery, machine learning, high-throughput imaging
Introduction
Research in developing computational algorithms for drug-target interaction (DTI) prediction and ADMET (absorption, distribution, metabolism, excretion, and toxicity) has shown stupendous growth in the past few years.1–5 Presently, the entire drug discovery and development processes require ~2 billion US dollars and approximately 12 years for any given drug and target to make it to market. Using virtual screening methods, it is possible to reduce the time and cost involved in the drug discovery process. Big pharma companies have adopted computational methods to make their drug discovery processes more efficient. DTI prediction is useful in lead compound identification, an important step in the multi-phase drug discovery process. Even though identifying the lead compound (discovery stage) takes less time compared with animal and human testing (development stage),6 the quality of the lead compound obtained at discovery stage plays an essential role in reducing the attrition rate during the development stage. Drug-target interaction prediction is also useful for other tasks like drug activity prediction and drug repurposing which are briefly discussed in this article.
For any given disease, a set of protein targets are initially identified such that their functional inhibition will reduce the ill effects of the disease. In lead compound identification, the aim is to identify a drug molecule that interacts with the binding sites of these protein targets, thereby inhibiting their functional activity.7 In an in vitro testing setup, thousands of small-molecule compounds are tested against the target protein to test for bioactivity. This procedure is slow, laborious, and expensive. With in silico methods, however, it is possible to reduce the search space to a smaller number of molecules by virtually screening the drugs that are more probable to interact with the target protein. If the three-dimensional (3D) structure of the target protein is known, then docking models can be used to prioritize a compound that binds well with the target protein. Unfortunately, the 3D structure is often unavailable for common protein target types (ie, G-protein-coupled receptors [GPCRs]).7,8 In cases where the 3D structure of a target is unknown, machine learning (ML) models that use compound structure and protein sequence information are used to perform virtual screening. These ML models are either similarity-based approaches8 or descriptor-based approaches.9,10 Both approaches use chemical structure information or mass spectroscopy information of compounds and amino acid sequence information of proteins as input data. Similarity-based approaches are more common and they calculate drug-drug similarities using scores like SIMCOMP11 and protein-protein similarities using Smith-Waterman (SW) scores.12 In one of the seminal papers in similarity-based DTI prediction, Bleakley and Yamanishi13 use a bipartite graph learning method to predict drug interaction profiles for targets and vice versa. They created a golden standard dataset that is later used by most DTI prediction algorithms as a test bed. The dataset contains 4 DTI networks corresponding to enzymes, GPCRs, ion channels, and nuclear receptors. For example, in the enzyme data, there are 445 drugs and 664 proteins (enzymes) with a total of 2926 known DTIs. Similarity matrices for drugs and proteins are calculated using SIMCOMP and SW scores. Using these matrices, embeddings (low-dimensional vectors) for all drugs and proteins are calculated such that a drug D1 and a protein P1 are close to each other if they are known to interact. Similarly, drug D1 and drug D2 are close to each other if their structural similarity is high and the same applies for proteins. This low-dimensional space where drugs and proteins interact is called the pharmacologic space. Later works also used the same dataset and built algorithms that use variations of these low-dimensional embeddings.2,3,13 On the other hand, descriptor-based models extract feature vectors from protein sequences and chemical structures and use standard ML techniques like support vector machines (SVMs) and artificial neural networks to build models that predict DTIs.9,10 In this study, we explore the utility of a new imaging-based descriptor obtained through RNA interference (RNAi) phenotyping. These imaging data corresponding to protein kinases are generated from an siRNA human kinome screen in engineered cell models that allow for imaging-based visualization and quantitation of several steps of the nuclear receptor gene transcription activation pathways. Feature descriptors are extracted from the imaging data to build descriptor-based ML models and similarity-based models.
Protein kinases have become some of the most significant drug targets in cancer therapy. They are known to modulate the activity of many human proteins through phosphorylation, an essential mechanism to regulate the molecular drivers of cell proliferation, an out-of-control process in cancer cells. Successful kinase-based cancer therapy demonstrates that it is possible to reduce the growth of cancer cells by regulating phosphorylation through protein kinase inhibition. To find additional small-molecule inhibitors of target kinases, we propose a novel, imaging-based approach using high-content analysis (HCA). To this end, we have used a large imaging dataset generated by high-throughput microscopy. This dataset is created from an siRNA human kinome screen to analyze the effects of each kinase on 2 molecular drivers known to be important in breast cancer growth, estrogens and progestins, via activation of their cognate receptors, estrogen receptor (ER) and progesterone receptor (PR), members of the nuclear receptor family of transcription factors. These molecules are essential regulatory hormones in the body during development and reproduction, and are implicated in the progression of multiple cancer types, including breast, ovarian, endometrial, and uterine.14 In addition to regulation by ligand, both ER and PR are regulated by multiple phosphorylation sites targeted by protein kinases that are part of diverse intracellular signaling networks.15 To visualize kinase-specific effects on these signaling pathways, an siRNA human kinome screen was performed using engineered cells containing a stable, microscopically visible, multi-copy integration of the ER-responsive prolactin promoter-enhancer unit (PRL-HeLa). These cell lines, following the expression of GFP-ERα or chimeric GFP-PRB-ERα, allow for direct and simultaneous visualization and quantitation of receptor DNA binding, chromatin remodeling, and transcriptional regulation in response to estrogens or progestins.16–19 These cell lines, combined with a custom automated image analysis platform,20 have been previously used to discriminate and classify the mechanistic effects of estrogens and progestins. These data have been included in mathematical models predicting the potential endocrine disrupting activity of compounds by the Environmental Protection Agency.21
From these imaging data, we extract 2 protein kinase descriptors that provide valuable information regarding drug-kinase interactions. To date, to the best of our knowledge, imaging-based descriptors for protein kinases have not been used within virtual screening. Recently, however, compound-imaging-based descriptors were proposed22 that show promising results that encourage more research in image-based feature extraction procedures. A detailed description of data sources, feature extraction procedures, and data type information is provided in the next section. Later, in section “Methods and Results,” ML models are built for ligand-based drug discovery and target-based drug discovery. We also discuss various approaches including single-task learning, multi-task learning, and collaborative filtering (CF), and their use in different drug discovery scenarios. In section “Discussion,” we discuss the benefits of image-based methods in target-based drug discovery and also comment on the pros and cons of different ML approaches.
Data
Three kinds of data are leveraged to build and test computational models that predict drug-kinase interactions:
Bioactivity data;
Kinase descriptors;
Compound descriptors.
Although our main aim is to show the utility of imaging descriptors for kinases through target-based discovery, we also provide additional models and results that use both kinase and drug descriptors. A detailed description of data sources, extraction procedures, and data types of all 3 kinds of data is provided below.
Bioactivity data
The end goal of virtual screening is to predict interactions between untested compound and target kinase pairs. For this purpose, we collected drug-kinase interaction data from DrugKiNET portal23 which has information of more than 800 compounds that have been experimentally determined to interact with human protein kinases. DrugKiNET has curated these data from several sources including (a) the National Center for Biotechnology Information (NCBI); (b) the PubChem Compound database24; (c) the Kinase SARfari database from the European Molecular Biology Laboratory (EMBL) European Bioinformatics Institute25; and (d) hundreds of research publications. Each drug, along with its binding affinities with different protein kinases, is provided in a list format on the website. Most of the binding affinities are measured using equilibrium dissociation constant (Kd) values and a few with half maximal inhibitory concentration (IC50). Because most drug-like compounds have Kd, IC50 values < 1 µM, we chose 1 µM as a concentration threshold to convert the binding affinity matrix to a binary DTI matrix. If the concentration is less than 1 µM, then a binary value of 1 is associated with it and vice versa. This results in a matrix that is 99% sparse (ie, only 1% of the values are non-zero entries that represent interacting drug-target pairs). The final matrix has a shape of 725 × 246 (drugs × targets).
Kinase descriptors
In target-based drug discovery, kinase descriptors are used as inputs to the ML models to predict their interactions with various drug compounds. Here, kinase descriptors are generated from HCA datasets that are used to determine the impact of kinase signaling networks on ER and PR signaling in response to hormones. An imaging dataset generated from an siRNA human kinome screen is used to analyze the signaling effects of each kinase on ER or PR activity. The Stealth RNAi Human Kinome Collection (Invitrogen) contains 636 human kinase targets with 3 individual non-overlapping Stealth RNAi duplexes per target. Library plates were thawed and siRNAs were printed into 2 replicate 384-well optical bottom plates in quadruplicate wells using a BioMek FX (Beckman Coulter) liquid handling platform. To reduce screening size, target replicates A, B, and C were printed into the same well. siRNA was complexed by the addition of 20 µL of diluted XtremeGENE (Roche) in Opti-MEM (Invitrogen) using a µFill (BioTek) followed by incubation for 30 minutes at room temperature. GFP-ER:PRL-HeLa or GFP-PRB-ER:PRL-HeLa cells were trypsinized and resuspended in growth media without penicillin-streptomycin and added at a concentration of 1500 cells/well using a µFill transfer device. GFP-ER:PRL-HeLa cells express full-length ERα with an N-terminal fusion to GFP (REF). GFP-PRB-ER:PRL-HeLa cells express full-length chimeric PRB with a region containing the PR DBD that has been swapped for a region containing the ERα DBD (amino acids 183-254) and an N-terminal fusion to GFP (Trevino REF). Cells were placed into a 37 C/5% CO2 humidified incubator for 72 hours, treated with either estrogen (E2) or progestin (R5020) for 2 hours, and then fixed and nuclei stained with 4′,6-diamidino-2-phenylindole (DAPI).
Image datasets were collected using a GE Healthcare IN Cell 6000 automated imaging cytometer using reflection-based autofocusing, a 40×/0.90 Nikon S-luor objective, and an sCMOS 5.5-megapixel camera and LED illumination. Z-stacks at 0.5 µm optical section intervals were collected and maximum-projected for analysis. Cell, nucleus, array segmentation, and signal quantification were performed using the myImageAnalysis web application powered by Pipeline Pilot software (Biovia) as described previously in Szafran and Mancini.20 Aggregated, mitotic, and apoptotic cells were removed using filters based on nuclear size, nuclear shape, and nuclear intensity. A final panel of 5 features capturing kinase siRNA effects on ER/PR expression, nuclear translocation, DNA binding, and chromatin remodeling was collected on a per-cell basis. Because hundreds of cells are associated with a single siRNA analysis, there are multiple five-dimensional (5D) features associated with each kinase. The following 2 aggregation methods are used to extract a single descriptor for each kinase:
Population-median-based feature. There is a 5D feature associated with each cell corresponding to 1 kinase. Therefore, the median feature of all the cells corresponding to an siRNA is used as the kinase descriptor.
Bag-of-words (BoW) feature. The median-based method mentioned above ignores heterogeneity across all cells in the image. This variance/heterogeneity can be well captured using a BoW-based feature vector.26 We compare model predictions using both of these feature descriptors in section “Methods and Results.” More information regarding the BoW feature extraction process is provided in section “Methods and Results.”
Compound descriptors
Drug-target interactions, also known as ligand-protein interactions, depend on the structure of both the ligand and the protein. Due to this reason, we assume that compounds that are structurally similar will interact with the same proteins, and vice versa. Descriptors such as extended-connectivity fingerprints (ECFPs) capture the structural information of compounds that are widely used by the drug discovery community for compound similarity searching, quantitative structure-activity relationship (QSAR) modeling for lead compound generation, and absorption, distribution, metabolism, excretion and toxicity (ADMET) prediction models. ECFPs are a class of circular fingerprints that can capture structural information of molecules. A brief overview of the ECFP generation procedure is provided in the supplementary section, and a more in-depth analysis can be obtained from previous studies.27,28 ECFPs provide substructure information by calculating features based on circular neighborhoods of atoms present in the molecules. In our study, we use a 1024-bit ECFP feature to represent each drug compound. Each bit indicates the presence/absence of a certain substructure. This substructure information is encoded in the ECFP algorithm in the form of hash tables. We have used RDKit, an open-source cheminformatics package, to extract these 1024-dimensional ECFPs.29
Methods and Results
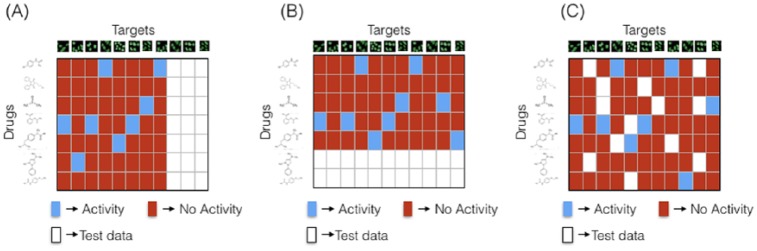
In this section, the following 3 types of drug discovery tasks are described and posed as ML problems (see Figure 1):
Figure 1.
The machine learning setups for various drug discovery tasks: (A) lead compound identification—the task is to predict drug interactions with new kinase targets to find lead compounds that show significant bioactivity when tested experimentally; (B) drug activity prediction—the task is to predict the target interactions of new drugs to find drug-like molecules; (C) drug repurposing—given partially known bioactivity data, the task is to predict unknown interactions. This is useful for finding new therapeutic uses for already established drugs.
Lead compound identification;
Drug activity prediction;
Drug repurposing.
We build models to solve the above tasks and then compare their performances using area under the receiver operating characteristic curve (AUC) and area under the precision-recall (AUPR) curve metrics.
Lead compound identification
In lead compound identification (eg, target-based drug discovery), kinase descriptors are used to predict the interactions of a particular target kinase with various drug compounds. Two datasets are used for this purpose. Dataset-1 contains the kinase descriptors extracted from the experimental data describing the effects of kinase knockdown on ER/PR activity. Dataset-2 contains kinase “interactions” derived from a publicly available database (DrugKiNET) that describes known drug-kinase interactions. Machine learning models attempt to bridge the 2 datasets to predict the probability of active drugs from a known kinase effect on ER/PR signaling. These models are trained with kinase descriptors as inputs and their interaction with drug compounds (binary labels: Activity/No Activity) as outputs. These models measure descriptor similarity of new kinases with existing kinases and use this information to predict the bioactivity of new kinases. As mentioned in section “Data,” we use 2 types of kinase imaging descriptors as input features to the learning models: a population-median-based feature and a BoW feature. To train ML models that have the ability to predict new kinase-drug interactions, we need to split the available data into training and testing data (see Figure 1A). The testing data are used only to validate the performance of the models. In total, 70% of the kinases and their drug interaction profiles are used for training, whereas the remaining 30% are considered as new kinase targets for which the drug interaction profile is unknown. In the next subsection, we discuss the BoW feature extraction procedure and its benefits, followed by a brief description of the different ML models used.
BoW feature extraction procedure
Bag-of-words-based features are frequently used in document classification and computer vision tasks.26,30 If an entity (eg, an image) has multiple distinct features associated with it, then using BoW it is possible to extract a single descriptor that contains information about all the different features. For example, consider an image classification task where the task is to classify a given image as a cat or a dog. Multiple randomly sampled image patches are used to represent each image. In case of a dog image, these random patches may contain nose parts, ears, tail, and other parts that constitute a typical dog. This patch sampling process is repeated for all the training images and each patch is represented as a point in a high-dimensional space. By clustering these points, one can observe that specific features like long ears of dogs and small noses of cats belong to the same clusters. This ability to capture complex information by leveraging heterogeneity of multiple local features across the image field makes the BoW descriptor well suited for image classification tasks.
In our work presented here, a kinase siRNA will impact one or more of the multiple imaging features available, each associated with an individual cell. Each imaging feature is represented as a point in the 5D space. The median-based method calculates the centroid of all the data points while ignoring the variance information. However, the BoW method tries to capture the variance by learning a distribution over all the available points. The steps involved in a BoW feature extraction procedure are as follows:
Cluster all data points from all kinase screens into k groups;
Multiple cells are analyzed in each kinase screen. Therefore, for each kinase, calculate a normalized histogram for which bins are the cluster indices and the frequency values are the number of points of that kinase belonging to that cluster index;
Use these normalized histograms (k-dimensional vector) as features for each kinase.
If the distribution (the BoW feature vector) is very narrow, then it implies that the feature variance for that particular kinase siRNA is low. On the contrary, if the distribution is wide, then the feature variance is high (see Figure 2 for examples of BoW vectors).
Figure 2.
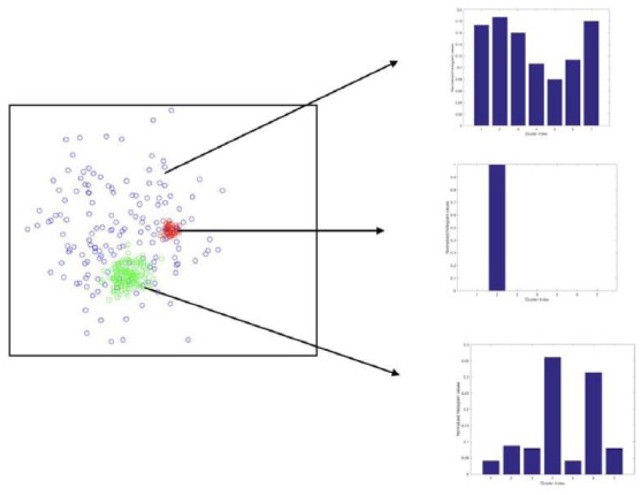
Bag-of-words. This is a simulated example used for illustration purpose only. We can observe that the blue-colored points are highly heterogeneous and, therefore, have a flatter histogram profile. The red-colored points are local (eg, very homogeneous and therefore have a narrow histogram profile).
Single-task learning and multi-task learning
In this subsection, we discuss single- and multi-task approaches for building DTI prediction models. In lead compound identification, predicting interactions of all test kinases with a single compound is considered as a “single task.” Therefore, the total number of tasks is equal to the number of compounds. When separate models are trained to predict kinase interactions for each compound, then that approach is called single-task learning. On the other hand, multi-task learning attempts to learn a single model to predict the bioactivities of a kinase with multiple compounds. In multi-task learning (see Figure 3), mainly multi-task neural networks, features from any kinase are extracted using a shared network and then separate models are learned using these features as inputs. This method can extract better initial features because data from all the compounds (more data) are used to build the shared network.31,32 We use a 2-layered multi-task neural network that predicts the entire drug interaction profile of each kinase. For single-task learning, we have used ML models that include (a) logistic regression, (b) k-nearest neighbor (KNN), (c) neural networks, (d) random forest, and (e) SVMs. The results for each of these single-task learning models and multi-task learning are shown in Table 1.
Figure 3.

(A) Single-task learning setup. Independent models are trained for predicting bioactivity for each kinase. For example, Task-1 represents the task of predicting the bioactivity of all compounds with a particular protein kinase (say AAK1). (B) Multi-task learning. A shared model is used to extract an initial set of features from all the drugs. These features are later used as inputs to smaller models which can make predictions on all the tasks.
Table 1.
Single-task learning—compound profile prediction AUC results of protein kinases using either population-median-based descriptor or bag-of-words-based descriptor.
| Model | AUC (with 95% confidence interval) | |
|---|---|---|
| Median feature | Bag-of-words feature | |
| KNN (k = 3) | 0.68 (0.65-0.69) | 0.68 (0.65-0.72) |
| Logistic regression | 0.8 (0.79-0.83) | 0.84 (0.81-0.87) |
| Linear SVM | 0.83 (0.79-0.86) | 0.82 (0.8-0.86) |
| Random forest | 0.83 (0.81-0.85) | 0.83 (0.81-0.85) |
| 2-layered neural network | 0.82 (0.8-0.84) | 0.84 (0.79-0.86) |
| Multi-task neural network | 0.85 (0.84-0.86) | 0.86 (0.84-0.87) |
Abbreviations: AUC, area under the receiver operating characteristic curve; KNN, k-nearest neighbor; SVM, support vector machine.
A simple linear SVM could provide very good performance on the test set. Average AUCs and confidence intervals are calculated over 100 independent trials.
The scikit-learn package in Python is used to implement all the single-task learning algorithms. For the random forest classifier, we have used 100 decision trees with a maximum depth of 5. For the neural network classifier, a 2-layered neural network with 50 hidden layer units and 1 output unit is used for predicting each task; a sigmoid activation function is used in both the hidden layer and the output layer. The Keras deep learning library is used to build the multi-task neural networks. Keras is an easy-to-use library built on TensorFlow with Python as the core language. A multi-task neural network with 50 hidden layer units and 725 outputs (725 is the number of drug compounds) is used to construct a model that predicts the entire compound interaction profile for any new kinase. In case of linear SVM and logistic regression, default parameters are used. In total, 100 independent trials are conducted where in each trial a new train-test split is created. 95% confidence intervals are calculated using the AUC33 values from each of these 100 trials. We have observed that most of the models perform similarly with multi-task neural networks slightly outperforming the other models (see Table 1). The receiver operating characteristic (ROC) curves corresponding to 10 independent simulations of a multi-task neural network are shown in Figure 4. The average AUC of all the ROC curves is 0.86, with a 95% confidence interval of [0.84-0.87].
Figure 4.

Receiver operating characteristic (ROC) curves of a multi-task neural network for predicting drug-target interactions with BoW-based kinase features as inputs. Each ROC curve corresponds to 1 experiment. The average AUC of all the ROC curves is 0.86, with a 95% confidence interval of [0.84-0.87]. AUC indicates area under the receiver operating characteristic curve; ROC, receiver operating characteristic.
AUPR curve
Although AUC (or AUROC) is a widely used metric in bioinformatics, it has few disadvantages in the context of DTI prediction performances. The AUC value does not provide insights into virtual screening efficiency. For example, an AUC value of 0.8 does not give any information about how many interactions the algorithm correctly predicted and how efficient it was in making those predictions. If we would like to know the efficiency of the virtual screening process, then a metric like precision score (eg, positive predictive value [PPV]) would be useful. Precision is the ratio between the number of true positives (TPs) to the total number of predicted positives (TP + FP). Therefore, a low precision score implies that the virtual screening process is inefficient, for example, the algorithm predicts many positives, of which only few are positive interactions. The precision score alone does not provide all the required information. There can be a situation where the algorithm predicts very few positives in total, most of which are TPs. In this situation, the model will receive a high precision score, but it is not useful because it ignores a lot of TPs that are of interest. Therefore, another metric that captures information about the number of predicted TPs compared with the total number of TPs needs to be calculated. Recall (eg, sensitivity or true-positive rate [TPR]) is defined as the ratio between predicted TPs and the total number of existing positives (TP + FN). A high recall score implies that a significant amount of positive labels are predicted correctly. Therefore, high precision and high recall scores result in an efficient and well-explored virtual screening process. For this reason, AUPR would be a better metric compared with the AUC. The AUPR results for lead compound identification are provided in Table 2. Note that a random classifier that predicts output as all ones with probability 0.01 and zeros with probability 0.99 (these values are chosen because the DTI input matrix has a sparsity of 1%) would result in an AUPR score of 0.01 and an AUC score of 0.5.
Table 2.
Single-task learning—compound profile prediction AUPR results of protein kinases using either population-median-based descriptor or bag-of-words-based descriptor.
| Model | AUPR (with 95% confidence interval) | |
|---|---|---|
| Median feature | Bag-of-words feature | |
| KNN (k = 3) | 0.16 (0.13-0.18) | 0.15 (0.13-0.17) |
| Logistic regression | 0.25 (0.22-0.3) | 0.33 (0.29-0.37) |
| Linear SVM | 0.3 (0.28-0.36) | 0.29 (0.23-0.33) |
| Random forest | 0.26 (0.24-0.3) | 0.26 (0.24-0.27) |
| 2-layered neural network | 0.3 (0.27-0.33) | 0.32 (0.29-0.36) |
| Multi-task neural network | 0.3 (0.27-0.33) | 0.32 (0.29-0.34) |
Abbreviations: AUPR, area under the precision-recall curve; KNN, k-nearest neighbor; SVM, support vector machine.
Average AUPR scores and their confidence intervals are calculated over 100 independent trials.
Drug activity prediction
In drug activity prediction (a.k.a. ligand-based drug discovery), compound descriptors are used as inputs and their kinase activities as outputs to the ML models. During the testing stage, this allows us to predict kinase interactions for new drug compounds. Drug activity prediction is very useful in the case of virtual screening because thousands of chemical compounds can be surveyed to discover possible drug-like molecules that are predicted to interact with at least 1 kinase. 1024-bit-length ECFPs were used as compound descriptors. For training and testing data split, 70% of the drugs and their kinase interaction profiles are used for training, whereas the remaining 30% are considered as new drug compounds for which the kinase interaction profile is unknown. These unknown interactions are treated as “missing data” in the DTI matrix as shown in Figure 1B. Both single- and multi-task learning approaches are used to assess the prediction performances. Similar to the lead compound identification problem mentioned previously, we have used ML methods like logistic regression, KNN, neural networks, random forest, and SVMs to build drug activity prediction models. Results for each of these single-task learning models and multi-task learning are provided in Table 3. Area under the precision-recall scores for the prediction of each model are also included in Table 3. Random forest classifiers and 2-layered multi-task neural networks provide the best performances on the test sets.
Table 3.
Drug activity prediction results using ECFPs as input features.
| Model | AUC (with 95% confidence interval) | AUPR (with 95% confidence interval) |
|---|---|---|
| KNN (k = 3) | 0.68 (0.63-0.7) | 0.2 (0.14-0.24) |
| Logistic regression | 0.8 (0.77-0.81) | 0.25 (0.22-0.29) |
| Linear SVM | 0.77 (0.76-0.79) | 0.21 (0.19-0.26) |
| Random forest | 0.8 (0.78-0.83) | 0.22 (0.17-0.28) |
| 2-layered neural network | 0.72 (0.7-0.74) | 0.12 (0.1-0.14) |
| Multi-task neural network | 0.8 (0.76-0.83) | 0.22 (0.19-0.26) |
Abbreviations: AUC, area under the receiver operating characteristic curve; AUPR, area under the precision-recall curve; ECFPs, extended-connectivity fingerprints; KNN, k-nearest neighbor; SVM, support vector machine.
Multi-task network and random forest methods are marginally better than the other methods.
Drug repurposing
Drug repurposing is a scenario where previously failed drugs are re-investigated for new therapeutic indications.34 This can be posed as an ML problem where the interaction data are partially available either for the drug or the target protein, and the bioactivities of the unavailable data are of interest. This scenario is illustrated in Figure 1C. Both single-task learning and collaborative-filtering-based methods can be used to predict interactions of the unavailable data. The CF methods35 use similarities between the target profiles of 2 compounds to make predictions on their missing interactions. Moreover, they use similarities between compound profiles of 2 targets to make predictions on missing interactions. As an example, assume that Drug-A and Drug-B interact with few common targets, then there is a high chance that Drug-A and Drug-B have the same interaction profile for some missing values. This procedure is unlike ligand-based/target-based drug discovery where compound descriptors/target-protein descriptors are used to make predictions.
The CF methods are extensively used in recommender systems like Netflix, Amazon, and YouTube, where user-item data are partially available. For example, in the Netflix movie recommendation problem,35,36 each user rates only a few movies and the goal is to predict his or her ratings on unseen movies. Similarly, for each movie, only a few users would have rated it, and the goal is to predict ratings of some user. Information is shared across users and across movies to predict a new value in the user-movie recommendation matrix. Low-rank matrix factorization (LRMF) is a common method used for CF. In this method, we assume that individual drug properties are governed by a set of low-dimensional features known as latent factors. Similarly, each protein has a low-dimensional feature associated with it. Each drug and each protein are considered to interact with each other if they have similar latent factors.
The LRMF method can be formulated as follows:
Let denote a binary matrix representing Activity/No Activity with +1 representing “Activity” and −1 representing “No Activity.” Assuming that there are “n” compounds and “m” kinases, then the size of is n × m. Initially, the entire matrix is known. To build and validate ML models, the dataset has to be split into training and test data. For this purpose, we randomly remove matrix values and label them as missing/test data as shown in Figure 1C. The model assumption is that drugs and targets are controlled by a few latent factors that dictate the interactions between them. Each drug and each target are represented by an embedded k-dimensional feature. A drug and a target protein are said to interact if they are close in this k-dimensional space. Let U and V be the drug and target embeddings, respectively. U is of size n × k and V is of size k × m (a transposed feature matrix is used for convenience) for which the product is the estimated interaction matrix . Let be the input training matrix containing the values −1, +1, and 0 corresponding to No Activity, Activity, and Unknown Activity, respectively. The goal of LRMF is to find a low-rank matrix that is closest to in the Frobenius norm. Note that the Frobenius norm is calculated only for the training values.37 As described above, the low-rank constraint can be forced into by learning 2 rectangular matrices U, V of rank “k,” the product of which is equal to (product of 2 rank-k matrices gives a rank-k matrix). So the optimization problem (or loss function) becomes
| (1) |
where U is of size n × k and V is of size k × m. The terms and are the regularization terms used to limit the matrix values,38 thereby giving better results.
This optimization problem is non-convex because it contains a product of 2 variable matrices U, V. However, if we assume that one of the matrices is constant, then the problem becomes convex. Therefore, an alternating optimization scheme can be used to solve the optimization problem, where we iteratively update one matrix while keeping the other fixed. We have used the convex optimization toolbox, “CVXPY,” which is available in Python to perform optimization on our dataset. The steps of the alternating optimization method are shown in Algorithm 1.
| Algorithm 1. Alternating optimization for matrix factorization. |
|---|
|
Procedure MF(Ytr, k) 1. Initialize matrices U, V with values from unit normal distribution N(0, 1) 2. Choose a convergence threshold 3. while (prevIterLoss – IterLoss > threshold) do 4. if (odd iteration) then # update U in odd iterations 5. U = argmin Loss; given Ytr, V 6. else # update V in even iterations 7. V = argmin Loss; given Ytr, U 8. end if 9. end while 10. return U, V 11. end procedure |
Here . Note that this loss function does not contain squared terms. We have used this loss because it is faster to optimize and has the same properties as the loss function in equation (1); prevIterLoss = loss function value in previous iteration; IterLoss = loss function value in present iteration.
argmin: Minimization is done using the cvxopt function in the CVXPY toolbox. This function uses the stochastic gradient descent (SGD) method to find the global minimum of any convex function. cvxopt outputs the minimizer and the corresponding loss function value. If the loss function is non-decreasing over successive iterations, then the algorithm is considered to converge to an optimal solution. The entire implementation on our dataset is provided on Github.39
We have used a 70-30 train-test split to build and test the LRMF model. 30% of the entries are randomly removed from the initial DTI matrix and are considered as unknown test data. An LRMF method with rank k = 20 is used to build a DTI prediction model. This model has resulted in an AUC of 0.93 and an AUPR score of 0.61. From these results, we can observe that CF provides better prediction AUCs even without using any feature descriptors. This happens when lots of interaction data are available at the training stage. However, if the input data are very sparse (>90% missing entries), then descriptor-based ML models perform better because they supply external information to the model in the form of feature descriptors. Figure 5 shows the comparison of the CF and logistic regression methods at varying levels of sparsity. The logistic regression model uses BoW-based kinase imaging descriptors as input features.
Figure 5.

Performance of the collaborative filtering (using LRMF) and kinase-feature-based methods (logistic regression model) at varying levels of training data sparsity. AUC indicates area under the receiver operating characteristic curve; LRMF, low-rank matrix factorization.
CF with side information
A significant number of existing DTI algorithms are similarity-based methods. These methods use drug networks and protein networks to build models that can predict DTIs. Yamanishi et al1 published a seminal paper in 2008 that uses both drug and protein networks to build a bipartite graph learning method. Drug networks contain drug compounds as nodes and structural similarity between them as the edge lengths; protein networks contain proteins as the nodes and their sequence similarity as the edge lengths. In their paper, low-dimensional embeddings of both drugs and proteins are computed by learning a mapping function that maps drugs/proteins from the compound/genomic space to a low-dimensional pharmacology space. Drugs and proteins close by in this space are said to interact with each other. Gonen2 showed better results with a similar method, but using Bayesian priors on the mapping matrices. A variational approximation is used to solve the Bayesian optimization problem. We have tested both of their methods on our dataset, but the performances were not satisfactory compared with the CF methods. Therefore, we have used a graph regularized alternating least squares (GRALS) method to perform CF when side information like drug and protein networks is available. Rao et al37 use the GRALS method on the MovieLens dataset with user social networks as side information and show that this additional side information improves the model prediction performance. Instead of using L2-regularizers (Frobenius norm) as in equation (1), a graph-based regularizer is used. Low-dimensional embeddings in this case are learned in such a way that any 2 drugs connected in the drug network will have their embeddings close to each other. Similarly, any 2 kinases connected in the kinase network will have embeddings close to each other in the low-dimensional space. Note that these constraints are placed in addition to the initial condition where drugs and targets connected in the DTI network need to have embeddings close to each other.
Therefore, optimal U, V should be calculated such that they satisfy both the interaction matrix criterion as well as the side information criteria. The above conditions can be formulated as follows
| (2a) |
| (2b) |
| (2c) |
Equations (2b) and (2c) can be represented in the following matrix forms, which make them easier to optimize. Here, and are the adjacency matrices of the drug similarity network and the kinase similarity network, respectively. For example, represents the similarity value between drugs i and j
| (3a) |
| (3b) |
where and are the graph Laplacian matrices40 of the drug and kinase networks, respectively.
and where is the degree matrix of the drug network. It is a diagonal matrix with representing the degree of the drug node “i.”
The combined loss function can be written as
| (4) |
An alternating optimization method similar to Algorithm 1 is used to minimize equation (4). For the drug similarity network, the nodes are represented by drugs and the edges contain the structural similarity values. We have used the Sorensen-Dice coefficient41 to calculate similarity between 2 ECFP features. Given any 2 fingerprint vectors X and Y (which are 1024-dimensional bit vectors in our case), the Sorensen-Dice coefficient is calculated as follows
| (5) |
where X ∩ Y is the “AND” operation between 2 binary vectors and|X| is the total number of ones in X.
For the kinase similarity network, kinases are represented by the nodes and the edges contain the kinase similarity values. Cosine similarity between the normalized kinase imaging features is used as a similarity metric. After the similarity matrices are created, we preserve only 5 nearest neighbors for each node in both the networks. This nearest neighbor truncation is applied because sparse similarity matrices are faster to train and perform inference. We have tested this collaborative filtering with side information (CFSI) model with rank k = 20, and the side information is the truncated drug and target similarity matrices. This has resulted in an AUC of 0.94 for the drug repurposing case as shown in Figure 1C. Results for the unknown drug case as in Figure 1B and unknown target cases in Figure 1A are very similar to the ones obtained through feature-based models.
Discussion
Quantitative structure-activity relationship methods have been well studied in the past 2 decades.42 Drug-target interaction prediction methods are a subclass of QSAR methods that are primarily used for virtual screening.43 Existing DTI prediction methods use information like compound chemical structures and amino acid sequences to describe drug compounds and target proteins. Recently, Simm et al22 showed that imaging-based features extracted from high-throughput screening can be used to describe drug compounds. These imaging features are not completely related to the chemical structure and therefore might contain mutually exclusive information regarding drug-target bioactivity. Their work has motivated us to look at new imaging-based descriptors for target proteins, especially kinases, that can be used in DTI prediction. We have shown the DTI prediction results in 3 different setups: lead compound identification, drug activity prediction, and drug repurposing as shown in Figure 1. A new approach to lead compound identification has been introduced using the image-derived kinase features, unlike most existing methods that use gene/protein sequence information to represent kinases.2–4 Two feature extraction approaches for kinase imaging data, namely, a population-median-based approach and a BoW-based approach, are used to build target-based drug discovery models. BoW features are generally favored over population median features because of their ability to capture heterogeneity across the imaging data. However, our results (see Tables 1 and 2) show that BoW does not provide a significant improvement over median-based features.
Multiple methods like single-task learning, multi-task learning, and CF are used to build models for DTI prediction. Various ML models like logistic regression, SVMs, KNN, neural networks, and random forests are used for the single-task learning setup. Whereas KNN performs poorly, all the remaining methods provide similar performances with random forests being marginally better than the others. In the multi-task learning setup, we have used a 2-layered neural network to build prediction models. We observe that the multi-task learning method provides slightly better results than the single-task learning methods (see Tables 1 to 3). For the CF setup, we have used 2 types of models, one that uses only the DTI data and the other that uses additional side information (ie, drug networks and protein networks) to build prediction models. Collaborative filtering methods outperform feature-based methods (single-task/multi-task learning) when a sufficient amount of training data are available (ie, if more than 10% of DTIs are known in the training phase). In cases where the available DTIs are reduced (sparser training data), the performance of the CF method drops and feature-based methods tend to perform better. Prediction performances of both the models are compared with varying levels of training data, and the results are shown in Figure 5. Even though the performance of the CF methods is impressive, it is important to note that predictions for drugs/targets that do not have any known interactions (ie, entirely new drugs/targets) are difficult. Collaborative filtering with side information overcomes this problem using data from drug/protein networks to make predictions. It is recommended to use CF with side information for DTI predictions because of its general use in all 3 tasks—lead compound identification, drug activity prediction, and drug repurposing—while giving the best accuracies. CF with side information44 is known to provide state-of-the-art results on the gold standard dataset from Bleakley and Yamanishi13 to predict DTI for 4 kinds of target proteins: enzymes, ion channels, GPCRs, and nuclear receptors. In general, variants of matrix factorization are known to perform well in DTI prediction. This has been the case for prediction of drug-kinase interactions using imaging-based descriptors. In this article, we have shown that feature descriptors extracted from HCA could be used for virtual screening, thereby making the drug discovery process more cost efficient. Our future work includes collecting more drug-kinase bioactivity data and experimentally validating the proposed models.
Footnotes
Funding:The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: A.R. and S.K. were supported by CCSG Bioinformatics Shared Resource P30 CA016672, an Institutional Research Grant from The University of Texas MD Anderson Cancer Center (MD Anderson), CPRIT RP170719, CPRIT RP150578, NCI R37CA214955-01A1, a Career Development Award from the MD Anderson Brain Tumor SPORE, a gift from Agilent Technologies, and a Research Scholar Grant from the American Cancer Society (RSG-16-005-01).
Declaration of Conflicting Interests:The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Author Contributions: SK and AR created the machine learning methodology and performed the required computational experiments. AS, MM and FS have performed wet lab experiments and provided the siRNA imaging data that is used for building machine learning models.
References
- 1. Yamanishi Y, Araki M, Gutteridge A, Honda W, Kanehisa M. Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics. 2008;24:i232–i240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Gonen M. Predicting drug-target interactions from chemical and genomic kernels using Bayesian matrix factorization. Bioinformatics. 2012;28:2304–2310. [DOI] [PubMed] [Google Scholar]
- 3. Cobanoglu MC, Liu C, Hu F, Oltvai ZN, Bahar I. Predicting drug–target interactions using probabilistic matrix factorization. J Chem Inf Model. 2013;53:3399–3409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. van Laarhoven T, Nabuurs SB, Marchiori E. Gaussian interaction profile kernels for predicting drug–target interaction. Bioinformatics. 2011;27:3036–3043. [DOI] [PubMed] [Google Scholar]
- 5. van Laarhoven T, Marchiori E. Predicting drug-target interactions for new drug compounds using a weighted nearest neighbor profile. PLoS ONE. 2013;8:e66952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Paul SM, Mytelka DS, Dunwiddie CT, et al. How to improve R&D productivity: the pharmaceutical industry’s grand challenge. Nat Rev Drug Discov. 2010;9:203–214. [DOI] [PubMed] [Google Scholar]
- 7. Hopkins AL, Groom CR. The druggable genome. Nat Rev Drug Discov. 2002;1:727–730. [DOI] [PubMed] [Google Scholar]
- 8. Ding H, Takigawa I, Mamitsuka H, Zhu S. Similarity-based machine learning methods for predicting drug–target interactions: a brief review. Brief Bioinform. 2013;15:734–747. [DOI] [PubMed] [Google Scholar]
- 9. Nagamine N, Sakakibara Y. Statistical prediction of protein–chemical interactions based on chemical structure and mass spectrometry data. Bioinformatics. 2007;23:2004–2012. doi: 10.1093/bioinformatics/btm266. [DOI] [PubMed] [Google Scholar]
- 10. Nagamine N, Shirakawa T, Minato Y, et al. Integrating statistical predictions and experimental verifications for enhancing protein-chemical interaction predictions in virtual screening. PLoS Comput Biol. 2009;5:e1000397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Hattori M, Okuno Y, Goto S, Kanehisa M. Development of a chemical structure comparison method for integrated analysis of chemical and genomic information in the metabolic pathways. J Am Chem Soc. 2003;125:11853–11865. [DOI] [PubMed] [Google Scholar]
- 12. Smith TF, Waterman MS. Identification of common molecular subsequences. J Mol Biol. 1981;147:195–197. [DOI] [PubMed] [Google Scholar]
- 13. Bleakley K, Yamanishi Y. Supervised prediction of drug–target interactions using bipartite local models. Bioinformatics. 2009;25:2397–2403. doi: 10.1093/bioinformatics/btp433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Lonard DM, O’Malley BW. Nuclear receptor coregulators: modulators of pathology and therapeutic targets. Nat Rev Endocrinol. 2012;8:598–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Anbalagan M, Huderson B, Murphy L, Rowan BG. Post-translational modifications of nuclear receptors and human disease. Nucl Recept Signal. 2012;10:e001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Stossi F, Bolt MJ, Ashcroft FJ, et al. Defining estrogenic mechanisms of bisphenol A analogs through high throughput microscopy-based contextual assays. Chem Biol. 2014;21:743–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Szafran AT, Stossi F, Mancini MG, Walker CL, Mancini MA. Characterizing properties of non-estrogenic substituted bisphenol analogs using high throughput microscopy and image analysis. PLoS ONE. 2017;12:e0180141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ashcroft FJ, Newberg JY, Jones ED, Mikic I, Mancini MA. High content imaging-based assay to classify estrogen receptor-α ligands based on defined mechanistic outcomes. Gene. 2011;477:42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Trevino LS, Bolt MJ, Grimm SL, Edwards DP, Mancini MA, Weigel NL. Differential regulation of progesterone receptor-mediated transcription by CDK2 and DNA-PK. Mol Endocrinol. 2016;30:158–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Szafran AT, Mancini MA. The myImageAnalysis project: a web-based application for high-content screening. Assay Drug Dev Technol. 2014;12:87–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Judson RS, Magpantay FM, Chickarmane V, et al. Integrated model of chemical perturbations of a biological pathway using 18 in vitro high-throughput screening assays for the estrogen receptor. Toxicol Sci. 2015;148:137–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Simm J, Klambauer G, Arany A, et al. Repurposing high-throughput image assays enables biological activity prediction for drug discovery. Cell Chem Biol. 2018;25:611.e3–618.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. DrugKiNET. http://www.drugkinet.ca. Accessed October 25, 2018.
- 24. Wang Y, Xiao J, Suzek TO, Zhang J, Wang J, Bryant SH. PubChem: a public information system for analyzing bioactivities of small molecules. Nucleic Acids Res. 2009;37:W623–W633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Gaulton A, Bellis LJ, Bento AP, et al. ChEMBL: a large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012;40:D1100–D1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Filliat D. A visual bag of words method for interactive qualitative localization and mapping. Paper presented at: International Conference on Robotics and Automation; April 10-14, 2007; Roma, Italy. doi: 10.1109/robot.2007.364080. [DOI] [Google Scholar]
- 27. Rogers D, Hahn M. Extended-connectivity fingerprints. J Chem Inf Model. 2010;50:742–754. [DOI] [PubMed] [Google Scholar]
- 28. Extended connectivity fingerprint ECFP. In: ChemAxon—DOCS. https://docs.chemaxon.com/display/docs/Extended+Connectivity+Fingerprint+ECFP. Accessed October 25, 2018.
- 29. Landrum G. RDKit. https://www.rdkit.org. Accessed October 25, 2018.
- 30. Yang J, Jiang Y-G, Hauptmann AG, Ngo C-W. Evaluating bag-of-visual-words representations in scene classification. Paper presented at: International Workshop on Workshop on Multimedia Information Retrieval (MIR ’07); September 24-29, 2007; Augsburg, Germany. doi: 10.1145/1290082.1290111. [DOI] [Google Scholar]
- 31. Dahl GE, Jaitly N, Salakhutdinov R. Multi-task neural networks for QSAR predictions. https://arxiv.org/abs/1406.1231. Up-dated 2014.
- 32. Ramsundar B, Kearnes S, Riley P, Webster D, Konerding D, Pande V. Massively multitask networks for drug discovery. https://arxiv.org/abs/1502.02072.
- 33. Bradley AP. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997;30:1145–1159. [Google Scholar]
- 34. Oprea TI, Mestres J. Drug repurposing: far beyond new targets for old drugs. AAPS J. 2012;14:759–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer. 2009;42:30–37. [Google Scholar]
- 36. Hu Y, Koren Y, Volinsky C. Collaborative filtering for implicit feedback datasets. Paper presented at: International Conference on Data Mining; December 15-19, 2008; Pisa, Italy. doi: 10.1109/icdm.2008.22. [DOI] [Google Scholar]
- 37. Rao N, Yu H-F, Ravikumar PK, Dhillon IS. Collaborative filtering with graph information: consistency and scalable methods. https://papers.nips.cc/paper/5938-collaborative-filtering-with-graph-information-consistency-and-scalable-methods.
- 38. Ng AY. Feature selection, L1 vs. L2 regularization, and rotational invariance. Paper presented at: International Conference on Machine learning (ICML ’04); July 4-8, 2004; Banff, AB, Canada. doi: 10.1145/1015330.1015435. [DOI] [Google Scholar]
- 39. Kuthuru S. Github weblink to access codes. github.com/srikanthkuthuru/DTI-prediction.
- 40. von Luxburg U. A tutorial on spectral clustering. Stat Comput. 2007;17:395–416. [Google Scholar]
- 41. Jackson DA, Somers KM, Harvey HH. Similarity coefficients: measures of co-occurrence and association or simply measures of occurrence? Am Nat. 1989;133:436–453. [Google Scholar]
- 42. Puzyn T, Leszczynski J, Cronin MT. Recent Advances in QSAR Studies: Methods and Applications. London, England: Springer Science & Business Media; 2010. [Google Scholar]
- 43. Ekins S, Mestres J, Testa B. In silico pharmacology for drug discovery: methods for virtual ligand screening and profiling. Br J Pharmacol. 2007;152:9–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zheng X, Ding H, Mamitsuka H, Zhu S. Collaborative matrix factorization with multiple similarities for predicting drug-target interactions. Paper presented at: International Conference on Knowledge Discovery and Data Mining (KDD ’13); August 11-14, 2013; Chicago, IL. doi: 10.1145/2487575.2487670. [DOI] [Google Scholar]