Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jul 6;35(23):7383–7387. doi: 10.1021/acs.langmuir.8b01276

Protein–Water–Ice Contact Angle

Jens O M Karlsson †, Ido Braslavsky ‡, Janet A W Elliott §,*
PMCID: PMC6563840  PMID: 29979046

Abstract

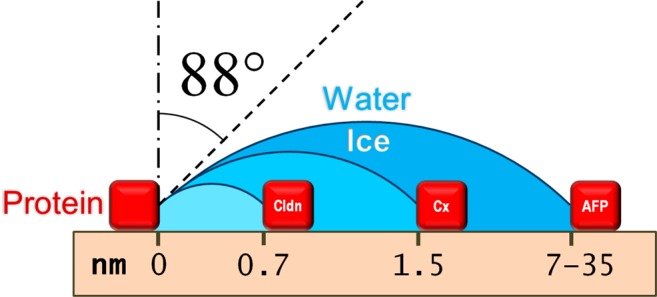
graphic file with name la-2018-01276k_0005.jpg

The protein–water–ice contact angle is a controlling parameter in diverse fields. Here we show that data from three different experiments, at three different length scales, with three different proteins, in three different laboratories yield a consistent value for the protein–water–ice contact angle (88.0 ± 1.3°) when analyzed using the Gibbs–Thomson equation. The measurements reinforce the validity of each other, and the fact that similar values are obtained across diverse length scales, experiments, and proteins yields insight into protein–water interactions and the applicability of thermodynamics at the nanoscale.

Introduction

The interaction of water with proteins and other biological molecules is fundamental to biology and a subject of intense current interest.1−4 Knowledge of the contact angle that an ice–water interface makes with a protein could add new insight to this interaction. Also, the protein–water–ice contact angle is a controlling parameter in processes in diverse fields including cloud physics,5,6 cell7 and tissue cryopreservation,8,9 food processing,10 artificial snow making,5 and natural biological adaptions in cold-climate-resilient plants, animals, and bacteria.11 Even though this property can be determined indirectly from the Gibbs–Thomson equation (the thermodynamic relationship that describes freezing-point depression due to interfacial curvature), this approach requires knowledge of geometric dimensions that are difficult to estimate at the nanometer length scales associated with protein–water–ice interactions. Consequently, it is common to assume speculative values for the contact angle7,8 or to use phenomenological parametrizations that lump the contact angle with other physical properties.5,12 Specifically in the field of cryobiology, inaccurate values of the protein–water–ice contact angle may lead to errors in the prediction of intracellular ice formation temperatures or of ice-binding protein activities.

Gibbs–Thomson Equation

The growth of ice in a confined space is limited by the geometrically imposed ice–liquid interface curvature and the ensuing freezing-point depression. See Figure 1. The relationship between freezing point depression ΔT (the amount that the equilibrium freezing point of the confined aqueous solution is below the freezing point of the unconfined aqueous solution8) and the curvature of a spherical ice front in a confining cylindrical pore of diameter d is given by the Gibbs–Thomson equation13

graphic file with name la-2018-01276k_m001.jpg 1

where Tf = 273.15 K is the equilibrium freezing point of unconfined pure water, vI = 1.091 × 10–3 m3/kg is the specific volume of ice at Tf, Lf = 3.337 × 105 J/kg is the specific latent heat of fusion of pure water at Tf, γ is the ice–water interfacial tension, and θ is the contact angle that the ice–water interface makes with the confining pore wall as measured through the liquid water. There are some important things to note in the application of the Gibbs–Thomson equation. First, because of the action of interfacial tension, the shape of the equilibrium ice–water interface is indeed approximately spherical when confined within a cylindrical pore. Liu et al. showed explicitly that the ice interface was spherical in glass capillaries of 6 to 20 μm diameter.14 Second, because of the elegant construction of the Gibbs dividing surface and the Gibbs surface of tension (whereby all effects of the existence of an interface are assigned for accounting purposes to surface excess properties), the composite system thermodynamics of Gibbs,15 on which eq 1 is based, is expected to be valid down to length scales (phase dimensions, radii of curvature, pore diameters) significantly smaller than the depth to which interface effects (such as the ordering of water molecules) extend into the bulk. To date, the validity of eq 1 has been experimentally confirmed for pore diameters down to 3.6 nm.16 Third, eq 1 predicts that the curvature-induced freezing-point depression does not become appreciable until the curvature reaches length scales below those easily accessible optically, making visual verification of the contact angle barely possible. That is, in systems for which the curvature-induced freezing-point depression is significant, the contact angle appearing in eq 1 is not known a priori.

Figure 1.

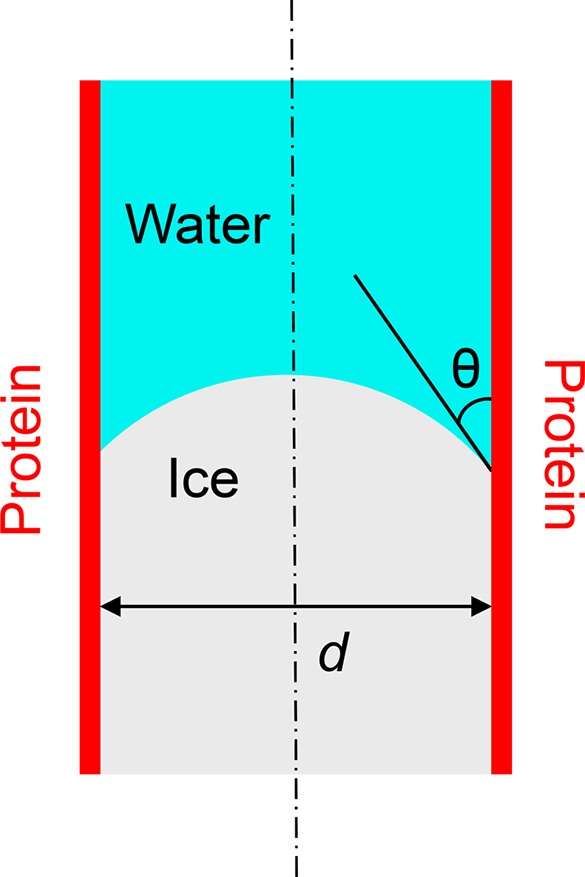
Figure 1

Open in a new tab

Schematic of ice in a cylindrical confining pore. The pore diameter, d, and the ice–water–wall contact angle, θ, are identified.

Results

The authors and their co-workers have independently undertaken three different experiments that examine the temperature at which ice can grow through pores formed by animal proteins.8,9,17 Each study used a temperature-controlled cryomicroscope to observe a biological material in which one or more proteinaceous pores separated a crystallized aqueous compartment from a supercooled aqueous compartment, allowing the temperature of ice growth through the pore to be determined by the visual detection of ice crystal formation in the adjoining liquid compartment. Thus, each paper reported a measurement of ΔT for a known circumstance of ice propagation in a confined space; the experimental methods and circumstances are elaborated in the paragraphs below and given in full in the cited references. In this work, using these previously published ΔT data together with the Gibbs–Thomson equation (eq 1) and suitable values for the constants appearing in that equation, we obtained estimates of the protein–water–ice contact angle. For the analysis of all three data sets, we used a single value for the ice–water interfacial tension of 30 mJ/m2, which has broad independent experimental support,14,18−20 and then performed a sensitivity analysis to determine the impact of uncertainties in this least-well-known parameter of eq 1.

Drori, Davies, and Braslavsky correlated measurements of thermal hysteresis (the difference between the melting point of ice and the lower temperature of an ice growth burst) with the surface density of hyperactive antifreeze protein from Tenebrio molitor adsorbed on the surface of ice crystals, and interpreted the thermal hysteresis as being due to the curvature-induced freezing-point depression ΔT resulting from the constraint that ice grow through voids between adsorbed antifreeze proteins.17 See Figure 2. It is important to understand that these antifreeze proteins have a unique interaction with the ice surface that enables them to adhere to ice crystals. Whereas the ice-binding domain of the protein has a high affinity for ice over liquid water, the outward-facing domains of the protein do not have this preference for ice.11,17 Here, we consider the contact angle resulting from interactions of the water–ice interface with the nonbinding surfaces of the antifreeze protein.

Figure 2.

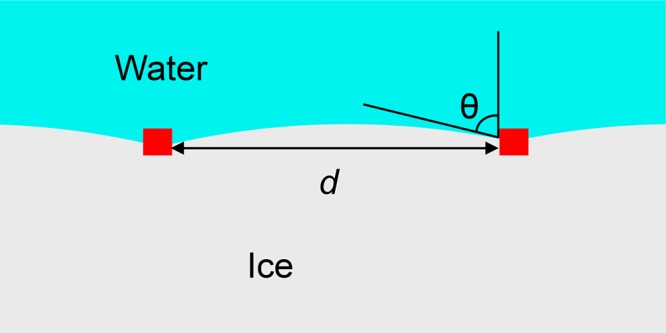
Figure 2

Open in a new tab

Schematic of ice blocked by ice-binding proteins (shown in red), depicting interactions between the curved ice–water interface and the protein surface.

If the spatial distribution of the ice-binding proteins is modeled as a Poisson point process, then the expected value of the diameter of circular voids is given by 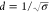Inline graphic, where σ is the average surface density of adsorbed antifreeze protein.21 For protein densities that yielded mean void diameters ranging from 7 to 35 nm, the thermal hysteresis was well fit by the relationship

graphic file with name la-2018-01276k_m003.jpg 2

When this expression is substituted into eq 1, the resulting value of the protein–water–ice contact angle is found to be 87.5 ± 0.2°. An estimate of the contact angle from a similar analysis was first published in ref (17); the value reported here differs slightly (by ∼2.5°) from the value given in ref (17) because the previous calculation assumed regular spacing of the adsorbed proteins and thus applied a different form of the Gibbs–Thomson equation.

Higgins and Karlsson used high-speed imaging techniques to observe the mechanism of initiation of intracellular ice formation in pairs of genetically modified MIN6 (mouse insulinoma) cell strains, and found that intracellular freezing was preceded by a paracellular ice penetration process in which growing extracellular ice crystals inoculate pockets of supercooled solution that are trapped between apposing membranes at the cell–cell interface.9 See Figure 3. They observed that although the rate of incidence of paracellular ice penetration events varied by nearly an order of magnitude in the four different MIN6 strains investigated, the probability of paracellular freezing vanished abruptly at temperatures above a threshold temperature that fell within a narrow range (−5.92 to −5.41 °C) for each of the four cell strains. Following the evidence and arguments presented in ref (9), we assume that paracellular ice penetration events occur when ice grows through claudin pores that regulate the paracellular permeability of tight junction strands. Paracellular claudin pores are estimated to have diameters in the range of 0.65–0.8 nm.22,23 Substituting that value for d in eq 1 along with the measured freezing-point depression for paracellular ice penetration relative to the freezing point of the unconfined aqueous solution, which was −1.5 °C, i.e.,9

graphic file with name la-2018-01276k_m004.jpg 3

we calculate a protein–water–ice contact angle of 88.4 ± 0.3°. The value reported here is slightly different from the corresponding one previously reported in ref (9) (by ∼0.1°) due to improved estimates of the pore diameter and the ice–water interfacial tension value in eq 1.

Figure 3.

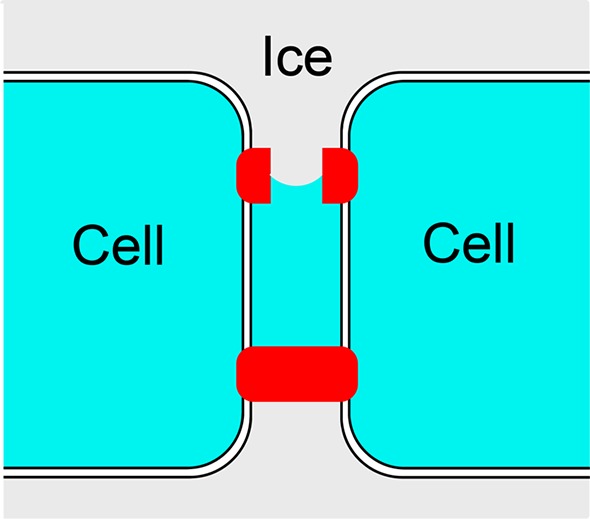
Figure 3

Open in a new tab

Schematic diagram of cell–cell interface with tight junctions (tight junction proteins shown in red) depicting the paracellular growth of extracellular ice through a claudin pore (which results in the inoculation of a liquid pocket located between the two cell membranes).

Acker, Elliott, and McGann observed the spatiotemporal pattern of intracellular ice formation in monolayer cultures of Madine–Darby canine kidney (MDCK) cells and interpreted the appearance of directed wavelike patterns of ice formation as evidence of ice growth through gap junctions.8 See Figure 4. They found that ice grew readily from cell to cell at −3 °C but not at higher temperatures. Because the unconfined isotonic solution produces a colligative freezing-point depression of 0.6 °C, the gap junction channels can be assumed to have contributed a curvature-induced freezing-point depression of

graphic file with name la-2018-01276k_m005.jpg 4

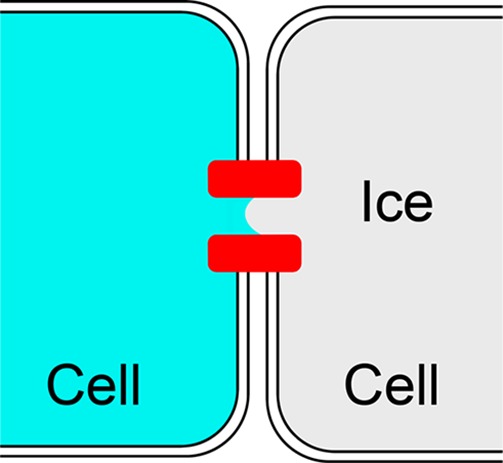
Figure 4.

Figure 4

Open in a new tab

Schematic illustration of ice growth from one cell to an adjacent cell through a gap junction pore. Gap junction proteins are shown in red.

When this ΔT together with a diameter for gap junction pores of 1.5 nm is used in eq 1, the protein–water–ice contact angle is found to be 88.1°. While 1.5 nm is an accepted estimate of the gap junction pore diameter in mammalian cells,24 gap junction pore diameters have been measured to range from 0.8 to 2.4 nm.25 Taking into account this uncertainty in the pore diameter, the contact angle resulting from this third experiment can be given as 88 ± 1°.

Discussion and Conclusion

Herein we used the Gibbs–Thomson equation together with data from three different experiments on ice propagation through protein pores and obtained estimates for the protein–water–ice contact angle with error bounds of 1° or less for each experiment. Significantly, all of the contact angles thus obtained agree with each other very closely, giving a contact angle of 88 ± 1° (in which the value and error represent the range of obtained results). We note that these experiments involve three different types of protein, in three different experiments, with three different geometries, in three different laboratories and with pore sizes spanning almost 2 orders of magnitude (0.65–35 nm). Furthermore, as the ice–water interfacial tension is the least well known constant in eq 1, performing a sensitivity analysis on the effect of varying the ice–water interfacial tension from 27 to 34 mJ/m2 (the largest range supported by the different results in refs (18−20) and more than adequate to cover any temperature dependence of the interfacial tension18) broadens our precision of the protein–water–ice contact angle reported here only slightly, to 88.0 ± 1.3°.

The results in this article are important for two reasons. First, the fact that the contact angle is close to 90° indicates that the protein–water interfacial tension is very similar to the protein–ice interfacial tension, which is consistent with the known phenomenon of water structuring by proteins.26−28 Because the precision of our reported value of the contact angle is high (±1.5%), it may be possible to use this parameter value to calibrate molecular dynamics simulations to gain additional insight into protein–water interactions.29,30 Second, the high degree of consistency among our three independent contact angle estimates justifies the application of eq 1 to each of the experimental systems. Specifically, within the limits of experimental uncertainty, the contact angles obtained from the two experiments with the smallest pore sizes (in the range 0.65–2.4 nm) are in agreement with each other, and these nanoscale measurements also agree with the values found from the experiments with larger pore sizes of up to 35 nm. Inasmuch as the validity of the Gibbs–Thomson equation is not in doubt for the larger pore dimensions, the agreement among all three experimental studies suggests that eq 1 is also valid for the nanometer-scale pores. Thus, our results represent the smallest length scale to which the Gibbs–Thomson equation has found support for validity.16,31,32

The results of our article beg the question, what is the smallest length scale at which it is possible for the Gibbs–Thomson equation to be valid? The Gibbs–Thomson equation has been previously experimentally verified for water in porous glass down to a diameter of 3.6 nm, and it was further shown that water molecules moved rather freely in pores of this dimension.16 For systems such as water in glass with contact angles near 0°,14 the first limit of validity of Gibbsian composite system thermodynamics is set by the scale at which disjoining pressure, which keeps the interface from approaching the pore wall, becomes an appreciable effect. For our systems, in which the contact angle is near 90°, the interface comes straight out from the wall and disjoining pressure makes no contribution to the contact angle. The next limit of possible validity of thermodynamics occurs as the pore size approaches the molecular size and molecules are excluded from the pore. The effective diameter of a water molecule has been estimated to be 0.274 nm,33 meaning that our smallest pore size is only 2.4 molecular diameters across. It is therefore unlikely that agreement with the Gibbs–Thomson equation will be found with length scales any smaller than the smallest pore size in this article.

The applicability of eq 1 to nanoscale phase transformations is a testament to the careful structure of Gibbsian thermodynamics of composite systems,15 which, because of the prescient constructs of the Gibbs dividing surface and the Gibbs surface of tension, is valid even in systems with dimensions comparable to or smaller than the length scale of the interface effects. Thus, beyond their importance for applications in biology and cloud physics, our results are broadly significant for the fundamental disciplines of thermodynamics and nanoscale science.

Acknowledgments

J.A.W.E. holds a Canada Research Chair in Thermodynamics and acknowledges funding from the Natural Sciences and Engineering Research Council of Canada (DG-194168 and RGPIN-2016-05502). I.B. acknowledges research grants from the European Research Council and the Israel Science Foundation. J.O.M.K. acknowledges grant support from the United States National Science Foundation and National Institutes of Health.

The authors declare no competing financial interest.

References

  1. Klebe G. Applying Thermodynamic Profiling in Lead Finding and Optimization. Nat. Rev. Drug Discovery 2015, 14, 95–110. 10.1038/nrd4486. [DOI] [PubMed] [Google Scholar]
  2. Moyano D. F.; Ray M.; Rotello V. M. Nanoparticle–protein Interactions: Water Is the Key. MRS Bull. 2014, 39, 1069–1073. 10.1557/mrs.2014.255. [DOI] [Google Scholar]
  3. Raschke T. M. Water Structure and Interactions with Protein Surfaces. Curr. Opin. Struct. Biol. 2006, 16, 152–159. 10.1016/j.sbi.2006.03.002. [DOI] [PubMed] [Google Scholar]
  4. Ball P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74–108. 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
  5. Sahyoun M.; Wex H.; Gosewinkel U.; Šantl-Temkiv T.; Nielsen N. W.; Finster K.; Sørensen J. H.; Stratmann F.; Korsholm U. S. On the Usage of Classical Nucleation Theory in Quantification of the Impact of Bacterial INP on Weather and Climate. Atmos. Environ. 2016, 139, 230–240. 10.1016/j.atmosenv.2016.05.034. [DOI] [Google Scholar]
  6. Murray B. J.; O’Sullivan D.; Atkinson J. D.; Webb M. E. Ice Nucleation by Particles Immersed in Supercooled Cloud Droplets. Chem. Soc. Rev. 2012, 41, 6519–6554. 10.1039/c2cs35200a. [DOI] [PubMed] [Google Scholar]
  7. Mazur P. The Role of Cell Membranes in the Freezing of Yeast and Other Single Cells. Ann. N. Y. Acad. Sci. 1965, 125, 658–676. 10.1111/j.1749-6632.1965.tb45420.x. [DOI] [PubMed] [Google Scholar]
  8. Acker J. P.; Elliott J. A. W.; McGann L. E. Intercellular Ice Propagation: Experimental Evidence for Ice Growth through Membrane Pores. Biophys. J. 2001, 81, 1389–1397. 10.1016/S0006-3495(01)75794-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Higgins A. Z.; Karlsson J. O. M. Effects of Intercellular Junction Protein Expression on Intracellular Ice Formation in Mouse Insulinoma Cells. Biophys. J. 2013, 105, 2006–2015. 10.1016/j.bpj.2013.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Goff H. D. Formation and Stabilisation of Structure in Ice-Cream and Related Products. Curr. Opin. Colloid Interface Sci. 2002, 7, 432–437. 10.1016/S1359-0294(02)00076-6. [DOI] [Google Scholar]
  11. Bar Dolev M.; Braslavsky I.; Davies P. L. Ice-Binding Proteins and Their Function. Annu. Rev. Biochem. 2016, 85, 515–542. 10.1146/annurev-biochem-060815-014546. [DOI] [PubMed] [Google Scholar]
  12. Koop T.; Zobrist B. Parameterizations for Ice Nucleation in Biological and Atmospheric Systems. Phys. Chem. Chem. Phys. 2009, 11, 10839–10850. 10.1039/b914289d. [DOI] [PubMed] [Google Scholar]
  13. The origin of the Gibbs–Thomson equation merits some discussion. Thomson (Lord Kelvin) introduced the idea that interfacial curvature should cause an effect on phase equilibrium in 1871.34 However, because the concept of chemical potential was not yet known at the time, the equation appearing in Thomson’s paper is not thermodynamically correct. With the introduction of the chemical potential (1876–1878), Gibbs presented in general form all that is needed to correctly write down any condition for the thermodynamic equilibrium of a system containing a curved interface (e.g., the corrected liquid–vapor Kelvin equation,35 the solute–solution Ostwald–Freundlich equation,36−39 or the solid–liquid Gibbs–Thomson equation39−41) with eq 661 of his famous paper and the discussion that followed (i.e., the combination of chemical potential equality with the mechanical equilibrium describing the pressure difference across a curved surface with interfacial tension).15 While it was not until some years later that explicit forms of the chemical potentials of the liquid and solid phases were substituted into Gibbs’ equations to arrive at eq 1,40,41 the naming of eq 1 as the Gibbs–Thomson equation aptly recognizes the significance of the early contributions.
  14. Liu Z.; Muldrew K.; Wan R. G.; Elliott J. A. W. Measurement of Freezing Point Depression of Water in Glass Capillaries and the Associated Ice Front Shape. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2003, 67, 061602. 10.1103/PhysRevE.67.061602. [DOI] [PubMed] [Google Scholar]
  15. Gibbs J. W. On the Equilibrium of Heterogeneous Substances. Trans. Connecticut Acad. 1876, 2, 108–248. [Google Scholar]; The Scientific Papers of J. Willard Gibbs; Ox Bow Press: Woodridge, CT, 1993; Vol. 1, pp 55–353. [Google Scholar]
  16. Hirama Y.; Takahashi T.; Hino M.; Sato T. Studies of Water Adsorbed in Porous Vycor Glass. J. Colloid Interface Sci. 1996, 184, 349–359. 10.1006/jcis.1996.0629. [DOI] [PubMed] [Google Scholar]
  17. Drori R.; Davies P. L.; Braslavsky I. Experimental Correlation between Thermal Hysteresis Activity and the Distance between Antifreeze Proteins on an Ice Surface. RSC Adv. 2015, 5, 7848. 10.1039/C4RA12638F. [DOI] [Google Scholar]
  18. Wood G. R.; Walton A. G. Homogeneous Nucleation Kinetics of Ice from Water. J. Appl. Phys. 1970, 41, 3027–3036. 10.1063/1.1659359. [DOI] [Google Scholar]
  19. Hardy S. C. A. Grain Boundary Groove Measurement of the Surface Tension between Ice and Water. Philos. Mag. 1977, 35, 471–484. 10.1080/14786437708237066. [DOI] [Google Scholar]
  20. Hillig W. B. Measurement of Interfacial Free Energy for Ice/Water System. J. Cryst. Growth 1998, 183, 463–468. 10.1016/S0022-0248(97)00411-9. [DOI] [Google Scholar]
  21. Illian J.; Penttinen A.; Stoyan H.; Stoyan D.. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons, 2007 10.1002/9780470725160. [DOI] [Google Scholar]
  22. Yu A. S. L.; Cheng M. H.; Angelow S.; Günzel D.; Kanzawa S. A.; Schneeberger E. E.; Fromm M.; Coalson R. D. Molecular Basis for Cation Selectivity in Claudin-2-Based Paracellular Pores: Identification of an Electrostatic Interaction Site. J. Gen. Physiol. 2009, 133, 111–127. 10.1085/jgp.200810154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Van Itallie C. M.; Holmes J.; Bridges A.; Gookin J. L.; Coccaro M. R.; Proctor W.; Colegio O. R.; Anderson J. M. The Density of Small Tight Junction Pores Varies among Cell Types and Is Increased by Expression of Claudin-2. J. Cell Sci. 2008, 121, 298–305. 10.1242/jcs.021485. [DOI] [PubMed] [Google Scholar]
  24. Loewenstein W. R. Junctional Intercellular Communication: The Cell-to-Cell Membrane Channel. Physiol. Rev. 1981, 61, 829–913. 10.1152/physrev.1981.61.4.829. [DOI] [PubMed] [Google Scholar]
  25. Veenstra R. D. Size and Selectivity of Gap Junction Channels Formed from Different Connexins. J. Bioenerg. Biomembr. 1996, 28, 327–337. 10.1007/BF02110109. [DOI] [PubMed] [Google Scholar]
  26. Zhang L.; Yang Y.; Kao Y.-T.; Wang L.; Zhong D. Protein Hydration Dynamics and Molecular Mechanism of Coupled Water-Protein Fluctuations. J. Am. Chem. Soc. 2009, 131, 10677–10691. 10.1021/ja902918p. [DOI] [PubMed] [Google Scholar]
  27. Meister K.; Ebbinghaus S.; Xu Y.; Duman J. G.; DeVries A.; Gruebele M.; Leitner D. M.; Havenith M. Long-Range Protein-Water Dynamics in Hyperactive Insect Antifreeze Proteins. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 1617–1622. 10.1073/pnas.1214911110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Heyden M.; Tobias D. J. Spatial Dependence of Protein-Water Collective Hydrogen-Bond Dynamics. Phys. Rev. Lett. 2013, 111, 218101. 10.1103/PhysRevLett.111.218101. [DOI] [PubMed] [Google Scholar]
  29. Lupi L.; Hudait A.; Molinero V. Heterogeneous Nucleation of Ice on Carbon Surfaces. J. Am. Chem. Soc. 2014, 136, 3156–3164. 10.1021/ja411507a. [DOI] [PubMed] [Google Scholar]
  30. Pandey R.; Usui K.; Livingstone R. A.; Fischer S. A.; Pfaendtner J.; Backus E. H. G.; Nagata Y.; Fröhlich-Nowoisky J.; Schmüser L.; Mauri S.; Scheel J. F.; Knopf D. A.; Pöschl U.; Bonn M.; Weidner T. Ice-Nucleating Bacteria Control the Order and Dynamics of Interfacial Water. Sci. Adv. 2016, 2, e1501630. 10.1126/sciadv.1501630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Fisher L. R.; Israelachvili J. N. Direct Experimental Verification of the Kelvin Equation for Capillary Condensation. Nature 1979, 277, 548–549. 10.1038/277548a0. [DOI] [Google Scholar]
  32. Christenson H. K. Confinement Effects on Freezing and Melting. J. Phys.: Condens. Matter 2001, 13, R95–R133. 10.1088/0953-8984/13/11/201. [DOI] [Google Scholar]
  33. Zhang Y.; Xu Z. Atomic Radii of Noble Gas Elements in Condensed Phases. Am. Mineral. 1995, 80, 670–675. 10.2138/am-1995-7-803. [DOI] [Google Scholar]
  34. Thomson W. On the Equilibrium of Vapour at a Curved Surface of Liquid. Philos. Mag. 1871, 42, 448–452. 10.1080/14786447108640606. [DOI] [Google Scholar]
  35. Elliott J. A. W. On the Complete Kelvin Equation. Chem. Eng. Educ. 2001, 35, 274–278. [Google Scholar]
  36. Ostwald W. Über die vermeintliche Isomerie des roten und gelben Quecksilbersoxyds und die Oberflächenspannung fester Körper. Z. Phys. Chem. 1900, 34, 495–503. 10.1515/zpch-1900-3431. [DOI] [Google Scholar]
  37. Freundlich H.Akademische Verlagsgessellschaft: Leipzig. Kapillarchemie; Eine Darstellung der Chemie der Kolloide und verwanter Gebiete, Leipzig, 1909. https://searchworks.stanford.edu/view/666516 (accessed July 15, 2017).
  38. Eslami F.; Elliott J. A. W. Role of Precipitating Solute Curvature on Microdrops and Nanodrops during Concentrating Processes: The Nonideal Ostwald-Freundlich Equation. J. Phys. Chem. B 2014, 118, 14675–14686. 10.1021/jp5063786. [DOI] [PubMed] [Google Scholar]
  39. Liu F.; Zargarzadeh L.; Chung H.-J.; Elliott J. A. W. Thermodynamic Investigation of the Effect of Interface Curvature on the Solid-Liquid Equilibrium and Eutectic Point of Binary Mixtures. J. Phys. Chem. B 2017, 121, 9452–9462. 10.1021/acs.jpcb.7b07271. [DOI] [PubMed] [Google Scholar]
  40. Meissner F. Mitteilungen aus dem Institut für phys. Chemie der Universität Göttingen. Nr. 8. Über den Einfluß der Zerteilung auf die Schmelztemperatur. Z. anorg. allg. Chem. 1920, 110, 169–186. 10.1002/zaac.19201100112. [DOI] [Google Scholar]
  41. Rie E. Über den Einfluß der Oberflächenspannung auf Schmelzen und Gefrieren. Z. Phys. Chem. 1923, 104, 354–362. 10.1515/zpch-1923-10425. [DOI] [Google Scholar]

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES