Neurite Orientation Dispersion and Density Imaging of Mouse Brain Microstructure

Abstract

Advanced biophysical models like neurite orientation dispersion and density imaging (NODDI) have been developed to estimate the microstructural complexity of voxels enriched in dendrites and axons for both in vivo and ex vivo studies. NODDI metrics derived from high spatial and angular resolution diffusion MRI using the fixed mouse brain as a reference template have not yet been reported due in part to the extremely long scan time required. In this study, we modified the three-dimensional diffusion-weighted spin-echo pulse sequence for multi-shell and undersampling acquisition to reduce the scan time. This allowed us to acquire several exhaustive datasets that would otherwise not be attainable. NODDI metrics were derived from a complex eight shell diffusion (1000 – 8000 s/mm²) dataset with 384 diffusion gradient encoding directions at 50 μm isotropic resolution. These provided a foundation for exploration of tradeoffs among acquisition parameters. A three-shell acquisition strategy covering low, medium, and high b values with at least angular resolution of 64 is essential for ex vivo NODDI experiments. The good agreement between neurite density index (NDI) and the orientation dispersion index (ODI) with the subsequent histochemical analysis of myelin and neuronal density highlights that NODDI could provide new insight into the microstructure of the brain. Furthermore, we found that NDI is sensitive to microstructural variations in the corpus callosum using a well-established demyelination cuprizone model. The study lays the ground work for developing protocols for routine use of high resolution NODDI method in characterizing brain microstructure in mouse models.

Introduction

Diffusion magnetic resonance imaging (MRI) affords unique insight into tissue microstructure and fiber tractography due to its sensitivity to the displacement pattern of water molecules during diffusion time (Zhang et al. 2012a; Alexander et al. 2010; Grussu et al. 2017; Glasser et al. 2016; Vu et al. 2015). The most commonly used approach, diffusion tensor imaging (DTI), is based on a Gaussian water displacement distribution (Basser et al. 1994). The metrics obtained from DTI such as fractional anisotropy (FA) and mean diffusivity (MD) have been used to assess tissue properties. However, these parameters may not be directly related to specific aspects of tissue structure because DTI model does not consider the hindered and restricted diffusion properties in the tissue (Zhang et al. 2012a; Basser et al. 1994). Following the basic tensor model, there is growing interest in observing tissue microstructure by diffusion MRI (Zhang et al. 2012a; Barazany et al. 2009; Kaden et al. 2016; Genc et al. 2018). Modeling techniques have been used to infer more specific tissue characteristics from the diffusion signal including axon diameter, neurite density dispersion, permeability, and cell size (Sepehrband et al. 2015; Beaujoin et al. 2018; Sepehrband et al. 2016).

Neurite orientation dispersion and density imaging (NODDI) is a non-Gaussian biophysical model that assumes three types of microstructural environments (intra-neurite, extra-neurite, and CSF compartments) (Zhang et al. 2012a; Anderson et al. 2018). The neurite density index (NDI), isotropic volume fraction (V_iso), and the orientation dispersion index (ODI) are the most common quantitative metrics derived from NODDI. Kamagata et al. found that high-resolution NODDI analysis may be useful for early diagnosis of Parkinson disease (PD) as well as assessment of its subsequent progression since NDI and ODI are significantly correlated with disease duration (Kamagata et al. 2016). Schneider et al. demonstrated that NODDI is a viable technique for multiple sclerosis (MS) patients and it may improve sensitivity and provide greater specificity to microstructure features than DTI parameters (Schneider et al. 2017). Edwards et al. proposed a NODDI-DTI signal model that allows interpretation of standard single-shell DTI data in terms of biophysical parameters in healthy human white matter (Edwards et al. 2017). The NODDI model has also been used for animal studies and validated with histology (Kleinnijenhuis et al. 2013b; Crombe et al. 2018). In a tau pathology mouse model of Alzheimer’s disease, NODDI identified potential tissue sources contributing to DTI indices and may provide greater specificity to pathology such a (Colgan et al. 2016). A recent study shows NODDI may suffer from limitations in grey matter structures in capturing the subtle neurodegenerative process at the early stage of experimental multiple sclerosis compared to simpler but more robust DTI model (Crombe et al. 2018). Extending NODDI to microscopic studies of cytoarchitecture and myeloarchitecture are challenging due to the relatively long scan time for high spatial resolution (Kleinnijenhuis et al. 2013b; Crombe et al. 2018).

In clinical studies, parallel imaging allows faster acquisition by undersampling the k-space and reconstructing the data using the encoding capability provided by multi-channel receiver arrays (Deshmane et al. 2012). Simultaneous MultiSlice (SMS) acquisition using parallel imaging can further reduce the scan time (Barth et al. 2016). Applying these techniques to studies in the mouse brain is challenging due to the small coil size (supplemental figure 1) and the limited space in the probe (Johnson et al. 2012; Petiet et al. 2008; Larkman and Nunes 2007). Diffusion MRI with single-shot echo planar imaging (EPI) readout is widely used in clinical application and neuroscience research due to its short scan time and insensitivity to motion. Segmented readout EPI has the advantage of reducing susceptibility to off-resonance artifacts by dividing the k-space into multiple interleaved acquisitions (Holdsworth et al. 2008). In general, EPI is more susceptible to a number of artifacts, such as eddy current artifacts, Nyquist ghosting, image blurring, and magnetic field inhomogeneity (Alomair et al. 2015). EPI readout also suffers from limited spatial resolution because of T2* or T2 decrease at high magnetic field. Our specific interest in the mouse brain requires spatial resolution up to 100,000 times that of clinical scans. 3D Stejskal-Tanner spin echo diffusion-weighted imaging sequence provides high spatial resolution and shows great immunity to magnetic susceptibility (Alomair et al. 2015). However, this sequence is time consuming and allows a limited number of DWIs within a reasonable scan time. Thus, any method to accelerate dMRI experiments is highly desirable. Compressed sensing (CS) is an accelerated imaging method, which enables reconstruction of under sampled data by exploiting image sparsity (Wang et al. 2018b; Lustig et al. 2007). Undersampling both phase encoding directions helps to fully explore the 2D sparsity preferred in CS reconstruction (Lustig et al. 2007; Wang et al. 2019).

In this study, we accelerated microscopic-resolution diffusion MRI for the mouse brain using the modified three-dimensional (3D) diffusion-weighted spin-echo pulse sequence (Stejskal and Tanner 1965) by sparse sampling both phase encoding directions in k-space. First, a four-shell diffusion dataset at 50 μm isotropic resolution was acquired with an CS acceleration factor (AF) of 5.12, and the NODDI metrics were compared with the fully sampled dataset at 100 μm isotropic resolution. Then, a more complex eight shell diffusion (1000 – 8000 s/mm²) dataset was acquired with total 384 diffusion weighted images (DWIs) (48 angles/shell, AF = 5.12) at 50 μm isotropic resolution to validate against conventional histochemical stains for the demonstration of myelin and neuronal cell bodies. The effects of b value selection and angular resolution were investigated in detail. Finally we explored the utility of the NODDI indices in a well-established demyelination cuprizone model (Matsushima and Morell 2001).

Methods

Animal Preparation

Animal experiments were carried out in compliance with the Duke University Institutional Animal Care and Use Committee. Five wild-type adult male C57BL/6 mice (Jackson Laboratory, Bar Harbor, ME) were chosen for MR imaging. One mouse at age of 90 days was scanned with 4 shells at both 50 μm and 100 μm isotropic resolution; one mouse at the same age was scanned with 8 shells at 50 μm isotropic resolution (details in MR histology protocol). For demyelination study, two cuprizone-fed mice (CUPZ) received a diet of chow mixed with 0.2% w/w cuprizone at 56 days old (Sigma Aldrich, St. Louis, MO) over the course of 5 weeks (CUPZ5) and 13 weeks (CUPZ13) to induce an acute and chronic state of central nervous system (CNS) demyelination (Doan et al. 2013; Matsushima and Morell 2001). An adult mouse with a normal diet of chow was used as control (CTRL).

MR histology protocol

Animals were sacrificed and perfusion fixed with a 1:10 mixture of ProHance-buffered (Bracco Diagnostics, Princeton, NJ) formalin. Specimens were immersed in buffered formalin for 24 hours and then moved to a 1:200 solution of ProHance/saline to shorten T1 (to about 110 ms) and reduce scan time.

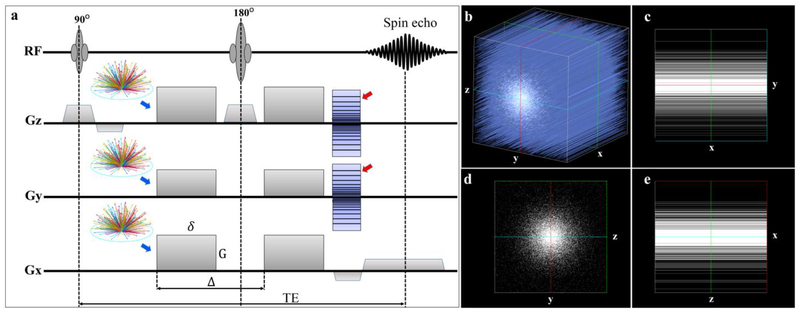
MR images were acquired on a 9.4T Oxford 8.9-cm vertical bore magnet (Oxford Instruments, Abingdon, United Kingdom) with an Agilent VnmrJ 4.0 imaging console with maximum gradient slew rate of 6000 T/m/s. We used a three-dimensional (3D) diffusion-weighted spin-echo pulse sequence with that was modified to support k-space undersampling and varying b values with different diffusion gradient directions (Figure 1). A 3D CS strategy fully sampled the readout dimension and under sampled the two phase encoding dimensions using a sparsifying approach, which has been described in detail previously (Wang et al. 2018a). Acceleration factors (AF) of 1.0, 4.0, and 5.12 were used in this study, where 1.0 stands for the fully sampled data. To achieve multi-shell diffusion MRI acquisition, the diffusion gradient orientations (distributed over half sphere) were determined using the method proposed by Koay et al. to ensure the uniformity within each shell while maintaining uniformity across all shells (Koay et al. 2012).

Figure 1:

The modified 3D Stejskal-Tanner diffusion-weighted spin-echo pulse sequence used in this study. Raw k-space data is fully sampled along the readout (x) dimension and under sampled in two phase dimensions (y and z, red arrows)) with the acceleration factor of 4.0 or 5.12. The diffusion gradient encoding directions for multi-shell (different b values) acquisition (blue arrows) is also implemented to the pulse sequence to ensure the maximum uniformity of the diffusion measurements in each shell as well as the diffusion measurements in all shells. The variable density undersampling patterns in 3D k-space (Fig 1b) and its projection in 2D plains are illustrated in Fig 1c–1e. G is the strength of the gradient pulse, δ is the duration of the pulse, Δ is the time between the two pulses.

We developed four protocols: 1) A fully sampled dataset was acquired using a multi-shell acquisition (b value = 1000, 2000, 4000, 8000 s/mm²) at 100 μm isotropic resolution, 31 DWIs and 3 b0 images in each shell, and one repetition. Total scan time was 62 hours (0.46 hours/volume). 2) An under sampled (AF = 5.12) dataset was acquired using the same parameters as the fully sampled dataset for comparison, except the spatial resolution was increased to 50 μm. The total scan time was 48.5 hours (0.36 hours/volume). 3) A second under sampled dataset (AF = 5.12) was acquired with multiple shells (b value = 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000 s/mm²) at 50 μm isotropic resolution, 48 directions DWIs and 4 b0 images in each shell, and one repetition. The total scan time was 148 hours (0.36 hours/volume). The vectors of these 384 diffusion gradient directions are plotted in supplemental figure 2. This dataset was further subsampled by different b values and gradient orientations to assess the performance of NODDI fitting results (next paragraph). 4) Based on this comprehensive study, a third compressed data protocol (AF=4.0) was developed with multiple shells (b value = 500, 1000, 2000, 4000, 6000, 8000 s/mm²) at 60 μm isotropic resolution, 39 DWIs and 4 b0 images in each shell, and one repetition. This protocol took 66 hours (0.26 hours/volume) and was used to image the CUPZ specimens. Temperature (~ 20°C) was monitored throughout all the scans and fluctuation was less than 1°C. All the scans kept the same TE of 15.2 ms and TR of 100 ms. Gradient separation time was 7.7 ms, the diffusion gradient duration time was 4.8 ms, and the maximum gradient amplitude was 134 G/cm. The maximum variation of DWIs signal (b0) is about ~ 2.3 % during the scans without notable signal drift (supplemental figure 3). Details of the acquisition parameters are summarized in Table 1.

Table 1:

The scan parameters of both fully sampled data and the under sampled scans.

AF	Resolution (μm)	Shells	b-value (s/mm2)	Gradient Orientations	TR (ms)	TE (ms)	FOV	Matrix Size	Scan time (hours)	Mice Numbers
1.0	100	4	lk,2k,4k,8k	31/shell	100	15.2	21.0*12.8*12.8	210*128*128	62	1
5.12	50	4	lk,2k,4k,8k	31/shell	100	15.2	21.0*12.8*12.8	420*256*256	48.5
5.12	50	8	lk,2k,3k,4k, 5k,6k,7k,8k	48/shell	100	15.2	20.0*12.8*12.8	380*256*256	148	1
4.0	60	6	0.5k,lk,2k, 4k,6k,8k	39/shell	100	15.2	19.2*11.52*11.52	320*192*192	66	3

AF: acceleration factor.

To assess the effect of angular resolution, the diffusion dataset acquired using protocol 3 was subsampled to 192, 96, 64, and 48 gradient orientations for NODDI model fitting (Sepehrband et al. 2017). This dataset was also subsampled by different shells to assess the effect of b values: 4 shells (b = 1000, 2000, 3000, 4000 s/mm²; b = 5000, 6000, 7000, 8000 s/mm²; b = 1000, 3000, 5000, 7000 s/mm²), 3 shells (b = 1000, 4000, 8000 s/mm²), and 2 shells (b = 1000, 4000 s/mm²), respectively. The 3-shell dataset (b = 1000, 4000, 8000 s/mm²) was further subsampled to 128, 96, 64, and 48 diffusion gradient orientations.

CS Reconstruction

Reconstruction of the under sampled k-space data has been described in previous studies (Hollingsworth 2015; Lustig et al. 2007; Wang et al. 2018b). In particular, acceleration factor of 4.0 and 5.12 means the acquisition time is 1/4^th and 1/5.12^th the time for a fully-sampled dataset. For example, the scan time for protocol 3 (details in MR histology protocol) took 148 hours, the scan time for the fully sampled dataset would take 148*5.12 = 757.76 hours (more than 30 days). The reconstruction was implemented on a Dell Cluster where an initial Fourier transform along the read out axis yielded multiple 2D images from each acquisition which could be spread across the cluster for parallel reconstruction (Wang et al. 2018a). The image SNR was calculated as the ratio of the average signal value to the standard deviation of the background.

Diffusion metrics

All the DWIs were registered to the baseline image (b0) to correct the eddy currents. Generalized Q- sampling imaging (GQI) is a model-free reconstruction method that quantifies the density of diffusion water at different orientations (Yeh et al. 2011). Quantitative anisotropy (QA) was obtained using DSI Studio software with a maximum of four fibers resolved in one voxel (Yeh et al. 2013). DTI was also used to calculate the tensor and the scalar indices at the b value of 1000 s/mm²: fractional anisotropy (FA) and mean diffusivity (MD).

NODDI fitting

The NODDI toolbox for Matlab was used for fitting the data (Zhang et al. 2012a). The software default value of intrinsic diffusivity (D_in) for ex vivo fixed tissue was 0.6 × 10⁻³ mm²/s. This parameter was varied from 0.6 × 10⁻³ − 1.2 × 10⁻³ mm²/s in this study to optimize the fitting results (supplemental figures 4, 5). The default value of isotropic diffusivity of 2.0 × 10⁻³ mm²/s was used for D_iso value (Holz et al. 2000). For ex vivo NODDI model, a relatively small dot-compartment (the diffusion is restricted in all directions) was included for the fitting (Dhital et al. 2018). The parameters derived from the NODDI model were ODI, NDI, and V_iso. DTI metrics (FA and MD) and NODDI metrics (ODI, NDI, and V_iso) are available from: https://civmvoxport.vm.duke.edu/voxbase/login.php?return_url=%2Fvoxbase%2F upon request.

Histological analysis

Histological examinations were performed on the specimens after the MRI scans. Coronal 8-μm thick slices were stained for the demonstration of myelin using a standard Luxol Fast Blue (LFB) protocol. Adjacent sections were stained by means of immunocytochemistry for the demonstration neuronal cell bodies using antibodies directed against the neuronal nuclear antigen (NeuN) (MAB377, lot 2967854, Millipore, Burlington, MA). Slides were imaged using Axioscop2 FSmot optical microscope with EC PlanNeofluar Zeiss lens at 20× magnification, 0.3 aperture under the same settings and light conditions. In order to quantitatively compare histology results with MRI results (Kamagata et al. 2017; Sato et al. 2017), the intensity of LFB/NeuN was measured based on the transmitted light intensity (luminosity) by the equation below:

$$I_{ii}=\frac{(maxlum-lumROI)}{maxlum}$$

Where ii stands for LFB or NeuN, maxlum is the maximum luminosity of the image, lumROI represents the luminosity of a specific ROI. The I_ii is normalized by the maxlum to [0 1], the same range as NODDI metrics.

Results

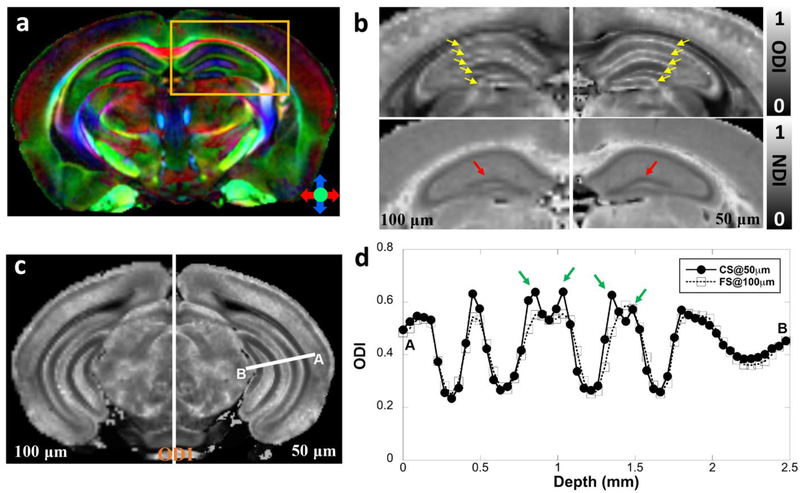
Figure 2 shows representative ODI and NDI images of the fully sampled (FS) dataset at 100 μm isotropic resolution (left panels of b, c) and CS results at 50 μm isotropic resolution (right panel of b, c). The color FA at 50 μm isotropic resolution is also shown in Figure 2a. The quantitative mappings from CS (right panels) are visually comparable with the FS results (left panels) from NODDI models, however, the utility of the higher resolution images is evident upon close inspection of the images. For example, ODI images in panels b and c show greater definition of laminar and sublaminar features in neuronal and molecular layers of the hippocampus (yellow arrows in Figure 2b). Thus, the ODI image highlights multiple discrete, high intensity features in the 50 μm image that are not resolved at 100 μm. In Figure 2c, such features are more discrete and better resolved in the 50 μm ODI images. Note, both scans retained the same 4 shells and the same angular resolution (31 DWIs and 3 B0 images per shell, Table 1), which results in the scan time of 62 hours for FS scan and 48.5 hours for CS scan, respectively. The profile of the ODI (Figure 2d) between CS results and FS results confirmed the robust nature of the CS reconstruction, while subtle laminar and sublaminar features are better resolved with higher spatial resolution (green arrows). In order to investigate the influence of CS effect, the 50 μm CS dataset was down sampled to 100 μm and compared with the FS dataset at 100 μm spatial resolution. The calculated ODI and NDI images from CS dataset were comparable to the references (results from FS dataset) with major information qualitatively preserved and negligible artifacts (supplemental figure 6).

Figure 2:

The metrics calculated from NODDI (ODI, NDI) of fully sampled (FS) dataset at 100 μm isotropic resolution (left panel of 2b and 2c, enlarged from the yellow box in 2a) and compressed sensing (CS) results at 50 μm isotropic resolution (right panel of 2b and 2c). The color FA at 50 μm isotropic resolution is also shown in panel a. Both NODDI and DTI metrics derived from CS data are found to be visually comparable with the fully sampled results. However, the subtle sublaminar features in the neuronal and molecular layers of the hippocampus could be better resolved with higher spatial resolution (green arrows, d) in ODI profiles. The ODI profiles in panel d are derived from the white line area in panel c. The comparison is from the right hemisphere of the same mouse.

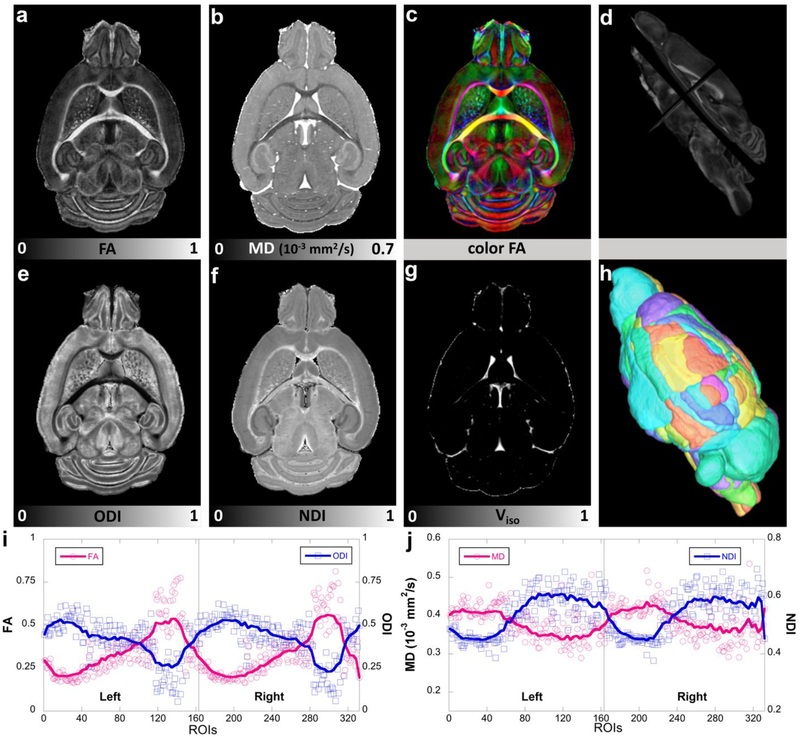
Figure 3 compares FA, MD with ODI, NDI images and the corresponding quantitative values at different ROIs from protocol 3 (see Methods) with 8 shells (48 DWIs/shell) at 50 μm isotropic resolution. The whole brain is divided to 332 regions (166 in each hemisphere) based on a prior parcellation of the mouse brain (Calabrese et al. 2015). In general, FA and ODI images show opposite contrast, as do MD and NDI images. Thus, the correlation coefficient between FA and ODI is − 0.94, and the correlation coefficient between MD and NDI is − 0.81 (supplemental Figure 7).

Figure 3:

DTI metrics (FA, MD, color FA), NODDI metrics (ODI, NDI, V_iso) and the corresponding quantitative values at different ROIs. The whole brain is divided to 332 regions (166 in each hemisphere, h) based on a previous parcellation of the mouse brain atlas. Figure 3d shows the FA images in different views. FA and ODI images show opposite contrast, where higher FA regions exhibits lower ODI values (i). The same inverse contrast is also found between MD and NDI images (j). Left: left hemisphere; Right: right hemisphere.

Modification of the fixed parameters, D_in, in the NODDI model produced considerable systematic changes in the outcome metrics, which may due to the fixation process for the specimens (Zhang et al. 2011; Hutchinson et al. 2017). When D_in is lower than 0.6, apparent artifacts are shown at hippocampus regions in both NDI and V_iso images. When D_in is larger than 1.0, the ODI values in some cortex region rise to 1 (supplemental figures 4, 5). In this study, we selected a moderate D_in of 0.9 × 10⁻³ in mm²/s to avoid the artifacts in NDI and V_iso images at lower D_in and overestimating ODI at higher D_in.

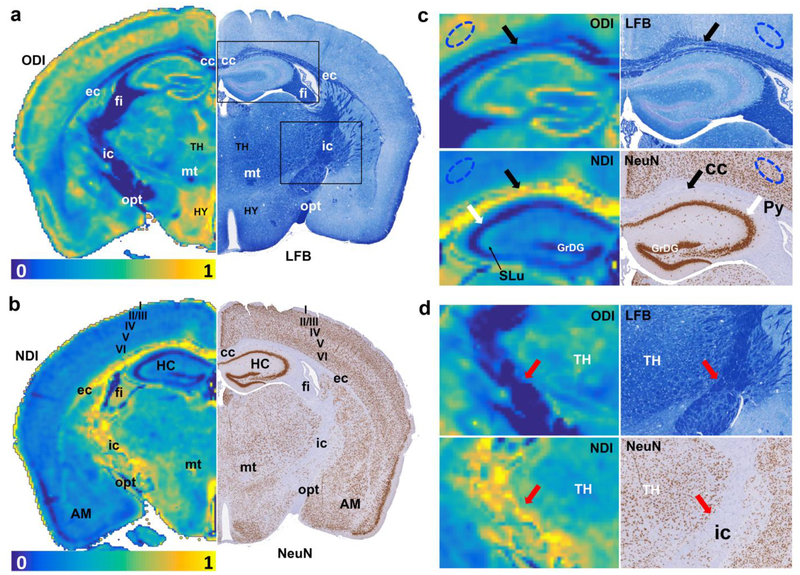
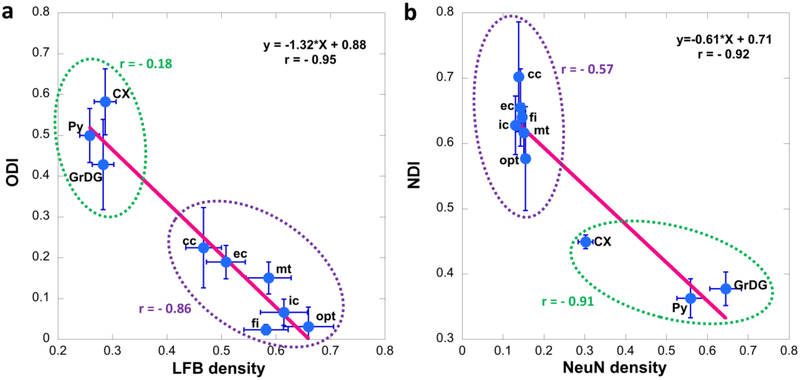
Figure 4 shows the ODI (4a) and NDI (4b) images with the corresponding histology images (LFB and NeuN). Heavy myelinated white matter bundles (corpus callosum (cc), external capsule (ec), fimbria (fi), internal capsule (ic), mammillothalamic tract (mt), and optic tract (opt)) exhibit lower ODI values, light myelinated region (such as neocortex) has higher ODI values. NDI shows lower values in the pyramidal cell layer of the hippocampus (Py), the granule cell layer of the dentate gyrus in the hippocampus (GrDG), corresponding to higher neuron contents in NeuN images. Stratum lucidum of the hippocampus (SLu), the track of the mossy fiber projections, shows slightly higher NDI than the surrounding sublaminae. Furthermore, NDI shows higher values in major white matter bundles (cc, ec, fi, ic, and opt), which are largely devoid of neuronal cell bodies, as shown in the corresponding image of NeuN staining.

Figure 4:

The ODI and NDI images with the corresponding histology images (LFB and NeuN). Heavy myelinated white matter bundles (cc, ec, fi, ic, mt, and opt) exhibit lower ODI values, light myelinated region (neocortex) has higher ODI values. NDI shows lower values in Py and GrDG, corresponding to higher neuron contents in NeuN images. SLu shows slightly higher NDI than the surrounding tissues. Laminar appearance of neuron density is observed at the cortex area in NeuN staining, where the variation at cortex layer IV (internal granular layer) and V (large pyramidal layer) in NeuN staining is illustated in NDI image. The different contrast for NODDI and histology images in cc (black arrows), ic (red arrows), Py (white arrows) and neocortex (blue eclipse) are enlarged in Figure c-d. All the images are obtained from the right hemisphere. cc: corpus callosum; ec: external capsule; fi: fimbria; ic: internal capsule; mt: mammillothalamic tract; opt: optic tract; Py: pyramidal cell layer in hippocampus; GrDG: granule cell layer of dentate gyrus in hippocampus; SLu: Stratum lucidum of the hippocampus; AM: amygdala; TH: thalamus; HY: hypothalamus.

In addition, the layers of the neocortex, which are evident in NeuN staining, show striking variation in both ODI and NDI images. For example, both NODDI metrics are highest in layer I, which is a molecular layer enriched in the largely symmetrical apical dendritic tufts of cortical pyramidal neurons and the thalamocortical and cortico-cortical axons that innervate them, with only a sparsely distributed population of neuronal cell bodies. Similarly, cortical layer V, which features a relatively low density of neuronal cell bodies and a high density of neuritic elements, displays higher values of ODI and NDI. The high values of ODI in cortical layer V presumably reflects the rich abundance and, on average, isotropic distribution of basal dendrites of the large pyramidal neurons that are a characteristic feature of this cortical layer. The similar results are observed in different cortical areas (Bregma 0.74 mm, supplemental figure 8). The laminar features of cerebral cortex are also shown in averaged DWIs (supplemental figure 9) and evident through the whole cortex regions (supplemental figure 10).

The different contrast for NODDI and histology images in cc (black arrows), ic (red arrows), Py (white arrows) and neocortex (blue eclipse) are enlarged in Figure 4c–d. Other brain regions show enrichments in ODI and/or NDI without obvious correlates in either the LFB or NeuN histological preparations; these include the lateral nucleus of the amygdala, the hypothalamus, and certain nuclear divisions of the thalamus. The quantitative NODDI and histology results yield strong negative correlations between ODI and LFB density (−0.95, p < 0.001) and between NDI and NeuN density (−0.92, p < 0.001) (Figure 5). The correlation between ODI and LFB density in major WM tracts (cc, ec, mt, ic, fi, and opt) is −0.86, the correlation between NDI and NeuN density in major WM tracts is −0.57. The correlation between ODI (CX, Py and GrDG) and LFB instnsity in GM is −0.18, between NDI and NeuN density in GM is −0.91.

Figure 5:

The correlation between ODI and LFB density (a) and between NDI and NeuN density (b). The correlation was further calculated by separating the ROIs to WM (cc, ec, mt, ic, fi, and opt, purple circles) and GM (CX, Py, and GrDG, green circles). The error bars represented the standard deviation. cc: corpus callosum; ec: external capsule; fi: fimbria; ic: internal capsule; mt: mammillothalamic tract; opt: optic tract; Py: pyramidal cell layer in hippocampus; GrDG: granule cell layer of dentate gyrus in hippocampus; CX: cortex; SLu: Stratum lucidum of the hippocampus.

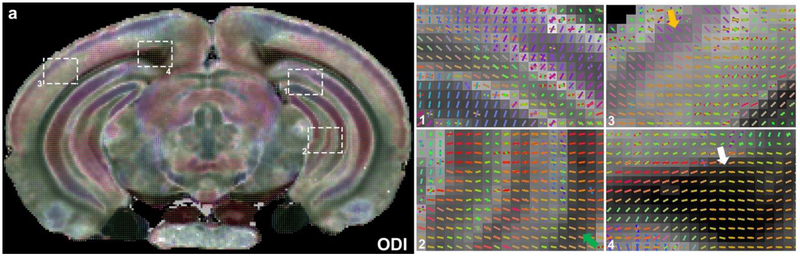
Figure 6 demonstrates the relationship between ODI and fiber orientation distributions with four enlarged areas (cortex, corpus callosum, and two regions in hippocampus). At this particular level (Bregma −3.40 mm), there are multiple layers resolved in the 50 μm ODI image. The fiber orientation map superimposed on ODI image show numerous crossing fibers at higher ODI areas, while fewer crossing fibers exist in lower ODI regions. There are few crossing fibers in corpus callosum (region 4 with white arrow, low ODI), fewer crossing fibers in the radiatum layer of the hippocampus (region 2 with green arrows, low ODI). There are complex fiber orientation distributions in the cortex, where many areas have crossing fibers. However, layer II/III, the cortical region with lowest ODI values (yellow arrows) shows the fewest crossing fibers.

Figure 6:

The relationship between ODI and fiber orientation distributions. Four selected areas showing hippocampus (1 and 2), neocortex (3), and subcortical white matter just posterior to the splenium of the corpus callosum (4) are enlarged in panels to the right. Throughout the brain, higher ODI regions show more crossing fibers, while lower ODI regions show few crossing fibers. Note the absence of resolved crossing fibers in the subcortical white matter (white arrow in 4) and the strong coherence of anisotropic voxels in the stratum radiatum of the hippocampus (green arrows in 2). The cortex showed complex fiber orientation distributions, where most areas have crossing fibers. However, neocortical layer II/III features lower ODI values (yellow arrow in 3), which presumably reflects the prominence of the apical dendrites of cortical pyramidal neurons passing through this region.

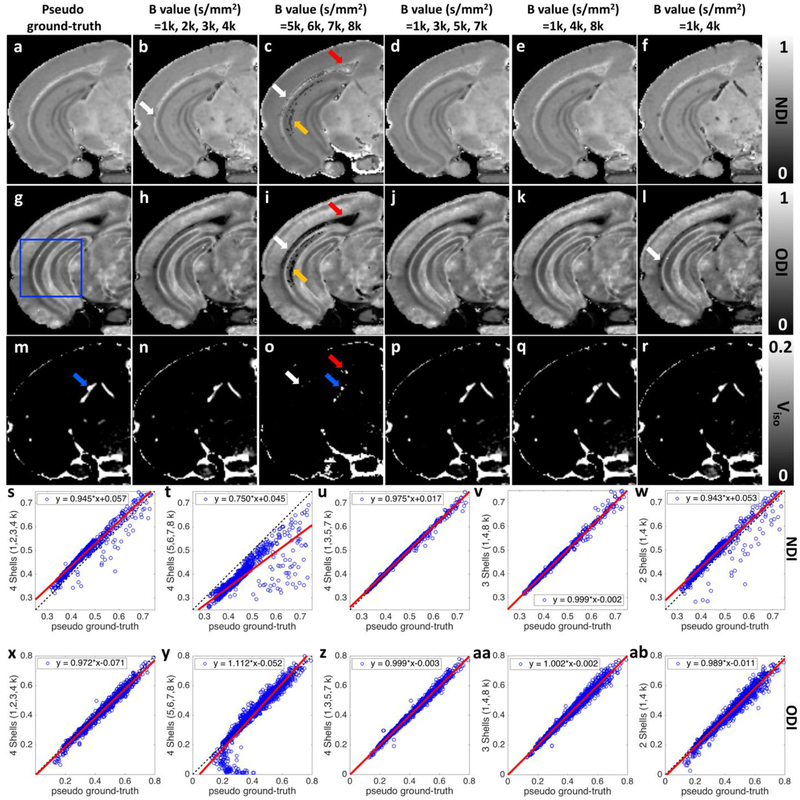
To evaluate the impact of b value selection on the NODDI model fitting, ODI, NDI, and V_iso maps derived from 2, 3, and 4 shells (subsampled from 8 diffusion shells) are shown in Figure 7. Plots of voxel correspondence for the selection of shells vs the pseudo ground truth (all 8 shells) are shown for the ROI (blue box) in figure 7s – 7ab. Significant artifacts are evident in both ODI and NDI in the external capsule and hippocampus in figure 7c and 7i, i.e. when fitting with the 4 highest b value shells (5000, 6000, 7000, 8000 s/mm²), probably due to less accurate estimation of the free water diffusivity derived from lower b values (figure 7o). The corresponding plots of correspondence (figure 7t and 7y) show a large dispersion. In contrast, plots of correspondence using 4 shells (figure 7u and 7z) with equally spaced b values (1000, 3000, 5000, 7000 s/mm²), demonstrate good agreements. Finally, use of only 3 shells (figure 7e, 7k, 7q, 7v, 7aa) yields correspondence nearly comparable to that of best selection of 4 shells. Use of only 2 shells (figure 7f and 7l) leads to a significant dispersion, particularly in the NDI. These last two points suggest that use of 3 shells with equally spaced b values as a potential protocol for routine use.

Figure 7:

ODI, NDI, and V_iso maps derived from 2, 3, and 4 shells (subsampled from 8 shells diffusion dataset as the pseudo ground-truth). Plots of voxel correspondence for the selection of shells vs the pseudo ground truth are shown for the ROI (blue box) in figure 6s – 6ab. Significant artifacts are shown in both ODI and NDI (white, red, and yellow arrows, c, i) maps when using the highest four b values (5000, 6000, 7000, 8000 s/mm²). The inconsistences also show in V_iso images (white, red, and blue arrows, o). The calculated ODI and NDI show visually inconsistent results in some specific areas when only using lowest four b values (1000, 2000, 3000, 4000 s/mm²). The results become more consistent with the pseudo ground-truth when using 4 shells (1000, 3000, 5000, 7000 s/mm²) or 3 shells (1000, 4000, 8000 s/mm²). All the images are obtained from the left hemisphere.

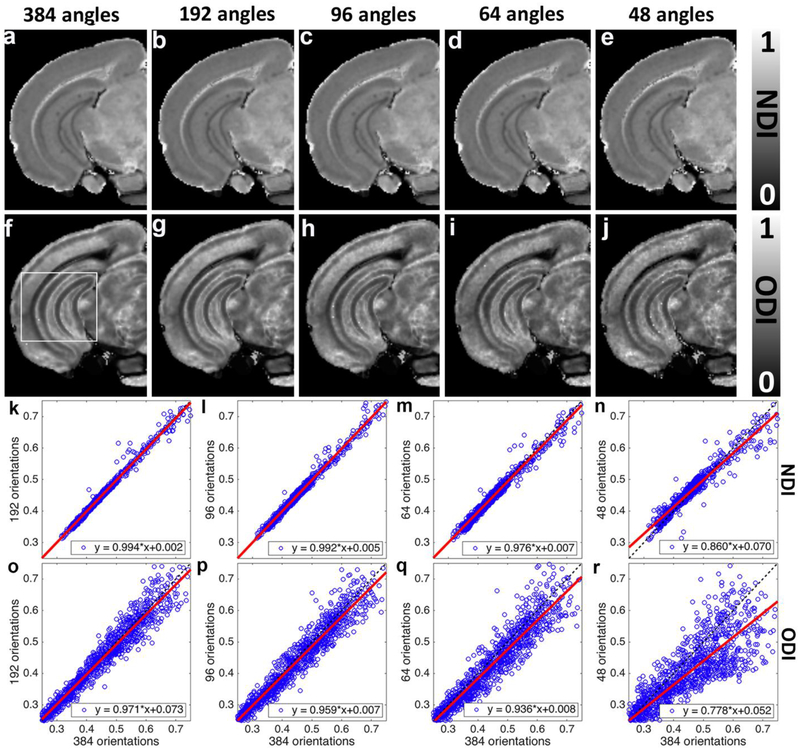
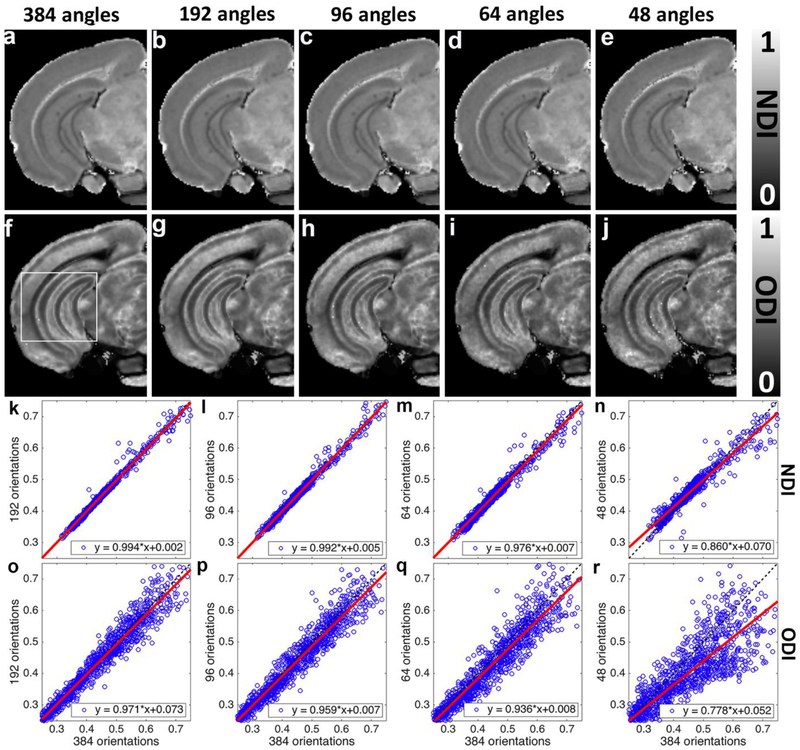
To assess the impact of the angular resolution on NODDI model fitting, the pseudo ground-truth dataset (8 shells with 384 diffusion gradient directions) was subsampled 2, 4, 6, and 8 times to 192, 96, 64, and 48 diffusion gradient directions datasets (Figure 8). Plots of voxel correspondence for the selection DWIs vs the pseudo ground truth are shown for the ROI (White box) in figure 8k – 8r. All of the subsampled datasets keep the same 8 shells as the pseudo ground-truth dataset. For example, subsampled dataset with 96 diffusion gradient directions contains 8 shells from 1000 to 8000 s/mm² with 12 gradient directions in each shell. NDI and ODI images with more than 64 diffusion gradient directions are visually comparable to the pseudo ground-truth results. In general, subsampled NDI shows less deviations from pseudo ground-truth than ODI images (Figure 8k–r). Larger deviation is found with lower angular resolution, especially with only 48 diffusion gradient directions (Figure 8r). As one might expect, the fitting results are suboptimal with lower angular resolution.

Figure 8:

NODDI model fitting results from the subsampled (2, 4, 6, and 8 times) diffusion gradient directions datasets. Each of the subsampled datasets keeps the same 8 shells as the pseudo ground-truth dataset. NDI and ODI images with 64 diffusion gradient directions are visually comparable to the pseudo ground-truth results (a-j). However, the images become noisier with lower angular resolution, as quantified in the plots showing voxel-wise comparison (k-r). NDI shows less dependence on the angular resolution than ODI. All the images are obtained from the left hemisphere.

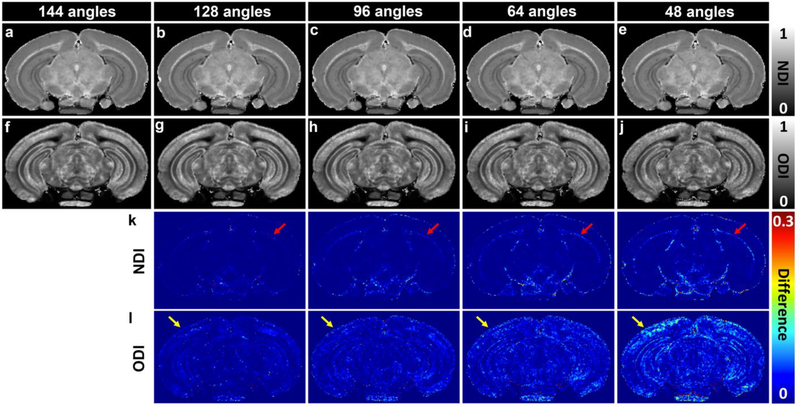
The 3-shell (1000, 4000, 8000 s/mm² with 48 DWIs in each shell) dataset yields correspondence nearly comparable to that of pseudo ground truth, therefore, this 3-shell dataset is further subsampled to 128, 96, 64, and 48 diffusion gradient directions datasets (Figure 9). All of the subsampled datasets keep the same 3 shells. NDI and ODI images with 64 or higher diffusion gradient directions are visually comparable to the 3-shell dataset with 144 DWIs. NDI images always shows less dependence on the angular resolution than ODI images (Figure 9k–l) and larger deviation is found with lower angular resolution (red arrows for external capsule, yellow arrows for neocortex).

Figure 9:

NODDI model fitting results (48 to 128 angles) subsampled from the 3-shell dataset (1k, 4k, and 8k s/mm² with 48 angles in each shell). Each of the subsampled dataset keeps the same 3 shells. NDI and ODI images with more than 64 diffusion gradient directions are visually comparable to the pseudo ground-truth results (144 angles). The variations become higher with lower angular resolution (red and yellow arrows for external capsule and neocortex). NDI shows less dependent on the angular resolution than ODI.

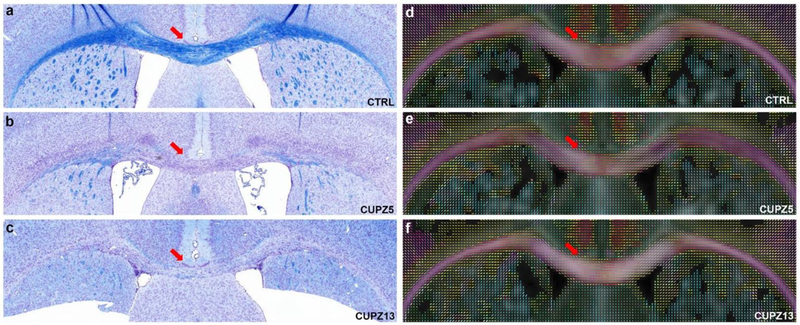
Figure 10 shows representative brain slices through the corpus callosum of CTRL, CUPZ5, and CUPZ13 mice stained with Luxol Fast Blue (LFB). The corresponding fiber orientation distribution images are shown on the right as comparison. Exposure of mice to dietary cuprizone for 5 weeks induces significant loss of myelin in the corpus callosum (red arrows, b) with continued demyelination at 13 weeks (red arrows, c). The fiber orientations (red arrows, d, e, f) show limited difference between control mice and cuprizone treated at both 5 weeks and 13 weeks, where few crossing fibers are observed in corpus callosum region and external capsule region.

Figure 10:

The representative brain slices of CTRL, CUPZ5, and CUPZ13 mice stained with Luxol Fast Blue (LFB) in the region of the body of the corpus callosum, with the corresponding fiber orientation distribution images shown on the right. Exposure of mice to dietary cuprizone for 5 weeks and 13 weeks induces significant loss of myelin in the corpus callosum (red arrows, b and c). The fiber orientations in cc (red arrows, d, e, and f) show limited difference among control mice and cuprizone administrated mice. Few crossing fibers are observed in corpus callosum region and external capsule region.

However, NODDI parameters reveal additional features that correspond with the appearance of demyelination evident in the LFB staining in the cuprizone treated animals. Figure 11 shows the ODI, NDI and color QA images at the same location and time points as the data shown in Figure 10. The corpus callosum (yellow arrows) has lower ODI values compared to the surrounding gray matter (GM) and does not differ significantly between the control and cuprizone induced mice. The fiber orientation in the corpus callosum is consistent regardless of cuprizone administration (yellow arrows, Figure 11c, 11f, and 11i). However, there is an apparent contrast change in the NDI images. The corpus callosum in the CTRL condition has a much higher NDI (brighter) than the surrounding GM; however, the NDI in the corpus callosum is lower (darker) after 5 weeks of cuprizone administration. The contrast between the corpus callosum and surrounding GM is almost absent in the NDI image after 13 weeks cuprizone administration. The FA, MD, ODI, and NDI changes at different demyelination stages is summarized in supplemental figure 11.

Figure 11:

The ODI, NDI and color quantitative anisotropy (QA) images of CTRL, CUPZ5, and CUPZ13 mice in corpus callosum regions. Corpus callosum (yellow arrows) shows lower ODI values compared to the surrounding gray matters (GM) in both control and cuprizone induced mice. On the contrary, dramatic contrast change is evident in the corpus callosum, relative to surrounding gray matter, when NDI images are compared among control and cuprizone treatment conditions. Corpus callosum in CTRL shows higher NDI (brighter) than the surrounding GM, however, corpus callosum exhibits lower NDI (darker) after 5 weeks cuprizone administration. The contrast between corpus callosum and surrounding GM is largely diminished after 13 weeks cuprizone administration, which may reflect microanatomical changes that contributes to a subtle increase in NDI and QA in the corpus callosum.

Discussion

Diffusion MRI provides a number of different ways to characterize brain microstructure in neurological and psychiatric conditions, most of the methods require multiple b values with high angular resolution (Kaden et al. 2016; Zhang et al. 2012a; Barazany et al. 2009; Basser et al. 1994). The mouse brain is a particularly interesting target since there are numerous genetic models in which biophysical models derived from dMRI might provide insight into cytoarchitectural and white matter microstructure variants. Extending the methods to the microscopic domain results in extremly long scan times to the accommodate both high spatial and high angular sampling. The use of compressed sensing has allowed us to acquire a foundational dataset that can be served as a high resolution reference template. This dataset has been systematically subsampled to determine the impact of angular resolution and b values on NODDI model fitting. Furthermore, we demonstrated that the NDI metric is particularly sensitive to microstructural variations in the corpus callosum in the cuprizone model of demyelination.

Effects of experimental parameters for NODDI fitting

Zhang et al demonstrated that NODDI affords a clinically feasible technique for in vivo neurite orientation dispersion and density imaging at clinical resolution (~ 2 mm³), and reliable ODI and NDI could be obtained using two shells with the maximum b-value of 2000 s/mm² (Zhang et al. 2012a). Higher b values (5000, 6000 s/mm²) were not particularly useful because of the signal loss due to long TE imposed by the limitations of clinical gradients. The NODDI model has been extended to ex vivo fixed tissue studies. Ex vivo diffusivities are significantly lower than in vivo measurements. But ex vivo FA values differ less from in vivo FA values in the mouse brain (Zhang et al. 2012b). Rane et al. found the in vivo ADC was larger by a factor of 5 compared to fixed rhesus macaque brains, and white matter FA was 28% higher in the in vivo study as compared to the ex vivo experiments (Rane and Duong 2011). In a recent ex vivo mouse brain NODDI study, the maximum b value of 10,000 s/mm² was performed to evaluate the NODDI fitting results (Hutchinson et al. 2017). In the current study, the maximum b value of 8,000 s/mm² was chosen to balance the signal loss due to longer TE (15.2 ms) and requirement for higher b value in fixed tissue. The SNR at b of 8000 s/mm² is about 12.9 at 50 μm isotropic resolution. This relatively high SNR may improve the performance of the NODDI model. In addition, higher b value is useful for resolving the crossing fibers in CNS (Vu et al. 2015). Including higher b value also helps to compare the ODI and fiber orientation distributions directly (Figure 6), where more crossing fibers are found in higher ODI regions.

In this study, we used a fixed D_in parameter for our NODDI fitting, which is consistent with the original NODDI fitting protocol. Since obtaining the ground truth of D_in value is still challenging, the calculated NODDI metrics are parametrically dependent on this value (Jelescu et al. 2016; Lampinen et al. 2017). The default D_in value in NODDI toolbox is 0.6 × 10⁻³ mm²/s, however, this value may need to be adjusted for ex vivo specimens because the fixation process may be non-identical among labs or variably successful among animals (Zhang et al. 2012a; Jelescu et al. 2015). We selected a moderate D_in to avoid apparent artifacts in NDI, ODI, and V_iso images with lower D_in and overestimating ODI with higher D_in. Hutchinson et al. found that fitting the NODDI model with D_in as a free parameter reveals heterogeneity in this value across the brain, thus, anatomical contrast evident on the D_in map may also call for caution in interpreting the NODDI fitting results for ex vivo specimens (Hutchinson et al. 2017). The use of exogenous contrast agents is helpful to improve the SNR and also reduce the T1 relaxation time for ex vivo studies. The effect of contrast agent on the DTI metrics and the diffusivity of water has been studied previous, this may also contribute to the final NODDI results (Zolal et al. 2012). Furthermore, the fixation process, scan temperature and postmortem interval may all affect the D_in value, which calls extra attention for biophysical model results derived from dMRI. As NODDI depicts a single and fixed intrinsic diffusivity over the whole brain, which may hold the potential to overestimate the free-water content in the cerebral white matter (Kaden et al. 2016). In addition, NODDI model assumes the neurite orientation distribution using a single Watson distribution without accounting for fiber crossings, the current results may be improved with multiple Bingham distributions or spherical mean technique (SMT) (Kaden et al. 2016; Tariq et al. 2016).

By comparing combinations of b values and angular samples to the comprehensive scan (8 b values, 384 angular samples at 50 μm resolution) we can judiciously choose acquisition parameters (three b values of 1000, 4000, 8000 s/mm², and angular sampling between 64–128) that yield good agreement with the foundation set with reasonable scan time. A 3-shell acquisition with 64 angular samples at 50 μm resolution can be completed in 24.7 hrs. Since this work was started, we have demonstrated that compression factors up to 8× can be used with limited impact on the conventional DTI metrics which could further reduce the acquisition time to 15.8 hr (Wang et al. 2018a).

Validating the NODDI model with histology

Diffusion MRI has been used most frequently to characterize the fractional anisotropy in cerebral white matter (Le Bihan et al. 2001; Basser et al. 1994). Higher-order tensors provide a powerful mathematical tool to analyze the complex diffusion data generated by single- and multi-shell high angular resolution diffusion-weighted imaging (HARDI) (Zhang et al. 2012a; Kaden et al. 2016). The major limitation of diffusion imaging on the cortex and hippocampus is the low level of resolution that can be achieved in comparison to the actual size and the relatively lower fractional anisotropy in these regions (Assaf 2018). However, recent studies provide meaningful information on the micro-structure characteristics of gray matter using diffusion MRI (Assaf 2018; Kleinnijenhuis et al. 2013a). Colgan et al. demonstrated that only NDI from the NODDI model correlated with the histological measurements of the levels of hyperphosphorylated tau protein and NODDI may provide greater specificity to pathology in Alzheimer’s disease (Colgan et al. 2016). There is significant correlation between myelin density estimated by absolute tissue density from NODDI (ABTIN) and myelin density obtained from electron microscopy in the mouse corpus callosum (Sepehrband et al. 2015). Kleinnijenhuis et al. fitted the NODDI tissue model to multi-shell DWI data revealing that NODDI has more potential for capturing cortical microstructure than DTI metrics with various histological markers (Kleinnijenhuis et al. 2013b). The relationship between the high spatial diffusion MRI signal and the cellular components of the cortex was also explored with the comparison of histology.

The main orientation/alignment of the diffusion tensor corresponds with the orientation of the axons and dendrites in both neocortex and hippocampus, which suggested that high resolution diffusion MRI holds the potential to detect intrinsic cortical architecture with high sensitivity (Assaf 2018). The fiber orientation density function has been used to reveal the directions of ordered aligned fibers in neocortex. We found high ODI regions show more crossing fibers, while low ODI regions show fewer crossing fibers by directly mapping fiber orientation distribution imaging to ODI. The NODDI metrics are not homogeneous throughout the neocortex, instead, both ODI and NDI demonstrate laminar patterns, which is consistent with previous findings in high resolution FA and MD images (Assaf 2018). The relative homogeneity of fiber alignment in heavy myelinated white matter bundles shows lower ODI than the neocortex and hippocampus, which demonstrates good agreement between LFB staining and ODI in these white matter structures. Major white matter tracts contain largely axons that are tightly bundled into compact parallel fascicles, corresponding to higher neurite density. In contrast, GrDG and Py are known to have densely packed cell bodies with relatively low neuropil volume and therefore show low axon/dendrite density. In this study, the good agreement between NDI and NeuN suggests high resolution NODDI could be a biomarker for characterizing the microstructure in the brain.

NODDI for cuprizone mice model

The cuprizone mouse model is a well-established demyelination model, and MRI studies demonstrated that various MRI techniques can detect white matter abnormality noninvasively (Thiessen et al. 2013; Tagge et al. 2016). Guglielmetti et al. reported that both T2 and MTR measures are highly correlated to the brain microstructure and underlying histopathological events following cuprizone administration (Guglielmetti et al. 2016a). Sun et al. found that axial diffusivity and radial diffusivity can be used as a noninvasive marker to probe the extent of axonal injury and myelin loss in vivo (Sun et al. 2006). In this study, we choose two different demyelination stages to investigate the ODI and NDI variations: acute demyelination (5 weeks cuprizone administration) and chronic demyelination (13 weeks cuprizone administration). It has been shown that demyelination, a hallmark of multiple sclerosis, is not a prerequisite for axon damage (Nikic et al. 2011). Since significant demyelination was found in both acute and chronic stages of treatment from the evaluation of the LFB staining of myelin, the marked NDI variation in the corpus callosum may not only cause by the demyelination itself. It may suggest that NODDI could be sensitive biomarkers to probe the different stages of white matter pathology between acute demyelination and chronic demyelination (Matsushima and Morell 2001).

Demyelination is linked to myelin and oligodendrocyte loss, axon damage, active gliosis, and astrocytic hypertrophy (Lin et al. 2017; Zhang et al. 2012b; Nikic et al. 2011; Simons et al. 2014; Skripuletz et al. 2008). Xie et al. found the axon diameter values were reduced after 4 weeks of cuprizone and the axonal atrophy persisted at 12 weeks of cuprizone treatment, however, the total density of axons were not significantly different in the densities of total neurofilament profiles throughout cuprizone treatment up to 12 weeks in the corpus callosum (Xie et al. 2010). The similar pattern of fiber orientation distributions in the corpus callosum and consistent ODI results after 5 weeks and 13 weeks cuprizone administration in the present study may suggest that the relatively less alteration of the major axon bundle orientations (at least in microscopic scale), even though the axon damage and reduction of axon diameter are confirmed by the immunohistochemical evaluations through the previous studies (Guglielmetti et al. 2016b; Aggarwal et al. 2012; Xie et al. 2010; Skripuletz et al. 2008; Matsushima and Morell 2001). Furthermore, it’s unlikely that the NDI variations in is purely attributed to axon damage, since the NDI is lower than the surrounding GM in acute demyelination (CUPZ5) but then elevates in chronic demyelination mice (CUPZ13). It’s reported that demyelinated areas have extensive infiltration and amplification of cells that distort the normal tissue structure in acute demyelination cuprizone model (Aggarwal et al. 2012; Sun et al. 2006). This swelling due to infiltration of immune cells in the cuprizone model may play an important role for the dramatic NDI decrease after 5 weeks cuprizone administration. These subtle dynamics between 5 and 13 weeks cuprizone treatment could reflect microanatomical changes in the response of glial constituents (microgliosis and/or astrogliosis) and immune-related activity in the demyelinating corpus callosum. The pathology changes at different MS stages may also be attributed to the decoupling between intra-axonal and extra-axonal diffusivity, which may also affect the calculated NODDI metrics and need substantial investigation in further studies (Jelescu et al. 2015; Jelescu et al. 2016).

There are several limitations to our study. CS was only applied in undersampling k-space, however, diffusion MRI is known to be much sparser in q-space. Joint reconstruction of k-q space may further reduce the scan time (Cheng et al. 2015). An obvious limitation is the relatively long scan time for both high spatial and angular resolution diffusion magnetic resonance histology scans. The dataset with 384 diffusion encoding gradients with 8 shells at 50 μm provides a pseudo ground truth, however, a relatively high-throughput protocol, derived from the analysis of this dataset including three b values and 64–128 angular samples may be applied for population studies. Third, we only compared the demyelination process at two timing points (acute and chronic), further studies of cuprizone model are also warranted to determine the time course of demyelination using NODDI model. In addition, mapping the whole brain ODI and NDI remains a matter for precise, hypothesis-driven investigation. Quantitative comparison between NODDI metrics and histology results are warranted in further studies.

To summarize, we have extended the spatial resolution in NODDI for whole mouse brain to 50 μm. We have acquired a foundation set that has allowed us to systematically understand the tradeoff in number of shells, b value, and angular samples. This leads to a protocol which can be executed in ~ 24 hours with NDI and ODI metrics very nearly comparable to the longer (148 hours) acquisition. The NODDI protocol demonstrated unique tissue contrasts in the mouse brain. The distinctive delineation of densely packed neuronal regions and heavily myelinated white matter bundles has interesting implications for studies investigating neuronal defects in the hippocampus, neocortex, and white mater tracts in mouse models of related disorders. The finding that NDI is sensitive to microstructural white matter variations in the cuprizone model also renders this technique useful for applications in mouse models of white matter disorders. The potential to provide routine mouse brain maps of NODDI metrics at high spatial resolution is truly exciting. The promise is not yet fully realized but this study will hopefully add to the work of others in realizing this potential.