A non-randomized procedure for large-scale heterogeneous multiple discrete testing based on randomized tests

Summary:

In the analysis of next-generation sequencing technology, massive discrete data are generated from short read counts with varying biological coverage. Conducting conditional hypothesis testing such as Fisher’s Exact Test at every genomic region of interest thus leads to a heterogeneous multiple discrete testing problem. However, most existing multiple testing procedures for controlling the false discovery rate (FDR) assume that test statistics are continuous and become conservative for discrete tests. To overcome the conservativeness, in this article, we propose a novel multiple testing procedure for better FDR control on heterogeneous discrete tests. Our procedure makes decisions based on the marginal critical function (MCF) of randomized tests, which enables achieving a powerful and non-randomized multiple testing procedure. We provide upper bounds of the positive FDR (pFDR) and the positive false non-discovery rate (pFNR) corresponding to our procedure. We also prove that the set of detections made by our method contains every detection made by a naive application of the widely-used q-value method. We further demonstrate the improvement of our method over other existing multiple testing procedures by simulations and a real example of differentially methylated region (DMR) detection using whole-genome bisulfite sequencing (WGBS) data.

1. Introduction

Recent developments of next generation sequencing (NGS) technology have revolutionized genomic research with its unprecedented throughput, scalability and speed. NGS data are typically presented in the form of short read counts and invoke large-scale multiple discrete testing. For example, in a whole-genome bisulfite sequencing (WGBS) experiment, input DNA is treated with sodium bisulfite and sequenced to help understand the DNA methylation pattern. Along the genome, the CpG sites are regions of DNA where a cytosine nucleotide occurs next to a guanine nucleotide in the linear sequence of bases along its length, and a comparative WGBS experiment gives methylated and unmethyated counts at each CpG site between the control and treatment samples. To identify the differentially methylated regions (DMRs) based on these discrete counts, a rudimentary method is to conduct Fisher’s Exact Test (FET) at each CpG site and then a DMR is detected as a genomic region of adjacent CpG sites that are differentially methylated (Challen et al., 2012; Gu et al., 2010). FET as a conditional test depends on its marginal counts, i.e. the sum of read counts between two samples, which is highly varying at different CpG sites. Thus testing at all the CpG sites leads to a heterogeneous multiple discrete testing problem, that is, tests with different discrete null distributions. However, most existing multiple testing methods are designed for continuous tests and lack sufficient power when applied to discrete tests (Pounds and Cheng, 2006). In this paper, we study how to overcome the conservativeness for general heterogeneous multiple discrete testing problems.

When testing multiple hypotheses, the false discovery rate (FDR) proposed by Benjamini and Hochberg (1995) is widely adopted to measure the overall error rate. Suppose that we test m hypotheses and reject R of them, out of which V tests are erroneously rejected. The false discovery proportion (FDP) is then the proportion of false rejections among all the rejections, i.e. $\text{FDP}=\frac{V}{\max (R,1)}$. The FDR is defined as the expectation of FDP, i.e. $\text{FDR}=\mathbb{E}(\text{FDP})=\mathbb{E}\left\{\frac{V}{\max (R,1)}\right\}=\mathbb{E}\left(\frac{V}{R}|R>0\right)\mathrm{Pr}(R>0)$. A slight variant of FDR, the positive FDR (pFDR) (Storey, 2002), is defined as the conditional FDR given at least one rejection, i.e. $\text{pFDR}=\mathbb{E}\left(\frac{V}{R}|R>0\right)$. The pFDR can be interpreted as a Bayesian Type-I error rate under a mixture model involving i.i.d. p-values (Storey, 2003). Storey (2002) also provided estimates of pFDR under the above mixture model for a single-step procedure that are related to the empirical Bayes FDR of Efron et al. (2001). When the number of tests is large, Pr(R > 0) is close to 1 and the pFDR serves as an good approximation to the FDR.

Over the past decade, a large number of multiple testing methods on controlling the FDR or pFDR have been proposed in the literature, such as Benjamini and Hochberg (1995); Efron and Tibshirani (2007); Pounds and Cheng (2004); Ruppert et al. (2007) and Storey (2002). Most of them assume that test statistics are continuously distributed and heavily rely on the resulting fact that under null hypotheses, the p-values follow Unif(0,1), i.e. the uniform distribution on the interval (0,1), for example, the BH algorithm (Benjamini and Hochberg, 1995) and the q-value method (Storey, 2003). However, when the continuity assumption no longer holds in discrete tests, ignoring the discreteness leads to FDR estimators with inflated standard error, conservativeness and lower detection power (Efron, 2008; Pounds and Cheng, 2006). The challenges imposed by discrete tests come from two major parts. The first challenge is that the p-values from discrete tests follow discrete distributions that are stochastically larger than the Unif(0,1) distribution, which leads to the conservativeness of directly applying conventional multiple testing methods. To alleviate the discreteness of p-values, Gilbert (2005) proposed a two-step procedure combining Tarone’s adjustment (Tarone, 1990) with the BH-algorithm, by first removing tests that can not be rejected even with their smallest possible p-values. Heller and Gur (2011) suggested applying the BH-algorithm to mid p-values (Lancaster, 1961) instead of the raw p-values, but this approach does not guarantee controlling the FDR at the nominal level. Habiger and Pena (2011) and Habiger (2015) proposed a unifying framework that applies traditional multiple testing methods such as the BH-algorithm or q-value method to the randomized p-values. It avoids the issue of discreteness since the randomized p-values are continuously distributed. However, due to its random decision, this approach can be difficult for practitioners to adopt. Habiger (2015) suggested using this approach as additional information for understanding the properties of usual multiple testing procedures. The second challenge lies in that discrete tests usually have different null distributions of p-values, for that many discrete tests are conditional tests, unlike p-values always follow Unif(0,1) in continuous tests. To handle this heterogeneity, Chen and Doerge (2015) proposed grouping discrete tests into groups with similar null distributions of p-values, then controlling the FDR by a weighted FDR-control procedure proposed by Hu et al. (2010). We note that there are special cases where tests are highly homogeneous, i.e. the p-values have discrete but identical distributions, such as those induced by permutation tests. This paper does not target on this scenario and we refer readers to the novel class of FDR estimators proposed by Liang (2016).

In this paper, we propose a novel procedure for heterogeneous multiple discrete testing based on the marginal critical function (MCF) of randomized tests (Kulinskaya and Lewin, 2009). Our MCF-based method reduces the discreteness of each individual test utilizing the idea of randomized tests, and also provides non-random decisions based on the ranked MCF values. The MCF of a randomized test is the conditional probability that a randomized p-value is less than a given threshold and can serve as a measure of evidence against the null hypothesis (Kulinskaya and Lewin, 2009). Compared to the approach in Habiger (2015) which relies on a single realization of randomized p-values, our MCF-based method utilizes more distributional information of the randomized p-values and is shown to result in a higher detection power and a more stable control of FDR, i.e. a smaller standard deviation of the FDP. When tests are heterogeneous enough, specifically when Condition 3.1 in Section 3 satisfies, we prove that the pFDR of our method is asymptotically controlled at the nominal level, and provide an asymptotic upper bound for the pFNR of our method. We also show empirically that our MCF-based method outperforms many other existing methods designed for multiple discrete testing.

The paper is organized as follows. We describe our MCF-based method in Section 2, with its theory given in Section 3. In Section 4, we evaluate our method based on various simulated datasets. Section 5 presents its application to DMR detection using WGBS data from NGS experiments. Section 6 contains concluding remarks and discussions. Proofs of the theorems and additional numerical results, algorithms, figures and tables are provided in the Supplementary Material.

2. Methods

Tocher (1950) showed that a single discrete test may not achieve an exact significance level for that its raw p-value is not continuously distributed. He further suggested using an efficient randomized test strategy as a remedy. Specifically, consider a right-tailed test (similarly for left-tailed and double-tailed) with discrete test statistics T, whose observed value is denoted by t. Let P denote the raw p-value of this test (viewed as a random variable), and its observed value be p = P(t) = Pr₀(T ⩾ t) calculated under the null distribution of T. Since in a discrete test, the support of P is discrete, the test can not obtain certain significance level α exactly (Tocher, 1950). This difficulty can be solved by the introduction of randomized tests. Given observed test statistic t, the randomized p-value is defined as $\tilde{P}(t)={\mathrm{Pr}}_0(T>t)+U\cdot {\mathrm{Pr}}_0(T=t)$ for U ~ Unif(0,1). The randomizer U can be interpreted as a need for an extra Bernoulli experiment with probability of rejection (α − Pr₀(T > t))/Pr₀(T = t) when T = t. Given p, let p⁻ = Pr(T > t) be the largest possible value less than p in the support of the raw p-value (Geyer and Meeden, 2005), then

$$\tilde{P}|P=p\sim \text{Unif}(p^{-},p).$$ (1)

Marginally, when integrating out P, $\tilde{P}$ follows the Unif(0,1) distribution under the null hypothesis, and the exact level-α test can be achieved. Next we generalize the idea of randomized tests to multiple testing.

Consider testing m hypotheses with discrete test statistics. Let P₁, …, P_m be their corresponding raw p-values and ${\tilde{P}}_1,\dots ,{\tilde{P}}_m$ be their randomized p-values. To reduce the conservativeness caused by the discrete raw p-values, Habiger (2015) suggested utilizing the randomized p-values instead. First assume that, when integrating out P_i, ${\tilde{P}}_i$, i = 1,2, …m, independently follow the two-component mixture model,

$${\tilde{P}}_i|{\Delta }_i\sim (1-{\Delta }_i)\cdot \text{U}\left[0,1\right]+{\Delta }_i\cdot F_{1i},$$ (2)

where ∆_i is the indicator function that equals zero if the ith null hypothesis is true (true null) and equals one if it is false (true non-null), and F_1i is the alternative distribution of ${\tilde{P}}_i$. Suppose that Pr(∆_i = 0) = π₀ and Pr(∆_i = 1) = π₁ = 1 − π₀, where π₀ and π₁ are called the null proportion and non-null proportion, respectively.

Under the above mixture model, Storey (2003) showed that the pFDR corresponding to a threshold λ on the randomized p-values is $\text{pFDR}(\lambda )=\frac{{\pi }_0\lambda }{{\pi }_0\lambda +{\pi }_1{F}_1(\lambda )}$, where $F_1(t)=\frac{1}{m}{\sum }_{i=1}^m{F}_{1i}(t)$. Given a nominal FDR level 0 < α < 1, Habiger (2015) then defined

$${\lambda }^{*}\left(\alpha \right)=\sup \left\{\lambda :\text{pFDR}(\lambda )=\frac{{\pi }_0\lambda }{{\pi }_0\lambda +{\pi }_1{F}_1(\lambda )}⩽\alpha \right\},$$ (3)

and suggested to reject the ith tests if ${\tilde{P}}_i\hspace{0.17em}\hspace{0.17em}⩽\hspace{0.17em}\hspace{0.17em}{\lambda }^{*}\left(\alpha \right)$ (referred as Habiger’s method hereafter). We refer λ^*(α) as λ^* when no confusion. Habiger’s method is shown to control the FDR under the nominal level α (Habiger, 2015).

Although enjoying good theoretical properties, Habiger’s method is likely undesirable by practitioners due to its random decisions. In order to resolve this, we consider a related measure called the marginal critical function (MCF) of randomized test (Kulinskaya and Lewin, 2009).

Definition 1: Suppose that p is the observed p-value from a discrete test and p⁻ is the largest possible value less than p in the support of p-value. If not such p⁻ exists, let it be 0. For a given threshold λ ∈ (0, 1), the marginal critical function (MCF) of a randomized test is defined as

$$r(p,\lambda )=\{\begin{array}{ll}1,\hfill & \text{if}\hspace{0.17em}p<\lambda ,\hfill \\ \frac{\lambda -p^{-}}{p-p^{-}},\hfill & \text{if}\hspace{0.17em}{p}^{-}<\lambda \hspace{0.17em}⩽\hspace{0.17em}p,\hfill \\ 0,\hfill & \text{if}\hspace{0.17em}\lambda \hspace{0.17em}⩽\hspace{0.17em}{p}^{-}.\hfill \end{array}$$

It follows from the conditional distribution of $\tilde{P}$ in (1) that $r(p_i,\hspace{0.17em}\hspace{0.17em}{\lambda }^{*})=\mathrm{Pr}({\tilde{P}}_i<{\lambda }^{*}|p_i)$. In other words, the MCF represents the conditional probability of a test being rejected by Habiger’s method. Therefore, the tests with larger MCF values are more likely to be true non-null and shall be rejected. For simplicity, we use r_i to refer to the MCF r(p_i, λ^*) conditionally on p_i.

Define the random indicators $X_i=1\left\{{\tilde{P}}_i\hspace{0.17em}⩽\hspace{0.17em}{\lambda }^{*}|p_i\right\}$, i = 1, 2, …, m, then Habiger’s method rejects the ith test if X_i = 1. To avoid the random decision in Habiger’s method caused by the random variable X_i’s, we make decisions relying on the expected value of each X_i, E(X_i|p_i) = r_i, which is fixed given observed p_i. We also make the same proportion of rejection as in Habiger’s method to ensure that the FDR is controlled. Specifically, following the two-component model (2), given level λ^*, the expected proportion of rejections by Habiger’s method is $u=\frac{1}{m}{\sum }_{i=1}^m\text{Pr}({\tilde{P}}_i<{\lambda }^{*})={\pi }_0{\lambda }^{*}+{\pi }_1{F}_1({\lambda }^{*})$. Define the (1 − u)-th quantile of the empirical distribution of the pooled MCF’s {r₁, …, r_m} as

$$Q\left(1-u\right)=\inf \left\{x\in ℝ:1-u\hspace{0.17em}⩽\hspace{0.17em}\text{CDF(}x\text{)}\right\},$$ (4)

where $\text{C}\text{DF}\left(x\right)=\frac{{\sum }_{i=1}^{m}1\{r_i\hspace{0.17em}⩽\hspace{0.17em}x\}}{m}$ is the empirical cdf of the r_i’s. We then reject the ith test if r_i > Q(1 −u). When some tests are homogeneous and they have the same observed p-values, there exist ties in the MCF values and the proportion of rejections by our MCF-based method will be smaller than Habiger’s method. However, when the tests are not highly homogeneous, ties happen rarely and the difference in their proportions of rejections is small. Our simulation studies in Section 4 also show that even though our MCF-based method may result in slightly smaller number of rejections, it often has higher detection power than Habiger’s method due to its usage of more informative MCFs.

Our method is summarized in the following Algorithm 1.

$$\underset{\_}{\begin{array}{l}\overline{\mathbf{\text{Algorithm}}\hspace{0.17em}\mathbf{1}\text{:}\hspace{0.17em}\text{MCF-based}\hspace{0.17em}\text{Multiple}\hspace{0.17em}\text{Testing}\hspace{0.17em}\text{Procedure }\hspace{0.17em}}\\ \overline{\begin{array}{l}\hspace{0.17em}\mathbf{\text{Step}}\hspace{0.17em}\mathbf{1}\hspace{0.17em}\text{:}\hspace{0.17em}\text{Estimate}\hspace{0.17em}\text{the}\hspace{0.17em}\text{null}\hspace{0.17em}\text{proportion}\hspace{0.17em}{\pi }_{\text{0}}\hspace{0.17em}\text{and}\hspace{0.17em}\text{the}\hspace{0.17em}\text{proportion}\hspace{0.17em}\text{of}\hspace{0.17em}\text{rejections}\\ \begin{array}{l}\hspace{0.17em}F(\lambda )={\pi }_{\text{0}}\lambda +{\pi }_{\text{1}}{F}_{\text{1}}\text{(λ),}\hspace{0.17em}\text{which}\hspace{0.17em}\text{is}\hspace{0.17em}\text{the}\hspace{0.17em}\text{denominator}\hspace{0.17em}\text{in}\hspace{0.17em}\left(\text{3}\right)\text{;}\hfill \\ \hspace{0.17em}\mathbf{\text{Step}}\hspace{0.17em}\mathbf{2}\hspace{0.17em}\text{:}\hspace{0.17em}\text{For}\hspace{0.17em}\text{a}\hspace{0.17em}\text{given}\hspace{0.17em}\text{FDR}\hspace{0.17em}\text{level}\hspace{0.17em}\alpha \text{,}\hspace{0.17em}\text{calculate}\hspace{0.17em}\text{the}\hspace{0.17em}\text{threshold}\hspace{0.17em}\lambda *\hspace{0.17em}\text{(}\alpha \text{)}\hspace{0.17em}\text{in}\hspace{0.17em}\left(\text{3}\right)\text{;}\hfill \\ \hspace{0.17em}\mathbf{\text{Step}}\hspace{0.17em}\mathbf{3}\hspace{0.17em}\text{:}\hspace{0.17em}\text{From}\hspace{0.17em}\text{Definition}\hspace{0.17em}\text{1,}\hspace{0.17em}\text{calculate}\hspace{0.17em}\text{the}\hspace{0.17em}\text{MCF}\hspace{0.17em}\text{value}\hspace{0.17em}\text{corresponding}\hspace{0.17em}\text{to}\hspace{0.17em}\lambda *\hspace{0.17em}\text{(}\alpha \text{),}\hspace{0.17em}{r}_i\text{,}\hspace{0.17em}\text{for}\hspace{0.17em}\text{each}\hspace{0.17em}\text{test;}\hfill \\ \hspace{0.17em}\mathbf{\text{Step}}\hspace{0.17em}\mathbf{4}\hspace{0.17em}\text{:}\hspace{0.17em}\text{Calculate}\hspace{0.17em}\text{the}\hspace{0.17em}\text{(1}-u\text{)-th}\hspace{0.17em}\text{quantile}\hspace{0.17em}\text{in}\hspace{0.17em}\left(\text{4}\right)\hspace{0.17em}\text{and}\hspace{0.17em}\text{reject}\hspace{0.17em}\text{the}\hspace{0.17em}i\text{th}\hspace{0.17em}\text{test}\hspace{0.17em}\text{if}\hspace{0.17em}{r}_i\hspace{0.17em}>Q\hspace{0.17em}(1-u)\text{.}\hfill \end{array}\end{array}}\end{array}}$$

In Step 1, common estimation methods for multiple continuous tests can be directly applied because the randomized p-values are continuously distributed (Nettleton et al., 2006; Pounds and Cheng, 2006; Storey, 2002). This is another advantage of our method as we avoid the complications to account for discreteness. To estimate π₀, we generate B set of samples of the randomized p-values, $\left\{{\tilde{p}}_1^b,{\tilde{p}}_2^b,\dots ,{\tilde{p}}_m^b\right\}$, b = 1, 2, …, B and apply Storey’s estimator ${\widehat{\pi }}_0^b(t)=\frac{{\sum }_{i=1}^{m}1\left\{{\tilde{p}}_i^b>t\right\}}{m(1-t)}$ with threshold t. We then estimate π₀ by ${\widehat{\pi }}_0(t)=\frac{1}{B}{\sum }_{b=1}^B{\widehat{\pi }}_0^b(t)$. Storey (2002) provided a bootstrap method to find the optimal threshold t in Storey’s estimator. However, they found that the difference of using different thresholds was not drastic, and optimal performance in estimating pFDR was nearly attained in almost all the situations they simulated (Storey, 2002). In the scenario of multiple discrete testing, we also found that using different threshold t led to similarly good estimators based on our simulated datasets (see details in Web Appendix D). Therefore in our work, we suggest setting t = 0.5 by convention. To estimate F (λ) = π₀λ + π₁F₁(λ), which is the denominator in (3), we use the empirical distribution of the pooled sample of randomized p-values, $\left\{{\tilde{p}}_1^1,\dots ,{\tilde{p}}_m^1,{\tilde{p}}_1^2,\dots ,{\tilde{p}}_m^2,\dots ,{\tilde{p}}_1^B,\dots ,{\tilde{p}}_m^B\right\}$, i.e. $\widehat{F}(\lambda )=\frac{{\sum }_{b=1}^B{\sum }_{i=1}^{m}1\left\{{\tilde{p}}_i^b<\lambda \right\}}{B\cdot m}$. In practice, a reasonably large B will ensure accurate estimations and we find B = 1000 often sufficient. In Step 2, there is generally no closed-form solution to calculate λ^*. However, following Genovese et al. (2006) we may assume that F₁ is concave, then based on Lemma 1 in the Web Appendix E, we know that $\frac{{\pi }_0\lambda }{{\pi }_0\lambda +{\pi }_1{F}_1(\lambda )}$ is non-decreasing in λ. This allows us to apply the bisection algorithm to find λ^* (see Web Appendix F).

3. Theoretical Results

In this section, we derive the upper bounds for the asymptotic pFDR and pFNR corresponding to our MCF-based method. We also show that our method gives a strictly larger set of detections than the q-value method.

3.1. Asymptotic upper bound of pFDR

Let ${\mathcal{P}}_i$ be the discrete support of the raw p-value P_i, i = 1, 2, …, m. Similar to the two-component model (2) of ${\tilde{P}}_i$, we assume that the raw p-value P_i also follows a mixture model,

$$P_i|{\Delta }_i\sim (1-{\Delta }_i)\cdot H_{0i}+{\Delta }_i\cdot H_{1i},$$ (5)

where ∆_i is defined as in (2), H_0i and H_1i are the null and alternative cdf of P_i, respectively, and H_0i(p) = p for any $p\in {\mathcal{P}}_i$ (Geyer and Meeden, 2005). Let h_0i and h_1i denote the pmf of H_0i and of H_1i, respectively. Given a threshold 0 < λ < 1, for the ith test, i = 1, …, m, let $b_{i\lambda }=\min \left\{p:p\hspace{0.17em}⩾\hspace{0.17em}\lambda ,p\in {\mathcal{P}}_i\right\}$ and $a_{i\lambda }=\max \left\{p:p\hspace{0.17em}<\hspace{0.17em}\lambda ,p\in {\mathcal{P}}_i\cup \left\{0\right\}\right\}$, i.e. a_iλ < λ ⩽ b_iλ are two consecutive values in ${\mathcal{P}}_i$ around λ. Notice that, in the special case that b_iλ is the smallest value in ${\mathcal{P}}_i$, we let a_iλ be 0. By Definition 1, the MCF value r_i = r(p_i, λ) takes value in $\left\{0,w_i=\frac{\lambda -a_{i\lambda }}{b_{i\lambda }-a_{i\lambda }},1\right\}$ and follows a two-component model,

$$r_i|{\Delta }_i\sim (1-{\Delta }_i)\cdot G_{0i}+{\Delta }_i\cdot G_{1i},$$ (6)

where the cdf’s G_ji, j = 0, 1, are step functions with jumps at {0, w_i, 1} and the corresponding step sizes, i.e. pmf values, are {H_ji(a_iλ), h_ji(b_iλ), 1 − H_ji(b_iλ)}. Marginally over m tests, the average null and alternative cdf of the MCF values are $G_0^m=\frac{1}{m}{\sum }_{i=1}^m{G}_{0i}$ and $G_1^m=\frac{1}{m}{\sum }_{i=1}^m{G}_{1i}$, which have jumps at {1, w₁, …, w_m, 1} with corresponding step size $\left\{\frac{1}{m}{\sum }_{i=1}^m{H}_{ji}(a_{i\lambda }),\frac{1}{m}{h}_{j1}(b_{1\lambda }),\dots ,\frac{1}{m}{h}_{jm}(b_{m\lambda }),\frac{1}{m}{\sum }_{i=1}^m[1-H_{ji}(b_{i\lambda })]\right\}$. for j = 0, 1. As the number of tests m → ∞, each step size $\frac{1}{m}{h}_{jk}(b_{k\lambda })$ goes to 0 as hj_k (b_kλ) is bounded by 1. When tests are highly heterogeneous, in the sense that there are not infinitely many w_i’s having the same value, and w_i’s spread well within (0,1), we make the following assumption to linearly approximate the steps in $G_0^m$ and $G_1^m$.

Condition 3.1: For any threshold λ ∈ (0, 1), and j = 0, 1, suppose there exist constants $a_j^{*},b_j^{*}\in (0,1)$, such that as m → ∞, $\frac{1}{m}{\sum }_i^m{H}_{ji}(a_{i\lambda })\to a_j^{*}$ and $\frac{1}{m}{\sum }_i^m{H}_{ji}(b_{i\lambda })\to b_j^{*}$. Let $G_j^{*}$ be a random variable with cdf

$$G_j^{*}(x)=\{\begin{array}{ll}{a}_j^{*}\hfill & \text{if}\hspace{0.17em}x<0,\hfill \\ a_j^{*}+\left(b_j^{*}-a_j^{*}\right)x,\hfill & \text{if}\hspace{0.17em}\text{0}\hspace{0.17em}⩽\hspace{0.17em}x<1,\hfill \\ b_j^{*}\hfill & \text{if}\hspace{0.17em}x<1,\hfill \end{array}$$

then $G_j^m\stackrel{d}{\to }{G}_j^{*}$ as m → ∞ for j = 0, 1.

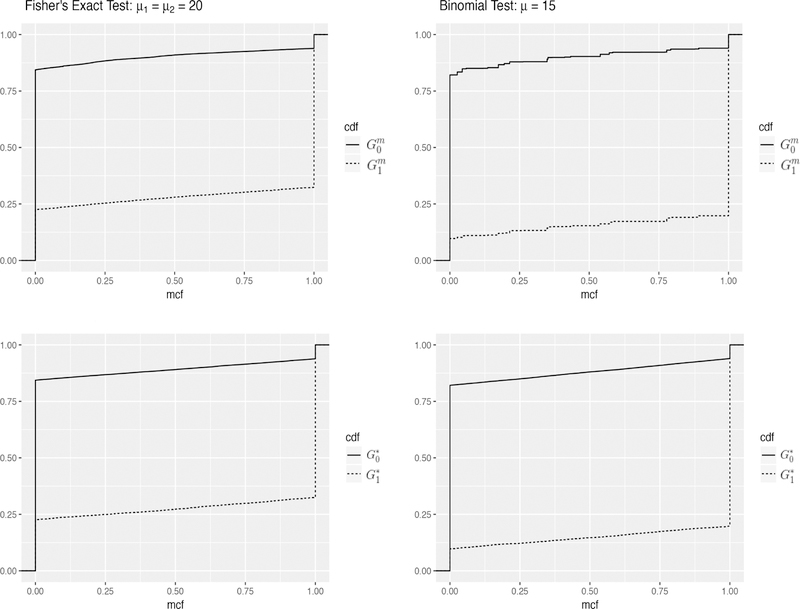
Condition 3.1 can be interpreted under a Bayesian hierarchical model setup. In discrete tests, for a given λ, the null and alternative distribution of the MCF value, (G_0i, G_1i), are usually determined by the configuration of ith test, i = 1, …, m. For example, the configuration of a Binomial test includes the sample size, the probability of success under the null and alternative hypotheses. Following a Bayesian hierarchical model setup, when the number of tests is large, the test configurations can be considered as independently generated from an underlying mechanism (Allison et al., 2002; Catelan et al., 2010; Tang et al., 2007). Thus for j = 0, 1, H_ji(a_iλ) and H_ji(b_iλ) are i.i.d. random variables, i = 1, …, m, and based on the law of large numbers (LLN), their mean converges under mild conditions as m → ∞ (Lehmann, 2004). Condition 3.1 also assumes that this underlying mechanism generates highly heterogeneous tests so that the linear approximations of $G_0^m$ and $G_1^m$ hold. Figure 1 below shows the empirical $G_0^m$ and $G_1^m$ from simulated datasets under two setups described in Section 4, and their corresponding linear approximations $G_0^{*}$ and $G_1^{*}$ defined in Condition 3.1.

Figure 1.

Empirical $G_0^m$ and $G_1^m$ (top) and their corresponding linear approximations $G_0^{*}$ and $G_1^{*}$ (bottom) described in Condition 3.1, under Setup 1 with µ₁ = µ₂ = 20 (left) and Setup 2 with µ = 15 (right).

When tests are randomly generated from a hierarchical model, although each test is discrete, when they are heterogeneous enough, the step sizes of the average distribution $G_0^m$ and $G_1^m$ are small and they can be well approximated on (0,1) by a continuous distribution as in Condition 3.1. In Section 5, we also show that the real application of DMR detection based on WGBS read counts leads to a highly heterogeneous multiple discrete testing problem, and our MCF-based method applies well. When tests are highly homogeneous, for example when each test is a permutation test with the same sample size as described in Liang (2016), Condition 3.1 may not hold and one may adopt other methods, such as Liang (2016).

Under Condition 3.1, Theorem 1 gives the asymptotic upper bound of the pFDR for our method. See Web Appendix A for the proof of Theorem 1.

Theorem 1: In a multiple testing problem with m discrete tests, denote by P_i and ${\tilde{P}}_i$ the p-value and randomized p-value of the ith test, i = 1, 2, …, m, respectively. Suppose that P_i independently follows the distribution (5) and ${\tilde{P}}_i$ independently follows the distribution (2). With probability 1, as m → ∞, suppose that $\frac{{\sum }_{i=1}^m(1-{\Delta }_i)}{m}\to {\pi }_0$ and $\frac{{\sum }_{i=1}^m{F}_{1i}(t)}{m}\to F_1^{*}(t)$ for any 0 ⩽ t ⩽ 1, where 0 < π₀ < 1 is a constant and $F_1^{*}$ is a continuous cdf. Given a nominal FDR level 0 < α < 1, let $u^{*}={\pi }_0{\lambda }^{*}(\alpha )+{\pi }_1{F}_1^{*}({\lambda }^{*}(\alpha ))$, and reject the ith test if r_i > Q(1 −u^*) where Q(1 − u^*) is the (1 − u^*)-th quantile of the pooled MCF values {r₁, …, r_m} as in (4). Suppose that Condition 3.1 holds, then as m → ∞, the corresponding pFDR satisfies,

$$\underset{m\to \infty }{\lim \sup }\hspace{0.17em}\text{pFDR(}m\text{)}\hspace{0.17em}⩽\hspace{0.17em}\alpha .$$ (7)

3.2. Asymptotic upper bound of pFNR

Next we investigate the Type-II error performance for our MCF-based method in terms of the positive false non-discovery rate (pFNR) (Storey, 2003). Let W denote the number of nonsignificant tests, out of which T tests are true non-nulls, then $\text{pFNR}=\text{E}\left(\frac{T}{W}|W>0\right)$. Theorem 2 below provides an asymptotic pFNR bound of our method. See Web Appendix B for the proof of Theorem 2.

Theorem 2: Under the assumptions of Theorem 1, the corresponding pFNR satisfies

$$\underset{m\to \infty }{\lim \sup }\hspace{0.17em}\text{pFDR(}m\text{)}\hspace{0.17em}⩽\hspace{0.17em}\frac{{\pi }_1(1-F_1^{*}({\lambda }^{*}))}{1-({\pi }_0{\lambda }^{*}+{\pi }_1{F}_1^{*}{\text{(λ}}^{*}))}.$$ (8)

In general, methods for controlling the FDR do not necessarily minimize the pFNR, but Theorem 2 enables us to quantify the pFNR by its upper bound.

3.3. Comparison to a naive application of the q-value method

As many FDR-control methods for discrete tests are developed only recently, the discreteness issue is often ignored by practitioners and hence common methods, e.g. the q-value method (Storey, 2003), are directly applied. The advantage of our MCF-based method compared to the q-value method is shown in the following theorem. See Web Appendix C for the proof of Theorem 3.

Theorem 3: In a multiple testing problem with m discrete tests, if a test is rejected after directly applying the q-value method to the raw p-values, it will also be rejected by our MCF-based method under the same nominal FDR level.

Theorem 3 claims that under the same nominal FDR level, our MCF-based method will not miss any significant test reported by the q-value method. In other words, our MCF-based method has a strictly larger detection power than the q-value method. This is also shown under various settings of simulations (Section 4) and in the real application to a WGBS dataset (Section 5). In contrast, Habiger’s method does not share this property as their decision solely depends on a one-time realization of the randomized p-values.

4. Simulation study

In this section, we demonstrate the performance of our method by simulations. We generate data under two different setups and consider testing m = 5000 hypotheses with the true null proportion π₀ = 0.9, which emulates typical multiple-testing applications with relatively sparse signals, i.e. true non-nulls.

• Setup 1: The ith test, i = 1, 2, …, m, is an FET to test if the probabilities of success from two Binomial distributions are the same. This is consistent with the setup of the DMR detection in the real application in Section 5, where at each CpG site an FET is conducted. The FET is built on the data given in the following 2 × 2 contingency table, which consists of the counts (C, N − C) from two Binomial distributions, Bin(n_1i, q_1i) and Bin(n_2i, q_2i).

	C	N − C	Total
Bin(n1i, q1i)	c1i	n1i − c1i	n1i
Bin(n2i, q2i)	c2i	n2i – c2i	n2i

We first generate the number of trials n_si ~ Poisson(µ_s) and then the count c_si ~ Binomial(n_si, q_si), s = 1, 2. Two cases are considered: µ₁ = µ₂ = 20 and µ₁ = µ₂ = 25. For the first π₀ · m = 4500 tests (true nulls), we generate the common value of q_1i and q_2i independently from U[0,1]. For the rest 500 tests (true non-nulls), q_2i = 0.5u_i, q_1i = q_2i + δ_i. where u_i ~ U[0, 1] and δ_i ~ U[0.2, 0.5]. Then we apply FET to test H_0i : q_1i = q_2i v.s. H_1i : q_1i ≠ q_2i, i = 1, …, m.

• Setup 2: The ith test, i = 1, 2, …, m, is an exact Binomial test to test if the probability of success in a Bernoulli experiment is 0.5 or not. We generate counts X_i from a Binomial distribution Bin(n_i, q_i) with success probability q_i = 0.5 for i = 1, …, 4500 and q_i = 0.5+δ_iϵ_i for i = 4501, …, 5000, where δ_i is the sign variable with equal probability being 1 and −1, and ϵ_i ~ U[0.2, 0.5]. Sample sizes n₁, n₂,…n_m were generated independently from a Poisson distribution with mean µ. Two cases are considered: µ = 10 and µ = 15. We then apply Binomial tests to test H_0i : q_i = 0.5 v.s. H_1i : qi ≠ 0.5, i = 1, …, m.

We run N = 100 Monte Carlo simulations to evaluate the average performance of our method. We keep n_si, q_si under Setup 1 and n_i, q_i under Setup 2 unchanged in different Monte Carlo samples and only update c_si under setup 1 and X_i under setup 2.

We compare our method with Habiger’s method and three other methods designed for multiple discrete testing (Chen and Doerge, 2015; Gilbert, 2005; Heller and Gur, 2011), in their true FDR and statistical power at different nominal FDR level α, where the statistical power is defined as the ratio between the number of correct rejections and the number of true non-null hypotheses.

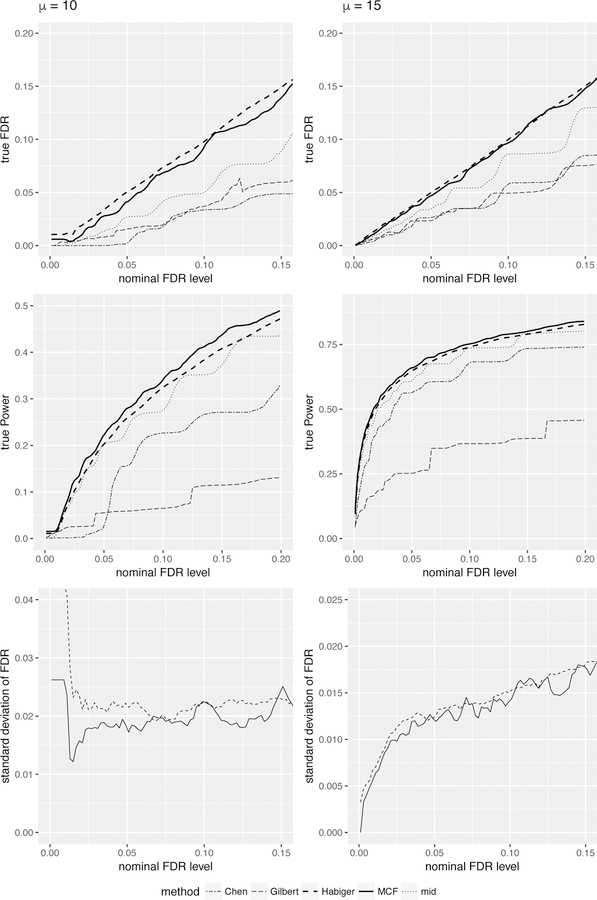
The top rows of Figures 2 and 3 plot the average FDP of each method. We see that all five methods control the FDR under nominal level, i.e. below the 45 degree line. However except our method and Habiger’s method, the other three methods are too conservative based on the graph, i.e. far below the diagonal line. Although our MCF-based method results in a smaller FDR than Habiger’s method, it is not conservative and even more powerful than Habiger’s method according to the statistical power. The second rows of Figures 2 and 3 display the statistical power of each method, and our method achieves the best performance and very close to Habiger’s method. In addition, the third rows of Figures 2 and 3 plot the standard deviation of the FDP’s over the N = 100 Monte Carlo samples, i.e. $\sqrt{{\sum }_{i=1}^N({\text{FDP}}_i-\hspace{0.17em}\overline{\text{FDP}}{)}^2/N}$, where FDP_i is the FDP based on the ith sample and $\overline{\text{FDP}}={\sum }_{i=1}^N{\text{FDP}}_i/N$. We can see that our MCF-based method is more stable than Habiger’s method with a lower standard deviation, which is expected as our method utilized the distributional information of the randomized p-values comparing to utilizing their one-time realizations as in Habiger’s method. We also plot the FNR corresponding to our method and Habiger’s method, and the asymptotic pFNR upper bound proposed in Theorem 2 (see Web Figures 2 and 3 in Web Appendix I). We see that the FNR of our method is similar but slightly lower than that of Habiger’s method, and the asymptotic pFNR upper bound proposed in Theorem 2 is usually effective and close to the true FNR.

Figure 2.

Performance comparisons among different multiple testing methods for Setup 1. The average FDR vs. nominal FDR level (first row), the statistical power vs. nominal FDR level (second row) and the sample standard deviation of FDR (from 100 simulations) vs. nominal FDR level (third row), for Setup 1 with µ₁ = µ₂ = 25 (left column) and µ₁ = µ₂ = 20 (right column).

Figure 3.

Performance comparisons among different multiple testing methods for Setup 2. The average FDR vs. nominal FDR level (first row), the statistical power vs. nominal FDR level (second row) and the sample standard deviation of FDR (from 100 simulations) vs. nominal FDR level (third row), for Setup 2 with µ = 10 (left column) and µ = 15 (right column).

5. Applications

In this section, we apply our MCF-based multiple testing method to DMR detection, using a WGBS dataset from the NIH Roadmap Project (http://www.ncbi.nlm.nih.gov/geo/roadmap/epigenomics) in the Gene Expression Omnibus (GEO) database. We use three different types of sample cells: Brain, Skin and H1ES (Kundaje et al., 2015), where each sample has only 1 biological replicate. Following Challen et al. (2012), we considered three pairwise comparisons for detecting differentially methylated CpG sites between two biological samples, i.e., Brain versus H1ES, Skin versus H1ES and Brain versus Skin, by running FET at each CpG site. The data at the ith CpG sites can then be expressed as the following 2 × 2 contingency table.

	Methylated	Unmethylated	total
Sample 1	m1i	n1i − m1i	n1i
Sample 2	m2i	n2i − m2i	n2i

The CpG sites with at least one of the total counts (n_1i, n_2i) less than 15 were excluded from our analysis to ensure the reliability of the data source. The threshold 15 is applied to achieve a good compromise between the test accuracy and the genome coverage, as CpG sites with low read counts may not be measured accurately. We also repeated the same analysis using the cutoffs of 10 and 20, and our results were little affected by the cutoff value (see Web Appendix G). The three comparisons then contained 10,023,559, 15,894,438 and 9,384,917 tests, respectively. Boxplots of the total read count at different CpG sites in each sample (see Web Figure 4 in Web Appendix I) shows that these read counts are highly variated. Since FET is a conditional discrete test depending on the marginal counts, i.e. the total read counts, thus combing all CpG sites leads to a heterogeneous discrete multiple testing problem, which is an ideal application setting for our MCF-based method. We then compared our method with the widely-used q-value method under two nominal FDR levels α = 0.05 and 0.1, respectively. Because Habiger’s method produces random decisions, and the method of Chen and Doerge (2015) is computationally too intense to handle multiple testing at this large scale, we did not include them.

Results in Table 1 show that our MCF-based method always gave more discoveries than the q-value method. Across three comparisons, our MCF-based method resulted in 13–44% more discoveries. Moreover, our MCF-based method detected every discovery made by the q-value method, in that the number of significant CpG sites found by the q-value method is always the same as the number of significant CpG sites found by both the MCF-based method and the q-value method, and this is consistent with Theorem 3 in Section 3. Hereafter, we refer to the significant CpG sites found by the MCF-based method but not the q-value method as the “additional” sites, and the significant CpG sites found by both methods as “overlap” sites. We plotted the number of significant CpG sites detected by the two methods at different nominal FDR levels (from 0 to 0.2 with step size 0.001) (see Web Figure 5 in Web Appendix I), which shows that our MCF-based method consistently detected more significant CpG sites than the q-value method. We also plotted the histogram of the standardized methylation level difference between two genomic samples at each significant CpG site (see Web Figure 6 in Web Appendix I). The standardized methylation level difference at the ith CpG site is defined as $\frac{{\widehat{q}}_{1i}-{\widehat{q}}_{2i}}{\sqrt{{\widehat{q}}_i(1-{\widehat{q}}_i)\{1/n_{1i}+1/n_{2i}}}$, where ${\widehat{q}}_{1i}=\frac{m_{1i}}{n_{1i}}$, ${\widehat{q}}_{2i}=\frac{m_{2i}}{n_{2i}}$ and ${\widehat{q}}_i=\frac{m_{1i}+m_{2i}}{n_{1i}+n_{2i}}$ Then from the overlaps of histograms between the additional sites and the overlap sites, we see that the additional power of our method was not due to a simple shift of the cutoff on the standardized methylation level difference.

Table 1.

Number of the significant CpG sites. “MCF” represents the number of significant CpG sites found by the MCF-based method, “q-value” the number of significant CpG sites found by q-value method, “both” the number of significant CpG site found by both methods.

	α = 0.05			α = 0.1
	MCF	q-value	both	MCF	q-value	both
Brain vs H1ES	1,572,027	1,136,401	1,136,401	2,225,930	1,541,358	1,541,358
Skin vs H1ES	2,239,725	1,986,017	1,986,017	2,715,394	2,325,530	2,325,530
Brain vs Skin	1,593,047	1,250,206	1,250,206	2,082,701	1,545,953	1,545,953

We further plotted the histograms of $p_i-p_i^{-}$ for the additional CpG sites and the overlap CpG sites in Figure 4. We see that the additional CpG sites are usually associated with large values in $p_i-p_i^{-}$‘s, i.e. p_i is not very small but $p_i^{-}$ is. The intuition is that, for a CpG site with small a $p_i^{-}$, even though the observed p_i is not very small, a small $p_i^{-}$ means that if we run a repeated experiment at this CpG site, it is likely that the observed p-value will shift to $p_i^{-}$ due to the sampling variation. In other words, our procedure does not solely rely on the observed p-values, but also consider their possible values in a repeated experiment. Also from Definition 1, if p_i and λ are fixed, the smaller $p_i^{-}$ is, the larger its MCF would be, and more likely the CpG site will be claimed as significant. Therefore, for those CpG sites that are not detected by the q-value method, our MCF-based method gains power by looking at their $p_i^{-}$‘s and identifies those sites as significant if their $p_i^{-}$‘s are small.

Figure 4.

Histogram of $p_i-p_i^{-}$ at each significant CpG site. The light color represents the overlap CpG sites, the dark color represents the additional CpG sites.

The goal of a WGBS experiment usually does not stop at identifying individual CpG sites that show statistical significance between two samples, but to find differentially methylated regions (DMRs), which are regarded as possible functional regions involved in gene transcriptional regulation and chromatin remodeling (Hebestreit et al., 2013). A DMR involves a group of adjacent CpG sites that are mostly differentially methylated and we used a merging technique in Feng et al. (2014) to combine nearby CpG sites into DMRs (see details in Web Appendix H). The results are presented in Table 2, which shows that our MCF-based method gave 14% − 78% more detections than the q-value method at the DMR level.

Table 2.

Number of the significant DMRs. “MCF” represents the number of DMRs found by the MCF-based method, “q-value” the number of DMRs found by q-value method, “both” the number of DMRs found by both methods.

	α = 0.05			α = 0.1
	MCF	q-value	both	MCF	q-value	both
Brain vs H1ES	18,177	12,390	12,387	32,547	18,283	18,268
Skin vs H1ES	51,218	44,956	44,955	63,746	54,134	54,132
Brain vs Skin	34,573	25,001	24,994	51,837	33,827	33,818

To validate the performance of our MCF-based method and to ensure that the additional DMRs detected by our method are biologically meaningful, we performed an enrichment analysis on the additional DMRs at the nominal FDR level α = 0.05. We used the Genomic Regions Enrichment of Annotations Tool (GREAT) (McLean et al., 2010) and presented the biological pathway ontology enrichment results using the Pathway Commons database (http://www.pathwaycommons.org/ ) (see Web Figures 7–9 in Web Appendix I). Biological pathway is one of the most widely used gene ontology types and includes biochemical reactions, complex assembly, transport and catalysis events, and physical interactions involving proteins, DNA, RNA, small molecules and complexes. GREAT performs both the binomial test over genomic regions and the hypergeometric test over genes to provide an accurate picture of annotation enrichments for genomic regions. A pathway is claimed as statistically enriched if it shows significance in both tests as well as its value in Binom Fold Enrichment (column 3 in Web Figures 7–9 in Web Appendix I) is greater than 2. The Binom Fold Enrichment is defined as k/(n * p), where k is the number of DMRs that hit the annotation, n is the number of the total genomic regions and p is the fraction of the genome annotated. For details about the GREAT analysis, refer to http://bejerano.stanford.edu/help/display/GREAT/Output. From the enrichment analysis results in Web Figures 7–9 in Web Appendix I, for the three comparisons of Brain versus H1ES, Skin versus H1ES and Brain versus Skin, there are 32, 9 and 31 biological pathways enriched, respectively, based on the additional DMRs detected by the MCF-based method. Many of these enriched pathways are related to the specific biological functions of the compared sample cells. For example, in the comparison between Brain and H1ES cells the ceramide signaling pathway was enriched, in the comparison between Skin and H1ES the vitamin C ascorbate metabolism pathway was enriched, and in the comparison between Brain and Skin the glutamate degradation pathway and organic anion transport pathway were enriched. The enrichment analysis thus shows that, the additional DMRs detected by our MCF-based method provided biological meaningful information in retrieving the functional profile of biological samples, and using MCF-based methods helped identify more biologically functional regions comparing to the traditional q-value method.

6. Conclusion and Discussion

In this paper, we proposed a novel MCF-based method for multiple testing of heterogeneous discrete tests. Our proposed method utilizes the MCF of randomized tests to achieve a powerful testing procedure. Rather than making decisions directly according to a one-time realization of the randomized p-values, our method performs better by using more distributional information of the randomized p-values. Our test decision is non-random and can be easily applied in practice comparing to the randomized testing approach in Habiger (2015). When tests are heterogeneous enough, specifically when Condition 3.1 satisfies, we proved that the pFDR of our method is asymptotically controlled under nominal level, and provided an asymptotic upper bound for the pFNR. Our method results in more detections than a naive application of the q-value method and does not miss any significant test detected by the q-value method. Another advantage of our method is that to estimate the null proportion and the alternative distribution of the randomized p-values, we can generate samples of the randomized p-values and apply common estimation methods without being concerned about the discreteness. Under different simulation settings, we showed that our MCF-based method outperformed many other existing methods with a higher detection power, and a controlled and more stable FDR. In a real application of DMR detection using WGBS data, our method improved the detection power by reporting more biologically meaningful regions. We also understood that our proposed method gains power from rejecting the tests that are likely to have smaller p-values if repeated experiments are conducted. Furthermore, our MCF-based method is designed for general heterogeneous multiple discrete testing, therefore besides the DMR detection mentioned in this paper, it has a broad range of applications in the analysis of the next-generation sequencing experiments and many other scientific fields, where data are collected as discrete read counts.