Transformation model estimation of survival under dependent truncation and independent censoring

Abstract

Truncation is a mechanism that permits observation of selected subjects from a source population; subjects are excluded if their event times are not contained within subject-specific intervals. Standard survival analysis methods for estimation of the distribution of the event time require quasi-independence [1] of failure and truncation. When quasi-independence does not hold, alternative estimation procedures are required; currently, there is a copula model approach that makes strong modeling assumptions, and a transformation model approach [2] that does not allow for right censoring. We extend the transformation model approach to accommodate right censoring. We propose a regression diagnostic for assessment of model fit. We evaluate the proposed transformation model in simulations and apply it to the National Alzheimer’s Coordinating Centers autopsy cohort study and an AIDS incubation study. Our methods are publicly available in an R package, tranSurv [3].

Introduction

Truncation is a mechanism that yields a biased sample from a source population; subjects are excluded if their event times fall outside of subject-specific intervals. One-sided intervals yield left (or right) truncation. Truncation differs from censoring, which causes incomplete observations from the entire population. Left truncation refers to the sampling requirement that the event time exceeds the truncation time, while right truncation refers to the sampling requirement that the event time precedes the truncation time. While left truncation is often accompanied by right censoring, right truncation typically does not involve any censoring. In the absence of censoring, and for the purpose of nonparametric survivor function estimation, a method that accommodates left-truncated data also accommodates right-truncated data, through a simple reversal of the timescale [4, Chapter 5.3].

Standard survival analysis methods for estimation of the distribution of the event time in the presence of truncation and censoring [5, 6] require independent censoring and quasi-independence [1] of failure and truncation. Quasi-independence means that the joint density of the event time and the truncation time is proportional to the product of their marginals in the observable region. While independent censoring cannot be empirically tested [7], quasi-independence of event and truncation can be tested using the observed data. When quasi-independence does not hold, the simple truncation-adjusted Kaplan–Meier and Turnbull estimators are biased [8]. This is problematic because in many settings it is of interest to disentangle the marginal survivor distribution from the sampling and observation processes that are particular to the given study. The marginal survivor distribution is substantively meaningful and generalizable, and can be estimated under an assumed dependence model. Thus, in the presence of quasi-dependence, such a model and accompanying alternative estimation procedures are required. We note that in some contexts, the nature of the dependence relationship is of primary scientific interest and calls for careful investigations. In this paper, however, we presume that the dependence is a nuisance with regard to our primary objective of estimating the marginal survivor distribution.

Truncation arises from observational studies in which some selection occurs, and often this is dependent on the failure mechanism. The primary goal of a National Alzheimer’s Coordinating Centers (NACC) study is to estimate the distribution of the duration of Alzheimer’s disease (AD) measured from the age of cognitive impairment to the age at death. The duration of AD is left-truncated by the time from cognitive impairment to NACC entry for the participants who experienced cognitive impairment prior to their NACC study entry. One might suspect that age of entry to the sample is associated with risk of death, and thus time to death. On the other hand, an AIDS incubation study [1] retrospectively sampled hemophiliacs who had received blood transfusions and were diagnosed with AIDS. Thus, only infected individuals who were diagnosed with AIDS prior to the end of the study period were included in the study; this is an example of right truncation with truncation time being the length of the study period. In this study, a longer duration from HIV infection to AIDS onset is associated with a shorter duration from HIV infection to sampling, suggesting a longer incubation period later in calendar time. In each of these examples, quasi-independence of truncation and failure is rejected and thus the simple truncation-adjusted Kaplan–Meier estimator [5] cannot be used for the event time distribution.

Several tests of quasi-independence have been proposed in the literature. A conditional version of a Kendall’s tau [9] test of association was established for one sided truncation [1], and was extended to more complicated truncation settings in the presence of independent censoring [10, 11]. Other approaches include weighted log-rank statistics [12], tests of the Markov condition in the illness-death model [13], copula based tests [14], and thresholded minimum p-value tests [15]. Currently, there are no software packages available for testing quasi-independence.

There is a limited literature on survivor function estimation in the presence of dependent left truncation and right censoring. A “semi-survival” Archimedean copula model that links the conditional distributions of the truncation and event was proposed to account for dependence while leaving the marginal distributions of truncation and event unspecified [16]. Methods for estimation of this model include semi-parametric conditional likelihood [17], nonparametric likelihood [18], and estimating equations [19]. However, identification of the marginal distributions relies upon the copula assumption in the entire positive quadrant, and interpretation may not be natural. There is an open source R [20] package for implementation of the copula methods [21]. An alternative to the copula model is assumption of a fully parametric model, such as bivariate normality [22]. Both of these approaches make strong assumptions and are not broadly applicable. Limited goodness of fit tests are available for copula selection [23], copula identifiability [24], and the bivariate parametric model [25].

In the absence of censoring, a structural transformation [2] was proposed to model a latent quasi-independent truncation time as a function of the observed dependent truncation time and the event time and an unknown transformation parameter. Critically, the model ensures that the transformation is monotone and hence the truncation ordering is preserved. The transformation parameter is chosen to minimize the dependence between the original failure time and the transformed truncation time, as measured by Kendall’s tau. Estimation of the latent truncation times follows immediately by plugging in the transformation parameter to the transformation model. This procedure places us in an independent truncation setting and thereby enables us to estimate the marginal distribution. Thus, estimation of the event time distribution follows by applying standard methods, such as the Kaplan–Meier estimator [5] and the Nelson–Aalen estimator [26, 27] to the quasi-independent latent truncation time and observed event time. This is an attractive approach, but it is limited in not being applicable to right censored data and in the unavailability of software.

Motivated by the dearth of available estimators for quasi-dependent left-truncated and right censored data, the limitations of the copula and fully parametric approaches, and the appeal of the transformation approach for uncensored data, we propose an extension of the transformation model approach that accommodates censored data. Our approach applies the transformation only to the uncensored observations, and properly accounts for this selection in its estimation. It relies on a consistent estimator for the conditional Kendall’s tau [11] that uses uncensored observations only for estimation of the transformation parameter. We also propose two diagnostics for goodness of fit: convergence (or not) of the estimation procedure and a regression based approach.

We note that this approach of uncovering a latent, quasi-independent truncation time in order to estimate a marginal survivor function, is not applicable in all dependent truncation settings. One such setting is the Channing House study [28], which followed retirees from their entry to the retirement home to death or end of study or departure from the home. Subjects were included in the study only if they lived long enough to enter the retirement home; thus, the event time of interest, the age at death, is left-truncated by the time to the retirement home entry and right-censored by the end of follow-up or departure from the home. However, age at death cannot be separated from entry to the Channing House and cannot be separated from the event of entry to the House. In this example, a conditional survivor estimator is most appropriate given the dependent entry process.

Transformation approach for uncensored data

Let T denote the left truncation time and let X denote the event time; subjects are sampled only if T < X. The transformation approach for uncensored data [2] assumes that there is a latent, quasi-independent truncation time that would have accompanied X in the absence of the dependence. Let T′(a) = (T + aX)/(1 + a) denote the latent truncation time for some unknown transformation parameter, a. This transformation model satisfies T′(a) < X if and only if T < X as long as a > −1. Depending on the event times, the between-subjects ordering of truncation times can be different after transformation. In general, the transformed truncation time, T′(a), and the event time, X, are uncorrelated over the entire sample space if a = −ρσ_T/σ_X, where ρ is the correlation of T and X, and σ_T and σ_X are the corresponding standard deviations. This is a stronger condition than quasi-independence because the latter requires independence only in the observable region. Complete independence of T′(a) and X holds when (T,X) is bivariate normal.

The conditional Kendall tau’s test [1] for quasi-independence of T′(a) and X can be inverted to obtain an estimate for a [2]. Given random vectors $\left(X_1,T_1^{\prime }(a)\right)$ and $\left(X_2,T_2^{\prime }(a)\right)$, the conditional Kendall’s tau is defined as ${\tau }_c(a)=\text{E}\left[\text{sgn}\left\{\left(X_1-X_2\right)\left(T_1^{\prime }(a)-T_2^{\prime }(a)\right)\right\}|{\mathrm{\Omega }}_{12}\right]$, where sgn(u) = −1 for u < 0, 1 for u > 0, and 0 for u = 0 and ${\mathrm{\Omega }}_{12}=\left\{\max \left(T_1^{\prime }(a),T_2^{\prime }(a)\right)\le \min \left(X_1,X_2\right)\right\}$ is the event of comparability of the observations. This restriction to comparable pairs is required so that τ_c(a) has expectation zero under the null hypothesis. A consistent U-statistic estimator of τ_c(a) [10] is given by

$${\widehat{\tau }}_c(a)=\frac{1}{M}\sum _{i=1}^{n-1}\sum _{j=i+1}^n\text{sgn}\{(X_i-X_j)(T_i^{\prime }(a)-T_j^{\prime }(a))\}I({\mathrm{\Omega }}_{ij}),$$

where I(A) denotes the indicator function of the event A and $M={\sum }_{i=1}^{n-1}{\sum }_{j=i+1}^{n}I\left({\mathrm{\Omega }}_{ij}\right)$ is the number of comparable pairs. Operationally, the estimate of the transformation parameter, a, is the value that minimizes $\left|{\widehat{\tau }}_c(a)\right|$.

There are two extreme cases to consider if a does not converge to some value interior to (−1,∞): a → −1 and a → ∞. In the first case, the latent truncation times are separated from the event times since T′(a) → −∞, and effectively there is no truncation. This means that if $\left|{\widehat{\tau }}_c(a)\right|$ converges to zero as a → −1, the transformation model estimator of the survivor function of the event time is simply the Kaplan–Meier estimator, unadjusted for any truncation. If $\left|{\widehat{\tau }}_c(a)\right|$ does not converge to zero as a → −1, a transformation model estimator does not exist. As a → ∞, T′(a) → X, and there will be no comparable pairs as long as there are no ties among the event times. This means that ${\widehat{\tau }}_c(a)$ does not exist, and thus a transformation estimator does not exist. If there are ties, then it is possible that ${\widehat{\tau }}_c(a)\to 0$ and a transformation estimator will exist. If there are multiple zero-crossings for ${\widehat{\tau }}_c(a)$, either the transformation model does not fit the data, or there is numerical instability.

Transformation approach for censored data

Let C denote the censoring time, let Y = min(X,C) denote the observation time, and let δ = I(X < C) denote the failure indicator. Subjects are sampled only if T < Y. We assume that censoring is independent of failure and truncation in the observable region: (T,X) ⊥ C|T <Y. As in the case with no censoring, we assume the transformation model, T′(a) = (T + aX)/(1 + a), for the relationship between the latent independent truncation time T′ and (X,T). Since X is not observed for censored observations, neither is T′(a), and it is not obvious how to estimate a in the presence of censored event and truncation times. For this reason, we restrict to the uncensored data for estimation, with correction for this restriction.

We propose to estimate the transformation parameter, a, by ninverting an inverse probability weighted version of Kendall’s tau measure (or test) of dependence between T′(a) and X that adjusts for selection of the uncensored observations [11]. This version of Kendall’s tau is given by ${\widehat{\tau }}_c^{\prime }(a)=U_c(a)/U_M(a)$, where

$$\begin{gathered} U_c(a)={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\times \\ \sum _{i=1}^{n-1}\sum _{j=i+1}^n\frac{\text{sgn}\left\{\left(Y_i-Y_j\right)\left(T_i^{\prime }(a)-T_j^{\prime }(a)\right)\right\}I\left({\eta }_{ij}(a)\right)}{\left\{{\widehat{S}}_C\left(Y_i\right){\widehat{S}}_C\left(Y_j\right)\right\}/\left\{{\widehat{S}}_C\left(T_i^{\prime }(a)\right){\widehat{S}}_C\left(T_j^{\prime }(a)\right)\right\}}, \\ {U}_M(a)={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\times \\ \sum _{i=1}^{n-1}\sum _{j=i+1}^n\frac{I\left({\eta }_{ij}(a)\right)}{\left\{{\widehat{S}}_C\left(Y_i\right){\widehat{S}}_C\left(Y_j\right)\right\}/\left\{{\widehat{S}}_C\left(T_i^{\prime }(a)\right){\widehat{S}}_C\left(T_j^{\prime }(a)\right)\right\}}, \end{gathered}$$

where ${\eta }_{ij}(a)=\{\max \left(T_i^{\prime }(a),T_j^{\prime }(a)\right)\le \min \left(Y_i,Y_j\right)\cap \left({\delta }_i{\delta }_j=1\right)\}$, and ${\widehat{S}}_C(u)$ is the Kaplan–Meier estimator for Pr(C > u), which is estimated using the truncation adjusted Kaplan–Meier estimator based on all of the data, and adjusts for quasi-independent left truncation of C by T and independent right censoring of C by X.

We then use the uncensored observations, along with their associated latent independent truncation times, T′(a), to estimate the distribution of X. Restriction to the uncensored data would amount to right truncation of X by C, except that C is not observed for the uncensored data. Nonetheless, the likelihood can accommodate this restriction. The likelihood of these restricted data, expressed for discrete random variables, is

$$\begin{gathered} L=\prod _{i:{\mathrm{\Delta }}_i=1}Pr\left(X_i=x_i|T_i^{\prime }(a)=t_i^{\prime }(a),X_i>T_i^{\prime }(a),X_i<C_i\right) \\ =\prod _{i:{\mathrm{\Delta }}_i=1}\frac{f_X\left(x_i\right){\widehat{S}}_C\left(x_i\right)}{{\int }_{t_i^{\prime }(a)}^{\infty }{f}_X(x){\widehat{S}}_C(x)\text{d}x}, \end{gathered}$$

where f_X is the density of X. This expression elucidates that f_X can be estimated using a weighted Kaplan–Meier estimator [29] with S_C as the sampling weight.

Because there is no survival information prior to time $T_{(1)}^{\prime }(\widehat{a})=\min \left\{T_i^{\prime }(\widehat{a});{\delta }_i=1\right\}$, and our estimation procedure removes information after the maximum observed event time, X_(n) = max{X_i;δ_i = 1}, the survival estimator at time x is actually an estimator of $\text{Pr}(X>x|T_{(1)}^{\prime }(\widehat{a})<{X<X}_{(n)})$, in contrast to other estimators for left-truncated data that estimate $\text{Pr}(X>x|T_{(1)}^{\prime }(\widehat{a})<X)$. Noting that

$$\begin{gathered} \text{Pr}(X>x|X>T_{(1)}^{\prime }(\widehat{a}))= \\ \text{Pr}(X>x|T_{(1)}^{\prime }(\widehat{a})<X<X_{(n)})(1-r)+r, \end{gathered}$$ (1)

where $r=\text{Pr}\left(X>X_{(n)}\right)/\text{Pr}\left(X>T_{(1)}^{\prime }(\widehat{a})\right)$, and viewing the right hand side of (1) as a monotone increasing function of r, it follows that our estimator provides a lower bound for the common target of estimation, $\text{Pr}(X>x|X>T_{(1)}^{\prime }(\widehat{a}))$, at the lower bound for r. A simple lower bound for r is the proportion of censored observations out of the whole sample that exceed X_(n). An upper bound for $\text{Pr}(X>x|X>T_{(1)}^{\prime }(\widehat{a}))$ is obtained via an upper bound for r. A sensitivity band is constructed through evaluation of the estimator at the lower and upper bounds for r. We demonstrate this in Data examples.

We note that this estimation approach based on restriction to uncensored observations requires sufficient numbers of large censored observations to adequately estimate the distribution function S_C throughout the support of the uncensored observations for use as weights in the calculation of both ${\widehat{\tau }}_c^{\prime }$ and in the estimation of the distribution of X. There also must be sufficient numbers of uncensored observations to adequately estimate the distribution of X. This is a vague notion, and in practice, our simulated and real data examples achieve this balance and we have not encountered problems due to it. If several of the uncensored observations exceed the maximum of the censored observations, we will instead restrict estimation to those observations that fall below the maximum observed censoring time and estimate the corresponding conditional survivor function of X. Consistency of the estimator under the transformation model follows from consistent estimation of a in conjunction with analysis of the Nelson–Aalen form of the survivor estimator. We demonstrate this property in our simulations.

Goodness-of-fit for the transformation model

A clear indicator of lack of fit of the transformation model is the lack of a unique solution for the transformation parameter, a. There may also be true dependence models that do not satisfy the transformation model, and yet yield a single, well-behaved estimated, a. For example, inversion of the conditional Kendall’s tau may create non-monotone dependence, which could yield a Kendall’s tau close to zero, rather than the desired quasi-independence. For these potential scenarios, we require a goodness-of-fit assessment. A goodness-of-fit assessment of the transformation model must focus on the model linking T′(a) to (X,T) and not on comparisons between survival-related quantities that are empirically estimable and their model-based counterparts. This is because our estimator is essentially nonparametric, with the only model-based aspect of it being the dependence model for (X,T).

We propose several assessments of goodness-of-fit of the transformation model. Our first approach is to test for residucal dependence between $T^{\prime }(\widehat{a})$ and X, which might arise if there is non-monotone dependence that is not captured by a single Kendall’s tau. This would be problematic as it would imply that the estimated transformation model would not yield a latent quasi-independent truncation variable. One such test involves incorporation of $T^{\prime }(\widehat{a})$ (or categorized versions of it) as covariates in a Cox model [30]. Another is the minp1 test proposed by Chiou et al. [15]. Our second approach is to consider the following regression model, which is implied by the transformation model:

$$\begin{gathered} X-T=-(1+a)E\left\{T^{\prime }(a)\right\}+ \\ (1+a)X-(1+a)\left[T^{\prime }(a)-E\left\{T^{\prime }(a)\right\}\right] \\ ≔{\beta }_0+{\beta }_{1}X+ϵ. \end{gathered}$$

Under the independence assumptions involving censoring, this model holds approximately when restricted to uncensored observations. The regression estimates, ${\widehat{\beta }}_0$ and ${\widehat{\beta }}_1$, can be obtained nonparametrically adjusting for left truncation of X − T by zero and under the assumption that ϵ is symmetric [e.g. 31, 32]. We use this relationship to evaluate goodness-of-fit of the transformation model by directly assessing the linearity in X. We do this by considering larger models that are nonlinear in X and within which this implied model is nested. Although these diverse assessments may each suffer from low power, because they target different types of dependence, together they may present evidence as to whether or not residual dependence after transformation is present. If there is evidence of dependence even after transformation, we recommend alternative transformations, such as those described in the Discussion, or an expanded transformation model that fits separate transformation models to subsets of the data suggested by the nonlinear model. We discuss this in greater detail in Web Appendix A and demonstrate these diagnostic strategies in our simulations for consistency and robustness and in our real data examples.

Simulation

Consistency

We performed simulations under an ideal condition when the transformation model holds exactly. Although, in reality, the true relationship between the failure time X and truncation time T is unknown, such a simulation is necessary to evaluate the consistency of the proposed procedures when the transformation model holds. The failure time X was generated from a generalized extreme value (GEV) distribution, gev(μ, σ, ξ), where μ, σ, and ξ are the location, scale, and shape parameters. We generated the latent quasi-independent truncation time T′(a) from an exponential distribution with rate p, and the censoring time C from gev(c, 1, 1). We set μ = σ = ξ = 1 and constructed dependent truncation times by inverting the transformation model: T = (1 + a)T′(a) − aX. We repeated this process until we obtained n = 200 observations that satisfied T ≤ Y = min(X,C). The truncation probability is defined as Pr(T ≥ Y ). The additional parameters, c, p and a, were tuned to obtain moderate truncation (i.e., Pr(T ≥ Y ) = 50%), moderate pre-truncation association between (T,X) (i.e., τ = 0.3), and three levels of censoring after truncation at 0%, 20%, and 40%. Specifically, we set (p, a) = (0.4,−0.2) for 0% censoring, (c, p, a) = (5.8,0.6,−0.19) and (1,1,−0.085) for 20% and 40% censoring, respectively. For each configuration, we simulated 1000 datasets. We compared the averaged results of the transformation model estimator (implemented using our R package tranSurv [3]) with the Clayton and Frank copula estimators [16], as implemented in the R package depend.truncation [21], and with the Kaplan–Meier estimator adjusted for quasi-independent truncation. We applied the simple bootstrap with 300 re-samples to obtain the standard error for the proposed transformation model.

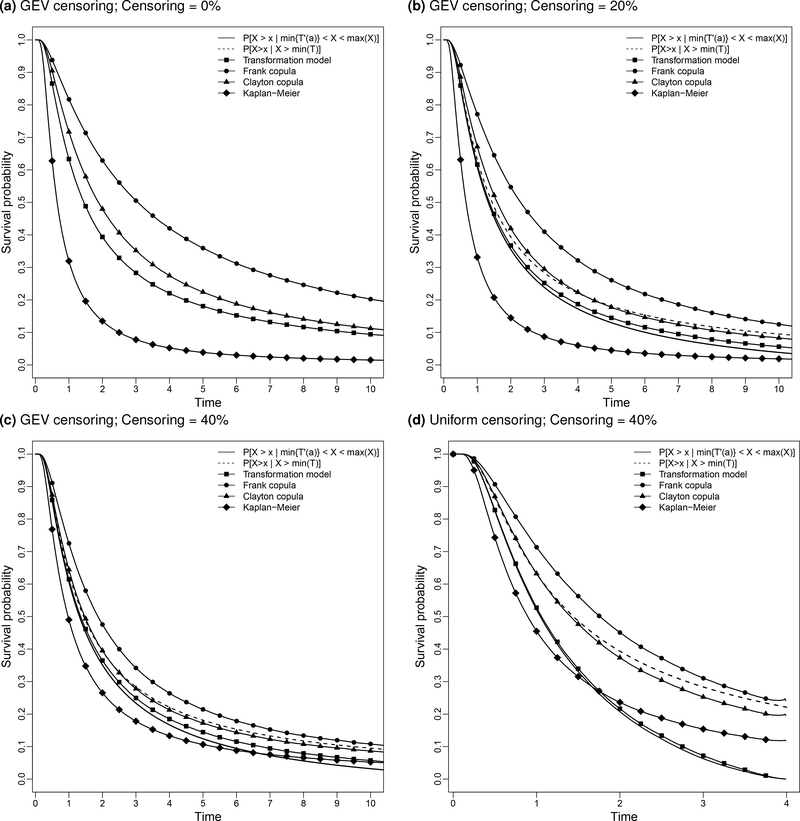
Table 1a lists the average bias, empirical standard error, average standard error and the average MSE for the three estimators and Figure 1 displays the averaged estimates of the survival function. These quantities are compared to the estimable quantities given the truncation, and in the case of the transformation estimator, the restriction to uncensored observations. These are $\text{Pr}(X>x|T_{(1)}^{\prime }(\widehat{a})<X<X_{(n)})$ for the transformation estimator and Pr(X > x | X > T₍₁₎) for the copula estimators; these are quite close to the unconditional distribution of X. This is because the averaged P(X > X_(n)) are quite small: 0.002, 0.057, and 0.068 for 0%, 20%, and 40% censoring rates, respectively, and the estimated values for Pr(X > T₍₁₎) are close to $\text{Pr}(X>T_{(1)}^{\prime }(\widehat{a}))$, and on average, both are greater than 0.999 for all scenarios considered.

Table 1.

Simulation results with 1000 repetitions; S*(x) is the target survival probability.

(a) Simulation 1: linear transformation model holds (n = 200). ESE is the empirical standard error, ASE is the average bootstrap standard error with 300 bootstrap samples, and MSE is the averaged mean square error.
		Transformation				Frank’s estimator			Clayton’s estimator
censoring	S*(·)	bias	ESE	ASE	MSE	bias	ESE	MSE	bias	ESE	MSE
	C ~ GEV distribution
0%	0.8	−0.002	0.055	0.054	0.003	0.090	0.030	0.009	0.059	0.036	0.005
	0.6	−0.002	0.056	0.057	0.003	0.178	0.031	0.032	0.093	0.042	0.010
	0.4	−0.001	0.049	0.049	0.002	0.225	0.035	0.052	0.092	0.044	0.010
	0.2	0.000	0.032	0.032	0.001	0.196	0.039	0.040	0.051	0.035	0.004
20%	0.8	0.007	0.054	0.053	0.003	0.090	0.029	0.009	0.033	0.042	0.003
	0.6	0.011	0.057	0.057	0.003	0.158	0.034	0.026	0.047	0.048	0.004
	0.4	0.014	0.052	0.050	0.003	0.173	0.044	0.032	0.036	0.049	0.004
	0.2	0.015	0.039	0.035	0.002	0.107	0.055	0.015	0.005	0.040	0.002
40%	0.8	0.003	0.044	0.043	0.002	0.064	0.030	0.005	0.011	0.040	0.002
	0.6	0.008	0.050	0.052	0.003	0.096	0.042	0.011	0.013	0.048	0.002
	0.4	0.013	0.050	0.052	0.003	0.085	0.053	0.010	0.003	0.049	0.002
	0.2	0.016	0.043	0.045	0.002	0.036	0.054	0.004	−0.010	0.042	0.002
	C ~ Uniform distribution
40%	0.8	0.005	0.053	0.055	0.003	0.058	0.031	0.004	0.005	0.042	0.002
	0.6	0.009	0.062	0.057	0.004	0.082	0.043	0.009	−0.002	0.050	0.003
	0.4	0.008	0.064	0.060	0.003	0.089	0.050	0.006	−0.020	0.047	0.003
	0.2	0.009	0.057	0.055	0.004

(b) Simulation 2: linear transformation model does not hold (n = 200). ESE is the empirical standard error, ASE is the average bootstrap standard error with 300 bootstrap samples, and MSE is the averaged mean square error.
		Transformation				Frank’s estimator			Clayton’s estimator
censoring	S*(·)	bias	ESE	ASE	MSE	bias	ESE	MSE	bias	ESE	MSE
0%	0.8	−0.275	0.189	0.187	0.063	−0.354	0.174	0.154	−0.477	0.188	0.262
	0.6	−0.238	0.140	0.140	0.051	−0.256	0.147	0.087	−0.364	0.143	0.152
	0.4	−0.180	0.090	0.088	0.035	−0.174	0.109	0.042	−0.254	0.094	0.073
	0.2	−0.106	0.050	0.050	0.014	−0.110	0.053	0.015	−0.144	0.042	0.023
20%	0.8	−0.145	0.089	0.088	0.023	−0.292	0.170	0.098	−0.389	0.172	0.155
	0.6	−0.135	0.074	0.073	0.020	−0.202	0.147	0.055	−0.295	0.135	0.094
	0.4	−0.118	0.057	0.055	0.015	−0.131	0.116	0.029	−0.207	0.095	0.050
	0.2	−0.073	0.037	0.033	0.006	−0.088	0.061	0.011	−0.124	0.046	0.017

(c) Rejection probabilities of goodness-of-fit tests of the transformation model on the basis of lack of unique solution for a or global tests of equality of slopes in piecewise linear regression. K is the number of changepoints in the piecewise linear model.
	Simulation 1				Simulation 2
	n = 100		n = 200		n = 100		n = 200
censoring	K = 1	K = 2	K = 1	K = 2	K = 1	K = 2	K = 1	K = 2
0%	0.029	0.027	0.025	0.048	0.412	0.554	0.552	0.862
	C ~ GEV distribution				C ~ Uniform distribution
20%	0.024	0.032	0.018	0.025	0.520	0.561	0.623	0.754
40%	0.020	0.027	0.021	0.024	0.370	0.411	0.604	0.572
	C ~ Uniform distribution
40%	0.056	0.168	0.044	0.175

Figure 1.

Averaged survival function estimates under the linear transformation model: n = 200 and 1000 repetitions. When there is no censoring, the target survival curves, Pr(X >x | $T_{\left(1\right)}^{\prime }(\widehat{a})$ < X < X_(n)) and Pr(X > x | X > T₍₁₎), coincide with the transformation estimator in Figure 1a.

In general, the transformation estimator exhibits lower bias and MSE than the other estimators (Table 1a and Figure 1). The Kaplan–Meier estimator adjusted for independent truncation underestimates the true survivor distribution (Figure 1), because the sizes of the risk-sets at each event time are smaller when T and X are positively associated than when they are quasi-independent. The average bootstrap standard errors are in close agreement with the empirical standard errors. Interestingly, the biases of the copula estimators and the simple truncation-adjusted Kaplan–Meier estimator decrease as censoring increases. For example, in terms of bias and MSE, the Clayton estimator is as efficient as the transformation estimator at 40% censoring. This is in part due to fortuitous proximity of the Clayton model to the truth and in part because under heavy censoring, which is independent of X and T, misspecification of the dependence structure is less problematic and there are fewer observations available for the transformation model estimation procedure.

We performed our goodness-of-fit diagnostic procedures to assess the adequacy of the transformation model. For each of the 1000 repetitions and scenarios in Table 1a we obtained well-behaved solutions for the transformation parameter, a, and a battery of tests of quasi-independence did not reject quasi-independence between $T^{\prime }(\widehat{a})$ and X. We additionally checked the model-imposed linearity using piecewise truncated regression models, with either one or two changepoints, using tests for the regression coefficients using the R package truncSP [33]. The rejection proportions are listed in the top three rows of the left panel of Table 1c; all are less than 0.05, supporting the validity of the linear transformation model.

Robustness to misspecification

We next investigated the performance of the transformation model when it does not hold. To do this, we first generated T from a uniform distribution over (0, 3. 5) and set X = 3 +0.65(T – 1)(T – 2)(T – 3) + ϵ, where ϵ ~ Norm(0, 0.1²). Without censoring, 12% of X were truncated. We generated the censoring time, C, from an independent uniform distribution over (0,c) such that c = 7 yielded a truncation probability of 35% and a censoring rate of 20% while c = 4.5 yielded a truncation probability of 46% and a censoring rate of 40%. The truncation probability increases with the censoring rate because truncation is applied to the minimum of X and C. For each setting, the unconditional Kendall’s tau for (T,X) before truncation was 0.42. We retained n = 200 observations that satisfied T < min(X,C) for each of 1000 repetitions. We applied the nonparametric bootstrap with 300 bootstrap samples to obtain the standard error of the transformation estimator. We compare the performances of the transformation estimator and the two copula estimators under the misspecified model.

Figure 2 provides a visual display of the average of the survival estimates. The simple truncation-adjusted Kaplan–Meier estimator that assumes quasi-independence exhibits the worst performance, and the transformation estimator departs the least from the target survival curve. As censoring increases, all estimators become closer to the corresponding target survival curves because the dependence structure is weakened by the censoring effect. Overall, these observations indicate that the proposed transformation estimator can exhibit acceptable performance in the presence of censoring even under a misspecified model. The numerical results summarized in Table 1b confirm these findings.

Figure 2.

The average of the estimators of the distribution of X when the dependence structure of (T, X) is assumed to have a nonlinear form. The results are based on 1000 data sets and a sample size of n = 200. When there is no censoring, the target survival curves, Pr(X > x | $T_{\left(1\right)}^{\prime }(\widehat{a})$ < X < X_(n)) and Pr(X > x | X > T₍₁₎), are almost indistinguishable in Figure 2a, 2b, and 2c.

Of greater interest in this simulation is the performance of the proposed goodness-of-fit diagnostics. The right panel of Table 1c lists the rejection probabilities based on nonconvergence of the transformation model estimate to a unique solution or lack of linearity of X − T and X. The transformation model is rejected with moderate to large probabilities, which increase with sample size and decreases with extent of censoring, as expected given the obscuring effect on dependence. These results indicate that the data are able to reveal that the linear transformation model is not appropriate.

In the Web Supplement, we also examined scenarios in which copula models hold. In these scenarios (Web Table 1 and Figure 1), the transformation model performs better than a misspecified copula model. This additionally supports the robustness of the transformation model.

Restricted target of estimation

Since our procedure restricts to the uncensored data for estimation, the target of our estimation is slightly different from that of alternative estimators for dependently truncated data (1). This divergence is inconsequential under censoring distributions that enable observation of the upper limit of the support of the event time. When censoring prevents this and the quantity r in (1) is non-negligible, the sensitivity band that we have proposed via (1) will be wide. We have conducted a simulation to illustrate this point. As in our first simulation, we generated X from gev(1, 1, 1), but generated T′(a) from an exponential distribution with rate 0.9 and set a = −0.11. In addition, we generated C from a Uniform distribution over (0, 4) to yield a 40% censoring rate after truncation. These settings result in the same truncation rate (50%) and pre-truncation association (τ = 0.3) as in our first study. In this setting r is approximately equal to 0.25. Figure 1d displays the averaged estimates of the survivor function. The transformation estimator is very close to its target, but far from the common target based on left-truncated data of $\text{Pr}(X>x|X>T_{(1)}^{\prime }(\widehat{a}))$. The sensitivity band is indeed wide, and covers this target. When comparing to the corresponding target of estimation, the transformation estimator yields negligible bias throughout, while the Clayton estimator is more biased at the later times and the Frank estimator is more biased at the early times (Table 1a, bottom). The rejection proportions from the goodness-of-fit diagnostic procedures are all very small, as they should be (Table 1c bottom left), supporting the linear transformation model. This example demonstrates the usefulness of the proposed sensitivity band when censoring has a large impact on the target of estimation.

Data examples

National Alzheimer’s Coordinating Centers cohort study

The NACC database is a large multicenter longitudinal cohort study involving Alzheimer Disease Centers across the United States [34]. Participating subjects undergo a baseline visit and annual follow-up visits at which demographics and standard motor, behavioral, functional, and neuropsychological assessments are recorded. It has been a long-standing research focus to identify predictors of increased risk of death among subjects with cognitive impairment; this is important for the purpose of planning for medical care at end of life and for predicting the impact of Alzheimer’s disease on health care usage [35]. For this analysis, we included 7436 subjects from the 2005–2017 cohort who had no diagnosis of cognitive impairment due to medical illness, medication use, depression, or alcohol at the initial visit, who had at least one follow-up visit, and who did not have missing values for key covariates. A total of 6467 of these subjects experienced onset of cognitive impairment prior to their entry to NACC, and thus their times to death or last follow-up from onset of cognitive impairment were left-truncated by their times from onset of impairment to NACC entry. There were 3192 deaths (57% censoring) among the 7436 subjects.

Quasi-independence between the time to death and time to NACC entry seems implausible; many dependence structures are reasonable alternatives. For example, subjects who are diagnosed with cognitive impairment at younger ages may be at an earlier stage of impairment (e.g., due to vigilant monitoring), may enter NACC later after diagnosis due to good health, and may have longer survival times from onset than those who are diagnosed at older ages and at later stages of impairment, and who have shorter times to NACC entry from diagnosis and shorter times to death. This scenario results in positive dependence. We confirmed this hypothesis via the conditional Kendall’s tau tests (τ_c = 0.228 with p <0.001, ${\tau }_c^{\prime }=0.329$ with p < 0.001).

We fit the transformation model and assessed its goodness-of-fit by testing for residual quasi-independence between the transformed truncation times and the original times to event. Quasi-independence was rejected by the Cox model test and the minp1 permutation tests (p < 0.011 for all tests). We thus relaxed the assumed single transformation model and instead assumed separate transformation models within subsets of a 3-segment partition of X (cutpoints at 6.8 and 13.5). The significantly different slopes (p < 0.001) associated with this partition in a piecewise linear goodness-of-fit regression model for X − T suggest the lack of fit of the single transformation model. We thus transformed each T according to the segment to which it belonged and the associated estimated value of the transformation parameter, a (i.e., −0.175, −0.506, −0.931). Figures 3a,3b,3c display the zero crossings for τ_c and the p-value curves for each segment of the partition of X. Figure 3d displays the resulting transformation estimate, as well as the copula estimates and the truncation-adjusted Kaplan–Meier estimate that assumes quasi-independence. There are modest differences among the estimates; the copula estimates and the truncation-adjusted Kaplan-Meier estimate lie entirely below the transformation estimator. Such underestimation is consistent with our simulation results presented in Robustness to misspecification where the true dependence structure was assumed to be nonlinear. This example indicates the importance of adjusting for dependent truncation and demonstrates the flexibility of the transformation method in accommodating a non-linear dependence structure.

Figure 3.

Summary plot and estimated survival curves for the NACC data.

AIDS Incubation Study

The AIDS incubation study [1] retrospectively sampled hemophiliacs who received blood transfusions after January 1978 and who were diagnosed with AIDS before July 1986 (i.e., 102 months from January 1978). The study consists of 295 subjects, and includes measurements of T, the number of months from January 1978 to HIV infection, X, the months from HIV infection to AIDS, and age. Subjects were included in the study only if T + X < 102; i.e., X^∗ = 102 − X is left-truncated by T. This “time reversal” allows us to apply our methods for left-truncated data to estimate the survivor function of X*, which we can easily transform to obtain the survivor function for X, which is of scientific interest. Specifically, Pr(X* > x) = Pr(X < 102 − x) = 1 − Pr(X > 102 − x). The distribution of the induction time from HIV infection to AIDS, X, is of interest and has been analyzed in different ways [e.g., 36, 37, 38]. These approaches all assumed quasi-independence between X* = 102 − X and T. In fact, there is a significant positive association between T and X^∗ (${\widehat{\tau }}_c=0.115$,p < 0.001), which is a negative association between T and X. This could potentially be due to a changing nature of the disease over calendar time. This calendar time dependence might be of substantive interest, along with the marginal distribution of the incubation time, X, in which case the conditional distribution of time from HIV infection to AIDS given calendar date of HIV infection could be estimated. In practice, this would require a much larger sample size than available in this study, and as in previous analyses of these data, we focus on the marginal estimator for the induction time distribution.

We fit the linear transformation model and obtained $\widehat{a}$ = −0.522. After transformation, additional hypothesis tests did not reject the null of quasi-independence between T′(a) and X (e.g., Cox model p = 0.444). And the global test of equality of three slopes based on the two-changepoint piecewise linear regression model did not indicate a lack of linearity (p = 0.78). Figure 4a displays the transformation estimate, along with the Kaplan–Meier, and the Frank and Clayton copula estimates; there is wide disparity among them. Given the empirical affirmation of the transformation model based on the diagnostics, it appears that the simple, truncation adjusted Kaplan–Meier estimate, and the copula estimates exhibit bias.

Figure 4.

Estimated survival curves obtained from the AIDS data.

To illustrate the performance of the transformation estimator in the presence of censoring, we artificially imposed independent censoring; i.e., we generated censoring times, C, such that (T,X*) ⊥ C|T < X*,T < C. In particular, we generated C ∼ log-norm(4.3,σ_c), where we selected σ_c to achieve a truncation probability of 70% and three levels of censoring probabilities: 20%, 30% and 40%. In the presence of artificial censoring, and for 1000 repetitions, the estimated $\widehat{a}$’s are −0.517, −0.489 and −0.457 for 20%, 30% and 40% censoring, respectively. These exhibit some bias at high censoring relative to the “truth”: $\widehat{a}$ = −0.522 for the 0% censoring case. This trend is reflected in Figures 4b, 4c and 4d, which display the averages of the transformation estimates, the copula estimates and the simple truncation-adjusted Kaplan–Meier estimates. Under 20% censoring, our estimate is nearly indistinguishable from the “truth”, which we obtained from the original, uncensored data. The corresponding sensitivity band, constructed with r ∈ (0, 0.1], covers the truth, as expected. As the censoring rate increases, the transformation estimates display an increasing, though relatively small amount of bias.

Discussion

We have extended the transformation model of [2] to accommodate censored data. Our approach uses the uncensored failure times only, but adjusts for this selection through inverse weighting by the censoring distribution. We have assumed that censoring is quasi-independent of truncation in the observable region. We use this property in our construction of the weights for the survivor function estimate for time to failure; these weights are the survivor function estimates for time to censoring. If quasi-independence of C and T does not hold, we suggest fitting a separate transformation model for C, and iterating between estimates of S_C and S_X until convergence.

The restriction to uncensored event times also has implications for the target of our estimator; we estimate a conditional event time distribution given the observed range of event times. In practice this is not problematic as this range usually covers the range of interest. Nonetheless, we have derived bounds for the usual target of truncated event time estimation for sensitivity analysis. Our approach does not require any assumptions about the unobservable region and reduces to nonparametric estimation via weighted truncation-adjusted of risk-sets following application of the derived transformation. We have demonstrated its low bias and variability in simulation studies and its applicability in real studies. Importantly, we have derived useful diagnostics for goodness-of-fit for our model, which are essential for real applications. These include tests of residual dependence following transformation and a regression model in which our model is nested, and thus can be tested.

The transformation model differs from copula models [16] in interpretation. The transformation model assumes an independent, unobserved truncation time, whereas the copula model assumes the conditional independence of the observed truncation time and failure time, given a frailty parameter. Different contexts may be more appropriate for one model than the other. The availability of the transformation model increases the possibilities for estimation under dependent truncation.

We have presented just one member of a whole class of transformation models that could be used to achieve quasi-independence. Although different in functional form, alternative transformation models would involve the same general estimation procedure. The key requirement for an alternative transformation model is that it must preserve the original truncation ordering, T′(a) < X if T < X. A general additive model that accomplishes this is

$$T^{\prime }(a)=f_a^{-1}\left(T+f_a(X)-X\right),$$

for some monotone non-decreasing function, f(·) that is indexed by a dependence parameter, a. The model that we have considered in this paper takes f_a(y) = (1 + a)y. A general multiplicative model that retains the truncation ordering is

$$T^{\prime }(a)=g_a^{-1}\left(\frac{T{g}_a(X)}{X}\right),$$

for some monotone non-decreasing function g(·) that is indexed by a dependence parameter, a. These can also be composed any number of times to obtain even more complex transformation, such as

$$T^{\prime }(a,b)=f_b^{-1}\left\{g_a^{-1}(\frac{T{g}_a(X)}{X}\right\}+f_b(X)-X]$$

and

$$T^{\prime }(a,b)=g_b^{-1}\left[\frac{f_a^{-1}\left\{T+f_a(X)-X\right\}{g}_b(X)}{X}\right],$$

for example. These are written as functions of two dependence parameters, a and b, which allows for a sequence of inversions to quasi-independence, if desired. All of these possibilities allow for deviations from the strong linearity of the simple transformation model.