Statistical analysis of Goal Attainment Scaling endpoints in randomised trials

Abstract

Goal Attainment Scaling is an assessment instrument to evaluate interventions on the basis of individual, patient-specific goals. The attainment of these goals is mapped in a pre-specified way to attainment levels on an ordinal scale, which is common to all goals. This approach is patient-centred and allows one to integrate the outcomes of patients with very heterogeneous symptoms. The latter is of particular importance in clinical trials in rare diseases because it enables larger sample sizes by including a broader patient population. In this paper, we focus on the statistical analysis of Goal Attainment Scaling outcomes for the comparison of two treatments in randomised clinical trials. Building on a general statistical model, we investigate the properties of different hypothesis testing approaches. Additionally, we propose a latent variable approach to generate Goal Attainment Scaling data in a simulation study, to assess the impact of model parameters such as the number of goals per patient and their correlation, the choice of discretisation thresholds and the type of design (parallel group or cross-over). Based on our findings, we give recommendations for the design of clinical trials with a Goal Attainment Scaling endpoint. Furthermore, we discuss an application of Goal Attainment Scaling in a clinical trial in mastocytosis.

1 Introduction

For diseases with very heterogeneous courses or stages where symptoms differ substantially between patients, the evaluation of new treatments can be challenging when no standardised outcome measure, applicable to all concerned patients is available. This is of special concern in rare diseases where separate clinical trials in homogeneous subgroups of patients are not feasible because of the small number of patients available. Examples of such heterogeneous disorders are mitochondrial DNA diseases where the same underlying mitochondrial defect may have a wide range of symptoms, varying from coordination disturbance and muscle weakness to developmental delay and hearing loss. A drug that targets the mechanism underlying the disease could lead to an improvement in groups of patients with very heterogeneous symptoms. However, an outcome measure such as a walking or a hearing test will only be able to describe improvements in the subgroup of patients that are affected by the corresponding symptom. Restricting a clinical trial to such specific subgroups with homogeneous phenotypes may lead to too small sample sizes due to the low disease prevalence of 9.2 in 100,000.¹

Another example is Duchenne muscular dystrophy, a disabling and life-threatening X-linked recessive genetic disorder that primarily affects males.^2,3 It results from defects in the gene for dystrophin, a structural protein required to maintain muscle integrity. First signs of Duchenne are increasingly abnormal ambulation due to proximal muscle weakness. Problems with falling while walking, standing up from supine position or climbing stairs are typically encountered before the age of 8. By 10–14 years of age, most boys with the disease are restricted to a wheelchair. Except for walking abnormalities including stride length and cadence, major disease manifestations are impairments in upper and lower extremity movements and strength, such as elbow flexion, elbow extension, knee flexion, knee extension and shoulder abduction, but also endurance, and cardiorespiratory status. A currently often used outcome measure for ambulatory Duchenne patients is the 6-min Walk Test. This endpoint, however, has been criticised because it is restricted to ambulatory patients and provides insufficient information in case of loss of ambulation.^4–6

A general tool to quantify the treatment benefit in a population with very heterogeneous symptoms is Goal Attainment Scaling (GAS) introduced by Kiresuk and Sherman.⁷ It has been proposed as a patient centred outcome measure capturing the treatment effect across a range of manifestations. GAS has been used as an endpoint in rehabilitation research,^8,9 in geriatric trials to measure changes in the health status of frail elderly patients,^10,11 to evaluate health care,^12,13 educational programs¹⁴ and psychosocial interventions,¹⁵ but rarely in comparative clinical drug trials to assess the effect of an experimental treatment compared to a control.¹⁶ Examples for such randomised controlled trials are studies assessing botulinum toxin treating patients with upper limb spasticity^17–19 and a trial to evaluate donepezil²⁰ for the treatment of Alzheimer’s disease.

GAS endpoints are assessed in a procedure with several steps. First, patients formulate one or more goals together with a treating physician. Such goals can be, for example, to improve the maximum walking distance, to improve independence in a selected activity of daily living such as eating or to be able to use a computer mouse. Typically, the choice of goals is a process in which both the patient and the investigator take part. The investigator supports the trial participant to identify goals that are most relevant for the disease, are feasible, and can be measured objectively. In some settings, each patient and/or the caregiver is interviewed and the investigators define the goals for the specific patient based on this interview. Note that especially for diseases with very heterogeneous manifestations, the chosen goals may be unique to the patient. Furthermore, the number of chosen goals may vary across patients, a result of the goal setting step. In addition to the goals, criteria defining attainment levels for each goal are specified. The number of attainment levels is the same for all goals and often a scale with five measurement levels from −2 to 2 is chosen as suggested in the original article about GAS by Kiresuk and Sherman.⁷ Finally, patients can optionally choose weights for the goals to differentiate between goals of different relevance or importance. This concludes the goal setting steps. After the treatment intervention, at a given follow-up time, the assessment of the goal attainment levels for each patient is performed according to the pre-specified assessment criteria.

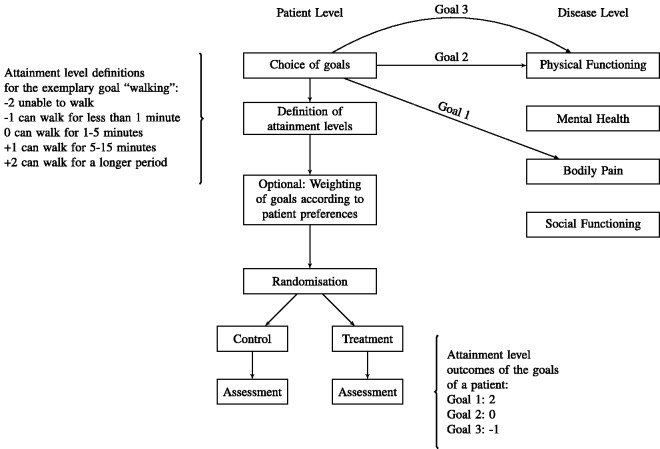
Figure 1 gives a schematic illustration of the application of GAS as endpoint in a double-blind randomised clinical trial. To avoid bias, the goals, the criteria for the assessment of their attainment, and the weights are chosen before the patient is randomised to one of the treatment groups. This can prevent systematic differences in the choice of goals between treatment groups even if patients and/or physicians cannot be fully blinded. However, blinding is important for the assessment of goal attainment at the time of follow-up to avoid imbalances between treatment groups. If blinding of patients and physicians is not possible, the validity of the assessment can be improved if the assessment of goal attainments is performed by an assessor blinded to the assigned treatment.

Figure 1.

Illustration of the application of a GAS endpoint in a randomised clinical trial. Supported by an investigator, each patient chooses disease related goals he or she wants to attain. The type and the number of goals are chosen individually and can correspond to different dimensions of symptoms. In the example, the patient chooses two goals related to physical functioning and one goal related to bodily pain but no goal related to the other dimensions. For each goal criteria, specific attainment levels are defined before the intervention. Additionally, goals can optionally be weighted to quantify differences in importance and relevance of the goals. After the goals are set, patients are randomised and allocated to the treatment groups. After a predefined follow-up period, the attainment level for each goal is assessed according to the pre-specified criteria.

The statistical analysis and interpretation of GAS endpoints is challenging because the goals of each patient may be unique and the number of goals across patients may vary. As a consequence, current practice and opinions differ substantially.^9,21–23

An important advantage of GAS as an endpoint for clinical trials in rare diseases is the potential to include patients with very heterogeneous disease manifestations. This allows one to broaden the pool of potential trial participants and to speed up recruitment. Furthermore, the involvement of patients in the choice of goals can increase the relevance of the endpoint to the patient which is an important factor of patient-focused drug development (see literature²⁴ for a recent discussion). However, practical challenges, such as the training and time required for goal setting as well as a lack of scientific literature on study design and analysis methods may be an obstacle in the application of GAS as an endpoint in clinical trials. Recently, several systematic literature reviews addressing the psychometric properties of the GAS scale, i.e. its validity, reliability and responsiveness have been performed^16,25 but only general, qualitative recommendations^9,21,26 regarding the statistical analysis of GAS endpoints are available.

In this article we address the statistical analysis and study design of comparative clinical trials with a GAS endpoint. Especially, we study the statistical properties of different analysis methods and explore the impact of the number of goals per patient, the distribution of effect sizes across goals, the correlation of goal attainment levels and other factors that may have an influence on the power and type I error rate of statistical tests. To this end, in Section 2.1 we propose a probabilistic model for GAS data in clinical trials. In Sections 2.2, 2.3 and 2.4, analysis methods to demonstrate a treatment effect in randomised clinical trials with a GAS endpoint are introduced and in Section 2.5 models accounting for goal-specific weights are discussed. In Section 2.6 the robustness of the testing procedures with regard to the model assumptions is explored. In Section 3 we introduce a hierarchical model to simulate GAS data and report the results of a simulation study investigating the power and type I error rate of the considered analysis methods under a range of scenarios. The extension of the testing procedures to cross-over trials is discussed in Section 4. In Section 5 an example from a clinical trial is presented. Finally, in Section 6 we discuss the limitations of the approach and give some recommendations for the analysis and design of studies with a GAS endpoint.

2 A probabilistic model for GAS and hypothesis tests

2.1 Data model

Consider a randomised parallel group trial comparing an experimental treatment to a control with respect to a GAS endpoint. Let m denote the total number of subjects and for each subject $i=1,\dots ,m$, let $g_i=0,1$ denote the treatment group indicator (where g_i = 0 for the control and g_i = 1 for the experimental treatment group). We first address GAS without weighting of goals and discuss the case of weighting in Section 2.5. For each subject, a vector of goal attainment levels ${\mathbf{X}}_i={(X_{\mathit{ik}})}_{k=1}^{ni}$ is observed, where $n_i\le n_{\text{max}}$ denotes the number of goals chosen by patient i, and n_max the maximum number of goals that can be chosen by a patient. The design parameter n_max is considered identical for all patients and has to be pre-specified. The goal attainment levels X_ik take values from a set $M\subseteq \mathbb{Z}$. A common choice is $M=\{-2,-1,0,1,2\}$.

Let F_g denote the distribution of ${\mathbf{X}}_i$ conditional on $g_i=g,g=0,1$ and we assume that ${\mathbf{X}}_i$ are (conditional on g_i) stochastically independent across $i=1,\dots ,m$. Thus, F₀, F₁ denote the distribution of the outcome vectors for patients in the treatment and control group. These are distributions on the sample space $\{{(a_k)}_{k=1}^{ni}|n\in \{1,\dots ,n_{\text{max}}\},a_k\in M\}$ and specify a distribution on the goal attainments X_ik as well as on the number of goals n_i.

Let ${\overline{X}}_i=\frac{1}{n_i}\sum _{k=1}^{n_i}{X}_{\mathit{ik}}$ denote the mean goal attainment of subject i and define ${\mu }_g=E\{{\overline{X}}_i|g_i=g\}$ to be the expected mean goal attainment for patient i allocated to group g = 0, 1. Then, a (one-sided) null hypothesis for these means is given by

$$H_0:{\mu }_1\le {\mu }_0\text{ against }{H}_1:{\mu }_1>{\mu }_0$$ (1)

We make two assumptions on the distributions F₀, F₁:

1. The distribution of n_i is independent of g_i.

2. For $g\in \{0,1\}$ we have $E({\overline{X}}_i|n_i=n,g_i=g)=E({\overline{X}}_i|n_i=n\text{'},g_i=g)$ for all $n,n\text{'}=1,\dots ,n_{\text{max}}$.

Assumption (A) states that the distribution of the number of goals per patient is equally distributed in both treatment groups. This can be achieved if, for example, the goals are set before randomisation. Assumption (B) implies that the expected mean attainment of goals is independent of the number of goals a patient sets. In Section 2.6 we discuss the validity of statistical hypothesis tests in settings where these assumptions are not satisfied.

We consider several testing approaches to test the null hypothesis H₀ that take the dependence between observations from the same patient into account.

2.2 T-Test and Mann–Whitney U Test on per-subject means

A two-sample Welch’s t-test applied to the per-subject means ${\overline{X}}_i$ directly tests the null hypothesis H₀. Because the means ${\overline{X}}_i$ are independent between patients, Welch’s t-test statistic follows asymptotically a normal distribution. For finite m, the distribution can be approximated by a t-distribution with appropriate degrees of freedom. If, under the null hypothesis, the distribution of the per-subject means ${\overline{X}}_i$ is equal in both groups, also Student’s t-test or the Mann–Whitney U test can be applied.

2.3 Generalised estimating equations (GEE) approach

The variance of ${\overline{X}}_i$ depends on the variances and covariances of X_ik and on n_i and will be smaller for larger n_i. The t-test described above is based on the unweighted mean of ${\overline{X}}_i,g_i=g$ as estimate of $E({\overline{X}}_i|g_i=g)$, which is not efficient in the presence of unequal variances. Efficiency can be increased by using a weighted mean, with weights equal to the inverse of the variance of each $\overline{X_i}$. In an actual application, these variances are unknown. However, a weighted t-test can be performed in terms of a GEE model.²⁷ There, weights are derived from a working covariance structure. The larger the gain in efficiency, the closer the assumed covariance structure is to the true one. A robust sandwich variance estimator is used, such that misspecification of the covariance structure does not affect type I error rate control of the resulting test, at least asymptotically.

Assuming a working covariance structure with equal correlations ρ_x for all pairs $(X_{\mathit{ik}},X_{\mathit{ik}\text{'}})$ (conditional on $n_i\ge k,k\text{'}$) and zero correlation between observations from different patients, the weights are given by

$$w_i=\frac{n_i}{1+(n_i-1){\rho }_x}$$ (2)

and an estimator for the mean attainment level μ_g in group g = 0, 1 is given by

$${\hat{\mu }}_g=\frac{\sum _{i=1}^m{w}_i{\overline{X}}_i{1}_{\{g_i=g\}}}{\sum _{i=1}^m{w}_i{1}_{\{g_i=g\}}}$$ (3)

where $1_{\{·\}}$ denotes the indicator function.

Following the GEE approach, both ρ_x and ${\mu }_g,g\in \{0,1\}$ may be estimated in an iterative way by using the newly estimated ρ_x in the estimation of μ_g and vice versa.²⁷ Alternatively an arbitrary value ${\rho }_x>-\frac{1}{n_{\text{max}}-1}$ may be chosen. A sandwich variance estimator that accounts for the correlation of goal attainments of the same subject is given by

$$\widehat{\mathit{var}}({\hat{\mu }}_g)=\frac{\sum _{i=1}^m{1}_{\{g_i=g\}}}{(\sum _{i=1}^m{w}_i{1}_{\{g_i=g\}}{)}^2}\frac{\sum _{i=1}^m(w_i{\overline{X}}_i-w_i{\hat{\mu }}_g{)}^2{1}_{\{g_i=g\}}}{\sum _{i=1}^m{1}_{\{g_i=g\}}-1}$$ (4)

Now, the Wald test statistics to test (1) is given by $T=\frac{{\hat{\mu }}_1-{\hat{\mu }}_0}{\sqrt{\widehat{\mathit{var}}({\hat{\mu }}_1)+\widehat{\mathit{var}}({\hat{\mu }}_0)}}$ and is approximately standard normal under the null hypothesis. For small sample sizes, a t-distribution with m − 2 degrees of freedom gives a better approximation.

Two important special cases are covered by the GEE approach. For the case ${\rho }_x=0$ the weights are w_i = n_i, and the estimates of ${\mu }_g,g=1,2$ (3) become the grand mean $\sum _{i=1}^m{1}_{\{g_i=g\}}\sum _{k=1}^{n_i}{X}_{\mathit{ik}}/\sum _{i=1}^m{n}_i{1}_{\{g_i=g\}}$. For the case ${\rho }_x=1$ the weights are w_i = 1, and the estimate reduces to the mean of the per-subject means. In the latter case, the corresponding hypothesis test asymptotically reduces to the t-test of the per-subject means discussed in the previous section.

2.4 Standardised means (Kiresuk and Sherman)

In their initial proposal of GAS, Kiresuk and Sherman⁷ proposed to standardise the per-subject means of the goal attainment levels ${\overline{X}}_i$ by their standard deviation, such that the resulting standardised means have unit variance regardless of the number of chosen goals n_i. The standard deviation of the ${\overline{X}}_i$ depends on the variances and covariances of the vector of goal attainments $(X_{i1},\dots ,X_{{\mathit{in}}_i})$, which are, however, unknown. Kiresuk and Sherman therefore suggested to assume that the variance of the X_ik is one for all goal attainment levels and the common correlation is ${\rho }_x=0.3$ without giving a formal justification. The resulting standardised per-subject mean for subject i is then given by ${\overline{Z}}_i=\sqrt{w_i}{\overline{X}}_i$, where w_i is defined in equation (2).

Several authors have applied tests based on the standardised means^,8,15,20 with t-tests or Wilcoxon tests. For parallel group comparisons, the t-test tests the null hypothesis that the difference of means of the standardised per patient means is non-positive. Under assumptions (A) and (B) this is equivalent to the null hypothesis H₀ (formulated for the non-standardised means), i.e. $E\{{\overline{X}}_i|g_i=1\}\le E\{{\overline{X}}_i|g_i=0\}\iff E\{{\overline{Z}}_i|g_i=1\}\le E\{{\overline{Z}}_i|g_i=0\}$, and thus the Welch’s t-test applied to the scores ${\overline{Z}}_i$ is an asymptotically valid test for this null hypothesis.

2.5 Goal-specific weights

All the above testing approaches are based on per-subject averages of the individual goal attainment scores ${\overline{X}}_i$. They differ in the way the contribution of each patient is weighted in the overall test statistics; however, all goals within a single patient have the same weight. This can be generalised by introducing goal-specific weights $v_{\mathit{ik}}\ge 0,i=1,\dots ,m,k=1,\dots ,n_i,\sum _{k=1}^{n_i}{v}_{\mathit{ki}}=1$, that, e.g., may reflect within-patient differences in the importance of the goals.⁸ Then, the weighted per-subject mean of the goal attainment scores of subject i is given by ${\overline{X}}_i\text{'}=\sum _{k=1}^{n_i}{v}_{\mathit{ik}}{X}_{\mathit{ik}}$. The standardised weighted means are given by

$${\overline{Z}}_i\text{'}=\frac{\sum _k(v_{\mathit{ik}}{X}_{\mathit{ik}})}{\sqrt{(1-{\rho }_x)\sum _k{v}_{\mathit{ik}}^2+{\rho }_x(\sum _k{v}_{\mathit{ik}}{)}^2}}$$ (5)

where ρ_x is defined as above. Note that Kiresuk and Sherman⁷ proposed to use the equivalent rescaled scores $T_i=50+10{\overline{Z}}_i\text{'}$ instead.

Now, as discussed in Sections 2.2 and 2.4, the t-test can be applied to the means ${\overline{X}}_i\text{'}$ of the weighted goal attainment levels or standardised means of the ${\overline{Z}}_i\text{'}$ using weighted goal attainment levels. Similarly, the GEE approach for a weighted analysis can be performed.

The weighted tests, however, in general test a different null hypothesis than the unweighted test. Let ${\mu }_g\text{'}=E\{{\overline{X}}_i\text{'}|g_i=g\},g=0,1$, then the null hypothesis $H{\text{'}}_0:{\mu }_1\text{'}\le {\mu }_0\text{'}$ is tested by the above approaches with weighted goal attainment levels.

In any case, to ensure the control of the type I error rate, the weights need to be chosen independently of the treatment assignment and thus before randomisation. For example, they can be chosen at the time the individual goals are set. Weights can either be used to reflect patient preferences regarding the different importance of the goals or the weights could be chosen to maximise the power of the test, by giving more weight to goals where a larger treatment effect (i.e., larger difference to the control group) is expected. Furthermore, we assume that assumption (B) with ${\overline{X}}_i$ replaced by ${\overline{X}}_i\text{'}$ holds.

2.6 Robustness of the testing procedures

The type I error rate control of the testing procedures above may be compromised, if the assumptions defined in Section 2.1 are not satisfied.

If only condition (A) is relaxed and the distribution of the number of goals per patient may differ between the treatment groups, the per patient means ${\overline{X}}_i$ are still asymptotically normally distributed in each treatment group. However, the variances may differ between groups and the t-test for equal variances may not control the type I error rate. On the other hand, the t-test for unequal variances (i.e. the Welch’s t-test) is asymptotically still valid in this setting. Furthermore, the GEE procedure discussed in Section 2.2 still controls the type I error rate, because, similar to Welch’s test, the variances are estimated separately for both groups.

The t-test for the standardised means (Section 2.4) does, however, not control the type I error rate. To see this, consider a simple example: Assume that in the control group each subject chooses one goal, while in the treatment group two goals are chosen. Furthermore, let ${\rho }_x=0$ such that w_i = n_i. Then, under the null hypothesis ${\mu }_0={\mu }_1$, we have $E({\overline{Z}}_i|g_i=0)={\mu }_0$ but $E({\overline{Z}}_i|g_i=1)={\mu }_0\sqrt{2}$ for $i=1,\dots ,m$. Hence, if ${\mu }_0={\mu }_1>0$, the t-test based on standardised mean scores favours the treatment group even though the null hypothesis holds.

Consider now the case that only assumption (B) is not satisfied such that the attainment of goals depends on the number of goals a patient sets while the distribution of the number of goals is equal across treatment groups. This may result, for example, if there is a trend where patients choosing more goals tend to choose increasingly challenging goals. Also in this setting, the per patient means ${\overline{X}}_i$ are still asymptotically normally distributed and the t-test is still valid. The t-tests based on standardised means and the GEE approach do not necessarily control the type I error rate, though, because patients with different number of goals, and hence different expected goal attainment levels have different weights in the overall estimate. As illustrative example, assume for both groups that exactly half of the patients choose one goal and the other half choose two goals and that ρ = 0. For the control group assume $E({\overline{X}}_i|n_i=1,g_i=0)=E({\overline{X}}_i|n_i=2,g_i=0)=1$, while in the treatment group $E({\overline{X}}_i|n_i=1,g_i=1)=0$ and $E({\overline{X}}_i|n_i=2,g_i=1)=2$. Thus $E({\overline{X}}_i|g_i=0)=E({\overline{X}}_i|g_i=1)=1$; however, the weighted estimates used for the hypothesis test in the GEE approach are $E({\hat{\mu }}_0)=1<E({\hat{\mu }}_1)=4/3$. Similarly the expected values of the standardised means are $E({\overline{Z}}_i|g_i=0)=(1+\sqrt{2})/2<E({\overline{Z}}_i|g_i=1)=\sqrt{2}$.

However, if (A) but not (B) holds, the GEE and standardised means tests are valid tests for the stronger null hypothesis $E({\overline{X}}_i|n_i=n,g_i=0)\le E({\overline{X}}_i|n_i=n,g_i=1)$ for all $n=1,\dots ,n_{\text{max}}$. Then the expectation of the weighted mean ${\hat{\mu }}_g$ (for the GEE test) or ${\overline{Z}}_i$ (for the standardised means test) in the treatment group will be less than or equal to the respective expectation in the control group under the stronger null hypothesis. Note that in the GEE approach the sandwich variance estimate $\widehat{\mathit{var}}({\hat{\mu }}_g)$ is consistent even if (A) and (B) are violated because $w_i{\hat{\mu }}_{g_i}$ is asymptotically unbiased for $E(w_i{\overline{X}}_i|g_i=g)$, even if ${\hat{\mu }}_g$ is biased and not consistent.

Finally, if neither assumption (A) nor (B) holds, Welch’s t-test based on the patient-wise means will still be valid, due to asymptotic normal distribution of the ${\overline{X}}_i$. Because of the issues outlined above, the GEE and the t-test based on the standardised means may inflate the type I error rate in this setting.

Table 1 gives an overview of the validity of the hypothesis tests in the different settings.

Table 1.

Type I error rate control of the testing procedures dependent on the validity of assumptions (A) and (B).

Assumption		Testing procedure
(A)	(B)	Welch t-test for means	GEE	Welch t-test for standardised means
✓	✓	✓	✓	✓
✓	✗	✓	(✓)	(✓)
✗	✓	✓	✓	✗
✗	✗	✓	✗	✗

✓: (asymptotic) control of the type I error rate for the test of H₀, (✓): Type I error control for the stronger null hypothesis $E({\overline{X}}_i|n_i=n,g_i=0)\le E({\overline{X}}_i|n_i=n,g_i=1),n=1,\dots ,n_{\text{max}}$. ✗: no control of the type I error rate for the test of H₀.

3 Simulation study

3.1 A data generating model for GAS data

To investigate the properties of different analysis approaches for GAS endpoints, we introduce a data generating model for the observed goal attainment scores X_ik based on continuous latent variables Y_ik. They allow one to parametrise the treatment effect as well as the between- and within-patient variability. Let $n_i\sim D$, where D denotes the distribution of the number of goals chosen by patient i. Now, for $k=1,\dots ,n_i$

$$Y_{\mathit{ik}}=b_0+u_i+g_i{b}_{\mathit{ik}}+{\epsilon }_{\mathit{ik}}$$ (6)

denotes a continuous goal attainment score for goal k of subject i. Here, b₀ denotes the mean response in the control group, $u_i\sim N(0,{\sigma }_u^2)$ a patient-specific random effect (introducing correlation between goal attainments of different scores within a patient), $b_{\mathit{ik}}\sim B$ is the effect of the experimental treatment on the attainment of goal k in subject i and ${\epsilon }_{\mathit{ik}}\sim N(0,{\sigma }_{\epsilon }^2)$ is a random error term. Furthermore, we assume that the b_ik are non-negative random variables and that $n_i,u_i,b_{\mathit{ik}}$ and ε_ik are independent between subjects and b_ik and ε_ik additionally within subjects for different goals. Modelling the treatment effects by the random variable b_ik reflects the assumption that each patient chooses separate and different goals (and potentially no goal is chosen more than once). Note that, as special case, the treatment effect b_ik can be a constant. The correlation of Y_ik and $Y_{\mathit{ik}\text{'}},k\ne k\text{'}$ is then given by

$${\rho }_g={\sigma }_u^2/({\sigma }_u^2+g{\sigma }_B^2+{\sigma }_{\epsilon }^2)$$ (7)

where ${\sigma }_B^2$ denotes the variance of b_ik. Thus, if ${\sigma }_B^2>0$, the correlation in the treatment group is smaller than in the control group. The discrete goal attainment levels X_ik are defined by discretising Y_ik via a set of thresholds $-\infty =c_0<c_1\dots c_{2l+1}=\infty$, such that $X_{\mathit{ik}}=s-l-1$ if $c_{s-1}<Y_{\mathit{ik}}\le c_s,s=0,\dots ,2l+1$. Note that the distribution of the vectors ${\mathbf{X}}_i$ in this model satisfies the conditions (A) and (B).

3.2 Simulation scenarios

We performed a simulation study to compare the power of the considered hypothesis tests to detect a treatment effect in a GAS endpoint in a parallel group design with equal per group sample sizes $m/2$. In the reference scenario, the overall sample size was set to m = 40 and thresholds $c_j={\Phi }^{-1}(0.2j),j=0,\dots ,5$ are used, where ${\Phi }^{-1}$ denotes the inverse of the cumulative standard normal distribution function. The number of goals n_i are uniformly distributed on $\{1,\dots ,n_{\text{max}}\}$ with n_max = 5. The treatment effects b_ik are assumed to be uniformly distributed on $(0,2\delta )$ for fixed constants δ, i.e. $B=U(0,2\delta )$, such that $E(b_{\mathit{ik}})=\delta$ and $\mathit{var}(b_{\mathit{ik}})=\frac{{\delta }^2}{3}$. The mean response in the control group is set to zero, i.e. $b_0=0$ such that ${\mu }_0=0$. To investigate the impact of the correlation of treatment scores on the outcomes, we fixed different correlations ρ₀ in the control group and set ${\sigma }_u^2={\rho }_0,{\sigma }_{\epsilon }^2=1-{\rho }_0$ such that ${\sigma }_u^2+{\sigma }_{\epsilon }^2=1$. In the computation of the weights (2) to calculate the standardised means ${\overline{Z}}_i$, we set ${\rho }_x=0.3$.

Besides the unweighted case, we considered two choices of goal specific weights (see Section 2.5): (i) a setting where the weights v_ik ($v_{\mathit{ik}}\in U\{1,\dots ,n_i\}$ for $k=1,\dots ,n_i$ where $v_{\mathit{ik}}\ne v_{\mathit{ij}}$ for $k\ne j$) represent patient preferences (e.g. the importance of the goal to the patient) and are therefore assumed to be stochastically independent of the treatment effect variable b_ik and (ii) a setting where weights are chosen to increase the power of the applied testing procedure by giving more weight to goals for which a larger treatment effect is expected. To this end, we choose the weights

$$v_{\mathit{ik}}=\frac{b_{\mathit{ik}}}{\sum _{l=1}^{n_i}{b}_{\mathit{ik}}}·n_i$$ (8)

assuming that the effect sizes b_ik for each of the goals are known, but still $b_{\mathit{ik}}\sim U(0,2\delta )$. These weights have a certain optimality property: if ρ = 0, they maximise the ratio $[E(\sum _{k=1}^{n_i}{v}_{\mathit{ik}}{Y}_{\mathit{ik}}|g_i=1)-E(\sum _{k=1}^{n_i}{v}_{\mathit{ik}}{Y}_{\mathit{ik}}|g_i=0){]}^2/\mathit{var}(\sum _{k=1}^{n_i}{v}_{\mathit{ik}}{Y}_{\mathit{ik}})$, i.e. the effect over variance ratio of the latent variable within patient i.²⁸ For each simulation 10⁴ simulation runs were performed, except for the calculation of the type I error rate where 10⁵ simulation runs were used.

We compared three testing procedures: the Welch t-test based on the per-subject mean specific scores (see Section 2.2), the GEE test (see Section 2.3) and the t-test based on the standardised means (see Section 2.4) were performed. All simulations were performed in R. The GEE models were fitted with the R-package geepack.²⁹

3.3 Results of the simulation study

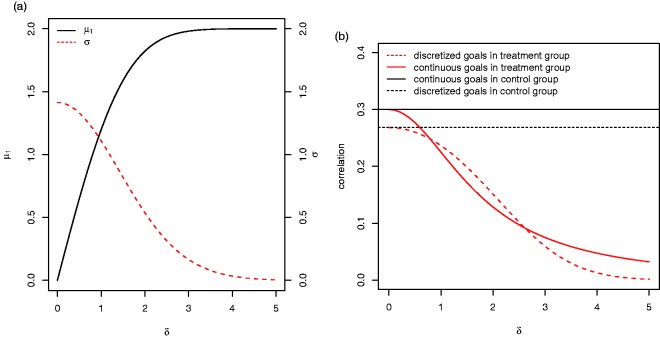
Due to the discretisation of the continuous variables, the dependence of the expected value of the goal attainment scores X_ik on δ is not linear in the treatment group but levels off for large δ due to a ceiling effect (see Figure 2(a)). Correspondingly, their variance decreases to zero for increasing δ. As noted above, also the correlation between the goal attainment scores of patients in the treatment group depends on the effect size. Figure 2(b) shows that the correlations of $X_{\mathit{ik}},X_{\mathit{ik}\text{'}}$ and $Y_{\mathit{ik}},Y_{\mathit{ik}\text{'}},k\neg =k\text{'}$ in the treatment group decrease with increasing δ. Expressions for the mean, variance and covariance of the discretised attainment levels in the proposed model are given in Appendix 1.

Figure 2.

(a) The expected value of the goal attainment scores X_ik in the treatment group μ₁ and their variance σ as function of δ in the reference scenario described in Section 3.2. (b) The correlations of the continuous and discretised goal scores $X_{\mathit{ik}},X_{\mathit{ik}\text{'}}$ and $Y_{\mathit{ik}},Y_{\mathit{ik}\text{'}},k\neg =k\text{'}$ within a patient as function of δ for ${\rho }_0=0.3$.

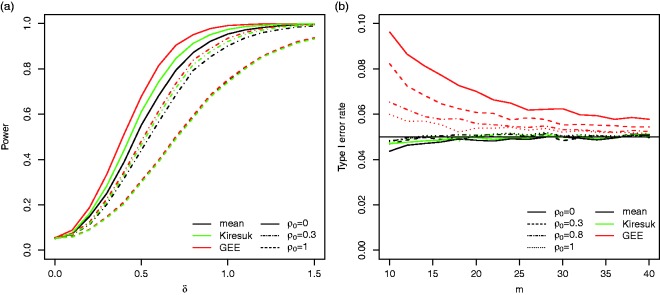
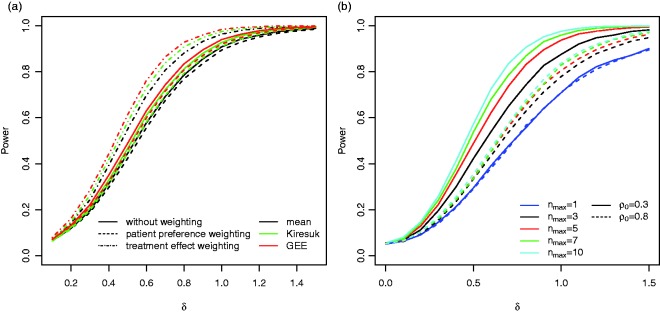
Figure 3(a) shows that for the reference scenario the power of the GEE approach is largest, followed by the t-test for standardised means and the t-test for the raw means. For example, for ${\rho }_0=0,\delta =0.5$ the power is 68% for the GEE approach compared to 61% for the t-test on the standardised per-subject means and 55% for the t-test on the non-standardised means. The differences in power become smaller for increasing ρ₀. For ${\rho }_0=1$ all three testing procedures have the same power. In addition, for increasing ρ₀ the power of all procedures decreases. Figure 5(a) shows the power of the t-test for standardised means for the case where correlations ${\rho }_x\neg ={\rho }_0$ are chosen in equation (2) to compute the standardised means ${\overline{Z}}_i$. Especially, if ${\rho }_0=0$, choosing a ${\rho }_x>>{\rho }_0$ leads to a drop in power.

Figure 3.

The power (a, 10⁴ simulation runs) and type I error rate (b, 10⁵ simulation runs) of the t-test based on the per-subject means (mean), the t-tests based on the standardised per-subject means (Kiresuk), and the test based on the GEE model (GEE) for the reference scenario.

Figure 5.

(a) The power of the t-test for standardised means for the case where correlations ${\rho }_x\neg ={\rho }_0$ are chosen in equation (2) to compute the standardised means ${\overline{Z}}_i$ for the reference scenario. Figure (b) shows the power under the assumption that the effect size follows a mixture distribution with weight $1-p$ on 0 and weight p on a uniform distribution on $[0,2\delta ]$, using the t-test applied to the per-subject means (mean) and standardised per-subject means (Kiresuk), and the test based on the GEE model (GEE) for the reference scenario.

For sufficiently large sample sizes, the type I error rate is controlled for all three procedures. However, the GEE approach is liberal for small sample sizes: for a sample size of m = 20, the type I error rate for ${\rho }_0=0$ is 0.07 instead of the nominal $\alpha =0.05$ and reduces to 0.0545 for m = 40 (see Figure 3 (b)).

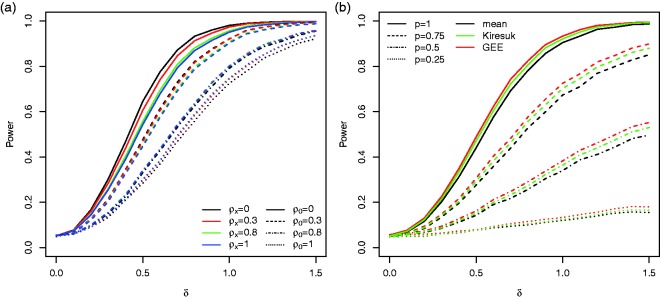
If goal specific weights are applied that are independent of the effect sizes (Case (i) in Section 3.2) the power drops for all three testing procedures. However, if we assume that the weights are chosen according to equation (8) (Case (ii) in Section 3.2), the power increases compared to the tests based on the unweighted goal attainment scores (see Figure 4(a)). The latter scenario serves as benchmark only, as it requires that the exact effect sizes of each goal are known in advance. If estimates based on historical data are used instead, the increase in power may be smaller.

Figure 4.

(a) The power of the three considered testing procedures without weighting, with patient preference weighting (Case (i) in Section 3.2) and with treatment effect weighting (Case (ii) in Section 3.2) in the reference scenario for ${\rho }_0=0.3$ and n_max = 5. (b) The power of the GEE approach for different maximum number of goals $(n_{\text{max}}=1,3,5,7,10)$ and correlations ${\rho }_0=0.3,0.8$. For the respective power curves for the t-tests applied to the mean and standardised mean scores, see Figures S1 in the Supplementary Material.

Figure 4(b) shows the impact of the maximum number of goals per patient on the power for the reference scenario. As expected the power increases with increasing n_max and the increase is more prominent for lower correlations ρ₀.

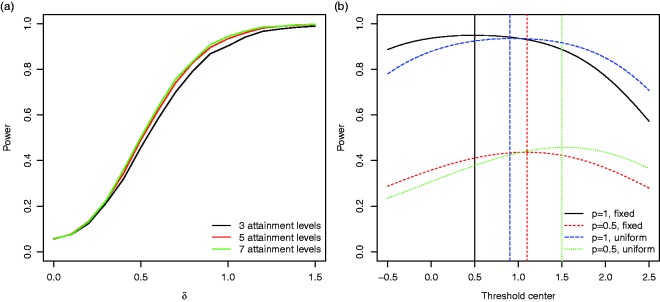
To assess the robustness of the procedures, we performed simulations for several alternative scenarios and modifications of the procedure: To investigate the impact of the inclusion of goals on which the treatment has no effect, we consider a scenario where b_i follows a mixture distribution with point mass $1-p$ on 0 and probability p on a $U(0,2\delta )$ distribution. For decreasing p we observe a sharp drop in power (see Figure 5(b)). Figure 5(a) shows the consequences of a misspecification of the average correlation between the goals on the power of a test using the Kiresuk aggregation formula. The impact of the number of attainment levels used (i.e. the number of categories applied in the categorisation of the continuous latent variable) is shown in Figure 6(b). Increasing the number of attainment levels leads to a gain in power. However, while an increase from 3 to 5 levels gives a noticeable improvement, going beyond 5 levels has only a marginal impact. In the reference scenario, the thresholds for the discretisation of the continuous normal variables are chosen as quantiles of a standard normal distribution such that in the control group the x_ik have a discrete uniform distribution. If instead quantiles of a normal distribution that is centred between 0 and δ is chosen, the power can be improved. Figure 6(a) shows the respective power curves under the assumption that b_ik follows a mixture distribution, either between the points 0 and δ or between 0 and uniform distribution on $[0,2\delta ]$. The optimal categorisation threshold centre depends on the assumed effect size distribution.

Figure 6.

(a) The power for the GEE approach for discrete goal attainment scales with $L=3,5,$ and 7 levels such that $c_j={\Phi }^{-1}(j/L),j=1,\dots ,L$ and other parameter values are as in the reference scenario. For the respective power curves for the t-tests applied to the per-subject mean and standardised mean scores, see Figure S1 in the Supplementary Material. (b) The Power of the t-test based on per-subject means if the discretisation of the continuous attainment levels, which is centred around 0 in the reference scenario, is based on other threshold centre values. For different threshold centre values t, we set $c_j={\Phi }_{t,1}^{-1}(j0.2),j=0,\dots ,5$, where ${\Phi }_{t,1}^{-1}$ denotes the quantiles of the normal distribution with mean t and variance 1. The distribution of effect sizes was either assumed to be a mixture distribution on 0 and δ (fixed effect) or 0 and a uniform distribution on $[0,2\delta ]$ (uniform) with weights $1-p$ and p.

4 Extension to cross-over designs

4.1 Hypothesis tests for cross-over designs

For the investigation of treatments with short-term effects on a chronic condition, cross-over designs may provide advantages to parallel group designs.³⁰ In a two-armed cross-over trial, each patient is exposed to both treatments in randomised order, over a sequence of treatment periods. The outcome variables are observed at the end of each period. Effect estimates and hypothesis tests are then based on within-patient comparisons and precision and power are determined by the within-patient variance rather than the typically larger between-patient variance determining the properties of a parallel group design. Therefore, a cross-over design may lead to a higher power or require a smaller sample size than a parallel group design.

Consider a cross-over trial with a goal attainment scaling endpoint, where each patient chooses a single set of goals and attainment categories which are used in both treatment periods. Such a design can be useful for the investigation of symptomatic treatments in stable, chronic diseases where a short-term endpoint is available.

4.2 Extension of the testing approaches to cross-over designs

The three hypothesis tests proposed in Section 2 can be extended to a two groups–two periods cross-over design:

4.2.1 Paired t-test based on per-subject means

For patient $i=1,\dots ,m$, let $(X_{i1g},\dots ,X_{{\mathit{in}}_{i}g})$ denote the observed goal attainment levels under treatment g = 0, 1. Then the per-subject means under treatment g are ${\overline{X}}_{\mathit{ig}}=\sum _{k=1}^{n_i}{X}_{\mathit{ikg}}/n_i$. The null hypothesis H₀ as defined in (1) can then be tested by a paired t-test applied to the pairs of per-subject means $({\overline{X}}_{i0},{\overline{X}}_{i1})$.

4.2.2 Paired t-test based on standardised per-subject means

For patient i under treatment g, let ${\overline{Z}}_{\mathit{ig}}=\sqrt{w_i}{\overline{X}}_{\mathit{ig}}$ denote the standardised means, where w_i is defined as in (2), then a paired t-test can be applied to the pairs $({\overline{Z}}_{i0},{\overline{Z}}_{i1})$ to test H₀.

4.2.3 GEE approach 1

The GEE approach reduces to an intercept only GEE model applied to the differences ${\Delta }_{\mathit{ik}}=X_{\mathit{ik}1}-X_{\mathit{ik}0}$, with subject as clustering variable. We assume, analogous to (B), that $E({\overline{\Delta }}_i|n_i=n)$ does not vary with $n=1,\dots ,n_{\text{max}}$, where ${\overline{\Delta }}_j=\sum _{k=1}^{n_i}{\Delta }_{\mathit{ik}}/n_i$. The null hypothesis for the paired GEE test is $E({\overline{\Delta }}_i|n_i=n)=0$ for all $n=1,\dots ,n_{\text{max}}$. Here the same goals are measured for each patient in each period.

4.2.4 GEE approach 2

The GEE approach could also be applied to model $E(X_{\mathit{ikg}}|n_i=n)$ while accounting for patient as clustering variable. The null hypothesis for this second paired GEE test is $E(X_{\mathit{ik}1}|n_i=n)=E(X_{\mathit{ik}0}|n_i=n)$ for all $n=1,\dots ,n_{\text{max}}$.

Remarks: (i) With the exception of GEE approach 1, the above hypothesis tests can be extended to adjust for co-variables such as the treatment period. To this end, the paired t-tests are replaced by a linear model for ${\overline{X}}_{\mathit{ig}}$ (or ${\overline{Z}}_{\mathit{ig}}$), with patient, treatment group and period as categorical independent factors.³⁰ To include a period effect in the GEE approach 2, the treatment period is added as co-variable in the marginal model for $E(X_{\mathit{ikg}}|n_i=n)$, with subject as clustering variable. (ii) The hypothesis tests can directly be extended to GAS with goal-specific weights. To this end, the goal attainment levels are multiplied by the respective goal-specific weights as discussed in Section 2.5. (iii) Cross-over trials with GAS endpoints face all limitations of cross-over trials based on more traditional outcomes, as susceptibility to carry-over effects or time trends. The latter can be adjusted for in the model (see Remark i) but even the unadjusted test does not lead to bias if the sequences are balanced. (iv) For progressive diseases, one can consider cross-over designs where patients may select different goals (and even different numbers of goals) for the second treatment period, to account for changes in their needs due to the disease progression. Also, in this case the paired t-tests based on per-subject means and standardised means remain valid. Furthermore, the GEE approach 2 that pairs the mean goal attainment levels per patient can be applied. GEE approach 1 that pairs individual goal attainment levels is, however, not applicable. In addition, as a period effect is expected in the progressive disease setting, the adjusted models (see Remark (i)) are more suitable. An alternative to the selection of new goals in the second period is the adjustment of the definition of goal attainment levels to avoid ceiling effects if the disease progresses. Also, in this setting the above hypothesis tests can be applied. If the second period goals (or the definitions of attainment levels) are chosen after randomisation, blinding is essential to reduce the potential for bias.

4.3 A data generating model for cross-over trials

Data for the cross-over trial are modelled similarly as for the parallel group design based on continuous goal attainment scores defined by

$$Y_{\mathit{ikg}}=b_0+u_i+{\mathit{gb}}_{\mathit{ik}}+{\epsilon }_{\mathit{ikg}}$$ (9)

where Y_ikg is the response of patient i on treatment g = 0, 1 in goal $k=1,\dots ,n_i$. The discretised scores X_ikg are defined as in the parallel group case. All random variables in equation (9) as well as n_i are defined as for the parallel group design. However, we allow that the correlation ${\rho }_{\epsilon }=\mathit{Cor}({\epsilon }_{\mathit{ik}0},{\epsilon }_{\mathit{ik}1})$ between the noise in the treatment and control group differs from 0, all other pairs of ε_ikg are ${\epsilon }_{i\text{'}k\text{'}g\text{'}}$ are assumed to be independent. Then, as in the parallel group design, the correlation between goal attainment levels of the same patient for each treatment group g = 0, 1 is ${\sigma }_u^2/({\sigma }_u^2+g{\sigma }_B^2+{\sigma }_{\epsilon }^2)$. The correlation of the goal attainment levels between periods is (for the same goal and patient) $({\sigma }_u^2+{\rho }_{\epsilon }{\sigma }_{\epsilon }^2)/(\sqrt{{\sigma }_u^2+{\sigma }_B^2+{\sigma }_{\epsilon }^2}\sqrt{{\sigma }_u^2+{\sigma }_{\epsilon }^2})$.

In Section 5, we compare the cross-over design to the parallel group design in an example.

5 Example: Assessment of the efficacy of recombinant human diamine oxidase in mastocytosis

In November 2014 the Medical University of Vienna seeked scientific advice concerning planned clinical trials for the treatment of mastocytosis patients with the active substance recombinant human diamine oxidase (rhDAO) in order to achieve Marketing Authorisation. With a prevalence of less than 3 in 10,000 (EMA/OD/75/2014), mastocytosis is considered an orphan disease. It is characterised by too many mast cells in various organs of the body, and patients with recurrent anaphylaxis are even much rarer.

Due to the diversity of symptoms of mastocytosis patients, it is especially difficult to perform clinical studies with a single standardised endpoint. Symptoms include a broad spectrum ranging from minor inconveniences compromising the quality of life like flushing (redness), pruritus (itching), urticaria, abdominal pain (cramps), nausea, vomiting, heartburn, palpitations (tachycardia), dyspnoea (difficulty breathing) and hypotension (low blood pressure) to its most severe form with life-threatening hypersensitivity reactions (anaphylaxis). All these symptoms have as a common cause an excess of activated mast cells in various parts of the body. About 70% of mastocytosis patients feel that they suffer from a disability caused by their disease.³¹

There is an unmet medical need for some patients despite optimised available treatment because they still experience recurrent episodes of anaphylaxis and are living with the daily fear of a fatal outcome. For this subgroup of mastocytosis patients suffering from recurrent anaphylaxis, marketing approval under exceptional circumstances was envisaged, justified by the rarity of the indication. Variability of anaphylactic episodes may require individualised outcome measures to show the effect of rhDAO for single patients. For example one patient had anaphylactic shocks at least 60 times in the last 15 years and needed to be transported to the hospital every time despite being treated with intramuscular epinephrine, anti-histamines and glucocorticoids. In this case, it could be of an advantage to measure the time to resolution of anaphylactic shock defined by reaching a sustained mean arterial pressure of at least 70 mmHg. In another patient, the recurrent episodes of anaphylaxis are triggered by acute infections and only after days of fever, headaches and nausea, the patient came to the hospital because of urticaria and flush. Besides measuring the mean arterial pressure, the bioactive histamine in urine samples could be quantified. In yet another case, a mastocytosis patient suffers from recurrent anaphylactic attacks when his skin is exposed to mechanical or thermal stress. For this patient, tolerance towards elevated temperature and rubbing of the skin could be an adequate outcome to measure the efficacy of rhDAO. Table 2 gives an example of how a GAS scale could look like for this goal of a patient as proposed in the request for scientific advice. To summarise the effect on the different endpoints of the different patients, the use of an individual goal attainment scale was suggested. The Medical University of Vienna planned to perform a cross-over trial using either rhDAO or placebo in addition to standard of care to demonstrate that degradation of histamine by repeated injection of rhDAO will be safe and effective in alleviating chronically debilitating symptoms in mastocytosis patients not controlled by conventional standard therapy.

Table 2.

Example of a Goal Attainment Scale for a mastocytosis patient taken from the request for scientific advice at the EMA.

Goal score	Definition
−2	Patient only tolerates showers with lower temperatures
	AND tolerates gentler rubbing/drying of skin
−1	Patient only tolerates showers with lower temperatures
	OR tolerates gentler rubbing/drying of skin
0	Patient does not experience any changes
+1	Patient tolerates showers with higher temperatures
	OR tolerates rougher rubbing/drying of skin
+2	Patient tolerates showers with higher temperatures
	AND tolerates rougher rubbing/drying of skin

In the protocol assistance provided by the European Medicines Agency (EMA), it was recommended that the study is focused on patients with stable cutaneous and indolent systemic mastocytosis and that all patients are well educated about their disease, factors triggering symptoms and the use of rescue therapy. The EMA suggested performing an open (multinational) trial in this population, where patients and/or emergency physicians inject rhDAO, but to use a differentiated or individualised approach in defining suitable endpoints as triggers and presentation of anaphylaxis can vary substantially between patients. The outcome of such a trial could be a series of cases treated and observed under a common, well-defined protocol including a number of amendments or notifications to fit individual patient needs. Additionally they suggest to further explore the feasibility of a within patient, placebo-controlled, on top of standard of care study in those patients considered suitable for self-administration of rhDAO.

Note that the exemplary goal definition (Table 2) as proposed in the request for scientific advice can be refined by defining separate goals for tolerable temperatures and pressures. Furthermore, quantitative thresholds for temperature and pressure defining the attainment levels could be specified.

We simulated the statistical power of a clinical trial in a setting similar to the example above. Especially, we compared the properties of a parallel group design with 30 patients to a cross-over design with 15 patients where each patient serves as his or her own control (Table 3). Note that while both have the same number of outcome measurements, the former requires twice as many patients. We used the data generating model (9) with parameters as in the reference scenario in Section $3.2$ and a uniform effect size distribution on $[0,2\delta ]$ and correlations of goal attainment levels between goals ρ₀ of 0 and 0.3. For the cross-over trials, we considered correlations ${\rho }_{\epsilon }$ between periods of 0 and 0.3.

Table 3.

Operating characteristics of a parallel group trial with 30 patients compared to a cross-over trial with 15 patients for the example in Section 5 with expected effect size δ = 1.

Design	ρ 0	Method	Power			T1E
			no w	patient w	effect w	no w	patient w
Parallel		Mean	0.81	0.79	0.90	0.050	0.050
Group	0.3	Kiresuk	0.83	0.81	0.92	0.050	0.050
Design		GEE	0.85	0.83	0.94	0.056	0.056
Cross-		Mean	0.92	0.90	0.99	0.049	0.050
Over	0.3	Kiresuk	0.95	0.93	0.99	0.050	0.051
design		GEE 1	0.97	0.95	0.98	0.067	0.070
${\rho }_{\epsilon }=0$		GEE 2	0.98	0.96	0.99	0.055	0.055
Cross-		Mean	0.98	0.97	1.00	0.048	0.049
over	0.3	Kiresuk	0.99	0.98	1.00	0.050	0.049
design		GEE 1	0.99	0.98	0.99	0.066	0.068
${\rho }_{\epsilon }=0.3$		GEE 2	1.00	0.99	1.00	0.054	0.055
Parallel		Mean	0.88	0.86	0.93	0.049	0.050
group	0	Kiresuk	0.92	0.89	0.96	0.050	0.050
design		GEE	0.96	0.93	0.98	0.062	0.062
Cross-		Mean	0.86	0.83	0.97	0.047	0.050
over	0	Kiresuk	0.90	0.87	0.97	0.049	0.050
design		GEE 1	0.94	0.90	0.97	0.068	0.070
${\rho }_{\epsilon }=0$		GEE 2	0.94	0.90	0.98	0.055	0.056
Cross-		Mean	0.92	0.90	0.99	0.047	0.047
over	0	Kiresuk	0.95	0.92	0.99	0.048	0.049
design		GEE 1	0.97	0.95	0.98	0.066	0.068
${\rho }_{\epsilon }=0.3$		GEE 2	0.98	0.95	0.99	0.054	0.055

Note: The power (10⁴ simulation runs) and type I error rate (T1E, 10⁵ simulation runs) are given for the unweighted (no w), patient preference weighted (patient w), and treatment effect weighted (effect w) scores. Note that under the null hypothesis, the treatment effect weighted and unweighted case coincide.

As expected, for a correlation of goal attainment levels within patients of ${\rho }_0=0.3$, the cross-over trial has a substantially larger power than the parallel group design. The power for all designs decreases if GAS with patient preference weighting is used and increases if GAS with effect size weighting is used. For ρ = 0, the cross-over trial has slightly lower power than the parallel group design. This is due to the fact that in this case the true standard error of the treatment effect estimates in the cross-over analysis is the same as in the parallel group design, but in the paired analysis corresponding estimate has fewer degrees of freedom.³² Because of the lower degrees of freedom in the cross-over trial, analysing a cross-over trial as if the observations are obtained by two independent groups of patients (as in a parallel group design) can increase the power if the sample size and the correlations are low.^32,33 In the considered scenarios for cross-over trials, the GEE 1 and 2 approaches have similar power and are superior to the other approaches. The GEE 2 approach has a lower type I error rate compared to GEE 1, due to the larger degrees of freedom in the variance estimate. These findings remain valid if lower effect sizes ($\delta =0.5$) are considered (see Table S1 in the Supplementary Material).

6 Discussion

We propose a probabilistic model for data from a GAS endpoint that can be useful to assess the appropriateness of different analysis approaches and to calculate the sample size for trials with a GAS endpoint. The proposed model covers a number of important features of these endpoints, such as the varying number of goals per patient and the individual choice of goals for each patient (reflected by modelling the treatment effects as a random variable). We focused on parallel group superiority trials and considered three testing procedures, t-tests on per patient mean scores or standardised mean scores as well as an analysis by a GEE approach. Randomised treatment allocation and the choice of goals and weights before randomisation avoids systematic imbalances between the treatment groups. In particular, systematic differences in the quality, attainability and importance of goals are prevented.

A clinical interpretation of the tested null hypothesis as well as the considered alternative hypotheses is challenging because the GAS endpoint depends not only on the preferences of the patients included in the trial but also on the scope of goals available to the patients and the process of choosing individual goals. The goals and patient preference weights, which are chosen before randomisation, can be considered as a baseline characteristic of the patient, as age or sex. The observed value of a GAS endpoint can be regarded as an attribute of the patient under the specific treatment, similar to the observed value of a traditional clinical endpoint. Therefore, observing a significant treatment effect in the mean (weighted) goal attainment in a randomised trial allows for the conclusion that, under the same process of selecting goals (and weights), on average the (weighted) goal attainment levels of other patients from the same population will be higher under treatment than under control. If the study sample cannot be assumed to be a random sample, but patients are randomised between treatment groups, a conditional interpretation is possible and study results may be generalised to a population with properties matching those of the study sample. The issue of conditional and unconditional inference is not specific to GAS endpoints but has been discussed for clinical trials with traditional clinical endpoints as well, as the applicability of the random sampling model for clinical trials has been challenged. Note that, at least asymptotically, conditional re-randomisation tests and unconditional tests often coincide (see e.g. Sections 4.1 and 4.2 of literature^34,35 for a recent discussion). It is well understood for clinical trials with a traditional endpoint that the interpretation of trial results is only meaningful if the trial population is sufficiently specified by appropriate inclusion/exclusion criteria based on baseline characteristics. Furthermore, the possibility to generalise trial results may depend on how well the trial population including their goal preferences reflects a future patient population to be treated with the treatments under investigation. Similarly, for a clinical interpretation of results of a trial with a GAS endpoint, appropriate criteria for valid goals have to be specified. These criteria can help to assess the generalisability of trial results, similar to classical inclusion/exclusion criteria. The criteria need to be flexible enough to cover all important goals for a heterogeneous patient population, but need to make sure that the goals are relevant and clinically useful. The choice of the goal to reach a certain level of the experimental drug in the blood, for example, will typically not be a valid goal and may bias the analysis.

For the interpretation of outcomes of trials with a GAS endpoint, it is essential that the chosen goals are reported in a similar way as baseline variables are traditionally reported in randomised controlled trials. If a full listing of goals is not feasible, a categorisation of goals based on pre-specified categories and reporting of the corresponding frequencies can be an important tool for the interpretation. Furthermore, such a categorisation can be the basis for stratified randomisation and stratified analysis to ensure a balance across treatment groups and potentially increase the power of respective tests.

Goal attainment scaling can be viewed as a type of combined endpoint, where the components may change from patient to patient such that potentially only one observation per component is available. Therefore, the treatment effects for specific goals cannot be estimated. This limitation in the interpretation is a price for the possibility to choose individualised endpoints such that more heterogeneous patients can be included in the trial.

The interpretation of GAS endpoints shares several limitations with more standard combined endpoints, where the same components are measured for each patient. Especially, positive effects in some components can mask negative effects in other components.³⁶ For GAS this masking of effects is more difficult to assess because the analysis of individual components is not feasible if the goals are chosen individually. However, based on a categorisation of goals, a separate descriptive analysis for each of the categories could be considered.

If the number of goals per patient or the correlation between goal attainments varies between patients, not all patients provide the same amount of information on the treatment effect. Then, appropriate weighting of goals or patients can increase the power of hypothesis tests. For the considered data generating model, tests based on a GEE model lead to the highest power. The GEE model is based on a more efficient estimator of the average treatment effect across goals and patients compared to methods based on the mean or the standardised mean. Tests based on the standardised means, although widely used, have the disadvantage that they may not control the type I error rate conditional on the number of goals chosen for each patient.

While weighting of goals according to patient preferences can increase the clinical relevance of the GAS endpoints, such weighting reduces the power of hypothesis tests if the weights are not correlated with the treatment effect of the respective goals. This is due to the additional variability introduced by the weighting. On the other hand, power can be gained by choosing weights that correlate with the unknown treatment effects for the different goals. As an alternative to weights that are normalised within each patient, as discussed in Section 2.5, weights on an absolute scale could be used to reflect the relevance of a goal compared to different goals of different patients.

We also considered statistical testing procedures for cross-over designs with a goal attainment endpoint. As in such designs each patient serves as his own control, at most half the number of patients are required. If there is a strong correlation of goal attainments within patients, the required sample size is further reduced. For stable, chronic diseases and symptomatic treatments which are not disease modifying, the same goals can be used in both treatment periods. This not only reduces the variability for within patient comparisons, but can also limit the potential for bias as the analysis is stratified by goal. Allowing for different goals in the two treatment periods of randomised trials gives additional flexibility to adjust to changes in the patients’ needs, for example, due to a progressive disease. However, if goals or definitions of attainment levels are modified after randomisation of the treatment sequence, there is an additional potential for bias and blinding is paramount.

The power of the considered testing procedures for GAS endpoints depends on a number of factors, such as the number of chosen goals, the correlation of goal attainments within patients, the variability of goal attainments, the choice of the goal attainment levels, and the distribution of effect sizes for the chosen goals. The large number of parameters which are typically unknown at the planning stage imposes a substantial challenge for sample size planning. However, a few recommendations can be derived by our simulation study:

• Number of goals: The power of a between-group comparison increases with the number of goals per patient, assuming the distribution of treatment effects and correlation of goal attainments stay constant as the number of goals increases.

• Sensitivity of goals: Including goals that are not affected by the treatment can lead to a substantial loss in power and should be avoided.

• Hypothesis tests: Overall the GEE approach has the largest power, with minimal inflation of the type I error rate for moderate sample sizes. T-tests for the per-subject means of goal attainment levels are the most robust testing approach and control the type I error rate in all considered scenarios.

• Dependency between goals: For parallel group designs, goals within a patient should be weakly correlated. The increase in power by adding goals is less pronounced, the higher the correlation between goals.

• Number of scale levels: A goal attainment scale with five levels appears to be sufficient, as a further increase in the number of levels has little effect on the power.

• Definition of GAS attainment levels: The optimal scale (maximising the power) depends on the effect sizes of the individual goals.

• Parallel or cross-over trial: If applicable, a cross-over design may allow for a substantial reduction of the required sample size.

Utilising a GAS endpoint in a clinical trial requires substantial additional effort and time resources, as well as particular training of involved study team members, to choose goals with each patient individually and to evaluate the goal attainment. However, in rare diseases with very heterogeneous symptoms, where traditional clinical endpoints are not sufficiently sensitive in the overall population, the possibility to include a broader patient population may outweigh the increased complexity. The proposed statistical model enables the assessment of the operating characteristics of trials with a GAS endpoint. This can be the basis to evaluate if a GAS endpoint should be chosen, to facilitate the planning of trials with a GAS endpoint and to guide the data analysis and interpretation.

Appendix 1. Computation of the first two moments of the discretised goals ${(X_{\mathit{ik}})}_{k=1}^{ni}$ for model (6)

Note that for specific $k,k\text{'}$ the random variables $Y_{\mathit{ik}},Y_{\mathit{ik}\text{'}}.X_{\mathit{ik}},Y_{\mathit{ik}\text{'}}\dots$ are only defined conditionally on $n_i\ge k,k\text{'}$. To simplify notation, in this section all random variables are understood conditional on n_i = n, for some $n\ge k,k\text{'}$. Let f_b denote the density of b_ik, and set z_ik = $u_i+{\epsilon }_{\mathit{ik}}$, such that ${(z_{\mathit{ik}})}_{k=1}^{ni}$ is multivariate normal with mean 0, $\mathit{var}(z_{\mathit{ik}})={\sigma }_u^2+{\sigma }_{\epsilon }^2$ and $\mathit{cov}(z_{\mathit{ik}},z_{\mathit{ik}\text{'}})={\sigma }_u^2$. Then the continuous goal scores defined in equation (6) can be written as $Y_{\mathit{ik}}=b_0+g_i{b}_{\mathit{ik}}+z_{\mathit{ik}}$ and the discretised goal scores are defined by $X_{\mathit{ik}}=m$, if $c_{m-1}<Y_{\mathit{ik}}\le c_m$, with $m\in M\subset \mathbb{Z}$. Now, the marginal probability distribution of the X_ik is given by

$$P(X_{\mathit{ik}}=m|g_i=g,b_{\mathit{ik}}=b)=\Phi (\frac{c_m-\mathit{gb}-b_0}{{\sigma }_u^2+{\sigma }_{\epsilon }^2})-\Phi (\frac{c_{m-1}-\mathit{gb}-b_0}{{\sigma }_u^2+{\sigma }_{\epsilon }^2})$$

The joint probability distribution of $X_{\mathit{ik}},X_{\mathit{ik}\text{'}}$ for $k\ne k\text{'}$ is given by

$$\begin{array}{c}\multicolumn{1}{c}{P(X_{\mathit{ik}}=m,X_{\mathit{ik}\text{'}}=m\text{'}|g_i=g,b_{\mathit{ik}}=b,b_{\mathit{ik}\text{'}}=b\text{'})}\\ \multicolumn{1}{c}{=P(z_{\mathit{ik}}\in (c_{m-1}-\mathit{gb}-b_0,c_m-\mathit{gb}-b_0],z_{\mathit{ik}\text{'}}\in (c_{m-1}-\mathit{gb}\text{'}-b_0,c_m-\mathit{gb}\text{'}-b_0])}\end{array}$$

where $m,m\text{'}\in M$. This probability can be directly computed from the cumulative distribution function of the bivariate normal distribution. Now, for a > 0, the non-central moments are given by

$$\begin{array}{c}\multicolumn{1}{c}{E(X_{\mathit{ik}}^a|g_i=g)={\int }_{\stackrel{\sim }{B}}E(X_{\mathit{ik}}|g_i=g,b_{\mathit{ik}}=b)f_b(b)\mathit{db}=\sum _{m\in M}{m}^a{\int }_{\stackrel{\sim }{B}}P(X_{\mathit{ik}}=m|g_i=g,b_{\mathit{ik}}=b)f_b(b)\mathit{db}}\\ \multicolumn{1}{c}{E(X_{\mathit{ik}}{X}_{\mathit{ik}\text{'}}|g_i=g)={\int }_{\stackrel{\sim }{B}}{\int }_{\stackrel{\sim }{B}}\sum _{m\in M}\sum _{m\text{'}\in M}mm\text{'}P(X_{\mathit{ik}}=m,X_{\mathit{ik}\text{'}}=m\text{'}|g_i=g,b_{\mathit{ik}}=b,b_{\mathit{ik}}=b\text{'})f_b(b)f_b(b\text{'})\mathit{dbdb}\text{'}}\end{array}$$

Thus, the central moments are ${\mu }_g=E(X_{\mathit{ik}}|g_i=g),{\sigma }^2=\mathit{var}(X_{\mathit{ik}}|g_i=g)=E(X_{\mathit{ik}}^2|g_i=g)-E(X_{\mathit{ik}}|g_i=g{)}^2$, and ${\rho }_{x,g}=\mathit{cov}(X_{\mathit{ik}},X_{\mathit{ik}\text{'}}|g_i=g)=E(X_{\mathit{ik}}{X}_{\mathit{ik}\text{'}}|g_i=g)-{\mu }_g^2$.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work has been funded by the FP7-HEALTH-2013-INNOVATION-1 project Advances in Small Trials Design for Regulatory Innovation and Excellence (ASTERIX) (grant no. 603160). Website: http://www.asterix-fp7.eu/

Supplemental material

Supplemental material for this article is available online.