Short abstract
Objective
To compare the full age spectrum (FAS) equation with the Modification of Diet in Renal Disease (MDRD) and the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equations in predicting glomerular filtration rate (GFR) in patients with obstructive nephropathy.
Methods
Adult patients with obstructive nephropathy who had undergone a GFR measurement using technetium-99m diethylenetriaminepentaacetic acid radioisotope renography were enrolled in the study. The measured GFR was taken as the reference value. Bias, precision and accuracy were compared between the three equations. Kappa test and the Bland–Altman method were used to evaluate the classification and the agreement. Receiver operating characteristic (ROC) curve analysis was used to describe the diagnostic accuracy of each equation.
Results
A total of 327 patients were enrolled. The P30 value for the FAS equation was 60.2% in the overall study cohort. The FAS equation had the highest diagnostic accuracy (ROCAUC = 0.87, 95% confidence interval [CI] 0.84, 0.91) compared with the MDRD equation (ROCAUC = 0.86, 95% CI 0.82, 0.89). The median bias of the FAS equation was significantly higher than that of the MDRD equation (8.7 versus 7.6 ml/min/1.73 m2, respectively).
Conclusions
Despite the drawbacks associated with each equation, the FAS equation was probably closer to ideal to estimate GFR in patients with obstructive nephropathy.
Keywords: Full age spectrum, glomerular filtration rate, equation, obstructive nephropathy
Introduction
Obstructive nephropathy is one of the most common causes of chronic kidney disease (CKD).1 It is often caused by kidney stones, cancer or prostatic hyperplasia.2 Obstruction of the urinary tract may lower renal blood flow and the glomerular filtration rate (GFR),1 leading to renal fibrosis.3 To optimize patient outcomes, it has been suggested that renal function should be monitored during follow-up to estimate the condition of the disease and the effects of treatment.4
Glomerular filtration rate is considered the ideal indicator to evaluate renal function in patients with CKD.5 There are several newly developed equations to evaluate GFR, which are much more convenient and cheaper than the conventional methods that use renal clearance of exogenous inulin or other alternative exogenous markers. For example, the Modification of Diet in Renal Disease (MDRD) equation and the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation are the most commonly used equations worldwide.6,7
Recently, a new equation, full age spectrum (FAS), was developed and validated in a purely Caucasian population based on normalized serum creatinine.8 The FAS equation showed less bias and a better performance than the CKD-EPI equation in studies in which reference GFR values were obtained by various methods, but none of the studies used radioisotope renography with technetium-99m diethylenetriaminepentaacetic acid (99mTc-DTPA).8,9 However, the FAS equation has not been validated in Chinese patients with obstructive nephropathy compared with 99mTc-DTPA radioisotope renography as the standard method for measuring GFR.
The objective of this study was to estimate the performance of the FAS equation in patients with obstructive nephropathy and to compare this equation with the MDRD and CKD-EPI equations. To the best of our knowledge, few studies have validated these equations in a cohort of patients who only have obstructive nephropathy.2
Patients and methods
Patient population
This retrospective study enrolled consecutive adult patients with obstructive nephropathy who had undergone a GFR measurement using 99mTc-DTPA radioisotope renography at the Department of Nephrology, Ningbo No. 2 Hospital, Ningbo University School of Medicine, Ningbo, Zhejiang Province, China, between 1 January 2011 and 30 April 2016. Demographic data were recorded for each patient, including age, sex, height and weight. Exclusion criteria included the following: (i) acute kidney injury; (ii) treatment with dialysis; (iii) prior renal transplantation; (iv) severe malnutrition; (v) infection; (vi) severe liver or cardiac dysfunction; (vii) pleural or abdominal effusion: (viii) treatment with medication that can affect renal function, such as vitamin C or a large dose of steroids.
Based on the measured GFR (mGFR) value from the 99mTc-DTPA radioisotope renography, patients were divided into four groups according to the Kidney Disease Improvement Global Outcomes guidelines as follows:10 group 1, eGFR ≥90 ml/min/1.73m2 (stage 1 CKD); group 2, eGFR 60-89 ml/min/1.73m2 (stage 2 CKD); group 3, eGFR 30-59 ml/min/1.73m2 (stage 3 CKD); group 4, eGFR 15-29 ml/min/1.73m2 (stage 4 CKD).
The study was approved by the Ethics Committee of Ningbo No. 2 Hospital, Ningbo University School of Medicine, Ningbo, Zhejiang Province, China (No. PJ-NBEY-KY-2016-021-01). Due to the retrospective design of this current study, written informed consent was not required from the participants.
Measurement of GFR
The mGFR was measured using 99mTc-DTPA radioisotope renography on a Siemens e.cam single gamma camera with high dynamic range detector technology as described previously (Siemens Healthcare, Erlangen, Germany).11 5 mCi 99 mTc-DTPA (purity 95–99%; Atom-Hitech Isotope Limited Company, Hangzhou, China) was injected into the patient after their height and weight measurements had been taken, and they had consumed 500 ml of drinking water and had emptied their bladder. mGFR was calculated using a personal computer using the Gates method and corrected by body surface area with the Du Bios equation.
Measurement of serum creatinine
All whole blood samples were drawn from the median cubital vein in the morning following a minimum 8-h fast. Approximately 5 ml of whole blood was added to a test tube containing no anticoagulant as required for the production of serum and stored at room temperature for 1 h. The blood samples were centrifuged at 4128 g for 5 min at 4 C in a Thermo Scientific™ Heraeus™ Multifuge™ X1 Centrifuge (ThermoFisher Scientific, Rockford, IL, USA). Serum creatinine was measured using the sarcosine oxidase method (Purebio Biotechnology, Ningbo, China) on an ADVIA® 2400 Clinical Chemistry System (Siemens Healthcare).
Estimation of GFR
All three equations, MDRD, CKD-EPI and FAS, were used to estimate the GFR for each patient. The three equations are presented in Table 1.
Table 1.
The equations used to estimate glomerular filtration rate (eGFR) based on serum creatinine (SCr) levels, age and sex in a study that compared three equations: Modification of Diet in Renal Disease (MDRD) equation, the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation and the full age spectrum (FAS).6–8
| eGFR equation | Equation | |
|---|---|---|
| MDRD | 175 × (SCr)–1.154 × (Age)–0.203 × 0.742 (if female) | |
| CKD-EPI | ||
| Female: SCr ≤0.7 mg/dl | 144 × (SCr/0.7)−0.329 × 0.993Age | |
| Female: SCr > 0.7 mg/dl | 144 × (SCr/0.7)−1.209 × 0.993Age | |
| Male: SCr ≤0.9 mg/dl | 141 × (SCr/0.9)−0.411 × 0.993Age | |
| Male: SCr > 0.9 mg/dl | 141 × (SCr/0.9)−1.209 × 0.993Age | |
| FAS | ||
| Female: 18 ≤age ≤40 years | Q = 0.70 mg/dl | 107.3/(SCr/Q) |
| Female: age > 40 years | [107.3/(SCr/Q)]*0.988(age–40) | |
| Male: 18 ≤age ≤40 years | Q = 0.90 mg/dl | 107.3/(SCr/Q) |
| Male: age > 40 years | [107.3/(SCr/Q)]*0.988(age–40) | |
Statistical analyses
All statistical analyses were performed using SPSS software, version 19.0 (IBM Corp, Armonk, NY, USA) and MedCalc software, version 15.2.2 (MedCalc®, Ostend, Belgium). The data are presented as mean ± SD for normally distributed continuous variables, median (interquartile range) for not normally distributed continuous variables, and frequencies and percentages for categorical variables. Confidence intervals (CIs) were calculated using the Bootstrap method. The subjects were stratified by mGFR (< 60 versus ≥ 60 ml/min/1.73m2) and age (< 70 versus ≥ 70 years).
Bias, precision and accuracy were analysed to compare the performance of the three equations. Bias was calculated by determining the eGFR value minus the mGFR value. Precision was expressed as the root mean square error (RMSE). The accuracy of each equation was defined as P30, the percentage of eGFR values within 30% deviation of the mGFR.
Paired t-test was used to compare the bias. McNemar’s test and Kappa test were employed for accuracy and classification agreement between eGFR and mGFR. The Bland–Altman method was used to evaluate the agreement between eGFR and mGFR. Additionally, correlations between eGFR and mGFR were assessed using Pearson’s correlation analysis. Area under the receiver operating characteristic (ROC) curve was used to describe the diagnostic efficacy of the equations. The cut-off for GFR stratification was <60 ml/min/1.73m2. A P-value <0.05 was considered statistically significant.
Results
This study enrolled 327 adult patients with obstructive nephropathy who had undergone a GFR measurement using 99mTc-DTPA radioisotope renography. The detailed demographic and clinical characteristics of the patients are presented in Table 2. There were 133 females and 194 males, with a mean ± SD age of 56.25 ± 14.19 years. A total of 51 of 327 (15.60%) patients had bilateral obstructions and 276 of 327 (84.40%) patients had unilateral obstructions. The main aetiology was urinary tract stones, accounting for 69.42% of the total (227 of 327 patients). The mean ± SD mGFR was 69.58 ± 21.15 ml/min/1.73m2 and the mean ± SD eGFR of the three methods were GFRmdrd 77.18 ± 33.627 ml/min/1.73 m2, GFRepi 78.50 ± 30.627 ml/min/1.73m2 and GFRfas 78.33 ± 33.17 ml/min/1.73m2. Based on the mGFR value, there were 54 (16.51%), 166 (50.76%), 97 (29.66%) and 10 (3.06%) patients with stages 1, 2, 3 and 4 CKD, respectively.
Table 2.
Demographic and clinical characteristics of patients (n = 327) with obstructive nephropathy that participated in this study to compare three equations used to estimate glomerular filtration rate (eGFR) compared with measured GFR.
| Total cohort n = 327 | Females n = 133 | Males n = 194 | |
|---|---|---|---|
| Age, years | 56.25 ± 14.19 | 56.07 ±14.20 | 56.38 ± 14.23 |
| Weight, kg | 61.85 ± 10.43 | 56.82 ± 8.41 | 65.31 ± 10.30 |
| Height, cm | 164.72 ± 7.07 | 158.95 ± 5.07 | 168.68 ± 5.32 |
| Body mass index, kg/m2 | 22.73 ± 3.12 | 22.48 ± 3.14 | 22.90 ± 3.10 |
| Body surface area, m2 | 1.77 ± 0.15 | 1.67 ± 0.12 | 1.84 ± 0.14 |
| Serum albumin, g/l | 38.07 ± 6.00 | 38.82 ± 5.34 | 37.56 ± 7.37 |
| Serum creatinine, μmol/l | 80.00 (63.10–110.10) | 64.60 (56.20–82.60) | 89.40 (73.70–128.02) |
| Serum urea nitrogen, mmol/l | 5.92 ± 3.77 | 5.13 ± 2.81 | 6.46 ± 4.22 |
| Measured GFR, ml/min/1.73m2 | 69.58 ± 21.15 | 70.41 ± 20.31 | 69.02 ± 21.74 |
| Chronic kidney disease stage | |||
| 1 | 54 (16.51) | 23 (17.29) | 31 (15.98) |
| 2 | 166 (50.76) | 70 (52.63) | 96 (49.48) |
| 3 | 97 (29.66) | 36 (27.07) | 61 (31.44) |
| 4 | 10 (3.06) | 4 (3.01) | 6 (3.09) |
Data presented as mean ± SD, median (interquartile range) and n of patients (%).
The performance of the FAS equation compared with the MDRD and CKD-EPI equations is summarized in Table 3. The FAS equation produced a higher eGFR compared with mGFR and there was an obvious positive bias of 8.7 ml/min.1.73m2, which was not significantly different to that of the CKD-EPI equation (bias, 8.9 ml/min/1.73m2), but significantly higher than that of the MDRD equation (bias, 7.6 ml/min/1.73 m2; P = 0.01). The P30 value for the FAS equation was 60.2% in the overall study cohort, a little lower than the MDRD equation, but this was not significantly different compared with the CKD-EPI equation. In terms of precision, the RMSEs showed no statistically significant difference among the three equations.
Table 3.
The performance of three different equations used to estimate glomerular filtration rate (eGFR) compared with measured GFR (mGFR) according to age and mGFR groups in patients (n = 327) with obstructive nephropathy.
| Analytical groups | mGFR, ml/min/1.73 m2 | eGFR equation | Root mean square error | Bias, ml/ min/1.73m2(95% CI) | P30, %(95% CI) | Pearson’s correlation analysis (95% CI) | Kappa |
|---|---|---|---|---|---|---|---|
| Overall study cohort | 69.58 ± 21.15 | ||||||
| MDRD | 26.0 (24.2, 28.2) | 7.6 (4.6, 10.4)a | 60.6 (54.7,65.7) | 0.672 (0.603, 0.736)* | 0.401 | ||
| CKD-EPI | 23.3 (21.7, 25.3) | 8.9 (6.7, 11.3) | 56.3 (51.1,62.1) | 0.709 (0.645, 0.766)* | 0.351 | ||
| FAS | 25.1 (23.3, 27.2) | 8.7 (6.1, 11.3) | 60.2 (55.1, 65.7) | 0.707 (0.646, 0.768)* | 0.426 | ||
| Adults 18–70 years | 72.49 ± 20.77 | ||||||
| MDRD | 26.7 (24.6, 29.1) | 7.9 (4.8, 11.25)a | 62.1 (56.3, 67.5) | 0.666 (0.585, 0.739)* | 0.390 | ||
| CKD-EPI | 23.9 (22.1, 26.1) | 9.9 (7.3, 12.5) | 56.7 (50.5, 62.5) | 0.669 (0.622, 0.769)* | 0.325 | ||
| FAS | 26.3 (24.2, 28.6) | 10.7 (7.9, 13.5) | 59.2 (53.1, 65.0) | 0.686 (0.610, 0.758)* | 0.376 | ||
| Older adults ≥70 years | 53.46 ± 15.21 | ||||||
| MDRD | 22.4 (18.7, 27.8) | 5.9 (–0.1, 12.0)a | 52.0 (38.0, 66.0) | 0.473 (0.160, 0.701)* | 0.284 | ||
| CKD-EPI | 19.8 (16.5, 24.6) | 3.5 (–2.1, 8.9)b | 54.0 (40.0, 68.0) | 0.445 (0.118, 0.685)* | 0.270 | ||
| FAS | 17.5 (14.7, 21.8) | –1.9 (–6.6, 3.1) | 66.0 (52.0, 78.0) | 0.468 (0.168, 0.706)* | 0.375 | ||
| mGFR < 60ml/min/1.73m2 | 45.49 ± 10.40 | ||||||
| MDRD | 22.3 (19.7, 25.8) | 4.5(0.4, 8.5) | 47.7 (38.3, 57.0) | 0.538 (0.393, 0.680)* | 0.117 | ||
| CKD-EPI | 22.8 (20.1, 26.3) | 5.9 (1.9, 10.6)b | 43.0 (33.6, 52.3) | 0.566 (0.403, 0.687)* | 0.093 | ||
| FAS | 20.8 (18.3, 24.0) | 4.6 (1.1, 8.8) | 53.3 (43.0, 62.6) | 0.588 (0.403, 0.685)* | 0.138 | ||
| mGFR ≥ 60ml/min/1.73m2 | 81.30 ± 13.86 | ||||||
| MDRD | 27.7 (25.3, 30.5) | 9.1 (5.5, 12.5)a | 66.8 (60.5, 72.7) | 0.417 (0.286, 0.532)* | 0.177 | ||
| CKD-EPI | 23.6 (21.6,26.0) | 10.4 (7.5, 13.2) | 62.7 (55.9, 69.1) | 0.425 (0.289, 0.533)* | 0.110 | ||
| FAS | 27.0 (24.7, 29.8) | 10.8 (7.4, 14.0) | 63.6 (57.7, 70.0) | 0.457 (0.321, 0.565)* | 0.169 |
aP < 0.05 GFRfas compared with GFRmdrd; bP < 0.05 GFRfas compared with GFRepi.
*P < 0.05 Pearson’s correlation analysis.
CI, confidence interval; MDRD, Modification of Diet in Renal Disease equation, CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration equation; FAS, full age spectrum.
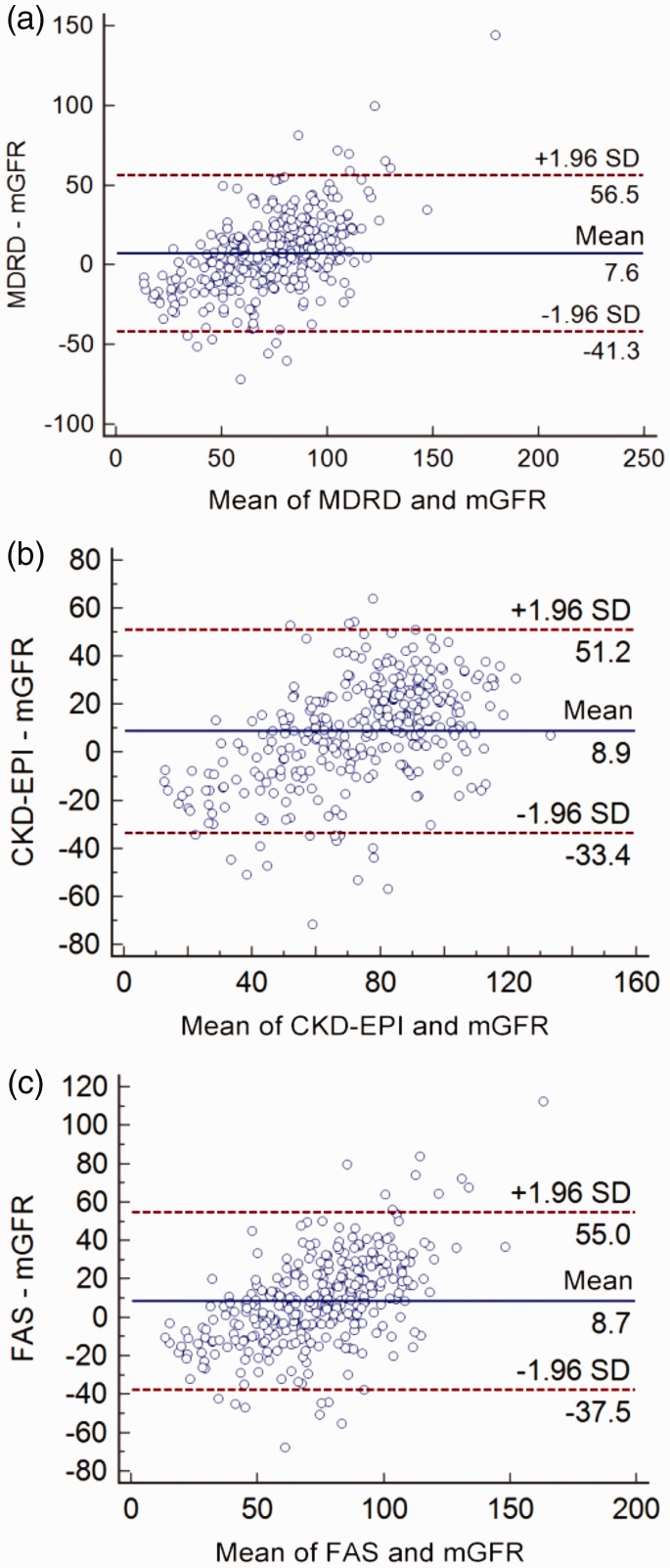
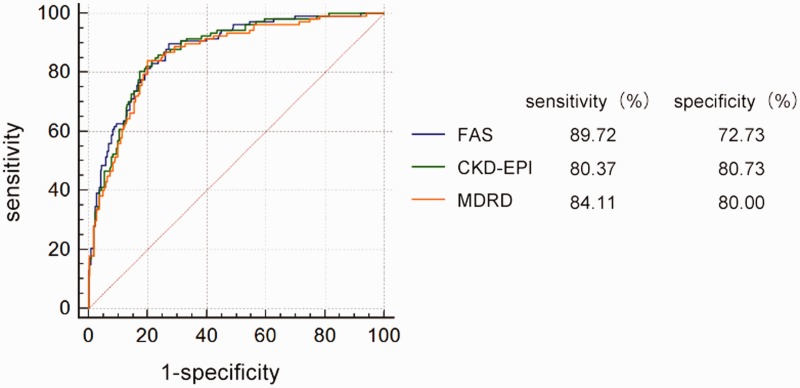
There was a significant correlation between the mGFR and eGFRfas by Pearson’s correlation analysis (r = 0.707, P <0.05). Similar correlations between mGFR and eGFR using the other two equations were observed (rmdrd = 0.672, P <0.05; repi = 0.709, P <0.05). The Bland–Altman plots of the three eGFR equations against mGFR are shown in Figure 1. Compared with mGFR, the agreement with eGFRfas (–37.5, 55.0 ml/min/1.73m2; P <0.01) and eGFRepi (–33.4, 51.2 ml/min/1.73 m2; P <0.01) was narrower than that between eGFRmdrd and mGFR (–41.3, 56.5 ml/min/1.73 m2; P <0.01). The Kappa coefficient of the FAS equation for staging consistency was 0.426 (Table 3), while the other two groups had poor agreement. Table 4 presents the diagnostic values of the three equations to identify patients with mGFR <60 ml/min/1.73 m2. The FAS equation gave the best diagnostic accuracy (ROCAUC = 0.87; 95% CI 0.84, 0.91) and was significantly superior to the MDRD equation (ROCAUC = 0.86; 95% CI 0.82, 0.89; P = 0.036; Figure 2).
Figure 1.
Bland–Altman plots of the estimated glomerular filtration rate (eGFR) and measured GFR (mGFR) for the three eGFR equations: Modification of Diet in Renal Disease (MDRD) equation (A), the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation (B) and the full age spectrum (FAS) equation (C). A positive difference in ‘eGFR – mGFR’ indicates an overestimation by the eGFR equation, whereas a negative difference indicates an underestimation. The solid lines indicate the mean difference; the dashed lines indicate the lines of agreement, calculated as the mean difference ± 1.96 SD of this difference. The colour version of this figure is available at: http://imr.sagepub.com.
Table 4.
Diagnostic measures of three different equations used to estimate glomerular filtration rate (GFR) using a cut-off of 60 ml/min/1.73m2.
| Diagnostic measures | Equations used to estimate GFR |
||
|---|---|---|---|
| MDRD | CKD-EPI | FAS | |
| AUC (95% CI) | 0.86 (0.82, 0.89)* | 0.87 (0.83, 0.91) | 0.87 (0.84, 0.91) |
| Standard error | 0.02 | 0.02 | 0.02 |
| Sensitivity, % | 84.11 | 80.37 | 89.72 |
| Specificity, % | 80.00 | 82.73 | 72.73 |
| Youden | 0.64 | 0.63 | 0.62 |
*P = 0.036 GFRfas compared with GFRmdrd.
MDRD, Modification of Diet in Renal Disease equation, CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration equation; FAS, full age spectrum; AUC, area under the curve; CI, confidence interval.
Figure 2.
Receiver operating characteristics curve analysis for the diagnostic ability of the three equations: Modification of Diet in Renal Disease (MDRD) equation, the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equation and the full age spectrum (FAS) equation. The values of the areas under the curve are listed in Table 4. The colour version of this figure is available at: http://imr.sagepub.com.
In the subgroup stratified by age (≥70 years), the FAS equation showed the lowest bias compared with mGFR with a mean difference of –1.9 (95% CI –6.6, 3.1) ml/min/1.73 m2. The value showed no statistical difference from 0, indicating that the FAS equation showed no bias in this setting (Table 3). The FAS equation was significantly superior to the other two equations in this age group in terms of bias (P <0.05 for both comparisons). The highest P30 value was 66.0% for the FAS equation, although there was no significant difference among the three equations. The precision of eGFR as calculated by the FAS equation was similar to that of the other two equations without there being a statistically significant difference in the RMSEs. There was poor consistency between eGFRfas and mGFR based on the correlation and the Kappa values, which were similar to the other eGFR equations.
In the subgroup stratified by mGFR (<60 ml/min/1.73 m2), the FAS equation had a significantly lower bias compared with the eGFRepi equation (P = 0.009). In terms of P30 accuracy and RMSE precision, these were highest with the FAS equation, but there were no significant differences between the three equations. As for the Kappa values, there was a poor staging consistency between eGFRfas and mGFR values.
Discussion
It is necessary to periodically monitor kidney function using convenient and accurate methods in order to facilitate an early diagnosis of kidney problems and to improve patient outcomes.4 This current study demonstrated that the FAS equation was nearly equivalent to the MDRD and CKD-EPI equations in terms of bias, accuracy and precision, and also positively correlated with the mGFR. The FAS equation gave the best diagnostic efficiency among the three equations. Especially in older patients and patients with GFR <60ml/min/1.73 m2, the FAS equation was superior to the other two equations in terms of bias and it was as good in other aspects.
Until now, over 10 equations to estimate the GFR have been developed. The MDRD and CKD-EPI equations are the most widely used equations worldwide.12 A previous study suggested that the MDRD and CKD-EPI equations were validated to estimate GFR in patients with obstructive nephropathy, despite the pathogenetic, pathological and physiological changes associated with obstructive nephropathy being different from those in diffuse renal diseases.2 In 2016, a novel eGFR equation, the FAS equation, was developed based on the concept of population-normalized serum creatinine, denoted as SCr/Q.8 To the best of our knowledge, this current study is the first to compare the FAS equation with the CKD-EPI and MDRD equations in the patients with obstructive nephropathy in China.
Bias, precision and accuracy are the most important indicators to evaluate the validity of the method used to determine the GFR.13 In this current study, the values of these indices for the MDRD and CKD-EPI equations were consistent with those demonstrated previously.2 The FAS equation was nearly equivalent to the other two equations in terms of bias, accuracy and precision. And among these three equations, the FAS equation gave the best diagnostic efficiency, significantly surpassing the MDRD equation.
In the subgroup of older patients (≥ 70 years), the mean bias of the FAS equation was nearest to zero and lower than that of the MDRD and CKD-EPI equations. The FAS equation showed the highest accuracy and precision compared with the MDRD and CKD-EPI equations, although without reaching a statistically significant difference. This finding was consistent with previous research that validated the FAS equation in 14 databases.8 Some studies demonstrated that the MDRD and CKD-EPI equations were not very suitable for elderly patients.14,15 These current findings suggest that the FAS equation may be suitable for older patients with obstructive nephropathy.
The agreement and staging consistency between eGFRfas and mGFR were not ideal. The kappa value was only 0.426 in the overall study cohort and it was poorer in the subgroups stratified by age or mGFR. The agreement between eGFRfas and mGFR was wider than that between eGFRepi and mGFR, but narrower than that between eGFRmdrd and mGFR, with all exceeding the acceptable limits of consistency defined as ± 30 ml/min/1.73m2 among these three equations. This result was consistent a previous study that validated the FAS equation in diffuse renal disease.11 All of these findings suggest that the FAS equation may not be ideal for the direct estimation of GFR in the patients with obstructive nephropathy in China. However, in adults and the older subgroups, the previous study demonstrated that the FAS equation showed a higher accuracy rate in correctly classifying subjects into matched GFR categories than that of CKD-EPI equation with a statistical difference.8
The possible reasons of these differences might be as follows: (i) an appropriate Q-value for the FAS equation is crucial. The Q-value for the FAS equation was derived from a Belgian population,16 which was lower than that of Korean males;9 (ii) in addition, the performance of the eGFR equation could be improved by using coefficients specific for local ethnic groups.7,17 Therefore, it is better to obtain the Q-value of the serum creatinine specifically for different ethnicities;18 (iii) the only aetiology was obstructive nephropathy in this current study, which was different to a previous study,8 in which the main aetiology was diffuse renal diseases; (iv) the difference in the serum creatinine measuring methods and the different reference measurements should be taken into consideration when evaluating the different equations. In this current study, serum creatinine was measured using an enzymatic assay, rather than using an isotope dilution mass spectrometry traceable creatinine method; (v) mGFR was obtained using 99 mTc-DTPA radioisotope renography in this current study, while iothalamate was applied for the CKD-EPI equation,19 and iohexol, inulin and iothalamate measurements were used for the FAS equation.8
This current study had several limitations. First, the study population was from a single centre with a small sample size and with no patients at with stage 5 CKD, so the study cohort is not representative of the general population. Secondly, the study did not estimate eGFR using the cystatin C equation or the combination of plasma creatinine and cystatin C, which may be more reliable predictors of GFR.
In conclusion, despite the drawbacks associated with each eGFR equation, the FAS equation was probably closer to the measured GFR in patients with obstructive nephropathy.
Acknowledgements
We would like to thank Professor Chang-Zheng Dong from Ningbo University School of Medicine, Ningbo, China for his assistance with the statistical analyses.
Declaration of conflicting interest
The authors declare that there are no conflicts of interest.
Funding
This study was supported by the Medical Scientific Research Foundation of Zhejiang Province, China (2019KY174).
References
- 1.Klahr S. Obstructive nephropathy. Intern Med 2000; 39: 355–361. [DOI] [PubMed] [Google Scholar]
- 2.Chen MX, Xia JM, Pei GC, et al. A more accurate method acquirement by a comparison of the prediction equations for estimating glomerular filtration rate in Chinese patients with obstructive nephropathy. BMC Nephrol 2016; 17: 150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Klahr S, Morrissey J. Obstructive nephropathy and renal fibrosis. Am J Physiol Renal Physiol 2002; 283: F861–F875. [DOI] [PubMed] [Google Scholar]
- 4.Stevens LA, Coresh J, Greene T, et al. Assessing kidney function – measured and estimate glomerular filtration rate. N Eng J Med 2006; 354: 2473–2483. [DOI] [PubMed] [Google Scholar]
- 5.National Kidney Foundation. K/DOQI clinical practice guidelines for chronic kidney disease: evaluation, classification, and stratification. Am J Kidney Dis 2002; 39: S1–S266 [PubMed] [Google Scholar]
- 6.Xie P, Huang JM, Lin HY, et al. CKD-EPI equation may be the most proper formula based on creatinine in determining glomerular filtration rate in Chinese patients with chronic kidney disease. Int Urol Nephrol 2013; 45: 1057–1064. [DOI] [PubMed] [Google Scholar]
- 7.Earley A, Miskulin D, Lamb EJ, et al. Estimating equations for glomerular filtration rate in the era of creatinine standardization: a systematic review. Ann Intern Med 2012; 156: 785–795. [DOI] [PubMed] [Google Scholar]
- 8.Pottel H, Hoste L, Dubourg L, et al. An estimated glomerular filtration rate equation for the full age spectrum. Nephrol Dial Transplant 2016; 31: 798–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jeong TD, Cho EJ, Lee WC, et al. Accuracy assessment of five equations used for estimating the glomerular filtration rate in Korean adults. Ann Lab Med 2017; 37: 371–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kidney Disease: Improving Global Outcomes (KDIGO) CKD Work Group. KDIGO 2012 clinical practice guideline for the evaluation and management of chronic kidney disease. Kidney Int Suppl 2013; 3: 1–150. [Google Scholar]
- 11.Chai L, Wang M, Cai K, et al. Full age spectrum equation may be an alternative method to estimate the glomerular filtration rate in Chinese patients with chronic kidney disease. Clin Nephrol 2018; 89: 413–421. [DOI] [PubMed] [Google Scholar]
- 12.Matsushita K, Mahmoodi BK, Woodward M, et al. Comparison of risk prediction using the CKD-EPI equation and the MDRD study equation for estimated glomerular filtration rate. JAMA 2012; 307: 1941–1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lee CK, Swinford RD, Cerda RD, et al. Evaluation of serum creatinine concentration-based glomerular filtration rate equation in pediatric patients with chronic kidney disease. Pharmacotherapy 2012; 32: 642–648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Changjie G, Xusheng Z, Feng H, et al. Evaluation of glomerular filtration rate by different equations in Chinese elderly with chronic kidney disease. Int Urol Nephrol 2017; 49: 133–141. [DOI] [PubMed] [Google Scholar]
- 15.Tarantini L, McAlister FA, Barbati G, et al. Chronic kidney disease and prognosis in elderly patients with cardiovascular disease: comparison between CKD-EPI and Berlin Initiative Study-1 formulas. Eur J Prev Cardiol 2016; 23: 1504–1513. [DOI] [PubMed] [Google Scholar]
- 16.Hoste L, Dubourg L, Selistre L, et al. A new equation to estimate the glomerular filtration rate in children, adolescent and young adults. Nephrol Dial Transplant 2014; 29: 1082–1091. [DOI] [PubMed] [Google Scholar]
- 17.Stevens LA, Claybon MA, Schmid CH, et al. Evaluation of the chronic kidney disease epidemiology collaboration equation for estimating the glomerular filtration rate in multiple ethnicities. Kidney Int 2011; 79: 555–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pottel H, Hoste L, Delanaye P, et al. Demystifying ethnic/sex differences in kidney function: is the difference in (estimating) glomerular filtration rate or in serum creatinine concentration? Clin Chim Acta 2012; 413: 1612–1617. [DOI] [PubMed] [Google Scholar]
- 19.Levey AS, Stevens LA, Schmid CH, et al. A new equation to estimate glomerular filtration rate. Ann Intern Med 2009; 150: 604–612. [DOI] [PMC free article] [PubMed] [Google Scholar]