Adversarial Learning of Knowledge Embeddings for the Unified Medical Language System

Abstract

Incorporating the knowledge encoded in the Unified Medical Language System (UMLS) in deep learning methods requires learning knowledge embeddings from the knowledge graphs available in UMLS: the Metathesaurus and the Semantic Network. In this paper we present a technique using Generative Adversarial Networks (GANs) for learning UMLS embeddings and showcase their usage in a clinical prediction model. When the UMLS embeddings are available, the predictions improve by up to 6.9% absolute F₁ score.

Introduction

Deep learning techniques have shown great promise in representing patient data from Electronic Health Records (EHRs), facilitating Big Data methods for clinical predictive modeling, as evidenced by Deep Patient¹. More recently, scalable and accurate deep learning methods² were capable of predicting multiple medical events from multiple centers without site-specific data harmonization. Deep learning methods have the advantage that they can easily handle large volumes of data extracted from EHRs, learning key features or patterns from the data, as well as their interactions. The data input of deep learning techniques takes the form of low-dimensional vector representations, also called embeddings, which need to be learned from the EHR data. For example, when considering only the medical concepts from clinical narratives available in the EHR, methods for learning their embeddings were presented in Choi et al. (2016)³ and compared with medical concept embeddings produced from medical journals or medical claims. Alternatively, medical concept embeddings were obtained in Beam et al. (2018)⁴ by first mapping the concepts into a common concept unique identifier space (CUI) using the thesaurus from the Unified Medical Language System (UMLS)⁵, producing the cui2vec embeddings. As noted in Choi et al. (2016)³, learning these forms of embeddings relies on the context in which the medical concepts are mentioned, reflecting the medical practice. However, in addition to their usage in various contexts throughout the EHRs, medical concepts are also organized and encoded in the Unified Medical Language System (UMLS)⁵, comprising the Metathesaurus and the Semantic Network.

Each concept encoded in the UMLS Metathesaurus has specific attributes defining its meaning and is linked to the corresponding concept names in various source vocabularies (e.g. ICD-10). Moreover, several types of relations connect concepts, e.g. “Is-A”, “Is-Part” or “Is caused by”. Moreover, each concept from the Metathesaurus is assigned one or more semantic types (or categories), which are linked with one another through semantic relationships. The UMLS Semantic Network is a catalog of these semantic types (e.g. “anatomical structure” or “biological function”) and semantic relationships between them (e.g. ”spatially related to” or ”functionally related to”). While there are over 3 million concepts in the UMLS Metathesaurus, there are only 180 semantic types and 49 semantic relationships in the UMLS Semantic Network. The UMLS Metathesaurus graph along with the UMLS Semantic Network graph encode a wealth of medical knowledge, capturing ontological and biomedical expertise which could also be used by deep learning methods, in addition to the concept embeddings derived from the EHRs. To enable the usage of the knowledge encoded in UMLS in deep learning methods, we need to learn knowledge embeddings which represent (1) the UMLS concepts; (2) the relations between UMLS concepts; (3) the nodes of the UMLS Network, representing the semantic types assigned to concepts; and (4) the semantic relations shared between the nodes of the UMLS Semantic Network (i.e. the semantic types).

There have been several models for learning knowledge graph embeddings proposed in the past years, which represent the concepts and relations from a knowledge graph as vectors: RESCAL⁶, which produces knowledge embeddings by using matrix factorization; TRANSE⁷ - producing translation-based knowledge embeddings; TRANSD⁸, which extended TRANS E by dynamically projecting the concept embeddings into various spaces; DISTMULT⁹, which simplifies RESCAL by using a diagonal matrix and more recently KBGAN¹⁰, which uses adversarial learning to produce knowledge embeddings. The structure of the UMLS knowledge encoding poses a challenge to the applicability of any of these models of learning knowledge embedding, which assume a single knowledge graph, while UMLS encodes two different and jointly connected graphs, namely (a) the UMLS Metathesaurus; and (b) the UMLS Semantic Network. In this paper we present an extension of the KBGAN model capable of learning UMLS knowledge embeddings representing concepts, relations between them, semantic types and semantic relations.

To showcase the impact of using UMLS knowledge embeddings, we have considered the task of building a predictive model based on deep learning for discovering (1) the incidence of opioid use disorders (OUD) after onset of opioid therapy and (2) chronic opioid therapy (COT) achievement and persistence. OUD is defined as a problematic pattern of opioid use that causes significant impairments or distress. Addiction and dependence of opioids are components of OUD. OUD is part of the current opioid use epidemic, which is among the most pressing public health issues in the United States. Opioid related poisonings and deaths have increased at alarming rates since 2014. This epidemic has urged a national call to action for healthcare systems to invest in surveillance, prevention, and treatment of OUD. Moreover, long-term opioid therapy poses a much higher risk of OUD and other adverse outcomes. In 2014, US retail pharmacies dispensed 245 million prescriptions for opioid pain relievers. Of these prescriptions 65% were for short term therapy (< 3 weeks). However, 3-4% of the adult population (9.6-11.5 million patients) were prescribed longer term (> 90 days) opioid therapy. Our predictive model for discovering the incidence of OUD after onset of opioid therapy and COT achievement and persistence uses a deep learning architecture based on hierarchical attention. We produced superior predictions when the model was informed by the UMLS knowledge embeddings generated with the methodology presented in this paper. We have made both the learned UMLS knowledge embeddings and the knowledge embedding learning methodology publicly available†.

Data

In addition to the data available from UMLS, we have used a large clinical dataset that enabled us to use the UMLS embeddings for predicting the incidence of OUD after onset of opioid therapy and COT achievement and persistence. This clinical dataset was available from the University of Washington Medical Center and Harborview Medical center. For this dataset, we considered adult patients (age ≥ 18 years), eligible in this study if they were prescribed with COT for chronic non-cancer pain between 2011-2017 (7 years). We defined COT as 45+ days supply of opioid analgesics in a calendar quarter (3 months) for at least one quarter within the 7-year time range. As such COT achievement occurs when the conditions for COT are first noted while COT persistence is observed when a patient continues to be prescribed a 45+ days supply of opioid analgesics in consecutive quarters. With the described inclusion/exclusion criteria, we created a cohort of 6355 patients receiving COT with a total of 23,945 COT quarters (avg:3.77, min:1, max:27). There were 3446 patients (54%) with 1 COT quarter, 1856 patients (29%) with 2-5 COT quarters, 420 patients (6.6%) with 6-10 COT quarters, and 680 patients (10.7%) with >10 COT quarters. A longitudinal dataset was created for the selected patients. We collected both structured clinical data and unstructured patient notes created during their treatments between 2008-2017 (10 years), but in this paper we used only structured data, namely we used the ICD-10 codes, the medication ordered and the laboratory results, which we also mapped into UMLS. We extended the data range to 10 years to capture a wider range of background clinical data. Our dataset contained 1,089,600 outpatient, 20,449 inpatient, and 25,232 emergency department visits. For structured data, we collected basic demographics (age, gender, ethnicity), hospital administrative data (to capture the nature of each visit), laboratory and test orders (for illicit drug abuse screen and opioid confirmation), medications (both administered and ordered), billing diagnoses, physician diagnoses, and problem lists. The dataset contained around 14 million data elements and each data element had a time-stamp to capture patient trajectories through time. In future work, we plan to use the entire structured and unstructured data. The retrospective review of the described de-identified longitudinal dataset has been approved by University of Washington Institutional Review Board as well as the University of Texas at Dallas Institutional Review Board.

Methods

Learning UMLS Knowledge Embeddings: When learning knowledge embeddings for knowledge bases represented as graphs, we have represented multi-relational data corresponding to concepts (i.e. nodes in the knowledge graph) and relations (i.e. edges in the knowledge graph) by modeling concepts as points in a continuous vector space, ℝ^d, called the embedding space, where d is a parameter indicating the dimensionality of the embedding space. In our previous work¹¹, we relied on the TransE⁷ method which represents relations between medical concepts also in ℝ^d. TransE, like all knowledge embedding models, learns an embedding, $\overrightarrow{c_i}$, for each concept c_i encoded in the knowledge graph and an embedding, $\overrightarrow{r}$, for each relation type r. TransE considers that the relation embedding is a translation vector between the two concept embeddings representing its arguments. This means that for any concept c_i, the concept most likely to be related to c_i by the relation r should be the concept whose embedding is closest to ($\overrightarrow{c_i}+\overrightarrow{r}$) in the embedding space. By modeling the concepts as points in the embedded space and the relations between them as translation vectors, it is possible to measure the plausibility of any potential relation between any pair of medical concepts using the geometric structure of the embedding space: $f(c_s,r,c_d)=\left|\right|\overrightarrow{c_s}+\overrightarrow{r}-\overrightarrow{c_d}|{|}_{L_1}$ where || · ||_L1 is the L1 norm. The plausibility of a relation between a source medical concept and a destination medical concept, represented as a triple, ⟨c_s, r, c_d⟩, is inversely proportional to the distance in the embedding space between the point predicted by the TransE model $(\overrightarrow{c_s}+\overrightarrow{r})$ and the point in the embedding space representing the destination argument of the relation, i.e. ($\overrightarrow{c_d}$). In addition to TransE, several other knowledge graph embedding models, which represent concepts and relations as vectors or matrices in an embedding space, have shown promise in recent years. We list in Table 1 two additional models that we have used when learning UMLS embeddings. TransD⁸ learns two embedding vectors for each concept in a knowledge graph: $[\overrightarrow{c},\overrightarrow{c_p}]$ as well as two embeddings for each relation in the graph: $[\overrightarrow{r},\overrightarrow{r_p}]$, where the first vector represents the “knowledge meaning” of the concept or relation while the second vector is a projection vector (with subscript p), used to construct a dynamic mapping matrix for each concept/relation pair. If the knowledge meaning of a concept or relation refers to the reason why the concept or relation was encoded in the knowledge graph, the projection of concepts in the space of the relations is used to capture the interaction between concepts participating in relations and relations holding various concepts as arguments. Essentially, TransD constructs a dynamic mapping matrix for each entity-relation pair by considering the diversity of entities and relations simultaneously. As each source concept c_s is translated into a pair $[\overrightarrow{c_s},\overrightarrow{c_{sp}}]$ and each destination concept is translated into a pair $[\overrightarrow{c_d},\overrightarrow{c_{dp}}]$, while the relation between them is translated into $[\overrightarrow{r},\overrightarrow{r_p}]$, the plausibility of the relation is measured by the scoring function listed in Table 1. DistMult⁹, another knowledge embedding model, is a simplification of the traditional bilinear form of matrix decomposition using only a diagonal matrix that has been shown to excel for probabilistic models. Its scoring function, listed in Table 1, is equivalent to the dot product between the vector representations of the source concept, the relation and the destination concept. Any of these scoring functions can be used for (a) assigning a plausibility score to each triple ⟨c₁, r, c₂⟩, encoding a relation between a pair of concepts from the UMLS Metatheraurus; as well as (b) assigning another plausibility score to each triple ⟨t₁, sr, t₂⟩ encoding semantic relationships (sr) between semantic types (t₁, t₂) encoded in the UMLS Semantic Network. However, from the learning standpoint, training the embeddings models requires positive examples encoded in the knowledge graph (in our case UMLS), and negative examples obtained by removing either the correct source or destination concept (or semantic type) and replacing it with a concept (or semantic type) randomly sampled from a uniform distribution. As noted in Cai and Wang (2018)¹⁰, this approach of generating negative examples is not ideal, because the sampled concept (or semantic type) may be completely unrelated to the source UMLS concept (or source UMLS semantic type), resulting in a learning framework using too many obviously false examples. To address this challenge, we have extended the KBGAN¹⁰ adversarial learning framework, which is currently one of the state-of-the-art learning methods for knowledge embeddings.

Table 1:

Scoring functions used in models that learn knowledge embeddings. I is the identity matrix.

Model	Scoring Function
TRANSE	${\Vert {\overrightarrow{c}}_s+\overrightarrow{r}-{\overrightarrow{c}}_d\Vert }_{L1}$
TRANSD	$\begin{array}{c}\Vert \left(I+{\overrightarrow{r}}_p\times \overrightarrow{c_{sp}{}^T}\right)\times \overrightarrow{c_s}+\overrightarrow{r}\\ {-\left(I+\overrightarrow{r_p}\times \overrightarrow{c_{dp}{}^T}\right)\times \overrightarrow{c_d}\Vert }_{L1}\end{array}$
DISTMULT	${{\displaystyle {\sum }_i\overrightarrow{c}}}_s{}^i\cdot \overrightarrow{r^i}\cdot \overrightarrow{c_d{}^i}$

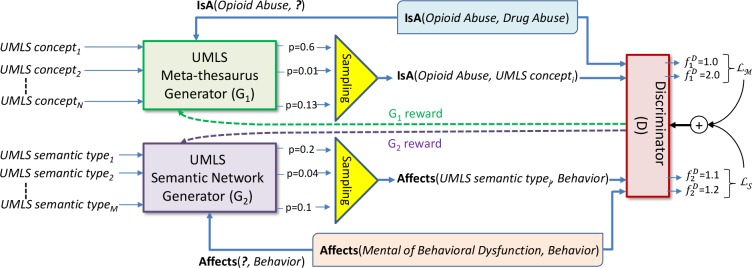
Generative Adversarial Networks (GANs) are at the core of our framework for learning knowledge embeddings for UMLS. GANs typically use a generator and a discriminator, as introduced in Goodfellow et al. (2014)¹². Metaphorically, the generator can be thought of as acting like a team of counterfeiters, trying to produce fake currency and use it without detection. The discriminator can be thought of as acting like the police, trying to detect the counterfeit currency. Competition in this game enabled by the GAN drives both teams to improve their methods until the counterfeiters are indistinguishable from the genuine articles. In the KBGAN¹⁰ framework, the discriminator learns to score the plausibility of a given relation triple and the generator tries to fool the discriminator by generating plausible, yet incorrect, triples. In order to accomplish this goal, the generator calculates a probability distribution over a set of negative examples of relation triples and then samples one triple from the distribution as its output. However, a single generator is not sufficient for creating UMLS embeddings, because the UMLS graph contains two types of relations, namely (1) relations between UMLS concepts and (2) semantic relations between UMLS semantic types. Therefore, we extended the KBGAN by using two different generators: an UMLS Metathesaurus generator G₁ and an UMLS Semantic Network generator G₂, as illustrated in Figure 1. Given any relation between two concepts encoded in the UMLS Metathesaurus, G_i calculates the probability distribution over a set of candidate negative examples of the relation, samples it and produces a negative example. Given the ground truth relation triple R₁ =IsA (Opioid Abuse, Drug Abuse) from the Metathesaurus G₁ will produce the negative example $R_1^N=IsA$(Opioid Abuse, UMLS concept_i), as illustrated in Figure 1, where UMLS concept_i is any UMLS concept which is not in an IsA relation with Opioid Abuse. Similarly, given a ground truth semantic relation triple R₂ = Affects(Mental or Behavioral Dysfunction, Behavior), G₂ generates the negative example, $R_2^N=Affects$(UMLS Semantic Type_j, Behavior) where UMLS Semantic Type_j is not in an Affects relation with UMLS semantic type Behavior. Both negative examples generated by G₁ and G₂ are sent to the Discriminator D along with the two ground truth relation triples: R₁ and R₂, respectively. D uses the function $f_1^D$ to compute the scores for R₁ and $R_1^N$ while it uses the function $f_2^D$ to compute the scores for R₂ and $R_2^N$. Both for $f_1^D$ and $f_2^D$ we experimented with two alternatives: (1) the scoring function of TransE, and (2) the scoring function of TransD, listed in Table 1.

Figure 1:

Adversarial Learning Framework for Producing Knowledge Embeddings for UMLS.

Intuitively, the discriminator D should assign low scores produced by the functions $f_1^D$ and $f_2^D$ to high-quality negative samples generated by G₁, and G₂ respectively. Moreover, the discriminator D should assign even lower $f_1^D$ and $f_2^D$ scores to the ground truth triples than to the high-quality negative samples. Suppose that G₁ produces a distribution of negative triples p_G1 (c₁’, r, c₂’|c₁, r, c₂) for a positive example ⟨c₁, r, c₂⟩ encoded in the UMLS Metathesaurus and generates ⟨c₁’, r, c₂’⟩ by sampling from this distribution. Similarly, suppose that G₂ produces a distribution of negative triples p_G2 (t₁’, sr, t₂’|t₁, sr, t₂) for a positive example ⟨t₁, sr, t₂⟩ encoded in the UMLS Semantic Network. Let $f_1^D$ and $f_2^D$ be the two scoring functions of D. Then the objective of the discriminator is to minimize the marginal loss between the ground truth (or positive) triples and the negative example triples generated by G₁ and G₂. To jointly minimize the marginal loss of D, we extend the marginal loss function of KBGAN¹⁰ to have two terms: (i) the Metathesaurus loss function, ${\mathcal{L}}_M$ and (ii) the Semantic Network loss function ${\mathcal{L}}_S$. We defined ${\mathcal{L}}_M$ as:

$${\mathcal{L}}_M={\displaystyle \sum _{\langle c_1,r,c_2\rangle \in \mathcal{M}}\left|\right|f_1^D(c_1,r,c_2)-f_1^D(c_1{}^{\prime },r,{c^{\prime }}_2)+{\gamma }_1\left|\right|}$$ (1)

where $\mathcal{M}$ represents all valid triples from the Metathesaurus, while $f_1^D(c_1,r,c_2)$ measures the plausibility of the triple ⟨c₁, r, c₂⟩ and γ₁ is a margin hyper-parameter. We defined ${\mathcal{L}}_S$ as:

$${\mathcal{L}}_S={\displaystyle \sum _{\langle t_1,sr,t_2\rangle \in \mathcal{S}}\left|\right|f_2^D(t_1,sr,t_2)-f_2^G(t_1{}^{\prime },sr,t_2{}^{\prime })+{\gamma }_2\left|\right|}+{\displaystyle \sum _i\left[\overrightarrow{t_i}-\frac{1}{|\delta (t_i)|}\times {\displaystyle \sum _{c\in \delta (t_i)}c}\right]}$$ (2)

where S represents all valid triples from the UMLS Semantic Network, while $f_2^D(t_1,sr,t_2)$ measures the plausibility of the triple ⟨t₁, sr, t₂⟩ from the UMLS Semantic Network expressing the semantic relation sr between the semantic types t₁ and t₂ in the UMLS Semantic Network and γ₂ is a margin hyper-parameter. The embedding of the UMLS semantic type t_i is denoted by $\overrightarrow{t_i}$ and δ(t_i) represents the set of UMLS concepts having the semantic type t_i. In this way, the centroid of the embeddings of UMLS concepts having the UMLS semantic type t_i is represented as $1/\delta (t_i)\times {\displaystyle {\sum }_{c\in \delta (t_i)}c}$. This allows us to measure in ${\mathcal{L}}_S$ not only the margin between the semantic relation produced by G₂ to the ground truth semantic relation encoded in the UMLS Semantic Network, but also the cumulative distance between the embeddings of each semantic type t_i and the centroid of the embeddings corresponding to the UMLS concepts sharing the semantic type t_i. Hence, ${\mathcal{L}}_S$ measures the loss of (a) not correctly recognizing a plausible semantic relation from the UMLS Semantic Network, but also (b) the loss of not recognizing plausible semantic types in the UMLS Semantic Network, given as reference all the UMLS semantic concepts that share same semantic type. This ensures that we learn embeddings of semantic relations from UMLS by taking into account the semantic types and the concepts that are encoded in UMLS.

In the adversarial framework presented in Figure 1, the objective of generator G₁ is to maximize the following expectation:

$${\mathcal{R}}_{G_1}={\displaystyle \sum _{\langle c_1,r,c_2\rangle \in \mathcal{M}}\mathbb{E}[-f_1^D(c_1{}^{\prime },r,c_2{}^{\prime })](c_1{}^{\prime },r,c_2{}^{\prime })~p_{G_1}(c_1{}^{\prime },r,c_2{}^{\prime }|c_1,r,c_2)}$$ (3)

Similarly, the objective of generator G₂ is to maximize the following expectation:

$${\mathcal{R}}_{G_2}={\displaystyle \sum _{\langle t_1,sr,t_2\rangle \in \mathcal{S}}\mathbb{E}[-f_2^D(t_1{}^{\prime },sr,t_2{}^{\prime })](t_1{}^{\prime },sr,t_2{}^{\prime })~p_{G_2}(t_1{}^{\prime },sr,t_2{}^{\prime }|t_1,sr,t_2)}$$ (4)

Both G₁ and G₂ involve a sampling step, to find the gradient of R_G1 and R_G2 we used a special case of the Policy Gradient Theorem¹³, which arises from reinforcement learning (RL). To optimize both R_G1 and R_G2, we maximized the reward returned by the discriminator to each generator in response to selecting negative examples for the relations encoded in UMLS, providing an excellent framework for learning the UMLS embeddings that beneits from good negative examples in addition to the abundance of positive examples. Finally, both generators G₁ and G₂ need to have scoring functions, defined as f_G1 (c₁, r, c₂) and f_G2 (t₁, sr, t₂). Several scoring function can be used, selecting from those that have been implemented in several knowledge graph embeddings, listed in Table 1. In our implementation, we have used for both generators the same scoring function as the one used in DIST MULT. Then given a set of candidate negative examples for the UMLS Metathesaurus: $Ne{g}^{\mathcal{M}}(c_1,r,c_2)=\{\langle c_1{}^{\prime },r,c_2\rangle |c_1{}^{\prime }\in \mathcal{C}\}\cup \{\langle c_1,r,c_2{}^{\prime }\rangle |c_2{}^{\prime }\in \mathcal{C}\}$ (where $\mathcal{C}$ represents all the concepts encoded in the UMLS Metathesaurus), the probability distribution p_G1 is:

$$p_{G_1}(c_1{}^{\prime },r,c_2{}^{\prime }|c_1,r,c_2)=\frac{\exp (f_{G_1}(c_1{}^{\prime },r,c_2{}^{\prime }))}{{\displaystyle {\sum }_{\langle c_1^{*},r,c_2^{*}\rangle \in Ne{g}^{\mathcal{M}}}\exp (f_{G_1}(c_1^{*},r,c_2^{*}))}}$$ (5)

Similarly, given a set of candidate negative examples for the UMLS Semantic Network $Ne{g}^{\mathcal{S}}(t_1,sr,t_2)=\{\langle t_1{}^{\prime },sr,t_2\rangle |t_1{}^{\prime }\in \mathcal{T}\}\cup \{\langle t_1,sr,t_2{}^{\prime }\rangle |t_2{}^{\prime }\in \mathcal{T}$ (where $\mathcal{T}$ represents all the semantic types encoded in the UMLS Semantic Network), then the probability distribution p_G2 is modeled as:

$$p_{G_2}(t_1{}^{\prime },sr,t_2{}^{\prime }|t_1,sr,t_2)=\frac{\exp (f_{G_2}(t_1{}^{\prime },sr,t_2{}^{\prime }))}{{\displaystyle {\sum }_{\langle t_1^{*},sr,t_2^{*}\rangle }\exp (f_{G_2}(t_1^{*},sr,t_2^{*}))}}$$ (6)

In this adversarial training setting, the generators G₁ and G₂ and the discriminator D are alternatively trained towards their respective objectives, informing the two forms of embeddings for the UMLS: knowledge embeddings for the UMLS Metathesaurus and knowledge embeddings for the UMLS Semantic Network.

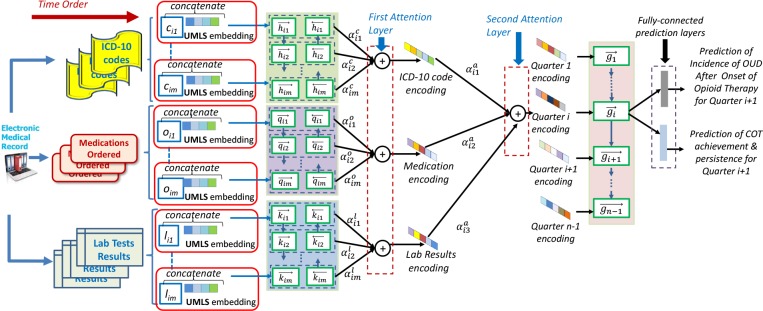
Using the UMLS Knowledge Embeddings in Clinical Prediction Models: In previous work¹⁴ we developed a model for predicting (1) the incidence of Opioid Use Disorders (OUD) after onset of opioid therapy and (2) Chronic Opioid Therapy (COT) achievement and persistence, which benefits from a deep learning method using a hierarchical attention mechanism. The predictive model was trained and tested on the clinical database from the University of Washington Medical Center and Harborview Medical center, described in the Data Section. Because we used a deep learning method for the predictions, as illustrated in Figure 2, we needed to generate embeddings to represent ICD-10 codes, medications ordered and laboratory results. To produce these embeddings, we considered that if a patient had records spanning N quarters, each having at most M different diagnostic codes assigned during the quarter, we could denote each diagnostic code as d_it, to represent the t-th ICD-10 code in the i-th quarter, with i ∈ [1, N]. To encode each diagnostic code d_it as a low-dimensional vector c_it (also called ICD-10 code embedding) we compute: $c_{it}=\mathbb{Q}\times d_{it}$, with t ∈ [1, M], in which ℚ represents the embedding matrix obtained from WORD2VEC¹⁵. As shown in Figure 2, each ICD-10 code embedding was concatenated with an UMLS knowledge embedding, such that the knowledge from clinical practice (ICD-10 code WORD 2VEC embeddings) can be combined with complementary knowledge, available from the UMLS ontology. The concatenation of UMLS knowledge embeddings was informed by the mapping of the ICD-10 vocabulary into UMLS concepts proved by the UMLS. We were then able to encode this combined knowledge representation pertaining to diagnoses and their ICD-10 codes as well as UMLS concepts representing them using a Recurrent Neural Network (RNN), implemented with bi-directional gated-recurrent units (GRUs). More speciically, for each concatenated embedding cc_it, we computed two vectors: (1) $\overrightarrow{h_{it}}=\overrightarrow{GRU}(c{c}_{it}))$ for t ∈ [1, M]; and (2) $\overleftarrow{h_{it}}=\overleftarrow{GRU}(c{c}_{it})$, for t ∈ [M, 1]; generating the encoding $x_{it}=[\overrightarrow{h_{it}},\overleftarrow{h_{it}}]$. Similarly, we computed the encodings of medications ordered o_it and of laboratory results l_it using the same type of RNNs as we did for ICD-10 codes. These encodings were also concatenated with corresponding UMLS embeddings. The medications and laboratory results are mapped to UMLS concepts using MetaMap Lite¹⁶. For the concatenated encodings of medications ordered o_it with UMLS embeddings, denoted oo_it, embeddings for medications were produced using again bi-directional GRUs as: $y_{it}=[\overrightarrow{q_{it}},\overleftarrow{q_{it}}]$, where $\overleftarrow{q_{it}}=\overrightarrow{GRU}(o{o}_{it})$ and $\overleftarrow{h_{it}}=\overleftarrow{GRU}(o{o}_{it})$. When concatenating the encodings of laboratory results l_it with UMLS embeddings, denoted ll_it, the bi-directional GRUs generated embeddings for laboratory results: $z_{it}=[\overrightarrow{k_{it}},\overleftarrow{k_{it}}]$, where $\overrightarrow{k_{it}}=\overrightarrow{GRU}(l{l}_{it})$ and $\overleftarrow{k_{it}}=\overleftarrow{GRU}(l{l}_{it})$. In addition, since not all ICD-10 codes, medications or laboratory results contribute equally to the clinical picture of the patient, we introduce an attention mechanism, that enables the predictive model to pay more attention to the more informative ICD-10 codes, medications and laboratory test results. Attention mechanisms are a new trend in deep learning, loosely based on visual attention mechanisms in humans, that have been successfully used in caption generation¹⁷ and medical predictions^18,19. In our predictive model, illustrated in Figure 2, we used a form of hierarchical attention mechanism, inspired by the work of Yang et al. (2016)²⁰. The first layer of attention learned how each of the combinations of ICD-10 codes and corresponding UMLS embeddings, ordered medications and corresponding UMLS embeddings and laboratory test results and corresponding UMLS embeddings contribute to the predictions and how to pay more attention to the more impactful ones. In the case of ICD-10 code embedding, attention is learned through the following equations: $u_{it}=tanh(W_c\times x_{it}+b_c)$; ${\alpha }_{it}^c=\exp (u_{it}\times c{c}_{it})/{\displaystyle {\sum }_t\exp (u_{it}\times c{c}_{it})}$; $IC{D}_{10}^{encod}={\displaystyle {\sum }_t{\alpha }_{it}^c\times x_{it}}$. As illustrated in Figure 2, similar attention mechanisms are implemented in the irst attention layer for the medication and for the laboratory results encodings, with the attention parameters ${\alpha }_{it}^o$ and ${\alpha }_{it}^l$ respectively.

Figure 2:

Architecture of a Hierarchical Attention-Based Prediction Model incorporating the UMLS embeddings.

A second layer of attention was also implemented, since we wanted the prediction model to also learn which form of clinical information combined with UMLS knowledge was the most impactful in deciding for the following quarter the COT achievement/persistence and the OUD incidence. Therefore, we learned an encoding for each quarter from the clinical picture and therapy of the patients available from ICD-10 codes, medications ordered and laboratory results of all hospital visits in a given quarter. The attention mechanism of the second layer uses parameters: ${\alpha }_{i1}^a$ (for ICD-10 codes encodings), ${\alpha }_{i2}^a$ (for medications ordered encodings) and ${\alpha }_{i3}^a$ (for laboratory result encodings). The results of the second layer of the hierarchical attention mechanism feed into a GRU which feeds into a fully prediction layer, as illustrated in Figure 2, allowing one binary classiier to decide whether COT will be achieved or persist in the next quarter, whereas a second binary classifier decides whether the incidence of OUDs will be observed.

Results

Both an intrinsic and an extrinsic evaluation of the UMLS knowledge embeddings was performed. The intrinsic evaluation measured the quality of the UMLS knowledge embeddings produced by the methodology presented in this paper against other models. The extrinsic evaluation measured the impact UMLS knowledge embeddings have on the results of a clinical prediction model. The quality of the UMLS knowledge embeddings was evaluated in terms of plausibility and completeness. The plausibility estimation was cast as a link prediction problem that can be seen as relation triple classification (RTC). For this purpose, we defined two plausibility functions informed by the scoring functions used in the Discriminator: the first operating on the UMLS Metathesaurus, defined as $P_1=-f_1^D$ and the second operating on the UMLS Semantic Network, defined as $P_2=-f_2^D$. Therefore, we measured how well P₁ can be used to predict a correct relation ⟨c₁, r, c₂⟩ encoded in the UMLS Metathesaurus, e.g. answering the questions “Is OPIOID ABUSE a kind of DRUG ABUSE?”, or how well P₂ can be used to predict a semantic relation ⟨t₁, sr, t₂⟩ encoded in the UMLS Semantic Network, e.g. answering the question “Can MENTAL OR BEHAVIORAL DYSFUNCTION affect BEHAVIOR?”. For this purpose, we used a validation set of 100,000 UMLS Metathesaurus triples to determine a threshold value, T₁ of the plausibility function P₁ above which all triples will be classified as true (i.e. P₁ (c_s, r, c_d) ≥ T₁) and below which all triples will be classified as false. Similarly, we relied on a validation set of 600 Semantic Network triples and the plausibility function P₂ to determine a threshold value T₂ above which all semantic relations are true. To evaluate the results of RTC, we relied on a set Π_M of 100,000 triples from the UMLS Metahesaurus held out from training and create a corrupted, false, version of each triple by randomly replacing either the source or destination concept. We then classified each of these 200,000 triples from the entire test set ${\Phi }_M^T$ as true if their plausibility value P₁ ≥ T₁ and false otherwise. Similarly, we used a Π_SN of 600 semantic relations extracted from the UMLS Semantic Network held out from training and we created an additional 600 semantic relations obtained by corrupting each triple by randomly replacing either the source or destination concept, obtaining a test set ${\Phi }_{SN}^T$ of 1200 semantic relations. Whenever the classification of these semantic relations had a plausibility P₂ ≥ T₂ the semantic relations was deemed correct. The results of the RTC were evaluated in terms of Precision, denoted as RTC-P, and Recall, denoted as RTC-R. The plausibility of the model for learning knowledge embeddings was quantified by RTC-P, whereas the completeness was quantified by RTC-R.

RTC-P for the UMLS Metathesaurus was defined by the number of correctly classified positive triples normalized by the size of the test set ${\Phi }_M^T$ (200,000). When measuring RTC-P on the UMLS Semantic Network, we normalized the number of correctly predicted semantic relations by the size of the test set ${\Phi }_{SN}^T$ (1200). The evaluation of RTC-R on the UMLS Metathesaurus measured the number of true relations that were predicted by the model out of all the true relations from the test set, i.e. Π_M (100,000). Similarly, RTC-R evaluated on the UMLS Semantic Network counted the number of true semantic relations predicted out of all the true semantic relations from the test set, i.e. Π_SN (600). We experimented with several methods for learning knowledge embeddings, and list their results in Table 2. It can be noted that the plausibility and completeness obtained by the GAN-based model, presented in this paper, consistently obtained the best results. We evaluated the performance of six knowledge embedding models using (a) the scoring functions (TRANSE and TRANSD), (b) incorporating information from the UMLS Semantic Network, and (c) the generative (GAN) adversarial learning framework. The TRANSE and TRANSD models were trained using only the Metathesaurus loss function, ${\mathcal{L}}_M$ shown in equation 1. The TRANSE_SN and TRANSD_SN models incorporated the Semantic Network by using both ${\mathcal{L}}_M$ and the Semantic Network loss function, ${\mathcal{L}}_S$ shown in equation 2. The GAN (TRANSE_SN+DISTMULT) and GAN (TRANSD_SN+DISTMULT) are trained with the full adversarial framework described in the Methods section, using the T RANSE and TRANS D scoring functions in their discriminators, respectively. Both GAN models use the DistMult scoring function for both their Metathesaurus (G ) and Semantic Network (G₂) generators. Each model was trained for 13 epochs using 9,169,311 Metathesaurus triples between 1,726,364 concepts spanning 388 relation types. The results for the Metathesaurus evaluations were obtained using the entire Semantic Network (6217 triples between 180 semantic types spanning 49 relation types), however to evaluate the Semantic Network knowledge embeddings, we reserved a test set of 600 triples, training on 5,617. We selected the dimension of the embedding space N = 50 from [25, 50,100,200] and the margin parameters γ₁, γ₂ =0.1 from [0.1,1.0,5.0] using grid search on a validation set of 10% of the training relation triples. All models are optimized using Adam²¹ with default parameters. TRANS E and TRANS D models are learned with the usual constraint that the L₂-norm of each embedding is ≤ 1 and the DISTMULT models use L₂ regularization. Table 2 shows that the GAN-based models outperform the non-adversarially learned models in each evaluation for the Metathesaurus and Semantic Network, demonstrating their effectiveness.

Table 2:

Plausibility and completeness of the UMLS knowledge embeddings. _SN indicates the incorporation of the Semantic Networkin the embeddings, which otherwise were learned only from the Metathesaurus.

Model	UMLS Metathesaurus					UMLS Semantic Network
	RTC-P	RTC-R	PPA	H@10	MRR	RTC-P	RTC-R	PPA	H@10	MRR
TRANSE	0.7712	0.6479	0.9340	0.2161	0.1400	–	–	–	–	–
TRANSD	0.9080	0.8895	0.9734	0.2780	0.1674	–	–	–	–	–
TRANSE_SN	0.8649	0.8019	0.9746	0.2240	0.1425	0.5105	0.7790	0.9150	0.7125	0.4882
TRANSD_SN	0.9188	0.8915	0.9729	0.2775	0.1670	0.6840	0.8771	0.9017	0.7300	0.4680
GAN (TRANSE_SN+DISTMULT)	0.8959	0.8424	0.9833	0.2727	0.1650	0.6109	0.7898	0.9367	0.7883	0.5373
GAN (TRANSD_SN+DISTMULT)	0.9311	0.9130	0.9803	0.3164	0.1886	0.8419	0.8546	0.9200	0.7867	0.5236

Table 2 also list three additional evaluations metrics for quantifying the plausibility of knowledge embeddings learned from UMLS: (1) Pairwise Plausibility Accuracy (PPA); (2) Hits at 10 (H10) and (3) Mean Reciprocal Rank (MRR). Given a test triple ϕ_M ∈ Π_M (or ϕ_SN ∈ Π_SN) and its corrupted version, z, created by randomly replacing either the source or destination argument with a random UMLS concept (or random UMLS semantic type), PPA measures the percentage of triples having the plausibility higher than plausibility of their corrupted triple. PPA demonstrates how well the knowledge embedding model can differentiate between a correct, ϕ, and an incorrect triple, z, even if the model had never encountered ϕ. In addition, the scoring functions $f_1^D$ and $f_2^D$ can be used to rank the triplets from the test sets ${\Phi }_M^T$ and ${\Phi }_{SN}^T$. For each triple ϕ in either test set, we created a set of candidate triples obtained by replacing the source argument and replacing it with every concept (or semantic type) from UMLS which was not seen in any training, development or test set (or selected before). This set of candidate triples is combined with ϕ to produce the set, Π_R. The scoring function $f_1^D$ (or $f_2^D$ respectively) was used to rank the triples from Π_R. We repeat this process for the destination argument, resulting in two rankings for each test triple. The rankings obtained in this way could be evaluated by metrics used in Information Retrieval: Hits at 10 (H@10) and Mean Reciprocal Rank (MRR). H@10 measures the percentage of test-set rankings where the specific test triple ϕ occurs in the top 10 highest ranked triples. MRR measures how high the correct triple, ϕ, is ranked. $MRR=\frac{1}{2\left|\Phi \right|}{\displaystyle {\sum }_{i=1}^{2\left|\Phi \right|}\frac{1}{ran{k}_i}}$ where rank_i refers to the rank of the triple ϕ in the i^th ranking and there are 2|Π| total rankings (2 for each test triple ϕ ∈ Π), with Π being either Π_M or Π_SN. The results listed in Table 2 indicate that the TRANSD models outperform the TRANSE models on the Metathesaurus evaluations (by 16% on H@10 and 14.3% on MRR), however TRANSE outperforms TRANSD on the Semantic Network evaluations, albeit by a lesser margin (1.8% on H@10 and 2.5% on MRR).

The impact of the UMLS knowledge embeddings on clinical prediction of the incidence of Opioid Use Disorders (OUD) after onset of opioid therapy and Chronic Opioid Therapy (COT) achievement and persistance was evaluated using a deep learning method using a Hierarchical Attention network (HAN). We trained two models, HAN^UMLS, conigured as described in the Methods section, and HAN, a baseline model that does not make use of the UMLS knowledge embeddings. HAN^UMLS uses the UMLS embeddings while HAN skips the concatenation step, using only the embeddings learned using word2vec. Both models are evaluated using F₁ score, sensitivity, specificity, Diagnostic Odds Ratio (DOR) and Area Under the Receiver Operating Characteristic curve (AUROC). The results, presented in Table 3, show that incorporating onto-logical knowledge in the form of UMLS knowledge embeddings improved performance when predicting Opioid Use Disorder while maintaining performance on Chronic Opioid Therapy achievement/persistence without major changes to the model.

Table 3:

The impact of UMLS knowledge embeddings on the prediction of incidence of Opioid Use Disorder (OUD) and the achievement/persistence of Chronic Opioid Therapy (COT). HAN^UMLS incorporates UMLS knowledge embeddings whereas HAN does not.

	OUD		COT
	HANUMLS	HAN	HANUMLS	HAN
F1 Score	0.843	0.774	0.778	0.776
Sensitivity	0.749	0.629	0.850	0.773
Specificity	0.963	0.981	0.717	0.792
DOR	77.86	72.99	14.30	12.99
AUROC	0.856	0.784	0.783	0.778

Discussion

This work demonstrates that adversarial learning of UMLS knowledge embeddings is an effective strategy for learning useful embeddings representing medical concepts, relations between them, semantic types and semantic relations. The learned knowledge embeddings exhibit interesting properties. For example, the 5 nearest neighbors of the UMLS concept ‘Malignant neoplasm of the lung’ (C0242379) are all different kinds of malignant neoplasm, including neoplasms of the skin (C0007114), brain (C0006118), pancreas (C0017689), bone (C0279530), and trachea (C0153489), each having the semantic type Neoplastic Process (T191). Likewise, the 10 nearest neighbors of the medical concept ‘Heroin Dependence’ are all Mental or Behavioral Dysfunctions (T048) indicating different drug abuse/dependency problems and the 10 nearest neighbors of ‘Quantitative Morphine Measurement’ (C0202428) are all Laboratory Procedures (T059) testing for some kind of opioid. The model does, however, struggle with concepts that have low connectivity in the knowledge graph (e.g. the 10 nearest neighbors of the concept ‘Stearic monoethanolamide’, which only appeared in 3 relation triples, are largely unrelated due to the low degree of that concept in the Metathesaurus graph). Moreover, we are currently unable to derive knowledge embeddings for concepts which do not participate in any relations. In future work, we plan to investigate methods capable of producing better representations for such isolated concepts.

The results also show that the UMLS knowledge embeddings improve the prediction of incidence of Opioid Use Disorder after onset of opioid therapy and Chronic Opioid Therapy achievement and persistence, out-of-the-box, by simply concatenating the UMLS knowledge embeddings with the traditional, WORD2VEC-style embeddings typically used in deep learning systems. We analyzed the attention weights assigned to each medical concept and to each class of concepts (i.e. ICD-10 codes, medications, and lab results) in the test set for both the HAN^UMLS and HAN models to determine the impact of the knowledge embeddings on the model. Interestingly, including the UMLS knowledge embeddings in the HAN^UMLS model caused the model to pay more attention to diagnoses (attention weight of 0.617 vs 0.4942) and less attention to medications (0.2706 vs 0.4762) on average indicating that the inclusion of the UMLS knowledge embeddings made the diagnoses more informative for prediction than the medications. Moreover, the diagnosis with the highest average attention weight in the HAN^UMLS model is ‘Chronic pain syndrome’ (C1298685) with an average attention weight of 0.5750 while in the HAN model, the diagnosis with the highest weight of 0.8092 was ‘ Predominant Disturbance of Emotions. In future work, we plan to investigate the impact of the knowledge embeddings on other predictive modeling tasks and investigate more sophisticated ways of including the embeddings in deep learning models.

Conclusion

In this paper we have presented a method for producing UMLS embeddings based on a generative adversarial network (GAN). These embeddings, which we make publicly available, can be used in a multitude of deep learning methods to benefit from the knowledge encoded in UMLS. We showcase how we have used the embeddings to improve performance in a clinical prediction model.