A Machine Learning Approach to Predicting the Stability of Inpatient Lab Test Results

Abstract

A primary focus for reducing waste in healthcare expenditure is identifying and discouraging unnecessary repeat lab tests. A machine learning model which could reliably predict low information lab tests could provide personalized, real-time predictions to discourage over-testing. To this end, we apply six standard machine learning algorithms to six years (2008-2014) of inpatient data from a tertiary academic center, to predict when the next measurement of a lab test is likely to be the “same” as the previous one. Out of 13 common inpatient lab tests selected for this analysis, several are predictably stable in many cases. This points to potential areas where machine learning approaches may identify and prevent unneeded testing before it occurs, and a methodological framework for how these tasks can be accomplished.

Introduction

Healthcare costs in developed nations are rising at an unsustainable rate¹. Ever-rising expenses with inconsistent improvements in outcome have led care providers and societies to express concern over waste in healthcare systems. In response, the American Board of Internal Medicine Foundation has championed the “Choosing Wisely” initiative, now supported by over 70 medical specialty societies, with the primary goal of discouraging unneeded tests and procedures^2,3. They encourage patients and clinicians to choose procedures that are “supported by evidence, not duplicative of other tests or procedures already received, free from harm, and truly necessary”³. One of the primary targets for waste is routine (often daily) lab testing, which comprises a large body of tests which are ordered out of habit or “just to be sure,” rather than to answer a specific clinical question. As a result, repeated lab testing is ubiquitous, with many of these repeat tests contributing little to no new information about the patient’s status.

The contribution of these lab tests to the large-scale waste in American Healthcare may be quite substantial. Although testing is the highest volume medical activity⁴, an estimated 25 to 50 percent of these tests may be unnecessary^5,6. Researchers estimate that eliminating low-information lab tests could save up to $5 billion United States dollars annually⁷. To do this, one must (1) identify which lab tests are truly unnecessary, and (2) encourage clinicians and patients to avoid ordering these low-yield tests. Consortia for a variety of medical societies now offer general guidelines on low-value tests and procedures, which are primarily based upon expert opinion or manual assessments^8,9. Most of these existing efforts involve manual top-down clinical guidelines and alerts¹⁰ based on simple rule triggers (e.g., avoiding vitamin D testing¹¹) However, attempts to incentivize clinicians against over-testing have been met with variable success⁹, often due to fear of medical-legal concerns and a well-intentioned desire to check “just to be safe.” One problem with the blanket guidelines may be that they are too general: patients and care providers are primarily concerned with the specific case rather than the general one. They want assurance that, in this moment, for this patient, ordering another test really is or is not necessary.

Here, we take a machine learning approach to supply data-derived insights into lab test predictability. An advantage of this methodology is that a well-calibrated model for lab test stability can provide personalized predictions: identifying whether the next test is likely to be unnecessary for a specific patient, given their previous medical history and test results. There are few examples in the literature that use machine learning predictive models as an approach to target such opportunities. Those that do exist tend to focus on focal analysis of single tests (e.g., ferritin¹²). In the past, researchers have demonstrated the feasibility of building classification models to predict whether a test result will be normal or abnormal¹³. However, normality is not the practitioners’ only concern. Even “abnormal” results may not be actionable, particularly if the result is highly predictable or repetitive from prior repeat assessments. What may be more useful to the care provider is whether or not a lab test result will “change” or “stay the same” as the previous measurement. If the patient’s status is almost certainly unchanged since the last test was ordered, the testing again may be unnecessary, wasteful, and detrimental to the patient.

We hypothesize that a substantial number of inpatient lab test results are largely unchanged between measurements, and therefore may not need to be re-measured. If this is true, it points to the usefulness of a predictive model which can identify when a lab test result is likely to offer no new information in light of the previous measurement. Such a tool could be used to consider lab test orders on a case-by-case basis and urge care providers against ordering more testing whenever the results are highly predictably stable. With this in mind, we aimed to (i) quantify the proportion of repeat lab tests which are unchanged with respect to the previous measurement, and (ii) assess the extent to which the stability of a lab test is predictable. That is: given that we know the previous measurement of a lab test component, how accurately can we predict that the next test result will be the same (within some level of allowable noise)?

One of the primary challenges in addressing this research goal is selecting a suitable definition of what it means for a lab test result to “stay the same.” Different definitions may be more appropriate or interpretable for different tests or scenarios: A 10 unit difference in creatinine kinase may be very different from a 10 unit difference in phosphorus. A “percent change” is an intuitive alternative, but if a previous result is very large, a “±X% change” refers to a much larger margin than if the previous measurement was small. This may be useful in some cases when we care more about small fluctuations when the previous measurement was very small, but in other scenarios this may be inappropriate.

We consider another definition of change in terms of absolute units rather than percent; the standard deviation (SD) of the result distribution. For example, we consider the SD of creatinine kinase to be the standard deviation of all creatinine kinase measures for all patients. Then one could say, for example, that a lab test result is “stable” or “unchanged” if the next creatinine kinase measure is within 1/10 of a standard deviation of the previous measurement. The value of this measure is that it captures the spread of values a clinician expects to see for a given lab test. This way, if a lab test naturally tends to show very wide variation between measurements and individuals, a +/- 0.1SD threshold for “stability” is looser than for a lab test which tends to show very little variation between individuals. This allows more ready comparison between lab tests, whereas +/- 1 “unit” may mean a very different thing for magnesium results than for creatinine kinase.

With this complexity in mind, we separately consider both definitions of “stability”: percent change, and standard deviation (SD) change. Within each framework, we evaluate: (i) the overall volume of “stable” repeat tests and (ii) predictability of these “stable” lab tests. By assessing the potential of these different frameworks for identifying low-yield “unchanged” lab results, we lay the groundwork for the development of a predictive model which can identify low information lab tests before they are ordered.

Methods

Study Data

For this study, we analyzed six years (2008-2014) of inpatient data from Stanford University Hospital, a tertiary academic hospital. Because the percent and standard deviation definitions of “change” we used for this approach do not apply to categorical lab test results (such as blood cultures) we restricted our analysis to lab tests with numeric results. For this study, we focused on non-panel tests (i. e., single order yields a single result) for clarity on the potential for prediction and decision support that links a predicted result to the ordering decision. This as opposed to panel tests (e.g., basic metabolic panel) where the individual components may be predictable, but it is unclear how to drive decision making for the overall panel. We ultimately evaluated 13 common inpatient lab tests that fit these criteria as in Figure 1.

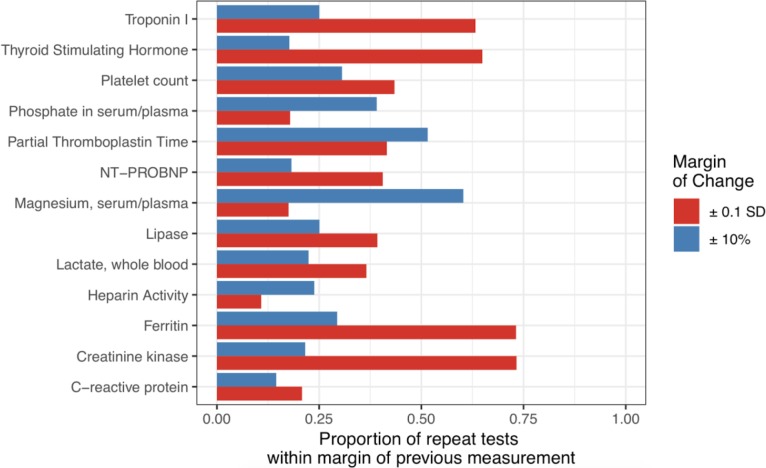
Figure 1:

Stability of repeat lab tests for 13 common single-component tests. Horizontal bars indicate the percent of repeat lab tests which are “stable” in light of the previous measurement. Stability is considered in terms of SD (red), or percent (blue).

The unit of analysis for this study was an individual order for a lab test of interest. For each of the 13 lab tests under consideration, we extracted a random sample of 12,000 lab test orders (or all orders if there were fewer than 12,000), omitting orders without a numeric result. Each raw dataset contained lab tests from at least 440 unique individuals (median: 1797, maximum: 7627). In keeping with past work¹³, the ‘previous measurement’ of a lab test result was considered to be the most recent measurement in the past 14 days; if this was not present, the test order was considered a ‘non-repeat’ lab test, and therefore excluded. Each observation was additionally described by ~800 features describing the clinical context of the lab test. These include: patient demographics, hospital stay information (such as admission date and the treatment teams assigned to the patient), and comorbidities. We additionally included information about the timing and numeric values of the patient’s previous test results, both for the lab test under study and other common (daily) lab tests and vital sign measurements (for example temperature, sodium, potassium, white blood cell count, etc.). Missing data was filled in using mean imputation. The data extraction process, including the features set describing each observation, was modeled after previous work¹³.

After the initial data extraction, we added outcome labels according to several different definitions of “stability.” In total, we used ten different definitions for each lab test: 50, 40, 30, 20, and 10 percent change, and change by 0.5, 0.4, 0.3, 0.2, or 0.1 SD units. For example, under the “ 10 percent change” definition, a lab test with a previous measure of 100 units would be stable if the next measure was between 90 to 110. In order to use the SD measure to define “stability,” for any lab test, we first estimate the standard deviation for the results of the test in question. This measurement was made on a set of 300 lab test examples distinct from those included in the training and testing sets.

Training and Evaluation

For feature selection and model training, we used the implementations available from scikit learn (version 0.19.1)¹⁴. For each lab test and each definition of “change” selected, we pruned the ~800 input features by 95% via recursive feature elimination with cross validated selection (RFECV) using a RandomForest estimator, leaving approximately 40 features. This was done in keeping with previous work¹³.

Prior the training phase, 25% of the data was held aside for testing. The remaining 75% was used to build six different machine learning models for classification: a decision tree, a boosted tree classifier (adaboost), a random forest, a gaussian naive Bayes classifier, a lasso-regularized logistic regression, and a linear regression followed by rounding to 0 or 1. Care was taken to ensure that the train and testing sets represented data from non-overlapping sets of individuals. Where relevant, hyperparameters for each model were tuned using 10-fold cross validation on the training set. In the testing phase, we measured the performance of each classifier in two ways.

First, we measured AU-ROC (area under receiver operating characteristic), which takes on values from 0.5 to 1 (with random classifiers performing at 0.5 and a perfect classifier achieving a score of 1). This is a standard metric for classifier performance, though it may not be as relevant for the applied question asked here. For a more practically meaningful metric, we estimated what portion of lab orders were “highly predictable” as assessed by predictability₉₉. We define predictability₉₉ as the proportion of repeat lab tests we predict to be unchanged with expected >99% accuracy. The practical interpretation is as follows: When we implement a model in the clinic, we must select a threshold for how certain we are of stability before we are willing to advise the clinician against ordering the test. Ideally, we would like to be quite certain of stability before we advise against ordering a test to avoid false alarm fatigue. We look to the training data to empirically estimate a decision threshold that is meant to achieve a 99% accuracy on the examples we predicted to be stable (i.e., where precision = positive predictive value is estimated to be 99%). Predictability₉₉ reports the percent of repeat lab tests we would advise against under this classification scheme.

For each lab order type and stability definition, we measured AU-ROC and predictability₉₉ on the test set and reported the statistics for the best of the six models.

Predictable Charge Volume

We measured the proportion of all tests which are unchanged relative to the previous measurement. To avoid any risk of information leak between the training and test sets, all of these measurements were taken on the test set after training and evaluating all classifiers. Additionally, we estimated the annual volume of each type of repeat lab tests over the course of the year 2016. Last, we used publicly available chargemaster data to estimate the relative potential economic impact (predictable charge volume) for the predictable tests.

Results

Stability of Repeat Lab Tests

A model for predicting low-information stable lab tests is only useful if a substantial number of lab tests actually are low-information. With this in mind, we set out to understand how consistent lab tests tend to be across measurements. Using both percent and SD definitions of change, we estimated the proportion of repeat orders that were “stable” relative to the previous measurement (Figure 1). In terms of both percent and standard deviation, a substantial proportion of lab test results were similar to previous values. For example, more than 70% of repeat measurements of creatinine kinase or ferritin were within ± 0.1 SD of the last recorded measurement, and approximately 60% of repeat measurements of magnesium were within ± 10% of the previous value. Interestingly, the proportion of results within ± 0.1 SD of the previous was often quite different than the proportion within ± 10% of the previous measurement. While more than 60% of repeat Troponin I tests were within ± 0.1 SD of the previous value, only than 25% were within ± 10% of the previous. Thus, some tests which are quite stable in terms of absolute units (such as SD) may be very different from the previous measurement in terms of percent, and vice versa. This indicates that a large number of repeat lab tests may indeed be fairly close to the previous measurement, but that the metric for stability can have a profound effect on which tests are considered “stable” and which are not.

Predictability of Stable Lab Tests

Ultimately, we wanted to ask, “how often can we predict that the next test result will be ‘close-enough’ to the previous one?” In other words, how predictable are stable lab tests? To do this, we developed a pipeline to train six standard machine learning models for identifying lab test results that were “stable” or “changed.” Since it was unclear which definition of “stability” was most appropriate, we applied several, and compared our results. First, we defined a “stable” measurement to be one that was within 10, 20, 30, 40, or 50 percent of the previous measurement. Second, we considered “stable” to mean ‘within 0.1, 0.2, 0.3, 0.4 or 0.5’ standard deviations of the previous (see Methods). We applied each of these ten definitions to each of the 13 common tests in our data set to build a total of 130 different training and testing sets and separately applied our machine learning pipeline to each.

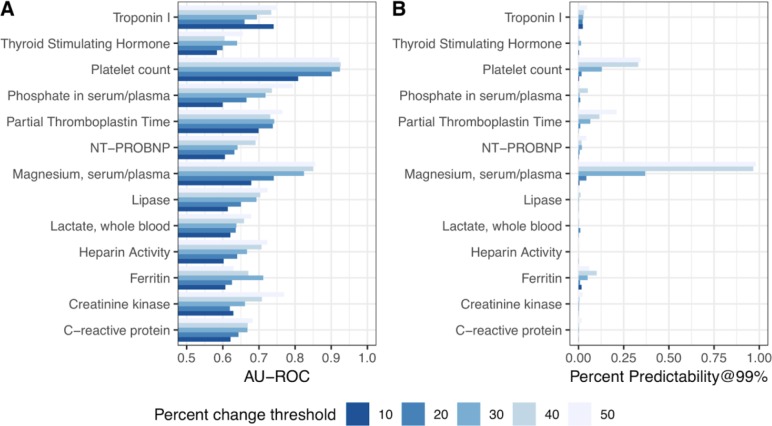
To evaluate the performance of each model, we used two metrics: the Area under the receiver operating characteristic curve (AU-ROC) and predictability₉₉ (see Methods). Here, we report the statistics for the best-performing model on the test set for each order. Generally, we achieve greater predictability₉₉ when our percent change threshold is large (Figure 2B) This is not surprising, since predictability is always upwardly bounded by the proportion of results which are stable, and this number increases as our definition of “stable” increasingly relaxed. However, our AU-ROC performance is quite high for some thresholds of percent change, even when predictability₉₉ is low (Figure 2). For example, when we considered a lab test result to be “stable” if it was within 30% of the previous measurement, we found that platelet count and magnesium had 12.9% and 36.9% predictability₉₉, respectively.

Figure 2:

Classifier performance for predicting whether a lab test will be “stable” compared to the previous one, in terms of percent change. Performance is shown in AU-ROC (A) and Predictability₉₉ (B) under 5 different definitions of “stability”: within ± 10, 20, 30, 40, or 50 percent of the previous measurement. For example, the predictability₉₉ ratings indicate that >30% of the orders for serum magnesium are “highly predictable” within a ± 30% threshold of a previous value.

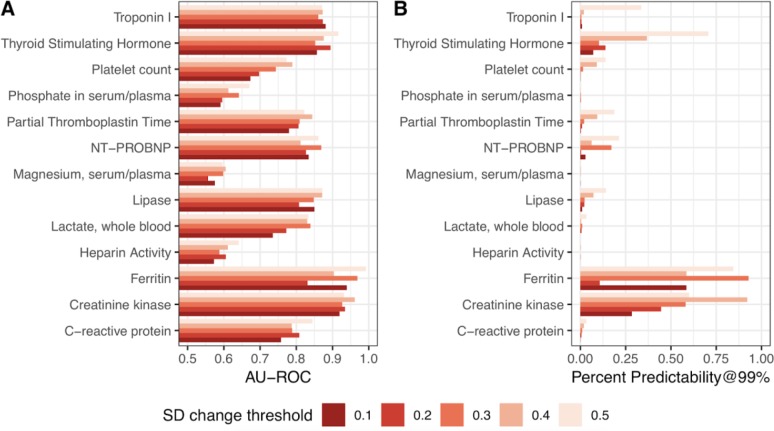
Generally speaking, AU-ROC and percent predictability are higher when we consider SD, rather than percent change (Figure 3). We achieve 28% predictability for predicting creatinine kinase results which are stable within ± 0.1 SD of the previous measurement, and up to 58% predictability for ferritin within ± 0.1 SD. Overwhelmingly, we find that the predictability of a test result’s stability varies heavily with the specific definition of “stability” we apply. In most cases, decision tree based learning methods (single decision tree, adaboost with a tree base learner, and random forest) outperformed other models (linear regression, logistic regression, and naive bayes).

Figure 3:

Classifier performance for predicting whether a lab test will be “stable” compared to the previous one, in terms of standard deviation. Performance is shown in AU-ROC and Predictability₉₉ under 5 different definitions of “stability”: within ± 0.1, 0.2, 0.3, 0.4, or 0.5 SD of the previous measurement.

Volume of predictable tests

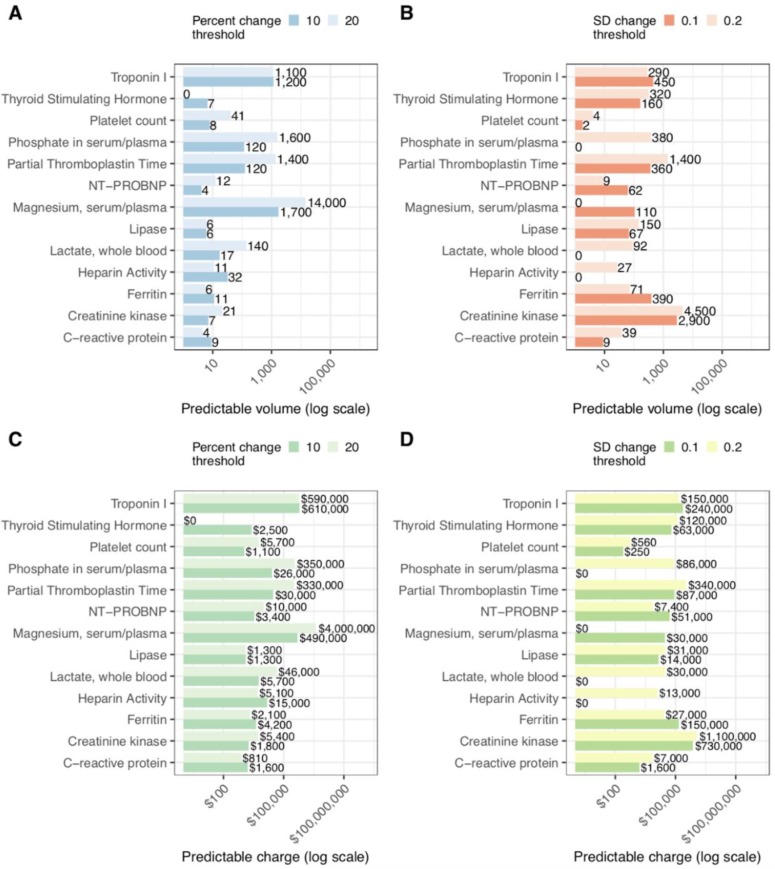
Next, we sought to estimate the volume of predictable tests, and roughly calculate the charges associated with these lab orders. To do this, we estimated the total number of repeat lab tests of each type in 2016. Since the true cost of a medical test is difficult to estimate and obtain for both practical and compliance reasons, we report public chargemaster data as a proxy for the relative expense of lab tests. Figure 4 gives estimates of the overall volume of predictable results and predictable charge volume on a log scale for six definitions of lab test “stability.” It is clear that some tests have far greater predictable volume than others. Of note Serum/Plasma Magnesium has an extremely large volume of repeat tests, and stability of Magnesium within ±20% is fairly predictable, amounting to large volumes of predictable lab testing. Also of note are Troponin I and Creatinine kinase tests, which are fairly predictably stable at ± 0.1 SD sensitivity.

Figure 4:

Estimates of predictable testing volume for percent (A) and SD change (B) for 2016 at Stanford University Hospital. Calculated charges of predictable tests under percent (C) and SD (D) frameworks for stability. All horizontal axes are on a logarithmic scale, with charges in United States Dollars (USD). For example, if we restrict only to predictions we can make with >99% accuracy, we estimate that approximately 1,200 repeat measurements of troponin I in 2016 can be predicted to be within ± 0.1 SD with of the previous measurement. This amounts to over $600,000 USD in charge volume.

Conclusion

Here, we interrogate two alternative formulations for discussing lab test “stability” by (i) quantifying the number of repeat tests which are “stable” with respect to the previous and (ii) assessing the extent to which stable lab test results are predictable. Our results demonstrate that, for certain common lab test types, there is promise in taking a machine learning approach to generate on-the-spot personalized predictions for identifying when a repeated lab test is likely to be contribute little new information.

We find that a large proportion of repeat tests are within ±10% or ±0.1 SD of the previous measurement, indicating that a large volume of repetitive testing may be contributing little new information (Figure 1). When we attempt to build models for predicting lab test stability, we find that some lab tests are predictably stable under certain definitions, while others are not (Figure 2, Figure 3). In particular, blood/serum magnesium, troponin I, and creatinine kinase testing stand out as potential targets where a large volume of repeat tests are often highly predictable, amounting to hundreds of thousands of dollars in estimated annual charge volume (Figure 4). In contrast, several lab test types do not appear easily predictable at all. This broad study indicates directions where future efforts are likely to be rewarded, as opposed to other less promising directions.

Several limitations to our approach are worth noting and may direct future work. First, because the true cost of a lab test to the hospital system is extremely difficult to ascertain for practical and compliance reasons, we used the lab test charge from public chargemaster data to estimate annual charge volume. This supplies some concept for the relative expenses of each test, but it is likely to be a gross overestimate of the “true cost” to the healthcare system of predictable lab tests. Finally, in this paper, we define a repeat test as one with a previous measurement within 14 days. Other time periods may be more appropriate for some tests. For example, considering a “repeat test” to be one with a measurement in the past 3 days may be more sensible for some lab tests. With large enough training set sizes, this may even boost the performance of the classifier, since, for example, predicting a lab test from a ≤ 3 -day-old measurement is likely to be much easier than from a ≤ 14-day-old measurement. The relative time dynamics of test ordering can itself be clinically important¹⁵ - this is why our models include consideration for what time of day, and what season of the year, that a test is ordered. Clinical users will similarly have to individualize interpretation of the performance ranges as checking the first repeated test in a month has different implications than checking a tenth repeat in a week. Future efforts in this field may employ temporal models for predicting the next result based on previous measurements.

Defining “clinically important” diagnostic test results requires more nuanced decision analyses on the relative impact of risks vs. benefits and consideration for more individual patient contexts than we attempt to address in this manuscript. These results are meant to lay the groundwork for future efforts towards identifying and avoiding low-information lab testing. The problem of deciding what “change” is relevant ultimately is a clinical question, not a mathematical one. For some tests, clinical guidelines may offer some direction for defining a “clinically relevant change.” For example, under the RIFLE criteria, an increase in serum creatinine of 0.3 mg/dl will cause a patient to be considered “at risk” for acute renal injury¹⁶. In other cases, the measurement error of the laboratory test itself might be considered a “gold standard” of precision for defining change. Certainly, if a test with measurement error of ±5% is not going to change by more than ±5% from the previous measure, then the repeat test should not be ordered. Future efforts may focus on developing predictive models for one or two promisingly predictable lab tests from these preliminary analysis, and define “stability” according to relevant clinical expertise.

Here, we offer two competing frameworks for “stability” which are qualitatively different in significant ways. While percent change may be more interpretable, it has the potentially problematic property that it is less sensitive when the previous measurement is large. Standard deviation units, on the other hand, are agnostic to the magnitude of the previous test result, but also may be less interpretable by clinicians and patients. If a system for predicting lab test stability were implemented, it would need to report not only the prediction that a result would be stable but also the interval of “stability” that specifically applies for each prediction (e.g. if the test is highly predictably stable at the 10% level with a previous value of 100, the system might report “There is > X% chance that the next result will be stable between 90 and 110”). At that juncture it would be the clinician and patient’s decision whether this range and confidence was tight enough to take the concrete (in)action of deferring the repeat test.

In conclusion, many repeated inpatient lab tests yield results that are predictably similar to prior results, based supervised machine learning models and readily available contextual data from patient electronic medical records. This work illustrates the opportunity and a methodologic framework to systematically target low value diagnostic testing.