Application of net reclassification index to non-nested and point-based risk prediction models: a review

Abstract

Much of medical risk prediction involves externally derived prediction equations, nomograms, and point-based risk scores. These settings are vulnerable to misleading findings of incremental value based on versions of the net reclassification index (NRI) in common use. By applying non-nested models and point-based risk scores in the setting of stroke risk prediction in patients with atrial fibrillation (AF), we demonstrate current recommendations for presentation and interpretation of the NRI. We emphasize pitfalls that are likely to occur with point-based risk scores that are easy to neglect when statistical methodology is focused on continuous models. In order to make appropriate decisions about risk prediction and personalized medicine, physicians, researchers, and policy makers need to understand the strengths and limitations of the NRI.

Introduction

The net reclassification index (NRI) has been proposed to assess the added value of new risk markers to existing prognostic models.¹ It was intended as a summary measure for the reclassification tables that display movement between risk categories which occurs when a new model is used in place of a previous standard, thereby emphasizing the implications to clinical practice of a new risk scoring strategy. The simplicity of this presentation may explain why it has been advocated and adopted so quickly in cardiovascular research.^2–4

Recent literature has identified several gaps in the calculation, reporting, and interpretation of the NRI, even in top-tier medical journals.^5–8 Furthermore, the NRI is being applied in new settings, and several forms of the metric have been proposed.^5,9–11 Original applications of the NRI involved nested models that evaluate the addition of new markers to an existing risk function with both models fit to a common data set. However, much of cardiovascular risk prediction involves non-nested models, which include externally derived prediction equations, nomograms, and point-based risk scores, with levels such as 0, 1, 2, 3, 4, 5+ that represent a tally of points associated with various patient characteristics.^12–15 These settings are particularly vulnerable to misleading results based on the forms of the NRI in common use.

In order to make appropriate decisions about risk prediction and personalized medicine, physicians, researchers, and policy makers need to understand the strengths and limitations of the NRI. This article provides current recommendations for presentation and interpretation of the NRI with special consideration given to applications of non-nested models and point-based risk scores in the setting of stroke risk prediction in patients with atrial fibrillation (AF).

Methods

Principles of risk prediction and metrics for model assessment were recently reviewed in the TRIPOD statement.¹⁶ Here, we focus on the best practices for use of the NRI, based on recent statistical literature. Although generalizable to risk prediction broadly, the principles are demonstrated in the context of a motivating example. Specifically, patients with AF are at elevated risk for stroke or systemic embolism (SSE). Oral anticoagulation (OAC) therapy can reduce the risk of SSE in patients with AF by 64%,¹⁷ and its use is guided by risk prediction algorithms.^13,18,19 Even among anticoagulated cohorts there is interest in identifying residual risk of SSE.^20,21 We focused on the latter problem where results are less established.

Data from the Outcomes Registry for Better Informed Treatment of AF (ORBIT-AF) study were used to compare algorithms for stroke risk prediction among anticoagulated patients. From 2010 to 2011, 10 135 patients with electrocardiographically confirmed AF were enrolled in ORBIT-AF from 176 sites in USA.²² Sites abstracted demographic and clinical data at baseline and conducted follow-up for outcomes, including SSE, at approximately 6-month intervals. After excluding patients without follow-up data (n = 392) and patients not on OAC therapy at baseline (n = 2301), there were 7442 patients eligible for this analysis.

An initial Cox regression model for SSE was fit and included history of stroke or transient ischaemic attack, diabetes, hypertension, age per 10 years, and heart failure. The selection of these covariates was influenced by variables included in the CHADS₂ score, a well-known risk score that predicts SSE for non-anticoagulated patients with AF by summing points based on these variables.¹⁸ The score itself is considered later. An augmented model was developed by adding the significant variables of female sex and vascular disease (myocardial infarction, peripheral artery disease, and aortic plaque) and removing diabetes, which was non-significant. The augmented model was compared with the initial model as a reference.

Nested vs. non-nested models

The original applications of the NRI concerned nested models: one or more biomarkers were added to an existing model. Best practices for application and interpretation of the NRI in this setting have been provided.^7,11 Here, we focus on non-nested models. Briefly, non-nested models encompass nearly any comparison where one model cannot be obtained by simply adding a set of covariates to the other and fitting them to the same data. Our ORBIT-AF example involves a non-nested model because factors are simultaneously added (female sex and vascular disease) and dropped (diabetes). Another important example arises when one or more risk prediction equations come from an external data set, as in a validation study. Although there are many parallels, the emphasis on non-nested models is important because problems arise that rarely occur in the nested setting: failure to establish statistical significance via modelling, lack of calibration, and numerous issues with point scores.

Results

Testing the incremental value of one model over another

In general, statistical testing based on metrics of incremental value has been discouraged.^23,24 If statistical testing is desired, it should rely on likelihood-based measures of model fit and not on the NRI. Instead, to compare nested models where one or more markers have been added to an existing model, the appropriate test is the likelihood ratio test of association for the coefficient(s) in a multivariable model.^23,24 Many questions of incremental value can be framed as nested models to facilitate this comparison. To compare two non-nested models, a similar method is given,²⁵ whereby the linear predictor for each model is obtained separately, and then the two linear predictors are included simultaneously in a model for outcome. Using this approach, the newer model in our example (adding female sex, vascular disease, and dropping diabetes) does significantly add to the initial model (initial model: χ² = 0.005, P-value = 0.94; augmented model: χ² = 5.06, P-value = 0.02).

Despite statistically significant incremental value, the area under the receiver operating characteristics curve (AUC)¹⁶ for the augmented model is 0.677, compared with 0.671 for the initial model. The numerical insensitivity of the AUC is not unusual, even in settings where statistically significant improvement has been established.^26,27 This, in part, motivated the use of alternative measures of added value, such as the NRI. However, a positive NRI should not be expected if traditional model-based P-values are non-significant or the AUC does not improve.^28,29 When this does occur, it likely reflects random chance or poor model fit.⁷ The careful approach to derivation and interpretation of the NRI described here will help avoid such discrepancies.

Review of the category-based net reclassification index

Timing

Interpretation of the NRI requires a clear time horizon for risk prediction, one that corresponds to the definition of risk thresholds.⁷ Studies of stroke risk in patients with AF have included variable follow-up from 1 to 3 years.^18,19,30 In ORBIT-AF, the time horizon for risk prediction and model assessment was chosen to be 3 years, just beyond the median follow-up of 2.5 years (25th percentiles, 75th percentiles: 2, 3 years), with 162 occurrences of SSE.

Reclassification tables and the category-based net reclassification index

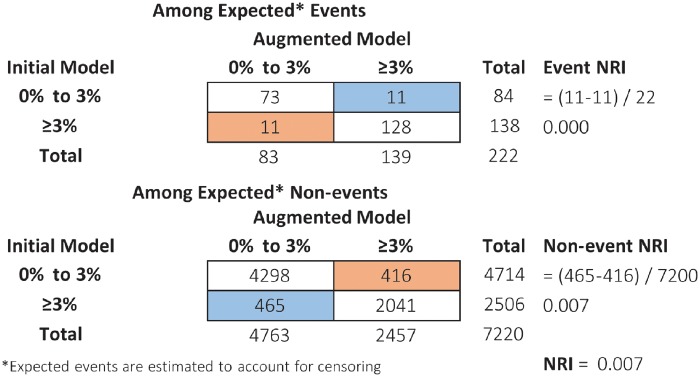
Suppose we are interested in differentiating ORBIT-AF patients with greater than 3% chance of stroke within the next 3 years, even with anticoagulation (alternative thresholds are considered later). We can obtain two sets of risk predictions ($p$) for every patient, first from the initial model and then from the augmented model. A reclassification table (Figure 1) illustrates how patients’ classification changes, above or below 3%, based on the initial risk predictions compared with the augmented risk predictions.¹ Separately, among patients who did or did not experience an event, the event NRI and non-event NRI, respectively, summarize net improvement in classification (Figure 1). The original version of the NRI simply adds the two components.¹ With the 3% threshold (low risk <3%, high risk >3%), the NRI for the augmented model compared with the initial model is 0.007 [95% confidence interval (CI) −0.04 to 0.06], reflecting a small magnitude of incremental value (Figure 1). Confidence intervals are obtained by bootstrapping.^6,31 In the ORBIT-AF example some patients are lost to follow-up prior to 3 years and thus have censored outcomes. In the presence of censoring, the NRI is defined the same way, but is estimated in a way that accounts for differential follow-up.^5,7

Figure 1.

Reclassification table where blue cells indicate patients whose risk prediction improved under the augmented model, and orange cells indicate patients whose risk prediction worsened under the augmented model (higher risk prediction is good for events and bad for non-events). Event NRI = up − # down]/total events; Non-event NRI =  # down − # up]/total non-events; NRI = Event NRI + non-event NRI. NRI, net reclassification index.

Selection of thresholds and net reclassification index at event rate

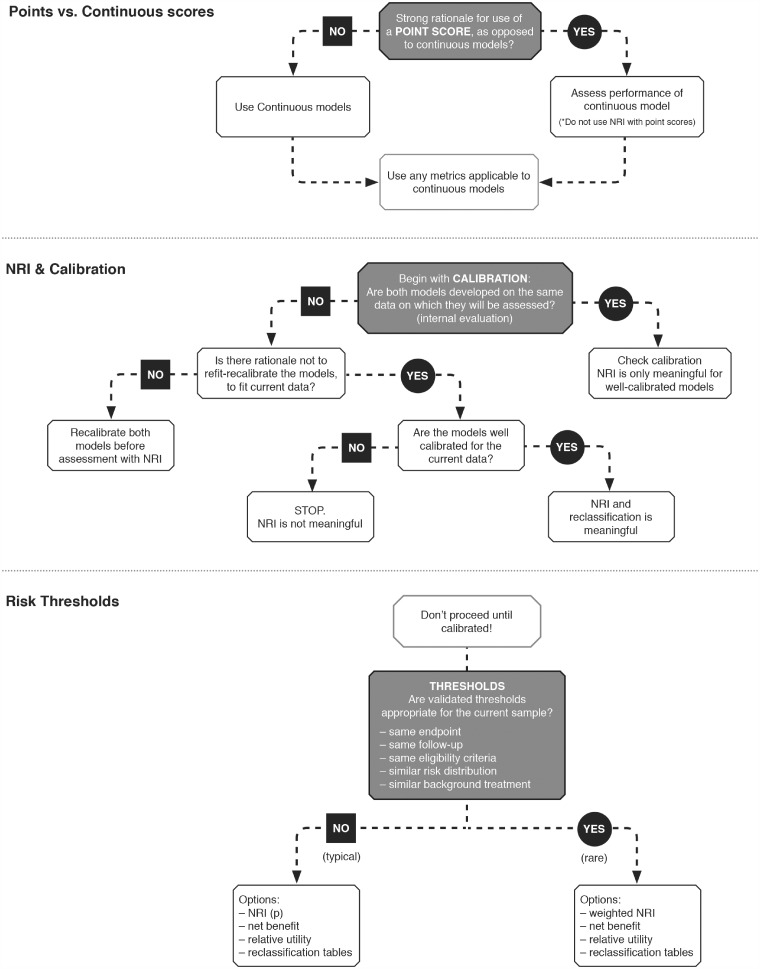
Validated risk thresholds should be aligned with current population eligibility criteria, endpoint, and follow-up duration (Figure 4). Recent literature reviews have found that risk cut-offs tend to be poorly motivated, rarely correspond to clear treatment decisions, and consequently yield inflated NRI values.^7,32 In the ORBIT-AF example, the three-category NRIs range from 0 to 0.04 depending on the choice of thresholds (<1%, 1–3%, >3%) and (<6%, 6–9%, >9%), respectively.

Figure 4.

Schema of key decisions that precede derivation of the net reclassification index.

These problems can be avoided by categorizing patients into two groups: above and below the sample event rate.^7,11 The NRI categorized at the event rate, denoted NRI(p), has many appealing statistical properties.²⁷ In particular, the NRI(p) is robust to model miscalibration and cannot be tricked by adding random noise (statistically proper).¹¹ To apply it in ORBIT-AF, we used the Kaplan–Meier methods to estimate the overall stroke rate at 3 years to be 3%. This motivates the selection of 3% as a risk threshold in ORBIT-AF (Figure 1).

Beware of miscalibration

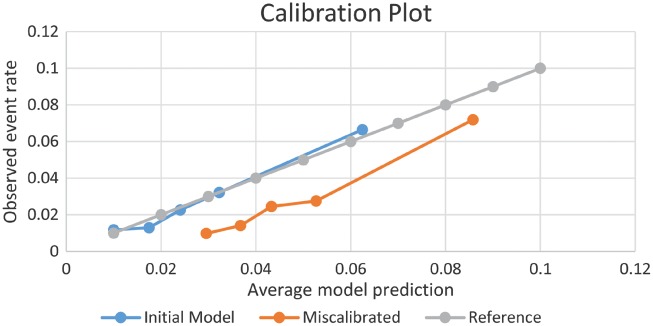
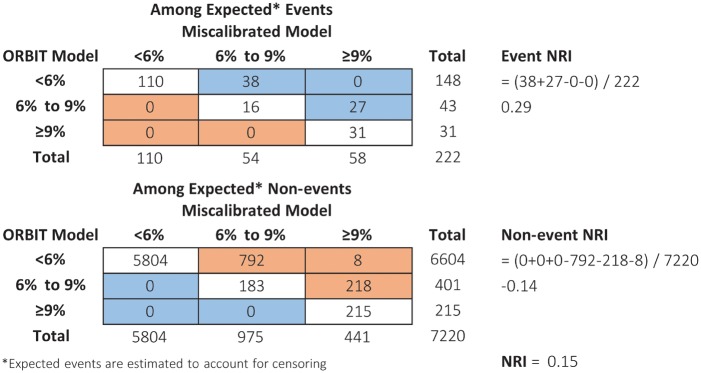
In contrast to rank-based measures such as the AUC, most forms of the NRI, with the exception of NRI(p), are sensitive to miscalibration.^7,11,33 This has important implications to non-nested models, particularly those derived in external data sets. Suppose that a new model was developed outside of ORBIT-AF in a population with higher risk. For illustration, we created such a model by artificially adding 0.02 to the predicted risk of the augmented ORBIT-AF model. The lack of calibration, where predictions are consistently too high, can be discerned from a calibration plot (Figure 2). Yet the NRI (<6%, 6–9%, >9%) is 0.15 (95% CI 0.07–0.23), suggesting that the miscalibrated model is better. To understand this, it is helpful to evaluate the reclassification table (Figure 3). Under the miscalibrated model, 38 + 27 = 65 expected events were favourably moved up. Consequently, the event NRI is positive at 0.29. However, 793 + 218 + 8 = 1018 expected non-events were also moved up, and the non-event NRI is –0.14. The NRI sums these proportions, 0.29 + (–0.14) = 0.15, and does not expose the trade-off. Inaccurate estimation of risk can appear favourable. The NRI (3%) at event rate is not fooled by our trick: it equals –0.21 (95% CI –0.28 to –0.11), indicating that the miscalibrated model is much worse.

Figure 2.

Agreement between average model predictions and observed event rates by quintiles of predicted risk.

Figure 3.

Reclassification table where blue cells indicate patients whose risk prediction improved under the miscalibrated model, and orange cells indicate patients whose risk prediction worsened under the miscalibrated model (higher risk prediction is good for events and bad for non-events). Event NRI = [# up – # down]/total events; Non-event NRI = [# down – # up]/total non-events; NRI = Event NRI + non-event NRI. NRI, net reclassification index.

Some amount of miscalibration is likely when a model is developed in an external data set.^7,34 In a validation study where the validation data are meant to represent the setting in which the model will be applied with respect to things like follow-up, definitions, and ascertainment, then lack of calibration may be a serious flaw in either the risk score or the data themselves (not being representative of the population of interest). If so, there is no need to proceed with reclassification assessment or the NRI.^33,35,36 Otherwise, note any lack of initial calibration and possible explanations (differences in follow-up, definitions, ascertainment, concomitant therapies, etc.) and recalibrate the models before calculating the NRI.^7,11 An easy approach to improve calibration is to refit both models (distinguished by two sets of covariates) to the current data, though other methods exist.^34,37

Event and non-event components of the net reclassification index

The event NRI and non-event NRI are individually important and should be reported separately, along with the reclassification table (Figure 1).^7,9,35 In the application to stroke prediction in ORBIT-AF, event NRI (0.03) = 0.00 (95% CI –0.03 to 0.05) and non-event NRI (0.03) = 0.007 (95% CI –0.003 to 0.012) (Figure 1). This is consistent with the impression of small gain given by the AUC. In addition to these two components, many researchers prefer to have an aggregate measure. As noted above, the NRI(p) is a proper measure. However, with respect to clinical interpretation, the event rate may not be a meaningful classification threshold. When alternative risk thresholds are well justified (Figure 4), the principles of decision analysis support the use of a weighted NRI, or its close cousins known as standardized net benefit or relative utility.^5,33,38 Rather than taking a simple sum, these metrics weigh events and non-events according to the differential costs of misclassification.

Interpretation

Interpreting the magnitude of the NRI requires consideration of multiple factors. Adding a variable that has a moderate or large effect size (Cohen’s D equal to 0.5 or 0.8, respectively) can yield NRI values between 0.004 and 0.392, depending on the version of the NRI and discrimination of the initial model (AUC).¹¹Table 2 illustrates this variation and gives a sense of meaningful reference ranges. For example, if moderate improvement in risk prediction is acceptable and the initial model has AUC = 0.75, an NRI(p) of 0.043 may be relevant. Clinical relevance can also be assessed using the reclassification tables directly, where practical trade-offs are evident.

Table 2.

Change in AUC (ΔAUC*), two-category NRI(p)^a, and three-category NRI(p/2, 2p) as a function of initial model discrimination (AUC) and effect size (Cohen’s D) of an added marker

Baseline		Cohen’s D
AUC		0.2	0.5	0.8
0.65	ΔAUC	0.009	0.049	0.103
	NRI(p)	0.014	0.074	0.157
	NRI(p/2, 2p)	0.032	0.181	0.392
0.75	ΔAUC	0.005	0.027	0.061
	NRI(p)	0.007	0.043	0.100
	NRI(p/2, 2p)	0.019	0.108	0.247
0.85	ΔAUC	0.002	0.013	0.031
	NRI(p)	0.004	0.025	0.060
	NRI(p/2, 2p)	0.010	0.059	0.141

AUC, area under the receiver operating characteristics curve; NRI, net reclassification index.

^aValues of ΔAUC and NRI(p) are true for any event rate p; three-category NRI(p/2, 2p) calculated at P = 0.10.

Net reclassification index with point-based risk scores

Risk prediction in AF is dominated by ordinal scores composed of a limited number of points that are easy to calculate at the bedside: CHADS₂, CHA₂DS₂-VASc, ATRIA-Stroke, and R₂CHADS₂ for SSE,^18,19,21,39 and HAS-BLED, ATRIA-Bleed, HEMMORHAGES, and ORBIT for bleeding.^12,40–42 CHADS₂, for example, is a sum of points; 1 point each for heart failure [C], hypertension [H], age 75 years or older [A], and diabetes [D], and 2 points for a previous stroke [S2] or transient ischaemic attack. Summed point values are then translated into a level of risk, typically based on the average event rate (per 100 patient-years) among such patients in the development sample. The NRI is frequently used to compare these point-based risk scores.^21,30,43,44

Threats to the validity of such applications are numerous. First, the fixed allocation of points to low/medium/high risk categories does not facilitate re-calibration, and the NRI may therefore favour a miscalibrated score (with no added information) over a well-calibrated alternative. Second, cut points (low/medium/high) associated with different scores generally do not have comparable meaning in terms of risk. Even if we attempt to apply common risk thresholds, results can be extremely sensitive to chance; moving a lot of people either above or below a given cut point. Bootstrap confidence intervals for the NRI will be wrong if either (i) miscalibration is present, or (ii) the bootstrap algorithm fails to incorporate re-calibration in each bootstrap sample. To the best of our knowledge, neither of these steps occurs in practice and as a result confidence intervals are too narrow; the NRI may appear ‘significant’ in whatever direction occurred by chance.

To illustrate a few of these issues, we compared CHADS₂ with CHA₂DS₂-VASc for stroke prediction in the anticoagulated ORBIT-AF population. Starting with the standard point allocation, we might compare CHADS₂ (low = 0, med = 1, high = 2+) to CHA₂DS₂-VASc (low = 0, med = 1, high = 2+), obtaining an NRI of –0.11 (95% CI –0.15 to –0.05). The negative value indicates that CHA₂DS₂-VASc is worse than CHADS₂. This contradicts a model-based comparison in which CHADS₂ (as a categorical variable) is not significant (P-value = 0.3) and CHA₂DS₂-VASc is (P-value < 0.001) when they are included in the same model. It also contradicts the finding of a nearly identical AUC of 0.653 and 0.657 for CHADS₂ and CHA₂DS₂-VASc. The discrepancy is attributable to poor calibration; thresholds of 0, 1, and 2+ are not the same in terms of actual risk for CHADS₂ and CHA₂DS₂-VASc, particularly in the anticoagulated population (Table 1).

Table 1.

Actual event rates (per 100 patient-years) in ORBIT-AF according to point-based scores CHADS₂ with CHA₂DS₂-VASc

CHA2DS2-VASc	Rate	CHADS2	Rate
0	0.0	0	0.4
1	0.3	1	0.4
2	0.4	2	0.8
3	0.6	3	1.1
4	0.8	4	1.9
5	1.2	5	2.8
6	1.6	6	3.0
7	2.4
8	3.9
9	4.5

AF, atrial fibrillation; ORBIT-AF, Outcomes Registry for Better Informed Treatment of AF.

Alternatively, we might attempt to recalibrate the points’ scores by applying common risk thresholds to the observed event rates, such as <2%, 2–3%, and >3% annually (selected by rounding the levels of risk originally intended for CHADS₂: 1.9 and 2.8 events per 100 patient-years). The NRI (<2%, 2–3%, >3% annual risk) for CHA₂DS₂-VASc vs. CHADS₂ would be 0.075 (95% CI 0.02 to 0.14). Perhaps an improvement, this result is extremely unstable. Using slightly different risk thresholds (<1.9%, 1.9–2.8%, >2.8% annual risk), the NRI for CHA₂DS₂-VASc vs. CHADS₂ is –0.11 (95% CI –0.18 to –0.01). Due to the coarse nature of point-based risk scores, small variation in either the threshold or observed risk can move a lot of people and dramatically influence the NRI. Typical confidence intervals do not take this large, chance variation into account. In this example, the NRI(p) at the event rate (reclassifying points above and below 1% observed annual risk) is more consistent with model-based results and AUC [NRI(1%) = 0.03; 95% CI –0.04 to 0.10].

Discussion

Whenever a new risk model is found to be superior to another, either by adding significant markers or better modelling of existing markers, the immediate question is ‘Does it positively impact patient care?’ Reclassification tables help us answer that question in terms of how many patients would be treated differently under the new risk prediction scheme, in settings where treatment decision-making is guided by firmly established risk thresholds. The NRI provides a summary metric of reclassification, but can be misleading if it is not applied carefully to non-nested models, particularly those developed externally. If statistical testing is desired, it should rely on likelihood-based measures of model fit and not on the NRI. Good calibration of both models should be ensured prior to calculating reclassification tables and the NRI.

The full reclassification table along with separate event NRI and non-event NRI are essential to interpretation, and the NRI should not be presented in isolation, particularly if it is not explicitly weighted. In the absence of firmly established risk thresholds that are appropriate for the current population, the sample event rate will be robust in many settings. The resulting NRI(p) is a proper measure that cannot be fooled by miscalibration. Where a clinically relevant decision threshold is established and differs from ‘p’, more clinically relevant summary measures of reclassification can be derived. These include the weighted NRI,⁵ standardized net benefit,³³ and relative utility.³⁸

When point-based risk scores are compared, it is easy to focus on points rather than absolute risk thresholds. In the field of AF, nobody is recommending using different cut points for CHADS₂ or CHA₂DS₂-VASc in different populations; the cut points derived for an initial population are synonymous with the score. When coupled with the fact that event rates in different AF populations vary many-fold, most forms of the NRI are impossible to interpret. A positive NRI may reflect added value of a marker, non-comparable cut points, miscalibration, incorrect confidence intervals, or the addition of random noise. While the NRI(p) exhibits robustness to some of these problems, its properties and the derivation of appropriate confidence intervals need further study in this context. We, therefore, caution against the use of the NRI with point-based risk scores.

Many of the challenges with point scores also apply to the AUC, particularly if scores are first categorized into low/medium/high and then evaluated. The AUC, however, does not require categorization and tends to be less sensitive to calibration problems. The best solution is to avoid point scores altogether and rely on continuous models. In fact, this may mitigate a related problem—that absolute risk according to fixed low/medium/high categories tends to differ drastically from data set to data set (i.e. good calibration is rarely seen). Simplification of a continuous risk profile into three categories based on coarse points may work fine on the training data but suffer challenges in terms of generalizability. In the era of electronic health records, the barriers to continuous risk prediction are disappearing. The challenges demonstrated here should further motivate that transition.

Conclusions

Careful application and interpretation of the NRI is particularly important in the setting of non-nested models. Additional steps are needed to ensure that a positive NRI is not explained by poor model fit or chance. Point scores are likely to yield misleading NRI with incorrect confidence intervals and the combination should be avoided.