Manipulation of eight-dimensional Bell-like states

Researchers manipulation and measure the eight hyperentangled Bell-like state in eight-dimensional Hilbert space.

Abstract

High-dimensional Bell-like states are necessary for increasing the channel capacity of the quantum protocol. However, their preparation and measurement are still huge challenges, especially for the latter. Here, we prepare an initial eight-dimensional Bell-like state based on hyperentanglement of spin and orbital angular momentum (OAM) of the first and the third orders. We design simple unitary operations to produce eight Bell-like states, which can be distinguished completely in theory among each other. We propose and illustrate a multiple projective measurement scheme composed of only linear optical elements and experimentally demonstrate that all the eight hyperentangled Bell-like states can be completely distinguished by our scheme. Our idea of manipulating the eight Bell-like states is beneficial to achieve the 3-bit channel capacity of quantum protocol, opening the door for extending applications of OAM states in future quantum information technology.

INTRODUCTION

Photons, as a carrier of messages, are encoded into their degrees of freedom (df), such as spin (or polarization) and orbital angular momentum (OAM). In quantum information, the information transfer is usually a process of preparation and measurement of the Bell states. The spin Bell states based on the spontaneous parametric down conversion (SPDC) process can be prepared with wave plates [half-wave plate (HWP) and quarter-wave plate (QWP)], while their complete measurement can be achieved with the aid of nonlinear optics (1), ancillary photons (2), or hyperentanglement (3, 4). Solution to these issues enables the spin-entangled states to be applied for quantum dense coding (4, 5), quantum teleportation (6, 7), quantum key distribution (8), entanglement swapping (9), and so on. Because of the limitation of dimension, the channel capacity of the quantum protocol based on the spin df can never be greater than 2 bits. To break this limitation, one must use high-dimensional (HD) entangled states.

However, thus far, the preparation with simple operations and complete discrimination of HD entangled states are still far from enough. Recently, Wang et al. (10) have prepared a complete set of Bell-like states in a four-dimensional Hilbert space structured by four OAM states (∣+1〉, ∣0〉, ∣−1〉, and ∣−2〉). The preparation of Bell-like states is not convenient enough for encoding information, and the Bell-like states are not distinguished, which restrict their practical applications.

Here, we generate an initial Bell-like state based on spin-OAM hyperentanglement in the eight-dimensional Hilbert space composed of the two-dimensional spin angular momentum and the four-dimensional OAM (±1 and ±3 orders). We then prepare eight Bell-like states from the initial one simply by operating a DP (Dove prism), an HWP, and a QWP, which is beneficial to encode the information. In theory, we can distinguish completely the eight Bell-like states when selecting a suitable basis set. Furthermore, we experimentally achieve the complete distinction of all the eight Bell-like states with a multiple projective measurement scheme using linear optical elements only. Our research on the eight Bell-like states will contribute to the channel capacity of quantum protocol up to 3 bits, which is promising for advanced applications.

RESULTS

Theory

First, we present the theoretical analysis to distinguish the eight Bell-like states. The eight two-photon Bell-like states we are to focus on can be formulated as follows

$$\mid {\mathrm{\Theta }}_{1,2}\rangle =[\mid {\mathrm{\Phi }}_{\text{spin}}^{\pm }\rangle \otimes (\mid {\mathrm{\Psi }}_1^{+}\rangle +\mid {\mathrm{\Psi }}_3^{+}\rangle )]/\sqrt{2}$$ (1A)

$$\mid {\mathrm{\Theta }}_{3,4}\rangle =[\mid {\mathrm{\Psi }}_{\text{spin}}^{\pm }\rangle \otimes (\mid {\mathrm{\Psi }}_1^{+}\rangle +\mid {\mathrm{\Psi }}_3^{+}\rangle )]/\sqrt{2}$$ (1B)

$$\mid {\mathrm{\Theta }}_{5,6}\rangle =[\mid {\mathrm{\Phi }}_{\text{spin}}^{\pm }\rangle \otimes (\mid {\mathrm{\Phi }}_1^{+}\rangle +\mid {\mathrm{\Phi }}_3^{+}\rangle )]/\sqrt{2}$$ (1C)

$$\mid {\mathrm{\Theta }}_{7,8}\rangle =[\mid {\mathrm{\Psi }}_{\text{spin}}^{\pm }\rangle \otimes (\mid {\mathrm{\Phi }}_1^{+}\rangle +\mid {\mathrm{\Phi }}_3^{+}\rangle )]/\sqrt{2}$$ (1D)

Here, spin and OAM Bell states are defined, respectively, as

$$\mid {\mathrm{\Phi }}_{\text{spin}}^{\pm }\rangle =(\mid H\rangle {}_A\mid H\rangle {}_B\pm \mid V\rangle {}_A\mid V\rangle {}_B)/\sqrt{2}$$ (2A)

$$\mid {\mathrm{\Psi }}_{\text{spin}}^{\pm }\rangle =(\mid H\rangle {}_A\mid V\rangle {}_B\pm \mid V\rangle {}_A\mid H\rangle {}_B)/\sqrt{2}$$ (2B)

$$\mid {\mathrm{\Psi }}_m^{+}\rangle =(\mid +m\rangle {}_A\mid -m\rangle {}_B+\mid -m\rangle {}_A\mid +m\rangle {}_B)/\sqrt{2}$$ (2C)

$$\mid {\mathrm{\Phi }}_m^{+}\rangle =(\mid +m\rangle {}_A\mid +m\rangle {}_B+\mid -m\rangle {}_A\mid -m\rangle {}_B)/\sqrt{2}$$ (2D)

where H (V) represents the horizontal (vertical) polarization, ∣+m〉 (∣−m〉) denotes a state of photon with an OAM of +mħ (−mħ), and m takes 1 or 3. Subscripts A and B label the two paths. Thus, all the eight Bell-like states described in Eq. 1 are in the identical eight-dimensional Hilbert space constructed by two-dimensional spin and four-dimensional OAM (±1 and ±3 orders).

We perform unitary operation U^O ⊗ U^S on the photon-A of state ∣Θ₁〉 to prepare the eight Bell-like states described in Eq. 1 (Fig. 1A).

• 1)For ∣Θ₁〉 ⇒ ∣Θ₁〉, without operation.
• 2)For ∣Θ₁〉 ⇒ ∣Θ₂〉, performing ∣H〉_A → e^+jπ/2 ∣H〉_A and ∣V〉_A → e^−jπ/2 ∣V〉_A with a QWP (11).
• 3)For ∣Θ₁〉 ⇒ ∣Θ₃〉, performing ∣H〉_A ↔ ∣V〉_A with an HWP (11).
• 4)For ∣Θ₁〉 ⇒ ∣Θ₄〉, performing ∣H〉_A → e^+jπ/2 ∣H〉_A, ∣V〉_A → e^−jπ/2 ∣V〉_A, and ∣H〉_A ↔ ∣V〉_A.
• 5)For ∣Θ₁〉 ⇒ ∣Θ₅〉, performing ∣+m〉_A ↔ ∣−m〉_A with a DP.
• 6)For ∣Θ₁〉 ⇒ ∣Θ₆〉, performing ∣+m〉_A ↔ ∣−m〉_A, ∣H〉_A → e^+jπ/2 ∣H〉_A, and ∣V〉_A → e^−jπ/2 ∣V〉_A.
• 7)For ∣Θ₁〉 ⇒ ∣Θ₇〉, performing ∣+m〉_A ↔ ∣−m〉_A and ∣H〉_A ↔ ∣V〉_A.
• 8)For ∣Θ₁〉 ⇒ ∣Θ₈〉, performing ∣+m〉_A ↔ ∣−m〉_A, ∣H〉_A → e^+jπ/2 ∣H〉_A, ∣V〉_A → e^−jπ/2 ∣V〉_A, and ∣H〉_A ↔ ∣V〉_A.

Fig. 1. Transformations and theoretical results of coincidence measurement for eight Bell-like states.

(A) Preparation of Bell-like states from ∣Θ₁〉 by manipulating unitary operation U^O ⊗ U^S on photon-A. Details on U^O ⊗ U^S are shown on the right side in (A). Here, YES (NO) means that the DP is (is not) in the optical path. @0° (@45° or @90°) means that the wave plate is oriented at 0° (45° or 90°, respectively) from the horizontal polarization direction. (B) Simulated coincidence measurement results of eight Bell-like states with projecting Bell-like states into {∣ψ_i〉_A∣ψ_j〉_B} (i, j = 1, 2, ..., 8). The colored small squares (empties) mean that there are (are no) coincidence counts.

Here, ∣H〉_A → e^+jπ/2 ∣H〉_A and ∣V〉_A → e^−jπ/2 ∣V〉_A are realized with setting the QWP@90°, ∣H〉_A ↔ ∣V〉_A is realized with setting the HWP@45°, and ∣ +m〉_A ↔ ∣ −m〉_A is realized by the use of the DP (see Fig. 1A for details). We should notice that the DP has no effect on spin, while HWP and QWP have no effect on OAM.

To distinguish the eight Bell-like states completely and accurately, we need to seek a suitable projective basis set, ensuring that any Bell-like state is a unique superposition. Inspired in (4, 12), here, we use the spin-OAM Bell states as a projective basis set

$$\mid {\mathrm{\psi }}_{1,2}\rangle =(\mid +1\rangle \mid H\rangle \pm \mid +3\rangle \mid V\rangle )/\sqrt{2}$$ (3A)

$$\mid {\mathrm{\psi }}_{3,4}\rangle =(\mid -1\rangle \mid H\rangle \pm \mid -3\rangle \mid V\rangle )/\sqrt{2}$$ (3B)

$$\mid {\mathrm{\psi }}_{5,6}\rangle =(\mid +1\rangle \mid V\rangle \pm \mid +3\rangle \mid H\rangle )/\sqrt{2}$$ (3C)

$$\mid {\mathrm{\psi }}_{7,8}\rangle =(\mid -1\rangle \mid V\rangle \pm \mid -3\rangle \mid H\rangle )/\sqrt{2}$$ (3D)

With Eq. 3, we rewrite Eq. 1 as follows

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_1\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B+\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B+\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B+\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B\hfill \end{array}$$ (4A)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_2\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B-\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B-\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B-\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B-\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B\hfill \end{array}$$ (4B)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_3\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B+\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B+\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B+\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B\hfill \end{array}$$ (4C)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_4\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B-\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B-\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B-\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B-\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B\hfill \end{array}$$ (4D)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_5\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B+\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B+\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B+\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B\hfill \end{array}$$ (4E)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_6\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B-\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B-\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B-\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B-\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B\hfill \end{array}$$ (4F)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_7\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B+\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B+\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B+\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B\hfill \end{array}$$ (4G)

$$\begin{array}{cc}\hfill \mid {\mathrm{\Theta }}_8\rangle \propto & \mid {\mathrm{\psi }}_1{\rangle }_A\mid {\mathrm{\psi }}_6{\rangle }_B+\mid {\mathrm{\psi }}_2{\rangle }_A\mid {\mathrm{\psi }}_5{\rangle }_B+\mid {\mathrm{\psi }}_3{\rangle }_A\mid {\mathrm{\psi }}_8{\rangle }_B+\hfill \\ & \mid {\mathrm{\psi }}_4{\rangle }_A\mid {\mathrm{\psi }}_7{\rangle }_B-\mid {\mathrm{\psi }}_5{\rangle }_A\mid {\mathrm{\psi }}_2{\rangle }_B-\mid {\mathrm{\psi }}_6{\rangle }_A\mid {\mathrm{\psi }}_1{\rangle }_B-\hfill \\ & \mid {\mathrm{\psi }}_7{\rangle }_A\mid {\mathrm{\psi }}_4{\rangle }_B-\mid {\mathrm{\psi }}_8{\rangle }_A\mid {\mathrm{\psi }}_3{\rangle }_B\hfill \end{array}$$ (4H)

From the above expressions, we can see that any Bell-like state is a unique superposition of 8 of the 64 possible combinations of the two-photon states. That is to say, all the Bell-like states are completely nondegenerate or incompatible. From Eq. 4 and the theoretical results of coincidence measurement for eight Bell-like states under the projective basis set {∣ψ_i〉} (Fig. 1B), it is evident that all the eight Bell-like states can be distinguished completely.

Experiment

It is well known that the HD entangled state can be generated on the basis of energy time (13, 14), time bins (15, 16), or frequency modes (17–19). Since the OAM entangled states can be easily produced via the SPDC process (20) and have the infinite dimension in principle, it should be one of the most promising candidates to provide access to the HD quantum states (21–29).

In our experimental setup (Fig. 2A) for the generation of the eight Bell-like states with the df of both spin and OAM hyperentanglement (30), the pump light is a femtosecond pulsed laser with a fundamental Gaussian mode, a power of 610 mW, a central wavelength of 405 nm, a pulse duration of ~140 fs, and a repetition rate of 80 MHz. On the basis of the SPDC process under the type I phase-matching condition, two 0.6-mm-thick β-barium borate (BBO) crystals with optic axes aligned in the perpendicular planes will produce down-converted photons at a degenerate wavelength of 810 nm in a 3.0° half-opening angle cone. The HD entangled state is described as

$$\mid {\mathrm{\Theta }}_{\text{SPDC}}\rangle =\mid {\mathrm{\Phi }}_{\text{spin}}^{+}\rangle \otimes (C_1\mid {\mathrm{\Psi }}_1^{+}\rangle +C_3\mid {\mathrm{\Psi }}_3^{+}\rangle )$$ (5)

where C_m is the amplitude fraction of mth-order OAM state. We should notice that the OAM states of other orders produced from the SPDC process have been filtered. Using linear optical elements [QWP, first/second-order q-plate, first-order q-plate (31–34), HWP, and polarizing beam splitter (PBS); see the Supplementary Materials for details], we characterize the ∣Θ_SPDC〉 state with coincidence measurement under the projective basis set {∣φ_i〉} (i = 1, 2, …, 8), here, ∣φ₁〉 = ∣+3〉 ∣H〉, ∣φ₂〉 = ∣+1〉 ∣ H〉, ∣φ₃〉 = ∣−1〉 ∣H〉, ∣φ₄〉 = ∣−3〉 ∣H〉, ∣φ₅〉 = ∣+3〉 ∣V〉, ∣φ₆〉 = ∣+1〉 ∣V〉, ∣φ₇〉 = ∣−1〉 ∣V〉, and ∣φ₈〉 = ∣−3〉 ∣V〉. As an example, we show the evolution of ∣φ₁〉 in Fig. 2B (see table S1 and eq. S3 for other details).

Fig. 2. Experimental setup for the generation and projection of Bell-like states.

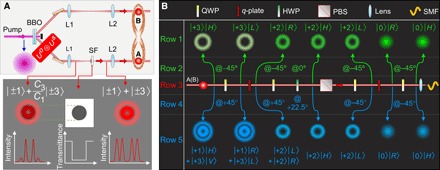
(A) An ultraviolet femtosecond laser pumps two 0.6-mm-thick BBO crystals to produce HD entanglement source. A spatial filter (SF) is used to obtain the maximum entangled state. Detail on function of SF has been given in the inset under the setup (see also the Supplementary Materials). (B) Projection of Bell-like states. The optical elements from left to right are QWP1, q-plate1, QWP2, HWP, PBS, QWP3, q-plate2, QWP4, lens, and single-mode fiber (SMF) in turn (as shown in row 3). Row 1 shows the evolution of the state ∣φ₁〉 = ∣+3〉 ∣H〉 by performing the operations (row 2) of the wave plates. Row 5 shows the evolution of the state ∣ψ₁〉 ∝∣+1〉 ∣H〉 + ∣+3〉 ∣V〉 by performing the operations (row 4) of the wave plates.

The experimental results (Fig. 3) show that the ∣Θ_SPDC〉 state is not a maximum HD spin-OAM entangled state (35). We estimate the ratio C₃/C₁ to be ~0.124 from the data in Fig. 3. To obtain the maximum entangled Bell-like state, we need distillation. Different from (36, 37), we implement the OAM concentration with a spatial filter (SF), which is a glass plate covered with a top hat–shaped copper thin film. To achieve C₃/C₁ ≈ 1, we place the SF in the back focal plane of lens L1, where the OAM states of ∣±1〉 and ∣±3〉 are spatially separated (the inset of Fig. 2A). The SF has a diameter of ~0.75 mm, which is almost the same as the size of the spatial mode ∣±1〉. From the experimental results (the inset of Fig. 3), ∣Θ_SPDC〉 behind the SF turns into

$$\mid {\mathrm{\Theta }}_{\text{SPDC}}^{\text{SF}}\rangle \propto \mid {\mathrm{\Phi }}_{\text{spin}}^{+}\rangle \otimes (\mid {\mathrm{\Psi }}_1^{+}\rangle +0.9654\mid {\mathrm{\Psi }}_3^{+}\rangle )\approx \mid {\mathrm{\Theta }}_1\rangle$$ (6)

Fig. 3. Experimental coincidence counts of ∣Θ_SPDC〉.

The coincidence counts under the projective basis set ∣φ_i〉(i = 1, 2, ..., 8) for eight-dimensional entangled state produced from the SPDC process directly. Inset shows the result after the distillation using the SF.

Once obtaining ∣Θ₁〉, we can prepare the other seven Bell-like states using the suitable unitary operations U^O ⊗ U^S (Fig. 1).

Next, we carry out the coincidence measurement for each Bell-like state under the basis set {∣ψ_i〉} (i = 1, 2, …, 8). The scheme for projection of {∣ψ_i〉} is shown in row 3 of Fig. 2B. As an example, we give the evolution of ∣ψ₁〉 in row 5 of Fig. 2B by the operations in row 4 of Fig. 2B (see the Supplementary Materials for details). QWP1@+45°, q-plate1, and QWP2@+45° convert ∣ψ₁〉 ∝∣+1〉 ∣H〉 + ∣+3〉 ∣V〉 into ∣+2〉(∣H〉 + ∣V〉) (31). Then, the HWP@+22.5° rotates the polarization state from ∣H〉 + ∣V〉 into ∣H〉, which can pass through the PBS. Last, the combination of QWP3@−45°, q-plate2, and QWP4@−45° converts ∣+2〉 ∣H〉 into ∣0〉 ∣H〉 (31), which can be coupled into a single-mode fiber and detected by a single-photon detector. The experimental results from the coincidence measurement (Fig. 4) demonstrate that any Bell-like state is a unique superposition of 8 of the 64 possible combinations of two-photon states, which agrees with the theoretical results (Fig. 1B). Therefore, we prove that all the eight Bell-like states can be distinguished completely in theory and experiment.

Fig. 4. Experimental coincidence measurement results for the eight Bell-like states.

The projective basis is ∣ψ_i〉 (i = 1, 2, ..., 8). Vertical axis represents the coincidence counts in 10 s.

DISCUSSION

To uniquely identify the entangled states, one should carry out the standard quantum tomography (38, 39), which requires a large number of measurements. In our situation, we need to do measurements up to 64² = 4096 for a full-state tomography, which is impractical. Alternatively, we do two things: the full-state tomography in every individual subspace and the signature of coherence between subspaces. For our eight Bell-like states, the measured density matrices (Fig. 5) verify the coherence in the three individual subspaces (spin, first-order OAM, or third-order OAM). In addition, the experimental coincidence measurement results under the projective basis set {∣ψ_i〉} (Fig. 4) reflect the coherence among the spin, first-order OAM, and third-order OAM subspaces (see the Supplementary Materials for the details).

Fig. 5. The real part of reconstructed density matrices and the corresponding fidelities in every subspace for the eight Bell-like states.

Taking ∣Θ₁〉 as an example, fidelities are calculated as $F_{\text{spin}}=\text{tr}({\mathrm{\rho }}_{\text{spin}}\mid {\mathrm{\Phi }}_{\text{spin}}^{+}\rangle \langle {\mathrm{\Phi }}_{\text{spin}}^{+}\mid )$ in the spin subspace, $F_1=\text{tr}({\mathrm{\rho }}_1\mid {\mathrm{\Psi }}_1^{+}\rangle \langle {\mathrm{\Psi }}_1^{+}\mid )$ in the first-order OAM subspace, and $F_3=\text{tr}({\mathrm{\rho }}_3\mid {\mathrm{\Psi }}_3^{+}\rangle \langle {\mathrm{\Psi }}_3^{+}\mid )$ in the third-order OAM subspace. Here, ρ_spin = [ρ_spin(+3) + ρ_spin(+1) + ρ_spin(−1) + ρ_spin(−3)]/4, ρ₁ = [ρ₁(H) + ρ₁(V)]/2, and ρ₃ = [ρ₃(H) + ρ₃(V)]/2. ρ_spin(m) is the measured density matrix of $\mid {\mathrm{\Phi }}_{\text{spin}}^{+}\rangle \mid m{\rangle }_A\mid -m{\rangle }_B$. ρ_m(H) and ρ_m(V) are the measured density matrices of $\mid {\mathrm{\Psi }}_m^{+}\rangle \mid H{\rangle }_A\mid H{\rangle }_B$ and $\mid {\mathrm{\Psi }}_m^{+}\rangle \mid V{\rangle }_A\mid V{\rangle }_B$, respectively. It should be pointed out that the imaginary parts of reconstructed density matrices in every subspace are almost zero for any Bell-like state.

In conclusion, we have presented the scheme for preparing the eight Bell-like states in an eight-dimensional Hilbert space constructed by spin and OAMs using the simple unitary operations with linear optics only. We have also proposed a solution (multiple projective measurement scheme) for completely distinguishing the eight Bell-like states under the spin-OAM projective basis set. In our experiment, we generated an initial Bell-like state first by the SPDC process with the aid of distillation of spatial mode and then prepared the other seven Bell-like states with the suitable unitary operations. We have achieved the complete distinction between the eight Bell-like states with our multiple projective measurement scheme using linear optics only. To achieve the goal of the quantum protocol of 3-bit channel capacity, we presented a practical eight-outcome Bell-like state analyzer scheme (see the Supplementary Materials for the details). However, it is a huge challenge to achieve this aim in the experiment due to the shortcomings of detection technology at present. Our multiple projective measurement scheme is equivalent to the eight-outcome Bell-like state analyzer for demonstrating the complete distinction between the eight Bell-like states. Once the bottlenecks of detection technology are broken, the channel capacity of quantum protocol will be undoubtedly increased up to 3 bits (see the Supplementary Materials for example). Note that the eight Bell-like states are in an eight-dimensional Hilbert space constructed by the two-dimensional spin and the four-dimensional OAM (±1st and ±3rd orders). Such an eight-dimensional Hilbert space has a total of 64 eight-dimensional Bell-like states. If more Bell-like states can be prepared and distinguished, then the channel capacity can be further increased.

METHODS

q-plate

The q-plate plays the key role in our experiment. In general, the function for an m′/2-order q-plate can be described as follows (31)

$$\mid m\rangle \mid R\rangle \stackrel{m\prime /2‐\text{order}q‐\text{plate}}{\to }\mid m+m\prime \rangle \mid L\rangle$$ (8A)

$$\mid m\rangle \mid L\rangle \stackrel{m\prime /2‐\text{order}q‐\text{plate}}{\to }\mid m-m\prime \rangle \mid R\rangle$$ (8B)

Here, ∣R〉 = ∣H〉 + j∣V〉 and ∣L〉 = ∣H〉 − j∣V〉 represent the right and left circularly polarized states, respectively. In this work, we used some first/second-order (which can convert the OAM state ∣+1〉 or ∣−1〉 into the fundamental Gaussian mode state ∣0〉) and first-order q-plates (which can convert the OAM state ∣+2〉 or ∣−2〉 into the fundamental Gaussian mode state ∣0〉).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/6/eaat9206/DC1

Section S1. Distillation of the HD entangled states

Section S2. Projection of the basis set {∣ψ₁〉, ∣ψ₂〉, ..., ∣ψ₈〉}

Section S3. Eight-outcome Bell-like state analyzer

Section S4. Sixty-four Bell-like states in the eight-dimensional Hilbert space

Section S5. Symmetry and antisymmetry of Bell-like states

Fig. S1. Distillation of the HD hyperentanglement source.

Fig. S2. Experimental coincidence measurement results under the projective basis set {∣φ_i〉} (i = 1, 2, ..., 8).

Fig. S3. Eight-outcome Bell-like state analyzer.

Fig. S4. Scheme for dense coding with eight Bell-like states.

Fig. S5. Theoretical results of coincidence measurement for 64 Bell-like states.

Fig. S6. Schematic diagram of coherence among three subspaces.

Fig. S7. Verification of Bell-like states.

Fig. S8. Coefficient distribution pattern(s) of Bell-like state(s).

Table S1. Scheme for projecting the basis set ∣φ_i〉 into ∣0〉.

Table S2. Scheme for projecting the basis set ∣ψ_i〉 into ∣0〉.