Assessment of Conformational State Transitions of Class B GPCRs Using Molecular Dynamics

Abstract

Class B G protein-coupled receptors (GPCRs) comprise a family of 15 peptide-binding members, which are crucial targets for endocrine, metabolic, and stress-related disorders. While their protein structures and dynamics remain largely unclear, computer modeling and simulations represent a promising means to help solve such puzzles. Herein, we present a basic introduction to the methodology of molecular dynamics (MD) simulations and two analytical methods to assess the conformational ensembles and transitions of Class B GPCRs, using our recent studies of the human pituitary adenylate cyclase activating polypeptide (PAC₁) receptor as an example. From long MD simulations, conformational ensembles with different roles in ligand binding and receptor activation are sampled to establish four states identified as either “open” or “closed” for the PAC₁ receptor. Next, the dynamical network can be applied to analyze the simulations and identify key features within each conformational ensemble, which help distinguish the ligand-bound states of the PAC₁ receptor from the ligand-free one. Further, the Markov State Model has emerged as a key approach to construct the transition network and connect the GPCR ensembles, providing detailed information for the transition pathways and kinetics. For the ligand-free PAC₁ receptor, the transitions within the closed states are near 10–30 times faster than the open-closed transitions, which is likely related to the activation mechanism of the receptor. Overall, long MD simulations and analyses are useful to assess conformational transitions for the Class B GPCRs and to gain mechanistic insight, which is difficult to obtain using other methods.

1. Introduction

G protein-coupled receptors (GPCRs), the largest family of trans-membrane proteins in the human genome, transduce a variety of signals, including hormones, neurotransmitters, odorants, tastants, and light, to regulate virtually all physiological responses for homeostasis [1, 2]. The more than 800 canonical heptahelical receptors are divided into 5 major classes based on sequence and structural similarities: rhodopsin (Class A); secretin (Class B); glutamate (Class C); adhesion and frizzled/taste. Class A is the largest class of more than 700 members with ~40 unique structures available. With just 15 members, the Class B secretin/glucagon/VIP family of GPCRs is critically important with respect to neural development, body calcium homeostasis, glucose metabolism, circadian rhythm, thermoregulation, inflammation, feeding behavior, pain modulation, stress and related endocrine responses [3–5]. Accordingly, these receptors are pharmacological targets for a variety of disorders including osteoporosis, hypercalcemia, type 2 diabetes, obesity, migraine and related chronic pain disorders, anxiety and depression. Despite the great pharmacological interests, only two full-length Class B receptor structures [6–8] have been determined. The three-dimensional molecular structures remain entirely or partially elusive among most Class B members. As a result, the detailed knowledge of receptor activation and regulation, such as the transitions among various states, is still incomplete. Therefore, for insight into ligand selectivity, activation, and regulation mechanisms, it is crucial to apply computer modeling to study the conformational states, as well as the associated transition pathways. Such insight will also serve as the foundation to design structure- and mechanism-based strategies to modulate Class B GPCRs.

Class B GPCRs are activated by well-studied peptide hormones, such as corticotropin-releasing factor (CRF), calcitonin gene-related peptide (CGRP), glucagon, glucagon-like peptide (GLP), pituitary adenylate cyclase activating polypeptide (PACAP), parathyroid hormone (PTH), secretin, and vasoactive intestinal peptide (VIP). The functional states are associated with distinct protein conformations as well as the presence of various ligands. One of the major challenges in studying the conformational transitions of Class B receptors is capturing the dynamics of the full-length receptor structure to accurately simulate the two-domain binding model for receptor activation [9]. In contrast to Class A GPCRs, which contain only the heptahelical transmembrane domain (7TM), each Class B receptor possesses an additional extracellular domain (ECD) of ~120 amino acid residues that is crucial for high affinity peptide binding and dynamics that allow bound-ligand presentation to the 7TM for receptor activation. Given such structural complexity, the choreography of Class B receptor activation—induced by the neuropeptide—is likely different from that of Class A receptors.

Although only few are available in full-length structures in Class B family, e.g. the glucagon receptor (GCGR, PDBIDs: 5XEZ and 5YQZ) and glucagon-like peptide 1 receptor (GLP-1R, PDBID: 5NX2), the construction of full-length models of other Class B receptors is viable with current knowledge of the 7TM and ECD structures. The 7TM structures of four members had been determined between 2013 and mid-2018: GCGR (PDBIDs: 5XEZ, 5YQZ, 5EE7, and 4L6R), corticotropin-releasing factor receptor (CRF₁R, PDBID: 4K5Y), GLP-1R (PDBIDs: 5NX2, 5VAI, 5VEW, and 5VEX), and calcitonin receptor (PDBID: 5UZ7). The ECD structures of nine members are known: glucose-dependent insulinotropic polypeptide (GIP) receptor (PDBID: 2QKH), GCGR (PDBIDs: 4ERS and 4LF3), GLP-1R (PDBIDs: 3IOL, 5E94, 3C59, 3C5T, and 4ZGM), PACAP receptor type 1 (PAC₁R, PDBIDs: 2JOD and 3N94), VIP/PACAP receptor type 2 (VPAC₂R, PDBID: 2X57), PTH₁ receptor (PDBIDs: 3CM4 and 3H3G), CRF₁R (PDBIDs: 2L27, 3EHS, and 3EHU), CRF₂R (PDBIDs: 1U34 and 3N96), and CGRP receptor (PDBIDs: 3N7P, 3N7R, and 3N7S). These experimental efforts allow the exploration of function-related conformational states and the assessment of transitions among these states via protein modeling and molecular dynamics (MD) simulations. Under physiological conditions, GPCRs are not static and often transition fluidly and fleetingly from one conformation to another, forming ensembles of receptor microstates that kinetically constitute macrostates. These constitutive macrostates may respond to binding of specific ligands and allosteric modulators or preferentially favor particular signaling events. Thus, long MD simulations (conventional or with enhanced sampling) followed by structural-based analysis are suitable to sample and distinguish these states, as well as to identify their transitions.

However, despite the large body of simulation studies of Class A GPCRs [10–16], the growth of MD simulations to investigate Class B GPCRs (with the full-length or 7TM models) has only emerged recently, due to the increasing amount of 7TM crystal structures. These simulation studies range from a few hundred nanoseconds to tens of microseconds and have provided valuable information regarding the molecular basis of receptor dynamics [17, 18], stabilizing effects from point mutations [19], hydrogen bonding network at an allosteric site [20], and inactive-to-active transitions focusing on TM displacement [21, 22]. Often in good agreement with experimental evidence, these recent studies provide invaluable mechanistic insight, which is typically costly and lengthy to study using experimental approaches alone. With advances in high-performance computing (HPC) [23, 24] and multiscale modeling technology [16, 17, 24–27], MD simulations have become useful tools to explore more complex systems (i.e., Class B GPCRs in the oligomeric states, the ligand-bound states, or the G protein/arrestin-bound states) on biologically relevant timescales. In this chapter, we provide a basic introduction to the methodology of MD simulation and the analysis to study conformational transitions of Class B GPCRs involving large-scale domain motions and helical displacements, using our studies of the PAC₁ receptor as an example.

2. Methods

2.1. Description of the MD Protocol

2.1.1. Conventional MD Simulations

An MD simulation describes the motion of a collection of molecules over time in a system of interest according to the physical and chemical principles. Such a system often contains essential chemical/biological components (such as proteins, water, lipids, and ions) in a three-dimensional box at a condition to mimic real-world experiments (such as temperature and external pressure). Generally, in an all-atom model, each atom is represented by a particle at a specific position in the simulation box with periodic boundary conditions, while the covalent bonds are treated like springs. The interactions between particles are described by equations and parameters—the so-called force field. According to the Newton’s laws, the particle motions are calculated in discrete time steps analogous to the film frames in a movie. The positions of atoms are updated from one step to the next; in a continuous fashion, as atoms move and time advances, a cinematic feature is constructed to show the conformational changes or transitions in the simulation box. In real practice, the time step for biological simulations is often chosen to be around 1 to 2 femtoseconds (fs). Therefore, for a typical simulation of 100 nanoseconds (ns), the number of steps approximates a million for over ten thousand atoms in the system; multiple simulation trajectories (or replicas) are needed for each model construct to ensure reliable data collection. With such high computational demands, MD simulations (i.e., for GPCRs) often require supercomputing resources.

In one of our studies of the PAC₁ receptor, for example, each model system contains a PAC₁ receptor model, a lipid bilayer of ~219 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) molecules, ~28,500 TIP3P water molecules, counter ions, and 0.15 M NaCl, totaling ~126,000 atoms in a periodic box of 95 × 95 × 134ų. All the simulations were performed with CHARMM36-cmap force field on the specialized Anton supercomputer using the Anton software 2.13.0 [23, 28]. Microsecond-long MD simulations (2–2.9 μs) for four conformational states were performed in an NPT ensemble (310 K, 1 bar, Berendesn thermostat and semi-isotropic barostat) with a time step of 2 fs (see Note 1).

2.1.2. Preparation of the Starting GPCR Models

The conformational transition between two states of biomolecules, initial state (A) and final state (B), is often under thermodynamic (downhill energy profile) and/or kinetic control (uphill energy profile) [29]. For systems where the probability of reaching B is very low, a strategy is to start with multiple intermediate points which may proceed to A or B while their early conformational evolutions can structurally overlap within a certain range (initial region). Our current class B GPCR study [17] indicated that in a microsecond-long MD simulation, the dynamic free-swinging process of the ECD, exposed to the solution, occurred during the first few hundred nanoseconds, after which the ECD interacted with the extracellular loops (ECLs) of the 7TM to greatly restrict its mobility. The large-scale domain motions lead to different ECD orientations with slight positional variations at the ECD–7TM interface. Thus, it is appropriate to choose initial conformations that have ECD free of interactions with ECLs and of different orientations relative to 7TM to initiate the conformational sampling. Notably, these starting conformations are likely metastable, and thus require them to be well equilibrated in short MD simulations. In our preparation of the PAC₁ receptor models, four homology models, differing in the ECD orientations by dihedral rotation at the linker region, were generated from multiple short MD simulations for microsecond-long production simulations [17]. Additionally, the initial models can also be generated using enhanced sampling methods, such as replica exchange [30], adaptive tempering [31], steered MD [32], and accelerated MD [33]. In particular, these methods can accelerate a kinetic-control process, for example, the transition from inactive to active receptor states and vice versa involving the displacement of the intracellular structures related to transmembrane helix 6 (TM6) [21, 22].

2.2. Analytical Methods for Conformational Transitions

While MD simulations provide direct visualization of GPCR conformations and conformational changes, the rich detail of atom positions also allows qualitative and quantitative characterizations of each conformational state and the transition from one state to another. For example, from four microsecond-long MD simulations [17], we obtained two major conformations distinct in the ECD orientations as the closed (G1, G2, and G3) or open (G4) states (Fig. 1), which implicate differential roles in ligand binding and receptor activation. Herein, we introduce two typical methods to analyze the conformational ensembles of Class B GPCRs and their transitions.

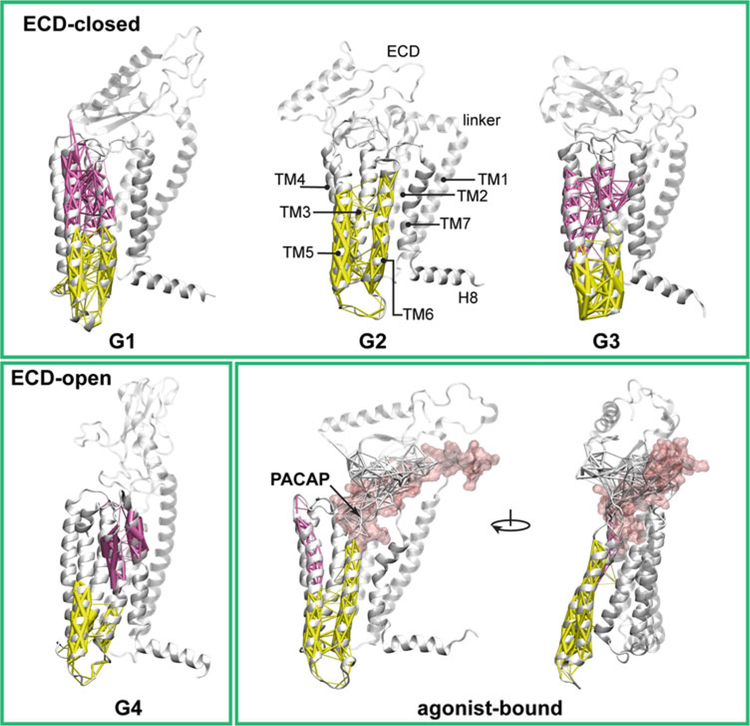
Fig. 1.

Community analysis of the ligand-free ECD closed and open states, and the agonist-bound active state of the PAC₁ receptor. The community decompositions of TM6 are displayed with weighted edges (thicker edges show greater correlation). The dynamical networks were created from the last 150 ns of each trajectory. In the ligand-free states G1, G3, and G4, TM6 splits into two communities, its extracellular half joins communities containing TM3 or TM7. In G2, TM6 merges into the community with the intracellular half of TM3. In the agonist-bound conformation, the entire TM6 behaves as a single community with the intracellular half of TM5 and fewer correlations with TM3. Thus, in the agonist-bound PAC₁ receptor, residues within TM6 can propagate information relatively easily through multiple routes from the extracellular side to the intracellular face of the receptor without perturbations from other TM helices

2.2.1. Dynamical Network Analysis

Given the conformational ensembles of variant ECD orientations, analysis of the dynamical network has been applied to identify the shared features of interactions and communication within the ligand-free PAC₁ receptor (G1, G2, G3, and G4), in comparison with a trajectory in the ligand-bound state. Such analysis can be readily carried out with the Network View plugin [34–36] in the VMD program [37]. Dynamical networks were created from the last 150 ns of each trajectory. To define the dynamical network, each Cα atom of amino acid residues represents a node; two nodes are connected by an edge if any two of their heavy atoms are within4.5Å for more than 75% of the simulation time [36]. The edge distances d_ij are derived from the pairwise correlations (C_ij) calculated by the program Carma v1.3 [38]. The community substructure of the network is obtained by the Girvan–Newman algorithm [39]. With correlation-based weights, communities correspond to sets of residues that move in concert with each other. The connections between nodes (representing amino acid residues) within one community should be stronger than the connections between nodes across different communities.

TM6 and the third intracellular loop (ICL3) play an essential role in the signaling process of GPCRs—by facilitating the binding of G proteins or other effector proteins at the intracellular receptor face after an outward conformational shift of the TM6/ICL3 segments (in the active state) [11]. The community decompositions of TM6 with weighted edges are displayed in Fig. 1 for four ligand-free states of the PAC₁ receptor, in comparison with a ligand-bound state. In the ligand-free G1, G3, and G4 states of the PAC₁ receptor, TM6 can be divided into two communities with its extracellular half (Fig. 1, purple) merging into communities containing TM3 or TM7. In G2, although the entire TM6 lies in the same community, it also joins the community containing the intracellular half of TM3. Thus, in all ECD open or closed ligand-free states, TM6 can be separated into two communities and exhibits topological dependency with adjacent TM helices (stronger correlations). By contrast, in the agonist-bound state, the entire length of TM6 behaves as a single community together with the intracellular half of TM5 and fewer correlations with TM3. The stronger communication within TM6 in the agonist-bound state may associate with signal propagation from the agonist-bound orthosteric pocket to the intracellular G protein-binding site. In direct terms, with fewer correlations with other neighboring TM helices, the single TM6 community permits an easier outward shift of the helix for the conformational changes necessary at the intracellular receptor face for G protein coupling and signaling.

2.2.2. Markov State Models

By applying the analysis based on the Markov State Model (MSM) to the extensive MD trajectory datasets, we have revealed the microsecond to millisecond-scale dynamics between open and closed PAC₁ receptor conformations, interconnected within an ensemble of transitional states—timescales toward GPCR activation. The open-to-closed transition, together with the intrinsic features of the receptor, can provide important insight into signaling mechanisms and potential druggable sites. In the following, we describe the general concept and implementation of MSM, our construction and validation of MSM, and our transition paths and timescales among the PAC₁ receptor ECD open and closed states.

We used the program MSMBuilder 3.2.0 [40, 41] to build a reversible MSM (see Note 2 for examples of execution). An MSM contains a set of state definitions and a transition matrix characterizing the kinetics on this state space. MSM can model long-time scale kinetics from much shorter trajectories by efficiently sampling transitions between these metastable states [42–45]. For MD simulations, the MSM approach first transforms a collection of MD trajectories into a discrete set of S = {1, …, m} microstates in the conformation space. A m × m transition matrix T(τ) is computed, where each element T_ij measures the probability of system going from one microstate (i) to another (j) within an observation time interval τ (lag time), by $T_{ij}=c_{ij}/{\sum }_{k=1}^m{c}_{ik}$. Here, c_ij counts the number of times the system traverses from i to j at time τ. At timescales slightly longer than the microstate lag time, i.e. 2τ, …, nτ, the transition counts become less between microstates and fewer microstates are kinetically connected in a transition matrix. For a Markov process, the vector of probabilities of the system to be in any of its microstate at time (nτ) must meet the Chapman–Kolmogorov equation [42, 46].

$$p(n\tau )=p(0)T(n\tau )\approx p(0){[T(\tau )]}^n$$ (1)

1. Dataset preparation.

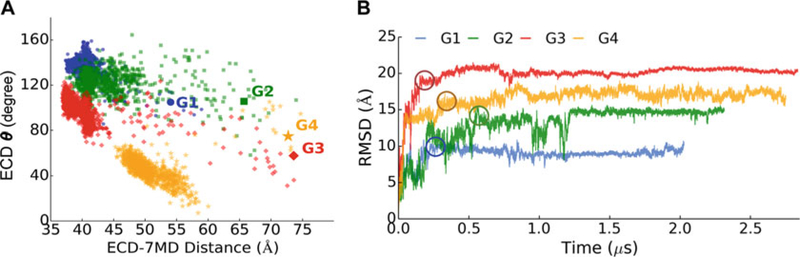
First, we prepared all trajectories using the C_α coordinates of residues 30–419 in the PAC₁ receptor, as the C_α atoms are often used to represent the overall protein structure. The first five and the last five amino acid residues were excluded, because they are highly dynamic in the N- and C-termini. The time evolutions of the receptor structures show that each PAC₁ receptor model reached a relatively stable structure after 200–500 ns; continuous structure relaxation improved the stability for another 1.5–2.5 μs (Fig. 2b). The last 1.5–2.5 μs of each microsecond simulation with stable final conformations were not included in building an MSM (see Note 3). Hence, the collected six shorter MD simulations of 20–50 ns each, and the first 200–550 ns of the microsecond long simulations, totaling 6324 configurations were used to build the MSM.

Fig. 2.

(a) Plot of the ECD tilt angle (θ) against the ECD–7TM distance. Starting points are labeled with larger markers. (b) Time evolution of overall RMSD of the PAC₁ receptor. RMSDs were computed by backbone alignments on initial structures with standard deviations of 0.34–0.56Å in the last ~1.5 μs. Each model of the PAC₁ receptor reached a relatively stable state after 200–500 ns, which had been continuously relaxed to demonstrate model stability for another 1.5–2.5 μs. The conformational states between which we calculated the shortest pathways are circled. Reprinted from Liao C, Zhao X, Brewer M, May V, Li J (2017) Sci Rep 7 (1):5427 with permission from Scientific Reports

2. Clustering.

Next, the MD trajectories were transformed into a dataset of microstates based on structural similarities. We used the k-centers algorithm [40] to group the dataset into 55 clusters by RMSD metric with a mean distance of ~0.34Å and a maximum distance of ~0.56Å, which were within the range of the RMSD standard deviations of the last ~1.5 μs in Fig. 2b. The small cluster number, different from the hundreds to thousands of intrinsic conformations of previous protein folding/unfolding studies [47, 48], is the result of limited conformational changes like the ECD rotation around the melting linker.

3. Lumping and validation.

A series of transition matrices in the evolution of the observation interval (lag time) at τ, 2τ, …, nτ were constructed using maximum likelihood estimation. As the lag time is increased, fewer microstates are kinetically relevant (kinetically reach each other on timescales faster than the lag time) [49]. Thus, those kinetically relevant microstates can be lumped into macrostates (larger and coarser grained) using the Perron-Cluster Cluster Analysis (PCCA) method [50]. Validation was carried out to examine if the model at lag time = τ appears Markovian with increasing lag time = 2τ, …, nτ using both implied timescales and the Chapman–Kolmogorov test [46]. If the macrostate partitions were less robust along implied timescales or if the Markov model errors between the true probability density at time nτ and the probability density predicted by the Markov model at the same time were large, then a refinement of the partition [46] or an improvement of the initial dataset [49] would be necessary.

4. Implied timescales.

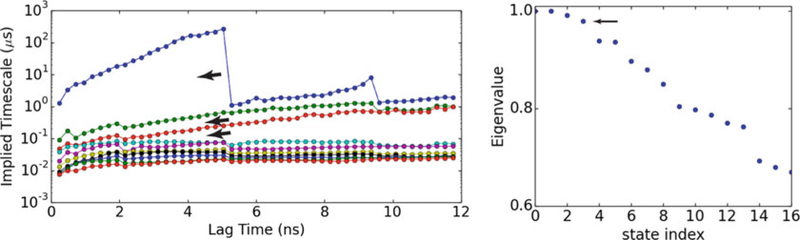
The implied timescales as a function of the lag time and the eigenvalues of the transition matrix are shown in Fig. 3. Four macrostates were selected, given the number of the major gaps of the implied timescales as well as the number of eigenvalues of the transition matrix that were close to 1 [50]. For a transition matrix of microstates, the partition of four macrostates was calculated from the eigenfunction structure using PCCA [50]. Consistently, the conformations of G1, G2, G3, and G4 were lumped into the four macrostates, labeled as A, B, C, and D, respectively.

Fig. 3.

Left panel: Implied timescales as a function of the lag time. There are three major gaps lasting from 2 to ~9 ns, implying four macrostate partitions (count as one more than the number of implied timescales above the major gap) [40]. Right panel: eigenvalues of the transition matrix at lag time of 4.8 ns. Only the first seventeen data are shown. There were four points close to 1. Reprinted from Liao C, Zhao X, Brewer M, May V, Li J (2017) Scientific Reports 7 (1):5427 with permission

5. Chapman–Kolmogorov test.

In general, given a set of states A that contains either an individual microstate or set of micro-states, we compared the true probability density of T(nτ) based on the transition counts (known as observed trajectory) and the probability density predicted by [T(τ)]ⁿ [46, 48]. The initial stationary distribution at time τ restricted to a set A is given by

$$w_i^A=\{\begin{array}{cc}\frac{{\pi }_i}{{\sum }_{j\in A}{\pi }_j}& i\in A\\ 0& i\notin A\end{array},$$ (2)

where π is the stationary probability of the m × m transition matrix T(τ). The trajectory-based time-dependence of the probability after time nτ with starting distribution w^A is given by

$$p_{\text{MD}}(A,A;n\tau )=\sum _{i\in A}{w}_i^A{p}_{\text{MD}}(i,A;n\tau ),$$ (3)

where p_MD(i, A; nτ) is the trajectory-based estimate of the stochastic transition function given by

$$p_{\text{MD}}(i,A;n\tau )=\frac{{\sum }_{j\in A}{c}_{ij}^{\text{obs}}(n\tau )}{{\sum }_{j=1}^m{c}_{ij}^{\text{obs}}(n\tau )},$$ (4)

where $c_{ij}^{\text{obs}}(n\tau )$ is the number of transition counts between states i and j at time nτ. Likewise, the probability to be at A by the Markov model is given by

$$p_{\text{MSM}}(A,A;n\tau )=\sum _{i\in A}{\left[{\left(w^A\right)}^T{T}^n(\tau )\right]}_i,$$ (5)

We tested how well the equality p_MD(A, A; nτ) = p_MSM(A, A; nτ) holds, as whether the solid line is within the error bar range of the dash line in Fig. 4. The uncertainties of the transition probabilities estimated from the MD trajectories are computed as:

$${ϵ}_{\text{MD}}(A,A;n\tau )=\sqrt{n\frac{p_{\text{MD}}(A,A;n\tau )-{\left[p_{\text{MD}}(A,A;n\tau )\right]}^2}{\sum _{i\in A}{\sum }_{j=1}^m{c}_{ij}^{\text{obs}}(n\tau )}}.$$ (6)

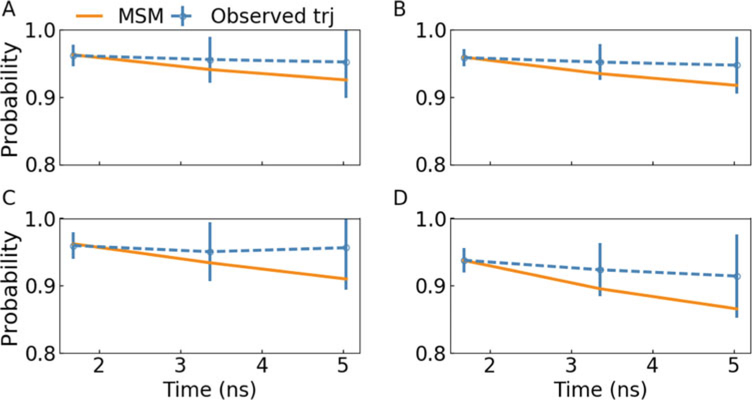
Fig. 4.

Microstates, which constitute the shortest and second shortest transition pathways between the closed and open states, were divided into four subsets (a, b, c, and d) according to the macrostate division and examined by the Chapman–Kolmogorov test. The transition probabilities from MSM agreed well with the probabilities in the observed trajectories within statistical uncertainty. Reprinted from Liao C, Zhao X, Brewer M, May V, Li J (2017) Scientific Reports 7 (1):5427 with permission

There are around 27 microstates that constitute the shortest and second shortest transition pathways between the closed and open states; they are identified as four subsets based on the macrostate division. The Chapman–Kolmogorov test of the four subsets is shown in Fig. 4, all of which ensure the test within statistical uncertainty. The transition probabilities from MSM agree well with the probabilities in observed trajectory within statistical uncertainty at a lag time of 1.68 ns. Thus, we built a four-macrostate MSM with 94% data in use with the lag time of 1.68 ns.

We used transition path theory (TPT) [48, 51–53] to calculate the minimum transition net flux of the shortest pathway connecting the ECD closed states or from the ECD open states to the closed states in the transition matrix. For state space S = {1, …, m}, we define the source set A, the target set B, and the intermediate set I. The rate of transitions observed from A → B per τ (time unit) is given by:

$$k_{\text{AB}}=F/\left(\tau {\sum }_{i=1}^m{\pi }_i\left(1-q_i^{+}\right)\right)$$ (7)

where F gives the total transition flux by $F=\sum _{i\in A}\sum _{j\notin A}{\pi }_i{T}_{ij}{q}_j^{+}$, π_i is the stationary probability at state i, and $q_i^{+}$ is a committor probability, $q_i^{+}=0$ for i ∈ A, $q_i^{+}=1$ for i ∈ B, $q_i^{+}=\sum _{j\in S}{T}_{ij}{q}_j^{+}$ for i ∉ {A, B} [48, 51, 54, 55]. With the lag time divided by the minimum transition net flux, we obtained the time to travel from one set of states to the other. The minimum transition net flux, number of micro-states, and the estimated transition time in the shortest pathway between the ECD closed and open states are summarized in Table 1. The pathways connecting the closed states (G1, G2, and G3) are relatively short, but from the closed states to the open states (G4) it is rather remote, suggesting a clear partition in the conformational states. Regarding the minimum transition flux, the reversible transitions within the closed states are about 10–30 times faster than the transition from open states to a closed one. Key conformations in the shortest pathways among closed and open states are summarized in Fig. 5.

Table 1.

The minimum transition net flux, the number of microstates, and the estimated transition time of the shortest pathways between the ECD closed and open states shown in Fig. 5

	G1–G2	G1–G3	G2–G3	G1–G4	G2–G4	G3–G4
Minimum net flux (10−5)	6.10	7.17	7.84	0.41	0.26	0.59
Number of microstates	3	5	3	13	12	11
Transition time (μs)	27.6	23.4	21.4	412.3	650	284.5

Note: G1, G2, G3, and G4 are represented by one or two microstates

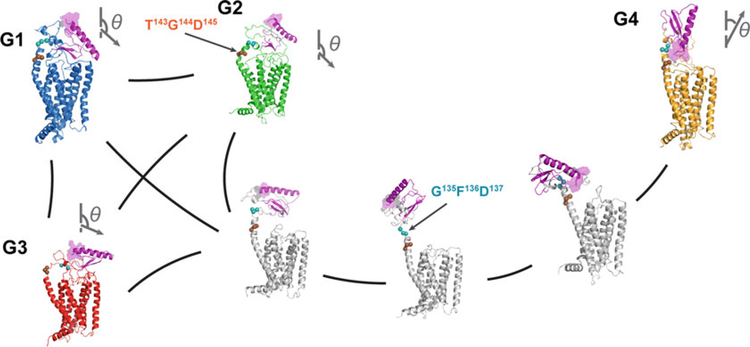
Fig. 5.

Illustration of the PAC₁ receptor’s conformational transition between the ECD open (G4) and closed (G1–G3) states with representative states from MSM and the transition-path theory. Vectors (showing the N-to-C direction of helix 1 in ECD) show the ECD orientations; and the ECD N-terminus is highlighted in a purple surface representation. Reprinted from Liao C, Zhao X, Brewer M, May V, Li J (2017) Scientific Reports 7 (1):5427 with permission

3. Conclusions

In summary, conformational ensembles with different roles in ligand binding and receptor activation can be discovered using long MD simulations. Using the dynamical network analysis, shared features can be revealed in conformational ensembles of variant ECD orientations, comparing with a ligand-bound state. With the construction of Markov State Model, the transition network kinetically connecting various GPCR ensembles can be identified. Overall, long MD simulations combined with these structural and kinetic analyses are useful tools to assess conformational transitions for the Class B GPCRs, based on which mechanistic insight can be gained to guide future designs of therapeutics to target these receptors.

4. Notes

1. In the MD simulations run by the program NAMD [56], we used the technology of Langevin dynamics [57] with a low damping coefficient of 1 ps⁻¹ for the temperature control and the Nose-Hoover Langevin piston pressure control [58, 59] with a piston period of 0.05 ps and a piston decay time of 0.025 ps (default settings). In the microsecond-long MD simulations performed on the Anton supercomputer, Berendesn thermostat/barostat were applied for the NPT ensemble.

2. Examples of Execution (Modules may change according to different versions of MSMBuilder):

   ### building microstates

   msmb KCenters --inp ‘trajectory_path/*.dcd’ --transformed kcenters_rmsd.h5 --metric

   rmsd --top trajectory_path/ca.pdb --n_clusters 55 --random_state 1746

   ### building a transition matrix (in python interface)

   from msmbuilder.dataset import dataset

   from msmbuilder.cluster import KCenters

   from msmbuilder.msm import MarkovStateModel

   ds = dataset(‘kcenters_rmsd.h5’)

   model = MarkovStateModel(lag_time=1, verbose=True).fit(ds)

   for i in range(0, len(model.transform(ds))):

                         print i, len(model.transform(ds)[i])

   sample = model.draw_samples(ds, 5)

   ###-scan implied_timescales---

   tscale=[]

   n=[]

   for i in range(1, 50):

                           model = MarkovStateModel(lag_time=i, n_timescales=10, verbose=True).fit(ds)

                           n.append(model.n_states_)

                           tscale.append(model.timescales_)

   ### lumping microstates to macrostates

   model.eigtransform(ds, right=True, mode=‘clip’)

   model.eigenvalues_

   ### choose number of macrostates base on model.eigenvalues_ that are closed to 1.

   from msmbuilder.lumping import PCCAPlus

   pcca = PCCAPlus.from_msm(model, n_macrostates=4)

   macro= pcca.microstate_mapping_

   ###-stationary population–

   model = MarkovStateModel(lag_time=1, verbose=True).fit(ds)

   mydict = {i:model.populations_[i] for i in range(0, model.n_states_)}

   top_pi=sorted(mydict, key=mydict.__getitem__, reverse=True)

   ### key attributes for Chapman-Kolmogorov test

   model.mapping_

   model.populations_

   model.countsmat_

   model.transmat_

   ### find the first five shortest paths

   from msmbuilder.tpt import net_fluxes

   from msmbuilder.tpt import paths

   netflux = net_fluxes(int, lst, model)

   topN = paths(int, lst, net, num_paths=5)

   commitor = committors(int, lst, model)

3. The last 1.5–2.5 μs of each microsecond simulation with stable final conformations were not included in building an MSM. A few trial tests showed that large population of final states caused the MSM to trim off the initial regions of less population and keep only some final states of large population to be most kinetically relevant.