Robustness analysis for external beam radiotherapy treatment plans: describing uncertainty scenarios and reporting their dosimetric consequences

Abstract

In external beam radiotherapy, uncertainties in treatment planning and delivery can result in an undesirable dose distribution delivered to the patient that can compromise the benefit of treatment. Techniques including geometric margins and probabilistic optimization have been used effectively to mitigate the effects of uncertainties. However, their broad application is inconsistent which can compromise the conclusions derived from cross-technique and cross-modality comparisons. This report describes robustness analysis as a framework that is applicable across treatment techniques and modalities. It identifies elements that are imperative to include when conducting robustness analysis and describing uncertainties and their dosimetric effects. The purpose of this more consistent approach to robustness analysis is to promote reliable plan evaluation and dose reporting, particularly during clinical trials conducted across institutions and treatment modalities.

Summary

Uncertainties in radiotherapy treatment planning and treatment delivery compromise the integrity of the desired dose distribution. Appropriate consideration of these uncertainties will improve the description of the delivered dose as well as our understanding of their clinical impact. This article identifies the elements required for a precise, unambiguous description of uncertainties and of their dosimetric effects.

In external beam radiotherapy, numerous uncertainties result in differences between the desired and delivered dose distributions. These include uncertainties in the information within planning images and models, limited machine precision, patient setup errors, and anatomy changes. Treatment plan robustness is the degree to which the desired dose distribution is resilient to these uncertainties, and it varies with treatment site, technique, and modality (Figure 1). Varied effects of uncertainties on treatment plans and varied techniques employed by treatment planners make accurate clinical comparisons challenging. This is especially true across treatment modalities where the target volume may be managed differently. For comparisons, the dose distribution to be assessed, reported, and correlated with clinical outcomes should be the best estimate of the actual delivered dose, including the influence of uncertainties. The risk of inaccurate comparisons has been a concern as there is currently no widely applied standard for quantifying and reporting plan robustness or the effects of uncertainties.

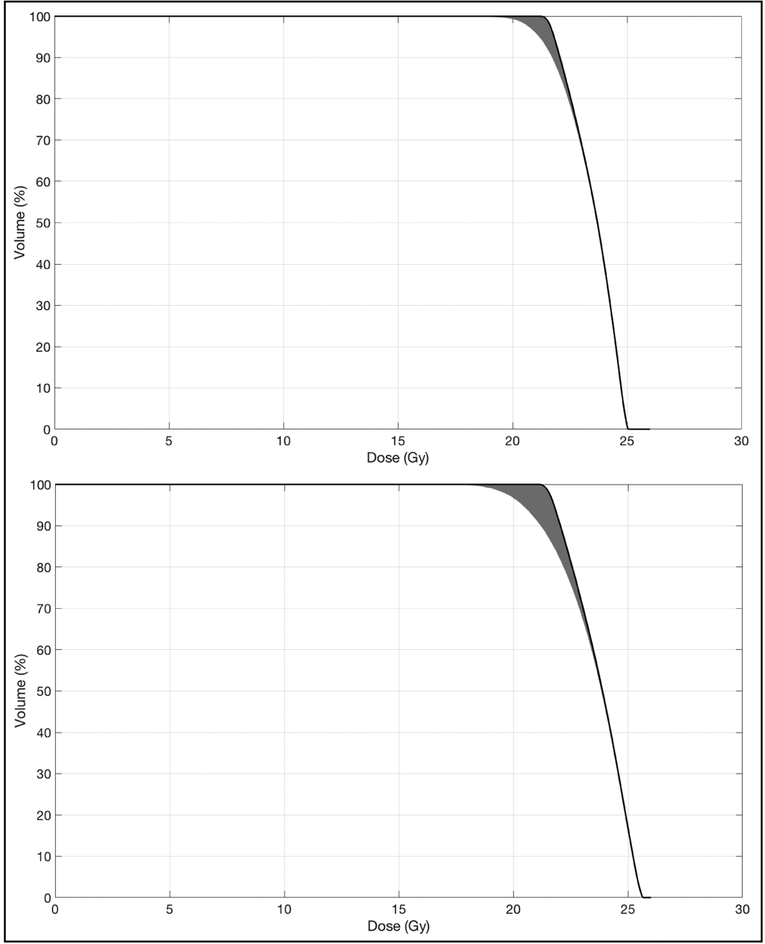
Figure 1:

Dose-volume histograms of two plans with similar static target coverage, but differing robustness. The black lines are the target DVH under the nominal dose distribution while the gray bands represent 1,000 example target DVHs that result from translations and rotations applied to the nominal plan. Prescription dose was 21 Gy.

This report has two aims. The first is to provide a brief overview of relevant uncertainties and use of robustness analysis in the treatment planning process. The second is to comment on considerations that are important when conducting and reporting treatment plan robustness analysis.

Addressing uncertainties in treatment planning

A common benchmark for dosimetric accuracy delivered in external beam radiotherapy is ±5% as recommended by the International Commission on Radiation Units and Measurements (1). The most widely used technique to mitigate the effects of uncertainties on a photon treatment plan is the use of safety margins described in ICRU Reports 50, 62, and 83 (2–4). These reports present the observable gross tumor volume (GTV), the clinical target volume (CTV) for microscopic disease, the internal target volume (ITV) for internal motion, and the planning target volume (PTV) for setup errors. By targeting the PTV, the treatment plan is presumed to deliver adequate dose to the CTV (5, 6).

The safety margin approach makes several assumptions. The first is that modest changes in patient position or anatomy do not affect the dose distribution. The treatment plan is considered a “static dose cloud” and independent of the changing patient. Englesman et al. conducted a phantom study considering systematic and random errors along with respiratory motion. They observed a maximum decrease of 3.3Gy (5%) for clinically relevant uncertainty parameters (7). Similarly, Beckham et al. observed a 5% maximum dose difference after simulations using a normal distribution of random errors with a 1.0cm standard deviation (8).

A second assumption is that effects of interplay between intrafractional motion and dynamic fluence patterns are negligible. This was broached several decades ago by Yu et al. (9). Under a static dose cloud approximation, effects of random and systematic setup errors can be represented by blurring and shifting the nominal dose distribution, respectively (6, 10). A blurred dose distribution was used by Bortfeld et al. to show that for breathing motion, the interplay does not strongly affect the expectation value of the dose (11). However, the point dose variance depends on treatment technique (11). Court et al. provide analysis of dose on target and MLC motion parameters (12, 13). Similarly, Jiang et al. evaluated the dose delivered to lung tumors with different dose rates, MLC modes, and respiratory phases. They found the mean dose difference to be 2–3% (14).

The implementation of safety margins depends on details of the treatment technique. Numerous investigators have evaluated the effect of image-guidance schedules on the necessary margin magnitudes and observed that increasing the frequency of image-guidance allows for smaller margins (15–20). The magnitude of margins has been shown to depend on the modality used for image-guidance (21, 22). It is anticipated that margins will continue to adapt to and improve with advances in image-guided radiotherapy techniques like real-time fiducial tracking (19) and advanced anatomic imaging (20).

The safety margin paradigm for photons cannot be directly extended to protons. The proton depth dose curve features a Bragg peak. Calculation uncertainties and temporal variations of the location of the Bragg peak render the static dose cloud assumption invalid, causing the conventional isotropic margin schema to fail. However, the PTV continues to be used.

Beyond uncertainties shared with photon therapy, there are additional proton therapy-specific uncertainties in range and the relative biological effectiveness (RBE). Discrepancies in proton range stem from uncertainties regarding Hounsfield Unit values, their conversion to relative proton stopping power, proton beam reproducibility, beam commissioning measurements, and, for scattered beams, range compensator fabrication (23). Equations can be used to determine the margin along each proton beam and are commonly based on Moyers et al.: Distal Margin = α% Range + βmm, where α relates to uncertainties in dose calculation and β relates to errors independent of dose calculation (24). Distal margins are beam-specific and not currently supported in commercial planning systems. Emerging technologies like proton CT show promise in reducing this uncertainty by directly measuring relative stopping powers (25).

Density variations along the beam axis displace the Bragg peak. For passive scattering deliveries, this is mitigated by smearing the range compensator. Reducing the proton beam conformity to the distal edge of the target promotes coverage under motion and setup errors. For scanned proton beams with no range compensator, either a margin is added along the beam or the potential displacement is factored into optimization. In addition, interplay between dynamic pencil beam delivery and target motion can result in dose heterogeneities approaching 20% error at the target edge (26). Techniques like re-painting spots, increasing spot size, and gating delivery can mitigate interplay effects (26).

Another major source of uncertainty is the RBE, often considered as a constant value of 1.1 (27). In reality, RBE varies and depends on linear energy transfer to the medium, dose per fraction, tissue and cell type, oxygenation level, and biological or clinical end point (28). Accurate quantification of these effects has not yet been achieved in vivo. It is believed that proton RBE correlates with linear energy transfer (LET). Because LET increases as proton energy decreases, the RBE is thought to increase at the end of the range (27). Currently, empirical methods are employed to account for this uncertainty.

Probabilistic approaches for plan robustness evaluation

An alternative to margins is to consider uncertainties from a probabilistic perspective. While generalizable to photon plans and passively-scattered proton therapy (PSPT) plans, this technique is essential for intensity modulated proton therapy (IMPT). As a result, IMPT plan assessment has been the primary arena for development of probabilistic robustness analysis techniques.

Many techniques start by determining the dose distribution under several instances of uncertainty conditions, such as translational shifts or proton range values (29–32). The effects of fractionation (33), interplay of treatment delivery and respiratory motion (30, 34, 35), and uncertainty in RBE values (36) have all been studied.

Numerous approaches exist to represent dose from this ensemble of uncertainty scenarios. One can consider the voxel-wise worst-case approach, where each voxel is evaluated based on the most undesirable dose it might receive (37–39). Alternatively, each dose distribution can be considered on the scale of the whole structure in a scenario-wise worst-case approach (40, 41). This avoids overly conservative dose depictions presented by the voxel-wise worst-case approach in physically unlikely configurations. A third option is to describe the simulation of scenarios according to the expectation value or variance of the delivered dose (37, 42, 43), or according to a model relating dosimetry to the uncertainty values (44). Techniques of minimizing the maximum optimization penalty (the “minimax” problem, or worst-case optimization) and optimizing the expected value have been described as specific cases of a general framework (45). These methods can be used to evaluate dose distributions and radiobiological parameters, or be incorporated into plan generation (32, 38, 39, 46–50). Incorporating these metrics into optimization of PSPT and IMPT is illustrated by Liu et al. (38, 39).

These techniques apply to photons as well, simplified by the validity of the static dose cloud approximation which allows for calculations with convolution (10, 11, 51–53). For photon-based IMRT, a static dose cloud may not be sufficiently accurate (54) and a voxel-wise uncertainty approach has been introduced (54–56). However, there is consensus that photon treatments are insensitive to uncertainties and the demand for robustness assessment is less.

It is clear different radiotherapy modalities vary in underlying physics, technology, and clinical implementation. Consequently, treatment planning techniques and evaluation metrics also differ, as do considerations and efforts made to address uncertainties. Treatment plan robustness analysis describes the dosimetric effects of uncertainties, leading to more accurate and more appropriate comparisons.

Robustness analysis and reporting results

Describing uncertainty scenarios

A logical technique to evaluate treatment plan robustness is to determine the dosimetric effects of delivering the plan under an ensemble of treatment scenarios, each featuring a different instance of uncertainty variables. Variations in dose will depend on details of the scenarios. It is imperative that characteristics of uncertainty scenarios be adequately described.

To begin with, the uncertainties considered in the analysis must be specified. These may include:

1. Uncertainties in position – e.g. rigid setup errors, internal anatomy non-rigid motion,

2. Uncertainties in imaging values or derived parameters – e.g. Hounsfield Units, electron density, stopping power ratios,

3. Uncertainties in physical or biological properties of the beam – e.g. depth doses, proton beam range, relative biological effectiveness.

Applications of robustness analysis should fully characterize the sources of uncertainty as well. Adequate characterization includes the magnitude and likelihood of uncertainty variable values, as well as the correlation between sources of uncertainties. To illustrate the need for this level of reporting, consider the following descriptions of two different sets of uncertainty scenarios potentially used as part of a robustness analysis. These hypothetical examples are similar enough that one might be tempted to directly compare them. However, the complete descriptions presented below reveal nuanced differences that will affect their results.

Description of Uncertainty Scenario Set 1

For robustness analysis, the dose was recalculated for 12 additional treatment scenarios comprised of individually combining a translational setup error of ± 5mm in the left-right, anterior-posterior, or superior-inferior directions with a ± 2% uncertainty in the photon beam data.

Description of Uncertainty Scenario Set 2

For robustness analysis, a static dose cloud was resampled for treatment scenarios derived from 1,000 random samples of a multivariate normal distribution of translational setup errors with mean μ and covariance matrix σ truncated at 3σ.

Description 1 features translational setup errors of a single magnitude and incorporates beam modeling uncertainty. Description 2 includes translational setup errors, but unlike Description 1, it considers combinations of errors in different directions and does not consider beam modeling uncertainties. Both descriptions convey the relative likelihood of each uncertainty scenario; Description 1 implicitly by providing the complete set of scenarios, and Description 2 by providing the form and parameters of the distribution (i.e. a multivariate normal distribution with μ and σ truncated at 3σ). Both descriptions provide sufficient information for others to replicate. Either description can serve as the basis for comparative robustness analysis. However, the two descriptions should not be compared with each other.

Lastly, a description of how dose is determined for each scenario must be included. The dose might be recalculated or approximated using a blurred dose distribution or static dose cloud.

Describing dosimetric consequences of uncertainty scenarios

Another important consideration is the representation of dosimetric variations resulting from the set of uncertainty scenarios. 3D dose distributions and dose-volume histograms (DVHs) can naturally be extended to depict dose from any particular scenario. Individually representing the many scenarios of robustness analysis may be impractical, particularly for 3D dose distributions. To simplify results, descriptive statistics such as minimum or maximum values, averages and standard deviations, or percentiles can be applied to 3D dose distributions or DVHs (42). Alternatively, the width of a band of DVHs resulting from dose based on uncertainty conditions is an indication of the treatment plan’s robustness (57). Plan quality metrics such as mean dose, target coverage, dose-volume points associated with specific toxicities, and dose heterogeneity indices can be presented statistically based on the worst-case scenario or with confidence intervals (30, 36).

It is important to recognize that results depend on how the statistics were performed. For example, one might determine the minimum dose to each voxel according to a set of uncertainty scenarios. An appropriately named “minimum DVH” could then be derived from this voxelized minimum dose distribution. This DVH is notably different, however, from the homonymous “minimum DVH” determined by first creating a DVH for each uncertainty scenario, and then determining the minimum value for each dose bin. The discrepancy between these methods is illustrated in Figure 2. Determining the minimum dose to each voxel before creating the “minimum DVH” severs the correlation of dose between voxels. This correlation is retained when a DVH is created for each scenario before determining the minimum DVH. While neither technique is inherently wrong, misinterpreting one of these “minimum DVHs” for the other could compromise conclusions from the robustness analysis. Therefore, the method used should be identifiable.

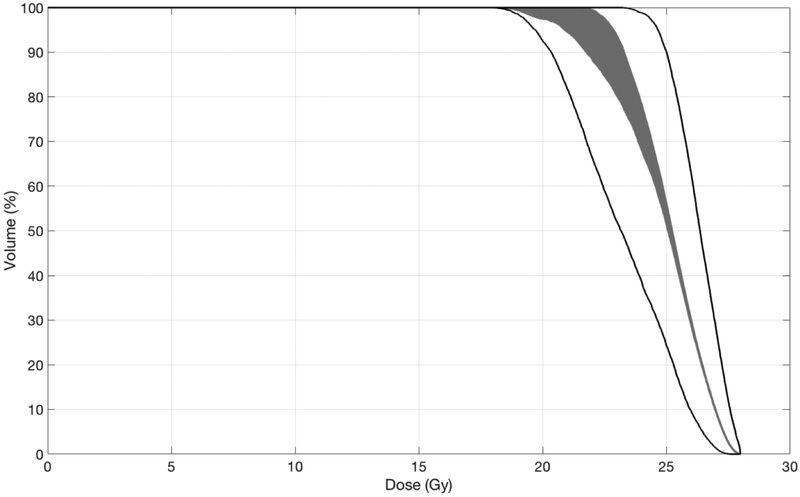
Figure 2:

Dose-volume histograms of a stereotactic radiosurgery target volume after 1,000 random rigid transformations. The large number of transformations provide a probabilistic description of the effects of errors for this example single-fraction treatment. Similar figures apply to conventionally fractionated treatments, in which case each curve will reflect an estimate of the cumulative dose delivered in one of many hypothetical treatment courses. The gray band is comprised of DVHs created from each of the 1,000 scenarios. The black lines are DVHs derived from the voxelized minimum and maximum doses. Note the discrepancy resulting from the order of determining the minimum or maximum dose and creating the DVH.

These considerations extend to radiobiological metrics derived from DVHs such as Equivalent Uniform Dose (EUD), Tumor Control Probability (TCP), or Normal Tissue Complication Probability (NTCP). For example, the average of the EUD calculated for each uncertainty scenario can be different from the EUD calculated from the average of the DVHs, or the EUD calculated from the DVH that was calculated from the average 3D dose distribution. However, all may be named the “average EUD.”

As when describing the set of uncertainty scenarios, a variety of techniques for describing their dosimetric results are valid (44): probability maps of failure (29), dose difference and standard deviation distributions (42), dose uncertainty or error-bar volume histograms (58, 59), volume histograms of the root-mean-square of dose distributions (60), difference in the area-under-the DVH curve (34), and population-based values (43). Elements for an unambiguous description of uncertainty scenarios and their dosimetric consequences are summarized in Table 1.

Table 1:

Elements required for unambiguous reporting of uncertainty scenarios and their dosimetric effects.

Element to Report	Example(s)
For Reporting Uncertainty Scenarios
Type of uncertainty	Lateral translations Rotations (pitch around lateral axis) Hounsfield Unit uncertainty
Magnitude of uncertainty value	+ 1 cm
Relative likelihood of uncertainty value	Represented as a probability distribution
Correlation between uncertainties	Covariance matrix for a multivariate normal distribution
Number of sample scenarios	1,000 random samples
Determination of dose for each scenario	Dose recalculated Dose resampled from the nominal dose distribution
For Reporting Dosimetric Effects of Uncertainty Scenarios
Form of the dosimetric representation	3D dose distribution DVH Equivalent Uniform Dose
Dosimetric representation descriptor	Mean Standard deviation Minimum Maximum nth percentile
Determination of the dosimetric descriptor	The “minimum DVH” as the DVH derived from the minimum dose per voxel of the 3D dose distributions under the uncertainty scenarios The “minimum DVH” as the dose-bin- wise minimum value of the many DVH’s under the uncertainty scenarios

Data representation for robustness analysis

To assess plan robustness, it is desirable to have a standard procedure for saving and transferring information. Information objects currently defined in DICOM can represent safety margins, but cannot represent uncertainties. A second generation DICOM RT currently in development (DICOM Supplement 177) extends the capabilities to describe statistical information and uncertainties used for plan evaluation. Several treatment planning systems incorporate robustness modules for plan evaluation or optimization. While functionality may vary, the importance of adequately understanding and describing uncertainty scenarios and their dosimetric effects applies broadly.

Conclusion

Treatment plan robustness analysis provides a more complete description of dose delivered in the presence of uncertainties and is vital for accurate, consistent, and appropriate comparison. The principles discussed here and the recommendations regarding complete reporting of uncertainty scenarios and their dosimetric effects apply regardless of treatment technique, modality, and dose-fractionation scheme. With improved awareness regarding robustness analysis and a common framework in which to conduct it, comparisons between plans, techniques, and modalities can be made based on best estimates of delivered dose. The benefit of this approach spans individual patient plan comparisons and large, multi-institution clinical trials. Robustness was perhaps first written into an NCTN trial in 2014 within ACNS1422. A proper foundation regarding the elements of robustness analysis may lead to future dosimetric studies with improved accuracy and clinical trials featuring increased signal-to-noise ratios when correlating this dose to clinical outcomes.