Fast shading correction for cone-beam CT via partitioned tissue classification

Abstract

The quantitative use of cone beam computed tomography (CBCT) in radiation therapy is limited by severe shading artifacts, even with system embedded correction. We recently proposed effective shading correction methods, using planning CT (pCT) as prior information to estimate low- frequency errors in either the projection domain or image domain. In this work, we further improve the clinical practicality of our previous methods by removing the requirement of prior pCT images.

Clinical CBCT images are typically composed of a limited number of tissues. By utilizing the low frequency characteristic of shading distribution, we first generate a ‘shading-free’ template image by enforcing uniformity on CBCT voxels of the same tissue type via a technique named partitioned tissue classification. Only a small subset of voxels in the template image are used in the correction process to generate sparse samples of shading artifacts. Local filtration, a Fourier transform based algorithm, is employed to efficiently process the sparse errors to compute a full-field distribution of shading artifacts for CBCT correction. We evaluate the method’s performance using an anthropomorphic pelvis phantom and 6 pelvis patients.

The proposed method improves the image quality of CBCT for both phantom and patients to a level matching that of pCT. On the pelvis phantom, the signal non-uniformity (SNU) is reduced from 12.11% to 3.11% and 8.40% to 2.21% on fat and muscle, respectively. The maximum CT number error is reduced from 70 to 10 HU and 73 to 11 HU on fat and muscle, respectively. On patients, the average SNU is reduced from 9.22% to 1.06% and 11.41% to 1.67% on fat and muscle, respectively. The maximum CT number error is reduced from 95 to 9 HU and 88 to 8 HU on fat and muscle, respectively. The typical processing time for one CBCT dataset is about 45 s on a standard PC.

1. Introduction

On-board cone-beam CT (CBCT) imaging has been playing an increasingly important role in modern radiation therapy. Advanced modalities of radiation therapy, including image-guided radiation therapy (Jaffray et al 2002, Letourneau et al 2005), adaptive radiation therapy (Yang et al 2007, Lutgendorf-Caucig et al 2011), and CBCT- guided proton therapy (Landry et al 2015, Arai et al 2017), require high accuracies of CBCT images. Despite the continuous development in imaging hardware and software, however, CBCT still suffers from severe shading artifacts, impeding its quantitative use. We recently proposed effective shading correction methods for CBCT in radiation therapy, using planning CT (pCT) as prior information to estimate low-frequency errors in either the projection domain (Niu et al 2010, 2012) or the image domain (Shi et al 2017a). These methods demonstrate high correction efficacy on both phantom and patient cases, with different advantages. In this work, we further improve the clinical practicality of our previous methods by removing the requirement of prior pCT images.

Shading artifacts lead to reduced soft tissue contrast and inaccurate HU values on CBCT images, causing problems in tumor delineation and dose calculation. In photon therapy, it has been reported that the dose discrepancy due to HU inaccuracy can be up to 11% without shading correction and less than 1% with correction (Li et al 2013). In recent years, proton therapy has been introduced to cancer treatment because of its superior precision in dose delivery and normal tissue sparing (Lomax et al 2001, 2004). It is expected that dose errors caused by shading artifacts are even more prominent in proton therapy than those in photon therapy, since calculations of proton range are more susceptible to small HU difference (Park et al 2015, Arai et al 2017).

A major source of shading artifacts on CBCT images is the scatter contamination stemming from irradiation of a large volume in a single projection. Scatter correction for volumetric CT has been an active research area for decades (Niu and Zhu 2010). Generic methods include scatter rejection by optimizing imaging geometry or using an anti-scatter grid, and scatter estimation for each projection via measurement (Tang et al 2001, Siewerdsen et al 2004), analytical modelling (Seibert and Boone 1988, Wiegert et al 2005, Sun and Star-Lack 2010, Shi et al 2017b), Monte Carlo simulation (Colijn and Beekman 2004, Zbijewski and Beekman 2006, Xu et al 2015, Shi et al 2016, Wang et al 2018) or primary modulation (Zhu et al 2006, Gao et al 2010, 2017, Zhu 2016). Despite promising results of image improvements, most of the existing methods are considered inconvenient for clinical use, as they require expensive computation, or modifications of imaging hardware and scanning protocols. Commercial systems therefore favor expedited software-based methods, at the cost of reduced correction efficacy. For example, Varian Medical Systems (Palo Alto, CA) developed a state-of-art correction scheme employing a fast adaptive scatter kernel superposition (fASKS) technique for use on their on-board CBCT of TrueBeam system (Sun and Star-Lack 2010). However, as documented in recent publications (Niu and Zhu 2010, Zhao et al 2016, Wang et al 2018), the image quality of TrueBeam CBCT still has a substantial margin for further improvements.

High-quality pCT images are routinely available in current radiation therapy, which opens possibilities of pCT-based shading correction specialized for CBCT in radiation therapy. Existing literatures have shown superior performances of these methods on improving the quality of CBCT images (Marchant et al 2008, Niu et al 2010, 2012, Shi et al 2017a). One of the key challenges is to avoid false anatomical information on pCT being carried over to the corrected CBCT. Using pCT as prior information, we have developed methods to remove lowfrequency errors of CBCT either in the projection domain (Niu et al 2010, 2012) or in the image domain (Shi et al 2017a). In the projection-domain method, we retain the anatomical difference between pCT and CBCT during the signal processing of shading correction, using the fact that scatter predominantly contains low-frequency components. To improve the computation efficiency and reduce the memory burden, we then translated the method to the image domain, removing the necessity of access to the projection data. A highly efficient algorithm, referred to as local filtration, is employed on sparse pCT samples to avoid false structural information on the corrected CBCT images. Although our pCT-based methods have shown promising results on both phantoms and patients, the requirement of pCT images remains as the last hurdle toward their clinical adoption. The signal processing of both methods includes registration between pCT and CBCT, which not only complicates the workflow but also reduces the method’s robustness. For example, the registration accuracy may significantly drop when a patient experiences significant weight loss over the entire course of radiation therapy treatment, or when CBCT contains severe truncation artifacts (Shi et al 2017a).

A few recent studies have shown promise on CBCT shading correction via an iterative workflow similar to that in pCT-based correction (Niu et al 2012) but without using prior pCT images (Li et al 2011, Wu et al 2015, Zhao et al 2016). The performances of these methods heavily rely on the accuracy of image segmentation: (Zhu et al 2006, Marchant et al 2008) performed thresholding based image segmentation on uncorrected CBCT to generate a template image, based on which a first-pass correction on each CBCT voxel is obtained. Li et al (2011) proposed a modified fuzzy C-mean (FCM) tissue classification model to iteratively estimate the shading distribution on uncorrected CBCT. Though these methods demonstrate promising results, direct segmentation employed on the uncorrected CBCT induce false classification and therefore requires a time-consuming iterative process to correct. In this work, we propose an improved method of CBCT shading correction without using prior pCT images. Distinct from existing approaches, the proposed method does not perform standard image segmentation or iteratively process the entire image domain. Instead, by utilizing the low frequency characteristic of shading distribution, it generates distributions of confidence scores for different tissues on partitioned regions of CBCT with little shading artifacts, and chooses only sparse samples with high confidence levels for CBCT correction. The proposed method is evaluated on one anthropomorphic pelvis phantom and 6 pelvis patients.

2. Method

As shown from the results of our previous pCT-based shading correction in the image domain (Shi et al 2017a), very sparse samples (<25% of the entire data) of pCT are sufficient to guarantee the correction performance. In this work, we develop a framework to generate a sparse template image directly on the uncorrected CBCT to replace the prior pCT, using a technique that we refer to as partitioned tissue classification. In this section, we lay emphasis on the derivation of this algorithm. Note that, in all the presented studies, we focus on CBCT imaging of the pelvis.

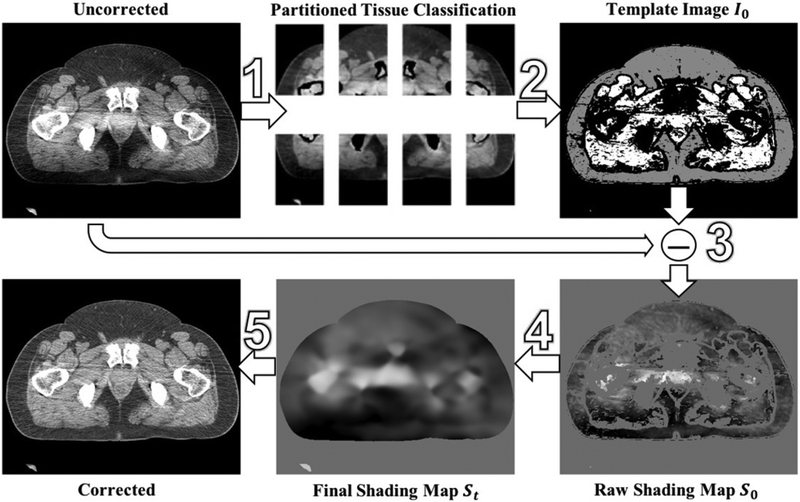
Figure 1 provides an overview of the proposed shading correction. By utilizing the low-frequency characteristic of shading artifacts in uncorrected CBCT, we first generate a template image I₀ via the method of partitioned tissue classification. Only sparse samples of shading errors obtained from I₀, referred to as S₀, are used to determine the entire shading distribution. The final shading map S_t is removed from uncorrected CBCT to obtain the corrected image. In the following sections, we elaborate the implementation for each step of the method.

Figure 1.

Workflow of the proposed shading correction.

2.1. Partitioned tissue classification

Our previous studies show that image-domain shading correction on CBCT requires only sparse sample of shading artifacts (Shi et al 2017a). When CBCT images contain low-frequency shading artifacts and the scanned structure is mainly composed of a limited number of different tissue types, we find it possible to determine the tissue compositions of the uncorrected CBCT images at sparse locations. In this paper, we perform tissue classification using an unsupervised FCM algorithm, a learning-based technique that has been widely used in image analysis and pattern recognition (Wang 1983, Pham and Prince 1999, Chen et al 2006). Distinct from an exclusive segmentation method where one data point is assigned to a definite group, FCM allows each data point to be assigned to two or more groups, i.e. a fuzzy classification.

The uncorrected CBCT images are first preprocessed using a 3D median filter with a width of five voxels along all three axes to suppress noise. The bone structures are then mostly removed by thresholding on HU values (we use 200 HU as the threshold value in all studies). FCM is then used to classify the remaining voxels into air, muscle, and fat, where muscle and fat are the two major soft tissues in pelvis.

Denoteu u_ki as the probability that the ith voxel belongs to tissue typek FCM computes uu via the following optimization framework:

$$\begin{array}{l}\text{minimize}\sum _{k=1}^c\sum _{i=1}^N{u}_{ki}^2{\Vert x_i-v_k\Vert }^2\\ \text{subject to}:\sum _{k=1}^c{u}_{ki}=1,\forall i;0⩽u_{ki}⩽1,\forall k,i.\end{array}$$ (1)

In equation (1), N is the total number of voxels and c is the total number of tissue types, a user-defined parameter. The parameter t ∈ [1, ∞) is another user-defined parameter to control the degree of separation. In all presented cases, we find that setting c value as 3 (i.e. fat, muscle, and air) and t value as 1.5 produces reliable classification results in this study. x_i is the value of the ith voxel, and v_k is the centroid value of the kth tissue type, calculated as:

$$v_k=\raisebox{1ex}{${\sum }_{i=1}^N{u}_{ki}{x}_i$}\!\left/ \!\raisebox{-1ex}{${\sum }_{i=1}^N{u}_{ki}$}\right..$$ (2)

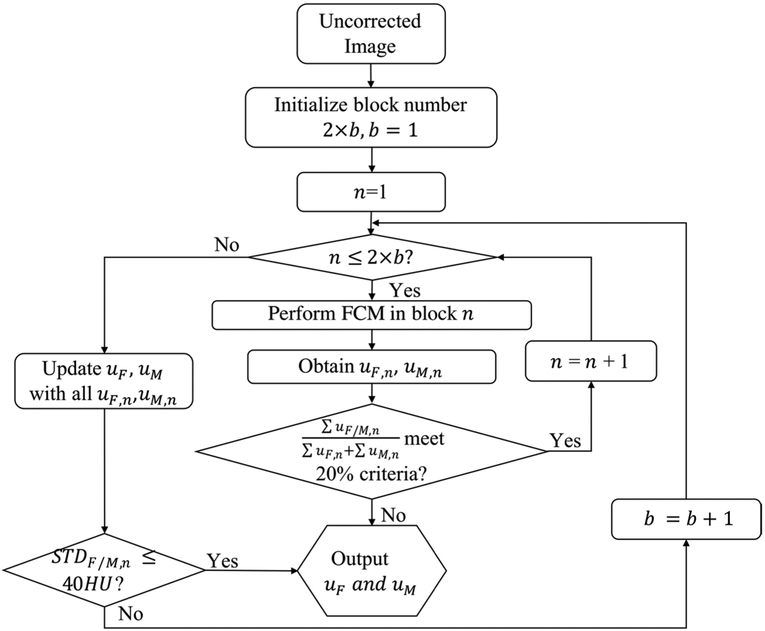
The performance of FCM is heavily dependent on the separability of clusters for different tissues in the histogram of one image. The shading artifacts smear these clusters and therefore degrade the quality of tissue classification. Given the fact that the shading artifacts vary slowly across image, one effective method to limit the range of shading artifacts is to perform FCM on small blocks of the input image. However, if one block has a small size, it may not contain sufficient voxels for each tissue type present in the overall image, which leads to significant errors in FCM. We propose to perform FCM independently on small blocks of the input image, with the block size and number automatically determined using an iterative scheme as shown in figure 2. The technique is referred to as partitioned tissue classification.

Figure 2.

Diagram of the block division scheme for the proposed partitioned tissue classification.

In partitioned tissue classification, the input CBCT is first evenly divided into 2 × b blocks in the axial plane (i.e. no division in the longitudinal direction). The iteration starts with b = 1 and FCM classifies each block into air, fat and muscle tissue. We use u_F,n and u_M,n to denote the probability maps for fat and muscle, respectively, in the nth block. To ensure one block contains sufficient voxels for both fat and muscle, we calculate the fraction of fat or muscle in each block, i.e. $\frac{\sum u_{F/M,n}}{\sum u_{F,n}+\sum u_{M,n}}$. If both fractions are larger than 20% for all blocks, the algorithm combines u_F,n and u_M,n to update the fat and muscle probability maps, u_F and u_M, for the entire images. Otherwise, the algorithm terminates and outputs u_F and u_M obtained in the previous iteration. After each iteration, we estimate the shading artifacts in each block by calculating the standard deviation of CT number for fat or muscle. If the standard deviation of both tissues in all blocks (i.e. STD_F,_n and STD_M,n) are less than a threshold, the block number and size used in current iteration are selected as the optimal ones. We set the termination threshold at 40 HU, which corresponds to the typical noise level in CBCT dataset. Otherwise, the iteration continues with b increased by 1 along the lateral direction in the axial plane. Due to the independent process of FCM in each block, we use parallel computation to accelerate the processing speed. Note that, to reduce the complexity of the proposed algorithm, the block number is fixed at 2 along the AP direction of axial plane where the body size is small compared to that in the lateral direction. As shown later in the result section, we find that this scheme guarantees sufficient voxels for each tissue type in the FCM algorithm and works well on all patient datasets in our study.

From partitioned tissue classification, we generate a template image I₀, calculated as:

$$I_0=H{U}_F\cdot u_F+H{U}_M\cdot u_M$$ (3)

where HU_F and HU_M are the reference HU values pre-determined from high-quality calibration scans or pCT images.

2.2. Image-domain shading correction on CBCT without prior images

I₀ obtained from equation (3) serves as a first-pass ‘prior image’ free of shading artifacts in the subsequent shading correction. To improve the accuracy and robustness, only a small subset of I₀ is used in the proposed correction, by enforcing the following two constraints:

High-probability constraint:

only voxels with high confidence levels in the partitioned tissue classification are used in CBCT correction, i.e. u_F > 0.99, u_M > 0.99.

Low-frequency constraint:

voxels in the tissue transition areas are discarded, i.e. |∇u_F (i, j, k)| < 0.01 and |∇u_M (i, j, k)| < 0.01.

The difference between the uncorrected CBCT and I₀ is considered as a raw shading map but only the signals within the selected region obtained from the above two constraints are used for shading correction, which are referred to as S₀. A local filtration algorithm (Zhu 2016, Shi et al 2017a) is used to efficiently process S₀ to obtain the final shading distribution S_t. Briefly, the local filtration can be implemented via fast Fourier Transform:

$$S_t(i,j,k)=\frac{\left(S_0\cdot f\right)\ast \ast \ast w}{f***w}$$ (4)

where f is the binary mask of the sampled region and w is a 3D Gaussian smoothing kernel with a standard deviation (σ) of 7 mm.

The workflow of the proposed algorithm shown in figure 1 can be summarized using the following Steps: Step 1: Perform partitioned tissue classification on uncorrected CBCT to generate a template image I₀ via equation (3).

Step 2: Apply high-probability and low-frequency constraints on I₀ to acquire a sparse I₀.

Step 3: Obtain a raw shading map, S₀, by taking the difference between uncorrected CBCT and sparse I₀ obtained in Step 2.

Step 4: Obtain a final shading map S_t from S₀ using local filtration via equation (4).

Step 5: Remove S_t from uncorrected CBCT for effective shading correction.

2.3. Evaluation

We evaluate the proposed method on an anthropomorphic pelvis phantom and 6 pelvis patients. All the CBCT scans are acquired from a kV on-board imager (OBI) on the TrueBeam system (Varian Medical Systems, Palo Alto, CA) with a typical clinical setting of 125 kVp and 80 mA. The OBI system operates in an offset-detector (half-fan) mode to avoid field of view truncation in the axial plane. The CBCT images are reconstructed using the system embedded software with a volume size of 512 × 512 × 81 voxels and a voxel size of 0.91 × 0.91 × 1.99 mm³. The reconstruction software on TrueBeam includes scatter correction using fASKS (Sun and Star-Lack 2010). However, the reconstructed image still suffers from severe residual shading artifacts. In this paper, we refer to the output CBCT images from TrueBeam as uncorrected CBCT images.

The proposed algorithm is implemented in Matlab 2014b on a standard laptop (2.5 GHz Intel Core i7 MacBook). Partitioned tissue classification typically takes about 40 s for one CBCT dataset with a block size of 2 × 2, with an almost linear relationship on the block size. The remaining signal processing takes about 2.5 s for shading correction on the entire CBCT volume.

The signal non-uniformity (SNU) of one tissue type (i.e. fat or muscle in our studies) is used as the evaluation metric and computed on five manually selected regions of interest (ROI), each of which has a size of 15 × 15 pixels:

$$SNU=\left({\overline{\mu }}_{max}-{\overline{\mu }}_{min}\right)/{\overline{\mu }}_{mean}$$ (5)

where the ${\overline{\mu }}_{max}$ and ${\overline{\mu }}_{min}$ are the maximum and minimum mean HU value of the selected ROIs and ${\overline{\mu }}_{mean}$ is the mean HU value over all pixels in the five ROIs.

To evaluate the improvement in HU accuracy by suppressing shading artifacts, we compute the maximum CT number error of the selected ROIs on CBCT with and without correction, using pCTas a reference. In all studies, we compare the image qualities of uncorrected CBCT, CBCT corrected by the proposed method, the pCT-based image domain method previously developed in our group (Shi et al 2017a), and the pCT.

The FCM algorithm used in our method implicitly assumes that the histogram of the processed image consists of a small number of narrow clusters. This assumption, however, might not be valid on clinical CBCT images when they contain structures of spatially-varying CT numbers. A typical example could be a tumor with necrosis in the middle but cancer-active around boundary. A study is specially designed to evaluate the proposed method on these challenging scenarios.

3. Results

3.1. Phantom results

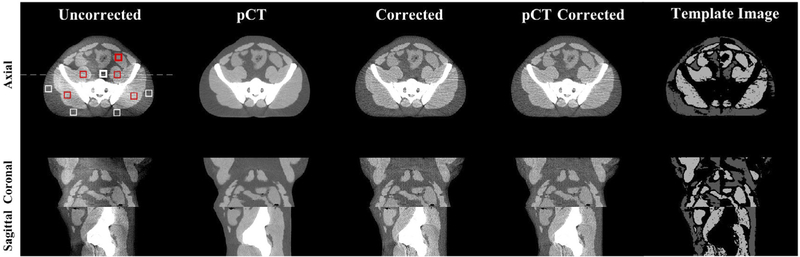
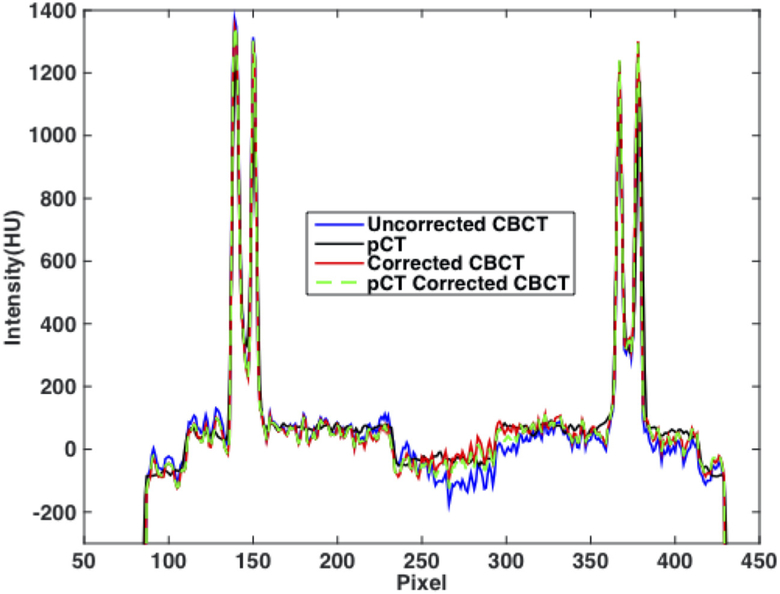
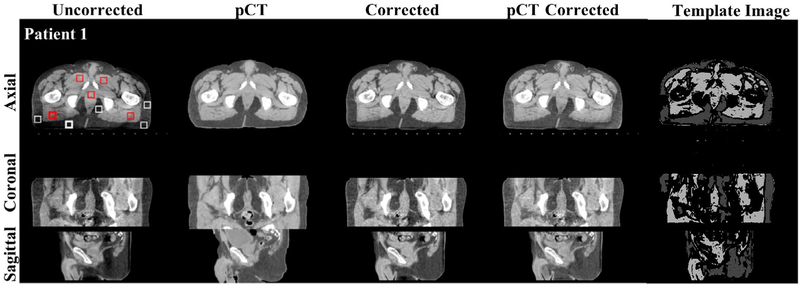
We first use an anthropomorphic pelvis phantom to demonstrate the feasibility of the proposed shading correction method. Figure 3 shows that, without prior information of pCT, the proposed method has a similar efficacy on the removal of shading artifacts compared with the pCT-based method (Shi et al 2017a), and the corrected image uniformity reaches a level similar to that of pCT. Figure 4 shows the line profiles extracted along the white dashed line in figure 3 on different images. Selected ROIs as indicated on the axial image of figure 3 are used to calculate SNU and the maximum CT number errors on fat and muscle. The results are reported in table 1. It is seen that our algorithm achieves a performance comparable to that of the pCT based method. SNU is reduced from 12.11% to 3.11% on fat and 8.40% to 2.21% on muscle and the maximum CT number error is reduced from 70 HU to 10 HU on fat and 73 HU to 11 HU on muscle.

Figure 3.

Shading correction results for the pelvis phantom. Images on the top, middle and bottom row show an axial, coronal and sagittal view, respectively. From left to right column: uncorrected CBCT, pCT, corrected CBCT obtained using the proposed method, the pCT-based method (Shi et al 2017a), and the template image after sparse sampling of the proposed method respectively. The white and red squares placed on the axial view of uncorrected CBCT are the selected ROIs for SNU calculation, where the bold square contains the maximum shading artifacts.

Figure 4.

Line profiles on axial images (i.e. uncorrected CBCT, pCT, corrected CBCT using the proposed and the pCT-based method), taken along the dashed line shown in figure 3.

Table 1.

Quantitative comparison for all studies.

SNU	On fat				On muscle
	pCT	Uncorrected CBCT	Proposed correction	pCT-based correction	pCT	Uncorrected CBCT	Proposed correction	pCT-based correction
Pelvis phantom	3.61%	12.11%	3.11%	3.05%	2.51%	8.40%	2.21%	2.29%
Patient 1	3.69%	9.11%	1.14%	2.58%	2.17%	9.24%	2.11%	1.94%
Patient 2	2.82%	8.62%	0.84%	2.57%	3.75%	11.25%	1.55%	4.08%
Patient 3	2.65%	9.26%	0.52%	2.74%	3.65%	9.53%	1.24%	4.04%
Patient 4	1.16%	10.69%	2.25%	2.49%	2.38%	9.84%	1.15%	3.24%
Patient 5	1.92%	9.05%	0.89%	0.99%	1.97%	10.69%	0.62%	2.19%
Patient 6	2.11%	8.58%	0.73%	1.96%	3.62%	17.88%	3.32%	3.56%
Average	2.39%	9.22%	1.06%	2.22%	2.92%	11.41%	1.67%	3.18%
Max CT number error (HU)		On fat				On muscle
		Uncorrected CBCT	Proposed correction	pCT-based correction		Uncorrected CBCT	Proposed correction	pCT-based correction
Pelvis Phantom		70	10	4		73	11	2
Patient 1		81	15	1		95	4	3
Patient 2		77	4	2		99	8	3
Patient 3		85	7	2		78	8	9
Patient 4		99	6	26		87	12	12
Patient 5		112	14	7		90	10	4
Patient 6		115	9	11		77	8	9
Average		95	9	8		88	8	6

3.2. Patient results

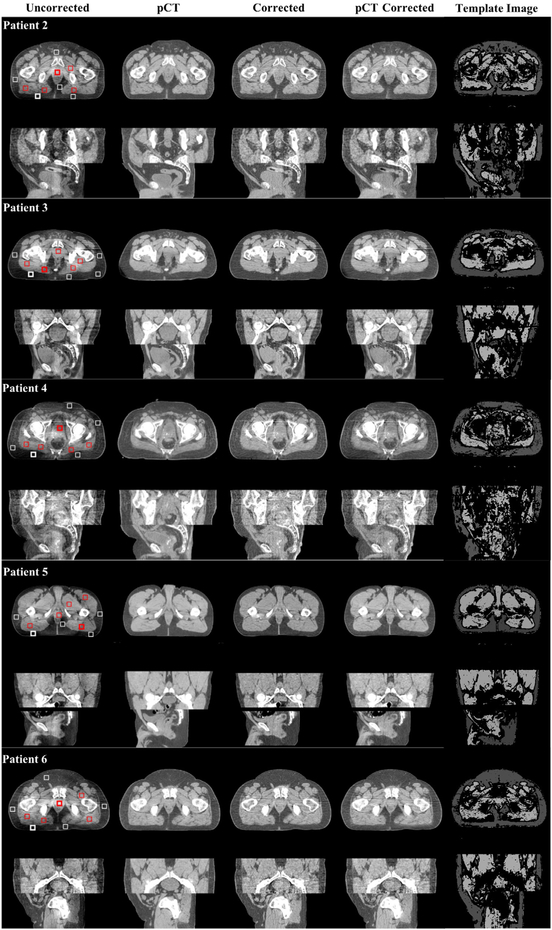
The same performance as seen in the phantom study is observed on patient images. One patient result is shown in figure 5 with large image sizes, and other patient results are shown in figure 6. The proposed method improves the CBCT image quality to a level matching that of pCT and the pCT-based correction. The quantitative comparison of SNU and maximum CT number error are listed in table 1: the average SNU for six patients is reduced from 9.22% to 1.06% on fat and 11.41% to 1.67% on muscle. This results even outperform the pCT based correction, which reduces the SNU to 2.22% on fat and 3.88% on muscle. The average maximum CT number error is reduced from 95 HU to 9 HU on fat, and 88 HU to 8 HU on muscle

Figure 5.

Shading correction results on one pelvis patient. The images in the top, middle and bottom row are axial, coronal and sagittal views, respectively. From left to right column: uncorrected CBCT, pCT, corrected CBCT using the proposed method, the pCT based method (Shi et al 2017a) and the template image after sparse sampling of the proposed method respectively. The white and red squares placed on the axial view of left column are the selected ROIs for SNU calculation, where the bold square contains the maximum shading artifacts. Display window: (−200 200) HU.

Figure 6.

Shading correction results on five additional pelvis patients. For each patient, the image is displayed the same way as figure 5. Display window: (−200 200) HU.

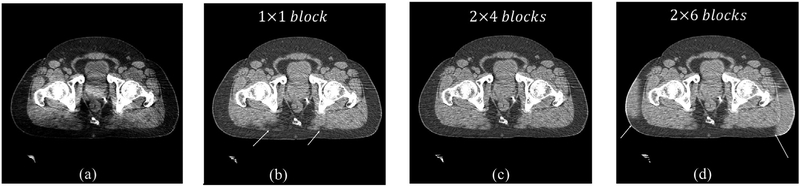
The block size selection in the partitioned tissue classification algorithm is essential in generating a reliable template image I₀ for shading correction. Figure 7 shows the effect of different block sizes on the performance of the proposed shading correction method. We manually set the blocker number in the partitioned tissue classification algorithm as 1 × 1,2 × 4 and 2 × 6. It is seen that the correction errors (indicated by white arrows in figure 7) appear for block number of 1 × 1 and 2 × 6. A large block size fails to suppress the shading artifacts, while a small block size fails to include sufficient representative tissues, therefore both scenarios of 1 × 1 and 2 × 6 blocks cause unreliable tissue classification. In this case, the proposed algorithm automatically finds 2 × 4 as the optimal block number, which obtains a superior image quality as seen in the comparison of figure 7. In all the studies present in this paper, we find that the optimal block number is typically between 2 × 2 and 2 × 4.

Figure 7.

Effect of block number on the performance of CBCT shading correction. (a) Uncorrected CBCT, and corrected CBCT (b) without using the block number selection, (c) with 2 × 4 blocks and (d) with 2 × 6 blocks. Display window: (−200 200) HU.

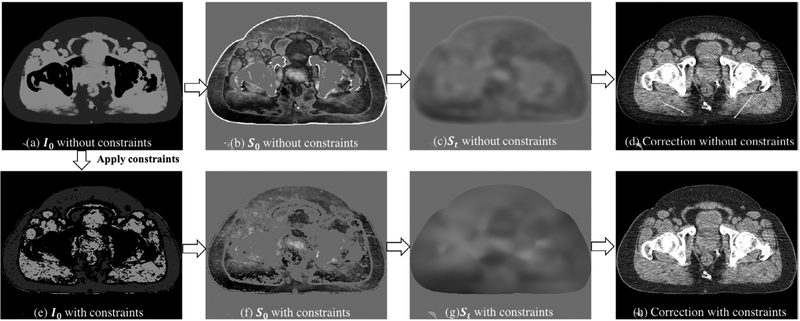
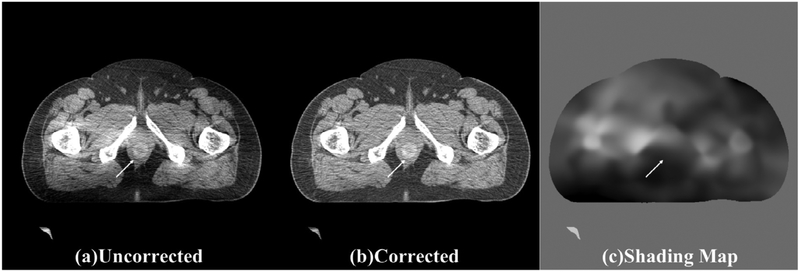
The high-probability and low-frequency constraints described in section 2.2 aim to remove most voxels of shading estimation with high potential of being errors, and therefore greatly improves the method accuracy. Figure 8 illustrates the effects of sparse signal selection in the shading correction, by comparing the corrected CBCT with and without applying the two constraints. As indicated by white arrows, shading correction with the proposed constraints obtains a better image quality especially around structure boundaries and in the regions initially with high shading artifacts.

Figure 8.

CBCT shading correction without (upper row) and with (bottom row) the high-probability and low-frequency constraints. The uncorrected CBCT image is shown in figure 7(a). From left to right are the template image I₀, first-pass shading map S₀ before local filtration, final shading map S_t after local filtration and corrected CBCT. Display window for I₀ and CBCT images: (−200 200) HU; for the shading images: (−100 100) HU.

3.3. Study with a manually-inserted tumor

To evaluate the method performance on structures with spatially-varying CT numbers, we manually insert a 3 cm tumor into the prostate region of one patient image, of which the contrast to background linearly changes from 0 HU at the center to 100 HU around the periphery. The results are shown in figure 9. The location of the inserted tumor is indicated by the white arrow. It is seen that the proposed correction faithfully retains the tumor structure as the shading map only contains low-frequency signals at the tumor region.

Figure 9.

Shading correction results for the case of a manually inserted tumor with spatially-varying CT numbers. (a) uncorrected CBCT, (b) corrected CBCT, and (c) shading map obtained using the proposed algorithm.

4. Discussion and conclusions

In this paper, we develop a new image-domain method to remove the low-frequency shading artifacts on CBCT images. Compared to our previously developed algorithms, the method does not require prior information of pCT images or access to projection data. A template image is first generated by enforcing uniformity in the area consisting of one tissue via the technique of partitioned tissue classification. Only sparse samples of the classified tissues are then used in the correction process, which substantially improves the method accuracy and robustness. Shading corrected images are efficiently generated using local filtration, a Fourier transform based method. We evaluate the method performance on an anthropomorphic pelvis phantom and 6 pelvis patients. The SNU is reduced from 12.11% to 3.11% on fat and 8.40% to 2.21% on muscle in the phantom study. The average SNU is reduced from 9.22% to 1.06% on fat and 11.41% to 1.67% on muscle for six patients.

Image-domain shading correction for CBCT is attractive in a clinical environment in that it does not require access to projection data and has low computational cost. Existing image-domain correction methods include an intermediate procedure of registration of pCT to CBCT or segmentation on CBCT. Such a procedure not only complicates the clinical workflow, but also reduces the method robustness since high accuracy of registration and segmentation is not guaranteed due to CBCT artifacts. The proposed method adopts a different framework. The fuzzy behavior of FCM allows indefinite classification of different tissues. Using the local filtration technique, we are able to discard signals of shading estimation with high potential of being errors. As such, our algorithm improves over the existing image-domain approaches with enhanced resistance to CBCT shading artifacts. Note that, we adopt a strategy of evenly distributed blocks in the proposed partitioned tissue classification algorithm, which might not be optimal as it limits the block number along the lateral direction. In future studies, we will design a more adaptive block division scheme and investigate the possible improvements on CBCT image qualities.

A limitation of our method is that it assumes the shading artifacts are only composed of low-frequency signals. As a result, our method is not able to recover the image contrast loss caused by high-frequency artifacts. Furthermore, in this study, we evaluate the proposed algorithm only on pelvis CBCT images. In our future research, we will continue the method evaluation on other anatomical sites.

5. Conclusion

We have developed a new image-domain method to remove the low-frequency shading artifacts on CBCT without access to pCT. The method is clinically attractive in that it is highly efficient and requires no modifications of existing clinical protocols.