Symbolic representation of numerosity by honeybees (Apis mellifera): matching characters to small quantities

Abstract

The assignment of a symbolic representation to a specific numerosity is a fundamental requirement for humans solving complex mathematical calculations used in diverse applications such as algebra, accounting, physics and everyday commerce. Here we show that honeybees are able to learn to match a sign to a numerosity, or a numerosity to a sign, and subsequently transfer this knowledge to novel numerosity stimuli changed in colour properties, shape and configuration. While honeybees learned the associations between two quantities (two; three) and two signs (N-shape; inverted T-shape), they failed at reversing their specific task of sign-to-numerosity matching to numerosity-to-sign matching and vice versa (i.e. a honeybee that learned to match a sign to a number of elements was not able to invert this learning to match the numerosity of elements to a sign). Thus, while bees could learn the association between a symbol and numerosity, it was linked to the specific task and bees could not spontaneously extrapolate the association to a novel, reversed task. Our study therefore reveals that the basic requirement for numerical symbolic representation can be fulfilled by an insect brain, suggesting that the absence of its spontaneous emergence in animals is not due to cognitive limitation.

1. Introduction

Matching specific numerosities with symbolic representations of that numerosity, such as Roman or Arabic numerals, is valuable for representing and manipulating numbers [1]. Some non-human animals have demonstrated symbolic number representation and ordinality of those signs. Pigeons have demonstrated learned symbolic number representation through peck number on a sign representing that numerosity [2,3]. The combination of ordinality and symbolic number representation has been demonstrated in an African grey parrot [4–6], chimpanzees [7–15] and rhesus monkeys [16]. Alex, a single African grey parrot, was able to learn the names of numerals and subsequently sum the quantities [5,17,18]. In addition, chimpanzees have been able to learn Arabic numerals and order them quantitatively [7–15], and rhesus monkeys have learned to choose the larger of two Arabic numerals to receive a corresponding number of food pellets [16] as well as match numbers of items to the correct Arabic numeral [19]. Nevertheless, there is no evidence that any species apart from Homo sapiens have ever spontaneously developed symbolic representations of numerosity, which opens the question of which animals are capable of learning symbolic number representations, which are capable of generating such representations, and whether this implies a fundamental difference in the mental processing of Homo sapiens compared with other animals [20–23].

There are two well-accepted mechanisms for numerical discrimination in humans and non-human animals which are involved for different number ranges [24–28]. The first is known as subitizing or the object file system, the quick and accurate estimation of four and fewer objects. The second mechanism is the approximate number system (ANS), also known as the analogue magnitude system (AMS) for quantifying numerosities above four objects. Animals that are able to process quantities above four are considered to be using the ANS/AMS mechanism of numerosity judgement. In humans, the ANS is thought to be an ancient evolutionary foundation, shared with non-human animals, for our ability to perform mathematics and use symbolic numerositiy mechanisms [29–32]. While symbolic number systems (such as the use of Arabic numerals) allows us to easily discriminate between two numbers, non-symbolic number systems, such as the ANS, show that ratio-dependent number discrimination exists. Thus, humans and non-human animals share the evolutionary ancient quantification system known as the ANS.

Honeybees are considered as a model species for studying numerical cognition in insects [33–38]. Previously, honeybees have demonstrated the capacity to evaluate quantities by counting the number of landmarks to reach a feeder [35,36], or matching the number of objects in pictures [38]. We recently demonstrated that bees can correctly value quantities up to six by choosing a stimulus with fewer elements between two alternative quantities [39]. Interestingly, bees spontaneously placed an empty set at the lower end of the numerical scale without specific training on the task, thereby demonstrating the ability to quantify an empty set as being lower than numbers one to six. This discovery challenges the postulate of zero being an unnatural abstract concept only reachable by large-brained animals [39,40]. Honeybees have also demonstrated an ability to learn and perform simple addition and subtraction operations of ‘plus one’ or ‘minus one’ using symbolic prompting and arrays of one to five objects [37]. This recent study was the first step in determining if insects could use a sign representation in numerical problem solving. The current study aimed to extend on this area of research by training honeybees to learn to associate numerosities with signs.

In the current study, honeybees were examined on their ability to match two numerical tags (signs; icons) to arrays of two or three elements. Bees were trained to perform either a sign-to-numerosity matching task (Group 1) or a numerosity-to-sign matching task (Group 2), and were subsequently tested on their ability to reverse their learned association.

2. Method

(a). Study species

We used 20 free-flying honeybee (Apis mellifera) foragers for this experiment. All bees were marked with a coloured dot on the thorax to identify individuals. A gravity feeder providing roughly 10–30% sucrose near the experimental set-up (distance: 20 m) maintained a regular number of bees for testing. Bees were recruited from over 25 hives maintained at Paul Sabatier University in Toulouse, France. Each experiment lasted for approximately 3–5 h per bee.

(b). Apparatus

Individual honeybees were trained to enter a Y-maze (as described in [41,42]; figure 1a,b) through a small entrance hole (approx. 5 cm diameter). The Y-maze arms were 40 × 20 × 20 cm (L × W × H). The bees had to fly through an initial entrance hole to enter a chamber where they would view the sample stimulus. This sample stimulus would be either a sign or quantity depending on the group being trained. Each bee could then fly through another hole into the decision chamber where it would be presented with two different options in each arm of the chamber. If the sample stimulus was a sign, then the two options would be quantities of two versus three elements; if the sample stimulus was a quantity of two or three elements, then the two options would be the two sign options (figure 1).

Figure 1.

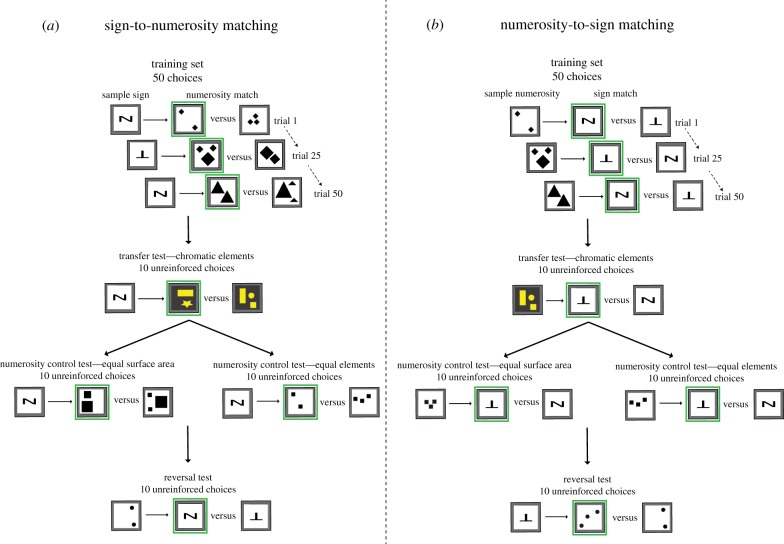
Apparatus set-up and stimuli examples for the (a) sign-to-numerosity-matching task and (b) numerosity-to-sign-matching task. Diagram shows parts of the Y-maze and the stimulus positions. (a) In the symbol-to-numerosity-matching task, when bees view a sample sign (N-shape or inverted T-shape), they must match it to the correct quantity of two or three elements. (b) In the numerosity-to-sign-matching task, when bees view a sample quantity (two or three elements), they must match it to the correct sign (N-shape or inverted T-shape). The entrance hole and wall into the first chamber are not visible in this diagram. (c) An example of the signs being matched to their corresponding correct quantity (N-shape to two elements; inverted T-shape to three elements). (Online version in colour.)

Stimuli were presented on grey backgrounds located 5 cm away from the decision lines. Two stimuli, one correct and one incorrect, were presented simultaneously in each arm of the Y-maze on the grey plastic background (figure 1a,b). A 10 µl drop of either a 50% sucrose solution (correct choice) or a 60 mM quinine solution (incorrect choice) were used as rewarding and punishing outcomes, respectively, during the training phase as this promotes enhanced visual discrimination performances in free-flying honeybees [43,44]. Each stimulus had a grey landing pole located below it which held either the drop of sucrose under the correct option or quinine under the incorrect option, so that bees would learn to associate stimuli with either a reward or punishment. Poles were replaced when touched by a bee and cleaned with 30% ethanol and water, then dried to exclude olfactory cues. The precise order by which stimuli were arranged in the Y-maze was randomly allocated between choices. If a bee made an incorrect choice and started to imbibe the quinine, it was allowed to fly to the pole in front of the correct stimulus to collect sucrose to maintain motivation, but only the first choice was used for statistical analysis. When the bee landed on the pole with sucrose, both the pole and bee were removed from the Y-maze; then a clean pole was placed into the Y-maze. Between each choice, stimuli and the positions of targets and distractors were randomized. Once the bee was finished imbibing the sucrose, it was allowed to fly back to the hive if satiated, or make another decision by re-entering the maze. During the non-reinforced tests, a drop of water was placed on each of the poles placed in front of the stimuli. Ten choices (touches of the poles) were recorded for each of the four tests to enable statistical comparisons.

(c). Stimuli

Each sign stimulus consisted of a 6 × 6 cm white square with a black sign (either an N-shape or an inverted T-shape; figure 1c), and stimuli containing quantities were 9 × 9 cm white square cards with elements presented on them, all covered with 80 µm Lowell laminate (figure 1). Sign stimuli had a surface area of 36 cm² (visual angle of 149° from the decision line) while quantity stimuli had a surface area of 81 cm² (visual angle of 165° from the decision line). Signs were based on the Xia et al. [2] paper on pigeons matching numerosities to signs [2]. The stimuli containing two or three numbers of elements were split into three different sets: (1) a set where surface area of all elements was equal (n = 32); (2) a set where each element was the same size (n = 32); (3) a set where random chromatic objects/shapes were used (for transfer test only; n = 8; electronic supplementary material, figure S1). Sets 1 and 2 consisted of squares, diamonds, circles or triangles which was pseudo-randomized between trials. Set 3 was used in testing as a control (electronic supplementary material, figure S1). Stimulus sets 1 and 2 were achromatic (white background with black elements) and set 3 was chromatic (grey background with salient yellow elements [45]). Stimulus sets were based on sets from [46].

(d). Training

We trained two groups (n = 10 per group) of bees to fly into a Y-maze apparatus and used a delayed-matching-to-sample (DMTS) framework for conditioning [38]. Upon flying into the Y-maze, one group of bees (Group 1; figure 2a) was presented with one of two possible signs (figure 1). After the bees flew into the next chamber, the decision chamber, they were presented with two options, one correct (two or three elements) and the other incorrect (two or three elements). The second group of bees (Group 2; figure 2b) was trained using the opposite DMTS framework, where they were first shown a quantity of elements in the first chamber and then presented with two signs in the arms of the Y-maze in the decision chamber.

Figure 2.

Examples of possible stimulus combinations during trials and tests in experiments on (a) sign-to-numerosity matching tasks and (b) numerosity-to-sign matching tasks. The diagrams show the sample stimulus (Group 1: sign; Group 2: numerosity) and the matched correct or incorrect options which would be presented in the two arms of the Y-maze (figure 1a,b). The four tests were conducted after the 50 appetitive–aversive trials had been completed and were conducted in the order of transfer test, numerical control tests (pseudo-randomized order) and then the reversal test. The first square on the right-hand side of the arrow (with green border) indicates which option is the correct answer for each of the example combinations. (Online version in colour.)

We used sets of stimuli with controlled surface area (set 1) and equal element size area (set 2) with achromatic properties (black elements on white background; electronic supplementary material, figure S1). The choice of stimuli for each trial was pseudo-randomized with regards to set (1 or 2), shape and arrangement of elements. Thus, bees were trained on both set 1 and set 2. Bees were trained for 50 choices using appetitive–aversive differential conditioning. The training phase lasted for approximately 2–4 h per bee.

(e). Testing

After the 50 training choices were completed, bees were removed from the apparatus following their final choice and given sucrose until they became satiated and returned to the hive. During the bee's absence from the experimental area, we prepared for the testing phase by placing test stimuli and clean landing poles into the Y-maze. Once bees returned from the hive (typically less than 5 min), individuals underwent four tests in the following order.

A transfer test was conducted for 10 unconditioned choices. In Group 1, this test consisted of showing a sign as the sample and then a randomized set of abstract objects not previously seen by bees (set 3: random set with chromatic properties). In Group 2, this test consisted of showing the random set of two or three elements and then both signs as the options (figure 2).

Two numerical control tests were conducted afterwards for 10 unconditioned choices in a pseudo-randomized order (two controlled sets: set 1, equal surface area of elements; set 2, equal element size; both with achromatic properties; figure 2).

A reversal test was finally conducted for 10 unconditioned choices. The Group 1 test consisted of showing a quantity as the sample and having the bee choose a corresponding sign. The Group 2 test consisted of showing a sign as the sample and having the bee choose a corresponding quantity (figure 2). This test aimed to determine whether bees could extrapolate the task to the reverse matching situation. Stimuli in this test were also achromatic and pseudo-randomly chosen from stimuli within set 1 or set 2 which had not previously been presented to bees during training. The tests were not randomized for order as the reversal test could have potentially confused bees with the switching of stimuli location, thus it was conducted last so that this would not impact the bees' performance on other tests. The testing phase lasted approximately 30 min to 1 h per bee. Between tests, we conducted refresher choices to maintain bee motivation and counter extinction effects of the unconditioned tests. The refresher choices consisted of bees being presented with the training set stimuli with appetitive and aversive outcomes (as in the training phase) for three to six choices (a single bout).

(f). Statistical analysis

To test for the effect of training on bee performance (number of correct choices), data from the training phase of 50 choices were analysed with a generalized linear mixed-effects model (GLMM) with a binomial distribution using the ‘glmer’ package within the R environment for statistical analysis. We fitted a full model with trial number as a continuous predictor, and subject as a random factor to account for repeated choices of individual bees.

To determine whether bees were able to learn to match a sign with the correct corresponding quantity, we analysed the test data by employing a GLMM including only the intercept term as fixed factor and subject as a random term to account for the repeated measures. The proportion of ‘correct’ choices (MPCC) recorded from the tests were used as response variable in the model. The Wald statistic (z) tested if the mean proportion of correct choices recorded from the tests, represented by the coefficient of the intercept term, was significantly different from chance expectation (i.e. H₀: MPCC = 0.5).

All analyses were performed within the R environment for statistical analysis [47].

3. Results

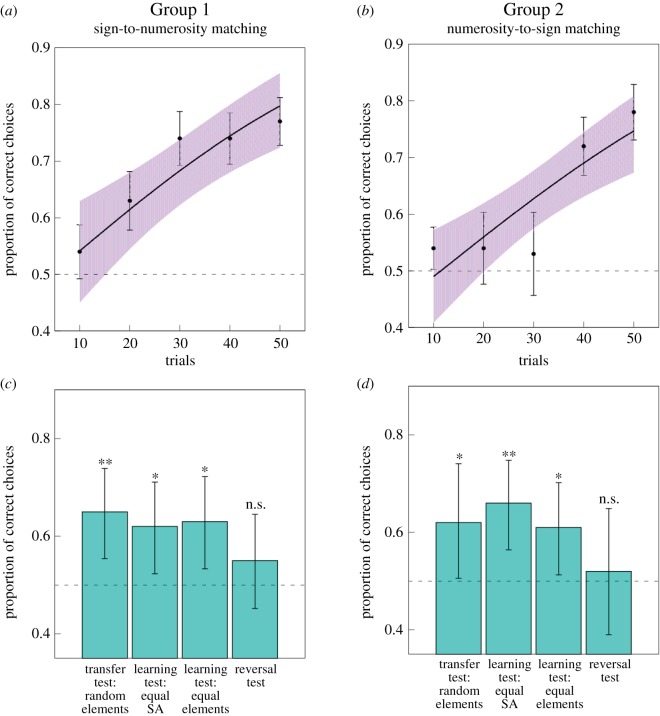
Bees in both groups demonstrated significant learning over the course of the appetitive–aversive trials to match either signs to numerosities (Group 1: z = 4.460, p < 0.001; figure 3a) or numerosities to signs (Group 2: z = 4.387, p < 0.001; figure 3b), demonstrating that bees learned the two signs had corresponding matching quantities associated with them. We also fitted a model with trial number, group and an interaction between trial number and group as continuous predictors, and subject as a random factor to account for repeated choices of individual bees to determine if the learning curve of the groups were significantly different. There was no significant effect of an interaction between trial number and group (z = −0.160, p = 0.873), nor a significant effect group in this model (z = −0.700, p = 0.484), demonstrating that both groups learned at an equal rate. Electronic supplementary material, figure S2a,b shows the individual learning curves that each bee obtained during the training phase.

Figure 3.

Results of the training and testing phases for the (a) group of bees trained to match a sign with a quantity (Group 1; n = 10) and for the (b) group of bees trained to match a quantity with a sign (Group 2; n = 10). (a,b) Performance during the training phase for (a) Group 1 and (b) Group 2. Dashed line at 0.5 indicates chance level performance. Solid black line represents a function describing the training phase of n = 10 bees as modelled by a generalized linear mixed model (GLMM). Points (closed circles) along the curve indicate the observed mean ± 95% CIs (shaded area) of correct choices for the bees. Increase in performance during the training phase was significant. (c,d) Performance during the testing phases for both (c) Group 1 and (d) Group 2. n = 10 for both test groups. Dashed line at 0.5 indicates chance level performance. Significance from chance level performance is indicated by * ≥ 0.05, ** ≥ 0.01, *** ≥ 0.001, n.s. > 0.05. Data shown are means ± 95% CI boundaries for all tests. See the electronic supplementary material, figure S2 for the individual learning curves obtained during training and proportion of correct choices per bee in the test phases. (Online version in colour.)

When bees were asked to transfer the matching task to completely novel stimuli, with chromatically coloured backgrounds and elements which were of novel shape and arrangement (set 3), bees in both groups performed this task at a level higher than expected by chance. Bees in Group 1 chose the correct numerosity at a proportion of 0.650 (95% confidence intervals (CIs) = 0.554, 0.739; z = 2.95, p = 0.003; figure 3c). Bees in Group 2 chose the correct sign at a proportion of 0.620 (CIs = 0.506, 0.741; z = 2.19, p = 0.029; figure 3d).

Bees were also tested on transferring their learned matching tasks to stimuli which were similar to the training set but of novel configuration. Bees in both groups were reliably able to choose the correct numerosity or sign in these tests. In the numerical control test, using novel stimuli from the set which had an equal surface area for quantities of both two and three, bees in Group 1 chose the correct option at a proportion of 0.620 (CIs = 0.523, 0.711; z = 2.38, p = 0.018; figure 3c) and bees in Group 2 chose the correct option at a proportion of 0.660 (CIs = 0.564, 0.748; z = 3.14, p = 0.002; figure 3d). In the numerical control test, using novel stimuli from the set in which all elements were of equal size for quantities of both two and three, bees in Group 1 chose the correct option at a proportion of 0.630 (CIs = 0.533, 0.722; z = 2.57, p = 0.010; figure 3c), and bees in Group 2 chose the correct option at a proportion of 0.610 (CIs = 0.513, 0.702; z = 2.18, p = 0.029; figure 3d).

Finally, bees were tested on their ability to transfer either the learned sign-to-numerosity matching task to a numerosity-to-sign matching task (Group 1), or their numerosity-to-sign matching task to a sign-to-numerosity matching task (Group 2). Stimuli used in this test were randomly selected from set 1 or set 2 using the stimuli which were not presented to bees during the training. Bees in both groups were unable to perform this reversal test at a level significant from chance expectation, with bees in Group 1 choosing the correct sign at a proportion of 0.550 (CIs = 0.452, 0.645; z = 1.00, p = 0.318; figure 3c) and bees in Group 2 choosing the correct numerosity at a proportion of 0.520 (CIs = 0.390, 0.649; z = 0.24, p = 0.346; figure 3d). Electronic supplementary material, figure S2c,d shows each bee's individual proportion of correct choices per test.

We fitted a model for each of the four tests to determine whether bees within the two groups performed significantly different from each other. We employed a GLMM including the intercept term and group as fixed factors, and subject as a random term to account for the repeated measures. There was no effect of the group factor on any of the four tests (p ≥ 0.556), thus demonstrating that performance on each test between the groups was not statistically different.

4. Discussion

Our findings show that independent groups of honeybees can learn and apply either a sign-to-numerosity matching task or a numerosity-to-sign matching task and subsequently apply acquired skills to novel stimuli. Interestingly, despite bees demonstrating a direct numerosity and sign association, they were unable to transfer the acquired skill to solve a reverse matching task. While independent groups of bees are able to learn the association in either direction with similar performances in training and tests, it seems the association itself is not reversible.

Piaget's theory on children's actions providing the basis for their own cognitive development gives some insight into our results [48]. Piaget considered ‘operations’ or ‘reversible actions’ as most conducive to a child's mental development. Operations are where an action can be undone by other actions, such as being able to turn a light on using a switch, and reverse this action by flicking the switch the other way [48]. Children will develop ‘operational schemes’ throughout their learning which allows them to think about the ability to reverse their actions [48]. If we consider a child knocking over a glass of milk, they will learn that this is an irreversible action and the milk cannot easily be put back into the glass. However, as in the previous example, a child is able to acquire the ability to understand reversing the state of a light as on or off via experimentation with these relative states, and individual actions.

If we consider Piaget's theories in terms of the results of the current study, it seems that bees have not learned ‘operations’ or ‘operational schemes’ in this instance. Our experiments show that bees can learn to perform the association of sign and numerosity in either direction but neither group can reverse the association. Thus, bees are not easily able to reverse a learned task unless they have had experience with the association in a specific direction. Thus, for cognitively demanding tasks like sign and numerosity matching, spontaneous reversion of the association appears to be beyond the capacity of an insect brain.

In a previous study by Gross et al. [38], honeybees were able to match two identical quantities differing by shape, colour and configuration in a DMTS framework [38], such as the method used in the current study. Another study by Zhang et al. [49] showed that bees were able to navigate by visual stimuli and memory recall of different groups of stimuli. Thus, bees were able to use symbol-like stimuli to inform their decision on which direction to choose in a maze [49]. Our current study takes the task of numerical matching and problem solving to a higher cognitive problem by training bees to match signs and quantities within a DMTS framework. In addition, honeybees were recently shown to learn simple addition and subtraction operations using this same DMTS framework [37]. When bees saw a blue array of elements, they learned to add one element to the quantity; however, when the array of elements was yellow, the bees learned to subtract one element from the quantity. The study demonstrated the use of colour as a symbolic cue as well as showing that honeybees had the capacity to perform simple arithmetic by using the symbolic colour cues.

The results demonstrate that while bees can perform both a sign-to-numerosity match and a numerosity-to-sign match, they are unable to reverse the task if it is only experienced in one direction. We do not know whether this inability to reverse the task is due to the numerical aspect of the task, or whether they are unable to reverse an association between any two stimuli within a DMTS framework. Interestingly, a similar result was observed by Gross et al. [38], where honeybees were trained to match two patterns based on only the quantity cue using a DMTS procedure, as in the current study. In their study, bees were given training to match patterns containing either two or three elements, and thus the bees experienced the task in both directions. They were trained to match a two-element pattern to a second two-element pattern in the presence of a three-element pattern. Bees were also trained to match a three-element pattern to a separate three-element pattern in the presence of a two-element pattern. Bees experienced matching patterns containing either two or three elements, thus performing the matching task in both directions and leading to the ability to match novel patterns containing two or three elements, even when in the presence of an incorrect novel pattern containing four elements. However, bees in this previous study were unable to consistently match novel patterns of four, five or six. Perhaps this was due to their inability to discriminate between numbers in the AMS/ANS range when trained with appetitive differential conditioning, or perhaps this was because bees are not able to perform a novel DMTS task without first learning the specific association in the correct direction. This suggests that the inability of bees to perform the reversal test in the current study may be due to the numerical nature of the task and the storage of numerical information, as discussed below, but it could also be that bees are unable to reverse any association which is presented in a DMTS task, thus an inability to process operational schemes or understand a reversible association [39]. Giurfa et al. [50] demonstrated that in a DMTS task bees were able to learn to match a sample visual or olfactory cue. Furthermore, bees could extrapolate this task in tests demonstrating neural flexibility in DMTS tasks. For example, if bees had been trained to match odours and were then tested to match novel visual stimuli such as colours, they succeeded despite having no training on colour matching [50]. The results from Giurfa et al. [50] suggest that the inability of the bees in the current study to perform a reversal test is due to the numerical nature of the task and not the DMTS task itself.

While it is currently unknown where and how numerical information may be processed in insect brains [40], evidence from vertebrates can inform us of how different numerical formats and abstract concepts may be formed, processed and stored. Monkeys performing spatial or temporal enumeration tasks activated different populations of neurons in the intraparietal sulcus; however, after the task was completed, a different neural population stored the cardinality information, regardless of whether the original enumeration task was temporal or spatial [51]. As the processing and final storage of temporal and spatial numerical formats are different in monkeys, the authors conclude on distinct processing stages for different numerical formats [51]. The lack of reversibility in the bees' understanding of the sign–numerosity matching tasks suggests that the symbolic and numerical information is processed and/or stored by different populations of neurons. Thus, sign and numerosity matching tasks are not able to be reversed without training in both the forward and backward directions (i.e. with two different neuronal populations for the processing of the two directions of associations). Recent work on sign and numerosity associations in rhesus monkeys shows that with training over several months, monkeys learn the association between Arabic numerals and their corresponding quantities. Eventually, this training resulted in the signs being responded to in a similar way to the quantities in the prefrontal cortex, and to a lesser extent in the parietal cortex [19]. Thus, perhaps with similar training on the quantitative value of multiple signs, honeybees would demonstrate a similar association and neuron populations could respond to the symbolic representation and quantities in the same way, which may facilitate the reversal task. However, currently such a complex conditioning paradigm has not been developed for training and testing bees as it would require a very complex experimental design within subject, using an animal that has a short lifespan. Bees would need to be trained on the valuation of different quantities (e.g. [39]), then to match those quantities with signs (as in the current study). The next phase of the experiment would then be to design a way to train bees to associate the quantitative value of the numerosity with the sign. Finally, bees would need to be tested on their ability to value the signs numerically. Considering the lifespan of the bee and the complexity of such a design, it is currently not possible to test this hypothesis.

It remains to be explored as to whether bees can learn specific numerosity and sign associations for more than two relations and use symbolic representations to order numbers by value, which would demonstrate both symbolic number representation and ordinality [52,53]. Thus, the results from the current study do not put honeybees on par with the use of symbolic representations of number in pigeons, chimpanzees, rhesus monkeys and Alex the parrot, as these other species were able to learn more than two sign–numerosity associations and even give the signs (or labels) quantitative value. The current study is valuable for refining our understanding of numerical abilities in insects and shows that at least the learning of symbolic and numerical representations is not restricted to vertebrates. Understanding how such apparently complex numerical skills are acquired by miniature brains will help enable our understanding of how mathematical and cultural thinking evolved in humans, and possibly other animals [1,22,23,29,54–58].

Data accessibility

Data available from the Dryad Digital Repository at: https://doi.org/10.5061/dryad.990m8h3 [59].

Authors' contributions

S.R.H., A.A.-W. and A.G.D. designed the experiment. S.R.H. and J.E.G. analysed the data. S.R.H. collected the data and wrote the manuscript. All authors were involved in data interpretation and gave final approval for submission.

Competing interests

We declare no competing interests.

Funding

S.R.H. acknowledges the Australian Government Research Training Program (RTP) Scholarship. A.D.G. is funded by the Australian Research Council through the Future Fellowship scheme, FT160100357.