Habitat preference modulates trans-oceanic dispersal in a terrestrial vertebrate

Abstract

The importance of long-distance dispersal (LDD) in shaping geographical distributions has been debated since the nineteenth century. In terrestrial vertebrates, LDD events across large water bodies are considered highly improbable, but organismal traits affecting dispersal capacity are generally not taken into account. Here, we focus on a recent lizard radiation and combine a summary-coalescent species tree based on 1225 exons with a probabilistic model that links dispersal capacity to an evolving trait, to investigate whether ecological specialization has influenced the probability of trans-oceanic dispersal. Cryptoblepharus species that occur in coastal habitats have on average dispersed 13 to 14 times more frequently than non-coastal species and coastal specialization has, therefore, led to an extraordinarily widespread distribution that includes multiple continents and distant island archipelagoes. Furthermore, their presence across the Pacific substantially predates the age of human colonization and we can explicitly reject the possibility that these patterns are solely shaped by human-mediated dispersal. Overall, by combining new analytical methods with a comprehensive phylogenomic dataset, we use a quantitative framework to show how coastal specialization can influence dispersal capacity and eventually shape geographical distributions at a macroevolutionary scale.

1. Introduction

From the outset of evolutionary biology, biologists have recognized the importance of long-distance dispersal (LDD) in shaping the geographical distributions of contemporary clades [1]. LDD refers to rare events that differ from instances of ‘regular' dispersal by covering geographical distances that are well outside a species' traditional range [2]. While LDD is plausible for flying or wind-dispersed organisms [2], it has been considered less so for others, in particular as an explanation for the presence of similar terrestrial vertebrates across large water bodies [3]. Instead, in the wake of the general acceptance of plate tectonics, vicariance-based hypotheses have frequently been proposed to explain the widespread distribution of closely related taxa. Yet, a growing number of phylogenetic studies suggest that continental break-up often predates the divergence times of widespread clades and have concluded that, in such instances, past LDD or human-mediated translocations are more parsimonious explanations for broad contemporary distributions [4–9]. Recent debates about LDD have largely focused on dating results and less so on organismal traits or environmental circumstances that could mediate the probability of LDD events. To move beyond the practice of merely reporting a dated phylogeny, the major challenge is now to integrate ecology in biogeographic models and understand why some taxa are widely dispersed while others are not [2,10].

The idea that the probability of LDD can depend on a specific ecological trait or a species' habitat affinity is longstanding [10–12]. In plants, dispersal mechanisms that promote LDD have been studied extensively and the functional importance of seed morphology is now generally acknowledged [13–15]. Some plant families have spread across vast distances solely owing to their occurrence in a specific habitat (e.g. coastal environment [16]) or because they are more frequently exposed to long-distance migrants (e.g. birds [15]). Unfortunately, similar empirical evidence remains scarce for most terrestrial animals, vertebrates in particular, even though trait-dependent variation in dispersal propensity could lead to substantial differences in species proliferation because geographical expansion and diversification are often intimately linked [17]. Thus, quantifying how ecological traits can modulate range evolution across the tree of life will shed further light on both the prevalence and eventual macroevolutionary implications of LDD.

Recent advances in the field of historical biogeography will greatly benefit the study of trait-dependent dispersal owing to the now widespread adoption of explicit, probabilistic models of biogeographic processes [18–23]. These models provide a statistical framework in which the mechanisms that mediate LDD can be studied, by comparing model fit using standard model choice procedures [24]. Here, we employ a recently introduced model variant that allows the probability of LDD to depend on a discrete trait which itself can evolve on a phylogeny [25,26] and use this model to ask whether habitat preference has influenced the rate of LDD in a recent lizard radiation with an exceptionally broad geographical distribution.

Lizards of the genus Cryptoblepharus are found on multiple continents and island archipelagoes across the Pacific and Indian Ocean; some over 10 000 km apart. The genus (approx. 62 species) is part of the Eugongylus skink radiation that diversified long after the break-up of Gondwana [27], suggesting that processes other than vicariance have played an important role in shaping their current distribution. A recent evolutionary analysis of Australian Cryptoblepharus demonstrated that continental species have repeatedly shifted between saxicolous (rock) and arboreal (tree) environments and the associated changes in adaptive traits emphasize the overall importance of habitat preference within this group [28,29]. However, while inland species have repeatedly adapted to specific substrates, a second axis of specialization can be detected at a broader geographical scale: inland versus coastal species. Within Australia, two species exclusively occur in close proximity to the coast and are sometimes even found on rocks in the intertidal zone, where they hide in crevices and hunt for small crustaceans [30]. Species with similar ecological profiles have been reported outside Australia as well [31], which raises the question of whether major range expansions might have been enabled by the evolution of a coastal habit.

To evaluate whether habitat preference can modulate the probability of LDD, we assembled, to our knowledge the first comprehensive phylogenomic dataset for all Cryptoblepharus. We sampled 135 representatives from all described and proposed taxa across their global distribution, used a custom exon-capture system to sequence thousands of loci and employed a coalescent-based method to infer relationships among taxa. The resulting phylogeny serves as the basis for a detailed evaluation of geographical range evolution, the probability of natural trans-oceanic dispersal and the role of habitat preference in expediting such rare events.

2. Material and methods

(a). Sampling, library preparation and exon capture

Previous studies [32] have shown that the current taxonomy of Cryptoblepharus is probably an underestimation of the true species diversity. We, therefore, took an opportunistic approach, sampled as many Cryptoblepharus populations as possible—across their global distribution—and used a mitochondrial marker to identify the main lineages (see the electronic supplementary material, Methods for a detailed description of taxon sampling strategy). In addition to 37 individuals previously sequenced [29], we selected 98 other individuals and generated individually barcoded genomic libraries, suitable for exon-capture and subsequent Illumina sequencing. We used a modified version of our original Eugongylus group skink exon-capture kit [33], which targeted exon sequences identified in the transcriptomes of Carlia rubrigularis, Lampropholis coggeri and Saproscincus basiliscus [34]. In the modified version, we removed target exons that failed in earlier captures, and expanded the taxonomic coverage of the target set. To do this, we added exonic targets based on transcriptomes for Cryptoblepharus ruber, Bassiana duperreyi and Pseudemoia entrecasteauxii. We also removed targets for S. basiliscus (to reduce the total target size), which is quite closely related to L. coggeri. We targeted a total of 2457 exons and our improved capture probe set was synthesized by Roche NimbleGen in a SeqCap EZ Developer Library.

Genomic libraries were prepared with approximately 1400 ng input DNA per sample and according to the protocol of Meyer & Kircher [35], using modifications of Bi et al. [36]. A detailed description of the library preparation protocol can be found in [29,33,37]. Barcoded libraries were pooled in equimolar ratios prior to hybridization and the exon-capture hybridization was performed following the SeqCap EZ Developer Library user guide (Roche Nimblegen). We assessed the quality of the hybridization as specified in [29] and genomic libraries were sequenced (100 bp paired end) on a single Illumina HiSeq 2500 lane (see the electronic supplementary material, table S1 for coverage statistics).

(b). Bioinformatic processing for phylogenetic inference

Each library was processed and assembled using an in-house developed and publically available workflow (archived in the Dryad Digital Repository: https://doi.org/10.5061/dryad.v1d32). Once contigs were assembled, they were used as a reference to map cleaned reads back for each individual. Mapping was performed using Bowtie2 (v. 2.2 [38]) and resulting SAM files processed with SAMTools (v. 0.1.19 [39]). We employed GATK (v. 3.6 [40]) to identify heterozygous sites, masked sites with a low-quality genotype call (GQ < 20) and used read-backed phasing to generate pseudo-phased haplotypes. We then calculated a range of summary statistics that characterize sequencing and assembly success for each individual, and enforced strict limits on library quality (see the electronic supplementary material, Methods for further details). The contigs for all remaining individuals were aligned and filtered using the EAPhy (v. 1.0 [41]) workflow to ensure alignment quality.

(c). Phylogenetic inference

We evaluated the major phylogenetic lineages across all Cryptoblepharus with a maximum-likelihood (ML) inference of our concatenated dataset (1196 loci; 537 674 bp). We used RAxML (v. 8.1 [42]) to estimate the most likely tree out of 10 tree search replicates, using a GTR + Γ substitution model, and subsequently generated 100 bootstrap replicates to quantify bipartition support. This exploratory analysis confirmed our prior conjecture—based on only a mitochondrial marker—that the current taxonomy is probably incomplete. We, therefore, chose two representatives from each species and/or major well-supported monophyletic lineage (i.e. divergence time judged to be greater than 1 Ma between terminal branches; electronic supplementary material, figure S1) for subsequent analyses. Future studies should examine whether these taxa indeed represent unique species or phylogeographic lineages (which is often a challenging question for island representatives), but here we mainly focus on the biogeographic patterns between these distinct units. We repeated the alignment and alignment filtering process as described before, for the reduced dataset that only included two representatives for each major lineage (electronic supplementary material, table S1).

To generate a time-calibrated phylogeny, we first inferred the species tree topology using a summary-coalescent approach and then fitted branch lengths a posteriori using a concatenated alignment [28]. Instead of a two-step approach as presented here, the joint estimation of topology and time-scaled branch lengths would be preferred [43], but is currently intractable in a coalescent framework with high-throughput sequencing datasets that include this many taxa and loci. We used Astral II (v. 4.8 [44] – multiind branch Github) to infer the summary-coalescent species tree, where we assigned two representatives of each major lineage as members of the same taxa. We then used JModelTest (v. 2.1.0 [45]) to identify the substitution model with the best fit for each locus and used RAxML to infer the most likely gene tree out of 10 replicates. To minimize the probability of erroneous inference owing to missing data, we only used alignments without missing individuals. We subsequently characterized differences in gene tree resolution between loci, by calculating the tree certainty value (TC; [46]) for each locus using the gene tree with the highest likelihood score and 100 bootstrap replicates. After having verified the robustness of our phylogenetic estimate with a sensitivity analysis based on TC scores [29], we used the complete dataset (i.e. 1225 loci—no missing taxa) and employed multi-locus bootstrapping [47] to quantify bootstrap support for each bipartition of the species tree topology. Lastly, we used BEAST (v. 2.5.1 [48]) to fit branch lengths using a concatenated alignment that used a single representative for each taxon. In the absence of Cryptoblepharus-specific fossils, we constrained the species tree topology and scaled the phylogeny using the relaxed clock log normal model that allows the clock rates to vary between branches. We used an empirically informed distribution (0.00075–0.00125 substitutions site⁻¹ Myr⁻¹) of clock rates as a prior, which was based on calibrations for nuclear loci in another group of lizards within the same family (Scincidae [49]). Furthermore, we set a prior on the crown age of all Cryptoblepharus based on an inferred crown age of all Eugongylus skinks around approximately 25 Ma [50] and a most recent common ancestor for the C. nigropunctatus, C. novocaledonicus and C. boutonii sub-clade around 7 Ma [51]. Given our current understanding of the Eugongylus radiation, it is likely that the crown age of all Cryptoblepharus should be somewhere between 10 and 15 Ma. We, therefore, placed a broad prior on the crown age, range 10–30 Ma, and sampled from a lognormal distribution with a sampling peak before 15 Ma (95% quantile between 10 and 28 Ma). We ran BEAST in duplicate for 20 million generations, each run with a different starting seed, and sampled the Markov chain Monte Carlo (MCMC) run each 2000 generations. Convergence was verified using Tracer (v. 1.6 [52]), the first 20% of the MCMC discarded, and we merged independent runs with LogCombiner (v. 2.4 [48]). A full description, the scripts used and output files for all phylogenetic analyses can be found in the electronic supplementary material, Data (see the Dryad Digital Repository: https://doi.org/10.5061/dryad.hf027dp [53]).

(d). Modelling trait-dependent dispersal

To investigate whether habitat preference is a good predictor of geographical range evolution, we first classified each lineage as being coastal or non-coastal and identified 17 biogeographic regions based on connectivity and geological history (see the electronic supplementary material, Methods for a detailed description). We then estimated model fit using maximum likelihood for the six basic biogeographic models (DEC, DIVALIKE, BAYAREALIKE; basic models + J) that make assumptions traditionally popular in historical biogeography. We subsequently modified each of these models with an additional parameter. First, a ‘+x' variant modifies dispersal probability as a function of relative distance between areas [23] to account for a possible relationship between distance and dispersal rate. Second, a trait-dependent dispersal model variant [25,26] modifies dispersal rate by multiplying it with ‘m_coastal'; a multiplier on dispersal rate that is applied if a lineage occupies state 2 of a binary character. Here, the binary character is habitat preference in Cryptoblepharus. Because ancestral habitat preference is not known exactly, it must be inferred jointly with the biogeographical history. We do this using a 2-rate Markov-k model (Mk [54]), where parameter t_nc-c specifies the rate of moving from state 1 (non-coastal; nc) to state 2 (coastal; c), and t_c-nc specifies the reverse rate. When m_coastal is fixed to the value 1, dispersal probability is not linked to the value of the binary trait, and the likelihood of the data is just the likelihood of the geographical range data (under a traditional biogeography model) plus the likelihood of the trait data (under the 2-rate Mk model). When m_coastal is estimated as a free parameter, the data consist of the combination of species trait states and their geographical ranges. If the likelihood of these data, when m_coastal is a free parameter, increases substantially over the likelihood when m_coastal is fixed to the value 1, this is evidence of improved model fit, and the value of m_coastal indicates the size of the effect of being coastal on dispersal probability. Furthermore, to characterize the approximate uncertainty around the ML estimate of m_coastal, we also constructed likelihood profiles of m_coastal by taking the ML solution and then varying m_coastal between 0 and 50 at intervals of 0.1 (which also includes the most optimal value for m_coastal as inferred when the parameter was free to vary). Overall, models ranged in complexity from two free parameters (d and e, as in standard DEC) to seven (d, e, j, x, t_nc-c, t_c-nc, m_coastal) and we used standard tools for statistical model comparison [55] as incorporated in BioGeoBEARS (v. 1.1; available at https://github.com/nmatzke/BioGeoBEARS). A full description, input files and results for biogeographic modelling in BioGeoBEARS can be found in the electronic supplementary material, Data on Dryad. Simulation-inference tests of the trait-dependent dispersal model, descriptions of code unit-tests, and additional advice for researchers using the model can be found in [25,26].

3. Results

Targeted sequencing of orthologous loci yielded an average of 2429 loci for each individual (electronic supplementary material, table S1) and allowed a time-calibrated species tree analysis based on 1225 nucleotide alignments (no missing individuals) that confirmed the recent origin of the genus (figure 1). Cryptoblepharus lizards emerged in the mid-Miocene (approx. 12 Ma) and subsequently diversified during the Plio-Pleistocene. The current taxonomy is probably an underestimation of the actual species diversity (electronic supplementary material, figure S1) and we, therefore, replicated each analysis using two alternative datasets; (I) either following the current taxonomy or (II) also including deep phylogenetic lineages that probably represent discrete species. Because there are no qualitative differences in inference across datasets, we focus on the latter dataset that is a more realistic reflection of the underlying species diversity (but see the electronic supplementary material, table S2 for all modelling results based on current taxonomy).

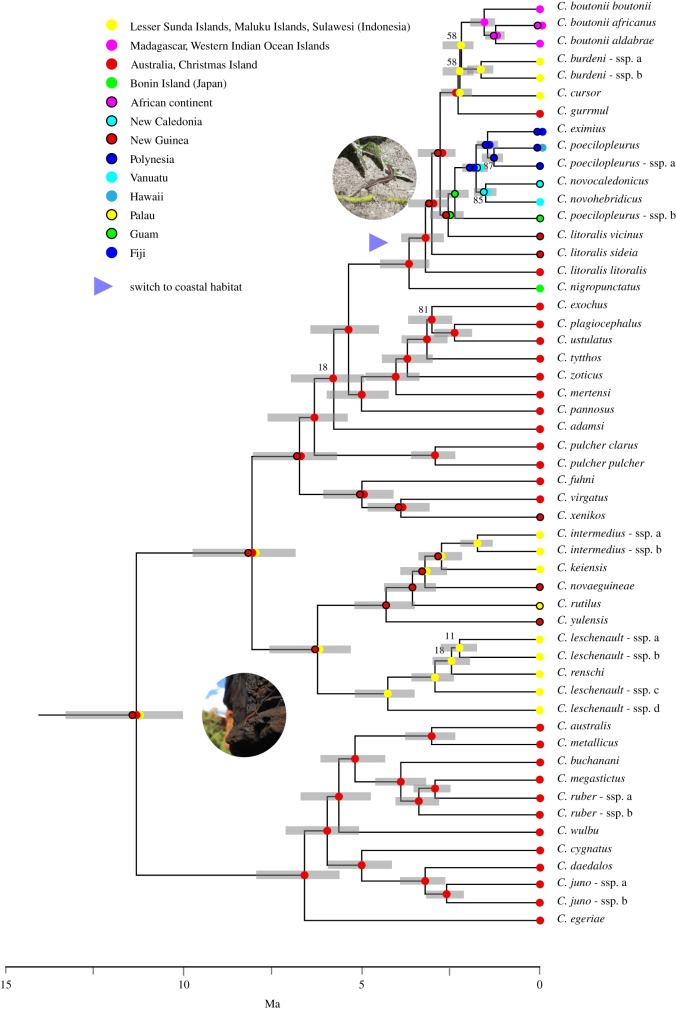
Figure 1.

Time-calibrated phylogeny for the major Cryptoblepharus lineages based on a summary-coalescent species tree analysis of 1225 loci. Confidence intervals for the node ages are highlighted in grey. The geographical region of origin has been annotated for each species using coloured orbs (see legend). Moreover, internal nodes have been annotated with the most probable ancestral regions as inferred using ancestral range estimation (see the electronic supplementary material, figure S2 for further details) and the colour scheme corresponds with figure 2. All nodes with multi-locus bootstrap support below 90 have been annotated and the blue arrow highlights the inferred branch where species switched from a non-coastal to coastal habitat (also see the electronic supplementary material, figure S3).

Ancestral range estimation suggests that the genus is of Indonesian or Sahul shelf (Indo-Australian) origin and then spread across the Pacific and Indian Ocean (figure 1; electronic supplementary material, figure S2). Initial range expansions were probably confined to the Indo-Australian area, with a species radiation across the region (including taxa on New Guinea and Micronesia), and the Australian continent was colonized in distinct waves with extant sister populations on the Lesser-Sundas and Christmas Island. The Australian continental radiation is, therefore, paraphyletic overall, with one large monophyletic group and a second group that includes many foreign representatives. Australian coastal species such as C. litoralis litoralis and C. gurrmul are for example more closely related to foreign coastal lineages than to inland congenerics (figure 1).

Major geographical range expansions, away from Indo-Australia, only commenced around 3–5 Ma (figures 1 and 2). The phylogenetic reconstruction indicates that the Pacific and Indian Ocean taxa are placed within one of the Indo-Australian clades but do not form a monophyletic group. The Indian Ocean taxa are most closely related to species that occur in northern Australia (C. gurrmul), the Lesser Sundas (C. burdeni) and Sulawesi (C. cursor). The Pacific taxa are more closely related to C. litoralis vicinus, which is a species that is distributed along the southern coast of New Guinea. In combination with the ancestral range estimation (figure 1; electronic supplementary material, figure S2), these results support a model where the oceanic populations have an Indo-Australian origin and spread outwards, possibly via a stepping stone process, in both directions. While the exact order of establishment remains unclear, populations that occur on islands closer to Indo-Australia are sister to the more distant populations for both the Pacific and Indian Ocean expansion (figure 1).

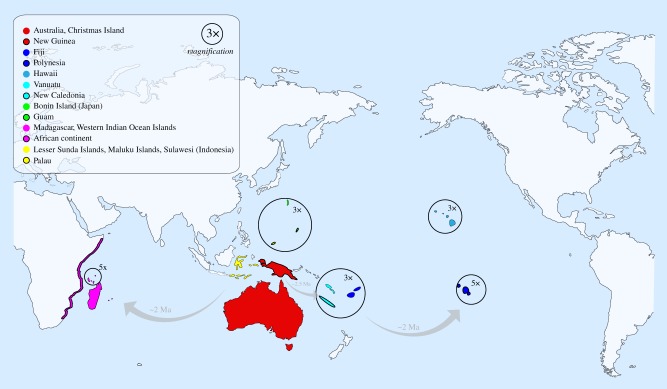
Figure 2.

Distribution map of the genus with the 17 geographical regions used in the biogeographic analyses. The colours and outlines of each region match with the orbs that highlight the geographical region of origin for each species (figure 1). Five geographical regions have been magnified to improve visualization, while regions within the Indonesian and Malagasy archipelagoes have been combined to improve clarity (though each of these regions were used independently in biogeographical models).

To investigate the biogeographic processes that have shaped the contemporary distribution of Cryptoblepharus lizards, we first considered six models that have been frequently used in historical biogeography (DEC, DIVALIKE, BAYAREALIKE; basic models + J). Among the six models, DEC + J was the best-supported model (table 1), with a considerable difference in the log-likelihood (LnL) between DEC + J (−117.5 LnL) and the worst performing model (BAYAREALIKE; −161.2 LnL), and a marginal difference between DEC + J and the second-best model (DIVALIKE + J; −119.3 LnL). While the comparison of traditional biogeographic models provides insight on the relative importance of dispersal in explaining contemporary distributions, it does not identify nor quantify predictors that can influence the frequency of LDD events. To investigate the latter, we modified the six traditional models and included two additional parameters; distance dependent dispersal probability (x) and trait dependent dispersal rate (m_coastal). Even though the trait-based models have two additional free parameters, ML estimates suggest that the increase in model fit is substantial and that the trait-based models significantly outperform all others (table 1; electronic supplementary material, table S2). Likelihood ratio tests also present significant support for the most complex models (electronic supplementary material, table S2) and, across all 24 possible models, the sample size corrected Akaike information criterion (AICc) model weights strongly support the DEC + J + x + m_coastal model as the overall model that best explains the data (table 1; 90.5%).

Table 1.

Statistical model comparison across all 24 models for the lineages dataset. (For all 24 models, the data includes both geographical ranges and the coastal/non-coastal discrete trait. Parameters in italics are fixed for the model in question. For p-values of likelihood ratio test comparisons of pairs of models, see the electronic supplementary material, table S2.)

dispersal predictor	base model	params	LnL	d	e	j	x	tnc-c	tc-nc	mcoastal	AICc	AICc weight (%)
none	DEC	4	−145.5	0.0067	0.0321	0	0	0.00613	0.00001	1	299.9	0.0
	DEC + J	5	−117.5	0.0018	1 × 10−12	0.0126	0			1	246.3	0.0
	DIVALIKE	4	−145.1	0.0071	0.0093	0	0			1	299.1	0.0
	DIVALIKE + J	5	−119.3	0.0020	1 × 10−12	0.0128	0			1	249.8	0.0
	BAYAREALIKE	4	−161.2	0.0089	0.1248	0	0			1	331.3	0.0
	BAYAREALIKE + J	5	−121.8	0.0016	1 × 10−12	0.0141	0			1	255.0	0.0
distance	DEC	5	−139.2	0.0925	0.0329	0	−1.206	0.00613	0.00001	1	289.8	0.0
	DEC + J	6	−109.5	0.0249	1 × 10−12	0.1848	−1.237			1	232.8	0.0
	DIVALIKE	5	−136.8	0.0962	0.0088	0	−1.210			1	284.8	0.0
	DIVALIKE + J	6	−110.5	0.0281	1 × 10−12	0.1748	−1.228			1	234.9	0.0
	BAYAREALIKE	5	−157.1	0.1018	0.1245	0	−1.096			1	325.4	0.0
	BAYAREALIKE + J	6	−112.9	0.0232	1 × 10−12	0.1860	−1.261			1	239.5	0.0
trait	DEC	5	−132.1	0.0021	0.0348	0	0	0.00610	0.00001	14.2	275.5	0.0
	DEC + J	6	−106.1	0.0005	1 × 10−13	0.0041	0	0.00610	0.00001	16.3	226.1	0.1
	DIVALIKE	5	−133.4	0.0029	0.0164	0	0	0.00579	0.00001	9.5	278.1	0.0
	DIVALIKE + J	6	−109.7	0.0008	1 × 10−13	0.0056	0	0.00609	0.00001	9.6	233.2	0.0
	BAYAREALIKE	5	−147.3	0.0024	0.1135	0	0	0.00611	0.00001	16.4	305.8	0.0
	BAYAREALIKE + J	6	−112.1	0.0004	1 × 10−13	0.0051	0	0.00610	0.00001	16.4	238.0	0.0
distance and trait	DEC	6	−126.2	0.0225	0.0350	0	−1.050	0.00610	0.00001	13.7	266.2	0.0
	DEC + J	7	−97.9	0.0065	1 × 10−13	0.0652	−1.177	0.00609	0.00001	13.7	212.4	90.5
	DIVALIKE	6	−125.2	0.0371	0.0141	0	−1.123	0.00610	0.00001	8.2	264.1	0.0
	DIVALIKE + J	7	−100.4	0.0104	1 × 10−13	0.0819	−1.188	0.00610	0.00001	8.8	217.2	8.1
	BAYAREALIKE	6	−142.3	0.0289	0.1124	0	−1.038	0.00613	0.00001	14.8	298.4	0.0
	BAYAREALIKE + J	7	−102.2	0.0061	1 × 10−13	0.0793	−1.217	0.00611	0.00001	14.8	220.9	1.3

The trait-based models are not only substantially favoured over others; individual parameter estimates measure how distance and the coastal preference modulate the probability of LDD (table 1). For the ‘+x’ models, where the dispersal probability is multiplied by (relative distance)^x, the value for x ranges from −1.038 to −1.261 (x; table 1), suggesting that dispersal probability declines roughly linearly with increasing distance (e.g. x = −1 means that dispersal probability drops by half when the relative distance doubles [23]). Furthermore, for models where dispersal probability changes with habitat preference, the rate of dispersal increases 13- to 14-fold (model averaged mean; table 1; electronic supplementary material, table S2) when comparing coastal to non-coastal species (m_coastal; table 1). Finally, the LnL profiles (electronic supplementary material, figure S6), produced by taking the ML model and only varying m_coastal, show that the spread of m_coastal values with similar likelihood scores is relatively large but that the likelihood curve drops precipitously as it approaches m_coastal = 1. Altogether, these results strongly suggest that jump-dispersal has played an important role in geographical range evolution and that, most notably, the probability of LDD substantially increases for species that occur in coastal habitats.

4. Discussion

Range evolution has undoubtedly shaped the macroevolutionary history of many taxa across the tree of life, but it has been challenging to study the frequency and determinants of LDD in a quantitative framework. Here, we combine new analytical methods with a comprehensive phylogenomic dataset to estimate how species-specific ecological features can influence the probability of trans-oceanic dispersal in a group of terrestrial vertebrates. Akin to habitat-dependent dispersal dynamics in plants, our results suggest that preference for coastal habitats has substantially increased the probability of natural trans-oceanic dispersal in Cryptoblepharus lizards and illustrate that such highly improbable occurrences should not be seen as mere random events. Instead, the evolution of novel traits or other ecological features can increase or decrease the likelihood of LDD and ultimately lead to major differences in geographical range evolution across clades.

While trait-dependent dispersal models provide a statistical framework to study the mechanistic processes that regulate LDD, accurate estimates of phylogenetic history are still required to appropriately model biogeographic history. We specifically employed a genomic approach and used a large sample of the genome (>1000 loci) to optimize the estimation of topology and branch lengths. The resulting coalescent-based species tree represents, to our knowledge, the first species-level phylogeny for all Cryptoblepharus, with most nodes fully resolved, and is largely congruent with previous phylogenetic estimates for the Malagasy and Australian clades alone [29,56]. The fossil record for skinks is unfortunately very scant and we, therefore, relied on an empirical clock rate calibration and our genomic dataset. The inferred node ages are relatively consistent with more broad scale studies that focus on all squamates [57] or Eugongylus skinks [50] alone, suggesting that the major timeline of the Eugongylus radiation is relatively well understood. Moreover, a comparison between the inferred node ages and the geological ages of landforms inhabited by Cryptoblepharus provides further support that our branch lengths are realistic. For example, Cryptoblepharus lizards are endemic to a number of young Pacific islands that are of volcanic origin and none of the associated divergence dates in the phylogeny substantially surpass island age [58]. A similar comparison between node ages (figure 1) and the known history of anthropogenic expansion across the Pacific also excludes the possibility that the observed dispersal patterns have been solely shaped by human intervention. Remote Pacific islands were among the last regions on Earth to be colonized by humans and many Polynesian islands have only been settled within the last 3000 years [59]. In this respect, Cryptoblepharus differs from other lizard taxa that are widely distributed across oceanic islands and for which genetic data supports a more recent expansion model [60–62].

Traditional models estimate biogeographic history, but the inclusion of additional parameters that account for variation in dispersal rates can provide explicit insights into the determinants that mediate LDD. First, model fit considerably improved when the rate of dispersal was not fixed but could vary with distance between regions (table 1). The geographical distance between Indo-Australia and the African mainland is close to 10 000 km and, even though Cryptoblepharus seems to disperse frequently at a macroevolutionary timescale, dispersal over long distances must be relatively rare in absolute terms [56,63]. The inverse relationship between distance and dispersal is congruent with expectations based on island biogeography [64] and our results generally support a model in which populations on nearby islands are more closely related. If dispersal rate between regions would be independent from geographical distance, distant regions should be colonized as frequently as nearby regions and result in a less structured phylogeographic distribution (figure 1). Second, in addition to distance, we find strong support for a model where dispersal rate is conditional on habitat preference. The inference of ancestral ranges and ecological states suggests that the distribution of Cryptoblepharus was largely confined to Indo-Australia until species adapted to a coastal habitat (figure 1; electronic supplementary material, figure S2). Once a coastal specialist emerged around 3–5 Ma, lineages dispersed in various directions and across vast geographical distances. These coastal species are on average 13 to 14 times more likely to disperse than non-coastal species (table 1), but the 95% confidence interval surrounding this estimate is relatively wide (electronic supplementary material, figure S6). Nonetheless, the likelihood curve drops substantially as it approaches m_coastal = 1, and is in line with the other statistical results (i.e. likelihood ratio test and AICc comparison), suggesting that models where m_coastal is higher than m_non-coastal have a significantly better fit to the data than models where they are equal. Statistical model choice therefore unambiguously supports a model in which habitat specialization has led to widespread dispersal across both the Pacific and Indian Ocean.

While statistical model comparison strongly suggests that habitat preference has led to a considerable change in LDD dynamics, future studies should investigate which aspects of being coastal might directly or indirectly enhance dispersal capacity. In the case of Cryptoblepharus, this may not be a straightforward question to address, because while there are many coastal taxa, coastal specialization is a derived state that only evolved once and these multiple dispersals represent phylogenetic pseudo-replication [65,66]. Any trait that is co-inherited with a coastal preference would show a similar signal of trait dependence and we, therefore, refrain from drawing any conclusions regarding the exact cause of the relationship between coastal habit and dispersal rate. Nonetheless, our results closely dovetail with the notion that ecological traits such as habitat preference can indeed shape the evolution of geographical ranges and suggests that trait-dependent LDD might be more widespread than previously thought. To date, much of this research has focused on plants and seed dispersal, but a limited number of studies have tried to identify coastal traits that increase dispersal capacity in other organisms. For example, experimental studies in lizards have focused on their ability to float [67], evaporative water loss [68] and various aspects of egg survival following exposure to seawater [69–71]. Similar experiments in arthropods have shown that survival rate between species exposed to seawater can vary [72], suggesting that some species might be better able to persist during long oceanic voyages. Unfortunately, experimental evidence remains scant for most animal groups and is much needed to be able to differentiate between a model in which coastal specialists have specific traits that enhance dispersal capacity or are simply more frequently exposed to dispersal enhancing circumstances. In the case of Cryptoblepharus, where it will be difficult to differentiate between both hypotheses, we will view traits that correlate with habitat preference as being part of a functional network [65] and suggest that most of these traits are directly or indirectly associated with coastal specialization. Similar collective changes in phenotype have been reported previously in Cryptoblepharus and lends further support to the idea that a change in environment can lead to a range of correlated changes [28,30].

In summary, we have outlined a probabilistic modelling framework in which the directionality, frequency and determinants of LDD can be simultaneously quantified, and investigated the role of ecology in shaping the contemporary distribution of a diverse genus of terrestrial vertebrates. Natural LDD across oceans has been a recurring process during the global radiation of Cryptoblepharus lizards, and the rate of dispersal substantially differs between species that occur in distinct habitats. These results demonstrate that LDD can have substantial macroevolutionary implications and, while rare, should not be merely seen as the outcome of a stochastic process. Instead, they should motivate future studies to further evaluate the prevalence of LDD across the tree of life and focus on the ecological determinants that can promote the evolution of geographical ranges.

5. Code availability

All scripts used for processing of exon-capture data can be found on Dryad: doi.org/10.5061/dryad.v1d32, while all scripts used for alignment and alignment filtering can be downloaded from https://github.com/MozesBlom/EAPhy. More specifically, a detailed description of scripts and project specific settings can be found in the electronic supplementary material, data also deposited in the Dryad Digital Repository: https://doi.org/10.5061/dryad.hf027dp [53].

Data accessibility

Raw nucleotide sequence data generated in this study have been deposited in the Short Read Archive (SRA) under PRJNA289283. The assembled exons, alignments, inferred phylogenies and input files for modelling of biogeographic history have been deposited in the Dryad Digital Repository: https://doi.org/10.5061/dryad.hf027dp [53].

Authors' contributions

M.P.K.B. and C.M. conceived the study; M.P.K.B., E.A., C.C.A., A.R.B., R.N.F., S.A.H., D.T.I., J.A.M., B.R.K., S.B.R., E.N.R., A.L.S., M.S., M.A., M.V. F.G., S.R and C.M. arranged permits and conducted the fieldwork; J.G.B. designed the exon-capture system; M.P.K.B. performed laboratory work; M.P.K.B., N.J.M. and J.G.B. performed data analysis; M.P.K.B., N.J.M. and C.M. interpreted the results; M.P.K.B., N.J.M., R.N.F., S.R. and C.M. provided theoretical discussion; M.P.K.B., N.M. and C.M. wrote the manuscript; M.P.K.B., C.C.A., R.N.F., J.A.M., S.R, M.A., M.V., F.G., M.S. and C.M. obtained funding. All authors read, gave comments and helped to revise the final version of the manuscript.

Competing interests

The authors declare no competing interests.

Funding

Fieldwork of M.P.K.B. was supported by a National Geographic Young Explorers Grant (9594-14) and the Mohamed bin Zayed Species Conservation Fund (14058475). Additional support was provided through grants from the Australian Research Council to C.M. and N.J.M. (DECRA no. DE150101773), the National Science Foundation to J.A.M. and C.C.A. (NSF DEB-1258185, DEB-1146033). N.J.M. was further supported by The Australian National University, the University of Auckland and Marsden grant nos 16-UOA-277, 18-UOA-034. Furthermore, R.N.F./S.A.H./A.R.B. received support from the Ecosystems Mission Area in USGS, Conservation International and SPREP, but the use of trade, product or firm names does not imply endorsement by the US government. Lastly, we also thank staff at various museums for providing access to tissues and would like to acknowledge the invaluable support of natural history collections.