Abstract
Self-report measures are vulnerable to response biases that can degrade the accuracy of conclusions drawn from results. In low-stakes measures, inattentive or careless responding can be especially problematic. A variety of a priori and post hoc methods exist for detecting these aberrant response patterns. Previous research indicates that nonparametric person-fit statistics tend to be the most accurate post hoc method for detecting inattentive responding on measures with dichotomous outcomes. This study investigated the accuracy and impact on model fit of parametric and nonparametric person-fit statistics in detecting inattentive responding with polytomous response scales. Receiver operating curve (ROC) analysis was used to determine the accuracy of each detection metric, and confirmatory factor analysis (CFA) fit indices were used to examine the impact of using person-fit statistics to identify inattentive respondents. ROC analysis showed the nonparametric HT statistic offered the most area under the curve when predicting a proxy for inattentive responding. The CFA fit indices showed the impact of using the person-fit statistics largely depends on the purpose (and cutoff) for using the person-fit statistics. Implications for using person-fit statistics to identify inattentive responders are discussed further.
Keywords: data quality, person-fit statistics, inattentive responding, response biases, nonparametric IRT
Response biases present a major threat to the validity of inferences made from self-report measures. Examples commonly found in educational and psychological research include social desirability bias, acquiescence, and inattentive responding (IR). In each case, the measurement process is systematically influenced by construct irrelevant variance resulting from participants’ perceptions of, and interactions with, the instrument. Response biases can influence results at both the item and scale levels, introducing measurement error, attenuating relationships, and increasing Type II errors (M. E. Clark, Gironda, & Young, 2003; Credé, 2010; Meade & Craig, 2012).
One such response bias, IR, is defined as failing to respond to the content of the items (Meade & Craig, 2012). This content nonresponsivity occurs when any response is made independent of the item content. Examples include responding without reading the item stem, or misinterpreting the item stem and/or response options. Previous studies have investigated IR and its impact on self-report results from a variety of perspectives (e.g., M. E. Clark et al., 2003; Maniaci & Rogge, 2014; Meade & Craig, 2012; Oppenheimer, Meyvis, & Davidenko, 2009). The mechanisms behind IR are hypothesized to be lack of participant ability to respond accurately (e.g., poor eyesight or a language barrier), responding randomly (e.g., selecting answers unsystematically), or systematic avoidance (deliberately answering items independent of content; Nichols, Greene, & Schmolck, 1989). IR has also been associated with a lack of motivation (Finn, 2015). In addition, it is hypothesized that IR is more prevalent in low-stakes, self-report measures that have little to no impact on the respondent.
Methods for Detecting IR
Methods for identifying IR can be categorized as either a priori or post hoc. As the name suggests, a priori methods are planned, and included, in a survey before the survey is administered. A priori methods often involve some sort of check to assess whether or not the participant is paying attention to the content of the items. Conversely, post hoc methods are implemented after a survey has been administered. Post hoc methods typically involve computing a statistic designed to identify aberrant response patterns. Several a priori and post hoc methods will be discussed further.
Instructed Response Items
Instructed response items are one of the most effective a priori ways to identify IR. Instructed response items are built with an item stem that instructs a participant to respond to an item in a particular way, or using a specific response option (e.g., For this item, select Response Option 5). If respondents do not endorse the instructed response option, it is assumed they are being inattentive. Including two instructed response items (each with five response options) was found to provide a .96 probability of screening out inattentive responders, assuming items are conditionally independent (Meade & Craig, 2012). However, recent research suggests that instructed response items have low specificity when identifying IR (Niessen, Meijer, & Tendeiro, 2016). It is possible that aberrant responders who are not completely disengaged from the survey (e.g., skimming the item stems and quickly selecting responses without thought) might be able to avoid identification by instructed response items.
Response Time
Response time is a commonly used post hoc method for detecting IR on online questionnaires. It is thought that a quick response time is evidence of IR, because it is unlikely that the participant had time to read, and fully consider, the item stem. In practice, it has been suggested that response time could be a useful indicator of IR if a meaningful cutoff, or related statistic, could be identified (Marianti, Fox, Avetisyan, Veldkamp, & Tijmstra, 2014; Meade & Craig, 2012; Wise & Kong, 2005). A major challenge with response time is identifying a threshold after which respondents are considered inattentive. Using empirical methods to determine a threshold, such as classification consistency, resampling, or receiver operating curve (ROC) analysis, may provide a method of making response time a useful indicator of IR.
Guttman Errors
Guttman errors can be used as a simple post hoc method for detecting aberrant response patterns (Emons, 2008; Karabatsos, 2003; Meijer, 1994; Meijer, Egberink, Emons, & Sijtsma, 2008). A Guttman error occurs when a respondent answers a difficult item correctly, but an easier item incorrectly. In practice, Guttman errors are used in one of two ways: (a) a simple count of Guttman errors or (b) the normed count of Guttman errors. Generally, both methods have been shown to accurately identify aberrant response patterns in data with dichotomous response scales (Emons, Sijtsma, & Meijer, 2005; Emons, 2008; Meijer, 1994). In some situations, Guttman errors were shown to detect IR better than more complex person-fit statistics (Emons et al., 2005; Karabatsos, 2003; Meijer, 1994; Meijer et al., 2008). However, Guttman errors have also been shown to have low sensitivity when detecting aberrancy in data with polytomous response scales (Niessen et al., 2016). Note that Guttman errors form the foundation of many nonparametric person-fit statistics, including the ones reviewed below, U3 and HT.
U3
The U3 person-fit statistic (van der Flier, 1982) provides another post hoc method for identifying IR. Although U3 has shown some promise in research (Karabatsos, 2003; Tendeiro & Meijer, 2014), a major limitation of U3 is that the equivalence between the theoretical and empirical sampling distribution is affected by item discrimination. Specifically, when the theoretical distribution is used to determine critical values, the Type I error rates are both inflated (in the tails of the distribution) and deflated (in the middle range of the distribution) when items have moderate to high levels of discrimination (Emons, Meijer, & Sijtsma, 2002; Tendeiro & Meijer, 2014). The polytomous generalization of U3 is given by Equations 1 and 2, where Equation 1 is the summation of the log odds of the JM item steps (where J is the number of items, and M is the number of response categories) that were passed for item k,
| (1) |
where yk is the vector of observed responses for item k, and is estimated item step difficulties. The summed log odds is then normed as
| (2) |
where max(W|X+) is the likelihood of the maximum number of item steps passed given person n’s total score, and min(W|X+) is the likelihood of the minimum number of item steps passed given person n’s total score.
HT
Proposed by Sijtsma (1986), HT is an application of the item scalability coefficient (Mokken, 1971) to respondents. The HT coefficient quantifies the degree to which data conform to the Guttman model for one respondent compared against the rest of the respondents in a sample. Conceptually, HT sums the covariances for person n with the rest of the sample and divides the maximum possible covariances for person n (i.e., the covariances that would have been observed with no Guttman errors) with the rest of the sample. HT reflects the concept of this covariance ratio as
| (3) |
where xn is the response vector for person n, and r(n) is the response vector of total scores calculated from all individuals in the sample excluding person n (this is also referred to as the rest score; Sijtsma & Molenaar, 2002). It should be noted that Equation 3 is mathematically equivalent to the definitional form of the HT equation (Sijtsma & Molenaar, 2002). HT has been shown to have high aberrant response detection rates in simulation studies involving data with dichotomous response scales under various conditions (Dimitrov & Smith, 2006; Karabatsos, 2003; Tendeiro & Meijer, 2014).
Standardized Log Likelihood
The standardized log likelihood (lz; Drasgow, Levine, & Williams, 1985) is a parametric person-fit statistic requiring estimates of both item and ability parameters. The lz statistic is the standardized log likelihood function:
| (4) |
where l0 is the polytomous log likelihood estimate, and E(l0) and V(l0) are the mean and variance of the log likelihood function, respectively. The lz statistic has been shown to approximate the standard normal distribution on long tests (i.e., 80 items or more; Drasgow et al., 1985). However, this approximate normality has been shown to degrade when estimated values of ability () are used, as is typically the case as true values of ability (θ) are generally unknown (Magis, Raiche, & Beland, 2012; Seo & Weiss, 2013). This often leads to an underdetection of person-misfit. It should be noted that a corrected form of the lz statistic (lz*) addressing this issue has been proposed, but it has only recently been generalized for use with polytomous data (Sinharay, 2016; Snijders, 2001). The lz statistic has been shown to have some ability to detect aberrancy depending on test characteristics (Armstrong, Stoumbos, Kung, & Shi, 2007; Reise & Due, 1991). Despite these issues, use of the lz statistic is common. Evidence suggests that lz is unable to detect aberrant response patterns as well as some nonparametric person-fit statistics on dichotomous response scales (Dimitrov & Smith, 2006; Karabatsos, 2003). In addition, lz has been shown to have low sensitivity when detecting aberrancy in data with polytomous response scales (Niessen et al., 2016).
Which Method Is Best?
Karabatsos (2003) compared 36 different person-fit statistics on how well they detected aberrant responding. These 36 person-fit statistics included HT, U3, number of Guttman errors (normed and raw), and lz. A simulation was conducted with three crossed conditions: five types of aberrant responding, four percentages of aberrant responders, and three test lengths. Data were simulated to be on a dichotomous response scale using the Rasch model. These 36 person-fit statistics were evaluated using ROC analysis, which compares the sensitivity (the ability of an index to identify actual aberrant responding), and specificity (the ability of an index to classify normal responding as such), of a predictor variable on some dichotomous outcome. Results indicated that HT provided the highest area under the curve (AUC; a measure of accuracy) when detecting all types of aberrant responding. U3 had the highest AUC for detecting respondents who were endorsing items at random. The number of Guttman errors and lz were also found have acceptable AUC in detecting aberrant response patterns, but did not have AUC greater than HT or U3. In addition, results indicated that there was essentially no difference in aberrancy detection between statistics based on the percentage of aberrant responders. However, as the percentage of aberrant responders increased, detection became more difficult overall. For test length, HT and the log likelihood function (not the standardized log likelihood) had the best detection rates across short, medium, and long tests. Overall, HT was determined to be the most accurate person-fit statistic across all conditions. U3 was also relatively accurate compared with the other 34 person-fit statistics. Some studies have found similar results under different conditions and with different types of aberrancy (Dimitrov & Smith, 2006; St-Onge, Valois, Abdous, & Germain, 2011; Tendeiro & Meijer, 2014). However, M. Clark et al. (2014) found that the Ico scalability index (a person-fit statistic based on factor analytic procedures; Ferrando, 2009) was able to more accurately detect cheating than HT and lz under certain conditions. Although, there were other conditions where all indices had poor detection rates. Sinharay (2017) also called into question Karabatosos’s method, suggesting that the effectiveness of nonparametric person-fit statistics degrades when ROC are calculated for each simulated dataset (rather than aggregated as Karabatsos had done). Taken together, these conflicting findings suggest that determining the “best” person-fit statistic for identifying aberrancy requires further investigation.
The studies just discussed show that person-fit statistics can be useful for identifying aberrant response patterns in simulated data with dichotomous response scales. However, empirical evaluations with polytomous data are limited. The current study extends previous research by comparing a few of the most promising parametric and nonparametric person-fit to determine the practical impact of applying these statistics in real-world, polytomous datasets. Specifically, this study examined the effectiveness of five aberrant response indices (HT, U3, normed Guttman errors, lz, and response time) in terms of two related research questions:
Research Question 1: Can the detection indices accurately flag IR, as approximated by instructed response items?
Research Question 2: After deleting IR using the detection indices, how much improvement in model fit can be obtained?
It should be noted that the instructed response item can only approximate true IR among participants. Some true IR went undetected and some false IR was flagged. However, in practice, the instructed response item is often the optimal a priori detection method. Thus, this study sought to provide practical guidance on the viability of person-fit statistics for detecting IR in real-world scenarios where instructed response items are not available.
Based on previous research, it is unclear whether the nonparametric person-fit statistics will outperform the parametric person-fit statistic in polytomous data (Dimitrov & Smith, 2006; Karabatsos, 2003; Sinharay, 2017). It is also unclear whether or not the person-fit statistics can provide an acceptable alternative to identifying IR in the absence of instructed response items. Thus, this study involves exploration via multiple stages of analysis. Overall, it was expected that the person-fit statistics would provide an acceptable alternative for identifying IR when instructed response data are not available. In addition, it was expected that HT and U3 would outperform lz and the normed number of Guttman errors in their detection of IR. Finally, it was expected that HT would outperform the U3. Response time was also investigated using an empirically derived cutoff to determine its accuracy in detecting IR.
Method
Data
Data were obtained from two baseline administrations of the Collegiate Active Learning Calculus Survey (CALCS), administered to undergraduate students across three universities. The purpose CALCS is to assess student attitudes, beliefs, and behaviors about mathematics in an attempt to improve teaching and learning in undergraduate courses. The 34 self-report items are designed to fit into four distinct factors: math usefulness (10 items), nonproductive beliefs about mathematics (seven items), flexible orientation toward math (seven items), and active learning (10 items). Two administrations of the survey were completed in January and August 2016, at the beginning of the spring and fall semesters. The survey was administered online, with students having the opportunity to receive extra credit and be included in a drawing for a gift card. Thus, the survey was low-stakes, and there was no direct incentive for students to respond attentively. Sample sizes for each administration were 1,368 and 3,831, respectively. These sample sizes represent the number of students who answered all items, after removing any duplicate responses by students, and removing any respondents that did not answer all of the items.
Analyses
Detection of approximate IR was compared for HT, U3, lz, normed Guttman errors, and response time. It should be noted that response time was measured as the duration that a respondent took to complete the entire survey, and did not provide any item-level information. A single instructed response item built into the CALCS served as an approximation for IR, and thus constituted the criterion for evaluating the accuracy of each detection method. The instructed response item, which appeared approximately two thirds of the way through the survey, instructed participants to choose Choice 4 on the 5-point rating scale. Responding at random across the entire survey, a participant has a .20 probability of selecting the correct response category, assuming the items were conditionally independent. The accuracy of each index was then evaluated using a ROC analysis, which also provided the basis for determining various empirical cutoffs. Three cutoffs were examined for each index: (a) a cutoff that minimized false positives to 1%, (b) a cutoff that minimized false negatives to 20%, and (c) a cutoff that maximized the AUC determined by the ROC.
The change in model fit obtained by using these metrics to remove inattentive responders was also examined. The indices were used to split each CALCS administration into seven datasets. The first dataset included all respondents who completed the questionnaire and had some variance in their responses, the second dataset removed all respondents who did not select the correct instructed response option, and the remaining datasets excluded flagged respondents based on the five detection indices. For each of these datasets, a confirmatory factor analysis (CFA) was conducted and fit indices were compared across datasets within a given administration. Each CFA was conducted using the maximum likelihood estimator, and modeled a four-factor solution with no residual covariances. Effective IR detection methods were expected to result in improved model fit when compared with model fit using data containing all respondents. Ideally, effective IR detection by the detection indices would also yield fit statistics that were comparable with the dataset which used the instructed response item to exclude respondent. All analyses were conducted in R (R Core Team, 2017) using the mokken (van der Ark, 2012), PerFit (Tendeiro, Meijer, & Niessen, 2016), pROC (Robin et al., 2011), and lavaan (Rosseel, 2011) packages.
Estimation of lz
As noted above, lz is parametric person-fit statistic, which means that it requires item and ability estimates. For the purposes of this study, item parameters were estimated using the Graded Response Model, as it provided the best fit to these data. In addition, the ability estimates were obtained using the Expected A Posteriori method. It should also be noted that the instructed response item was not included as part of the measurement model of the CALCS at any step of the analyses.
Determination of Cutoffs Using ROC
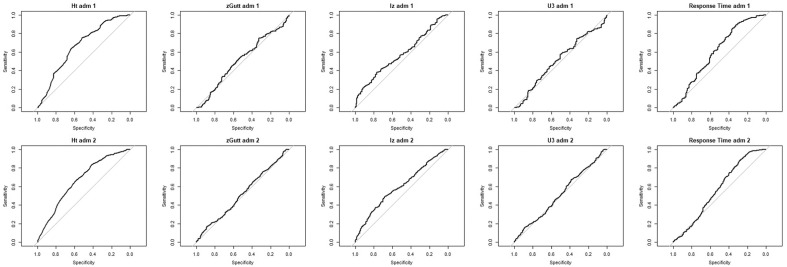
ROC analysis is a useful tool for determining empirical cutoffs, as it allows you to determine cutoffs for a variety of situations (e.g., limiting Type I or Type II errors). ROC analysis involves the creation of a ROC, which plots the sensitivity against the specificity, or sometimes the false positive rate (1 – specificity). Each point on the ROC is a sensitivity/specificity pair that corresponds to a particular threshold. These thresholds can be used to determine the cutoffs derived from ROC. To pick a cutoff, a threshold is identified that corresponds to a chosen level of either specificity or sensitivity. For example, to maintain a Type I error rate of 0.05 (α = .05), one would find the threshold that corresponds to a .95 sensitivity rate. Another useful way to determine cutoffs is to use the threshold that maximizes AUC, essentially the highest sensitivity/specificity pair. Many of the programs capable of conducting a ROC analysis contain options to automatically provide this threshold. Conceptually, maximizing the AUC is as simple as finding the point on the ROC that is furthest from the identification line (some ROC can be viewed in Figure 1).
Figure 1.
ROC plots for both administrations across all five identification indices.
Note. ROC = receiver operating curve; zGutt = normed Guttman errors.
Results
ROC Analyses
ROC plots are presented in Figure 1. In both administrations, HT has the highest AUC estimates (.66 in both administrations). The next highest AUC estimates were lz (.59 and .61) and response time (.61 and .57). The lowest AUC estimates were obtained from normed Guttman errors (.51 and .52) and U3 (.51 in both administration). AUC estimates can be roughly interpreted using an academic grading scale: AUC = 0.5 to 0.6 indicates an ineffective test, 0.6 to 0.7 is a poor test, 0.7 to 0.8 is considered a fair test, 0.8 to 0.9 is considered a good test, and 0.9 to 1.0 is considered an excellent test; AUC less than 0.5 indicates random chance is a more accurate predictor of the outcome than a particular criterion. According to this interpretation, it should be noted that none of the identification indices were classified better than poor predictors of the instructed response item. In addition to examining the AUC, the ROC was used to determine three empirical cutoffs for all the IR indices using the process described in the previous section.
CFAs
CFA fit indices were used to demonstrate the change in model fit obtained from using these person-fit indices to remove respondents. CFA model fit indices, along with sample size, are reported in Tables 1 to 3. It should also be noted that the intended measurement model for CALCS does not fit the full dataset particularly well, with fit statistic falling beyond recommended values. Results still allow for a relative comparison among the aberrant response indices. However, the poorly fitting models suggest that the measurement model, or the instrument itself, may need to be revised.
Table 1.
Model Fit Comparisons for Identification Indices When Minimizing False Positives.
| Adm. | CFI | RMSEA [90% CI] | SRMR | n |
|---|---|---|---|---|
| 1 | ||||
| Raw | 0.742 | .065 [.063, .068] | 0.064 | 1,236 |
| Inst. Res. | 0.770 | .062 [.059, .064] | 0.057 | 1,111 |
| H T | 0.748 | .063 [.061, .065] | 0.061 | 1,217 |
| zGutt | 0.754 | .061 [.059, .063] | 0.058 | 1,218 |
| lz | 0.772 | .060 [.059, .063] | 0.057 | 1,218 |
| U3 | 0.755 | .061 [.059, .063] | 0.058 | 1,218 |
| Resp. time | 0.751 | .062 [.062, .066] | 0.062 | 1,214 |
| 2 | ||||
| Raw | 0.730 | .066 [.065, .067] | 0.063 | 3,505 |
| Inst. Res. | 0.749 | .064 [.062, .065] | 0.058 | 3,176 |
| H T | 0.736 | .064 [.063, .065] | 0.060 | 3,465 |
| zGutt | 0.739 | .064 [.062, .065] | 0.059 | 3,461 |
| lz | 0.752 | .063 [.062, .064] | 0.058 | 3,460 |
| U3 | 0.738 | .064 [.062, .065] | 0.059 | 3,460 |
| Resp. time | 0.739 | .065 [.064, .066] | 0.061 | 3,447 |
Note. Adm. = administration; CFI = comparative fit index; RMSEA = root mean square error approximation; CI = confidence interval; SRMR = standardized root mean squared residual; Inst. Res. = instructed response; zGutt = normed Guttman errors; Resp. Time = response time.
Table 3.
Model Fit Comparisons for Identification Indices When Maximizing AUC.
| Adm. | CFI | RMSEA [90% CI] | SRMR | n |
|---|---|---|---|---|
| 1 | ||||
| Raw | 0.742 | .065 [.063, .068] | 0.064 | 1,236 |
| Inst. Res. | 0.770 | .062 [.059, .064] | 0.057 | 1,111 |
| H T | 0.702 | .062 [.059, .065] | 0.063 | 1,217 |
| zGutt | 0.642 | .057 [.052, .062] | 0.071 | 1,218 |
| lz | 0.800 | .057 [.053, .061] | 0.061 | 1,218 |
| U3 | 0.618 | .059 [.055, .062] | 0.071 | 1,218 |
| Resp. time | 0.768 | .062 [.059, .064] | 0.058 | 1,214 |
| 2 | ||||
| Raw | 0.730 | .066 [.065, .067] | 0.063 | 3,505 |
| Inst. Res. | 0.749 | .064 [.062, .065] | 0.058 | 3,176 |
| H T | 0.702 | .062 [.060, .063] | 0.060 | 2,836 |
| zGutt | 0.743 | .046 [.042, .049] | 0.055 | 563 |
| lz | 0.830 | .053 [.051, .055] | 0.048 | 1,670 |
| U3 | 0.687 | .058 [.057, .060] | 0.059 | 2,325 |
| Resp. time | 0.752 | .063 [.062, .064] | 0.058 | 3,030 |
Note. AUC = area under the curve; Adm. = administration; CFI = comparative fit index; RMSEA = root mean square error approximation; CI = confidence interval; SRMR = standardized root mean squared residual; Inst. Res. = instructed response; zGutt = normed Guttman errors; Resp. Time = response time.
Table 2.
Model Fit Comparisons for Identification Indices When Minimizing False Negatives.
| Adm. | CFI | RMSEA [90% CI] | SRMR | n |
|---|---|---|---|---|
| 1 | ||||
| Raw | 0.742 | .065 [.063, .068] | 0.064 | 1,236 |
| Inst. Res. | 0.770 | .062 [.059, .064] | 0.057 | 1,111 |
| H T | 0.769 | .050 [.045, .054] | 0.057 | 431 |
| zGutt | 0.654 | .055 [.049, .061] | 0.073 | 242 |
| lz | 0.825 | .053 [.049, .058] | 0.059 | 371 |
| U3 | 0.637 | .057 [.050, .063] | 0.074 | 228 |
| Resp. time | 0.762 | .065 [.060, .070] | 0.067 | 325 |
| 2 | ||||
| Raw | 0.730 | .066 [.065, .067] | 0.063 | 3,505 |
| Inst. Res. | 0.749 | .064 [.062, .065] | 0.058 | 3,176 |
| H T | 0.759 | .050 [.047, .053] | 0.052 | 777 |
| zGutt | 0.710 | .050 [.047, .043] | 0.056 | 757 |
| lz | 0.866 | .047 [.045, .049] | 0.044 | 1,155 |
| U3 | 0.698 | .049 [.046, .053] | 0.057 | 734 |
| Resp. time | 0.713 | .067 [.064, .071] | 0.061 | 619 |
Note. Adm. = administration; CFI = comparative fit index; RMSEA = root mean square error approximation; CI = confidence interval; SRMR = standardized root mean squared residual; Inst. Res. = instructed response; zGutt = normed Guttman errors; Resp. Time = response time.
First, removing participants who did not respond to the instructed response item correctly always offered significant improvement in model fit (where ΔCFI > –.01 is used to determine significant improvement between the raw dataset, and the flagged-respondents removed datasets; Cheung & Rensvold, 2002). HT offered significant improvements in model fit with cutoffs that minimized false positives and false negatives. Interestingly, HT did not significantly improve model fit when using a cutoff that maximized AUC. Normed Guttman errors also significantly improved model fit with cutoffs that minimized false negatives and false positives. However, normed Guttman errors did not significantly improve model fit with a cutoff maximizing the AUC. The lz index offered the most improvement in model fit when using cutoffs that maximized AUC and minimized false negatives. In addition, lz provided an improvement in model fit using all cutoffs in all administrations. The U3 index only offered significant improvement in model fit when using cutoffs minimizing false positives. Response time significantly improved model fit when using a cutoff that maximized AUC. Comparing the indices, lz improved model fit with all three cutoffs and in all administrations. The HT index and normed Guttman errors both improved model fit with cutoffs minimizing false positives and negative. Finally, U3 and response time improved model fit with just one cutoff. Table 4 contains the cutoff values used for each index based on the ROC analysis.
Table 4.
Cutoff Values for the Five Aberrant Response Indices Across Administrations.
| Minimizing false positives | 1 | 2 |
|---|---|---|
| H T | −0.07 | −0.03 |
| zGutt | 0.39 | 0.37 |
| lz | −6.21 | −5.63 |
| U3 | 0.38 | 0.36 |
| RT | 202.50 | 230.50 |
| Minimizing false negatives | 1 | 2 |
| H T | 0.33 | 0.39 |
| zGutt | 0.07 | 0.07 |
| lz | 1.23 | 1.12 |
| U3 | 0.06 | 0.06 |
| RT | 544.50 | 883.50 |
| Maximizing AUC | 1 | 2 |
| H T | 0.22 | 0.21 |
| zGutt | 0.08 | 0.06 |
| lz | 1.00 | 0.60 |
| U3 | 0.09 | 0.13 |
| RT | 289.50 | 342.50 |
Note. Response time cutoffs are reported in seconds. zGutt = normed Guttman errors; RT = response time; AUC = area under the curve.
Discussion
This study examined the accuracy of several methods for detecting approximate IR, and explored the impact on model fit of using these detection indices in practice. Specifically, it investigated the HT, U3, lz, normed Guttman errors, and response time indices. An instructed response item was used as a proxy for IR, to determine the accuracy of these indices when detecting IR. ROC analysis and CFA were conducted to clarify the accuracy and impact of using these indices as an alternative to instructed response items.
Using instructed response items to flag participants always improved model fit. However, the goal of the study was to determine the ability of the post hoc detection metrics to replicate the participants flagged by the instructed response item. The AUC estimates suggest that HT is more accurate than the other indices when detecting approximate IR. This is in line with previous research (Dimitrov & Smith, 2006; Karabatsos, 2003). However, CFA fit indices revealed interesting findings. Namely, that being able to more accurately predict the criterion (in this case, the instructed response item) does not necessarily always result in better model fit. In fact, it depends heavily on the type of cutoff used to flag respondents. This is supported by CFA model fit indices which show that HT, while having the highest AUC, does not improve model fit in all situations, and improves model fit less than normed Guttman errors when minimizing false positives. The lz index was the only index to improve model fit with all cutoffs. However, it is also important to note that lz and the maximum likelihood estimation use the likelihood function. In this way, the improve in model fit offered by lz is confounded with the estimation method. Because of this issue, AUC is the only result that gives useful information in determining whether lz is a viable alternative to instructed response. As lz had AUC around .60, it can be considered a poor predictor of instructed response items (the same as HT). Interestingly, response time does appear that it can be a useful index for identifying IR using an empirical cutoff. In fact, response time may be more useful for removing respondents than lz, it was comparably accurate to lz, but is not confounded with estimation method.
Recommendations and Conclusions
A priori methods for identifying IR are always recommended. Including instructed response items in a measure does take some planning, but it is a relatively simple procedure. There is little reason not to include these items on a measure, particularly if the measure is low stakes and the sample is vulnerable to IR. However, if a situation arises where a priori methods cannot be utilized, the question becomes: Are there any indices that can be used to remove aberrant responders? The answer to this question is a cautious yes, at least as far as IR is concerned.
In the absence of, or in addition to, a priori methods, several post hoc methods can be recommended. HT and response time (with an empirically derived cutoff) both were relatively accurate predictors of the instructed response item, and offered significant improvements in model fit with certain cutoffs. However, the indices’ improvement to model fit varied widely based on the type of cutoff used; if these identification indices are used to flag respondents, great care should be taken when choosing cutoff values. In addition, it should also be stated that no one metric should be used to make the overall decision about whether or not to keep or remove an individual from a dataset. Used in conjunction with other metrics of aberrant response, these person-fit statistics could provide additional information about particular participants’ response patterns. It is difficult to recommend the use of normed Guttman errors, lz, or U3. While normed Guttman errors and U3 improved model fit when minimizing false positive, they were not accurate predictors of the instructed response item. It is possible that the improvement in model fit when minimizing false positives is due to them detecting a different type of aberrancy. Finally, while using lz always improved model fit and was comparable to response time in its ability to predict the instructed response, it is unfortunately confounded with maximum likelihood estimation. It might be useful for detecting IR when other estimation methods are used, but further would be needed to recommend it for such a use.
Limitations
The main limitation of this study was the reliance on the instructed response item as a proxy for the criterion or True IR. Instructed response can be expected to identify IR to some extent, but not in every case. It is possible (especially if IR is viewed through a motivation lens) that some participants are partial inattentive respondents, that is, respondents who skim the item stem but still respond independent of the item content. If these types of respondents do exist, it is possible that they will avoid being detected by the instructed response item. Furthermore, the indices were only evaluated in terms of one type of response bias, IR. Based on these results, it is unclear if the statistics are identifying other types of aberrant response patterns, or if they are being overly sensitive and removing attentive responders with slightly deviant response patterns. It is possible that the indices are identifying individuals engaging in IR but were not identified by the instructed response item. It is also possible that the indices are identifying individuals engaging in other aberrant response patterns. Another limitation is the use of the multidimensional CALCS measure to assess these person-fit statistics. It is likely that using a unidimensional or identifying IR participants within factors (instead of across factors) would provide different results.
Future Directions
Some areas of future research were identified based on the results of this study. Whereas this study compared person-fit statistics in terms of their ability to detect IR in real items with polytomous response scales, it is still unclear how these indices would perform on real items with dichotomous response scales. It may be that these person-fit statistics do not work as well with polytomous items, but are still useful for identifying IR on dichotomous measures. In addition, other person-fit statistics and indices for identifying response biases should be investigated in items with polytomous response scales, as these scales are common in low-stakes measures. This study only investigated the effectiveness of aberrant response indices to identify one type of aberrant response pattern, IR. Future research should also investigate the effectiveness of these indices (and others) in identifying other types of response biases, such as cheating, social desirability responding, and acquiescence. Based on how widely the performance of the identification metrics varied based on the cutoff used, a future study could extend these results by determining cutoffs based on other empirical techniques (i.e., bootstrapping). In addition to simply identifying IR, steps should also be taken to investigate ways in which IR can be prevented.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The Collegiate Active Learning Calculus Survey (CALCS) instrument was developed in part with funding from a grant from the Helmsley Foundation to the Association of Public and Land grant Universities, with a subaward to the authors’ institution.
References
- Armstrong R. D., Stoumbos Z. G., Kung M. T., Shi M. (2007). On the performance of the lz person-fit statistic. Practical Assessment, Research & Evaluation, 12(16), 1-15. [Google Scholar]
- Cheung G. W., Rensvold R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling, 9, 233-255. [Google Scholar]
- Clark M., Skorupski W., Jirka S., McBride M., Wang C., Murphy S. (2014). An investigation into statistical methods to identify aberrant response patterns (Research report). Retrieved from https://www.pearson.com/content/dam/one-dot-com/one-dot-com/global/Files/efficacy-and-research/schools/021_Data-Forensics-RD-Research-Report-Person-Fit.pdf
- Clark M. E., Gironda R. J., Young R. W. (2003). Detection of back random responding: Effectiveness of MMPI-2 and Personality Assessment Inventory validity indices. Psychological Assessment, 15, 223-234. [DOI] [PubMed] [Google Scholar]
- Credé M. (2010). Random responding as a threat to the validity of effect size estimates in correlational research. Educational and Psychological Measurement, 70, 596-612. [Google Scholar]
- Dimitrov D. M., Smith R. M. (2006). Adjusted Rasch person-fit statistics. Journal of Applied Measurement, 7, 170-183. [PubMed] [Google Scholar]
- Drasgow F., Levine M. V., Williams E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38, 67-86. [Google Scholar]
- Emons W. H. M. (2008). Nonparametric person-fit analysis of polytomous item scores. Applied Psychological Measurement, 32, 224-247. [Google Scholar]
- Emons W. H. M., Meijer R. R., Sijtsma K. (2002). Comparing simulated and theoretical sampling distributions of the U3 person-fit statistic. Applied Psychological Measurement, 26, 88-108. [Google Scholar]
- Emons W. H. M., Sijtsma K., Meijer R. R. (2005). Global, local, and graphical person-fit analysis using person-response functions. Psychological Methods, 10, 101-119. [DOI] [PubMed] [Google Scholar]
- Ferrando P. J. (2009). Multidimensional factor-analysis-based procedures for assessing scalability in personality measurement. Structural Equation Modeling, 16, 109-133. [Google Scholar]
- Finn B. (2015). Measuring motivation in low-stakes assessment. ETS Research Report Series, 2015, 1-17. doi: 10.1002/ets2.12067 [DOI] [Google Scholar]
- Karabatsos G. (2003). Comparing the aberrant response detection performance of thirty-six person-fit statistics. Applied Measurement in Education, 16, 277-298. [Google Scholar]
- Magis D., Raiche G., Beland S. (2012). A didactic presentation of Snijders’s lz* index of person fit with emphasis on response model selection and ability estimation. Journal of Educational and Behavioral Statistics, 37, 57-81. [Google Scholar]
- Maniaci M. R., Rogge R. D. (2014). Caring about carelessness: Participant inattention and its effects on research. Journal of Research in Personality, 48, 61-83. [Google Scholar]
- Marianti S., Fox J., Avetisyan M., Veldkamp B. P., Tijmstra J. (2014). Testing for aberrant behavior in response time modeling. Journal of Educational and Behavioral Statistics, 39, 426-451. [Google Scholar]
- Meade A. W., Craig B. (2012). Identifying careless responses in survey data. Psychological Methods, 17, 437-455. [DOI] [PubMed] [Google Scholar]
- Meijer R. R. (1994). The number of Guttman errors as a simple and powerful person-fit statistic. Applied Psychological Measurement, 18, 311-314. [Google Scholar]
- Meijer R. R., Egberink I. J. L., Emons W. H. M., Sijtsma K. (2008). Detection and validation of unscalable item score patterns using item response theory: An illustration with Harter’s Self-Perception Profile for children. Journal of Personality Assessment, 90, 227-238. [DOI] [PubMed] [Google Scholar]
- Mokken R. J. (1971). A theory and procedure of scale analysis. The Hague, The Netherlands: Mouton. [Google Scholar]
- Nichols D. S., Greene R. L., Schmolck P. (1989). Criteria for assessing inconsistent patterns of item endorsement on the MMPI: Rationale, development, and empirical trials. Journal of Clinical Psychology, 45, 239-250. [DOI] [PubMed] [Google Scholar]
- Niessen S. M., Meijer R. R., Tendeiro J. N. (2016). Detecting careless respondents in web-based questionnaires: Which method to use? Journal of Research in Personality, 63, 1-11. [Google Scholar]
- Oppenheimer D. M., Meyvis T., Davidenko N. (2009). Instructional manipulation checks: Detecting satisficing to increase statistical power. Journal of Experimental Social Psychology, 45, 867-872. [Google Scholar]
- R Core Team. (2017). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. Available from https://www.R-project.org/
- Reise S. P., Due A. M. (1991). The influence of test characteristics on the detection of aberrant response patterns. Applied Psychological Measurement, 15, 217-226. [Google Scholar]
- Robin X., Turck N., Hainard A., Tiberti N., Lisacek F., Sanchez J. C., Müller M. (2011). pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics, 12, Article 77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosseel Y. (2012). lavaan: An R package for structural equation modeling. Journal of Statistical Software, 48(2), 1-36. Available from http://www.jstatsoft.org/v48/i02/ [Google Scholar]
- St-Onge C., Valois P., Abdous B., Germain S. (2011). Accuracy of person-fit statistics: A Monte Carlo study of the influence of aberrance rates. Applied Psychological Measurement, 36, 419-432. [Google Scholar]
- Seo D. G., Weiss D. J. (2013). lz person-fit index to identify misfit students with achievement test data. Educational and Psychological Measurement, 73, 994-1016. [Google Scholar]
- Sijtsma K. (1986). A coefficient of deviance of response patterns. Kwantitatieve Methoden: Nieuwsbrief voor Toegepaste Statistiek en Operationele Research, 7, 131-145. [Google Scholar]
- Sijtsma K., Molenaar I. W. (2002). Introduction to nonparametric item response theory (Vol. 5). Thousand Oaks, CA: Sage. [Google Scholar]
- Sinharay S. (2016). Asymptotically correct standardization of person-fit statistics beyond dichotomous items. Psychometrika, 81, 992-1013. [DOI] [PubMed] [Google Scholar]
- Sinharay S. (2017). Are the nonparametric person-fit statistics more powerful than their parametric counterparts? Revisiting the simulations in Karabatsos (2003). Applied Measurement in Education, 30, 314-328. [Google Scholar]
- Snijders T. A. B. (2001). Asymptotic null distribution of person fit statistics with estimated person parameter. Psychometrika, 66, 331-342. [Google Scholar]
- Tendeiro J. N., Meijer R. R. (2014). Detection of invalid test scores: The usefulness of simple nonparametric statistics. Journal of Educational Measurement, 51, 239-259. [Google Scholar]
- Tendeiro J. N., Meijer R. R., Niessen A. S. M. (2016). PerFit: An R package for person-fit analysis in IRT. Journal of Statistical Software, 74, 1-27. [Google Scholar]
- van der Ark L. A. (2012). New developments in Mokken scale analysis in R. Journal of Statistical Software, 48, 1-27. [Google Scholar]
- van der Flier H. (1982). Deviant response patterns and comparability of test scores. Journal of Cross-Cultural Psychology, 13, 267-298. [Google Scholar]
- Wise S. L., Kong X. (2005). Response time effort: A new measure of examinee motivation in computer-based tests. Applied Measurement in Education, 18, 163-183. [Google Scholar]