Muscle Response to Changing Neuronal Input in the Lobster (Panulirus interruptus) Stomatogastric System: Spike Number- versus Spike Frequency-Dependent Domains

Abstract

We aimed to determine the neuronal parameters controlling the contraction of slowly contracting, non-twitch (“tonic”) muscles driven by rhythmic neuronal activity. These muscles are almost completely absent in mammals but are common in lower vertebrates and invertebrates. Slow muscles are often believed to function primarily in tonic motor patterns. However, previous research and data presented here indicate that slow muscles are also driven by rhythmic neuronal inputs.

In rapidly contracting “twitch” muscles, motor unit force is believed to be primarily determined by motor neuron spike frequency. What determines slow muscle output is less well understood. We present a simple model that suggests that when motor neuron burst duration is brief compared with muscle summation time, spike number, not spike frequency, determines slow muscle contraction amplitude.

We present analyses that distinguish between spike number and spike frequency dependence in two slow muscles in the lobster stomatogastric system. Our analysis shows that, functionally, one muscle is spike number dependent, whereas the other is primarily spike frequency dependent. Thus, both of these parameters can determine slow muscle output. To predict the movements elicited by neuronal activity in preparations in which slow muscles are common, it may be necessary to determine spike number versus spike frequency dependence for each muscle.

Spike number dependence couples motor neuron burst duration and spike frequency in that changing either parameter alone alters spike number (and hence muscle contraction amplitude). Neural networks innervating spike number-dependent muscles may therefore have specific properties to compensate for the complexity intrinsic to spike number coding.

Variation is a general characteristic of motor patterns. For instance, we walk at different speeds, straight, in circles, uphill, and downhill. This variation arises from changes in the neural network activity that drives the muscles that produce the patterns. However, muscles often are not simple followers of their input but, instead, respond in complex ways to changing neural activity (Hoyle, 1983; Meyrand and Moulins, 1986; Meyrand and Marder, 1991). It is impossible to understand motor pattern variation, or the function of changing neuronal output, without understanding this neuron to muscle transform. Furthermore, because neural networks and their effectors co-evolved, some aspects of the synaptic connectivity and cellular properties of any given neural network may exist to fulfill particular needs imposed by its effector system. Thus, it may also be impossible to understand neural network design fully without considering network effectors.

A tremendous amount of research has been performed on the primary mammalian effectors (slow and fast twitch muscles). In these muscles tension is coded by (1) changing active motor unit number and (2) changing motor unit force by altering motor neuron spike frequency (rate coding) (for review, see DeLuca and Erim, 1994). Another effector type, non-twitch slow (“tonic”) muscle, is common in lower vertebrates and invertebrates (Hoyle, 1953, 1983; Atwood and Hoyle, 1965). These muscles contract very slowly, often taking seconds to contract fully in response to sustained tonic input. However, these muscles can be involved in relatively rapid, phasic motor patterns (Hetherington and Lombard, 1983; Carrier, 1989). The slow contractions of these muscles would never fully summate during relatively brief motor neuron bursts, and how contraction amplitude, force, etc. are coded under these conditions is largely unknown.

This lack of knowledge regarding non-twitch slow muscles is a particular concern, because the best understood neural networks are in invertebrate preparations, and several of these networks may drive slow muscles with relatively brief motor neuron bursts. We have been examining isotonic slow muscle responses to nerve stimulation that mimics physiological neural activity in the crustacean stomatogastric system. We have developed a simple, idealized model that predicts that slow muscle contraction amplitude should depend on spike number when burst duration is brief relative to muscle summation time, and on spike frequency when duration is long relative to this time. Our data on two stomatogastric muscles confirm this prediction and suggest that one muscle always functions in the spike number domain, whereas the other functions in the transition or spike frequency domain.

This functional difference between these two muscles may impose different constraints on their respective neural networks, in that different parameters (spike number and spike frequency) are used to determine contraction amplitude. These results reinforce the need to consider effector properties when interpreting neural network design and function. Moreover, because certain network properties may exist specifically to deal with differing effector constraints, these results also suggest caution in applying insights gained from systems with one effector type to those with different types.

Some of these data have been published previously in abstract form (Morris and Hooper, 1994, 1996).

MATERIALS AND METHODS

Lobsters (500–1000 gm) were obtained from Don Tomlinson (San Diego, CA) and maintained in aquaria with circulating artificial seawater at 12°C. Stomachs were dissected using standard techniques (Selverston et al., 1976) except that the cpv1a and 1b muscle origins on the hypodermis were preserved. Extreme care was taken to ensure that no digestive juices contacted the muscles and that the muscles were never stretched. Preparations were continuously superfused (40 ml/min) with chilled (12–15°C), oxygenated Panulirus saline (Selverston et al., 1976) containing 40 mm glucose. The data shown here were drawn from ∼25 experiments.

All electronics were standard. Extracellular nerve recordings and stimulation were made with stainless steel pin electrodes or polyethylene suction electrodes. Stimulation voltages were increased until maximum muscle contraction amplitudes were achieved, and hence presumably all motor neuron axons were being stimulated. Intracellular neuronal and muscle recordings were made with glass microelectrodes filled with 0.55 m K₂SO₄ and 0.02m KCl (resistance, 10–20 MΩ]) and an Axoclamp 2A. Muscle contractions were measured by attaching a Harvard Apparatus 60-3000 isotonic transducer to the hypodermis between the cpv1a or cpv1b muscle pair with a wire hook; transducer output was amplified 5- to 50-fold (depending on the muscle) by a Tektronix AM502 differential amplifier. Muscle length and loading were adjusted for each muscle to achieve optimal contractions; muscle overstretching between trials was prevented by placing a bar under the far end of the transducer arm. Contraction amplitudes were measured using Spike II (Cambridge Electronic Design) and Kaleidagraph (Synergy Software) software after transfer (Cambridge Electronic Design 1401 laboratory interface) to a Gateway 2000 P5 computer.

Figures 1 and 5 were made using a model developed with Stella II (High Performance Systems) software run on an Apple Macintosh Quadra 950 computer.

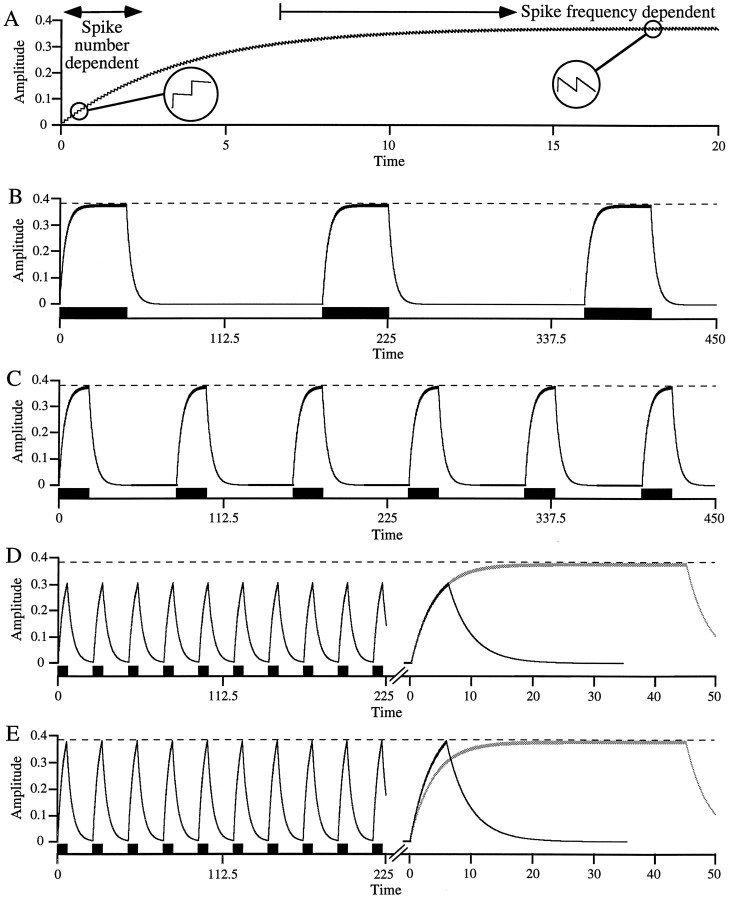
Fig. 1.

Simple model of slow, non-twitch muscle contraction showing spike number and spike frequency dependence.A, Each motor neuron spike induces a constant amplitude muscle contraction between which the muscle relaxes with a single exponential. Early in the stimulation, summated contraction amplitude is small, and hence interspike relaxation is small (left inset); summated contraction amplitude nearly equals spike number times unitary contraction amplitude and is thus spike number dependent. Because relaxation is exponential, as summated contraction amplitude increases so does interspike relaxation; when interspike relaxation equals unitary contraction amplitude (right inset), contraction amplitude reaches steady state. For times longer than this, contraction amplitude depends only on spike frequency. B, C, In a duty cycle maintaining a rhythmic pattern (such as the pyloric pattern), as cycle period decreases contraction amplitude remains constant, provided burst duration remains in the spike frequency domain. D,E, When cycle period decreases sufficiently that burst duration leaves the spike frequency domain, contraction amplitude decreases (D). Maintaining contraction amplitude in this burst duration range requires increased intraburst spike frequency (E) or other compensatory mechanisms (e.g., interburst potentiation). Right panels compare contractions in D and E (black trace) with those in B (gray trace) at an expanded time scale.

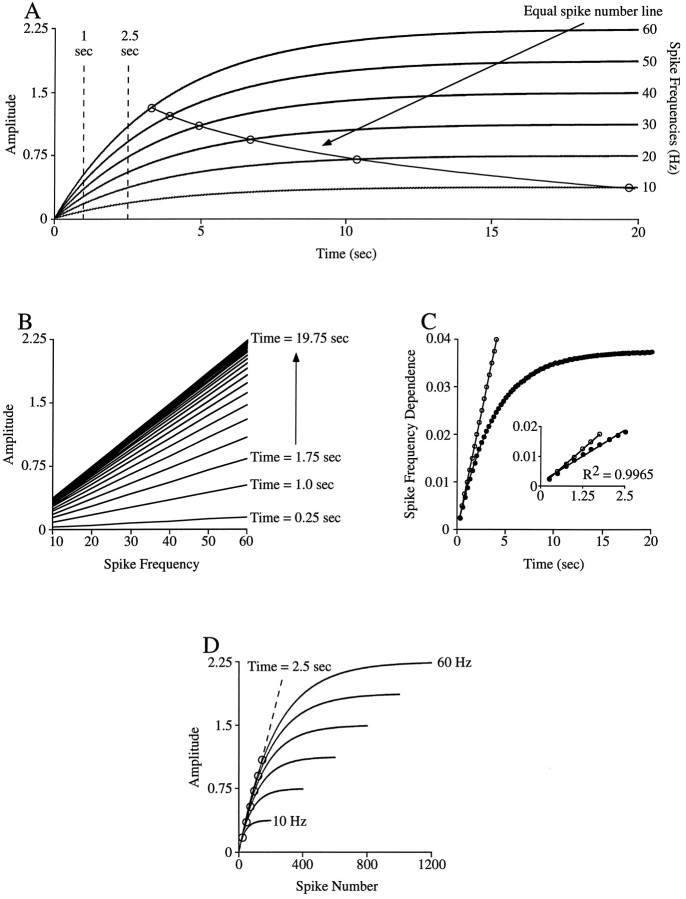
Fig. 5.

Analyses for revealing spike number and spike frequency domains. A, Tetanic contractions of model used in Figure 1 at 10–60 Hz spike frequencies. B, Contraction amplitudes of curves in A in 0.75 sec intervals from 0.25 to 19.75 sec plotted versus curve spike frequency. At early times into the train the lines are well separated but become more closely spaced as time into the train increases. This pattern indicates that as the train continues the dependence of contraction amplitude on burst duration becomes increasingly less. Furthermore, at early times into the train the dependence of amplitude on spike frequency (the slopes of the various lines) is small and increases as time into the train increases. C, Plot of the slopes of the lines (filled circles) shown inB versus time into the train; the linewith open circles shows the dependence expected if the interspike relaxation rate was zero (perfect spike number dependence). At very early times into the train the slopes of the model and the zero line agree. Inset, Expanded view of the plot at times <2.5 sec. The data points in this time domain are well fit with astraight line; in this domain the model is spike number dependent. D, Plot of the data in Aversus spike number. In the parts of the curves that overlie, equal amplitudes occur at equal spike numbers regardless of spike frequency. The dashed line marks the spike numbers (circles) at a time of 2.5 sec (the edge of the linear region shown in the inset in C). See Results for further explanation.

RESULTS

Two of the best studied neural networks are the pyloric and gastric networks of crustacean stomatogastric nervous systems (Harris-Warrick et al., 1992a). These networks are rhythmically active networks (central pattern generators) that generate the rhythmic motor patterns of, respectively, the pylorus and gastric mill of the crustacean stomach. One of the most interesting results of work in these networks is the observation that they produce multiple output patterns (Coleman et al., 1992; Nusbaum et al., 1992; Weimann et al., 1993; Coleman and Nusbaum, 1994; Nagy and Cardi, 1994; Skiebe and Schneider, 1994; Tazaki and Chiba, 1994; Blitz et al., 1995; Christie et al., 1995; Harris-Warrick et al., 1995; Johnson et al., 1995; Norris et al., 1996; for pre-1992 references, see Harris-Warrick et al., 1992b). Recently, it has also been shown that the pyloric network produces at least one pattern in a phase-constant manner (i.e., inter-neuronal delays and neuronal burst lengths proportionally alter when pyloric period changes) (Hooper 1997a,b). Similar abilities to produce multiple outputs, and to produce phase-constant patterns as cycle period changes, are present in several other neural networks (Berkinblit et al., 1978; Getting and Dekin, 1985; Soffe, 1993;DiCaprio et al., 1997).

The functional consequences—the changes in movement induced by these multiple outputs—are less understood. This is because the movements a musculoskeletal system produces, and how these movements change as neural output changes, are functions of specific properties particular to each system. Understanding how any given system transforms neural outputs into movement thus requires a detailed description of the contractile properties of every muscle involved and of the inertial and resistive properties of the skeletal components to which they attach. Analysis at this level of detail has seldom been performed, particularly in the systems that are best understood on the neural network level.

All lobster stomatogastric muscles that have been examined are non-twitch, slowly contracting muscles (Govind et al., 1975; Atwood et al., 1977, 1978). However, too little is known of the biophysical properties of these muscles to predict contraction amplitude and timing from recordings of neural activity. The effects that the changes in neural output noted above have on motor activity are therefore unknown. In an attempt to overcome this difficulty, we have been examining stomatogastric muscle responses to patterns of nerve stimulation that mimic the physiologically observed range of neural activity (Morris and Hooper, 1994, 1996; Ellis et al., 1996).

In considering these data, we realized that the slow, graded, non-twitch contraction properties of slow muscles (Hoyle, 1953, 1983;Atwood and Hoyle, 1965) could cause potentially general difficulties in predicting the response of such muscles to varying neural input. Consider the output of a slow, non-twitch muscle model (Fig.1). In this simple, idealized model, single motor neuron spikes induce a constant amplitude contraction that is followed by an exponential relaxation. Early in the train the amplitude of the summated contraction is small, and, because the relaxation is exponential, the magnitude of the relaxation between spikes is therefore also small (Fig. 1A, left inset). The summated contraction amplitude after any spike in this range is thus very nearly equal to the number of spikes the muscle has received times the contraction amplitude induced by a single spike. As will be shown later, in this part of the contraction, spike trains at different frequencies induce nearly equal contractions if the trains contain equal spike numbers. We therefore call this early part of the contraction the “spike number domain.”

As the train continues the summated contraction amplitude continues to increase, and hence, because the relaxation is exponential, the magnitude of the interspike relaxation also increases. Eventually, the summated contraction amplitude becomes large enough that the decline after each spike is equal to the contraction induced by the next spike (Fig. 1A, right inset). At this stable level the average contraction amplitude is determined only by spike frequency, not spike number (e.g., increasing spike number by increasing train duration does not alter contraction amplitude). We therefore call this late part of the contraction the “spike frequency domain.”

As an example of the possible complexity that slow muscle contraction could introduce, consider the response of the model to cycle period changes in a rhythmic pattern in which both duty cycle and intraburst spike frequency are constant (Fig. 1B–E). Figure1B shows the contractions with a long cycle period and hence long burst duration; the contractions fully summate to an amplitude that is maintained for the remainder of the burst. Within a certain range, decreasing cycle period (and hence shortening burst duration) does not alter contraction amplitude because burst duration is still long enough that the contractions fully summate (spike frequency domain) (Fig. 1C). However, as cycle period, and hence burst duration, decrease further, a point is reached at which the contractions no longer fully summate, and thus amplitude decreases (Fig. 1D). To maintain contraction amplitude in this range of pattern cycle periods, intraburst spike frequency must be increased (Fig. 1E), or other compensatory mechanisms must be present (e.g., interburst potentiation).

This model is extremely simple, and we do not pretend that it accurately reproduces the activity of any real muscle. However, it does suggest that for slowly contracting muscles a temporal domain could exist in which, for constant motor neuron intraburst spike frequencies, contraction amplitude depends on burst duration. This coupling of burst duration and contraction amplitude at short burst durations implies that, in the absence of compensatory mechanisms at the effector level (e.g., interburst potentiation), different strategies would be needed to control muscle contraction amplitude in the two domains. In the spike frequency domain, amplitude could be coded solely by intraburst spike frequency (changing burst duration would not alter amplitude). Alternatively, in the spike number domain, intraburst firing frequency and burst duration interact to determine contraction amplitude (e.g., to maintain a given amplitude, if duration shortens intraburst frequency must increase). Thus, in this domain nervous systems would need to coordinately vary both of these parameters to control contraction amplitude.

The issues noted above may be of more than academic interest. Real motor neurons can fire across a wide range of burst durations, because (as in Fig. 1) many neural networks produce constant duty cycle outputs as cycle period changes (Kristan et al., 1974; Grillner et al., 1988;Arbas and Calabrese, 1991; DiCaprio et al., 1997; Hooper, 1997a), and because individual motor neurons can participate in multiple motor patterns with very different temporal characteristics (Dickinson et al., 1990; Meyrand and Moulins 1991; Weimann et al., 1991; Meyrand et al., 1993; Soffe, 1993; Weimann and Marder, 1994). As such, a theoretical possibility that muscles could be required to function in both the spike frequency and spike number domains clearly exists. Although it is not difficult to believe that nervous systems could evolve strategies to solve the complexities inherent to such a situation, a more fundamental question is whether they ever need to. Given the wide range of muscle contraction properties that exist (Hoyle, 1983), an easy solution would be to make muscle summation time less than the shortest burst the muscle ever physiologically receives. The muscle would thus always be in the spike frequency domain, and contraction amplitude would never depend on burst duration.

We investigated this question with two lobster stomach muscles, cpv1a and cpv1b. Figure 2 shows a schematic of the fully dissected preparation. The bilaterally symmetric cpv1a and cpv1b muscle pairs originate on the carapace and insert on the lobster stomach near the junction of the gastric mill and pylorus. The individual cpv1a and cpv1b muscles of either side (right or left) of the stomach originate very near each other, insert on different but closely apposed ossicles, and hence are closely apposed along their entire length. The two muscle pairs were originally identified as being innervated by the pyloric dilator (PD) neurons of the pyloric network (Maynard and Dando, 1974), were believed to be agonists that participated in opening the cardiopyloric valve (Turrigiano and Heinzel, 1992), and have generally been considered to constitute a single group. In previous studies the combined activity of the two muscle pairs has generally been measured, although the cpv1a and cpv1b muscles have been reported to have different pharmacological sensitivities (Lingle, 1981).

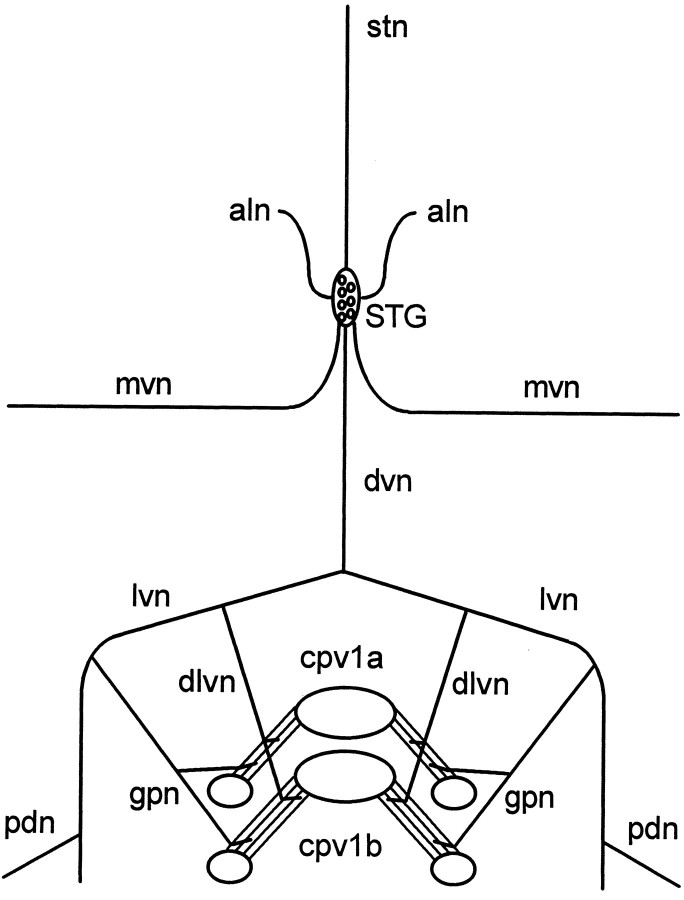
Fig. 2.

Schematic of fully dissected experimental preparation. The cpv1a and cpv1b muscles originate on the hypodermis/carapace (large ovals) very near each other, insert on different but closely apposed stomach ossicles (small ovals), and thus are closely apposed along their entire length. Muscle contractions were measured by attaching an isotonic transducer to the hypodermis between one or both muscle pairs with a wire hook. The muscles are innervated via the dorsal ventricular (dvn), lateral ventricular (lvn), dorsal lateral ventricular (dlvn), and gastropyloric (gpn) nerves. The cell bodies of the neurons that innervate the muscles are located in the stomatogastric ganglion (STG). Other important nerves for this work are the pyloric dilator nerve (pdn), which contains the axons of the PD neurons, and the aln, which contains the axons of the GM neurons. mvn, Median ventricular nerve;stn, stomatogastric nerve.

However, in preparations in which the stomatogastric ganglion was left attached to the cpv1a and cpv1b muscles, and simultaneous recordings were made of PD neuron activity [from the pyloric dilator nerve (pdn)] and of combined cpv1a and cpv1b muscle contractions, large, long-duration, slow-period contractions were observed in addition to small, PD neuron-timed contractions (Fig.3A). Recordings of the activity of individual cpv1a and cpv1b muscles showed that the large, long-duration, slow-period contractions were caused by cpv1a muscle activity, and the small, PD neuron-timed contractions were caused by cpv1b muscle activity (Fig. 3B,D).

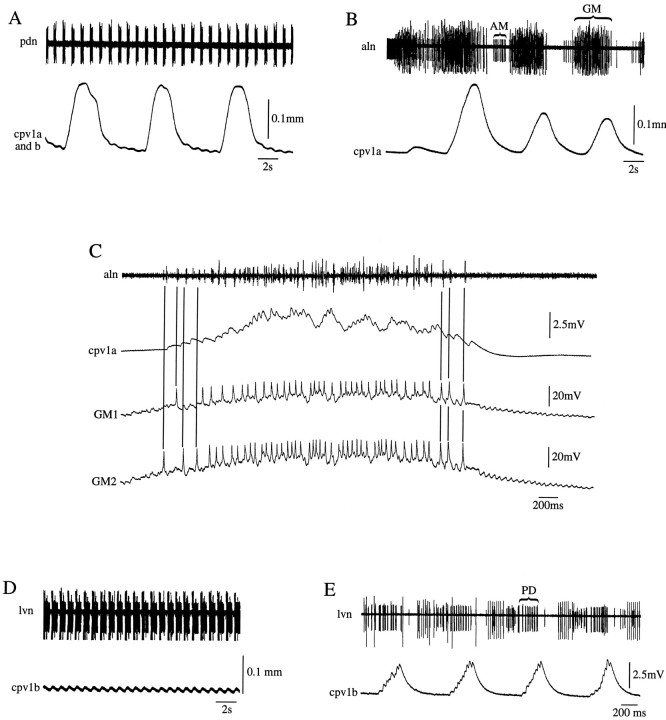
Fig. 3.

The cpv1a muscle is innervated by the GM neurons of the gastric network, and the cpv1b muscle is innervated by the PD neurons of the pyloric network. A, Simultaneous extracellular recording of PD neuron activity (pdn) and combined cpv1a and cpv1b muscle contractions. Note the large, long-duration, slow-period contractions and small PD neuron-timed contractions. B, Simultaneous extracellular recording of aln (this nerve contains the AM and GM neuron axons) activity and cpv1a muscle contractions; cpv1a muscle contractions match GM neuron activity. C, Simultaneous extracellular recording of aln activity and intracellular recordings of two GM neurons and the cpv1a muscle. cpv1a muscle EJPs match GM neuron spikes one for one. D, Simultaneous extracellular recording of PD neuron activity from the lvn and cpv1b muscle contractions; cpv1b muscle contractions match PD neuron bursts.E, Simultaneous extracellular recording of PD neuron activity (lvn) and intracellular recording from the cpv1b muscle; cpv1b muscle EJPs match PD neuron spikes one for one.

The period and duration of the cpv1a muscle contractions suggested they might be attributable to gastric network activity. Simultaneous recordings (Fig. 3B) from the anterior lateral nerve (aln), which contains the axons of the anterior median (AM; small unit) and gastric mill (GM; large units) neurons, and of cpv1a muscle contractions showed that the contractions occurred in GM neuron time. Simultaneous intracellular recordings of GM neuron activity and cpv1a muscle excitatory junctional potentials (EJPs) (Fig. 3C) showed one-for-one matching; hence the cpv1a muscle is actually innervated by the GM neurons of the gastric network. Simultaneous recordings of PD neuron activity and cpv1a muscle contractions or EJPs showed that the PD neurons do not innervate this muscle (data not shown), and so the cpv1a muscle is an exclusively gastric muscle.

Simultaneous recordings of PD neuron activity [in this case from the lateral ventricular nerve (lvn)] and cpv1b muscle contractions (Fig.3D) or EJPs (Fig. 3E) showed that this muscle is innervated by the PD neurons of the pyloric network. Simultaneous recordings from the cpv1b muscle and either extracellular recordings from the aln or intracellular recordings from the GM neurons showed that the GM neurons do not innervate this muscle (data not shown), and so the cpv1b muscle is an exclusively pyloric muscle. Throughout this article these muscles will therefore be referred to as the cpv1a(GM) muscle and the cpv1b(PD) muscle.

In vivo, the gastric network cycle period ranges from 4 to 70 sec, and presumed GM neuron burst duration (inferred from the durations in which the medial tooth of the stomach is in the forward position) ranges from 3 to 20 sec (Heinzel, 1988). The pyloric network cycle period ranges from 0.5 to 2 sec in vivo (Rezer and Moulins, 1983), and the PD neuron burst duration ranges from 100 to 500 msec when pyloric network frequency is varied through this range by current injection into the pacemaker neuron of the network (Hooper, 1997a). Both the cpv1a(GM) and cpv1b(PD) muscles therefore receive a wide range of burst durations, but the range for each muscle is very different (3–20 sec vs 100–500 msec). As such, these muscles were highly appropriate for investigating whether the temporal properties of muscle contraction and neural input are matched.

In a system as simple as the idealized model shown in Figure 1, this question can be answered by (1) inducing fully summated (tetanic) muscle contractions by tonic motor nerve stimulation at various frequencies, and once this is determined, (2) comparing physiological burst durations with muscle contraction dynamics (see Fig. 5). However, real muscle contractions often show strong history dependence (e.g., facilitation and potentiation), and hence data derived from tetanic stimulations may not be physiologically relevant, because tetanic and rhythmic stimulations may not induce the same muscle state.

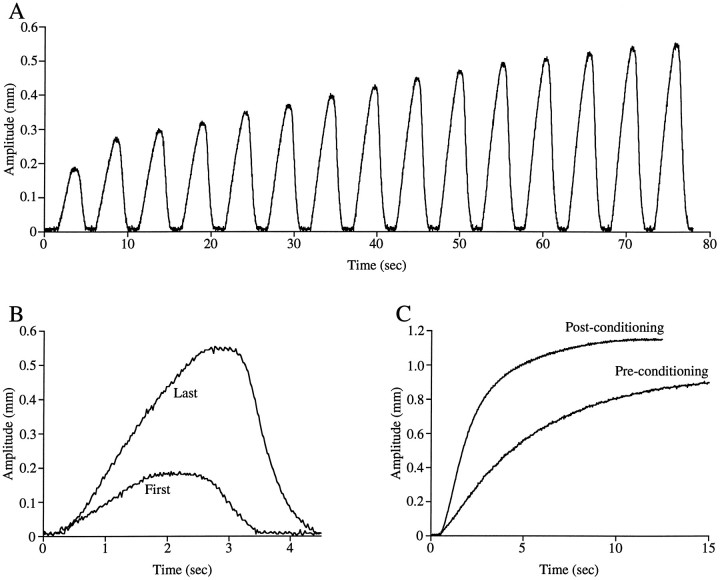
The validity of this concern is demonstrated in Figure4A, which shows cpv1a(GM) muscle contractions induced by rhythmic lvn stimulation with bursts of pulses. As the rhythmic stimulation proceeds, the muscle contraction amplitude and rate of rise initially increase and then stabilize (Fig.4B). Figure 4C shows the effect that previous rhythmic conditioning has on tetanic muscle contraction; conditioning decreases the time to half-maximum contraction from 4.2 to 1.9 sec. In all data shown here the cpv1a(GM) muscles were conditioned with rhythmic stimulations mimicking the most robust physiological input the muscle ever likely receives (burst duration, 2.5 sec; cycle period, 5 sec; intraburst spike frequency, 30 Hz). Similar history-dependent effects were not observed for the cpv1b(PD) muscle (data not shown), and this muscle was not rhythmically conditioned before tetanic stimulation.

Fig. 4.

cpv1a(GM) muscle tetanic rate of rise and amplitude increase as a result of previous activity. A, cpv1a (GM) muscle contractions in a rhythmic train of bursts (2.5 sec burst duration, 5 sec cycle period, 30 Hz spike frequency).B, Comparison of first and last contractions in the train shown in A; note rate of rise increase.C, Comparison of tetanic contractions induced before and after conditioning with a rhythmic train of trains; note rate of rise increase.

The analyses appropriate for determining the spike number and spike frequency domains of a muscle can be investigated with the model used to create Figure 1. Figure 5A shows the outputs of the model in response to long-duration (20 sec) input at frequencies from 10 to 60 Hz. The task is to use these data to determine how contraction amplitude depends on spike frequency and spike number at various times into the train and to compare these dependencies with those expected if contraction amplitude depended solely on spike frequency or spike number.

One way to address this issue is to measure the contraction amplitude of each train at various times into the train (Fig. 5A, vertical dashed lines) and to plot the amplitude versus train spike frequency line for each time. Figure 5B shows the result of this analysis at times into the train from 0.25 to 19.75 sec in 0.75 sec intervals. Two trends are apparent. First, as time into the train increases, the spacing between adjacent lines decreases. This means that as time into the train increases, the change in contraction amplitude induced by subsequent spikes decreases. For instance, in the 60 Hz train, going from a time of 0.25 to 1 sec causes an amplitude increase of 0.38, whereas going from a time of 19 to 19.75 sec causes an amplitude increase of 0.003. In each case an additional 45 spikes were added to the train, and hence the change in contraction amplitude induced by subsequent spikes becomes increasingly small as time into the train increases.

Second, as time into the train increases, the slope of the lines increases (the slope of the 0.25 sec line is 0.002, whereas the slope of the 19.75 sec line is 0.037). Because this is a plot of contraction amplitude versus spike frequency, these slopes show how amplitude depends on spike frequency. This plot thus shows that contraction amplitude increasingly depends on spike frequency as time into the train increases. This point is shown directly in Figure 5C, in which the slopes of the lines shown in Figure 5B are plotted against the time into the train each line represents. The dependence of contraction amplitude on spike frequency varies from an amplitude increase of 0.002 for each 1 Hz frequency increase at a time of 0.25 sec to an amplitude increase of 0.037 for each 1 Hz frequency increase at a time of ∼20 sec.

To understand fully the difference between the spike number and spike frequency domains, it is useful to consider the origin of the various slopes in Figure 5C. Late in the train the tetanic curves are flat (Fig. 5A), that is, contraction amplitude is constant. Spike number, of course, continues to increase as time into the train increases; thus in this time range amplitude is independent of spike number. Different spike frequencies, however, give rise to different amplitude contractions, and hence in this domain contraction amplitude does depend on spike frequency. This dependence arises because the tetani stabilize when interspike relaxation equals unitary contraction amplitude. As spike frequency increases, interspike interval decreases, and thus the magnitude of the interspike relaxation that occurs at any given contraction amplitude also decreases. Because relaxation is exponential, the magnitude of interspike relaxation is greater at larger contraction amplitudes. Contractions thus stabilize at larger amplitudes as spike frequency increases (interspike interval decreases), because only at these larger amplitudes are interspike relaxation and unitary contraction amplitude equal.

For this simple model the average stable contraction amplitude for each spike frequency can be explicitly calculated (see ). The dependence of contraction amplitude on spike frequency expected in the spike frequency domain can therefore also be explicitly calculated and is approximately or exactly (depending on how the average is defined; see ) equal to unitary contraction amplitude ×relaxation rate. For the parameters used here this value is 0.0375, in agreement with the slope achieved for long times shown in Figure 5C.

At early times into the train, contraction amplitude, and hence interspike relaxation magnitude, are small (Fig. 1A, left inset). Interspike relaxation is less than unitary contraction amplitude, and summated contraction amplitude increases with each subsequent spike. Furthermore, the difference in the interspike relaxation magnitude that occurs at different interspike intervals is very small [e.g., the magnitude of the relaxation that occurs in 100 msec (10 Hz spike frequency) and in 17 msec (60 Hz spike frequency) is essentially the same]. After any given number of spikes, the contraction of each subsequent spike is therefore “added” to essentially the same summated amplitude regardless of spike frequency. In this domain, spike frequency dependence (the slopes in Fig.5C) thus arises because spike trains with high frequencies have more spikes per time, not because an equilibrium between unitary contraction amplitude and interspike relaxation has been established.

To make this absolutely clear, consider the limit at which interspike relaxation is zero. In this case, the tetanic contractions never flatten out; contraction amplitude depends only on spike number; equal spike numbers give equal size contractions at all times into the train; and the dependence of amplitude on spike frequency can be explicitly calculated. At any spike frequency (freq_sp), the number of spikes in a given time is (time · freq_sp) + 1. Summated contraction amplitude (amp) equals unitary contraction amplitude (amp_unit) times spike number. The dependence of contraction amplitude on spike frequency is the change in contraction amplitude divided by the change in spike frequency, or:

$$\frac{{\text{amp at freq}}_{\text{sp}2}-{\text{amp at freq}}_{\text{sp}1}}{{\text{freq}}_{\text{sp}2}-{\text{freq}}_{\text{sp}1}}=\frac{[(\text{time}·{\text{freq}}_{\text{sp}2})+1]·{\text{amp}}_{\text{unit}}-[(\text{time}·{\text{freq}}_{\text{sp}1})+1]·{\text{amp}}_{\text{unit}}}{{\text{freq}}_{\text{sp}2}-{\text{freq}}_{\text{sp}1}}$$

$$=\text{time}·{\text{amp}}_{\text{unit}}.$$

This line is plotted on Figure 5C with open circles. At very short times into the train (≤0.75 sec), the dependence of contraction amplitude on spike frequency matches quite well the dependence expected were interspike relaxation zero (in which case amplitude would be strictly spike number dependent at all spike frequencies and times). That is, at these early times the differing interspike relaxation amplitudes that occur as spike frequency changes do not significantly alter the achieved contraction amplitude. Contraction amplitude is thus a linear function of spike number alone; the dependence on spike frequency arises solely because, at any given time, higher spike frequencies have greater spike numbers, not because they have less interspike relaxation time.

In reality, interspike relaxation is only small, not zero, and the simulation significantly diverges from the zero interspike relaxation line at times greater than 0.75 sec. However, the analysis below shows that the spike number domain (the time range in which equal spike numbers give approximately equal contraction amplitudes) is considerably longer than this time. Figure 5C,inset, shows an expanded view of the data from time 0 to 2.5 sec. A line with a constant slope (C) fits these data well (Fig. 5C, line through closed circles), and thus in this time range each point on this line equalsC × time. The points on this line are just the slopes of the corresponding amplitude versus spike frequency lines shown in Figure 5B. The family of equations for the lines in Figure 5B is amp = a +b · freq_sp, whereb is the slope of each line. For the linear region shown in Figure 5C, inset, b =C · time, and hence amp =a +C · time · freq_sp. Spike number (sp^#) equals (time · freq_sp) + 1, and thus freq_sp = (sp^#− 1)/time. Substituting gives amp =a − C +C ·sp^#, and thus as long as the spike frequency dependence is approximately linear with time (i.e.,C is a constant) and a is constant, contraction amplitude is an approximately linear function of spike number. In effect, nonzero interspike relaxation simply slightly reducesamp_unit, in the case at hand from 0.01 to 0.007 (Fig. 5C).

This analysis suggests that for times <2.5 sec, spike trains with equal spike numbers have equal contraction amplitudes. However, as is shown by the equal spike number line in Figure 5A, the times at which different frequency spike trains contain equal spike numbers are nonlinear functions of time (the points on this line are not in the spike number domain and hence do not give equal contraction amplitudes). It is therefore difficult in plots of amplitude versus time to identify the amplitudes corresponding to equal spike numbers in trains with different spike frequencies.

This difficulty can be overcome by transforming the amplitude versus time curves in Figure 5A to amplitude versus spike number curves (Fig. 5D). The initial portions of the curves overlie, and hence equal spike numbers give equal contraction amplitudes; this is the spike number domain. Each curve leaves the spike number domain (begins to flatten out) at a different spike number (∼25 spikes for 10 Hz stimulation and ∼150 spikes for 60 Hz). However, until they leave the spike number domain, different frequencies give equal amplitude contractions at approximately equal spike numbers (if the amplitude in question can be reached by that frequency; e.g., 10 Hz stimulation cannot give an amplitude of 0.5). For instance, a contraction amplitude of 0.1 occurs between 16 and 19 spikes at all frequencies, of 0.5 between 56 and 65 spikes in the 30–60 Hz frequency stimulations, and of 0.75 between 91 and 95 spikes in the 50 and 60 Hz stimulations. The dashed line connects the points that correspond to 2.5 sec into the various trains; in agreement with the discussion of Figure 5C, this time corresponds to the spike numbers at which the contractions leave the spike number domain.

The model of slow muscle contraction used for the analyses shown here is very simple, and it is important to point out under what conditions these analyses may fail. The key assumptions of the model are that interspike relaxation magnitude increases with contraction amplitude, and that when contraction amplitude is small, interspike relaxation magnitude is small compared with unitary contraction amplitude. If this is true, there will always be an early temporal domain in which the contraction of each spike simply “builds” on the contraction of the preceding spike (Fig. 1A, left inset), and summated contraction amplitude depends on spike number, not spike frequency (except for the trivial dependence that higher frequencies give more spikes per time).

In comparing this model with real muscles, two concerns immediately present themselves. The first is interspike facilitation (e.g., the first spike induces a unitary contraction of 1, the second of 2, etc.). If the amount of facilitation is constant at all physiological spike frequencies (i.e., the second spike induces an amplitude increase of 2 regardless of interspike interval), such muscles will still have a spike number domain, although each spike must be associated with the correct unitary amplitude (e.g., the amplitude after the third spike is 1 + 2 + 3 = 6). Alternatively, if interspike facilitation changes markedly within the physiological interspike interval range (e.g., the second spike induces a unitary contraction of 2 if it follows the first spike at 100 msec but one of 4 if it follows at 50 msec), then summated amplitude could nontrivially depend on spike frequency at all times into the train. The second concern is relaxation rate depending on spike frequency. If the interspike relaxation magnitude is markedly different at different physiological interspike intervals, nontrivial spike frequency dependence could again be always present.

In practice, single spikes are unlikely to produce measurable contractions in the slow, non-twitch muscles for which spike number dependence is likely of physiological importance. Therefore, how facilitation and relaxation depend on spike frequency cannot generally be measured, although changes in these parameters will change the rise time constants (time to 63% of maximum contraction amplitude) of the different tetanic contractions [note that in the model, because unitary contraction amplitude and relaxation rate are constant, the rise time constants of the curves are also constant (3.6 sec)]. However, if the goal is to determine whether a muscle is spike number or spike frequency dependent when driven by physiological burst durations, the discussion above of Figure 5C shows that measuring how unitary contraction facilitation and relaxation depend on spike frequency is unimportant. If the spike frequency dependence versus time plot (Figs. 5C, 6C, 8C) has an early linear portion and the lines in the amplitude versus spike frequency plot (Figs. 5B, 6B,8B) intercept the y axis at approximately the same value, the muscle has a spike number domain, and if all physiological burst durations are within this time range, the muscle is functionally spike number dependent.

Fig. 6.

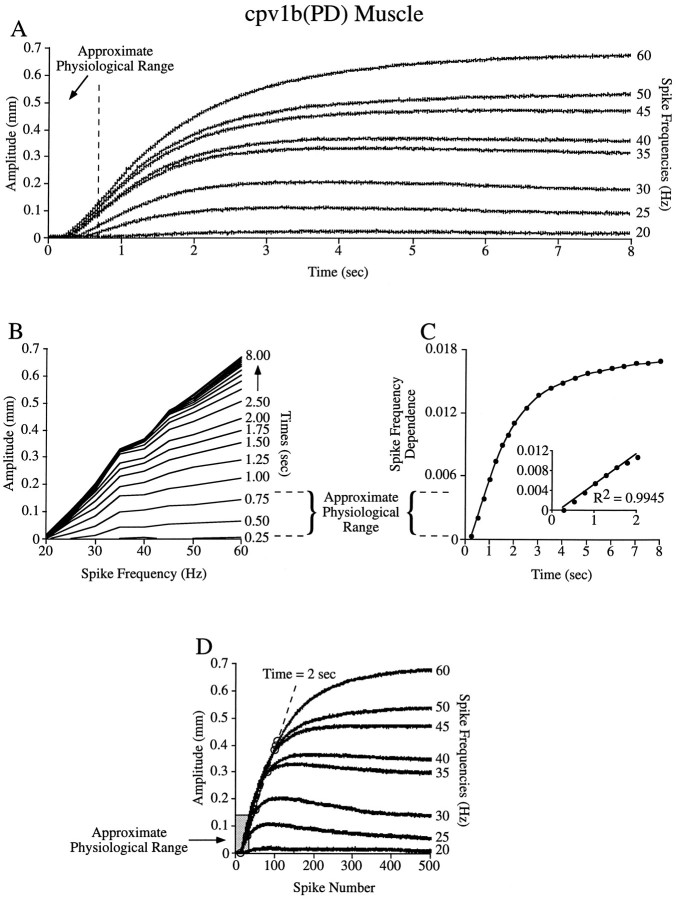
Tetanic stimulations suggest that the cpv1b(PD) muscle is spike number dependent at all physiological burst durations.A–D, Analyses of the type shown in Figure 5 with the cpv1b(PD) muscle. Note that the approximate physiological range (dashed lines in B and C,gray rectangle in D) is well within the spike number domain (e.g., the region of well spaced lines inB, the linear region in the inset ofC, and the overlay region in D).

Fig. 8.

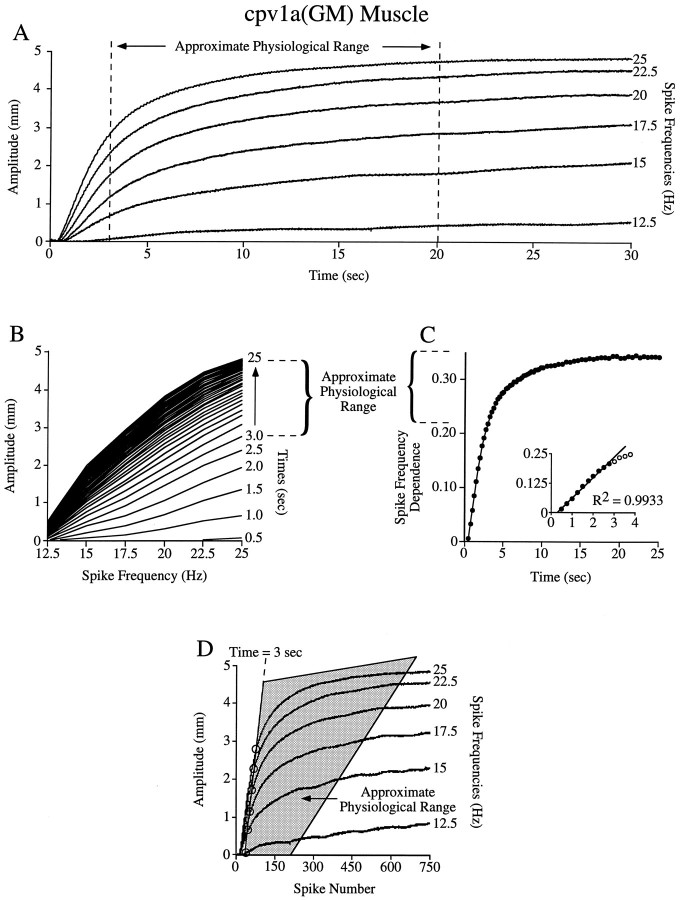
Tetanic stimulations suggest that the cpv1a(GM) muscle is in the transition or spike frequency domain at all physiological burst durations. A–D, Analyses of the type shown in Figure 5 with the cpv1a(GM) muscle. The approximate physiological range (dashed lines in Band C, gray area in D) is outside the spike number domain.

Before applying the analysis shown in Figure 5 to real muscles, it is important to make one additional point. In the model, stable contraction amplitude is determined only by spike frequency and interspike relaxation rate and hence increases without limit as spike frequency increases (i.e., the model has no maximum contraction amplitude). Alternatively, when real muscles are stimulated at increasing spike frequencies, beyond a certain frequency contraction amplitude does not increase. In this case the analyses shown in Figure5 fail (the lines in Fig. 5B level off at high spike frequencies). All data shown here were therefore performed at spike frequencies less than those that would induce an absolute maximum contraction of the muscle.

Figure 6 shows the results of this analysis on tetanic contractions induced in the cpv1b(PD) muscle. The PD neurons fire with spike frequencies between 20 and 60 Hz (Hooper and Thuma, 1996). Figure6A shows that in this range increasing stimulation frequency results in increased contraction amplitude (i.e., the muscle does not reach its maximum contraction amplitude at any of these frequencies), and thus the analyses shown in Figure 5 are appropriate. The muscle reaches its steady-state contraction amplitude at much longer times than the PD neuron burst durations (0.1–0.5 sec; Fig.6A, dashed line) observed as pyloric cycle frequency is altered in vitro (Hooper, 1997a). The cpv1b(PD) muscle thus clearly does not function in the spike frequency domain.

The analyses in Figure 6B–D suggest that this muscle always functions far within the spike number domain. Figure6B shows that the physiological range (dashed lines) is within the low-slope, well-separated region of the figure, and Figure 6C shows that this range is in the linear part of the spike frequency-dependent curve (the linear region extends to 2 sec; inset). Figure 6D shows that, when plotted against spike number, the 25–60 Hz contractions almost perfectly overlie in the physiological range (gray rectangle) and do not leave this range until 2 sec into the trains, much longer than the longest physiological burst duration. Note that this muscle does not have the same rise time constant at different spike frequencies (the 30 Hz curve has a rise time constant of 1.1 sec, whereas the 60 Hz curve has a rise time constant of 1.8 sec), and hence either unitary contraction amplitude or interspike relaxation rate or both change as spike frequency changes. However, as noted earlier, these changes are immaterial to determining functional spike number dependence; despite these changes, Figure 6C shows a linear region, and because this region is longer than the longest physiological burst duration, this muscle is likely functionally spike number dependent.

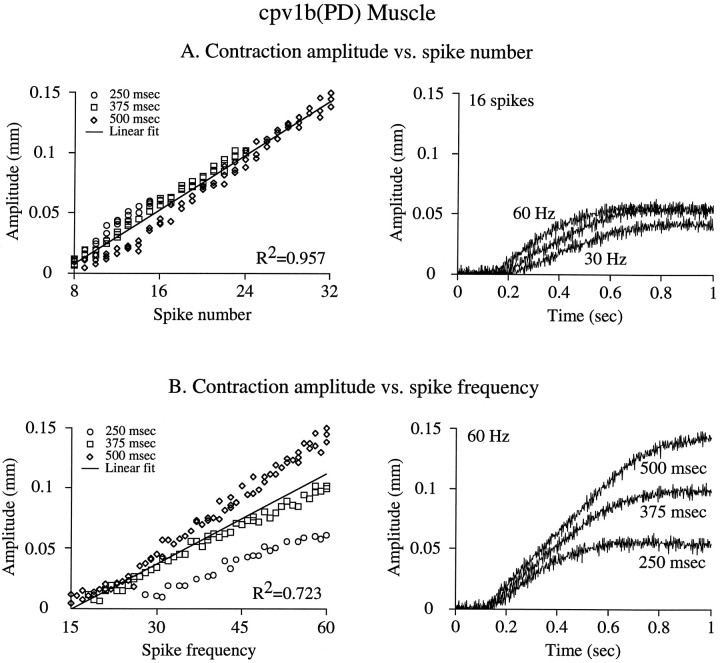
Although these data strongly suggest that the cpv1b(PD) muscles function in the spike number domain, they do not prove it because of the nonphysiological nature of tetanic stimulation. We therefore performed experiments in which cpv1b(PD) muscles were stimulated using bursts of different durations (250, 375, and 500 msec) and spike frequencies (15–60 Hz) mimicking muscle physiological input (Fig.7). These data contain bursts with equal spike numbers (e.g., 13 spikes are obtained with a 250 msec burst duration at 48 Hz, a 375 msec duration at 32 Hz, or a 500 msec duration at 24 Hz) and bursts with equal spike frequencies and thus allow direct comparison of which parameter best predicts contraction amplitude. Figure7A, left panel, shows amplitude plotted against spike number; amplitude is a linear function (note largeR² value) of spike number regardless of burst duration or spike frequency. Figure 7A, right panel, shows the contractions induced at the three burst durations with spike frequencies (60, 40, and 30 Hz) that gave 16 spikes in each burst; all three contractions have similar amplitudes. Figure 7B,left panel, shows contraction amplitude plotted against spike frequency; the data diverge into three distinct populations (note smaller R² value of linear fit). Figure7B, right panel, shows the contractions induced at the three burst durations at a constant (60 Hz) spike frequency (burst spike numbers 16, 23, and 31); the contractions have very different amplitudes. Comparison of Figure 7, A and B, shows that spike number predicts cpv1b(PD) muscle contraction amplitude much better than does spike frequency.

Fig. 7.

Burst spike number predicts cpv1b(PD) muscle contraction amplitude better than burst spike frequency when the muscle is stimulated with bursts of spikes. Burst durations of 250, 375, and 500 msec at spike frequencies from 15 to 60 Hz were used to induce single cpv1b(PD) muscle contractions with equal spike numbers and different spike frequencies and vice versa. A,Left panel, Contraction amplitude plotted versus burst spike number; a tight linear relationship exists (note largeR² value). Right panel, Contractions induced by 16 spikes in burst durations of 250, 375, and 500 msec (spike frequencies of 60, 45, and 30 Hz); note similar contraction amplitudes. B, Left panel, Contraction amplitude plotted versus burst spike frequency; three data populations (one for each duration) are apparent (note smaller R² value). Right panel, Contractions induced by 60 Hz stimulation at burst durations of 250, 375, and 500 msec (spike numbers of 16, 23, and 31); note the different contraction amplitudes.  

We were able to infer the physiological GM neuron burst duration range from published data but were unable to locate a reference for physiological intraburst spike frequencies. We stimulated the nerve containing the GM neuron axons (at voltages sufficient to activate all four GM neuron axons) across the entire frequency range in which summated contraction amplitude increased (12.5–25 Hz; Fig.8A). Under these conditions, GM neuron burst durations are sufficiently long that this muscle is spike frequency dependent for a large part of the physiological range (Fig.8A, dashed lines). Figure 8B–Dshows that this muscle functions in the transition or spike frequency domains. Figure 8B shows that the physiological range is in the high-slope, closely spaced region, and Figure 8Cshows that this range is outside the spike number domain [inset; the linear region (filled circles) ends around 3 sec]. Figure 8D shows that, when plotted against spike number, the physiological range (gray area) begins at the far edge of the spike number domain (dashed line). Thus, when the axons of all four GM neurons are activated, this muscle never functions in the spike number domain, and most of its physiological range is in the spike frequency domain [where the tetanic (Fig. 8A) and spike frequency dependence (Fig. 8C) curves are flat]. Again, also note that the analysis techniques used here continue to identify the spike number and spike frequency domains correctly [in particular, the time window (up to 3 sec) in which the spike number curves overlie (Fig. 8D) is correctly predicted from the linear region of Figure 8C], despite the fact that the rise time constants (and hence either unitary contraction amplitude or relaxation rate or both) of the tetanic curves change (from 3.4 sec at 25 Hz stimulation to 8.1 sec at 15 Hz) as spike frequency changes.

Because these stimulations activated all GM neuron axons, these data are comparable to gastric network activity in which all four GM neurons are simultaneously active. Although the GM neurons are electrically coupled, they have been observed to fire separately (Selverston and Mulloney, 1974). When decreased numbers of GM neurons fire, cpv1a(GM) muscle rise time would increase, and the duration of the spike number domain would increase. In this case, it is possible that the cpv1a(GM) muscle would function in the spike number domain. This concern does not affect the data for the cpv1b(PD) muscle, because when both PD neuron axons are stimulated (as in the data presented here) the spike number domain is much longer than physiological PD neuron burst durations are. Any increase in muscle rise time (as would occur if only one PD neuron fired) would simply increase the duration of the spike number domain, and thus the muscle would remain in the spike number domain.

DISCUSSION

This work was motivated by a simple observation and associated question. The observation was that slow muscles can have two domains: an early domain in which contraction amplitude depends on spike number (bursts of different durations and spike frequencies, but equal spike number, induce equal amplitude contractions) and a late domain in which amplitude depends on spike frequency (bursts of different durations and spike numbers, but equal spike frequency, induce equal amplitude contractions). The question was whether muscle contraction dynamics were matched to physiological burst durations so that muscles always functioned in the spike frequency domain, and thus spike frequency always coded contraction amplitude.

Our results show that the answer to this question is no. The cpv1b(PD) muscle always functions well within the spike number domain. The cpv1a(GM) muscle, alternatively, functions in the transition and spike frequency domains. Thus, at least in the stomatogastric system, no single aspect of neuron activity (spike number or spike frequency) codes for contraction amplitude. Understanding the functional consequences of stomatogastric neural activity changes will therefore require detailed examination of each of the muscles of the system. Moreover, because differing effector responses to varying neuronal input must be “taken into account” by the networks that drive the muscles, it is possible that certain aspects of the synaptic interconnectivity and cellular properties of the pyloric and gastric networks can be understood only by considering the differing properties of the muscles they innervate.

Implications for neural network activity

The observation that different aspects of neural activity code for cpv1b(PD) and cpv1a(GM) muscle contraction amplitude suggests that controlling contraction amplitude in these muscles should involve different strategies. Because the cpv1b(PD) muscle is always functionally spike number dependent, controlling the contraction amplitude of this muscle would require controlling the PD neuron burst spike number. This property means that intraburst spike frequency and burst duration need to be coordinated to produce the “correct” spike number. For instance, if PD neuron burst duration decreased, to maintain spike number, and hence muscle contraction amplitude, PD neuron spike frequency would need to increase. (Comparing the 500 msec, 60 Hz and 250 msec, 60 Hz cases in Fig. 7B shows that without this compensation, amplitude would decrease two-thirds as burst duration halved.) Alternatively, muscle contraction amplitude can be increased by increasing PD neuron burst duration alone, because increased burst duration will result in larger spike numbers.

The cpv1a(GM) muscle primarily functions in the spike frequency domain. In this domain spike number does not affect contraction amplitude, burst duration and intraburst spike frequency are decoupled, and controlling muscle contraction amplitude is more straightforward. At all burst durations, the same amplitude is achieved at the same spike frequency. At any burst duration, all amplitudes can be achieved by simply altering spike frequency without regard to its effect on spike number. The observation that this muscle sometimes functions in the transition zone (burst durations from 3 to 6 sec) is intriguing, because this is the most complex part of the muscle contraction with respect to the interaction of spike number and spike frequency. Furthermore, in this work all four GM neuron axons were activated, and the muscles used here were maximally conditioned (Fig. 4), both of which decrease the duration of the spike number domain. It is therefore possible that in vivo this muscle also functions in the spike number domain. Thus, if it is functionally important to maintain cpv1a(GM) muscle contraction amplitude across the full range of gastric network cycle periods, it is likely that the relationship between GM neuron spike frequency and burst duration is complex.

The possibility that all GM neurons need not be simultaneously active raises a potentially general concern for systems in which slow muscles are innervated by multiple motor neurons. Spike number versus spike frequency dependence is determined by how quickly contraction summation occurs. Thus, for the same burst duration, muscles could be spike number dependent when motor neurons fire individually but could become spike frequency dependent when the motor neurons fire as a group (because muscle rise time would decrease).

Implications for motor pattern production

The movements that the pyloric neural pattern induces (the pyloric motor pattern) are completely unknown. It is therefore unclear whether maintaining cpv1b(PD) muscle contraction amplitude as PD neuron burst duration changes is functionally required. The possibility that cpv1b(PD) muscle contraction amplitude often may not be maintained is supported by preliminary work suggesting that the PD neurons do not maintain spike number per burst when the pyloric cycle period is altered (Hooper and Thuma, 1996) and evidence that cpv1b(PD) muscle contractions show interburst temporal summation at fast cycle frequencies (Morris and Hooper, 1994, 1996). Moreover, the data shown here were taken under constant load conditions, and cpv1b(PD) muscle loading in vivo and how it changes throughout the pyloric motor pattern are unknown. Thus, although the data shown here are a necessary first step to predict the pyloric motor pattern from pyloric neural output, they are insufficient to fulfill this goal. The gastric motor pattern is much better described (Heinzel, 1988), but at the time of Heinzel’s work the cpv1a(GM) muscle was believed to be a pyloric muscle. What role this muscle plays in gastric mill function is unknown.

How general is spike number dependency?

Slow, non-twitch muscles are often called tonic muscles and are often considered to be used primarily for nonphasic motor patterns such as maintaining posture. However, slow muscles are used in iguana ventilation (Carrier, 1989), and the slow opercularis muscle in a bullfrog is driven with short (250 msec) rhythmic bursts at high cycle frequencies (0.5–1 Hz) (Hetherington and Lombard, 1983). The cpv1a(GM) and cpv1b(PD) muscles are almost certainly slow muscles given their several second summation time and nonspiking nature, yet cpv1b(PD) muscles are driven by burst durations of 100–500 msec at 0.5–2 sec cycle periods. It is thus clear that slow muscles can be driven by short burst durations in rapid motor patterns.

Spike number dependence is possible whenever slow muscle and short burst duration are matched. An expected property of spike number-dependent systems is that, to maintain muscle contraction amplitude, spike number will be constant as burst duration changes. Our results on other pyloric muscles and a review of the literature suggest that slow muscles and short burst durations may be matched in at least four well-defined model invertebrate systems; in two of these cases spike number is known to be maintained as burst duration changes.

Other pyloric muscles

Preliminary evidence suggests that two other pyloric muscles, p1 and p8 (innervated by the lateral pyloric and pyloric neurons, respectively), function largely or exclusively in the spike number domain (Ellis et al., 1996) (T. A. Ellis, S. L. Hooper, and L. G. Morris, unpublished observations).

The accessory radula closer (ARC) system in Aplysia

The ARC muscle is innervated by two motor neurons, B15 and B16. ARC recordings show that B15 and B16 fire 2–4 sec duration burstsin vivo. Muscle contractions induced by motor neuron stimulation show little or no sign of flattening out in these times (Cropper et al., 1990). ARC contractions induced by tetanic stimulation take ∼5–15 sec to fully summate (V. Brezina, personal communication). A significant portion of the physiological burst duration range is thus in the early part of the muscle contraction in which spike number dependence is possible.

Swimming in the leech, Hirudo medicinalis

In Hirudo, body wall muscles do not fully summate within the burst duration range observed during swimming (Mason and Kristan, 1982). In vivo, intraburst spike frequency varies inversely with burst duration as swim cycle period changes, and burst spike number is well maintained over a fourfold burst duration range (Murray et al., 1996). Assuming that maintaining muscle contraction amplitude is functionally important as swim cycle period changes, maintenance of burst spike number would be expected if the muscles were spike number dependent.

Ventilation in the green crab, Carcinus maenas

In vitro recordings show that, depending on pattern cycle frequency, the L2b motor neuron fires 60–600 msec bursts (Mercier and Wilkens, 1984; DiCaprio et al., 1997), and intraburst firing frequency increases as burst duration decreases (Mercier and Wilkens, 1984). This compensation can be sufficient to maintain the burst spike number rigidly as cycle period changes twofold, and burst spike number never varied more than 10 spikes as cycle period changed ninefold. In comparison with physiological burst durations, muscle contraction seems to develop slowly (Mercier and Wilkens, 1984), and isometric tension, at least at some stimulation frequencies, develops quite slowly (Josephson and Stokes, 1987).

Analyses such as those shown here must be performed to prove spike number dependence, and because that is not the case in the work above, these identifications are tentative. However, the frequent occurrence in lower vertebrates and invertebrates of slow, non-twitch muscles (Hoyle, 1983) suggests that spike number dependence may not be rare in these preparations. It may thus be important, when considering the functional consequences of changing neuronal activity in these systems, to determine muscle spike number versus spike frequency dependence. Finally, in systems with spike number-dependent muscles, certain neural network properties may be present specifically to compensate for the contraction amplitude control problems that spike number dependence entails.

The average amplitude (amp_ave) at which contractions stabilize in a system in which each spike induces a constant amplitude contraction (amp_unit) that decays with a single exponential e^−t/τ can be defined in two ways.

If amp_ave is defined as being midway between the maximum contraction amplitude that occurs immediately after a spike (amp_max) and the minimum contraction amplitude that occurs immediately before the subsequent spike (amp_min), thenamp_max = amp_ave +amp_unit/2. When the system is stable,amp_unit equals the interspike relaxation amplitude. Interspike interval equals the inverse of spike frequency, or 1/freq_sp. At the end of the interspike relaxation the contraction amplitude is thereforeamp_min =amp_maxe^{−(1/freq_sp)/τ}= (amp_ave +amp_unit/2)e^{−1/τ · freq_sp}.amp_unit equals amp_max −amp_min, or amp_unit= amp_ave +amp_unit/2 − (amp_ave+amp_unit/2)e^{−1/τ · freq_sp}.

Solving gives:

$${\text{amp}}_{\text{ave}}={\text{amp}}_{\text{unit}}\frac{1+e^{-1/\tau ·{\text{freq}}_{\text{sp}}}}{2(1-e^{-1/\tau ·{\text{freq}}_{\text{sp}}})}.$$

Series expansion of:

$$\frac{1+e^{-1/\tau ·{\text{freq}}_{\text{sp}}}}{2(1-e^{-1/\tau ·{\text{freq}}_{\text{sp}}})}$$

to the fifth term (further expansions do not significantly change the results) and gathering terms gives:

$$\tau ·{\text{freq}}_{\text{sp}}-\frac{1}{2\tau ·{\text{freq}}_{\text{sp}}}\times \left[\frac{\frac{1}{(\tau ·{\text{freq}}_{\text{sp}}{)}^3}-\frac{3}{(\tau ·{\text{freq}}_{\text{sp}}{)}^2}+\frac{10}{\tau ·{\text{freq}}_{\text{sp}}}-20}{\frac{1}{(\tau ·{\text{freq}}_{\text{sp}}{)}^4}-\frac{5}{(\tau ·{\text{freq}}_{\text{sp}}{)}^3}+\frac{20}{(\tau ·{\text{freq}}_{\text{sp}}{)}^2}-\frac{60}{(\tau ·{\text{freq}}_{\text{sp}})}+120}\right].$$

For all values of τ · freq_spgreater than ∼2, numerical solution shows that the expression in the brackets is very nearly −1/6 (maximum error is 0.7% at τ · freq_sp = 2), and thus this equation reduces to τ · freq_sp + 1/(12τ · freq_sp). The term 1/(12τ · freq_sp) is much smaller than τ · freq_sp for all τ · freq_sp ≥ 2 and becomes relatively smaller as τ · freq_sp increases.amp_ave therefore very nearly equalsamp_unit · τ · freq_sp, and hence the slope of amp_ave versusfreq_sp ≈amp_unit ·τ. The values of τ · freq_sp for which this approximation is true (τ · freq_sp ≥ 2) are in the physiological range of all pyloric and gastric muscle relaxation time constants and spike frequencies we have measured (Ellis et al., 1996;Morris and Hooper, 1996).

Another measure of average contraction amplitude is the average of the function defining the interspike relaxation,amp_maxe^−t/τ. The average of a function y =f(x), a ≤ x ≤b, equals:

$$\frac{1}{b-a} \underset{a}{\overset{b}{\int }} f(x)\text{dx}.$$

Taking the average over a single interspike interval (1/freq_sp) gives:

$${\text{freq}}_{\text{sp}} \underset{t=0}{\overset{1/{\text{freq}}_{\text{sp}}}{\int }} {\text{amp}}_{max}{e}^{-t/\tau }\text{dt}.$$

At stable state amp_max is constant, and thus the integral equalsfreq_sp · amp_max · τ · (1 −e^{−1/τ · freq_sp}).amp_max = amp_min +amp_unit, andamp_min =amp_maxe^{−1/τ · freq_sp}. Solving gives amp_max =amp_unit/ (1 −e^{−1/τ · freq_sp}), and thus at steady state the average of the functionamp_maxe^−t/τexactly equalsamp_unit · τ · freq_sp.