Abstract
The modulation of the pyloric rhythm of the stomatogastric ganglion of the crab, Cancer borealis, by crustacean cardioactive peptide (CCAP) is described. CCAP activated pyloric rhythms in most silent preparations, and altered the phase relationships of pyloric motor neuron firing in all preparations. In CCAP, the pyloric rhythms were characterized by long lateral pyloric (LP) neuron bursts of action potentials. The threshold for CCAP action was ∼10−10 M, with increasing effects at higher CCAP concentrations. The changes in motor pattern evoked by CCAP produced significant changes in LP-innervated muscle movement. These movements were additionally potentiated by CCAP applications to isolated nerve–muscle preparations. Thus, enhanced motor neuron firing and increase of the gain of the neuromuscular junctions are likely to operate coordinately in response to hormonally released CCAP. High CCAP concentrations sometimes resulted in modification of the normal 1:1 alternation between the pyloric dilator (PD) and LP neurons to patterns of 2:1, 3:1, or 4:1 alternation. CCAP seems to activate slow intrinsic oscillations in the LP neuron, as well as enhance faster oscillations in the pacemaker group of PD/anterior burster (AB) neurons. Simulations of fast and slow oscillators with reciprocal inhibitory coupling suggest mechanisms that could account for the mode switch from 1:1 alternation to multiple PD bursts alternating with one LP neuron burst.
Keywords: pyloric rhythm, crustacean neuropeptide, central pattern generator, neural oscillators, neuromodulator, computational modeling
Neurons with oscillatory and plateau properties are present in vertebrate and invertebrate nervous systems, and these processes are known to be important in central pattern generating networks responsible for the production of rhythmic movements (Cohen et al., 1988; Getting, 1989; Marder and Calabrese, 1996). Oscillatory and plateau properties are often subject to neuromodulatory control (Harris-Warrick and Marder, 1991), which allows flexibility and variability in the behaviors that are controlled by central pattern generating networks (Harris-Warrick and Marder, 1991; Harris-Warrick et al., 1992; Marder and Weimann, 1992; Marder and Calabrese, 1996).
In this paper, we describe the modulation of the pyloric rhythm of the stomatogastric ganglion (STG) of the crab Cancer borealis by the neuropeptide CCAP (Pro-Phe-Cys-Asn-Ala-Phe-Thr-Gly-Cys-NH2). CCAP was first purified and sequenced from the crab Carcinus maenas(Stangier et al., 1987), and has since been found in a large number of arthropod species (Stangier et al., 1989; Cheung et al., 1992; Furuya et al., 1993; Lehman et al., 1993; Dircksen, 1994).
Many of the modulatory substances that alter the motor patterns of the STG are found in neurons that project into the neuropil of the STG from somata in the paired commissural ganglia (CGs) and the unpaired esophageal ganglion (OG) (Coleman et al., 1992; Harris-Warrick et al., 1992). In contrast, CCAP is not found in neural inputs to the STG. The STG is situated in the dorsal artery, just anterior to the heart. CCAP is found in the pericardial organs in crabs, including C. borealis, and is likely to reach the STG as a result of hormonal delivery through the hemolymph from this neurosecretory structure (Stangier et al., 1987, 1988; Dircksen and Keller, 1988; Keller, 1992;Dircksen, 1994; Christie et al., 1995).
Circulating hormones can influence the movements produced by the stomatogastric nervous system by altering the neurally evoked motor patterns and/or by influencing the movement elicited by a given pattern of motor neuron discharge. CCAP alters both centrally driven motor patterns and the relationship between presynaptic discharge and muscle contraction.
Of particular interest are neuromodulatory processes that produce “mode switches” in which one pattern of activity is replaced by another, qualitatively different mode of activity. High CCAP concentrations sometimes produce a mode switch that illustrates some of the interesting dynamics that occur when oscillators of significantly different intrinsic periods are coupled synaptically. Some of these data have appeared previously in abstract form (Weimann et al., 1992).
MATERIALS AND METHODS
Animals and solutions. Experiments were performed with male C. borealis purchased from Neptune Lobster and Seafood or Commercial Lobster (both of Boston, MA). Animals were held in Instant Ocean filled aerated aquaria at 11–13°C until use, and weighed between 300 and 750 gm. C. borealisphysiological saline had the following composition (in mm): NaCl, 440; KCl, 11.3; CaCl2, 13.3; MgCl2, 26.3; Trizma Base, 11; maleic acid, 5.2, pH 7.4–7.6. CCAP was purchased from Bachem, Inc. (Torrance, CA).
Ganglion experiments. Physiological recordings were made as described previously in Weimann et al. (1991, 1993) from stomatogastric nervous systems dissected free from the animal. Extracellular pin electrodes insulated with Vaseline were used to record from nerves. Intracellular recordings were made with microelectrodes filled with either 0.6 mK2SO4 and 10 mm KCl or 2m potassium acetate and 10 mm KCl using either a Getting amplifier or an Axoclamp 2A. Data were collected with an eight-channel Gould thermal array chart recorder.
All preparations initially consisted of combined stomatogastric nervous systems, including the paired CG, OG, and STG with their associated motor and connecting nerves (Fig. 1). In most experiments, the STG was acutely isolated from the anterior ganglia either by cutting the stomatogastric nerve (stn) or by blocking impulse activity in the stn (Russell, 1979) by placing a Vaseline well around the desheathed stn and replacing the saline in the well with isotonic sucrose (750 mm).
Fig. 1.
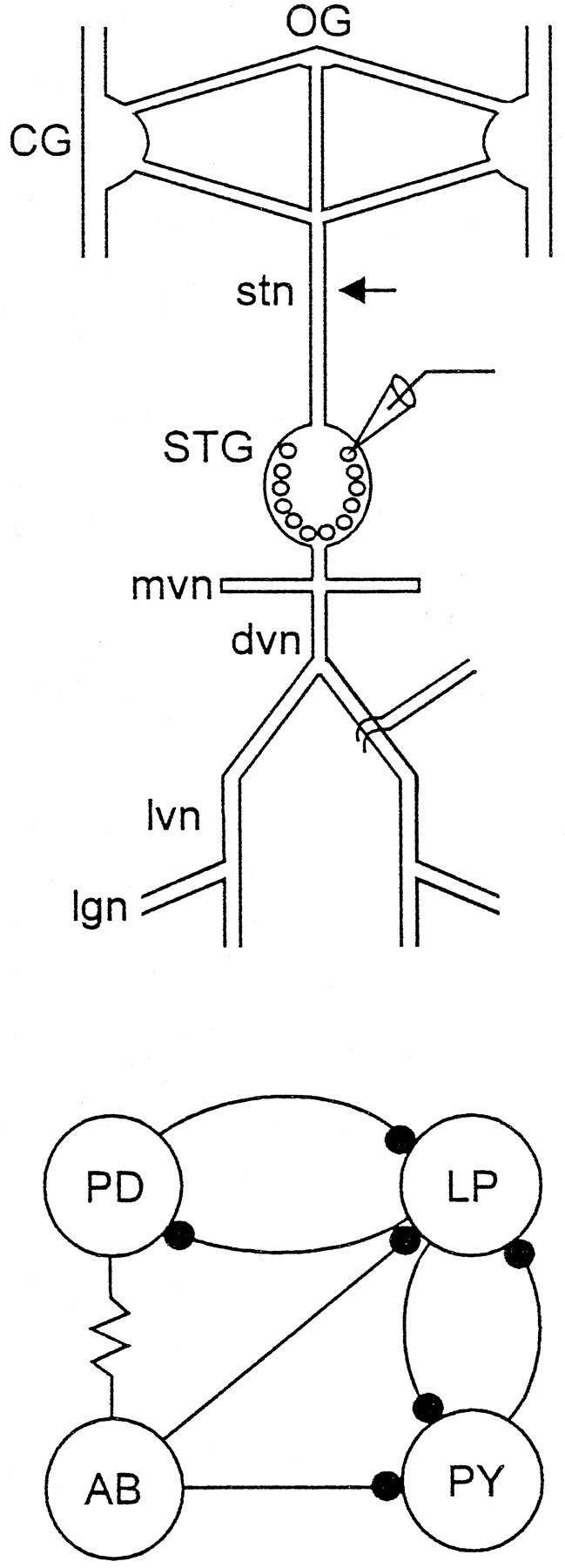
Organization of the stomatogastric nervous system.Top, Schematic of the stomatogastric nervous system showing the paired CG, OG, STG, and the associated nerves used in the recordings in this paper. These include the stn, mvn, dvn, lvn, and lgn. The arrow shows the position where the stn was cut or the Vaseline well used for blocking the stn was placed (Materials and Methods). Intracellular recordings were made from the somata (microelectrode) and extracellular electrodes used to record action potentials in the motor nerves. Bottom, Connectivity diagram of the pyloric network neurons that are the focus of this paper. The resistor symbol denotes an electrical connection, and the filled circles represent chemical inhibitory synaptic connections.
All preparations were continuously superfused with chilled C. borealis saline at 10–15 ml/min. CCAP was made up at the desired concentration and applied by means of a switching port in the superfusion system. The temperature was continuously monitored with a thermoelectric probe in the bath, and maintained at ∼12°C with a Peltier cooling system.
Neuromuscular preparations. Two of the muscles innervated by the LP neuron, cpv4 and cpv6 (Maynard and Dando, 1974; Weimann et al., 1991), were dissected from the stomach and pinned at one insertion to a small dish. The other insertion was attached by a thread to a Grass FT03 movement transducer modified to give increased sensitivity. The muscle was stretched to its resting length in the animal. The cut end of the motor nerve was stimulated with a suction electrode, and the resulting movements were recorded. The bath volume was 3 ml, and other conditions were as above.
Simulations. A simple mathematical model for the AB, PD, and LP neurons was used. The AB and PD neurons were lumped together and modeled as a single oscillator. The LP neuron was either modeled as a tonically firing neuron or a slow intrinsic oscillator. In all cases, only the slow envelopes of membrane potential trajectories, but not single spikes, were modeled.
The pair vAP,ndescribes the dynamics for AB/PD; vAPrepresents the transmembrane potential and n is the corresponding recovery variable. The equations are based on the Morris-Lecar (1981) system, whose modes of oscillation have been extensively studied. The equation forvAP is the sum of three standard intrinsic membrane currents, a constant injected currentIAP and a synaptic inhibitory current that both rises and decays quickly, with maximal conductancea1. The smooth functionHLP in the expression for the synaptic current is 1 if the voltage of the LP neuron,vLP, is above a certain threshold, and 0 otherwise.
When ε is small in the n equation, the oscillations generated by this system are of the relaxation type. We worked in this regime by using ε = 0.02. Except forIAP, sln, anda1, the parameters for AB/PD were kept constant in all the simulations shown. Their values are as follows: C1 = 1;gLAP = 0.007;VLAP = −80;g1AP = 70;V1 = −40,g1AP = 1,V2 = −60,Vsyn = −60. We variedIAP and sln to control the frequency and “strength” of this oscillator. By “strength” we mean its ability to continue to oscillate in spite of inhibition. This corresponds to the increased amplitude and frequency of the slow wave oscillation in the biological neuron. The parameter values used have no direct relationship to the actual physiological properties of the AB or PD cells. This model is only intended as a simple caricature of some of the oscillatory properties of the AB/PD pair.
The equations for the LP neuron were based on a two-dimensional system (similar to the Hodgkin–Huxley equations) developed by Manor et al. (1997), plus an additional current that can be thought of as a Ca2+-activated K+ current. The effect of the AB/PD group on LP was modeled as two inhibitory synaptic currents, one fast rising and fast decaying and the other quick-rising and slowly decaying. The dynamics for the model LP are described by the equations for vLP, w,h, s. As mentioned above,vLP corresponds to the membrane potential of LP, w is an inactivation variable, hcontrols the additional current, and s controls the time course of the slowly decaying synaptic current.
We have chosen this model because in the absence of the additional current and the two synaptic currents (i.e., wheng2LP = 0 anda2 = 0), it has three different behaviors (stable, excitable, and oscillatory) with varying the single parameter g1LP. In the relaxation regime (τw = 500), the model produces long plateaus, suitable for representing the behaviors of LP. The effect of the additional current (with maximal conductanceg2LP) is to make the duration of the hyperpolarized phase longer when the depolarized plateau lengthens.
The parameter values used for LP in all the simulations were:C2 = 0.15,gLLP = 0.25, g2LP = 0.5, ILP = −0.075, φ = 1, α = 0.001, β = 0.08,kf = 2,ks = 0.2. We changedg1LP, a2, and gsyn; their values for each simulation are described later in the text. a2and gsyn are the maximal synaptic conductances for the fast rising and decaying synaptic current and the rapidly rising and slowly decaying one, respectively. As in the AB/PD case, this model is extremely simplified. It portrays the behaviors of LP that we considered likely to be the most important in the mode switch. The specific values of the parameters are not associated with any actual physiological parameters of the LP neuron.
All simulations were performed using the package XPP (obtained courtesy of Bard Ermentrout atftp://ftp.math.pitt.edu/pub/bardware/xppaut2.52.tarz), both with RK-4 (stepsize = 0.01) and Gear methods. Initial conditions in all cases were: vAP = −59.5;n = 1; vLP = −59.5;W = 0.02; h = 0; s = 0. The equations now follow:
where
RESULTS
The STG of the crab C. borealis contains 25–26 neurons (Kilman and Marder, 1996), most of which are the motor neurons that innervate the muscles of the foregut. As in other decapod species, these neurons, together with the terminals of several of the modulatory neurons that project into the STG, form the networks that generate the pyloric and gastric mill rhythms of the crab (Weimann et al., 1991;Nusbaum et al., 1992; Coleman and Nusbaum, 1994; Weimann and Marder, 1994; Coleman et al., 1995). When inputs to the STG from the paired CG are left attached, robust pyloric rhythms (Fig.2A,B, control) are almost always observed, and spontaneous gastric mill rhythms are often observed. However, when the effects of the modulatory projection neurons found in the CG and the OG are removed by either cutting the stn or blocking impulse traffic in the stn with sucrose (Materials and Methods), the level of activity produced by the isolated STG is much reduced (Russell, 1979). Under these conditions, an ongoing gastric mill rhythm becomes silent, and the pyloric rhythm either becomes silent or displays low frequency activity (Fig. 2C,D, control).
Fig. 2.
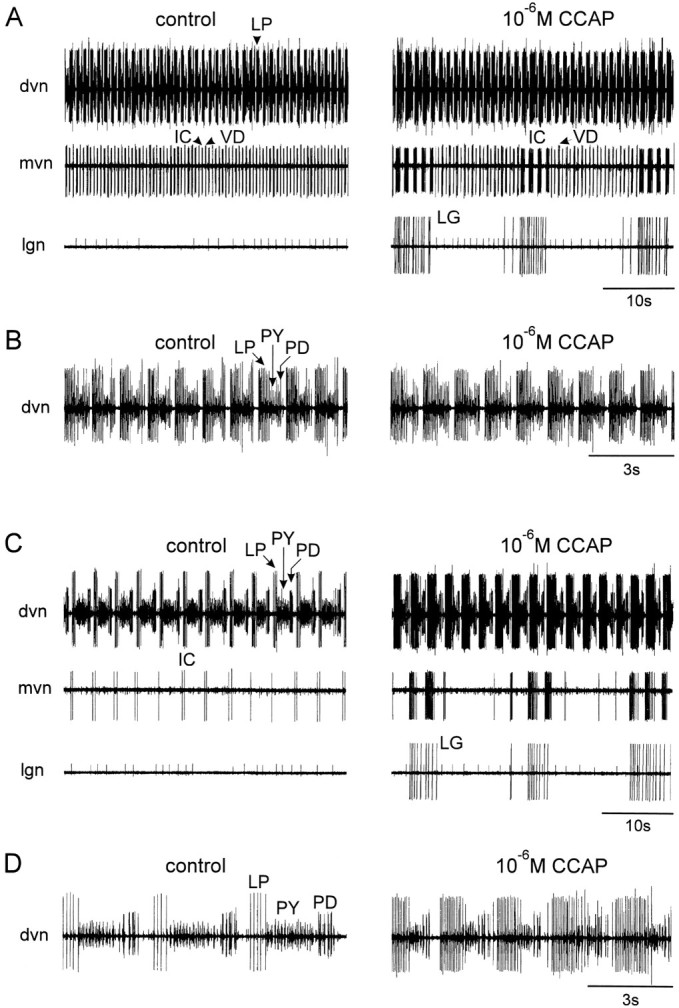
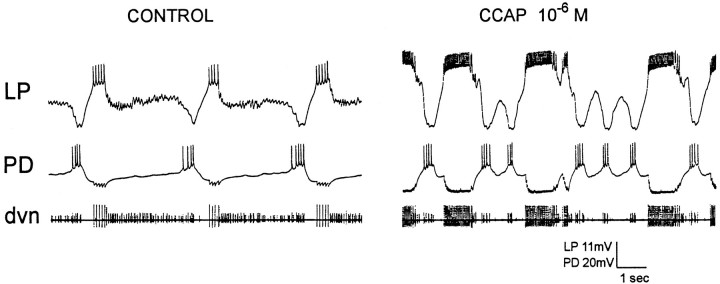
Comparison of the effects of CCAP on a preparation with different levels of starting activity.A and C, Simultaneous extracellular recordings from the dvn, mvn, and lgn.B and D, Faster chart speed of the dvn recordings in A and C, respectively. In all panels, left traces are in control saline andright traces are in the presence of 10−6m CCAP. In this experiment, CCAP was first applied to the combined preparation in which the CG and OG were left attached to the STG (A and B). Then thestn was cut, and 10−6m CCAP was applied to the STG again (C andD).
A variety of neuropeptides, including proctolin (Hooper and Marder, 1987; Nusbaum and Marder, 1989a,b), the extended FLRFamide-like peptides (Weimann et al., 1993), the arthropod tachykinins (Blitz et al., 1995), and red pigment concentrating hormone (Nusbaum and Marder, 1988), can strongly activate pyloric rhythms when applied to isolated STGs. The application of these substances to a preparation showing strong rhythmic activity often shows little or no effect, although they show extremely dramatic actions when applied to preparations that are quiescent or only slightly active (Nusbaum and Marder, 1989a,b). Therefore, we studied the actions of CCAP on combined preparations showing strong activity and on isolated STG preparations with considerably lower levels of activity.
Figure 2 compares the actions of bath application of CCAP to a preparation showing strong pyloric activity, because the CG were left attached (Fig. 2A,B), to the actions of CCAP on the same preparation after the stn was cut (Fig. 2C,D). Figure2A shows extracellular recordings from the dorsal ventricular nerve (dvn), median ventricular nerve (mvn), and lateral gastric nerve (lgn). The dvn shows activity of the LP, pyloric (PY), and PD neurons (this can be better seen in the faster chart speed expansion in Fig. 2B). The repeated sequence of alternating bursts in the LP, PY, and PD neurons is the characteristic pyloric rhythm. The mvn shows the activity of the ventricular dilator (VD) and inferior cardiac (IC) neurons, the activity of which is time locked to both the pyloric rhythm and the gastric mill rhythm (Weimann et al., 1991).
Bath application of 10−6m CCAP (Fig.2A, right) under these conditions produced a small decrease in the frequency of the pyloric rhythm, and the number of LP action potentials/burst and the LP neuron duty cycle increased (Fig. 2B). Obvious at the slow chart speed recordings of Figure 2A are the activation of the gastric lateral gastric (LG) neuron, and the LG-timed modifications of the IC/VD neuron alternating patterns of activity.
When the influence of the CG units on the STG was removed by cutting the stn, the pyloric rhythm slowed down considerably (Fig.2C,D). At that time, application of CCAP produced an increase in the frequency of the pyloric rhythm, as well as pronounced increases in the number of LP action potentials/burst (Fig.2C,D). The LG activation was less pronounced than that seen in Figure 2A, and the IC neuron again fired strongly in time with the LG neuron.
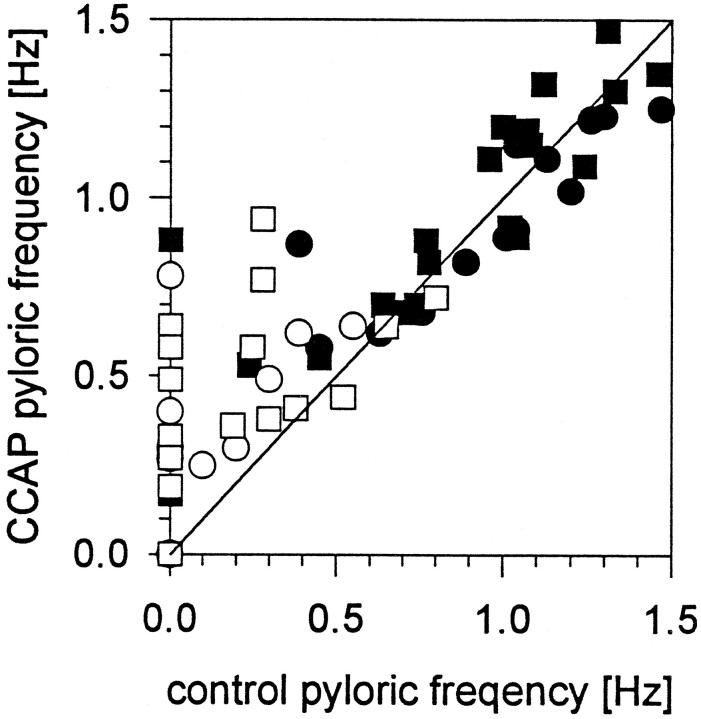
Figure 3 summarizes the effect of CCAP on the frequency of the pyloric rhythm in 43 preparations. In this plot, the frequency of the pyloric rhythm before CCAP application is plotted on the X-axis, and the frequency of the pyloric rhythm in CCAP is plotted on the Y-axis. All points found above the 45° line represent preparations that increased in frequency in CCAP, and those below the line represent preparations that decreased in frequency in CCAP. Fifteen of 43 preparations were silent after the stn was cut or blocked, and 2 of 43 were silent even with the stn intact. CCAP activated the pyloric rhythm in 12 of 17 silent preparations (Fig. 3). In some preparations, both 10−7m and 10−6mCCAP were applied (see Fig. 3, legend); therefore there are more than 43 points on the plot.
Fig. 3.
Effect of CCAP on pyloric rhythm frequency.X-axis, Frequency in control saline;Y-axis, frequency in CCAP. Points abovethe line are preparations in which the frequency was increased by CCAP. Points below the lineare decreases in frequency. ▪, 10−7m CCAP stn intact; •, 10−6m CCAP stn intact; □, 10−7m CCAP stn cut or blocked; ○, 10−6m CCAP stn cut or blocked.
Figure 3 illustrates that the effect of CCAP on pyloric frequency is complex. When the control frequency was low (<0.5 Hz), CCAP applications increased the frequency in 15 of 15 cases. When the control frequency was >0.7Hz, CCAP applications increased and decreased the pyloric frequency in about equal numbers of cases.
Dose dependence of CCAP action
The number of LP spikes/burst increased in all preparations to which CCAP was applied (n = 43). Figure4 shows the number of LP action potentials/burst in the presence of varying concentrations of CCAP in one experiment. In Figure4A the CG were left attached (resulting in a robust pyloric rhythm before CCAP application). In this experiment, CCAP increased the number of LP spikes/burst at all concentrations at 10−10m and higher, with approximately a doubling of the number of LP spikes seen at 10−6m CCAP. However, when the front end influences were removed (resulting in a weaker pyloric rhythm in control saline), the effects of CCAP were much more dramatic (Fig. 4B). The threshold for action was again at or below 10−10 M, with increasing effects at higher concentrations.
Fig. 4.
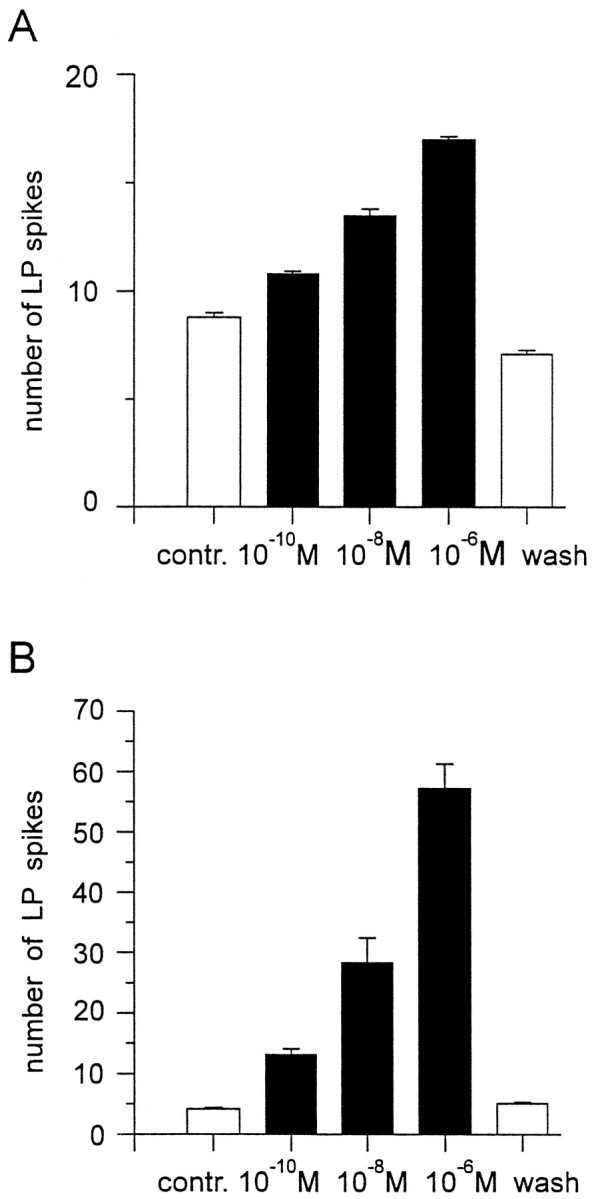
The dose dependence of CCAP action on the number of LP neuron action potentials/burst. A, CG and OG attached. Pyloric rhythm frequency, 0.74Hz. B, Stn cut. Pyloric rhythm frequency, 0.3 Hz. In both cases, all concentrations of CCAP ≥10−10m increased the number of LP neuron action potentials/burst. Note that theY-axis scale is different in the two plots, and the effect is much more pronounced with the lower starting level of activity. Error bars indicate SEM. All values are statistically different from the control and from each other (p < 0.01, t test).
We did 12 experiments in which CCAP was applied in increasing concentrations starting at 10−10 M. In 6 of these 12 experiments 10−10m CCAP clearly increased the number of LP spikes/burst, and in the remaining 6 experiments 10−9m CCAP did so.
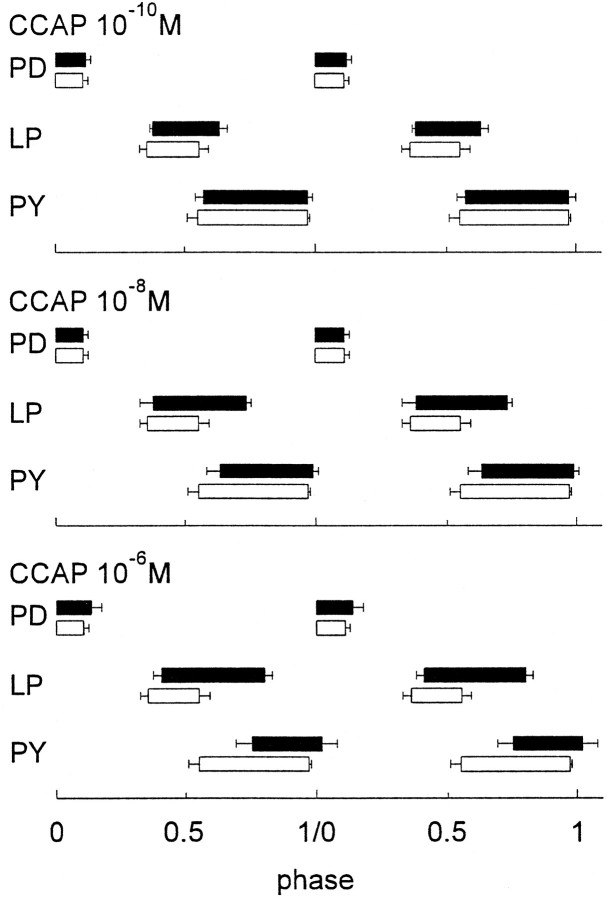
Even when CCAP produced no changes in the frequency of the pyloric rhythm, the activation of the LP neuron resulted in dose-dependent changes in the phase relations of firing between the LP and PY neurons, as illustrated in Figure 5. As the concentration of CCAP was increased from 10−10 to 10−6 M, the onset of the LP neuron firing was not much influenced by the application of CCAP. However, as the CCAP concentration was increased, the LP neuron extended its burst to terminate later in the cycle. The onset of PY neuron activity was phase delayed as a function of CCAP concentration, which is likely a result of the extension of the LP neuron burst, because LP synaptically inhibits PY.
Fig. 5.
The dose dependence of CCAP on the phase relationships of the pyloric network neurons. To make these plots, the start of the PD neuron burst was called phase 0. The phase of any event is calculated as the time from the start of the PD burst to that event, divided by the cycle period. In all panels, the CCAP data are shown inblack bars and the control data are shown inclear bars. Error bars indicate SD. Data correspond to the means of 10 cycles measured in each condition from a single experiment.
CCAP starts the pyloric rhythm
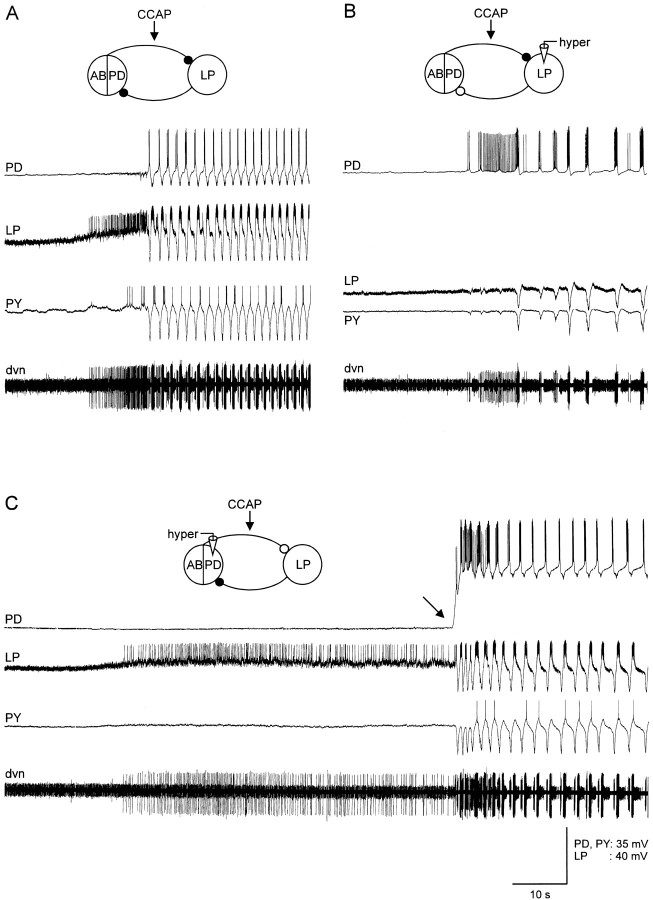
CCAP applications activated strong pyloric rhythms in the majority (12 of 17) of silent preparations. Figure6A shows simultaneous intracellular recordings from the PD, LP, and PY neurons in one such preparation to show the dynamics of CCAP activation. The CCAP reached the bath just before the onset of the traces shown here. Note that the first effect of the CCAP was depolarization of the LP neuron. Subsequently, the alternating pattern of LP, PY, and PD activity started.
Fig. 6.
CCAP starts the pyloric rhythm in silent preparations. All panels show simultaneous intracellular recordings from the PD, LP, and PY neurons with an extracellular recording from the dnv. The electrically coupled AB and two PD neurons are shown in the drawings as a linked ensemble. The black circlesshow the chemical inhibitory synapses in control saline. Theclear circles show the synaptic connections that are presumed to be no longer active because the presynaptic neurons were hyperpolarized below their synaptic release threshold. In each panel, 10−6m CCAP was applied to the preparation shortly before the recordings shown were taken. A, Control. Initial membrane potential: PD, −54 V; LP, −63 mV; PY, −60 mV. B, LP was hyperpolarized. Membrane potentials: PD, −53 mV; LP, −100 mV; PY, −61 mV. C, PD neuron was hyperpolarized. Membrane potentials: PD, −88 mV; LP, −64 mV; PY, −60 mV.
The LP neuron depolarization always preceded the start of the alternating full pyloric rhythm, suggesting that the activation of the pyloric rhythm could result entirely from the actions of CCAP on the LP neuron, which then indirectly activates the PD/AB neuron group by a postinhibitory rebound type mechanism. Alternatively, the oscillatory properties of the AB/PD neuron group could also be directly activated by CCAP. To distinguish between these possibilities, we hyperpolarized the LP neuron before CCAP applications to quiescent preparations. Figure 6B shows the effect of hyperpolarizing the LP neuron in the same preparation as that shown in Figure6A. With the LP neuron hyperpolarized, the PD neurons started to burst. However, the frequency and regularity of the PD burst seen under these conditions was less than that seen with the LP neuron also allowed to be active. Figure 6C shows the effect of hyperpolarizing the PD neuron before and during the beginning of the CCAP application. Note here the strong activation of the LP neuron, but the lack of rhythmic activity until the PD neurons were released from hyperpolarization (Fig. 6C, black arrow). Together, these experiments indicate that the CCAP activation of the pyloric rhythm occurs because of direct effects of the CCAP on both the LP neuron and on one or more neurons of the PD/AB neuron group.
Changes in movement associated with the effects of CCAP
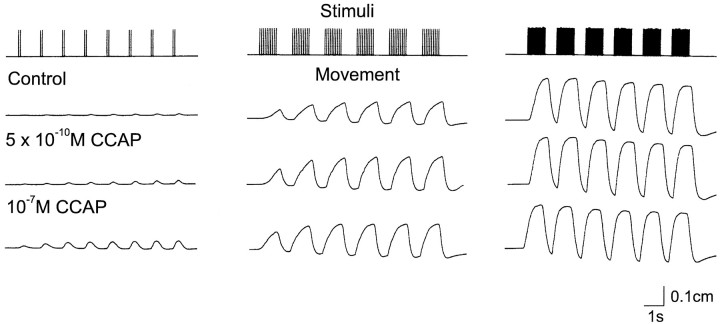
No matter how pronounced the changes in a motor pattern produced by a modulator, it is never self-evident that these modifications of motor patterns will translate into a change in movement. To determine whether the alterations in motor pattern evoked by CCAP will produce altered movements, we stimulated the motor nerve to several of the muscles innervated by the LP neuron in patterns that were designed to mimic those seen in different conditions. Figure 7 shows the results of one such experiment. In this experiment the motor nerve to muscles cpv4 and cpv6 (Maynard and Dando, 1974) was stimulated at 2, 10, and 20 spikes/burst to simulate the increase in the number of LP action potentials/burst seen in CCAP. Under control conditions, there was no movement evoked by the first burst of two spikes, and only very small movements evoked by later trains of 2 spikes/burst. At 10 spikes/burst, it is evident that the contractions increased in amplitude with successive trains of stimuli. At 20 spikes/burst, the first burst produced a large contraction, and subsequent stimuli produced no increase in peak amplitude.
Fig. 7.
Effects of CCAP on LP-innervated muscles. The cpv4 and cpv6 muscles with attached nerves were placed in a small dish and attached to a movement transducer. A suction electrode was used to stimulate the motor nerve at 2 spikes every 1.5 sec, 10 spikes every 2 sec, and 20 spikes every 1.8 sec. The top trace shows the stimulus pattern used. The next three traces are movement recordings of the muscle in response to the stimulus indicated in thetop panel in control saline and in the presence of CCAP at the indicated concentrations. The preparation was washed for 2 hr between the application of 5 × 10−10mCCAP and that of 10−7m CCAP. During that time, it returned to control levels (not shown). After more than 90 min of washing after the treatment with 10−7mCCAP, the preparation had not completely returned to control values (not shown). The slight downward slope of the baseline seen at high stimulus frequencies is a result of the elastic properties of the movement transducer at the upper portion of its operating range.
The recordings in control saline illustrate the significant change in muscle movement associated with the stronger LP neuron bursts that would result from the CCAP action on the ganglion alone. However, low concentrations of CCAP additionally amplify the strength of nerve-evoked contractions, as is illustrated in the recordings seen in the presence of CCAP (Fig. 7). Note that in the presence of 5 × 10−10m CCAP, there is movement evoked by even 2 spikes/burst, and at 10 spikes/burst enhancement of contraction was evident even in the first burst. However, when the muscle was stimulated at higher frequencies, CCAP had no additional effect on peak amplitude or relaxation rates. This is not a result of a ceiling effect, because even higher frequencies of nerve stimulation will produce larger amplitude contractions (data not shown). The effects of CCAP were dose dependent because 10−7m CCAP markedly increased the amplitude of the contractions produced by 2 spikes/burst, and further enhanced those at 10 spikes/burst. Similar results were obtained in seven preparations. The threshold for CCAP actions on these neuromuscular junctions was between 10−10and 10−9m (n = 3). In addition to action on the LP-innervated cpv4 and cpv6 muscles, CCAP also potentiated the responses of the muscles innervated by the IC (n = 3), DG (n = 3), and GM (n = 3) neurons (data not shown).
CCAP-evoked mode switch results from interactions between fast and slow oscillators
In approximately one-third of isolated STG preparations, CCAP applications produced a mode switch in which the normal alternating pattern of 1 PD burst/1 LP burst was replaced by a pattern of 2–4 PD bursts/1 LP burst. This pattern was characteristically produced in those preparations in which the pyloric rhythms in control saline were either silent or relatively weak (low frequency) before CCAP application. Figure 8 shows an experiment in which the pyloric rhythm had a frequency of about 0.2 Hz before CCAP application. In the presence of 10−6m CCAP (Fig. 8, right panel), the intense LP neuron bursts strongly inhibited the PD neurons, which then burst several times during the LP neuron interburst interval. These “novel” CCAP-induced modes were not seen in preparations in which a strong pyloric rhythm was present before CCAP application. Therefore, we hypothesized that these novel rhythms were occurring when the oscillatory properties in the AB/PD neuron group were relatively weak, and when CCAP applications to the LP induced slow intrinsic oscillatory activity from the LP neuron.
Fig. 8.
Altered modes of activity evoked by CCAP. Simultaneous intracellular recordings from the LP and PD neurons and extracellular recording from the dvn. Left, Slow pyloric rhythm with 1:1 alternation between the LP and PD neurons.Right, Altered pattern of activity seen in CCAP in which the PD neurons fire 2–3 bursts/LP burst. Most hyperpolarized point of recordings: LP, −82 mV; PD, −69 mV.
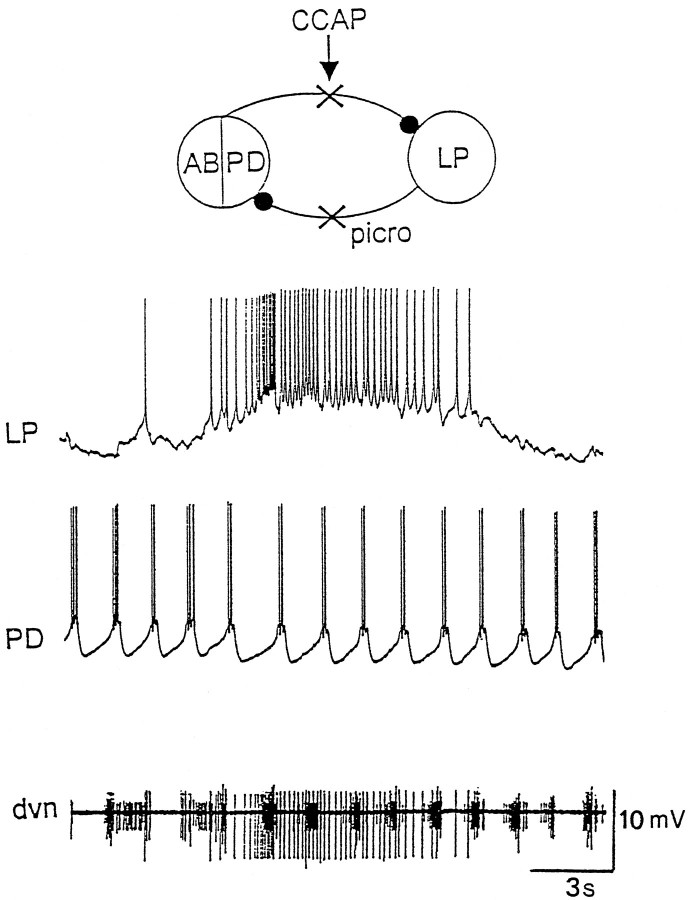
To test this hypothesis, preparations were placed in 10−5m picrotoxin to block the LP to PD inhibition and to block the AB to LP inhibition (Eisen and Marder, 1982; Marder and Eisen, 1984). Figure 9 shows simultaneous intracellular recordings from the LP and PD neurons in 10−8m CCAP in the presence of 10−5mpicrotoxin in one such experiment. The PD neurons were bursting in a normal pyloric manner. However, with the inhibition from the AB neuron blocked, the LP neuron fired in slow bursts, now uncoupled from pyloric time. In three preparations, the LP neuron in CCAP and picrotoxin was spontaneously generating slow oscillations. In two preparations, the LP neuron was tonically firing in CCAP and picrotoxin, but DC hyperpolarization evoked large amplitude slow oscillations, the frequency of which was dependent on the level of current injection (A. Swensen and J.M. Weimann, unpublished results). In four preparations, short depolarizing current pulses triggered, and short hyperpolarizing pulses terminated, plateau potentials in the LP neuron in the presence of CCAP (data not shown). Together, these data argue that CCAP increased the tendency of the LP neuron to generate slow voltage-dependent oscillations and/or plateaus.
Fig. 9.
Picrotoxin reveals fast and slow oscillators. Simultaneous intracellular recordings from the LP and PD neurons, and extracellular recording from the dvn. Preparation in 10−5m picrotoxin and 10−6m CCAP. The most hyperpolarized membrane potentials: LP, −50 mV; PD, −71 mV.
Simulations of the interaction between fast and slow oscillators
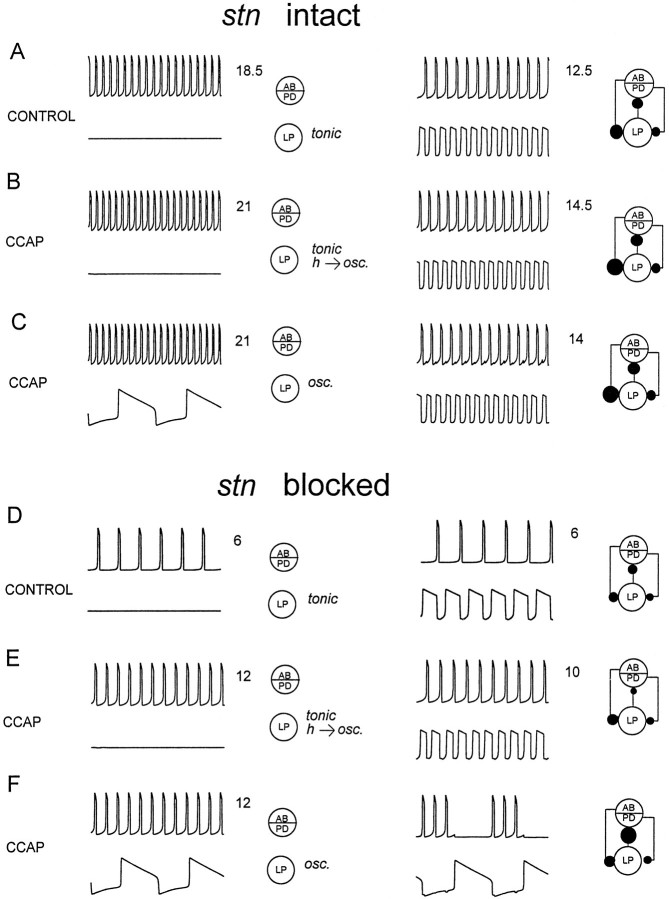
To gain further insight into the factors that might explain which conditions determine when CCAP applications increased the intensity of the pyloric rhythm without producing mode switches, and which conditions facilitate the CCAP-induced mode switch, we constructed a simple mathematical model. This model was studied in six different parameter regimes, chosen to represent the effects of anterior inputs and CCAP. The left panels of Figure 10 show the behavior of the isolated neurons, and the right panels of Figure 10show the behavior of the networks formed from these neurons. The AB/PD group was an oscillator the frequency and strength of which were varied to simulate the effects of anterior inputs and CCAP on the frequency and strength of the AB/PD oscillation. The LP neuron was modeled in three conditions: (1) tonically firing and unable to generate oscillations, (2) tonically firing but able to oscillate if hyperpolarized, and (3) slowly oscillatory. This oscillatory mode had the property that the duration of its hyperpolarized phase depended on the duration of its depolarized phase. That is, if the neuron remained depolarized for a long plateau, it required more recovery time before it could again depolarize into another plateau. This was done because many Ca2+ currents involved in sustained plateaus show voltage-dependent inactivation, and because Ca2+-dependent K+ currents that would retard a second burst would be more fully activated by a long burst than by a short one.
Fig. 10.
Mode switches can result from the interaction of fast and slow oscillators. The model neurons are described in Materials and Methods. In each panel, the left panel shows the behavior of the uncoupled cells, and theright panel shows the behavior of the coupled cells. Inhibitory synapses are shown as filled circles, the size of which was scaled to represent the actual strengths of the inhibitory synaptic conductances. The AB- and LP-evoked synapses are fast, and the PD-evoked synapse is slow (Materials and Methods). Thenumbers after each trace are the number of cycles depicted, so that it is possible to see easily the changes in frequency. A, D, The LP neuron was modeled as tonically active (at a constantly depolarized state), and would not generate slow oscillations in response to hyperpolarizing current. B, E, The LP neuron was tonically active with no imposed current, but would slowly oscillate if constant hyperpolarizing current was applied. C,F, The LP neuron was a slow oscillator, with no external current applied. Parameter values are listed in Table 1.
For simplicity, in both model neurons, the spike-generating mechanisms were ignored, and we concentrated on the envelopes of the voltage traces. Because these neurons release transmitter as a graded function of membrane potential, and graded transmission is thought to play the major role in pattern generation (Graubard et al., 1980, 1983; Johnson and Harris-Warrick, 1990; Johnson et al., 1995), this allowed us to model simply the network oscillations. Changes in oscillation amplitude were modeled by simply increasing the strength of the synaptic conductance, because this again is a direct consequence of graded transmitter release (Graubard et al., 1980, 1983; Johnson and Harris-Warrick, 1990, Johnson et al., 1995). The model neurons were connected with reciprocal inhibitory connections. In the drawings that describe the circuit configurations, chemical inhibitory synapses are shown as filled circles. The sizes of the filled circles are directly scaled to indicate the actual sizes of the synaptic currents used in the network simulations. Because both the AB and PD neurons inhibit the LP neuron, but the AB-evoked inhibition is rapid and the PD-evoked inhibition is slow (Eisen and Marder, 1982; Marder and Eisen, 1984), these connections were modeled separately, with different time courses.
Figure 10A is intended to simulate the pyloric rhythm with the stn intact, in the absence of CCAP. Here the isolated PD/AB oscillator was rapid, and the isolated LP neuron was modeled as tonically firing but not oscillatory. When these models were coupled together, a normal alternating pattern of activity was produced. The frequency of this rhythm was slower than that of the isolated oscillator. To simulate the effects of CCAP with the stn intact, two cases were considered. In the first case (Fig. 10B), the frequency of the isolated AB/PD neuron was modestly increased and the strength of the IPSPs evoked by the AB/PD group was also modestly increased. The parameters of the LP neuron (Table 1) were modified such that it was tonically firing in isolation but would be oscillatory if it were strongly hyperpolarized. When these neurons were coupled together, a normal alternating pattern of activity was produced at a lower frequency than that of the isolated fast oscillator.
Table 1.
Parameter values for the simulations shown in Figure10
| Parameter | IAP | sln | g1LP | a1 | a2 | gsyn |
|---|---|---|---|---|---|---|
| A left | 0 | 6.0 | 0.9 | 0 | 0 | 0 |
| A right | 0 | 6.0 | 0.9 | 0.5 | 0.12 | 0.045 |
| B left | 1.0 | 6.0 | 0.86 | 0 | 0 | 0 |
| B right | 1.0 | 6.0 | 0.86 | 0.6 | 0.135 | 0.06 |
| C left | 1.0 | 6.0 | 0.8 | 0 | 0 | 0 |
| C right | 1.0 | 6.0 | 0.8 | 0.6 | 0.135 | 0.06 |
| D left | −1.63 | 8.5 | 0.9 | 0 | 0 | 0 |
| D right | −1.63 | 8.5 | 0.9 | 0.02 | 0.06 | 0.0225 |
| E left | −1.0 | 8.5 | 0.86 | 0 | 0 | 0 |
| E right | −1.0 | 8.5 | 0.86 | 0.1 | 0.075 | 0.0375 |
| F left | −1.0 | 8.5 | 0.8 | 0 | 0 | 0 |
| F right | −1.0 | 8.5 | 0.8 | 1 | 0.075 | 0.0375 |
Figure 10C shows the case in which the LP is spontaneously oscillatory. The AB/PD neuron is the same as that in Figure10B. Note that with the AB/PD strongly oscillatory, the strength of the IPSP that they evoke is sufficient to terminate the LP burst. Therefore, although the intrinsic period of the LP is much longer than that of the PD/AB, it can still follow the oscillator, and the normal pattern persists.
To simulate the effect of blocking or cutting the stn (Fig.10D), the starting frequency of the AB/PD burst was decreased to approximately one-third of that in Figure10A (Table 1), and the synaptic strength decreased accordingly. The LP was modeled as tonically firing. When these neurons were coupled, the normal pattern of alternation was seen, with a frequency one-half that seen in Figure 10A. Figure10, E and F, models the effect of applying CCAP with the front end off. In Figure 10, E and F, the effects of CCAP on the AB/PD oscillator were modeled by increasing the frequency and strength of its oscillation. In Figure10E, the LP was tonically firing in isolation but would generate slow oscillations if strongly hyperpolarized. Under these conditions, and if the IPSP from LP to AB/PD was weak, the normal pattern of alternation was produced. In Figure 10F, the LP neuron was a slow oscillator in isolation, and the LP to AB/PD inhibition was strong. At this time the altered mode was produced. This altered mode depended on the ability of the LP to inhibit the AB/PD neuron group, and thus silence it during the active phase of the LP neuron. This allows the LP neuron to have a long active phase, and therefore a long silent phase. The inhibition of the AB/PD group could be accomplished by increasing the LP to AB/PD inhibition (as in Fig.10F) or by changing the properties of the AB/PD oscillation to make it easier to suppress (not shown).
DISCUSSION
A large number of neuroactive substances are known to modulate the motor patterns produced by the stomatogastric nervous system (Marder and Hooper, 1985; Harris-Warrick and Marder, 1991;Harris-Warrick et al., 1992; Marder and Weimann, 1992). Unlike most of the substances thus far known to modulate STG motor patterns, CCAP is not present in projection neurons that deliver the peptide directly to the STG neuropil. Rather, CCAP is released from neurosecretory structures such as the pericardial organs and therefore must reach the STG neuropil hormonally (Stangier et al., 1988; Christie et al., 1995). Because the pericardial organs release substances close to the heart, and the STG is found in the artery directly anterior to the heart, substances released by the pericardial organs are likely to reach the STG rapidly.
Biochemical studies in Carcinus maenas suggest that the release of only 1% of the CCAP in the pericardial organs would raise the bulk hemolymph concentration to more than 10−10m (Stangier et al., 1988), indicating that local concentrations significantly greater than 10−10m are likely to exist transiently. The threshold for CCAP in the studies reported here was in the 10−10m range, both for actions on the STG motor patterns and on the musculature. Therefore, we expect that circulating CCAP levels are likely to influence both the motor patterns produced by the STG and the movements evoked by these motor patterns. Obviously, the higher concentrations we used here were useful to characterize the CCAP responses, although it is unlikely that circulating CCAP levels would reach those concentrations, even transiently. However, it is possible that in the animal, other modulatory substances could act synergistically with CCAP, and that the effective CCAP thresholds and actions could be conditioned by other circulating or neurally delivered modulatory substances. This kind of enhancement of the action of one peptide by another is seen in Dickinson et al. (1997), demonstrating the enhancement of synaptic potentials in the stomatogastric nervous system.
We show here that CCAP alters both the motor patterns produced by the STG and the gain of the motor neuron to movement transfer function. CCAP is not unique in this; many other modulatory substances, including dopamine, serotonin, octopamine, proctolin, allatostatin, and FLRFamide-like peptides also have actions both on the pattern generating circuitry within the STG (Harris-Warrick et al., 1992;Marder and Weimann, 1992; Skiebe and Schneider, 1994) and on one or more of the neuromuscular junctions of the stomach (Lingle, 1981;Meyrand and Marder, 1991; Jorge-Rivera and Marder, 1995, 1996). However, in crabs, CCAP is unique in that it is only hormonally delivered to both its peripheral and central targets. From this, it is perhaps fair to argue that circulating levels of CCAP are likely to modify coordinately the STG motor patterns and to upregulate the gain of some of the neuromuscular junctions of the same motor neurons, the activity of which is enhanced by CCAP. Figure 7 shows clearly that the increased number of LP spikes/burst would, by itself, increase movement in the LP-innervated muscles, and that this is likely to be even further enhanced by the peripheral actions of CCAP. In this context, it would be interesting to determine how many and which of the approximately 40 muscles of the crab stomach are regulated by CCAP, to determine whether it acts to increase the general tone and strength of the whole musculature, or whether it selectively targets those muscles innnervated by motor neurons that are activated strongly in the peptide.
Although there is now an extensive literature documenting the presence of CCAP-like immunoreactivity in a large number of arthropod species (Cheung et al., 1992; Keller, 1992; Davis et al., 1993; Furuya et al., 1993; Lehman et al., 1993; Dircksen, 1994; Trube et al., 1994;Breidbach et al., 1995; Groome and Lehman, 1995; Würden and Homberg, 1995), the physiological actions of CCAP have been considerably less intensively studied. Although CCAP was initially named because of its cardioexcitatory actions on semi-isolated heart preparations of the crab C. maenas (Stangier et al., 1987), not all crustacean hearts seem to be sensitive to CCAP (McGaw et al., 1995). Moreover, the few physiological studies that are now available show that CCAP is likely to act on numerous other target organs, such as the retina (Gaus and Stieve, 1992) and midgut (Groome and Lehman, 1995), and now the STG and associated stomach muscles. Preliminary experiments studying the effects of CCAP injections into intact and behaving crayfish (Nieβen et al., 1995; B ohm et al., 1996) show that CCAP accelerates the heartbeat, ventilation, and pyloric rhythm, and can initiate the gastric rhythm. Because CCAP is found in a number of neurons in the crustacean nervous system, future work will almost certainly show that it functions as a neurally released neuromodulator, as well as a hormone.
At high concentrations, CCAP can produce an interesting mode switch, which we account for on the basis of a variable set of interactions between fast and slow oscillators. We speculate that the mode switch described here for the LP neuron may aid in coordinating stomach movements needed to move food from one area of the foregut to another. It is not clear whether this mode switch is representative of the actions of CCAP in the intact animal, but future endoscopic investigations should illuminate this point. Nonetheless, it raises a number of interesting issues about the interactions of oscillators with different properties on network dynamics. Similar looking switches can be produced by a variety of biophysical mechanisms (e.g., LoFaro et al., 1994). Our simple model was designed to capture the spirit of the biological data reported here. Although a significant body of theoretical literature is accumulating on the action of coupled oscillators in networks (Kopell, 1988; Wang and Rinzel, 1992; Skinner et al., 1994; Somers and Kopell, 1995; Marder and Calabrese, 1996), the bulk of this literature deals with networks formed from similar oscillators coupled in various architectures. Much less theoretical work has been done modeling oscillatory networks in which dissimilar neurons are coupled (LoFaro et al., 1994). The simulations included in this paper illustrate that the question, “Which neuron is most critical for controlling the frequency of the pyloric rhythm (or, for that manner, any other similar rhythmic circuit output)?” is difficult to answer. These simulations support the contention that different neurons are dominant in setting the frequency of the pyloric rhythm under different conditions, and that modulation, such as that provided by CCAP, may shift the primary pacemaker from one locus of control to another.
The simulations shown in Figure 10 are consistent with the interpretation that when the AB/PD group is strongly oscillatory, the normal pyloric rhythm will result, regardless of whether the LP neuron is tonically active or oscillatory. On the other hand, if the AB/PD group is only weakly oscillatory, and the LP neuron is strongly oscillatory, then the altered mode of activity will result. In the simulations in Figure 10, the LP oscillator had the property that the duration of the plateau phase determined the duration of the LP silent phase, so that if the AB/PD were unable to inhibit the LP plateau, then the LP silent phase would be long, allowing the AB/PD to burst several times during that silent phase. Thus, in this scenario, the LP neuron in CCAP was essentially identical with or without the stn blocked, but the difference in the behavior of the network comes from the strength of the oscillation in the AB/PD. It is not biologically implausible to assume that the LP neuron can recover from inhibition more rapidly if it is depolarized for a short time, but has a longer interburst interval if depolarized for a longer period of time. This could occur with either a Ca2+-activated K+ current or a voltage-dependent Ca2+ current that requires hyperpolarization to recover from inactivation.
The mechanism used in Figure 10 to account for the mode switch seen in high CCAP concentrations is not the only one that can do so. In other simulations (not shown), we obtained a similar mode switch by directly changing a parameter (gCa), thus lengthening the silent period of the LP, without the Ca2+-activated K+-like current. In both cases, the mode switch depended on the LP to AB/PD synapse being strong enough to shut down the AB/PD during the active phase of LP, and on a long LP silent phase. In the simulations shown in Figure 10, the LP is the same in both stn blocked and unblocked; removing the effects of the anterior inputs is modeled by changing synaptic strengths and the frequency of the AB/PD group. Alternatively, it is possible that the oscillatory properties of the LP neuron are different in the blocked or unblocked stn, with a longer silent period when the stn is blocked. In that scenario, CCAP would strengthen the LP to AB/PD synapse, and the alternative mechanism for the mode switch described above would produce results similar to those in Figure 10. Therefore, these simulations and their underlying assumptions make testable predictions about the oscillations that the LP generates under different conditions, and the role of these in network behavior. In particular, it will be crucial to determine how the period and interburst interval of the LP neuron oscillation are affected by hyperpolarizing and depolarizing perturbations.
The present study is the first to document the potential role of CCAP as an important modulator of central neuronal circuits in arthropods. The action of CCAP is similar to those evoked by proctolin in that both peptides can initiate strong pyloric rhythms in quiescent preparations and that both peptides strongly activate the LP neuron (Hooper and Marder, 1984, 1987). However, high proctolin concentrations do not produce the kind of mode switches seen in CCAP. Proctolin is known to strongly activate the burst generating mechanism in the AB neuron, but does not usually induce slow oscillatory action in the LP neuron, although it greatly enhances its spike rate (Hooper and Marder, 1987;Golowasch and Marder, 1992). In contrast, CCAP seems less effective than proctolin in activating the AB neuron burst, and more effective in eliciting slow bursts in the LP neuron. Thus, although a casual inspection might call the actions of CCAP and proctolin “redundant,” the actual dynamics of the networks in the two peptides are likely to be different, with the proctolin-activated network more dependent on strong oscillatory properties in the AB neuron, and the CCAP-activated network more dependent on strong rebound and oscillatory properties in the LP neuron.
Footnotes
This research was funded by National Institutes of Health Grants NS17813 (E.M.) and MH47150 (N.K.) and the Human Frontier Science Program Organization. J.C.J.-R. was the recipient of a Ford Foundation Dissertation Fellowship, and C.S. was the recipient of a CONACyT-Fulbright Fellowship. We gratefully acknowledge the W. M. Keck Foundation for support.
Correspondence should be addressed to Dr. Eve Marder, Volen Center, Brandeis University, Waltham, MA 02254.
Dr. Weimann’s present address: Department of Biological Sciences, Stanford University, Stanford, CA 94305.
Dr. Skiebe’s present address: Institut für Neurobiologie, Freie Universität Berlin, D-14195 Berlin, Germany.
REFERENCES
- 1.Blitz DM, Christie AE, Marder E, Nusbaum MP. Distribution and effects of tachykinin-like peptides in the stomatogastric nervous system of the crab, Cancer borealis. J Comp Neurol. 1995;354:282–294. doi: 10.1002/cne.903540209. [DOI] [PubMed] [Google Scholar]
- 2.Bohm H, Nieβen H, Hinterkeuser S, Heinzel HG. Modulation of vegetative rhythms in intact crayfish. Proc German Physiol Soc Meet. 1996;88.1:38. [Google Scholar]
- 3.Breidbach O, Dircksen H, Wegerhoff R. Common general morphological pattern of peptidergic neurons in the arachnid brain: crustacean cardioactive peptide-immunoreactive neurons in the protocerebrum of seven arachnid species. Cell Tissue Res. 1995;279:183–197. doi: 10.1007/BF00300703. [DOI] [PubMed] [Google Scholar]
- 4.Cheung CC, Loi PK, Sylwester AW, Lee TD, Tublitz NJ. Primary structure of a cardioactive neuropeptide from the tobacco hawkmoth, Manduca sexta. FEBS Lett. 1992;313:165–168. doi: 10.1016/0014-5793(92)81436-p. [DOI] [PubMed] [Google Scholar]
- 5.Christie AE, Skiebe P, Marder E. Matrix of neuromodulators in neurosecretory structures of the crab, Cancer borealis. J Exp Biol. 1995;198:2431–2439. doi: 10.1242/jeb.198.12.2431. [DOI] [PubMed] [Google Scholar]
- 6. Cohen AH, Rossignol S, Grillner S. Neural control of rhythmic movements in vertebrates. 1988. Wiley; New York: 1988. [Google Scholar]
- 7.Coleman MJ, Nusbaum MP. Functional consequences of compartmentalization of synaptic input. J Neurosci. 1994;14:6544–6552. doi: 10.1523/JNEUROSCI.14-11-06544.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Coleman MJ, Nusbaum MP, Cournil I, Claiborne BJ. Distribution of modulatory inputs to the stomatogastric ganglion of the crab, Cancer borealis. J Comp Neurol. 1992;325:581–594. doi: 10.1002/cne.903250410. [DOI] [PubMed] [Google Scholar]
- 9.Coleman MJ, Meyrand P, Nusbaum MP. Presynaptic inhibition mediates a switch between two modes of synaptic transmission. Nature. 1995;378:502–505. doi: 10.1038/378502a0. [DOI] [PubMed] [Google Scholar]
- 10.Davis NT, Homberg U, Dircksen H, Levine RB, Hildebrand JG. Crustacean cardioactive-immunoreactive peptide in the sphinx moth, Manduca sexta. J Comp Neurol. 1993;338:612–627. doi: 10.1002/cne.903380410. [DOI] [PubMed] [Google Scholar]
- 11.Dickinson PS, Fairfield WP, Hetling JR, Hauptman J (1997) Neurotransmitter interactions in the stomatogastric system of the spiny lobster: one peptide alters the response of a central pattern generator to a second peptide. J Neurophysiol, in press. [DOI] [PubMed]
- 12.Dircksen H (1994) Distribution and physiology of crustacean cardioactive peptide in arthropods. In: Perspectives in comparative endocrinology. pp 139–148. National Research Council of Canada.
- 13.Dircksen H, Keller R. Immunocytochemical localization of CCAP, a novel crustacean cardioactive peptide, in the nervous system of the shore crab, Carcinus maenas L. Cell Tissue Res. 1988;254:347–360. [Google Scholar]
- 14.Eisen JS, Marder E. Mechanisms underlying pattern generation in lobster stomatogastric ganglion as determined by selective inactivation of identified neurons. III. Synaptic connections of electrically coupled pyloric neurons. J Neurophysiol. 1982;48:1392–1415. doi: 10.1152/jn.1982.48.6.1392. [DOI] [PubMed] [Google Scholar]
- 15.Furuya K, Liao S, Reynolds SE, Ota RB, Hackett M, Schooley DA. Isolation and identification of cardioactive peptide from Tenebrio molitor and Spodoptera eridania. Biol Chem Hoppe Seyler. 1993;374:1065–1074. doi: 10.1515/bchm3.1993.374.7-12.1065. [DOI] [PubMed] [Google Scholar]
- 16.Gaus G, Stieve H. The effect of neuropeptides on the ERG of the crayfish Orconectes limosus. Z Naturforsch. 1992;47:300–303. doi: 10.1515/znc-1992-3-421. [DOI] [PubMed] [Google Scholar]
- 17.Getting PA. Emerging principles governing the operation of neural networks. Annu Rev Neurosci. 1989;12:185–204. doi: 10.1146/annurev.ne.12.030189.001153. [DOI] [PubMed] [Google Scholar]
- 18.Golowasch J, Marder E. Proctolin activates an inward current whose voltage-dependence is modified by extracellular Ca2+. J Neurosci. 1992;12:810–817. doi: 10.1523/JNEUROSCI.12-03-00810.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Graubard K, Raper JA, Hartline DK. Graded synaptic transmission between spiking neurons. Proc Natl Acad Sci USA. 1980;77:3733–3735. doi: 10.1073/pnas.77.6.3733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Graubard K, Raper JA, Hartline DK. Graded synaptic transmission between identified spiking neurons. J Neurophysiol. 1983;50:508–521. doi: 10.1152/jn.1983.50.2.508. [DOI] [PubMed] [Google Scholar]
- 21.Groome JR, Lehman HK. Characterization of crustacean cardioactive peptide-like immunoreactivity in the horseshoe crab, Limulus polyphemus. J Comp Neurol. 1995;357:36–51. doi: 10.1002/cne.903570105. [DOI] [PubMed] [Google Scholar]
- 22.Harris-Warrick RM, Marder E. Modulation of neural networks for behavior. Annu Rev Neurosci. 1991;14:39–57. doi: 10.1146/annurev.ne.14.030191.000351. [DOI] [PubMed] [Google Scholar]
- 23.Harris-Warrick RM, Marder E, Selverston AI, Moulins M. Dynamic biological networks: the stomatogastric nervous system. MIT; Cambridge, MA: 1992. [Google Scholar]
- 24.Hooper SL, Marder E. Modulation of a central pattern generator by two neuropeptides, proctolin and FMRFamide. Brain Res. 1984;305:186–191. doi: 10.1016/0006-8993(84)91138-7. [DOI] [PubMed] [Google Scholar]
- 25.Hooper SL, Marder E. Modulation of the lobster pyloric rhythm by the peptide proctolin. J Neurosci. 1987;7:2097–2112. doi: 10.1523/JNEUROSCI.07-07-02097.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Johnson BR, Harris-Warrick RM. Aminergic modulation of graded synaptic transmission in the lobster stomatogastric ganglion. J Neurosci. 1990;10:2066–2076. doi: 10.1523/JNEUROSCI.10-07-02066.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Johnson BR, Peck JH, Harris-Warrick RM. Distributed amine modulation of graded chemical transmission in the pyloric network of the lobster stomatogastric ganglion. J Neurophysiol. 1995;74:437–452. doi: 10.1152/jn.1995.74.1.437. [DOI] [PubMed] [Google Scholar]
- 28.Jorge-Rivera JC, Marder E. Convergent modulation of a neuromuscular junction by nine neurohormones. Soc Neurosci Abstr. 1995;21:2095. [Google Scholar]
- 29.Jorge-Rivera JC, Marder E. TNRNFLRFamide and SDRNFLRFamide modulate muscles of the stomatogastric system of the crab Cancer borealis. J Comp Physiol A. 1996;179:741–751. doi: 10.1007/BF00207353. [DOI] [PubMed] [Google Scholar]
- 30.Keller R. Crustacean neuropeptides: structures, functions and comparative aspects. Experientia. 1992;48:439–448. doi: 10.1007/BF01928162. [DOI] [PubMed] [Google Scholar]
- 31.Kilman V, Marder E. Ultrastructure of the stomatogastric ganglion neuropil of the crab, Cancer borealis. J Comp Neurol. 1996;374:362–375. doi: 10.1002/(SICI)1096-9861(19961021)374:3<362::AID-CNE5>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 32.Kopell N. Toward a theory of modeling central pattern generators. In: Cohen AH, Rossignol S, Grillner S, editors. Neural control of rhythmic movements in vertebrates. Wiley; New York: 1988. pp. 369–413. [Google Scholar]
- 33.Lehman HK, Murgiuc CM, Miller TA, Lee TD, Hildebrand JG. Crustacean cardioactive peptide in the sphinx moth, Manduca sexta. Peptides. 1993;14:735–741. doi: 10.1016/0196-9781(93)90106-q. [DOI] [PubMed] [Google Scholar]
- 34.Lingle C. The modulatory action of dopamine on crustacean foregut neuromuscular preparations. J Exp Biol. 1981;94:285–299. [Google Scholar]
- 35.LoFaro T, Kopell N, Marder E, Hooper SL. Subharmonic coordination in networks of neurons with slow conductances. Neural Comp. 1994;6:79–84. [Google Scholar]
- 36.Manor Y, Rinzel J, Segev I, Yarom Y (1997) Low amplitude oscillations in the inferior olive: a model based on electrical coupling of neurons with heterogeneous channel densities. J Neurophysiol, in press. [DOI] [PubMed]
- 37.Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- 38.Marder E, Eisen JS. Transmitter identification of pyloric neurons: electrically coupled neurons use different neurotransmitters. J Neurophysiol. 1984;51:1345–1361. doi: 10.1152/jn.1984.51.6.1345. [DOI] [PubMed] [Google Scholar]
- 39.Marder E, Hooper SL. Neurotransmitter modulation of stomatogastric ganglion of decapod crustaceans. In: Selverston AI, editor. Model neural networks and behavior. Plenum; New York: 1985. pp. 319–337. [Google Scholar]
- 40.Marder E, Weimann JM. Modulatory control of multiple task processing in the stomatogastric nervous system. In: Kien J, McCrohan C, Winlow W, editors. Neurobiology of motor programme selection: new approaches to mechanisms of behavioral choice. Pergamon; Oxford, UK: 1992. [Google Scholar]
- 41.Marder E, Skiebe P, Christie AE. Multiple modes of network modulation. Verh Dtsch Zool Ges. 1994;87:177–184. [Google Scholar]
- 42.Maynard DM, Dando MR. The structure of the stomatogastric neuromuscular system in Callinectes sapidus, Homarus americanus and Panulirus argus (decapoda crustacea). Philos Trans Roy Soc Lond B Biol Sci. 1974;268:161–220. doi: 10.1098/rstb.1974.0024. [DOI] [PubMed] [Google Scholar]
- 43.McGaw IJ, Wilkens JL, McMahon BR, Airiess CN. Crustacean cardioexcitatory peptides may inhibit the heart in vivo. J Exp Biol. 1995;198:2547–2550. doi: 10.1242/jeb.198.12.2547. [DOI] [PubMed] [Google Scholar]
- 44.Meyrand P, Marder E. Matching neural and muscle oscillators: control by FMRFamide-like peptides. J Neurosci. 1991;11:1150–1161. doi: 10.1523/JNEUROSCI.11-04-01150.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nieβen H, Böhm H, Heinzel HG. Modulation of vegetative rhythms in the crayfish Orconectes limosus. In: Burrows M, Matheson T, Newland PL, Schuppe H, editors. Nervous systems and behavior. Thieme Verlag; Stuttgart: 1995. p. 167. [Google Scholar]
- 47.Nusbaum MP, Marder E. A neuronal role for crustacean red pigment concentrating hormone-like peptide: neuromodulation of the pyloric rhythm in the crab, Cancer borealis. J Exp Biol. 1988;135:165–181. [Google Scholar]
- 48.Nusbaum MP, Marder E. A modulatory proctolin-containing neuron (MPN). I. Identification and characterization. J Neurosci. 1989a;9:1591–1599. doi: 10.1523/JNEUROSCI.09-05-01591.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nusbaum MP, Marder E. A modulatory proctolin-containing neuron (MPN). II. State-dependent modulation of rhythmic motor activity. J Neurosci. 1989b;9:1600–1607. doi: 10.1523/JNEUROSCI.09-05-01600.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nusbaum MP, Weimann JM, Golowasch J, Marder E. Presynaptic control of modulatory fibers by their neural network targets. J Neurosci. 1992;12:2706–2714. doi: 10.1523/JNEUROSCI.12-07-02706.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Russell DF. CNS control of pattern generation in the lobster stomatogastric ganglion. Brain Res. 1979;177:598–602. doi: 10.1016/0006-8993(79)90480-3. [DOI] [PubMed] [Google Scholar]
- 52.Skiebe P, Schneider H. Allatostatin peptides in the crab stomatogastric nervous system: inhibition of the pyloric motor pattern and distribution of allatostatin-like immunoreactivity. J Exp Biol. 1994;194:195–208. doi: 10.1242/jeb.194.1.195. [DOI] [PubMed] [Google Scholar]
- 53.Skinner FK, Kopell N, Marder E. Mechanisms for oscillation and frequency control in reciprocal inhibitory model neural networks. J Comput Neurosci. 1994;1:69–87. doi: 10.1007/BF00962719. [DOI] [PubMed] [Google Scholar]
- 54.Somers D, Kopell N. Waves and synchrony in arrays of oscillators of relaxation and non-relaxation type. Physica D. 1995;89:169–183. [Google Scholar]
- 55.Stangier J, Hilbich C, Beyreuther K, Keller R. Unusual cardioactive peptide (CCAP) from pericardial organs of the shore crab, Carcinus maenas. Proc Natl Acad Sci USA. 1987;84:575–579. doi: 10.1073/pnas.84.2.575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Stangier J, Hilbich C, Dircksen H, Keller R. Distribution of a novel cardioactive peptide (CCAP) in the nervous system of the shore crab Carcinus maenas. Peptides. 1988;9:795–800. doi: 10.1016/0196-9781(88)90124-6. [DOI] [PubMed] [Google Scholar]
- 57.Stangier J, Hilbich C, Keller R. Occurrence of crustacean cardioactive peptide (CCAP) in the nervous system of an insect, Locusta migratoria. J Comp Physiol B. 1989;159:5–11. [Google Scholar]
- 58.Trube A, Audehm U, Dircksen H. Crustacean cardioactive peptide-immunoreactive neurons in the ventral nervous system of crayfish. J Comp Neurol. 1994;348:80–93. doi: 10.1002/cne.903480104. [DOI] [PubMed] [Google Scholar]
- 59.Wang X-J, Rinzel J. Alternating and synchronous rhythms in reciprocally inhibitory model neurons. Neural Comp. 1992;4:84–97. [Google Scholar]
- 60.Weimann JM, Marder E. Switching neurons are integral members of multiple oscillatory networks. Curr Biol. 1994;4:896–902. doi: 10.1016/s0960-9822(00)00199-8. [DOI] [PubMed] [Google Scholar]
- 61.Weimann JM, Meyrand P, Marder E. Neurons that form multiple pattern generators: identification and multiple activity patterns of gastric/pyloric neurons in the crab stomatogastric system. J Neurophysiol. 1991;65:111–122. doi: 10.1152/jn.1991.65.1.111. [DOI] [PubMed] [Google Scholar]
- 62.Weimann JM, Heinzel HG, Marder E. Crustacean cardioactive peptide activation of the pyloric network in the STG of the crab, Cancer borealis. Soc Neurosci Abstr. 1992;18:1056. [Google Scholar]
- 63.Weimann JM, Marder E, Evans B, Calabrese RL. The effects of SDRNFLRFNH2 and TNRNFLRFNH2 on the motor patterns of the stomatogastric ganglion of the crab, Cancer borealis. J Exp Biol. 1993;181:1–26. doi: 10.1242/jeb.181.1.1. [DOI] [PubMed] [Google Scholar]
- 64.Würden S, Homberg U. Immunocytochemical mapping of serotonin and neuropeptides in the accessory medulla of the locust, Schistocerca gregaria. J Comp Neurol. 1995;362:305–319. doi: 10.1002/cne.903620302. [DOI] [PubMed] [Google Scholar]