How Is a Sensory Map Read Out? Effects of Microstimulation in Visual Area MT on Saccades and Smooth Pursuit Eye Movements

Abstract

To generate behavioral responses based on sensory input, motor areas of the brain must interpret, or “read out,” signals from sensory maps. Our experiments tested several algorithms for how the motor systems for smooth pursuit and saccadic eye movements might extract a usable signal of target velocity from the distributed representation of velocity in the middle temporal visual area (MT or V5). Using microstimulation, we attempted to manipulate the velocity information within MT while monkeys tracked a moving visual stimulus. We examined the effects of the microstimulation on smooth pursuit and on the compensation for target velocity shown by saccadic eye movements. Microstimulation could alter both the speed and direction of the motion estimates of both types of eye movements and could also cause monkeys to generate pursuit even when the visual target was actually stationary. The pattern of alterations suggests that microstimulation can introduce an additional velocity signal into MT and that the pursuit and saccadic systems usually compute a vector average of the visually evoked and microstimulation-induced velocity signals (pursuit, 55 of 122 experiments; saccades, 70 of 122). Microstimulation effects in a few experiments were consistent with vector summation of these two signals (pursuit, 6 of 122; saccades, 2 of 122). In the remainder of the experiments, microstimulation caused either an apparent impairment in motion processing (pursuit, 47 of 122; saccades, 41 of 122) or had no effect (pursuit, 14 of 122; saccades, 9 of 122). Within individual experiments, the effects on pursuit and saccades were usually similar, but the occasional striking exception suggests that the two eye movement systems may perform motion computations somewhat independently.

In the natural world, organisms collect and analyze sensory information for the purpose of guiding movements. For many visually guided movements, the neural pathway from sensory event to behavior begins with several processing stages in the visual cortex. Yet visual signals in the cerebral cortex differ substantially from those required to produce motor responses. Cortical sensory maps consist of arrays of neurons with different receptive field locations and different selectivities for stimulus features. Motor commands, however, encode movement parameters in a very different format: as graded firing rates specifying the muscle contractions for movements. To generate visually guided movements, cortical visual signals must be properly interpreted, or “read out,” by brain areas responsible for generating these motor commands.

How does the brain read out sensory signals to produce an appropriate behavioral response? We have explored this problem by manipulating neural activity with electrical microstimulation while rhesus monkeys made eye movements to moving visual targets. Specifically, we attempted to introduce artificial motion signals into the visual cortex by stimulating the middle temporal visual area (MT), an area known to provide visual motion signals for visually guided behavior (for review, see Newsome and Wurtz, 1988; Albright, 1993). MT neurons are tuned for both the direction and speed of visual stimuli (Dubner and Zeki, 1971; Zeki, 1974; Maunsell and Van Essen, 1983;Albright, 1984) and are organized topographically based on their direction selectivity; neurons sharing similar preferred directions are clustered together in columns (Albright et al., 1984; Malonek et al., 1994), although topography for speed tuning has not been demonstrated. We microstimulated within this velocity representation while monkeys tracked moving visual targets with their eyes. By analyzing the monkeys’ eye movements in response to this combination of visually and electrically evoked signals, we sought insight into the algorithms used for interpreting the motion map in area MT.

Tracking moving visual targets involves two kinds of eye movements: saccades, which are high velocity movements designed to bring a target of interest onto the fovea as quickly as possible; and pursuit movements, which match the direction and speed of the eyes to the direction and speed of the visual target, minimizing the slip of the target on the retina. Clearly, pursuit movements require a neural signal of target velocity to achieve their goal, whereas saccades are primarily concerned with the position of the target (Rashbass, 1961). (Throughout this article we use the term velocity in its vectorial sense, meaning both direction and speed rather than the scalar speed alone.) Because it takes time to generate a saccade, however, the saccadic system must use velocity signals as well. Just as basketball players aim passes at the future positions of moving teammates based on their current velocity, similarly the saccadic system must use a velocity signal to anticipate and compensate for ongoing target motion. This ensures that the end point of the saccade will fall on the target, not some distance behind it (Newsome et al., 1985; Ron et al., 1989; Keller and Steen Johnsen, 1990; Gellman and Carl, 1991; Schiller and Lee, 1994; Keller et al., 1996) (but seeHeywood and Churcher, 1981).

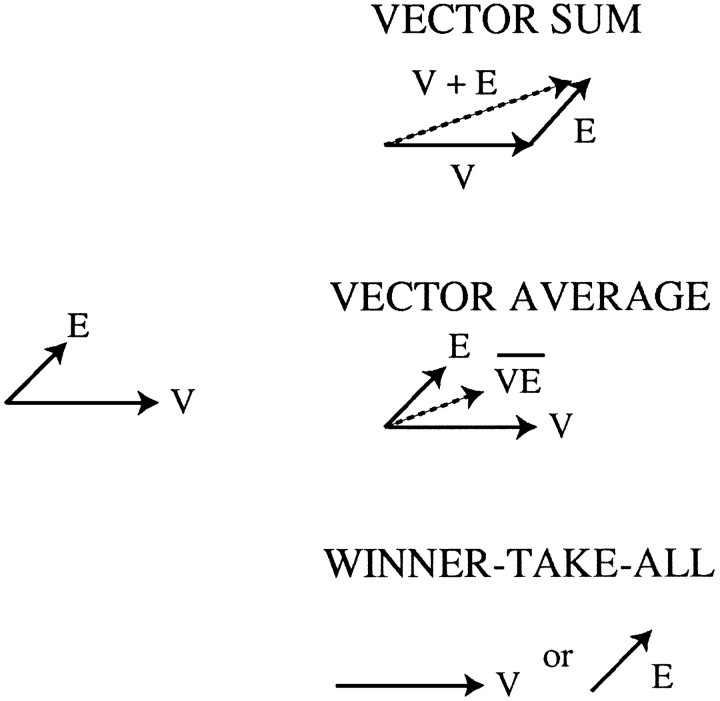
Although the motor commands ultimately generated by these two systems are quite different, both systems face the problem of computing a single velocity from an array of MT neurons having different preferred velocities and different firing rates. We considered three simple models for how a single velocity could be computed: vector summation, vector averaging, and winner-take-all. In these models, each neuron in MT can be thought of as “voting” for the vector of its preferred velocity, with the strength of its vote being proportional to its firing rate and to the synaptic weight(s) of its projection(s) to the hypothetical locus that computes a single velocity output. For vector summation, a single velocity is computed by adding together the preferred velocity vectors in proportion to the strength of the votes for each one. For vector averaging, the preferred velocities are averaged together, again in proportion to the strength of the vote for each. For winner-take-all, the winner is the single velocity vector receiving the most votes.

Any of these three mechanisms can compute the velocity of asingle visual stimulus viewed under normal conditions. If, however, an additional motion signal is introduced artificially through microstimulation, the types of errors predicted by each mechanism differ substantially. (Fig. 1, also see Fig. 7). As we will show, comparison of our data with these predictions suggests that vector averaging is the mechanism most commonly used by both the pursuit and saccadic systems for reading a velocity signal from MT.

Fig. 1.

Three algorithms for selecting a single velocity vector from two velocity signals in MT. The vectors labeledV correspond to a visual target moving rapidly to the right, whereas the vectors labeled E correspond to an artificial velocity signal produced by microstimulation in a column tuned for slower upward and rightward motion. A vector summation mechanism should cause the animal to track the target as if its velocity were the sum of the real velocity and the velocity signaled by the microstimulation. Under a vector-averaging scheme, the animal should track the target as if it were moving at the vector average of the visual and electrical velocity signals. Note that the sum and the average of two vectors have the same direction but different magnitudes (speeds). The behavior predicted by a winner-take-all mechanism depends on which velocity signal wins. If the visual signal wins, the animal should ignore the electrical velocity signal and behave normally on stimulated trials. If the electrical signal wins, the animal should ignore the real velocity of the visual target and behave as if the target were moving at the velocity signaled by the microstimulation. If the strengths of the electrical and visual signals are comparable, the animal should alternate between these two behaviors, producing a bimodal distribution of tracking velocities.

Fig. 7.

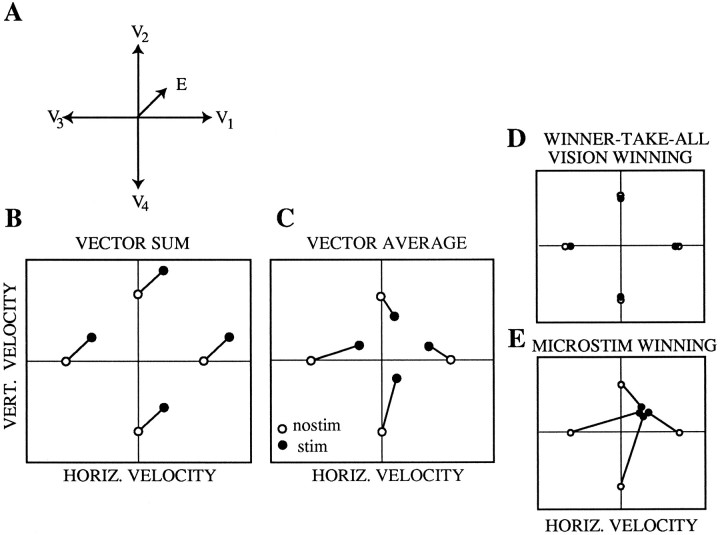
Pattern of results predicted by each hypothesis for a range of target velocities. Suppose microstimulation injects an artificial signal corresponding to slow upward and rightward motion, and four different visual target velocities are presented (up, down, left, and right) (A). B–E, Expected results for each possible mechanism. Pursuit velocity or saccadic target velocity compensation on nonstimulated trials for each visual target velocity are plotted as open circles, whereas stimulated trials for the same target velocities are plotted asfilled circles and connected to the corresponding nonstimulated data point.

Brief reports of this material have appeared previously (Born et al., 1995; Groh et al., 1995, 1996a,b).

MATERIALS AND METHODS

Monkeys and surgical procedures. One female and one male rhesus monkey (Macaca mulatta) served as subjects in these experiments. The experimental protocols were approved by the Stanford University Animal Care and Use Committee. In a sterile surgical procedure under halothane anesthesia, a coil of fine wire was implanted between the conjunctiva and the sclera for the measurement of eye position (Robinson, 1963; Judge et al., 1980). In the same procedure, stainless steel bone screws were implanted in the skull, and a fixture for immobilizing the head was attached using dental acrylic.

Behavioral training on a variety of oculomotor tasks began no sooner than 1 week after surgery. Monkeys were placed on a restricted fluid intake schedule and received water as reinforcement during training and experimental sessions. The animals were seated comfortably in a primate chair for these sessions. When behavioral training was complete, animals underwent a second surgery for implantation of a cylinder for chronic electrophysiological experiments in area MT.

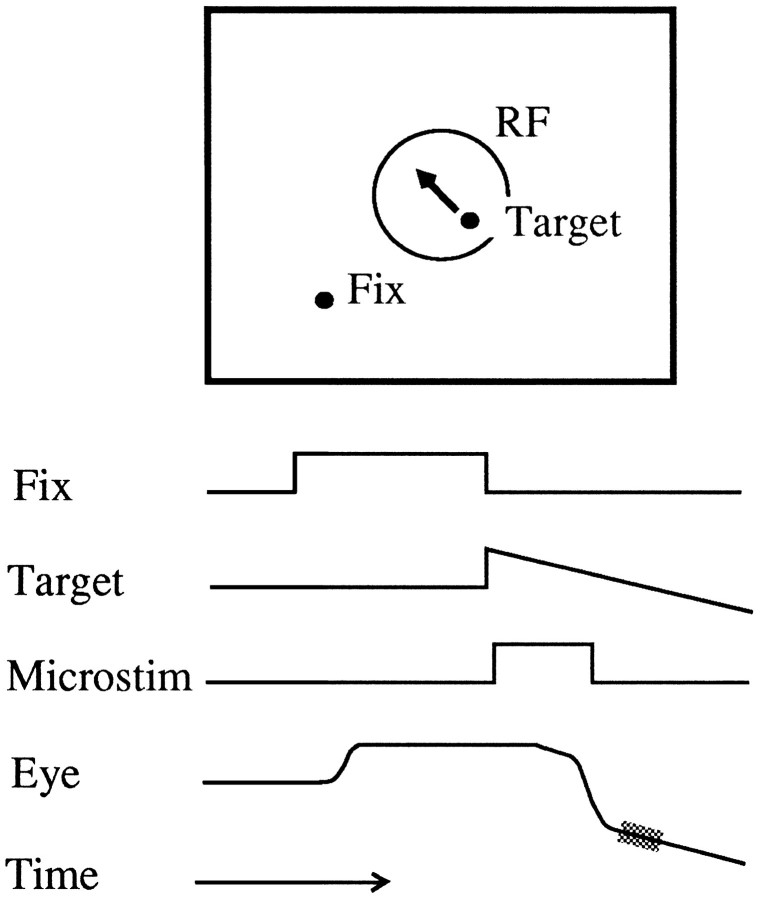
Visual stimuli and behavioral tasks. Visual stimuli were presented on a Mitsubishi monitor (21 × 27 inches, 24 inches away). Monkeys were trained to perform three types of behavioral tasks: (1) fixation trials, (2) saccade only or steptrials, and (3) combined saccade and pursuit or step–ramptrials (Fig. 2). On fixation trials, monkeys fixated within ±3° of a small red spot for 4.5–9.3 sec. This trial type was used for mapping receptive fields and assessing visual response properties of MT neurons. On step and step–ramp trials, the animal looked toward the red fixation spot for 500–1300 msec, at which time the fixation spot disappeared and a second spot appeared elsewhere in the visual field. This target could be either stationary (step trials) or it could move with a constant velocity (step–ramp trials). The animal made a saccade to this second target within 400 msec and either fixated (step trials) or pursued the target for 1.3–8 sec, depending on the speed of the target (step–ramp trials). Step trials were nearly always randomly interleaved with step–ramp trials. As described below, the step location and ramp velocity were tailored in each experiment to the receptive field location and velocity selectivity of the MT site to be stimulated. Monkeys sometimes received multiple rewards for longer fixation or tracking periods, in which case the first reward was delivered after at least 1.4 sec of tracking or fixation.

Fig. 2.

Schematic illustration of the events in the step–ramp task in space (top) and time (bottom) for a typical experiment. A monkey first looked at a fixation point, and then a moving target appeared in the receptive field of the cells at the microstimulation site. The monkey made a saccade to the position of the target and used smooth pursuit to move the eyes at the same velocity as the target. On half of the trials, a train of microstimulation (Microstim) pulses was delivered from the time of target onset until the saccade to the target. The velocity of pursuit was measured during the period 20–60 msec after the saccade to the target (shaded region). The saccadic target velocity compensation was measured by computing the difference between the end point of the saccade and the starting position of the target and dividing by the time elapsed between target onset and saccade offset.

Recording and microstimulation techniques. Standard electrophysiological recording techniques were used (for details, seeBritten et al., 1992). The electrodes entered the brain in V1 or V2 and moved anteroventrally in the sagittal plane toward MT. Transitions between gray and white matter were noted, and MT was identified based on its depth, prevalence of directionally selective visual responses, receptive field size, and visual topography. MT was easily distinguished from the neighboring middle superior temporal area MST based on the ratio of receptive field size to eccentricity, which is much lower in MT than in MST (Van Essen et al., 1981; Desimone and Ungerleider, 1986).

Once the electrode entered MT, we explored the receptive field properties of single units and multiunit clusters. While the animal maintained fixation, the borders of the receptive field were qualitatively identified using computer-generated stimuli such as moving or flashing bars or patches of moving dots. We then qualitatively assessed the direction tuning at the site using moving bars, dots, or both. This process was repeated every 100 μm until we identified a stretch of at least 200 μm in which the direction-tuning properties were similar. We then placed the electrode at or near the middle of the stretch in preparation for conducting a microstimulation experiment.^a

Before beginning microstimulation, we measured the sensitivity of the multiunit activity at the stimulation site to the speed of visual stimuli using either a patch of moving dots or a bar, usually moving at speeds of 5–30°/sec in the preferred direction. We judged the speed preferences of the site by ear at 36 experimental sites, and we stored multiunit data on speed selectivity and categorized the best speed off-line at a total of 68 sites in both monkeys. When dots were used as the visual stimulus, they were presented for 2 sec, and the average firing rate over the entire period was used as the response metric. For moving bars, the response metric was the average firing rate over a time window equal to the duration of the sweep of the bar through the receptive field. The duration of this window varied inversely, therefore, with the speed of the bar (Movshon, 1975; Orban et al., 1981). The best speed was defined as the stimulus speed that elicited the greatest response.

After collecting the speed-tuning data, we began the microstimulation phase of the experiment, stimulating through the same electrode that was used for recording. Stimulated trials were randomly interleaved with an equal proportion of nonstimulated trials and were identical to nonstimulated trials in all other respects. We used biphasic stimulating pulses (cathodal phase leading; phase length, 0.2 msec; interphase interval, 0.1 msec) at a frequency of 200 Hz (Bak Electronics pulse generator and stimulus isolation unit). In our initial series of 47 experiments, we tried several different current levels ranging from 10 to 80 μA for the purpose of choosing a standard current to use for the rest of the experiments. Based on the results of this first set of experiments, we chose 40 μA as our default current, and we used this current level for at least one block of trials for the rest of the experiments, although if time permitted we also used currents of 20 or 80 μA. When more than one current level was used, only the data for the current level that yielded the strongest effect were included in the present database.

To ensure that visually evoked and electrically induced activity in MT coincided in time, the train of pulses was turned on at, or 40 msec after, the onset of the visual tracking target. The 40 msec delay was chosen to approximate typical latencies of visual responses in MT (Maunsell and Van Essen, 1983; Maunsell, 1986; Mikami et al., 1986) (but see Raiguel et al., 1989) and was used for 102 of 122 experiments (all but the first 20). The stimulation train was terminated at the time of the saccade to the target, because the saccade removed the visual target from the receptive field of the stimulation site (Fig.2). Because of the variability in saccade reaction time, train durations could range from 60 to 360 msec but were usually between 110 and 180 msec.

The stimulation could influence the performance of the monkeys on the behavioral tracking task during the first several hundred milliseconds of target motion, after which they generally made corrective saccades and continued to track the target accurately through the completion of the trial (see Results). To ensure that the monkeys were not unduly penalized for stimulation-induced errors in their initial pursuit and saccades, we made the window around the target large enough so that the saccades brought the eyes into the window on both stimulated and nonstimulated trials for each stimulation site. It was also large enough that short duration disruptions in pursuit would not cause the eyes to leave the window. The typical target window size was ±4°, although for large microstimulation effects we made it as large as ±8°. Window sizes were the same on stimulated and nonstimulated trials. Reward was contingent on the monkeys continuing to track the target for at least an additional 900 msec after any stimulation-induced changes in saccades or pursuit. With these criteria, the frequency of aborted trials was the same on stimulated and on nonstimulated trials (nonstimulated trials, 94.8% correct; stimulated trials, 93.1% correct; t test, p> 0.05). Only successfully completed trials are included in the database.

Target position, directions, and speeds. Our database consists of 122 microstimulation experiments in which eye movement data were collected for targets moving at one or more speeds in both the preferred direction and the direction opposite to the preferred direction (the null direction). For the vast majority of these (111 of 122 experiments), data were obtained for at least two speeds in both directions. In later experiments in both monkeys, we also included target motion in directions orthogonal to the preferred–null axis (56 of 122). If time permitted, we conducted a more thorough sampling of velocity space, with as many as 25 different target velocities. Between 20 and 40 trials were conducted for each target velocity, with microstimulation occurring on a randomly selected 50% of the trials. Different sets of target velocities were often collected in separate blocks, which were combined if the effects for similar target velocities in the two blocks were reasonably stationary. Individual blocks of trials nearly always contained at least three or four target velocities, so that target velocity was unpredictable for the animal.

Targets were presented within the multiunit receptive field at the microstimulation site. To allow presentation of long ramps of target motion in different directions on our monitor, we positioned the initial fixation point at an eccentric location such that the receptive field was at the center of the monitor. For all targets, we centered the initial trajectory rather than positionwithin the receptive field. In other words, the initial positions of targets moving in different directions were offset from center of the receptive field so that the targets moved across the center and remained within the receptive field during the brief interval of microstimulation. For the first 103 experiments, targets moving at different speeds were offset by the same amount; for the last 20 experiments, targets were offset by an amount proportional to the speed. In 13 experiments, we interleaved two or more different starting locations for each target velocity to test for possible effects of target position on the microstimulation results. As will be shown in Results, the precise starting location of the target within the receptive field had little or no impact on the results over the range tested. For all experiments, targets were placed at the center of the receptive field for step trials. Because the targets were always presented in the multiunit receptive field of the microstimulation site, target location was roughly predictable from trial to trial. However, different directions and/or speeds of target motion were randomly interleaved and therefore not predictable.

Data collection and analysis. Horizontal and vertical eye position were sampled at a rate of 250 Hz and stored for further analysis. Eye velocity and acceleration were calculated off-line through software differentiation. A saccade-detecting algorithm marked the starting and ending positions of all saccades based on their acceleration profiles. Then, an error-checking routine discarded trials if any of the following conditions were met: (1) the latency of the saccade to the target was <100 msec or >400 msec; (2) the saccade to the target lasted more than 75 msec (which could happen if two saccades were erroneously lumped together by the saccade detector); (3) any nontargeting saccades were made before the saccade to the target; and (4) a corrective saccade occurred <60 msec after the saccade to the target, prematurely interrupting the epoch of pursuit after the targeting saccade. Fewer than 5% of trials were discarded based on these criteria. We tested the saccade detector and error-checking routine extensively and monitored their performance by visually inspecting selected trials and adjusting the parameters of the algorithm if necessary. The performance of the algorithm was highly reliable: on a randomly selected data set of 716 trials, we found that the saccade end points were identified correctly on 713 trials (99.6%).

To prevent any contamination of our pursuit velocity measurement by errors in saccade identification, we confined our analysis to pursuit starting 20 msec after the offset of the saccade. Our metric of pursuit was the average eye velocity over the period 20–60 msec after the saccade. Average eye velocity was calculated from the eye position samples; the total displacement in eye position across this interval was divided by the duration. We found that the microstimulation effects were largest and most stable during this period, and by 80 msec, the effects often started to decrease. Because of delays for visual processing (for review, see Lisberger et al., 1987), this epoch of pursuit was governed by the visual and electrical signals that were present before the saccade, in other words, when the visual target was in the receptive field and the microstimulation was turned on. We did not analyze pursuit initiated before the saccade, because the occurrence and magnitude of presaccadic pursuit were variable and depended on the geometry of target position and trajectory, with presaccadic pursuit being more pronounced for target motions toward the fovea.

To facilitate comparison of microstimulation on pursuit and saccades, we quantified the effects on saccades in the velocity domain. We measured the end point of each saccade and the latency from target onset until the end of the saccade. The difference between the saccade end point and the starting position of the target was then divided by the latency, yielding a measure of the velocity of target for which the saccade would have been appropriate. We refer to this metric as the saccadic target velocity compensation (Heywood and Churcher, 1981; Ron et al., 1989; Keller and Steen Johnsen, 1990; Gellman and Carl, 1991).^b Because even small systematic errors in saccade accuracy or in the calibration of the eye coil system could introduce a bias in this metric, we applied a correction for baseline saccadic target velocity compensation for each experiment. We estimated this bias by calculating the mean saccadic target velocity compensation on nonstimulated trials with stationary targets (step trials). (Under ideal conditions, with perfect calibration of the eye coil system, this quantity should be 0, because the target does not move on step trials.) We then subtracted this amount from the saccadic target velocity compensation on stimulated and nonstimulated trials for all target velocities. This correction was performed before the quantitative regression analysis described in Results and was applied to the data shown in Figures 8, 9, 13, and 14.

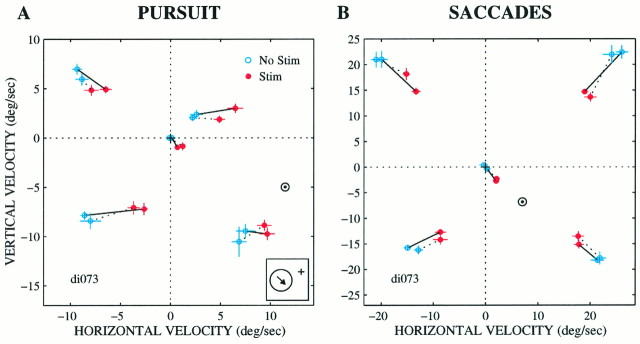
Fig. 8.

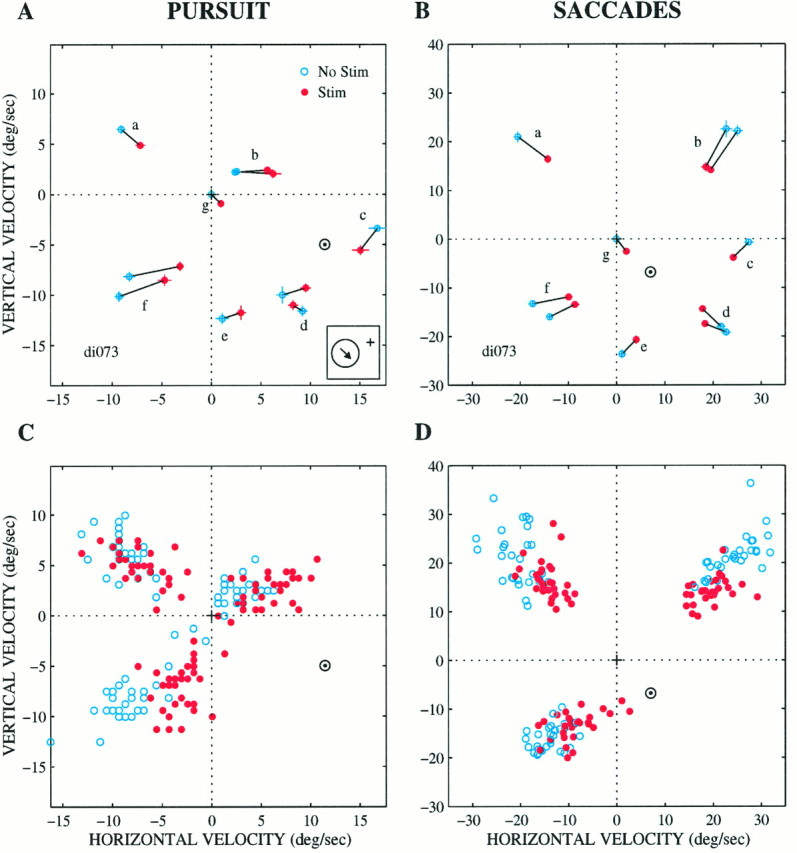
Actual pattern of microstimulation effects for a range of target velocities at one site in MT (same site as in Fig. 4).A, Plot of vertical versus horizontal velocity of pursuit for a number of different target velocities. Each point is the mean pursuit velocity for 15–20 nonstimulated (blue) or stimulated (red) trials for a particular target velocity [a, 135°, 25°/sec; b, 45°, 25°/sec (two sets)]; c, 0°, 25°/sec;d, 315°, 25°/sec (two sets); e, 270°, 25°/sec; f, 225°, 25°/sec (two sets);g, step trials, 0°/sec. A direction of 0° corresponds to straight right, 90° corresponds to straight up, etc. SE bars are shown as well. B, Saccadic target velocity compensation for the same trials in a similar fashion.C, D, Pursuit velocity and saccadic target velocity compensation on the individual trials for three of the target velocities: up right (b), up left (a), and down left (f) at 25°/sec. The velocity centroids calculated using the multivariate regression analysis (see Results for details) are plotted in each panel (⊙). The preferred direction for this site was down and to the right (inset). The current level was 40 μA. Note the different scales on the axes for the pursuit and saccade panels because of naturally occurring gain differences for pursuit and saccadic target velocity compensation.  

Fig. 9.

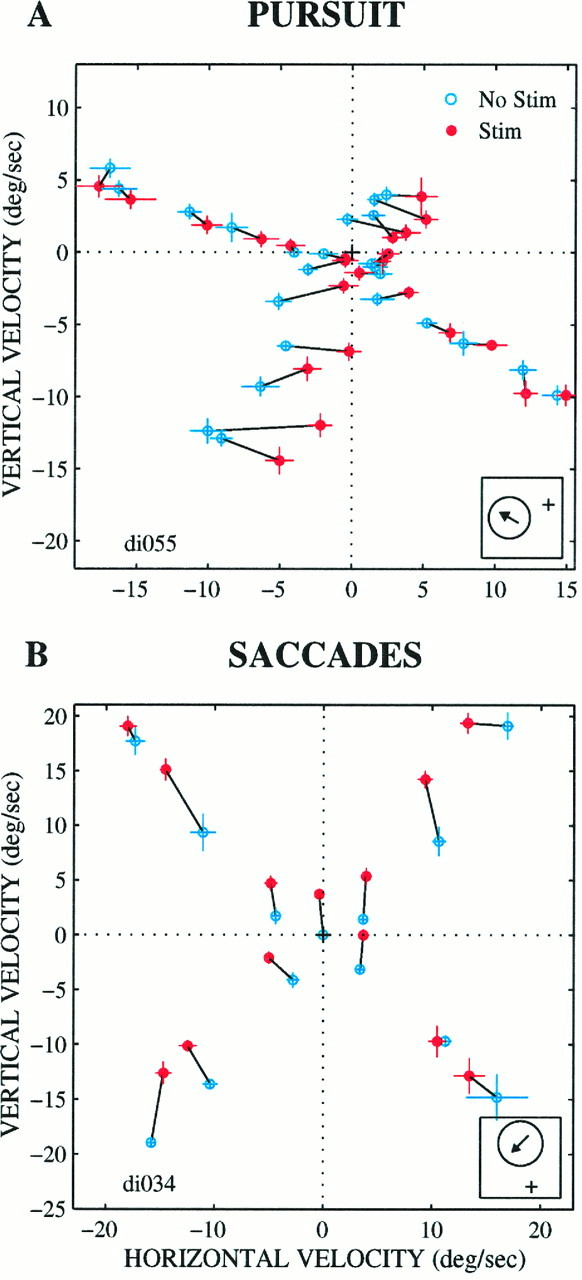
Vector summation patterns for pursuit (A) and saccadic target velocity compensation (B) at two different microstimulation sites. Conventions are similar to those in Figure 8. Insets, Receptive field locations and preferred directions for each site (A: receptive field position, 30° to the left, 10° down; receptive field diameter, 30°; preferred direction, 150°; preferred speed, 30°/sec; B: receptive field position, −1° horizontally, 4° vertically; receptive field diameter, 7°; preferred direction, 225°; preferred speed, 15°/sec). For the experiment shown in A, the target directions were 60, 150, 240, and 330°, and the target speeds were 5, 10, 15, 20, 25, and 30°/sec. For the experiment shown in B, the target directions were 45, 135, 225, and 315°. Target speeds were 0 (step trials), 5, 15, and 25°/sec. For both sites, the current level was 40 μA.

Fig. 13.

Two examples of experiments in which microstimulation affected pursuit and saccadic target velocity compensation differently. The data shown in C are the same as in Figure 9A. Conventions are the same as Figures 8, A and B, and 9. The receptive field location for the experiment in A andB was 27° to the left, 11° down, the preferred direction was 0° (inset), the receptive field diameter was 20°, and the preferred speed was 40°/sec. Targets moved in one of four directions (0, 90, 180, or 270°) at one of six speeds (5, 10, 15, 20, 25, or 30°/sec). The current level was 40 μA for both sites. Centroids (⊙) are shown in A, B, D. Because the data in C show a vector summation pattern, the magnitude of the centroid is undefined, and the direction of the centroid is shown by the arrow.

Fig. 14.

Influence of starting position of the target on the effects of microstimulation. The targets came on either in the center of the receptive field (solid lines) or offset from the center by 2.75° so that they crossed the center after about 110 msec (dotted lines). The microstimulation site is the same as in Figures 4 and 8. Conventions are similar to those in Figures 8, 9, and 13. The targets moved in one of four directions (45, 135, 225, or 315°) at 25°/sec. The current level was 40 μA.

A similar correction was necessary for the pursuit data. Both of the monkeys in our study exhibited a small amount of eye drift (average, 0.7°/sec), even when fixating stationary targets. To correct for this eye drift, we measured the average eye velocity during the 20–60 msec after the saccade on the nonstimulated step trials for each experiment. We then subtracted this velocity from the eye velocity for the same period on both stimulated and nonstimulated step and step–ramp trials for that experiment. Again, this correction was performed before the regression analysis described in Results and was applied to the data shown in Figures 8, 9, 13, and 14.

RESULTS

Influence of microstimulation on pursuit and saccadic target velocity compensation

Microstimulation could exert striking effects on both pursuit and saccadic target velocity compensation. In the next several figures (Figs. 3, 4, 5, 6), we will show individual examples of how microstimulation can alter the speed and direction of the motion estimates of these tracking eye movements. An appreciation for the raw data will set the stage for subsequent consideration of the vector summation, vector averaging, and winner-take-all hypotheses.

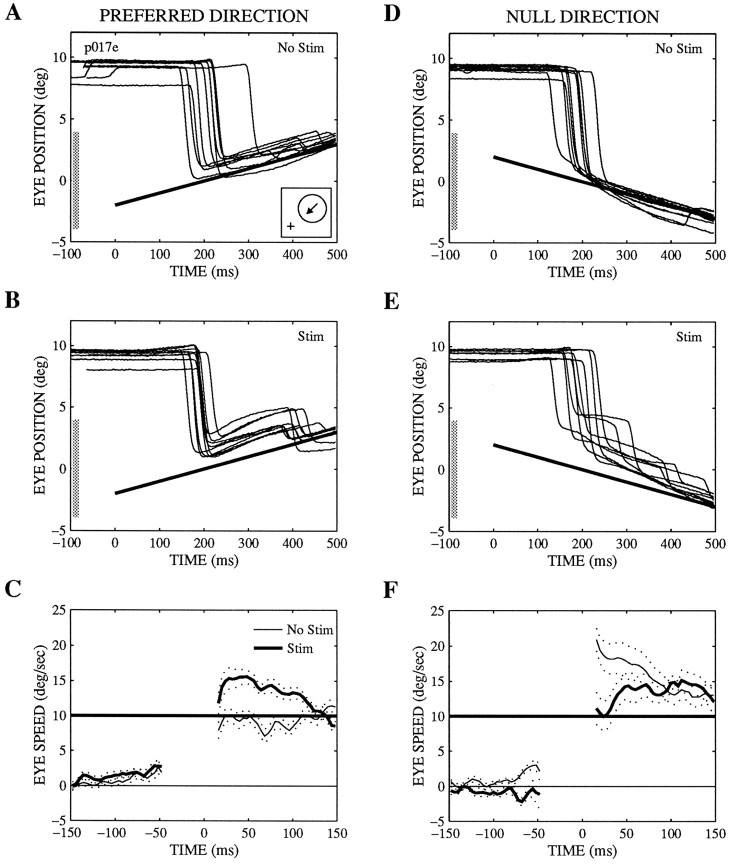
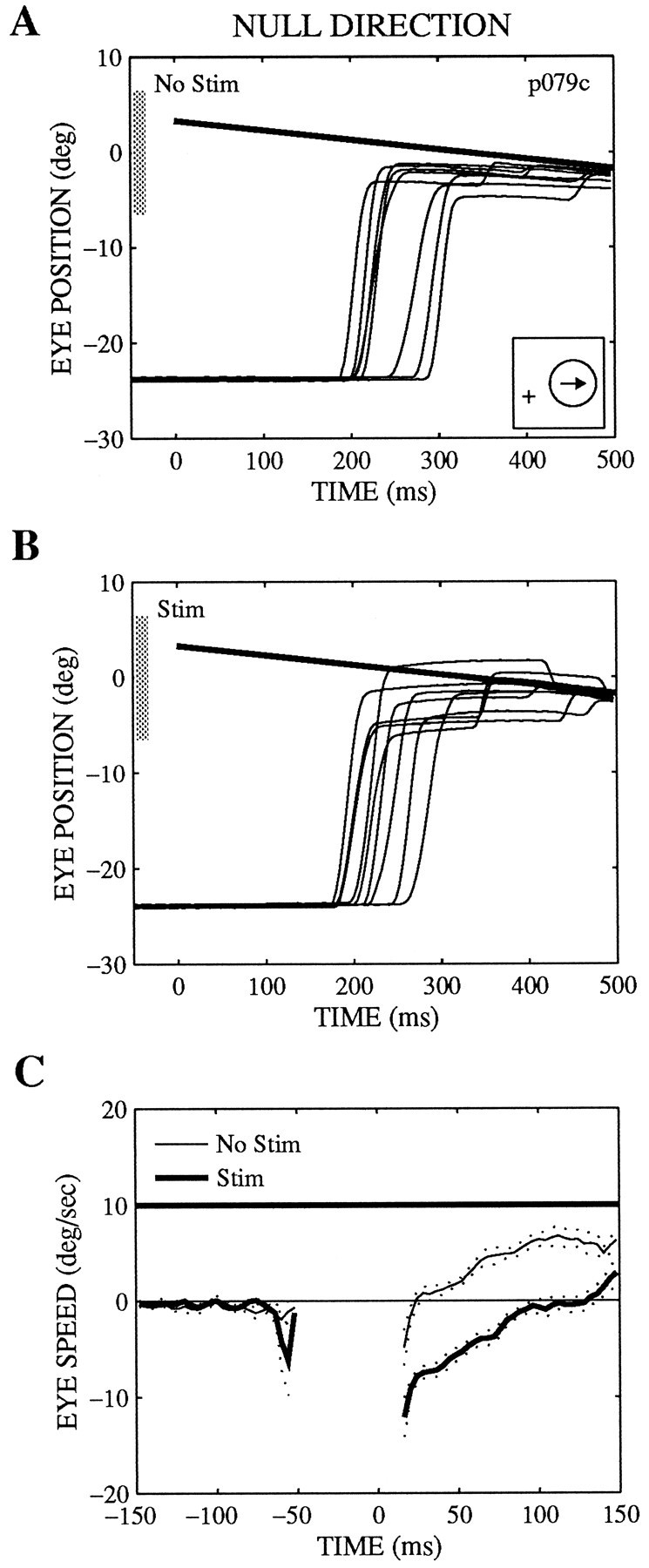
Fig. 3.

Effects of microstimulation on pursuit and saccadic target velocity compensation at one microstimulation site.A, B, D, E, Eye position versus time for targets moving in the preferred (A, B) or null (D, E) direction of the site on nonstimulated (No Stim; A, D) or stimulated (Stim; B, E) trials. The effects of stimulation on saccadic velocity compensation can be seen in these panels, whereas the effects on pursuit are best appreciated inC and F, which show averaged traces of eye speed versus time for the same trials. The dotted lines represent the SEs of the average traces. The individual trials were aligned on the end point of the saccade (time 0), and the saccade itself was excised before the average traces were computed. Note that the time axis is expanded in these panels to demonstrate more clearly the effects on pursuit during the first 20–150 msec after the saccade. [The greater speed of the initial pursuit on nonstimulated trials for null direction motion (F) than for preferred direction motion (C) reflects a naturally occurring asymmetry in pursuit speed.] The position traces show the position component along the preferred–null axis (with the preferred direction positive), whereas the speed traces show speed in the direction of target motion. The position traces (A, B, D, E) are aligned on target onset (time 0). The position and motion of the target are indicated by thethick straight lines. Inset in A,Receptive field location (circle, to the right 6.8°, up 5.6°) and the preferred direction of motion (arrow, 225°). As described in Materials and Methods, the fixation point was offset so that the receptive field was centered on the monitor (position 0). The diameter of the receptive field was 8°, as indicated by the shaded bars on the position axes of A, B, D, E. The preferred speed was not measured at this site. The current level was 20 μA on stimulated trials.

Fig. 4.

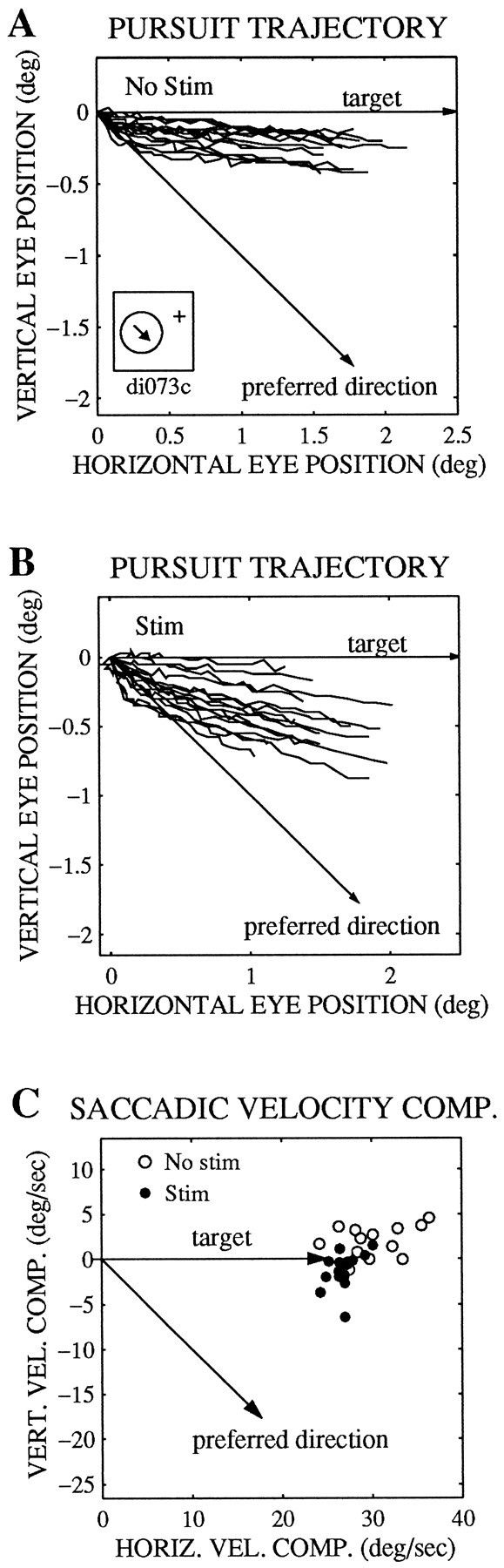
Microstimulation can alter the direction of pursuit and saccadic target velocity compensation. The trajectory of pursuit over the first 100 msec after the saccade to the target is shown for nonstimulated (No stim) trials inA and for stimulated (Stim) trials inB. The traces are aligned on the end point of the saccade in space. The saccadic target velocity compensation on stimulated (•) and nonstimulated (○) trials is shown inC. The target moved to the right at 25°/sec (arrow), and the preferred direction of this site was down and to the right (arrow). Inset inA, Receptive field location (circle, 10.8° to the left, 4.6° down) and preferred direction (arrow, 315°). The receptive field diameter was 11°, and the preferred speed was 25°/sec at this site. The current level was 40 μA on stimulated trials.

Fig. 5.

Microstimulation can cause pursuit in the direction opposite to the actual motion of the target. For all the trials shown, the target moved in the null direction. The position traces (A, B) show the eye position along the preferred–null axis, with downward deflections indicating null direction motion. C, Average eye speed in the direction of target motion as a function of time. The thick straight lines indicate the position and motion of the target.Inset in A, Location of the receptive field (circle, 24.6° to the right, 7.3° up) and the preferred direction (arrow, 0°) at this site. The receptive field diameter was 13.2° (shaded bars). The current level was 80 μA. The speed tuning of this site was not tested. No Stim, Nonstimulated trials;Stim, stimulated trials.

Fig. 6.

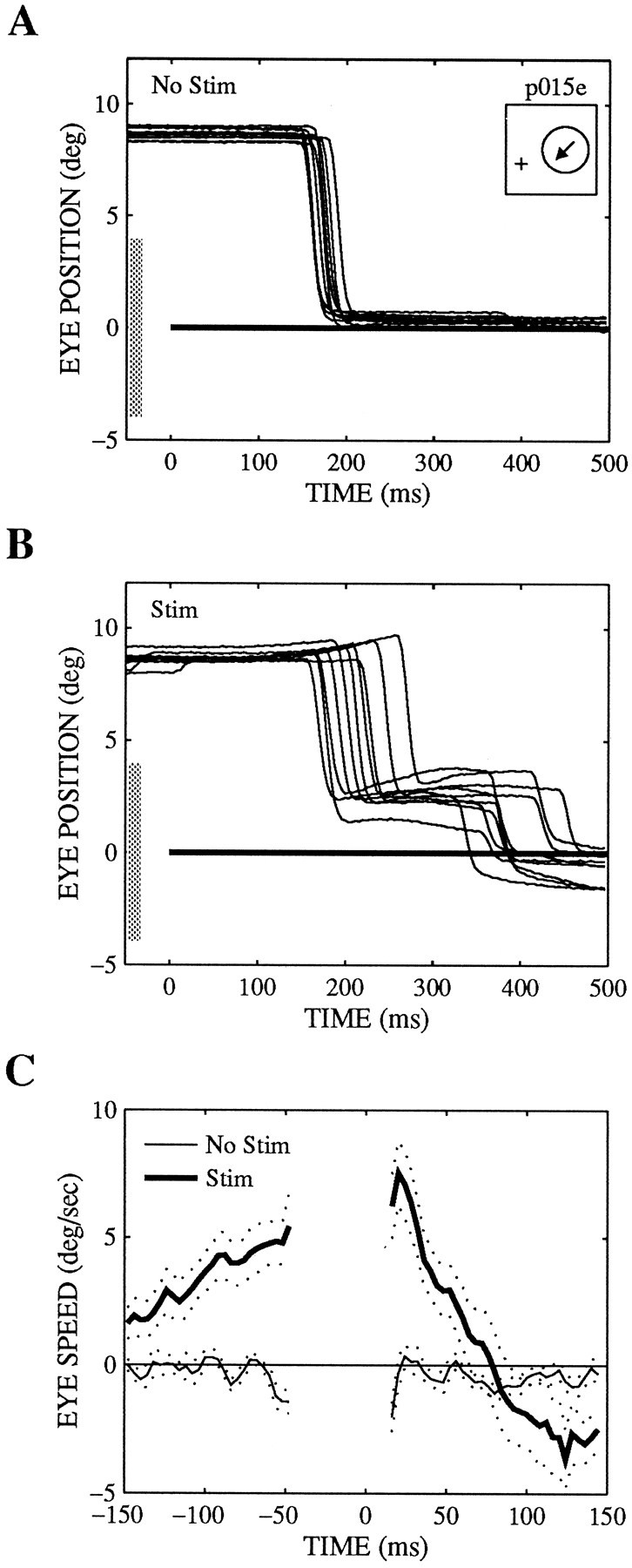
Microstimulation can elicit pursuit and saccadic target velocity compensation to stationary targets. The eye position and speed traces show the component along the preferred–null axis, with upward deflections corresponding to the preferred direction. The receptive field was located 8.6° to the right and 2.8° up, the preferred direction was 225° (inset), and the receptive field diameter was 8° (shaded bars). The current level was 80 μA. The speed tuning at this site was not tested. No Stim, Nonstimulated trials;Stim, stimulated trials.

Pursuit speed could be either increased or decreased by microstimulation, depending on the velocity of the target. Figure3 illustrates an example of such effects. In this experiment, the target “stepped” to the receptive field and moved at 10°/sec in the preferred (Fig. 3A–C) or null (Fig.3D–F) direction of the stimulated column (see Fig.3A, inset). The effects on pursuit are clearly apparent in the average velocity traces in the period immediately after the initial saccade (Fig. 3C,F). For motion in the preferred direction, microstimulation elicited an increase in pursuit speed of about 5°/sec during the 20–60 msec after the initial saccade (Fig.3C); for null direction motion, however, microstimulation caused a decrease in pursuit speed during the equivalent interval (Fig.3F). Saccades were affected in a qualitatively similar fashion; microstimulation on preferred direction trials caused the saccades to terminate slightly ahead of the target, as if the target were moving faster than it actually was (Fig. 3B). When the target moved in the null direction, microstimulation caused the end points of the saccades to fall behind the target, as if the speed of the target were systematically underestimated (Fig.3E). The animal then made secondary catch-up saccades to correct for the stimulation-induced errors on pursuit and saccadic target velocity compensation within about 200 msec of the initial saccade to the target (Fig. 3B,E).

In addition to altering the speed of pursuit and saccadic target velocity compensation, microstimulation could also alter thedirection of pursuit or saccadic target velocity compensation. Figure 4, A and B, shows plots of eye position in space, illustrating initial pursuit trajectories (first 100 msec after the saccade) for about 15 stimulated and nonstimulated trials. The pursuit target moved directly rightward, whereas the preferred direction of the stimulated column was down and to the right (Fig. 4A,B, arrows). Microstimulation shifted the pursuit trajectories toward the preferred direction even though pursuit speed was relatively unaffected for this target direction, as is evident from the roughly equivalent trajectory lengths for both stimulated and nonstimulated trials. Similarly, Figure4C shows that the target velocity compensation of the saccades shifted toward the preferred direction of the stimulated column.

In particularly striking cases, microstimulation caused the animal to pursue in a direction opposite to the actual direction of target motion. In Figure 5, for example, the target moved in the null direction of the MT column, but microstimulation caused the initial 100 msec of pursuit after the saccade to be in the preferred direction. The eye position traces are aligned, as usual, on target onset in Figure 5, A and B, whereas Figure5C shows average eye speed traces aligned on saccade offset. The “wrong way” pursuit reached a speed of approximately 7°/sec. The saccades in this particular example were only mildly affected by the stimulation.

Although microstimulation of MT did not seem to elicit pursuit or saccades in the absence of a visual target, it could elicit both pursuit and saccadic target velocity compensation when the visual target appeared but remained stationary (step trials). In the experiment shown in Figure 6, trials in which the target stepped into the receptive field but did not move were interleaved with step–ramp trials. On nonstimulated step trials, the monkey made a saccade to the target and held its eyes stationary. On stimulated step trials, however, the monkey initiated pursuit that reached a speed of about 5°/sec in the preferred direction of the stimulated column. This pursuit was apparent both before and after the saccade. Similarly, the saccade end points were shifted as though the monkey saw the stimulus moving at about 10°/sec in the preferred direction. The position (Fig. 6A,B) and velocity (Fig. 6C) traces in this figure have been rotated so that the preferred direction is reflected as upward, positive deflections.

Reading velocity from MT: models

As shown in the preceding figures, microstimulation in MT can exert striking effects on the motion computations underlying pursuit and saccadic eye movements. Careful analysis of such data can provide insight into the algorithms used by the brain to reconcile divergent motion signals and to compute a single velocity from activity within the motion map in MT. As indicated previously, we considered three possible mechanisms for producing such a velocity estimate: vector averaging, vector summation, and winner-take-all. However, these three mechanisms cannot be distinguished on the basis of measurements made at one or two target velocities as in the data shown in the preceding figures, especially if the precise direction and speed of the electrically induced velocity signal are uncertain. Rather, it is thepattern of results across several target velocities that allows us to differentiate between these mechanisms.

Figure 7 illustrates the pattern of results predicted by each of the three models. Suppose in thishypothetical experiment the tracking target moves at a constant speed in one of four different directions, as indicated by the four vectors labeled V in Figure 7A. On half of the trials, a second motion signal, E, is introduced via microstimulation. Predicted results of this experiment are shown in Fig. 7, B–E, which illustrates mean vertical eyevelocity plotted against mean horizontal eyevelocity for trials with (•) or without (○) microstimulation. The four data points for the nonstimulated (nostim) condition correspond to the velocities of the four visual targets in Fig. 7A, reflecting perfect pursuit. For the stimulated (stim) condition, the pattern of data points varies substantially for the vector sum and vector average models. If the visual and electrical velocity signals are combined according to a vector sum (Fig. 7B), the eye velocity observed on stimulated trials should change by the same amount for all four visual target velocities. If the visual and electrical signals are averaged (Fig. 7C), however, the eye velocity on the stimulated trials should shift toward the velocity encoded by the electrical signal, and the magnitude of this shift should be proportional to the difference between the visual and electrical velocity signals. Note that the direction of the change in velocity should reverse around the velocity encoded by the electrical signal.

The predictions of the winner-take-all mechanism are somewhat more complex. In this mechanism, the visual and electrically evoked velocities are evaluated separately, and the one receiving the most neural votes governs the monkey’s behavioral response. Three different outcomes can be obtained depending on the relative strength of the visual and electrical signals. If the visually evoked signal is substantially stronger, the monkey will always track the visual signal, yielding the same pattern of results on stimulated and nonstimulated trials (Fig. 7D). If the electrical signal is substantially stronger, the monkey will generate the same pursuit response on every trial regardless of the velocity of the visual target. The pursuit response will correspond to the velocity encoded by the electrical stimulus (Fig. 7E). If the two signals are roughly equal in strength, the visual stimulus will win the competition and govern the monkey’s behavioral response on a proportion of the trials, whereas the electrical signal governs behavior on the remainder. In this eventuality, plots of mean eye velocity across trials (like the hypothetical data illustrated in Fig. 7) will be similar for the vector average and winner-take-all mechanisms. These two mechanisms can be distinguished, however, by examining the distribution of pursuit responses that contribute to each data point. A vector-averaging mechanism will yield a unimodal distribution of velocities centered about the mean, whereas a winner-take-all mechanism will yield a bimodal distribution, with the two modes corresponding to the visual and electrically evoked velocity signals.

Although we have discussed the model predictions specifically in the context of pursuit responses, the same analyses and predictions are applicable to the target velocity compensation metric for the saccadic system.

Reading velocity from MT: data

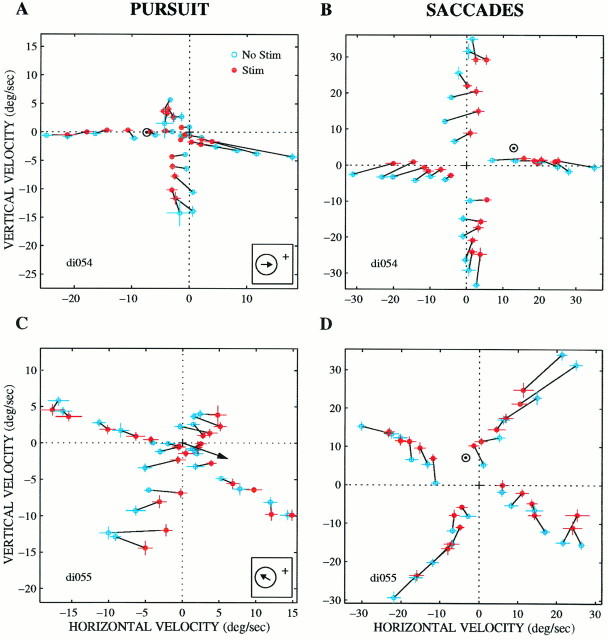
Figure 8 shows an example of the most common effect of microstimulation on pursuit (Fig. 8A) and saccades (Fig. 8B), a pattern that strongly suggests a vector-averaging mechanism. In this experiment, microstimulation shifted the animal’s behavior toward a downward and rightward velocity for both pursuit and saccades. If the target moved straight down (Fig.8A,B, e), microstimulation shifted the pursuit and saccades up and to the right, whereas if the target moved to the right (Fig. 8A,B, c, same data as in Fig. 4), microstimulation shifted pursuit and saccades down and to the left. Thus, microstimulation had the overall effect of drawing the eyes toward a velocity of about 10–12°/sec down and to the right (Fig.8A,B, ⊙). We will refer to the velocity toward which microstimulation draws the animal’s behavior as the velocitycentroid. The centroids for this site lie near the downward and rightward preferred direction of the neurons at the stimulation site (Fig. 8A, arrow).^c (The next section will explain how centroid locations were determined.)

It is important to note that the individual points in Figure 8,A and B, represent mean behavior across 10–20 trials for each target velocity. Thus the data could also be consistent with a winner-take-all mechanism if the individual data points were distributed bimodally (see preceding section). The winner-take-all interpretation is eliminated, however, by examination of the individual responses. Figure 8, C and D, show the individual responses for three of the target velocities (a, b, f). The stimulated trials form a unimodal distribution that is shifted toward the centroid. Individual trials do not form clusters around the target and centroid velocities, as would have been expected under the bimodal distribution of a winner-take-all mechanism. We never observed a plainly bimodal distribution of responses, and we therefore conclude that a winner-take-all mechanism does not operate for either pursuit initiation or saccadic target velocity compensation under the conditions tested in our experiments. A statistical analysis of the distribution of responses will be described in detail in the next section and .

Although most experiments exhibited a pattern of effects resembling vector averaging, a few produced a pattern more consistent with vector summation. Figure 9 illustrates two examples from different microstimulation sites, one for pursuit (Fig. 9A) and one for saccades (Fig. 9B). In the experiment of Figure9A, a rightward and slightly downward component was added to the pursuit response for most of the conditions tested. The direction of the microstimulation effect does not reverse within the range of velocity space tested, and there is no apparent point of convergence of the electrically evoked changes in pursuit velocity. If these data are to be explained by a vector-averaging model, the microstimulation signal must encode an exceptionally high velocity lying well outside the range tested, perhaps on the order of 100°/sec or more. The data are best accounted for by the addition of a single electrically evoked vector to each visual stimulus.

Similarly, the saccadic target velocity compensation data in Figure9B seem to reflect the addition of an upward motion vector to each visual signal. Although these data are somewhat less consistent across conditions than those in Figure 9A, there is no indication of a reversal in the direction of the stimulation effects, or even a point of convergence for the stimulation effects, within the large region of velocity space tested.

The direction of the microstimulation effect did not correspond to the preferred direction of the site in MT (arrows) for either of the experiments shown in Figure 9. In general, shifts in the null direction were surprisingly common for pursuit, although rare for saccadic target velocity compensation. We will analyze the correspondence between the preferred direction and the direction of the microstimulation effects in detail below.

Regression analysis for characterizing microstimulation effects

To characterize the microstimulation effects in an objective and quantitative fashion, we fit the data for all target velocities within a given experiment with a multivariate regression of the following form:

$$\mathrm{\Delta }\stackrel{\mathbf{⃗}}{\mathbf{V}}=\stackrel{\mathbf{⃗}}{\mathbf{C}}-g{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}},$$ Equation 1

where V⃗_ns (a vector) is the pursuit velocity or saccadic target velocity compensation on nonstimulated trials, ΔV⃗ (also a vector) is the change in velocity induced by microstimulation on matched trials,C⃗ is a vector constant, and g is a scalar gain term. ΔV⃗ was calculated from pairs of nonstimulated and stimulated trials for the same target velocity, matched in the order the trials were conducted. The derivation of this equation is explained in detail in .

This regression model was chosen because it can fit both vector averaging and vector summation patterns of effects (see ). The gain term g in the model is an indication of which type of pattern is exhibited by an individual experiment; vector summation patterns have gain terms close to 0, because the change in velocity caused by the microstimulation is basically a constant regardless of the velocity of the visual target (Fig. 7B). In contrast, the change in velocity for vector-averaging patterns depends critically on the velocity of the target (Fig. 7C), so the value ofg lies between 0 and 1. For a vector-averaging mechanism, the exact value of g corresponds to the relative weight of the microstimulation-induced velocity signal compared with the visual velocity signal. A gain of 0.5 corresponds to equal weights for the microstimulation and visual signals; higher values indicate that the electrical signal dominated, whereas lower values indicate that the visual signal dominated.

The regression model can also be used to calculate the position of the centroid in velocity space toward which microstimulation draws the monkey’s behavioral responses. This is the nonstimulated velocity for which microstimulation yields no change in eye velocity: Setting ΔV⃗ in Equation 1 to 0 and solving forV⃗, we obtain:

$$\stackrel{\mathbf{⃗}}{\mathbf{V}}=\frac{\stackrel{\mathbf{⃗}}{\mathbf{C}}}{g}.$$ Equation 2

For vector averaging, this velocity corresponds to the presumed velocity signal induced by microstimulation alone. For vector summation, the magnitude of this velocity vector, or the speed, should approach infinity, because g will be very small, but the vector will nevertheless have a meaningful direction.

Finally, the regression model provides tests of statistical significance for the microstimulation effects. Because g is a parameter that depends on which hypothesis is correct, we could not use tests of statistical significance that depend solely on this parameter (as does the correlation coefficient, for example). Instead, we tested whether the constant term was significantly different from 0 at the p < 0.05 level. Tests for significance of the regression terms are described in detail in .

Based on the statistical significance of the constant, we found that microstimulation affected smooth pursuit eye movements in 50.0% (61 of 122) and saccades in 59.0% (72 of 122) of the experiments (Table1). These experiments were classified as showingdirectional effects. Both pursuit and saccades showed directional effects in 44 experiments (36.1%). In addition to the experiments with directional effects, there were other experiments in which microstimulation caused a slowing of pursuit and/or saccadic target velocity compensation for targets moving in all directions and speeds. The constant terms (and hence the centroids) of such experiments occurred at a velocity that did not differ significantly from 0, but the gain terms were found to be significantly different from 0 [n = 47 of 122 (38.5%) for pursuit and 41 of 122 (33.6%) for saccades] when a similar test for significance (p < 0.05) was applied to this term. This type of effect has been reported by Komatsu and Wurtz (1988) in a previous study on the effects of microstimulation in MT on pursuit. This pattern is similar to the results of focal lesions in MT (Newsome et al., 1985) and may indicate that microstimulation impaired motion processing instead of injecting a systematic motion signal. For this reason, we excluded these experiments from the analyses described in succeeding sections, but we will consider this type of result further in Discussion.

Table 1.

Frequency of occurrence of the different classes of microstimulation effects

Regression parameters	Effect type	No. of experiments	%
Pursuit
C⃗ ≠ 0	Directional effect	61 /122	50.0
g ≠ 0	Vector average	55/61	90.2
g= 0	Vector sum	6/61	9.8
C⃗= 0, g ≠ 0	General slowing	47 /122	38.5
C⃗ = 0, g = 0	No effect	14 /122	11.5
Saccadic target velocity compensation
C⃗ ≠ 0	Directional effect	72 /122	59.0
g ≠ 0	Vector average	70/72	97.2
g= 0	Vector sum	2/72	2.8
C⃗= 0, g ≠ 0	General slowing	41 /122	33.6
C⃗ = 0, g = 0	No effect	9 /122	7.4

Figure 10, A and B, shows the distribution of gain terms for the experiments in which the constants differed from 0. For both pursuit and saccades, nearly all experiments had gain terms (g) that fell along a continuum between 0 and 1. For the bulk of the experiments, the gain terms were significantly different from 0 (Fig. 10, open regions). We classified these experiments as showing a vector-averaging pattern (Table 1). In a subset of the experiments, the gain terms did not differ significantly from 0 (Fig. 10, filled regions), and these experiments were classified as showing a vector summation pattern (pursuit, n = 6; saccade, n = 2).

Fig. 10.

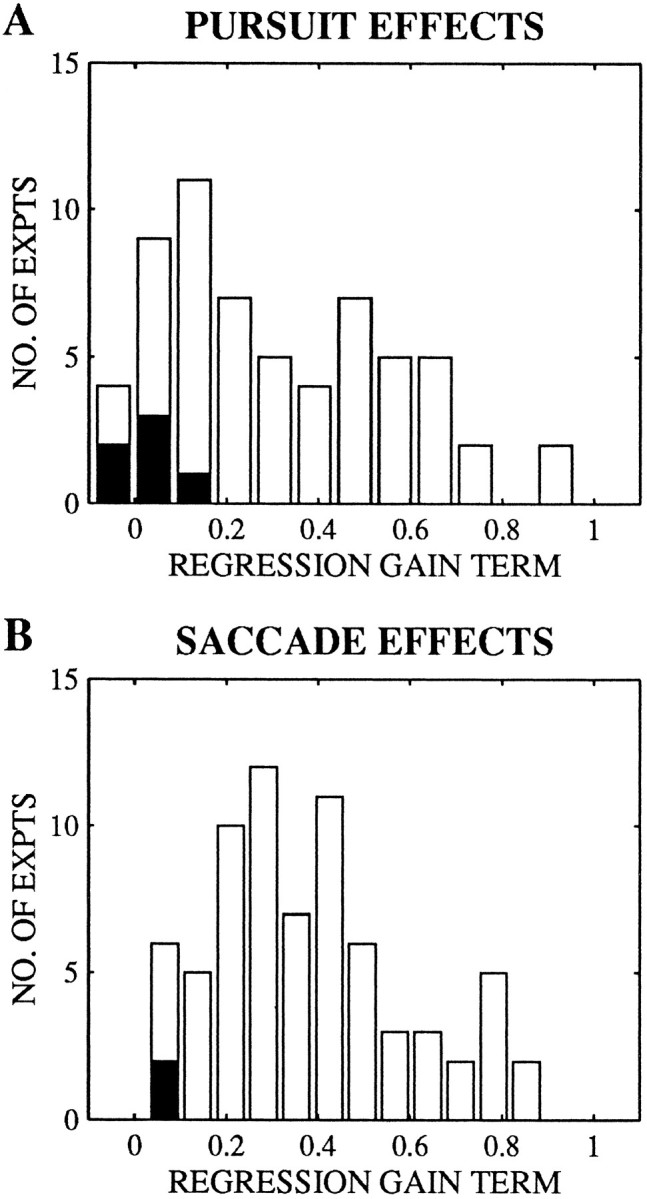
Frequency histograms of gain terms from the multivariate regression for pursuit (A) and saccadic target velocity compensation (B). Only experiments in which the constant terms differed significantly from 0 are included (n = 61 of 122 for pursuit, 72 of 122 for saccades). The filled regions of the bars indicate the experiments in which gain terms did not differ significantly from 0.

We conducted an additional statistical analysis on the experiments purportedly showing a vector-averaging pattern to ascertain whether any of these experiments might in fact have the bimodal distributions of responses indicative of a winner-take-all pattern. For each individual experiment, we compared the actual distribution of responses on stimulated trials with a unimodal distribution generated by transforming the nonstimulated trials, as described in . In no case could the unimodal distribution be rejected at thep < 0.05 level (χ²: pursuit, 0 of 41 tested; saccades, 0 of 50 tested).

Comparison of electrically evoked velocity signals to unit properties

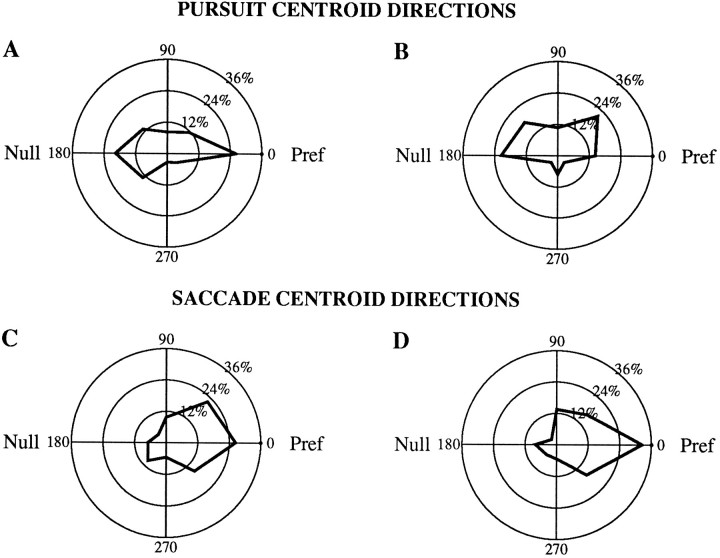
In two of the experiments shown thus far, microstimulation shifted pursuit or saccadic target velocity compensation toward thenull direction of the stimulation site rather than the preferred direction (Fig. 9). This was a surprisingly common occurrence for pursuit but relatively rare for saccadic target velocity compensation. Using the multivariate regression described above, we determined the centroid in velocity space that represented the effect of microstimulation for each experiment. Figure 11shows a polar frequency histogram of the direction of these centroids with respect to the preferred direction. For pursuit, the centroids were likely to lie along the preferred–null axis but could occur in either the preferred or null direction (Fig. 11A). For saccades, the centroids were more strongly biased toward the preferred direction rather than the null direction but were less tightly clustered around the preferred direction itself (Fig.11C). To control for the possibility that the bias of the pursuit effects to the preferred–null axis was related simply to a disproportionate use of targets moving along that axis, we examined separately the experiments that included targets moving in the orthogonal directions as well (Fig. 11B,D). Both the tendency of pursuit centroids to lie along the preferred null axis and the tendency of saccade target velocity compensation centroids to lie in the preferred direction were maintained in this subset, suggesting that these trends were not artifacts of the limited range of directions used in some experiments.

Fig. 11.

Polar frequency histograms of the distribution of the velocity centroids with respect to the preferred and null directions of the microstimulation sites. To construct each histogram, the preferred direction and velocity centroid for each site were rotated so that the preferred direction lay to the right at a direction of 0°. Thus, each bin represents the percentage of experiments in which the preferred direction and the direction of the velocity centroid differed by a given range of angles. The radial labels of the histograms indicate the percentage of sites in each bin. Only sites with directional effects (the constant terms of the multivariate regression differed significantly from 0) are included. A, Pursuit velocity centroids for all such experiments (n = 61 directional effects of 122 total experiments). B, Only the subset of experiments in which at least two target velocities that did not lie along the preferred–null axis were included (n = 28 directional effects of 55 experiments with off-axis target velocities; data from both monkeys). C, D, Corresponding data for saccadic target velocity compensation (C, n = 72 of 122; D,n = 37 of 55).

As mentioned in Materials and Methods, we measured the speed-tuning properties of the cells at the electrode tip before some microstimulation experiments. The speed of the electrically induced velocity signal was uncorrelated with the best speed of the site. We also categorized sites according to whether the cells preferred low (<15°/sec; n = 32) or higher (>20°/sec;n = 33) speeds. We found no difference in the frequency of occurrence of significant effects on either pursuit or saccades as a function of the speed-tuning properties of the site, nor was there any difference in the type of effect; the mean value of the gain term did not differ significantly as a function of the speed tuning. The lack of correlation of microstimulation effects with the speed-tuning properties of the stimulation site is perhaps not surprising, given that topographical organization for speed tuning has not been demonstrated in MT.

Comparison of effects on pursuit and saccades

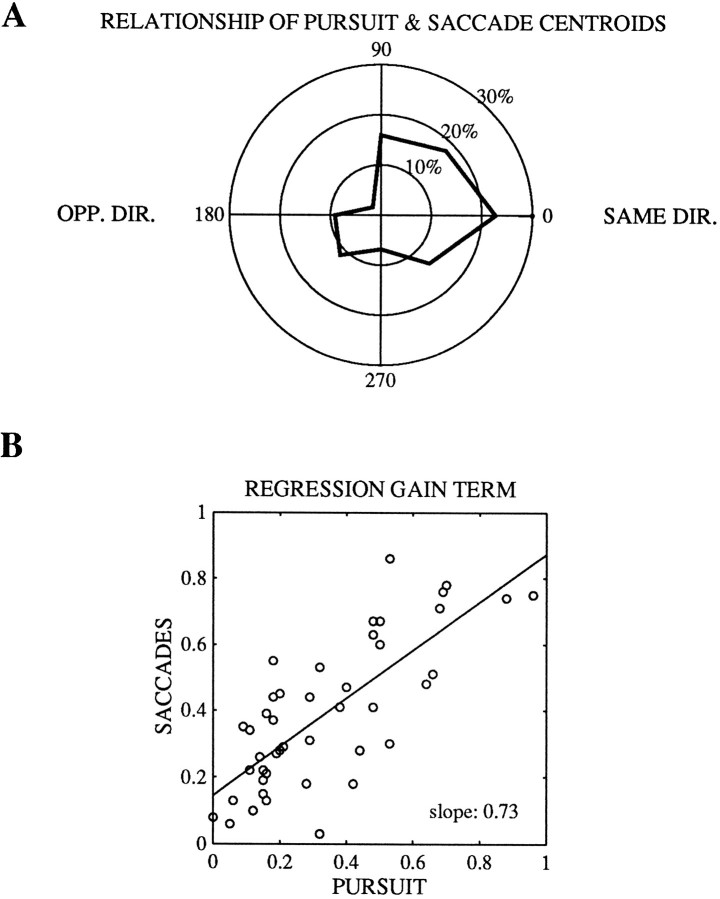
In the data presented in many of the preceding figures (Figs. 3,4, 6, 8), microstimulation affected pursuit and saccades in a qualitatively similar fashion within individual experiments. When microstimulation affected both pursuit and saccades (n= 44 of 122 experiments), we could compare the directionality of those effects using the centroids calculated from the regression analysis. The directions of the centroids for pursuit and saccadic target velocity compensation were correlated across the whole population of experiments (Fig. 12A), with the vast majority of the experiments having centroids for pursuit and saccades that were within 90° of each other. This correlation in the directions of the centroids for saccades and pursuit is about as tight as could be expected, given the fact that the pursuit centroids were best correlated with the preferred–null axis but the saccade centroids were best correlated with the preferred direction (Fig. 11). In general, the type of pattern (vector summation vs vector averaging) was similar for both pursuit and saccades within a given experiment. Figure12B shows that the gain values (g) for pursuit and saccades were correlated with one another, although there was a fair amount of scatter around the regression line (r = 0.76).

Fig. 12.

Comparison of the effects of microstimulation on pursuit and saccadic target velocity compensation in the subset of experiments in which microstimulation produced directional effects on both saccades and pursuit (constant terms differed from 0 for both;n = 44 of 122). A, Polar frequency histogram of the difference in direction between the pursuit velocity centroid and saccadic target velocity compensation centroid.B, Relationship between the gain terms of the multivariate regression model for pursuit and saccadic target velocity compensation. Only experiments in which the multivariate regression constant terms were significantly different from 0 for both pursuit and saccadic target velocity compensation are included.r = 0.76 between the saccade and pursuit gain terms.

Nevertheless, in individual experiments the effects of microstimulation on pursuit and saccadic target velocity compensation could differ strikingly (Fig. 13). For the experiment shown in Figure 13, A and B, microstimulation caused a vector-averaging pattern on both pursuit and saccadic target velocity compensation, but the locations of the centroids differed substantially. Microstimulation shifted the pursuit toward a centroid velocity of about 8°/sec in the null direction, whereas it shifted saccade target velocity compensation toward a centroid velocity of approximately 12°/sec in the preferred direction. Not only could the centroid velocities differ, but so could the basic pattern of effects; in the experiment shown in Figure 13, C and D, microstimulation caused a vector summation pattern on pursuit (same data as in Fig. 9A) but a vector-averaging pattern on saccadic target velocity compensation. Again, the directions of the effects differed as well; pursuit velocity was shifted to the right, whereas saccades were shifted toward an upward and leftward centroid velocity.

Does microstimulation mimic a position or a velocity signal?

In the experiments showing directional effects, microstimulation seemed to inject a velocity signal into MT. In theory, however, the signal might contain a position component in addition to velocity. For example, slight differences between the retinotopic locus of microstimulation and the actual position of the target might shift the end points of saccades or even affect the velocity of pursuit. In a few experiments, we tested this possibility by varying from trial to trial the starting location of targets with the same velocity. If microstimulation provided a position signal to the saccadic or pursuit systems, the direction or speed of the effect should vary as a function of the position of the target. Figure 14 shows an experiment in which the targets appeared either at the center of the receptive field (solid lines) or offset from the center by 2.75° so that the trajectory of the target crossed the center after about 110 msec (dotted lines). Microstimulation affected pursuit and saccades similarly regardless of the starting position of the target. In 11 of the 13 experiments for which we conducted this control, the directions of the saccade target velocity compensation centroids for both starting locations were within ±45° of one another; pursuit centroids were similarly aligned in 8 of the 13 experiments. Thus for both saccadic target velocity compensation and pursuit, the effects tended to be similar for both starting locations.

Effects of microstimulation on reaction times

Microstimulation could also alter the latency of saccades to the target (e.g., Fig. 6). The latency could be either shortened or lengthened. Often, effects on saccade latency occurred for some target velocities and not for others, varying with both the speed and the direction of target motion. These changes in saccade latency had no detectable effect on saccadic target velocity compensation or on the direction of pursuit. Our measurement of the speed of pursuit may have been affected in some cases, however. Because we measured pursuit during a window after the saccade to the target, a reduction in saccade latency would shift the pursuit window earlier with respect to target onset, whereas an increase in saccade latency would shift the pursuit window later. Because pursuit accelerates to its full speed over time, these latency changes could alter our measurement of pursuit speed. To control for this possibility, we repeated the population analyses shown in Figures 10, 11, 12 on the subset of experiments with little or no effects of microstimulation on saccade latency, excluding 42 experiments in which the reaction time was affected by ±40 msec for at least one target velocity. The frequency of significant effects, the correlation of the centroids with the preferred direction of the stimulation site, and the distribution of the gain terms in this subset were very similar to the results for the whole data set. We conclude that although the effects on saccade latency may have influenced our pursuit measurements for particular target velocities in individual experiments, they had little or no impact on our results as a whole.

DISCUSSION

Overview of microstimulation effects

Electrical microstimulation alters neural activity in a fashion that would not occur under normal physiological conditions. A rigid object at a particular location in space would normally have a unique velocity, and MT neurons responding to that object would represent only that single velocity vector. To differentiate between several potential neural algorithms for reading out this velocity code, we used microstimulation in an attempt to insert a second velocity vector into MT simultaneously with a visually evoked vector.

In about half of our experiments, microstimulation did seem to inject a nonzero velocity signal (directional effects). These experiments permit comparison with the predicted results of the vector-averaging, vector summation, and winner-take-all hypotheses. The pattern of stimulation-induced errors in the overwhelming majority of these experiments suggests that the pursuit and saccadic target velocity compensation pathways use a vector-averaging algorithm for extracting a single velocity signal from the distributed code for velocity in MT. Eye movements were generally biased toward a centroid in velocity space that presumably corresponds to the motion vector introduced by microstimulation. Indeed, pursuit could even be generated on trials in which the visual target was actually stationary, a finding that is particularly striking because pursuit eye movements are primarily elicited only in response to visual motion (Robinson, 1981).

A vector-averaging algorithm is quite sensible given a natural world in which objects appearing at a single retinotopic location generally have only one velocity. Computing a vector average of the preferred velocity vectors of neurons with receptive fields at the same position in space provides a rapid, accurate measurement of the velocity of an individual moving stimulus. In addition, vector averaging can provide an accurate measure of the aggregate velocity of nonrigid objects or objects that are simultaneously rotating and translating. Vector averaging has been reported in other contexts as well. A wide variety of studies have found evidence for vector averaging in the saccadic system using both physiological and behavioral techniques (Robinson and Fuchs, 1969;Robinson, 1972; Becker and Jurgens, 1979; Schiller et al., 1979;Findlay, 1982; Schiller and Sandell, 1983; du Lac and Knudsen, 1987;Lee et al., 1988; du Lac, 1989; van Opstal and van Gisbergen, 1990;McIlwain, 1991; Glimcher, 1993). Recently, Lisberger and Ferrera (1996)have examined the pursuit responses of monkeys when two moving visual targets are presented. They found evidence for both vector averaging (Lisberger and Ferrera, 1996) and winner-take-all mechanisms (Ferrera and Lisberger, 1995) depending on the conditions of the task.

In a small percentage of the experiments, the pattern of stimulation-induced errors was indicative of vector summation. These effects could perhaps emerge from a vector-averaging mechanism if thespeed of the electrically induced velocity vector were very high compared with the range of speeds of our visual-tracking targets. The average of two vectors with greatly disparate amplitudes will vary little, with modest changes in the small vector, leading to a result resembling vector summation. We can neither firmly support nor refute this hypothesis, however, because the apparent speed of the electrically induced velocity vector was typically uncorrelated with our measurements of speed tuning at a stimulation site.

In an additional third of our experiments, microstimulation caused a slowing of pursuit or saccadic target velocity compensation regardless of the velocity of the target. Nonspecific slowing of this nature has been observed previously after focal lesions of MT (Newsome et al., 1985) and during microstimulation of MT with higher currents (100 μA) than those used in our study (Komatsu and Wurtz, 1988). In microstimulation experiments, the most likely explanation for this effect is that the stimulating current spreads to columns representing multiple directions of motion, resulting in activation of neurons coding many different velocities. In the extreme, of course, a vector average of all possible velocity vectors should simply be 0. Consistent with this idea, the directional specificity of the effects of MT microstimulation on psychophysical motion judgments decreases with increasing current levels (Murasugi et al., 1993).

These different types of behavioral effects—vector averaging, vector summation, and general slowing—form a continuum that we have parsed using reasonable but somewhat arbitrary statistical conventions. The variability in our data are not surprising. The effects of stimulating current on a patch of cortex are likely to be complex and can differ from site to site because of variations in electrode placement with respect to the laminar and columnar architecture of MT. Furthermore, the electrically evoked signal may not always be independent of the visually evoked signal, as assumed in our model. Nonlinear interactions are possible, particularly in the case when the visual stimulus excites the same column to which electrical stimulation is applied (i.e., when the visual stimulus moves at the preferred velocity of the stimulation site). In this situation, microstimulation could interfere with or replace the visually evoked velocity signals, causing anomalies in the stimulation effects for target velocities near the preferred velocity. A fine-grained analysis involving a more thorough sampling of target velocity space would be necessary to test this possibility carefully.

Comparison of pursuit and saccadic target velocity compensation

Extrastriate area MT is highly specialized for analyzing visual motion information (Dubner and Zeki, 1971; Zeki, 1974; Maunsell and Van Essen, 1983; Albright, 1984), raising the prospect that MT could serve as a common source of motion signals for any effector system in need of such information. Our experiments allowed us to assess this conjecture simultaneously for two different, albeit related, motor systems: smooth pursuit and saccadic eye movements. Consistent with the hypothesis, microstimulation could affect both pursuit and saccadic target velocity compensation, and these effects tended to be correlated; in most experiments the pursuit and saccadic systems seemed to receive similar velocity estimates from MT (Fig. 12).

The fact that in some experiments the effects were strikingly different, with pursuit velocity and saccadic target velocity compensation shifted in opposite directions, provides an interesting insight into the neural pathways that must conduct these motion signals (also see Keller et al., 1996). In principle, the saccadic system could sample the MT velocity representation independently of the pursuit system, or it could obtain velocity information from a copy of the pursuit command, derived from somewhere along the pursuit pathway. In either case, under normal viewing conditions the pursuit and saccadic systems would receive substantially the same velocity signal. However, if the saccade system only had access to a copy of the pursuit command, then stimulating MT should always produce the same effect on saccadic target velocity compensation and pursuit. Because the effects on pursuit and saccades sometimes differed in our experiments, the saccadic system probably obtains its own velocity signal either directly from MT or perhaps indirectly from MST. That the saccadic system may receive a copy of the pursuit command in addition remains a possibility.

Relationship between physiological properties and microstimulation effects

For the experiments showing directional effects, the velocity centroids for both pursuit and saccadic target velocity compensation were correlated with the motion-tuning properties of the microstimulation site, albeit in somewhat different ways (Fig. 11). The velocity centroids for saccadic target velocity compensation were correlated with the preferred direction of the microstimulation site. Surprisingly, however, the pursuit velocity centroids were better correlated with the preferred–null axis than with the preferred direction.

Potential explanations for this preferred–null axis correlation exist, although none account for the difference between pursuit and saccadic target velocity compensation. Perhaps the most plausible possibility is that MT stimulation might frequently activate columns with the opposite preferred direction, because columns with opposing preferred directions tend to lie next to one another (Albright et al., 1984; Malonek et al., 1994). Alternatively, microstimulation might actually reduceoutput from the stimulated column if inhibitory neurons are activated preferentially (E. DeYoe, personal communication), causing a shift in pursuit velocity toward the null direction. Yet a third possibility is that MT stimulation might impart preferred direction motion to the visual background (the dim video screen surrounding the pursuit target), potentially inducing an apparent motion of the pursuit target in the null direction (Duncker, 1929). All such explanations stumble, however, on the fact that the same predictions should apply to the saccadic system as well.

Is the readout mechanism task-dependent?

Our results confirm that MT supplies motion signals to both the pursuit and saccadic target velocity compensation systems (Newsome et al., 1985; Komatsu and Wurtz, 1988; Schiller and Lee, 1994), and previous work from this laboratory has shown that MT provides motion signals for perceptual judgments as well (Newsome and Paré, 1988;Salzman et al., 1990, 1992; Salzman and Newsome, 1994; Britten et al., 1996). However, the algorithms used for reading the motion map in MT differ strikingly in these two sets of experiments. Salzman and Newsome (1994) trained monkeys to perform an eight-alternative, forced choice direction discrimination task in which the monkeys indicated their judgments by making an eye movement to one of eight targets corresponding to the eight possible directions of stimulus motion. When MT was microstimulated in this task, the monkeys tended to choose either the actual direction of motion of the stimulus or the preferred direction of motion of the stimulation site, rather than directions intermediate between the two. This pattern of results, then, was consistent with a winner-take-all mechanism rather than a vector-averaging mechanism.

Thus the distributed velocity map in MT seems to be read out according to different algorithms depending on the nature of the behavioral task. A possible explanation for these differences is that requirements differ depending on the type of behavioral response used. Winner-take-all mechanisms permit the segregation of distinct motion signals and may therefore be most appropriate for complex perceptual contexts in which different moving patterns abut or overlap each other in space. Requirements differ for other types of behavioral responses, however. Because pursuit and saccadic eye movements must be made very quickly (within a few hundred milliseconds) and to only one target at a time, the oculomotor system may simply average motion information in local regions of space to obtain a rapid “best guess” concerning the direction to be tracked.

Because these different algorithms are optimized for different purposes, it is likely that behavioral systems actually use a combination of methods for reading MT. For example, vector averaging of motion signals for pursuit and saccadic target velocity compensation probably only occurs within a circumscribed region of space. A winner-take-all mechanism may select the region of space from which motion signals will be used to guide these motor responses. Even for perceptual decisions the algorithm may depend on the precise details of the task; the winner-take-all results of Salzman and Newsome (1994) may relate in part to the fact that monkeys were asked to make discrete categorical judgments of motion direction. A vector-averaging scheme might predominate in a perceptual task that instead required fast, veridical estimates of target motion, such as those revealed by pursuit responses. Experiments are currently under way to resolve these issues.

APPENDIX

Regression analysis

The regression equation used to model the microstimulation results was chosen because it can fit the predicted results for all three hypotheses. The derivation of this equation is described below, first in the context of vector averaging or winner-take-all, and then for vector summation.

Let V⃗_ns equal the velocity of the animal’s behavior (pursuit or saccadic target velocity compensation) on nonstimulated trials,V⃗_s equal the velocity of the animal’s behavior on stimulated trials, andV⃗_e equal the value of the electrically induced velocity signal (an unknown).V⃗_ns corresponds to the velocity of the visual target but generally does not precisely equal target velocity, because pursuit and saccadic target velocity compensation are not perfectly accurate even on nonstimulated trials.

If a weighted vector average determined the animal’s behavior on stimulated trials, then:

$${\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{s}}}=g{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{e}}}+(1-g){\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}},$$ Equation 3

where g is a scalar weighting factor between 0 and 1 that indicates the relative contributions of the electrical and visual velocity signals. Note that the same equation could also model the results under winner-take-all, in which case g corresponds to the probability that a trial would be “won” by the electrical velocity signal.

For convenience, this equation can be solved for ΔV⃗, where:

$$\mathrm{\Delta }\stackrel{\mathbf{⃗}}{\mathbf{V}}={\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{s}}}-{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}},$$ Equation 4

yielding:

$$\mathrm{\Delta }\stackrel{\mathbf{⃗}}{\mathbf{V}}=g{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{e}}}-g{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}}.$$ Equation 5

Because g andV⃗_e are both unknowns, we can replace them with a single constant vector, C⃗, or:

$$\mathrm{\Delta }\stackrel{\mathbf{⃗}}{\mathbf{V}}=\stackrel{\mathbf{⃗}}{\mathbf{C}}-g{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}},$$ Equation 6

yielding the regression equation that we fit to the data for each stimulation site. The constant C⃗ corresponds to the regression estimate for the velocity on stimulated trials with a stationary visual target (step trials,V⃗_ns = 0).

An estimate of the value of the electrically induced velocity signal,V⃗_e, can be also be recovered from this equation. When the visual and electrical velocity signals are equal, the vector average of the two is identical to the visual velocity signal alone, and no change in velocity is produced by the microstimulation. Setting ΔV⃗ in Equation 6 to 0 and solving for V⃗_ns, we obtain:

$${\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}}=\frac{\stackrel{\mathbf{⃗}}{\mathbf{C}}}{g}={\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{e}}}.$$ Equation 7

Equation 6 can also fit the pattern of effects predicted by a vector summation pattern. For vector summation, the change in velocity induced by the stimulation is a constant vector. This can be seen from the vector summation equivalent to Equation 3, which is:

$${\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{s}}}=a{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{e}}}+{\stackrel{\mathbf{⃗}}{\mathbf{V}}}_{\mathbf{\text{ns}}},$$ Equation 8

where, a is a sealar weighting factor that is not constrained to any particular range. Once again substituting a single constant, C⃗, foraV⃗_e and solving for ΔV⃗ we have:

$$\mathrm{\Delta }\stackrel{\mathbf{⃗}}{\mathbf{V}}=\stackrel{\mathbf{⃗}}{\mathbf{C}}.$$ Equation 9

This equation is identical to Equation 6 when the value ofg is 0. Thus, a value of 0 for g serves as an indication of a vector summation pattern. Such patterns are distinguishable from vector averaging patterns in which the weight of the electrical signal is simply very low by the fact that the constant term, C⃗, should be significantly different from 0 for vector summation but not for a vector-averaging pattern in which the electrical signal is very weak. An estimate of the exact value of the electrically induced velocity signal is not possible for vector summation patterns, because the magnitude of this velocity vector cannot be distinguished from the weighting term a in Equation 8. However, the direction of the electrically induced velocity signal will be apparent from the direction of the constant term,C⃗, in Equation 9.

For each experimental site, we tested whether the constant,C⃗, and/or gain, g, were significantly different from 0 at the p < 0.05 level using the likelihood ratio:

$$\mathrm{\Lambda }=\frac{\mid \mathrm{\Sigma }\mid }{\mid {\mathrm{\Sigma }}_0\mid },$$ Equation 10

where Σ and Σ₀ are the maximum likelihood estimates of the variance–covariance matrix of the regression model with and without the parameter of interest, respectively (Finn, 1974). The likelihood ratio, Λ, can then be converted to a χ² distribution (adapted from Bartlett, 1947;Finn, 1974) by:

$${\chi }^2=-(n+q)ln\mathrm{\Lambda },$$ Equation 11

where n is the number of data points, andq is a correction factor related to the number of variables included in the full and reduced models [q = 3 for testing the significance of the constant, and q = 2.75 for testing the significance of the gain term (see Finn, 1974); becausen ≫ q, this correction factor has negligible impact]. The degrees of freedom are equal to the number and dimensions of the parameters being tested. Because the constant termC⃗ is a vector, it accounts for 2 df, whereas the gain term g accounts for 1 df.

Note that if neither C⃗ nor g is statistically significant, this indicates that the microstimulation had no effect, and the three hypotheses cannot be distinguished from one another.

Statistical analysis of distribution of stimulated trials

We conducted an additional statistical analysis to determine whether any experiments showed the bimodal distribution of responses predicted by the winner-take-all hypothesis. For each site, we compared the actual distribution of responses on stimulated trials with a unimodal distribution generated from the nonstimulated trials but having the same mean as the stimulated trials. For simplicity and statistical power, all data from a given experiment were transformed and normalized as described below to permit an analysis in one dimension.

For each target velocity at each stimulation site, the population of individual nonstimulated trials was first centered at 0 by subtracting their mean location. This mean was also subtracted from the centroid location and from the stimulated trials for that target velocity. Then, individual stimulated and nonstimulated trials were projected onto the axis containing the centroid, and their distance from 0 was normalized by the distance of the centroid. The result of these operations is that for each target velocity, the nonstimulated trials were centered at 0 and the centroid lay at a value of 1. These transformations permitted the pooling of data from different target velocities within an individual experiment. The expected unimodal distribution corresponding to vector averaging was generated by shifting all the nonstimulated data points by the mean location of the stimulated trials for each target velocity.

How well the unimodal distribution described the actual data was assessed by generating histograms for the unimodal and actual distributions and calculating the observed and expected values in each bin. A χ² value was calculated by computing:

$${\chi }^2=\frac{\mathrm{\Sigma } (\text{observed}-\text{expected}{)}^2}{\mathrm{\Sigma } {\text{observed}}^2},$$ Equation 12

with n − q − 1 df, wheren is the number of bins in the histogram, and qis the number of parameters estimated in the process of generating the expected distribution. The value of q in this case is 3, the means of the stimulated and nonstimulated trials, and the centroid (Larsen and Marx, 1986). If the χ² value was sufficiently small (<χ²_{0.95,n − q − 1}), the null hypothesis that the data could be described by a unimodal distribution was accepted (p > 0.05).

This test was conducted only on experiments in which both the constant and the gain terms of the regression were significantly different from 0. Within each experiment, we excluded data from target velocities in which the mean response velocity for the nonstimulated trials was less than 2 SD away from the centroid velocity. For these target velocities, any potential bimodality in the distribution of response velocities on stimulated trials would be obscured, because the mode corresponding to the visual signal “winning” would be too close to the mode for the electrical signal winning. Only experiments with enough trials to generate reasonable histograms with at least five bins (generally more than 50 stimulated and nonstimulated trials each) were included. Forty-one experiments met these criteria for pursuit, 50 for saccades.