Interneurons of the Dentate–Hilus Border of the Rat Dentate Gyrus: Morphological and Electrophysiological Heterogeneity

Abstract

Interneurons located near the border of the dentate granule cell layer and the hilus were studied in hippocampal slices using whole-cell current clamp and biocytin staining. Because these interneurons exhibit both morphological and electrophysiological diversity, we asked whether passive electrotonic parameters or repetitive firing behavior correlated with axonal distribution. Each interneuron was distinguished by a preferred axonal distribution in the molecular layer or granule cell layer, and four groups could be discerned, the axons of which arborized in (1) the granule cell layer, (2) the inner molecular layer, (3) the outer molecular layer, and (4) diffusely in the molecular layer. In our sample, interneurons with axons arborizing diffusely in the molecular layer were most frequent, and those with axons restricted to the granule cell layer were least frequent. Resting potential, input resistance, time constant, electrotonic length, and spike frequency adaptation (SFA) were not significantly different among the four groups, and the variability in SFA between cells with similar axonal distributions was striking. Clear differences in action potential morphology and afterhyperpolarizations, however, emerged when nonadapting interneurons were compared with those exhibiting SFA. Interneurons exhibiting SFA had characteristically broader spikes, progressive slowing of action potential repolarization during repetitive firing, and slow afterhyperpolarizations that distinguished them from nonadapting interneurons. We propose that the variability in repetitive firing behavior and morphology exhibited by each of these interneurons makes each interneuron unique and may provide a high level of fine tuning of inhibitory control critical to information processing in the dentate.

Interneurons of the dentate gyrus are remarkably diverse cells (for review, see Freund and Buzsáki, 1996) with variable morphology (Lorente de No, 1934; Ramón y Cajal, 1968;Amaral, 1978; Ribak and Seress, 1983; Seress and Ribak, 1983), axonal projections (Amaral, 1978; Han et al., 1993), and peptide content (Kohler, 1983; Kosaka et al., 1985; Kohler et al., 1986; Sloviter and Nilaver, 1987). The electrophysiological and functional correlates of the anatomical and histochemical diversity remain to be explored. Recent reports have stressed the specialization of function implied by dentate interneurons, the axons of which project to specific portions of the granule cell dendritic tree, soma, or axon initial segment (Halasy and Somogyi, 1993; Han et al., 1993; Soriano and Frotscher, 1993; Buhl et al., 1994; Buckmaster and Schwartzkroin, 1995a). In some cases, the dendritic trees of these interneurons are also restricted to certain areas of the dentate gyrus such as the hilus or molecular layer (Han et al., 1993; Halasy and Somogyi, 1993). These anatomical arrangements restrict the input and output functions of these cells and suggest that highly differentiated groups of interneurons serve specific functions in the control of dentate granule cell excitability and have selective effects on specific afferent inputs to the granule cells. These morphological specializations raise the question of electrophysiological specialization (Kawaguchi and Hama, 1987a; Halasy and Somogyi, 1993; Kawaguchi, 1993; Buckmaster and Schwartzkroin, 1995b; Scharfman, 1995). In particular, do electrophysiological characteristics of interneurons correlate with their morphological parameters?

In this study, we have attempted to explore this question by determining the axonal distribution and elementary electrophysiological properties of a sample of dentate interneurons located near the junction of the dentate granule cell layer and hilus, an area referred to by Amaral (1978) as the dentate hilus border of zone 4 or simply the D/H border zone, which is rich in GABAergic interneurons (Ribak and Seress, 1983; Kosaka et al., 1985; Sloviter and Nilaver, 1987; Houser and Esclapez, 1994). We asked whether the passive electrotonic properties or repetitive firing properties of these cells correlated with their axonal distributions. We found that when the D/H border zone interneurons were grouped by their apparent axonal distribution, no significant differences were seen among groups in passive electrotonic properties or repetitive firing properties. On the other hand, when interneurons were grouped by the extent of spike frequency adaptation into strongly adapting, normally adapting, and nonadapting cells, differences in spike morphology, spike repolarization, and hyperpolarizing aftercurrents did emerge that clearly distinguished adapting interneurons from nonadapting interneurons. These spike frequency adaptation groups were characterized by similar electrophysiology, but not by similar morphology. In fact, very often interneurons with identical axonal distribution patterns exhibited striking differences in repetitive firing behavior. Our conclusion is that the anatomical and electrophysiological properties of these cells do not necessarily correlate and that each cell has a distinct set of properties that confer a tremendous diversity on interneuron function in this area.

MATERIALS AND METHODS

Slice preparation and recording. Under deep halothane anesthesia, male Sprague Dawley rats (16–30 d old) were decapitated, and brains were removed and immersed in ice-cooled oxygenated ACSF (artificial cerebrospinal fluid). Transverse brain slices, 300 μm thick, were cut using a Vibraslicer (Campden 752, Berlin Germany), and the hippocampal formation was separated from the remainder of the brain slice. Hippocampal slices were incubated in warmed (32–34°C), bubbled ACSF containing (in mm): NaCl 120, NaHCO₃ 25, dextrose 10, KCl 3.3, NaH₂PO₄ 1.23, CaCl₂ 1.8, and MgSO₄ 1.2 and were bubbled with a 95% O₂/5% CO₂ gas mixture at pH 7.4. Slices were studied in a small submersion chamber (32–34°C) held in place by a bent piece of platinum wire resting on the surface of the slice and viewed with an upright Nikon Optophot microscope and a 40× water immersion objective using Hoffman Modulation Contrast optics and a video camera with infrared sensitivity.

Our whole-cell recording techniques have been described previously (Xie et al., 1992; Mott et al., 1993). Microelectrodes (3–6 MΩ) pulled from borosilicate glass capillary tubing (1.5 mm outer diameter, 1.05 mm inner diameter, World Precision Instruments, Sarasota, FL) on a Flaming-Brown microelectrode puller were filled with an intracellular solution containing (in mm): KGluconate 130, KCl 7, HEPES 10, MgATP 2, TrisGTP 0.3, pH-adjusted to 7.2 with KOH. Biocytin (Sigma, St. Louis, MO) 0.2–0.4% was added for later visualization of the neuron morphology. The osmolarity of the solutions was 265 mOsm for pipette solutions and 284 mOsm for the ACSF. Neuronal responses were amplified by the use of an Axopatch 1D amplifier and filtered at 3kHz. Pipette series resistance and capacitance were not compensated. Data were recorded on magnetic disks using a Nicolet digital oscilloscope (model 410) and also digitized by a Digidata 1200 A-D board (Axon Instruments, Foster City, CA) in a 486DX2 PC computer.

When excessive spontaneous synaptic activity obscured determination of thresholds, membrane potential trajectories, and passive firing patterns, it was blocked with 20 μm DNQX, 50 μmd-APV, 20 μm bicuculline methiodide, and 75 μm picrotoxin.

Fixation and histochemistry. In most cases a single cell was recorded from each slice. After this recording, each slice was fixed for at least 24 hr in 4% paraformaldehyde containing 0.1% gluteraldehyde in 0.1 m phosphate buffer (PB), pH 7.3, and then transferred to PB alone. Fixed slices were embedded in an albumin gelatin mixture (300 mg of chicken egg albumin, 15 mg of gelatin, and 30 μl of 25% gluteraldehyde/ml) and 75 μm sections were cut on a vibratome. Sections were collected in PB and washed three times for 10 min each. Endogenous peroxidase activity was eliminated by washing the sections in 50% (v/v) ethanol for 10 min, 70% for 15 min, and 50% for 10 min followed by three 10 min washes with PB. After these washes, slices were incubated in Avidin-HRP solution (Vectastain ABC Standard Kit) for 2–4 hr. After washing in PB for 30 min, slices were incubated in PB containing 0.05% 3′-3-diaminobenzidine tetrahydrochloride, CoCl₂ (0.025%), and NiNH₄SO₄(0.02%) for 15 min and then H₂O₂ (0.1% final concentration) was added. Incubation was continued for ∼10–15 min or until cells were visible. The slices were then washed in PB and mounted on a glass slide coated with chrome alum gelatin. The sections were dehydrated (70, 95, and 100% ethanol), cleared in xylene, and coverslipped. Shrinkage was measured by taking initial measurements of slice dimensions while the slice was in the submersion chamber. Measurements were taken using a calibrated eyepiece in theX–Y transverse plane from the top of the dentate molecular layer to the alveus below CA3 and at a right angle to this line from the alvear surface of CA3b to the alveus of CA1. Thickness of the slice in the longitudinal axis of the hippocampus or the Z-axis was also measured in the slice chamber. For measurements of theX–Y plane after fixation and mounting, slices were sectioned transversely and mounted as above, and the X–Ymeasurements were repeated. For measurements of the Z plane, slices were sectioned longitudinally (in the Z-axis), fixed and mounted, and measurements were made of the width of these sections to determine the thickness of the slice after mounting. Average shrinkage in the X–Y axis in three slices was 11 and 6%, respectively, and shrinkage in the Z-axis (slice thickness) was 15%.

Reconstruction of labeled neurons. For neuron reconstruction, cells and axons filled optimally were traced across all sections using a 100× oil immersion lens (NA = 1.25) and a three-dimensional neuronal reconstruction system consisting of an automated stage and a high-resolution monitor that was viewed through the microscope drawing tube (Neurolucida, Microbrightfield, Colchester, VT). The reconstructions were performed using all serial sections that contained the cell. At the edge of each section, the cell processes in the adjacent section were optimally lined up, and the incomplete endings from the previous section were then continued as required. The task of lining up incomplete processes was accomplished much more easily for the dendrites and proximal axons than for the complex web of distal axonal arborization. In many cases, it was virtually impossible to tell which tiny axonal process matched with which; however, because the distribution of the axonal fibers was the same on adjacent sections, this difficulty did not affect the overall distribution of the axonal arborization. Although the dendritic and axonal arborizations of the best-stained cells are quite extensive, it must be noted that, because of the preparation of thin (300 μm) hippocampal slices, processes were amputated unavoidably.

Electrotonic parameters. Resting membrane potential for each neuron was determined in current clamp at the beginning of the experiment by the voltage offset accompanying membrane rupture and rechecked at the end of the experiment. Although a junction potential of ∼10 mV has been reported using the pipette solution used in this study (Neher, 1992; Staley and Mody, 1992; Kawa, 1994), the potentials given in the tables have not been corrected for a junction potential. This correction would simply make these resting potentials and thresholds 10 mV more hyperpolarized if applied and would not change any other parameters. The input resistance (R_N) of each neuron was determined in current clamp from the amplitude of the voltage deflection produced by current injection (usually 50 pA).

The membrane time constant was determined at resting membrane potential from the decay curve of the membrane from a small (10–50 pA) current step, which caused a voltage deflection of less than 10 mV. The time constant was determined from the slowest component of a biexponential fit of the charging curve of the voltage response using the equation:

$$y(t)=a1*exp(-\text{t}/{\tau }_0)+a2*exp(-\text{t}/{\tau }_1),$$ Equation 1

where τ₀ is the longest time constant or membrane time constant and τ₁ is the shorter equalizing time constant derived from the biexponential fit to the charging curve. The goodness of fit of this equation was assessed by comparing the variance of the residual difference between the best fit of the data with the background variance of the data. In theory, if the data are poorly fit the residual variance will be significantly greater than the background variance. Therefore, a variance ratio (F = Var_res/Var_back) was determined for each fit. The data were considered to be well fit if the variance ratio (F) was less than 2. Responses were rejected if they displayed any obvious signs of active processes, such as a “sag” in the voltage response during the current step. Similarly, responses were not used if the time constant of the charging and discharging curve of the voltage response was substantially different (Turner, 1984; Spruston and Johnston, 1992) and measurements of decay time constant produced by both hyperpolarizing and depolarizing current steps were combined. For each neuron the reported membrane decay time constant represents the average of at least three responses in that cell.

The electrotonic length (L) expressed as length constants (λ) of each neuron was estimated based on a simple sealed-end cylinder model. According to this model, the cylinder represents the whole neuron, including both somatic and dendritic conductances. TheL value for this cylinder was calculated using the following equation (Rall, 1969):

$$L=\pi \times [({\tau }_0/{\tau }_1)-1{]}^{-1/2},$$ Equation 2

The estimate of L in this model is improved through the use of whole-cell recording techniques that reduce the somatic leak conductance commonly associated with sharp microelectrode recordings. This estimate, however, still suffers from errors caused by difficulty in extracting the appropriate membrane time constants and differences in the electrotonic length of dendritic branches.

In addition to the physiologically measured L values calculated as above, alternative derived electrotonic parameters for representative interneurons were calculated using the observedR_N and the somatic and dendritic parameters of the Neurolucida neuronal reconstruction. This calculation used a passive cable model (Turner, 1984) to calculate the derived values for specific membrane resistivity (R_m) and electrotonic length to each dendritic termination. The assumptions involved with this modeling included no conductance past observed dendritic endings, the use of the physiologically measuredR_N, no leak around the electrode, and specific internal resistivity (R_i) = 200 ohm/cm. Because each terminal possesses a summed L, histograms were constructed to indicate the dispersion and a mean was calculated for comparison to the average value of L from the electophysiological recordings. These values explicitly take into account the cell structure, but are also limited by the imprecision of matching dendritic processes and by any incompleteness of the reconstructed cell.

Action potential morphology and spike frequency adaptation.Action potentials were evoked by depolarizing rectangular current steps. Action potential threshold was determined by delivering current steps of increasing amplitude and measuring the membrane potential at which a spike was elicited. Action potential height was measured from the resting membrane potential to the peak of the action potential. Action potential duration was measured from the point at which the action potential started to rise until it again crossed that point in its downward deflection. The duration of the action potential at half-amplitude was measured at the point halfway between the potential at which the action potential began to rise and its peak. For each neuron the reported value of action potential height, duration, and duration at half-amplitude represents the average of three action potentials in that cell.

Spike trains were elicited by injections of depolarizing current of 700 msec duration. Whenever possible, the measurement of spike frequency adaptation was done using current levels between 0.1 and 0.2 nA. The initial frequency of spike firing during the depolarizing pulse was determined from the first two action potentials of the train. The extent of spike frequency adaptation was expressed as the ratio of the frequency of the last two spikes of the train to the frequency of the first two spikes and termed the adaptation ratio, which, if less than unity, indicates spike frequency adaptation occurred during the spike train. When more than one spike train at the same intensity of injected current was available, the adaptation ratio used was the average of the values for each train. Changes in the height and the duration of the action potentials during spike trains were determined by comparing the height and duration of the first and fifth spike of the train. The fifth action potential was selected for analysis because it represented the point in the spike train after which little additional change in the action potential occurred.

The amplitude of the fast afterhyperpolarization (fAHP) after an action potential was determined by measuring the peak downward deflection of the fAHP from the membrane potential at the point immediately before the action potential. The amplitude of the slow AHP (sAHP) after trains of 8–10 action potentials was measured as the peak downward deflection from the resting membrane potential immediately after the train.

After these experiments had been performed, we learned of the potential distortion of action potential morphology by patch-clamp amplifiers (Magistratti et al., 1996). To evaluate the effect of our Axopatch 1D on action potential waveforms, we used tape recorded action potentials as input for the head stage, with the voltage adjusted to physiological levels by a voltage divider. This input signal was placed as a voltage source between the headstage ground and a 10 MΩ resistor connected to the headstage input. As in our cell recordings, capacitance compensation was set at zero. Simultaneous recordings of the input voltage and the output of the Axopatch 1D demonstrated that this action potential waveform was distorted only mildly. There was an 8% increase in peak voltage, but no significant alteration in spike undershoot or width. We suggest that our conclusions, which are based on the comparison of action potential parameters between cells in these experiments all recorded in the same manner, are not invalidated by the distortion caused by the patch-clamp amplifier.

Data analysis and drug application. Acquired data were analyzed using Strathclyde Electrophysiology Software Whole Cell Program (version 1.1) developed and generously provided by John Dempster. Means and SE were calculated typically for quantitative data. Statistical significance was determined using one-way ANOVA and the Student’s t test. Gaussian curve fits were done using Origin version 4.1 (MicroCal Software, Northhampton, MA) χ² minimization routine.

6,7-Dinitroquinoxaline-2,3-dione (DNQX) andd(−)-2-amino-5-phosphonovaleric acid (d-APV) were purchased from Tocris Cookson (Bristol, England). Bicuculline methiodide and picrotoxin were purchased from Sigma. All drugs were bath-applied in the perfusion medium. All drugs were dissolved directly into the ACSF except DNQX, which was first dissolved in dimethyl sulfoxide and added to ACSF.

RESULTS

Morphological classification based on axonal arborization

Electrophysiological data were obtained from >60 D/H border interneurons. Of these, we were able to retrieve good biocytin stains of the axons, dendrites, and somata of 27 cells. In an additional 14 cells, there was incomplete staining of the soma and dendritic tree, usually because of loss or lysis of the soma. In these 14 cells, however, there was adequate axon staining to determine axonal distribution in the molecular layer (ML) or granule cell layer (GCL). Thus, in 41 of the interneurons studied, the axon distribution could be determined. We chose to group D/H border zone interneurons by the distribution of their axons, which has been a key feature in classifying these cells (Han et al., 1993; Halasy and Somogyi, 1993;Buckmaster and Schwartzkroin, 1995a,b). Thus, the 41 neurons with adequate axonal staining were grouped into four morphological classes as follows.

Interneurons with axonal arbors concentrated in the granule cell layer (GCL cells)

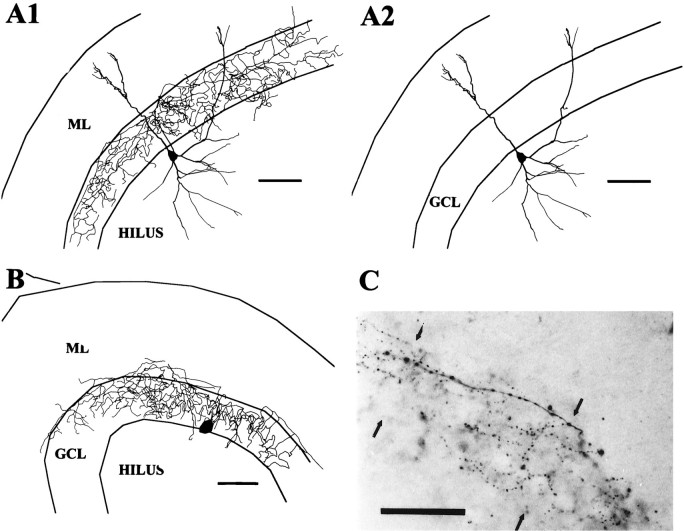
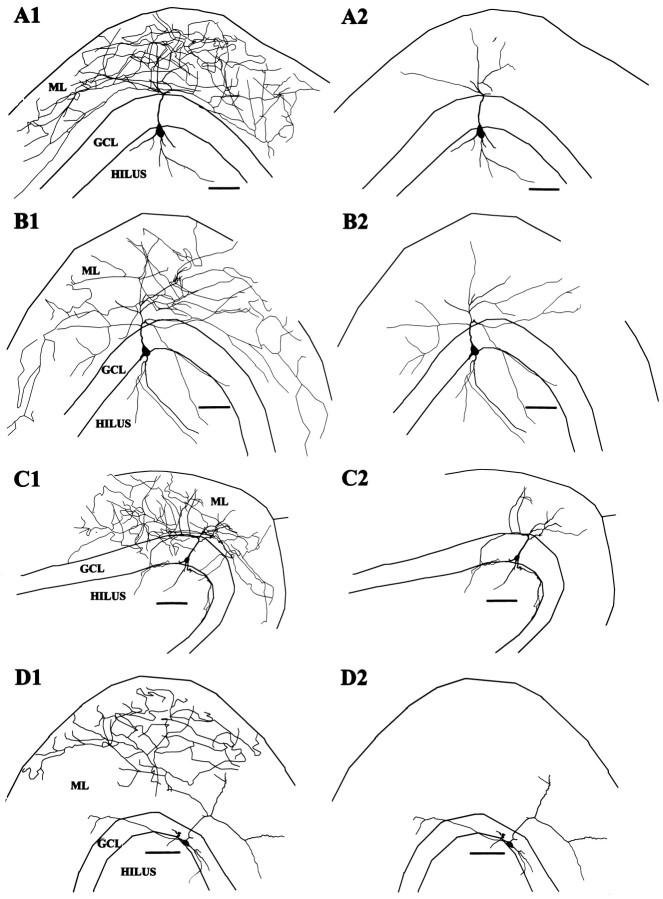
An axon arbor consisting of a delicate net-like arborization in the GCL (Amaral, 1978; Ribak and Seress, 1983; Han et al., 1993) was recovered in only four cells or ∼10% of the 41 cells with defined axonal domains (Fig. 1). The axon arborizations of these cells in the GCL had a delicate beaded appearance, and the branches of the axon were almost entirely confined to the GCL. In one cell, the soma and dendrites were exceptionally well preserved and it had the typical appearance of a pyramidal basket cell with a prominent apical dendrite. In one other, the soma and portions of the dendrites were recovered, showing that the soma was at the D/H border and dendrites extended into the hilus and ML. The dendrites of these cells were aspinous and varicose. Basket cells and axo–axonic cells are difficult to discern (Han et al., 1993), and we cannot be certain that all of these cells were basket cells rather than being a mix of basket cells and axo–axonic cells, and therefore these cells will be designated GCL cells. Axo–axonic cells, however, often have extensive axonal branching in the hilus as well as in the GCL (Han et al., 1993), favoring the interpretation that these GCL cells, which did not have extensive hilar axons, were indeed basket cells.

Fig. 1.

GCL cell reconstructions. A, This GCL cell shown in A1 with its axon and inA2 without its axon had a pyramidal-shaped soma and aspinous dendrites branching both in the hilus andML. The axon arborization was limited primarily to theGCL (scale bar, 100 μm). B, Only the axon and a portion of the soma of this cell were recovered; however, the distribution of the axon in the GCL suggests strongly that the cell was a basket cell (scale bar, 100 μm).C, Photograph of a section of axon arborization of cell in A. The axon with the string of beads appearance can be seen in the GCL (between thearrowheads) (scale bar, 50 μm).

Interneurons with inner molecular layer axons (IML cells)

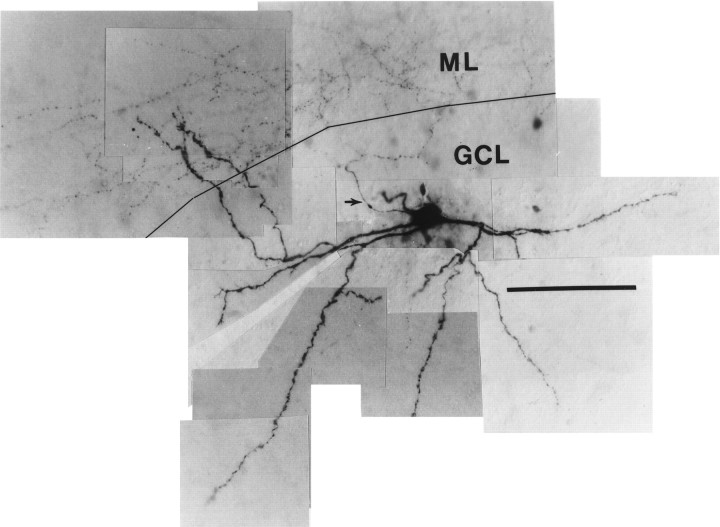
Eight cells had axons arborizing predominantly in the IML (Figs.2, 3). In most cases, the axons arose from apical dendrites, although in one case (Fig. 2) the axon clearly arose from the soma and ascended through the GCL to the IML. Soma shape was fusiform (n = 5) or pyramidal (n = 2) when the soma was visualized. The long axis of the fusiform cell soma could be parallel to the hilar border or, if the soma was embedded in the lower margin of the GCL, vertically oriented. Dendrites were aspinous (six cells) or sparsely spinous (two cells). Most of these cells also had several major dendrites ascending vertically from the soma to enter the ML directly. Occasional branches of the axons of the IML cells often entered the GCL but did not form the extensive and dense network of terminals in the GCL typical of the GCL cells, although one IML cell had a relatively large amount of axon in the GCL (Fig. 3C) similar to an interneuron innervating the IML described by Sik et al. (1997).

Fig. 2.

Photographic montage of IML cell. This cell exhibits the typical varicose dendrites of the interneurons seen in this study and, unlike most cells, also shows rare elongated spine-like processes on some of the dendrites. The axon (arrow) can be seen in this cell arising from the top lefthand margin of the soma and projecting to the nearby IML, where some of its tiny bead-like terminals can be discerned. The tracing of this cell is shown in Figure 3B. (Calibration bar, 100 μm; black line demarcates the junction of the GCL and ML.)

Fig. 3.

IML cell reconstructions. A, This IML cell with a fusiform soma distributed its axon primarily in the IML with very little overlap into the GCL (A1). InA2 the axon has been omitted, and the extent of the branching of its aspinous dendrites can be seen extending to theOML and along the D/H border. (In this and all following cell reconstructions, part 1 will show the cell with its axon included and in part 2 the axon is omitted. Scale bars in this and all subsequent reconstructions are 100 μm.) B, Reconstruction of the IML cell pictured in Figure 2. This cell had no dendrites reaching the OML, but a dendrite leaving the superior aspect of the soma may have been amputated judging from the stump-like process there. C, This IML cell had an axon that seemed to prefer both the GCL and the IML and a rather limited dendritic tree. Its soma was somewhat vertically oriented and situated more within the GCL than the cells in A and B.

Interneurons with outer molecular layer axons (OML cells)

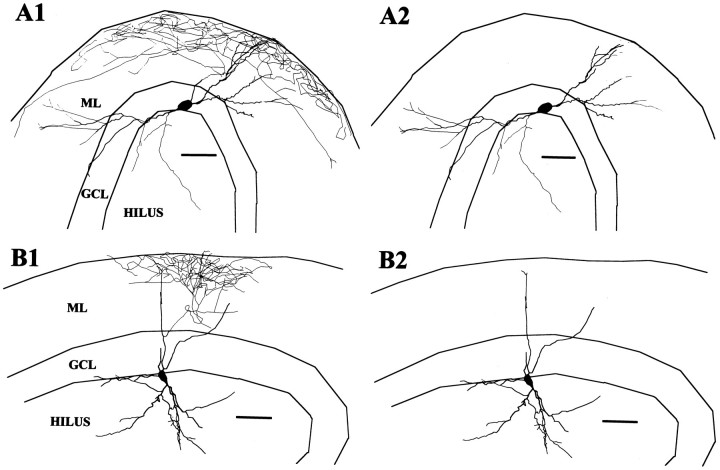
Six cells had axons that seemed to arborize preferentially in the outer half of the ML and are referred to as OML cells. Unfortunately, the soma and dendrites were well preserved in only two of these cells (Fig. 4). In one cell the axon arose from an ML dendrite and in the other cell it arose from the soma. Both cells had fusiform somata with aspinous dendrites entering both the hilus and ML and extending to the OML.

Fig. 4.

OML cell reconstructions. A, This cell had an extensive axonal arbor most densely distributed in the OML and a fusiform soma at the D/H border from which the axon arose. The dendrites spanned from the OML of the upper blade to the OML of the beginning of the lower blade. B, The axonal arbor of this cell was more limited; nevertheless, it seemed clearly preferentially located in the OML. This cell also had dendrites reaching the OML and a less expansive dendritic tree with a vertically oriented fusiform soma.

Interneurons with axons distributed diffusely throughout the molecular layer (TML cells)

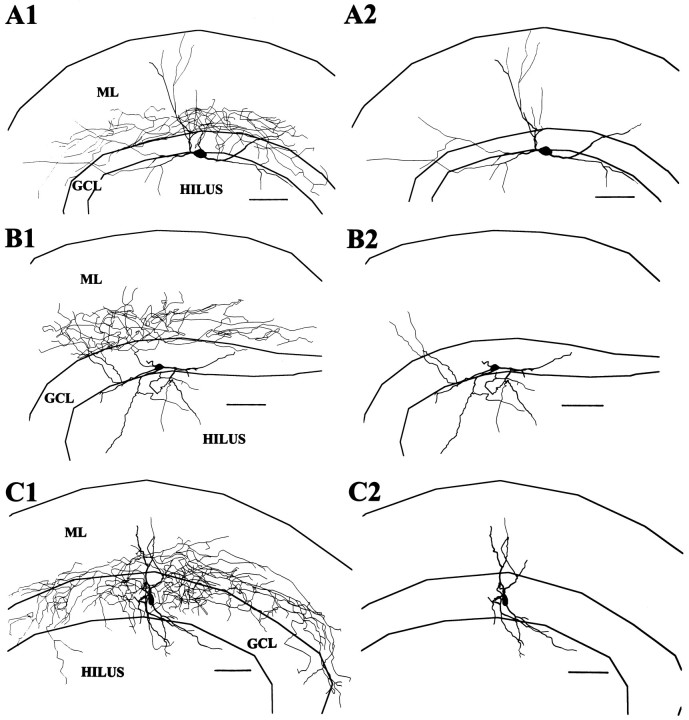
This was the most frequently encountered pattern in which the axon originated from an apical dendrite and branched in the ML with no clear concentration in any specific stratum of the ML (Fig.5). Of the 41 stained axonal arborizations, 22 showed this pattern, and, of these, 17 had adequately stained somatodendritic morphology as well. Compared with the IML and OML cells, the axonal arborization of these cells was not as dense and in many cases branches seemed to wander randomly over the entire thickness of the ML. In general, the axonal arborization was most concentrated in the ML directly overlying the soma, and in occasional cases the axon arborization extended widely in the transverse plane as well, occasionally nearly to the limits of the ML in both the suprapyramidal and infrapyramidal direction. Eleven of the TML cells also had axon branches entering the hilus.

Fig. 5.

TML cell reconstructions. Typical TML cells shown in A–D had axons that did not show a preferential distribution in either the OML or IML and were usually widely dispersed in the ML. Somata were most commonly pyramidal with prominent apical dendrites from which the axon typically arose. These cells strongly resemble the interneurons with extensive axonal arborization in the ML described by Soriano and Frotscher (1993).

Soma shape could be discerned in 16 cells and varied from pyramidal (n = 8) to fusiform (n = 5) or multipolar (n = 3), and dendrites extended typically into both the hilus and ML. The stained dendrites in our sections rarely reached the very outer limits of the OML and were varicose and aspinous (15) or sparsely spinous (2).

Passive membrane properties do not differ among morphological groups

Of the 41 interneurons with identified axonal projections, 26 neurons were selected for electrophysiological analysis. All selected neurons had resting membrane potentials below −40 mV without hyperpolarizing current injection and had an input resistance above 100 MΩ. With rare exceptions, these cells did not discharge spontaneously at rest. The selected neurons came from each of the four morphological groups and consisted of 13 TML cells, 3 GCL cells, 7 IML cells, and 3 OML cells. In addition to these four groups of neurons, we also determined the electrophysiological properties of 16 granule cells for comparison to the interneurons.

Comparison of the passive membrane properties of the morphological groups of interneurons revealed no statistically significant differences in resting membrane potential (RMP), input resistance (R_N), or membrane time constant (τ₀) among the groups (Table 1), except that the electrotonic length (L) of IML cells was long in comparison with TML and granule cells. The RMP of granule cells was significantly greater than that of interneurons, and there was a trend for the L of granule cells to be shorter than that of interneurons.

Table 1.

Passive membrane properties of interneurons classed by axonal arborization

	Cell type
	TML (n = 13)	GCL (n = 3)	IML (n = 7)	OML (n = 3)	Granule cells (n = 16)
RMP, mV	−54.5  ± 1.9	−51.7  ± 4.3	−60.5  ± 2.6	−57.0  ± 2.6	−75.3  ± 1.22
RN, MΩ	198.2  ± 23.8	228.5  ± 69.8	182.2  ± 27.2	252.3  ± 78.0	261.8  ± 38.2
τ1, msec	0.93  ± 0.13	1.48  ± 0.43	1.38  ± 0.20	1.11  ± 0.37	1.03  ± 0.18
τ0, msec	18.4  ± 1.1	15.9  ± 2.7	14.8  ± 1.8	16.9  ± 1.8	23.2  ± 4.3
L, cell	0.72  ± 0.07	0.98  ± 0.12	1.01  ± 0.071	0.80  ± 0.13	0.67  ± 0.04

This table exhibits the mean values and SEMs for the resting membrane potential (RMP), input resistance (R_N), membrane time constant (τ₀), equalizing time constant (τ₁), and electrotonic length calculated from τ₀ and τ₁ (L) for the four different morphological groups and the sample of granule cells.¹Note that there was no clear difference in these values among the different morphological groups in general with the exception that one-way ANOVA indicated that the L value for IML cells was longer than that of TML cells and granule cells (p < 0.05). ²The RMP of the granule cells was also significantly greater than all classes of interneurons (p < 0.01). The τ values for granule cells were determined at a membrane potential of −75 mV. All values in this and subsequent tables are means ± SEMs.  

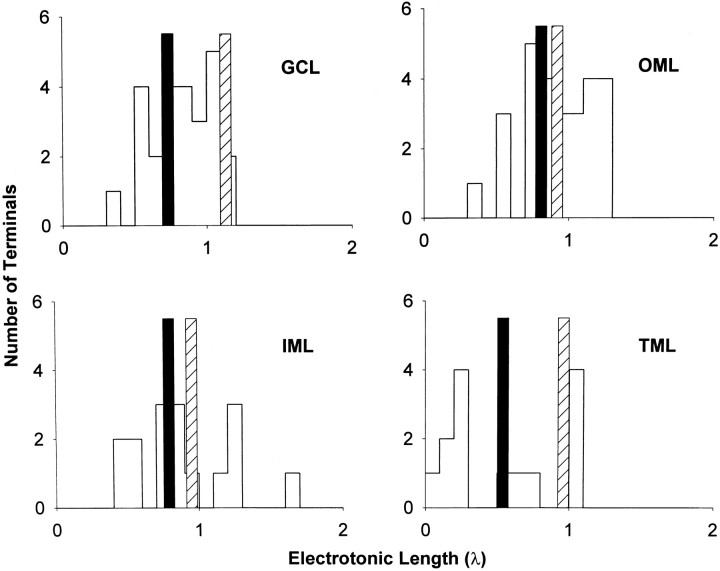
For a subset of interneurons with optimal reconstructions, anatomical and electrotonic values were calculated on the basis of the reconstructed cell image and the observed R_N(Table 2). In Table 2, the total axon and dendritic length, soma area, and cell area of the reconstructions are given. The cable model L values, calculated from the reconstructions, are compared to the physiological L values, calculated from the observed τ₀ and τ₁ parameters. Finally, specific membrane resistance (R_m) was also calculated for each class. The means of the values for all classes are also displayed as overall values. From the overall values of τ₀ and R_m, the average membrane capacitance was determined to be 1.098 μF/cm². Although the samples are too small to generalize about the properties of interneurons with differing axonal distributions, the greater dendritic length of the two OML cells does stand out and is also obvious from their displayed reconstructions in Figure 4. There was good agreement between the cable model L and physiological L for TML cells, but in the GCL cells and IML and OML cells, the cable modelL values were shorter than the physiological Lvalues (but not significantly different). The cable model Lvalues were calculated as the average of the distances to each dendritic termination, shown individually in Figure 6with examples of one neuron from each morphological group. Note that the physiological L values tended to be displaced toward the longer end of the histograms, suggesting that this electrical measurement may be strongly influenced by dendrites having the longest electrotonic lengths. The interneurons also demonstrated a relatively simple dendritic structure with a 4–9 branch order complexity and 18–25 dendritic terminations. In comparison, granule cells also tend to have relatively simple dendritic structures and total dendritic lengths comparable to these interneurons (Rihn and Claiborne, 1990) with branch orders from 6 to 8 (Pyapali and Turner, 1996). On the other hand, the pyramidal neurons of nearby CA3c have far more complex and extensive dendritic arbors (Turner et al., 1995).

Table 2.

Anatomical and electrotonic values of interneurons classed by axonal arborization

	TML (n = 6)	GCL (n = 1)	IML (n = 4)	OML (n = 2)	Overall (n = 13)
Axon length (mm)	5.12  ± 1.18	11.0	9.69  ± 2.01	8.2  ± 2.45	7.45  ± 1.04
Dendrite length (mm)	2.11  ± 0.43	2.46	2.39  ± 0.32	3.22  ± 0.68	2.39  ± 0.25
Soma area (103μm2)	0.74  ± 0.12	1.52	1.10  ± 0.16	1.89  ± 0.12	1.08  ± 0.14
Cell area (103 μm2)	7.24  ± 1.23	8.2	7.67  ± 0.49	12.1  ± 0.32	8.20  ± 0.74
Cable model L (λ)	0.77  ± 0.20	0.73	0.61  ± 0.13	0.55  ± 0.27	0.68  ± 0.10
Rm (103Ω-cm2)	13.4  ± 3.33	10.3	15.1  ± 2.98	23.4  ± 4.95	15.2  ± 2.06
Measured τ0	19.4  ± 1.18	12.7	15.8  ± 2.4	15.2  ± 0.85	16.7  ± 1.17
PhysiologicalL (λ)	0.78  ± 0.07	1.14	0.97  ± 0.08	0.72  ± 0.13	0.87  ± 0.06

This table shows mean values and SE, of total axon length, total dendrite length, soma area, cell area, and membrane resistivity (R_m) derived from neuronal reconstructions. Note that these cells are a subset of the total population recorded, because not every cell was adequately recovered and reconstructed. Cable model electrotonic length (L) expressed in units of space constant (λ) was calculated using the measured input resistance (R_N) and the soma and dendritic parameters of the Neurolucida neuronal reconstruction assuming specific internal resistivity of 200 ohm-cm. Physiological L expressed in units of space constant (λ) was calculated from the measured τ₀ and τ₁ values using the equationL = π × [(τ₀/τ₁) − 1]^−1/2.

Fig. 6.

Electrotonic distance histograms. Examples of histograms of calculated cable model L values to each individual dendritic termination are shown for the GCL cell shown in Figure 1A, the IML cell shown in Figure3A, the OML cell shown in Figure4A, and the TML cell shown in Figure5D. The mean of all individual dendritic terminationL values is shown as a vertical solid bar, and the physiologically determined L value for each cell is illustrated as a vertical striped barin each instance. In each case the physiologically determinedL was greater than the mean dendritic terminationL.

Morphological groups do not differ significantly in adaptation ratios

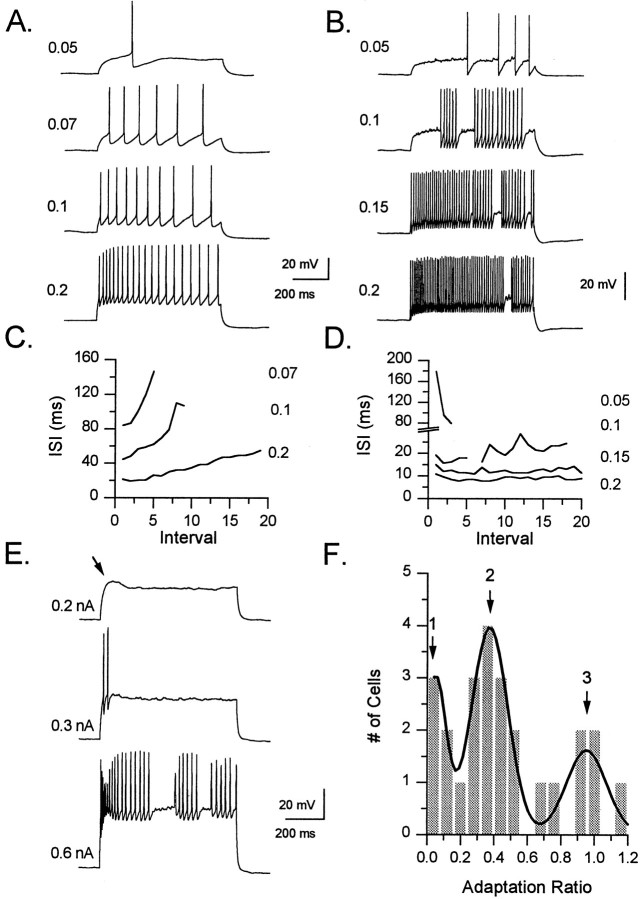
Given that passive membrane parameters did not seem clearly different among the four morphological groups, spike frequency adaptation (SFA) and patterns of repetitive firing were studied during depolarizing current injections. SFA was measured in each interneuron using the adaptation ratio (see Materials and Methods). Interneurons varied in their degree of SFA from only a slight slowing of action potential frequency to a complete cessation of action potential firing. This can be seen when the time interval between each successive spike in a train is plotted against the interval number (Fig.7). In most cells this plot indicates a progressive increase in the time between action potentials, as can be seen for the TML-projecting neuron in Figure7A,C. In other cells, however, this plot is almost flat, indicating little to no change in firing frequency as seen in the GCL cell of Figure7B,D.

Fig. 7.

Patterns of spike frequency adaptation in interneurons. A, B, Responses of a normally adapting TML cell (A) and a nonadapting GCL cell (B) to a series of 700 msec depolarizing current pulses are shown. The magnitude of the current injection (in nA) is indicated to the left of each trace. Note that with small-current injections SFA is apparent in the normally adapting cell, whereas in the nonadapting cell the rate of spike firing actually increases. C, This graph shows the interspike interval (ISI) during the train plotted against the number of the interval for the TML cell inA. The amplitude of the current injection (in nA) is indicated on the right. The increase in ISI duration is apparent at low current injection strengths as well as at higher currents, and in each case the ISI more than doubles by the end of the train. D, This is a similar graph for the GCL cell inB, showing the minimal SFA exhibited by this cell. Again the strength of the current injection (in nA) is given on theright of the graph. At the 0.1 nA level thepoint in the line corresponding to the pause in the spiking was deleted. Note the increase in firing rate at the lowest current injection. E, This IML cell is an example of the strongly adapting cells with a depolarizing hump (arrow). With the most intense current injection (0.6 nA), the rapid initial firing can be seen as well as the early decrement in spike amplitude which then recovers. F, This histogram plots the adaptation ratios of 25 cells (one cell with a value of 1.6 not shown). The histogram is better fit by a combination of three Gaussian functions (as shown by dark,smooth function; χ² = 0.54) than by a single Gaussian function (not shown; χ² = 1.09). This finding suggests that the distribution is composed of more than one population of cells, with three groups shown roughly by the peaks of the histograms (see text for details).

When comparisons were made among groups of interneurons, the mean adaptation ratios for the GCL, TML, IML, and OML cell groups were 0.67 ± 0.27, 0.41 ± 0.05, 0.50 ± 0.19, and 0.82 ± 0.42, respectively, and were not different significantly (p = 0.39, one-way ANOVA).

There were trends, however, suggesting that GCL cells might differ from TML cells with respect to SFA. The three GCL cells consisted of two cells with almost no SFA (adaptation ratios of 0.98 and 0.92) as would be expected for basket cells (Schwartzkroin and Mathers, 1978;Kawaguchi and Hama, 1987a; Kawaguchi et al., 1987), and one outlier cell that had marked SFA with an adaptation ratio of 0.13. On the other hand, all 13 TML cells displayed SFA with adaptation ratios ranging between 0 and 0.78. In addition, using a standard 0.2 nA current injection, the GCL cells showed the highest initial firing rate, with an initial mean frequency of 95.1 ± 40 Hz compared with initial frequencies of 13.5 ± 4.2, 26.5 ± 7.3, and 43.4 ± 6.1 Hz, respectively, for OML, IML, and TML cells.

Interneuron classification based on spike frequency adaptation

Despite these trends among some groups of cells, the above comparisons indicated primarily that for most cells there was only a weak correlation between morphological and electrophysiological properties. However, when electrophysiological properties of interneurons were compared, irrespective of morphological type, clear similarities among different cells became apparent. In particular, during depolarization-evoked trains of action potentials interneurons tended to display one of three different patterns of spike frequency adaptation. The three different patterns of SFA correspond approximately to the peaks on the adaptation ratio histogram in Figure7F.

Cells were considered as nonadapting with adaptation ratios of ≥0.9. The rightmost peak (peak 3) on the adaptation ratio histogram corresponds to the majority of these nonadapting cells. These cells displayed very little change or, in some cases, an increase in action potential firing frequency during the course of the depolarizing pulse. The six cells in this study that displayed this behavior consisted of two GCL cells, three IML cells, and one OML cell.

Interneurons with adaptation ratios between 0.15 and 0.9 were designated as normally adapting. The majority of interneurons in this study (n = 16) displayed this firing behavior. The mean of this group corresponds approximately to the central peak (peak 2) of the adaptation ratio histogram in Figure 7F.

Finally, neurons with adaptation ratios <0.15 were designated as strongly adapting. The upper limit of 0.15 was chosen because, using this cutoff, all four cells in this group had, in addition to very pronounced SFA, a distinct response to depolarizing current (Fig.7E). Invariably, when these neurons were depolarized from rest with current pulses, a transient depolarizing hump was evident. With higher currents, action potentials first appeared during this depolarizing hump. Further increases in the amplitude of the current step resulted in a rapid increase in the frequency of firing at the peak of this hump and eventually in action potential discharge during the remainder of the current pulse. Compared with the high frequency of firing during the burst, action potentials after the burst occurred at a markedly decreased frequency. Thus, by our measurements, these cells displayed unusually high levels of spike frequency adaptation. Despite their unusual behavior, these cells seemed electrophysiologically “healthy.” They had a resting membrane potential, input resistance, membrane time constant, and action potential height similar to other neurons in this study. One TML cell, one GCL cell, and two IML cells were of this type.

Using this classification, we again asked whether the morphological groups might show trends to have certain types of adaptation patterns. However, as a rule within each morphological group, there was a variety of SFA patterns. For example, the IML group contained three nonadapting cells, two normally adapting cells, and two strongly adapting cells. The OML group contained one nonadapting and two normally adapting cells. The GCL group contained two nonadapting cells and one strongly adapting cell. The TML group showed some homogeneity in that 12 of the 13 cells were normally adapting, but even so the range of adaptation ratios was from 0.2 to 0.78; one TML cell was strongly adapting.

Whereas the above comparisons demonstrated considerable variability among interneurons within morphological groups, they revealed that, when interneurons were compared on the basis of their extent of spike frequency adaptation, they fell into three distinct electrophysiological groups. The average adaptation ratio for each of these SFA groups was significantly different (p< 0.001, one-way ANOVA) with neurons in the nonadapting, normally adapting, and strongly adapting groups exhibiting mean adaptation ratios of 1.11 ± 0.11, 0.41 ± 0.04, and 0.03 ± 0.03, respectively. In comparison, granule cells had an average adaptation ratio of 0.54 + 0.13, a value that was similar to that found in normally adapting interneurons. Therefore, to better understand similarities among these cells, we reclassified interneurons into these three groups on the basis of the extent of adaptation observed in each cell.

Passive membrane properties do not correlate with SFA

The RMP, R_N, and τ₀ for each of the 6 nonadapting, 16 normally adapting, and 4 strongly adapting interneurons as well as for granule cells are shown in Table3. No differences in these parameters were seen comparing the strongly adapting, normally adapting, and nonadapting groups. Average RMPs of interneurons from all three SFA groups, however, were less than granule cells. The input resistance of granule cells was higher than input resistance of interneurons, and interneurons were again found to be less electrotonically compact than granule cells.

Table 3.

Passive membrane properties of interneurons classed by spike frequency adaptation

	Cell type
	Normally adapting (n = 16)	Nonadapting (n = 6)	Strongly adapting (n = 4)	Granule cells (n = 16)
RMP, mV	−55.8  ± 1.8	−54.0  ± 4.1	−58.0  ± 1.4	−75.3  ± 1.21
RN, MΩ	198.6  ± 23.4	211.6  ± 35.3	205.1  ± 51.5	261.8  ± 38.2
τ1, msec	1.19  ± 0.15	1.30  ± 0.29	1.49  ± 0.40	1.03  ± 0.18
τ0, msec	17.9  ± 0.9	15.3  ± 1.8	14.7  ± 3.4	23.2  ± 4.3
L, cell	0.84  ± 0.08	0.93  ± 0.082	1.04  ± 0.062	0.67  ± 0.04

In this table, the passive membrane properties of resting membrane potential (RMP), input resistance (R_N), membrane time constant (τ₀), equalizing constant (τ₁), and electrotonic length calculated from τ₀ and τ₁ (L) are compiled for the interneurons in the three classes of spike frequency adaptation and for the sample of granule cells. No significant differences were found in these parameters between the normally adapting, nonadapting, and strongly adapting interneurons. ¹The RMP of the granule cells was significantly greater than all classes of interneurons (p < 0.01). ²The L values of the nonadapting and strongly adapting cells were greater than theL values of granule cells (p < 0.05).

Action potential properties correlate with SFA

Properties of single-action potentials evoked by small depolarizing currents are listed in Table 4. Action potential threshold was similar in interneurons irrespective of the extent of SFA, and all interneurons had higher spike thresholds than did granule cells. Also, action potential amplitude did not differ among cells with different degrees of SFA. For all interneurons, rate of rise of the spike exceeded rate of decay, and all groups had similardV/dt ratios. The action potential duration in nonadapting interneurons, however, was significantly shorter than in normally adapting interneurons and shorter also than that of strongly adapting interneurons. Given the shorter action potential duration, it is not surprising that the rate of rise and rate of decay of the action potentials of the nonadapting cells were larger than action potentials of the adapting cells. It is notable that the rate of rise and rate of decay of granule cell spikes were greater than those same rates for interneurons.

Table 4.

Properties of single-action potentials

	Cell type
	Normally adapting	Nonadapting	Strongly adapting	Granule cells
Threshold, mV	−40.2  ± 1.7	−40.5  ± 2.5	−36.2  ± 3.4	−48.1  ± 1.42
Amplitude, mV	57.9  ± 2.9	59.0  ± 6.5	69.0  ± 4.9	109.7  ± 4.33
Duration, msec	2.4  ± 0.2	1.6  ± 0.11	2.1  ± 0.3	2.1  ± 0.1
Duration at 0.5 amp, msec	1.13  ± 0.07	0.86  ± 0.11	1.10  ± 0.11	1.07  ± 0.06
Rise, dV/dt	743.7  ± 63.8	887.3  ± 198.0	751.0  ± 146.8	1876.3  ± 168.64
Decay, dV/dt	397.2  ± 42.8	510.7  ± 133.2	452.0  ± 103.8	784.0  ± 59.84
dV/dt ratio	2.04  ± 0.14	1.84  ± 0.15	1.81  ± 0.34	2.50  ± 0.23

This table compares action potential properties of the three classes of interneurons based on spike frequency adaptation. Shown are spike threshold, spike amplitude measured from resting membrane potential, spike duration measured from the onset of rise to the point where the membrane potential returned to the level seen at the onset of the spike (duration), spike duration measured at a point halfway between the potential at which the spike began to rise and its peak (duration at 0.5 amp), the maximum rate of rise of the spike potential (rise, dV/dt), the maximum rate of decay or repolarization of the spike (decay, dV/dt), and the ratio of the maximum rate of rise to the maximum rate of decay (dV/dt ratio). ¹The spike duration was significantly shorter in nonadapting interneurons than in normally adapting interneurons and granule cells (p < 0.05), but no other differences were seen among the three different adaptation groups. ²Regarding differences of interneurons and granule cells, the threshold of granule cells was significantly more hyperpolarized than normally adapting, strongly adapting (p < 0.01), and nonadapting (p < 0.05) interneurons. ³The amplitude of granule cell spikes was significantly greater than all interneurons (p < 0.001) and ⁴the rise and decay of granule spikes were significantly faster than all interneurons (p < 0.01).

Changes in action potential properties during repetitive firing correlate with SFA

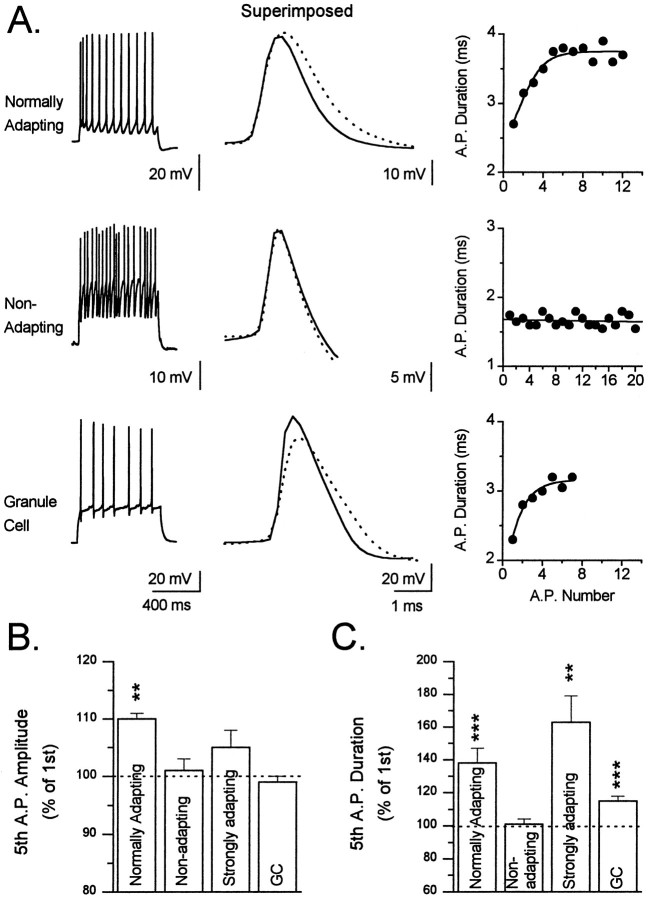
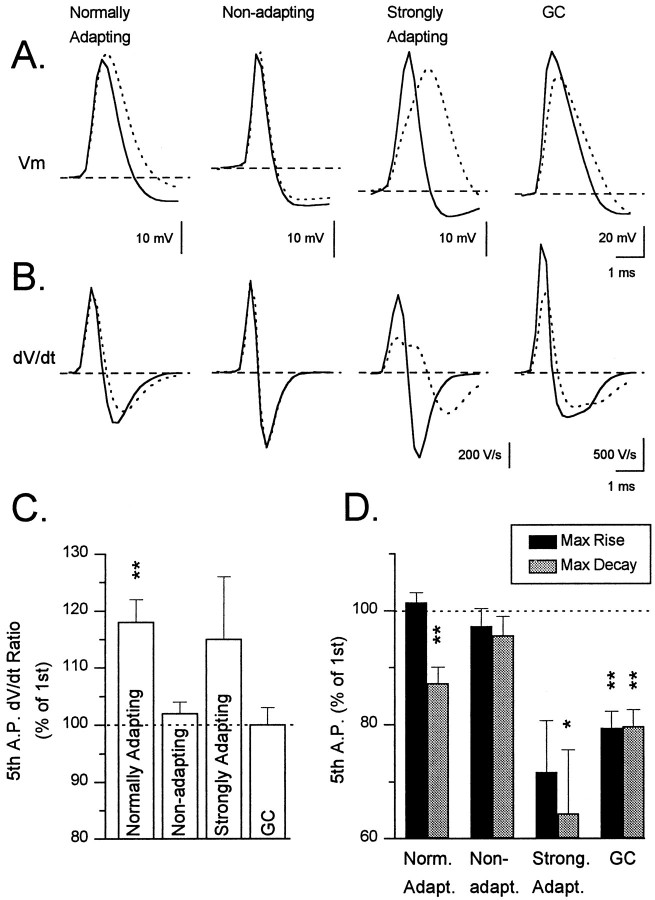
Action potential morphology typically changed during depolarization-induced trains of action potentials, and the evolution of action potential morphology during trains showed clear correlations with the pattern of SFA exhibited by the interneurons (Fig.8). Action potential amplitude increased significantly during a train in normally adapting interneurons and showed a tendency to increase in strongly adapting interneurons. Action potential amplitude, however, remained unchanged in nonadapting interneurons and in granule cells. The increase in amplitude was usually most dramatic on the second spike of the train and continued to increase until reaching a plateau by the fifth to seventh spike.

Fig. 8.

Changes in spike amplitude and duration during repetitive firing. A, Data from a normally adapting (TML cell; top row) and a nonadapting (GCL cell;middle row) interneuron and from a granule cell (bottom row). For each cell, a spike train elicited by injected depolarizing current (left column), thesuperimposed traces of the first (solid line) and fifth (dotted line) spike of the train (middle column), and a graph of spike duration (A. P. Duration) versus spike number (A. P. Number) during the train is shown. The depolarizing current injection was 0.2 nA for the interneurons and 0.14 nA for the granule cell. Note that in the nonadapting cell neither the spike amplitude nor duration changed during the train. In contrast, marked changes in both of these parameters were apparent in all other cell types tested.B, Comparison of the effect of repetitive firing on the amplitude of the action potential. The bar graph depicts the amplitude of the fifth action potential of a train expressed as a percentage of the first action potential of the train in each of the three classes of interneurons and granule cells. In this figure, bars and error bars represent the mean ± SEM (**p< 0.01). C, Comparison of the effect of repetitive firing on the duration of the action potential. The bar graph represents the duration of the fifth spike of the train as a percentage of the duration of the first spike (**p < 0.01; ***p < 0.001). Note the striking lack of a change in the spike duration in nonadapting cells as compared with all other cell types.

During the course of a train of action potentials, action potential duration increased significantly in normally adapting and strongly adapting interneurons and in granule cells (Fig. 8). This increase in action potential duration was most dramatic on the second spike of the train, reaching a plateau by the fifth to seventh spike. The increase in duration was quite variable among neurons with the action potentials of some interneurons exhibiting very little increase, whereas the action potentials of others almost doubled in width. In contrast to normally adapting neurons, action potential duration in nonadapting interneurons did not increase or increased by only a small amount.

The reason for the increase in action potential duration during the train was further investigated by examining the maximal rate of rise and maximal rate of decay of the action potentials (Fig.9A,B). Comparison of the dV/dt ratio (ratio of rate of rise to the rate of fall) for the first and fifth action potential revealed a marked increase in this ratio for both normally adapting and strongly adapting interneurons (Fig. 9C). To determine whether this change reflected an increase in the maximal rate of rise of the action potential or a decrease in the maximal rate of decay, we compared the maximal rate of rise and decay of the action potential for each group of interneurons (Fig. 9D). This comparison revealed that the change in the dV/dt ratio reflected a decrease in the decay rate of the action potential for both normally adapting and strongly adapting interneurons, indicating that the increase in action potential duration was caused by a decrease in the repolarization rate of the action potential. For strongly adapting interneurons, however, the rate of rise of the action potential also was reduced, suggesting the presence of an additional mechanism. In contrast, nonadapting interneurons did not exhibit a significant increase indV/dt ratio, nor did they show a change in either the rising or falling rate of the action potential during the train.

Fig. 9.

dV/dt changes during repetitive firing. A, These tracesillustrate the typical patterns of spike morphology during repetitive firing. They depict superimposed waveforms of the first (solid lines) and fifth spike (dotted lines) in the different classes of cells during spike trains. Note the lack of a change in spike morphology in the nonadapting cell. In addition, note the characteristic changes in each of the other groups of cells. For example, in the normally adapting cell the action potential broadens because of a slowing of the repolarization rate and increases in amplitude. In contrast, in both the strongly adapting cell and the granule cell, the rise and decay of the action potential are slowed and the amplitude is reduced. B, The time derivatives of the spikes in A demonstrate the changes in the maximumdV/dt values. C, Comparison of dV/dt ratios during spike trains. The bar graph depicts thedV/dt ratio of the fifth spike expressed as a percentage of the dV/dt ratio of the first spike of a train of action potentials in each cell type. Bars and error bars represent mean ± SEM (**p < 0.01). D, Comparison of the maximal rates of rise and decay in different cell types. The dark bars on the graph represent the maximal rate of rise of the fifth spike of the train expressed as a percentage of the maximal rate of rise of the first spike. Similarly, the lighter gray columnsrepresent the maximal rate of decay of the fifth spike expressed as a percentage of the first spike. The first two columnsfrom normally adapting cells confirm that the spike broadening in this group of cells was caused by a decrease in the rate of repolarization in the spikes and that the rate of rise did not change significantly. In contrast, nonadapting cells showed no significant change in either measurement, and both strongly adapting interneurons and granule cells exhibited pronounced reductions in both measurements.

The mechanism underlying spike broadening in granule cells seemed to differ from that in interneurons. Despite considerable broadening of action potentials (Fig. 9A), the dV/dtratio of these spikes did not change (Fig. 9C). For these cells, however, this lack of a change in thedV/dt ratio reflected approximately equal and significant declines in the rate of rise and fall of the action potential (Fig. 9B,D).

Interestingly, when action potential broadening was compared in the interneurons divided according to their morphological type, GCL cells exhibited a complete lack of spike broadening, whereas TML- (p < 0.01), IML- (p < 0.05), and OML- (p < 0.05) projecting interneurons displayed a significant increase in action potential duration. GCL cells also showed no change in eitherdV/dt ratio, maximal rate of rise of the action potential, or maximal rate of decay of the action potential. This is in marked contrast to all other morphological groups of interneurons, which showed an increase in dV/dt ratio, corresponding to a decrease in the repolarization rate of the action potential.

fAHPs after action potentials correlate with SFA

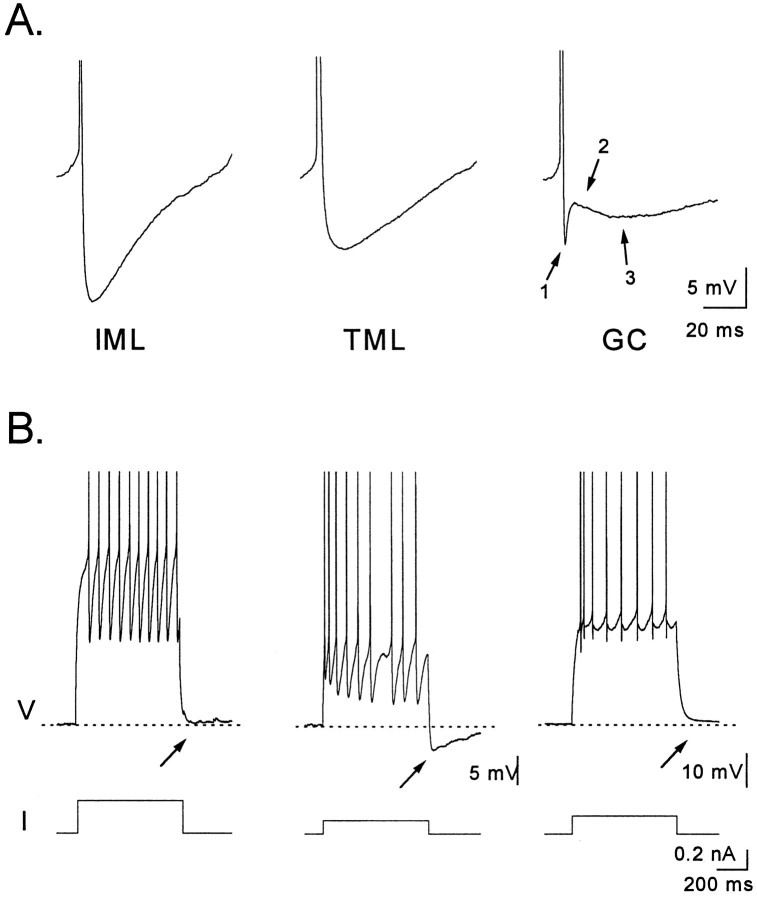
All interneurons displayed large monophasic fAHPs after action potentials, and the properties of these fAHPs are shown in Table5 and Figure 10. The amplitude of the fAHP after an action potential was dependent on membrane potential, increasing with depolarization. We measured fAHP amplitude at membrane potentials between −33 and −37 mV to account for this voltage dependence. The fAHP in normally adapting interneurons was significantly smaller (p < 0.05) than that in both nonadapting and strongly adapting interneurons. In general, the largest and fastest fAHPs were associated with action potentials in interneurons with the highest firing rates. The fAHP in granule cells (Fig. 10) was triphasic, with an initial hyperpolarization followed by a depolarization and then a later hyperpolarization as described previously (Assaf et al., 1981; Scharfman, 1992).

Table 5.

Properties of afterhyperpolarizations

	Cell type
	Normally adapting	Nonadapting	Strongly adapting	Granule cells
Fast afterhyperpolarization
Amplitude, mV	−7.2  ± 0.81	−14.4  ± 2.5	−12.2  ± 0.9	−11.2  ± 0.9
Slow afterhyperpolarization
Amplitude, mV	−1.7  ± 0.4	−0.5  ± 0.4	−3.9  ± 0.92,3	1.0  ± 0.34,5
Number of  spikes in the burst	8  ± 1	9  ± 3	9  ± 2	8  ± 1

This table shows the amplitudes of the fast afterhyperpolarizations (fAHPs) after individual spikes and the slow afterhyperpolarizations (sAHPs) after bursts of spikes in the different adaptation classes of interneurons and in granule cells.¹The amplitude of the fAHPs of both nonadapting and strongly adapting cells were greater than the fAHPs of normally adapting interneurons (p < 0.05). The sAHPs of strongly adapting cells were greater than the sAHPs of²normally adapting (p < 0.05) and³nonadapting (p < 0.01) interneurons. Granule cells did not have sAHPs and, in fact, the average potential after a burst in the granule cells was 1 mV depolarized [significantly different than the ⁴normally adapting, strongly adapting (p < 0.01) and ⁵nonadapting (p 0.05) interneurons]. The number of spikes in the bursts used for the measurements of the sAHP is given also.

Fig. 10.

AHPs of interneurons. A, Fast AHPs (fAHPs) from left to right are examples from a nonadapting (IML cell), normally adapting (TML cell), and a granule cell. Note the larger amplitude of the fAHP in the nonadapting cell. The triphasic appearance of the granule cell spike afterpotential with an initial fAHP (1), followed by a depolarizing phase (2), and then a slower hyperpolarizing phase (3) can be seen to contrast with the much less complex fAHPs of the interneurons. B, Bursts of 8–10 spikes (top traces) elicited by a depolarizing current injection (bottom traces) in the cells inA reveal that only the normally adapting interneuron, but not the nonadapting interneuron or the granule cell, is followed by a sAHP.

sAHPs correlate with SFA

After a burst of action potentials, many different types of neurons exhibit a sAHP. In this study we examined the sAHP by depolarizing each interneuron from rest to a level that would evoke a similar number (8–10) of action potentials and then measured the amplitude of the resulting sAHP (Table 5). We observed a sAHP in 15 of 16 normally adapting cells, 2 of 6 nonadapting cells, and 4 of 4 strongly adapting cells. The average amplitude of this sAHP differed substantially among these groups, with the largest sAHPs occurring in the cells with the strongest accommodation. Thus, the sAHP was largest in the strongly adapting neurons and significantly smaller in the group of normally adapting and nonadapting cells. Similarly, normally adapting cells had a substantially larger sAHP than the nonadapting cells (Fig. 10B). Interestingly, granule cells, which showed marked accommodation, did not exhibit a sAHP even when they were depolarized to −60 mV, close to the resting potential for interneurons.

Initial firing rate and pattern do not correlate with SFA

To examine the initial firing rates, we compared the frequency of the first two action potentials in each neuron evoked by a 700 msec, 0.2–0.3 nA depolarizing current pulse. We found no difference between the initial firing frequency of normally adapting and nonadapting neurons. In contrast, most strongly adapting neurons had a much higher initial firing frequency. Interneurons tended to have a greater initial firing frequency than granule cells, although with sufficient depolarization granule cells were capable of firing at frequencies equal to those achieved by interneurons.

To examine firing frequency further, we compared the rate of increase in spike frequency between interneuron groups as the intensity of the current pulse was increased. Graphs of spike frequency (from the first interspike interval) versus amplitude of the injected current (F–I curves) show a similar initial slope for normally adapting and nonadapting interneuron groups (Fig.11). Despite a similar initial firing frequency, nonadapting interneurons, because of their lack of accommodation, discharged more action potentials during a 700 msec depolarizing pulse than did all other neuron groups.

Fig. 11.

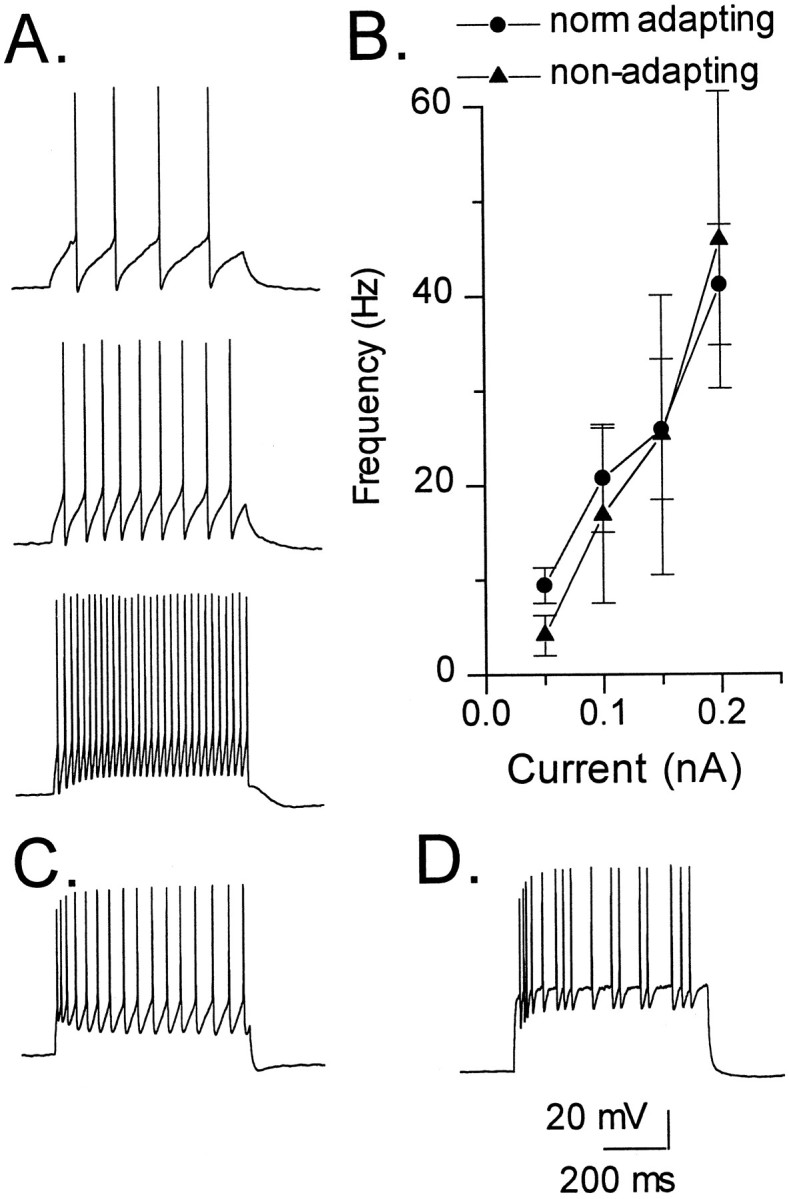
Frequency–current (F–I) curves and firing patterns of interneurons. A, This IML cell (shown in Fig.3B) is an example of the response of a nonadapting interneuron to increasing levels of depolarizing current (0.07, 0.1, and 0.2 nA, respectively). SFA was not apparent at any level of current injection. This cell fired action potentials in a continuous manner during a depolarizing current pulse. Note that this pattern of discharge remained constant even when the amplitude of the current pulse was increased. B,F–I curves of normally adapting (n = 12) (circles) and nonadapting (n = 4) (triangles) interneurons (symbols and error bars represent mean ± SEM). Note the lack of a difference in initial firing frequency between these groups of interneurons. C, D, Examples of TML cells with normal adaptation showing the two different patterns of discharge. The cell in C displays a continuous firing pattern in response to a 0.2 nA depolarizing current pulse, whereas the cell inD exhibits a discontinuous firing pattern in response to a 0.4 nA depolarizing current pulse.

Interneurons also differed in their pattern of action potential discharge during the current pulse (Fig. 11). These patterns of discharge were characterized as continuous firing (12 cells) and intermittent or discontinuous firing (14 cells). The pattern of continuous firing (Fig. 11A,C) was characterized by the regular discharge of the cell without erratic breaks or gaps in the train of action potentials during the current pulse. Cells from all three SFA groups displayed this firing pattern. The intermittent or discontinuous firing pattern (Fig.11D) was characterized by the presence of irregular gaps in the train of action potentials. This firing pattern was observed in interneurons, which in all respects seemed to be electrophysiologically “healthy.” In a few cells, the pattern of firing was reexamined at the end of the recording and remained consistent. The RMP, R_N, τ₀, and action potential height in neurons with this discontinuous firing pattern were no different from those in neurons displaying the continuous firing mode. Furthermore, this discharge pattern was evident immediately after breaking through the patch membrane at the beginning of the experiment and so is unlikely to represent cell run down. Firing pattern, whether continuous or discontinuous, did not seem to correlate with either SFA or morphology.

DISCUSSION

Our findings were the following: (1) In this sample of D/H border area interneurons, cells with ML-projecting axons outnumbered GCL cells; (2) interneuron electrophysiological properties did not usually correlate with the pattern of axonal arborization, although GCL cells may have some distinguishing features; (3) SFA was present in the majority of interneurons and was usually accompanied by spike broadening and sAHPs; and (4) a depolarizing hump and strong SFA distinguished a few interneurons.

Classification by axonal arborization

TML cells were the most common interneurons with axons targeting the ML without any clear preference for the OML or IML. Many of the TML cells may represent the pyramidal interneurons described bySoriano and Frotscher (1993) located in the D/H border area with extensive axonal arborization in the ML. The animals used in this study were 16–30 d old, and it is also possible that TML cells would be less frequent in older animals if the axon distribution were to become more laminated with maturation. Seress and Ribak (1990), however, reported that by 16 d the axonal plexus of basket cells was relatively mature and typically distributed, and therefore it is not clear that the axonal distribution of other dentate interneurons would be expected to change dramatically after 16 d.

OML cells resemble the hilar perforant pathway-associated (HIPP) cell of Han et al. (1993). OML cells could be somatostatin-containing cells like those described by Leranth et al. (1990) with both hilar and ML dendrites and OML axons. The IML cells probably correspond to the hilar commissural–associational pathway (HICAP) cell of Han et al. (1993). These cells may be examples of cholecystokinin-immunoreactive neurons with axons in the upper GCL and IML and dendrites in the hilus and ML (Sloviter and Nilaver, 1987; Freund and Buzsáki, 1996).

The paucity of GCL cells was unexpected because they are considered common in this area. Scharfman (1995), however, also reported finding few basket cells among D/H border area pyramidal interneurons. Furthermore, the somata of two of the five types of basket cells described in the dentate by Ribak and Seress (1983) were in the upper GCL or ML and would not have been sampled in our study.

Does morphology predict electrophysiology?

One question in the study of interneuron function is to what degree electrophysiology correlates with morphology (Kawaguchi and Hama, 1988; Buhl et al., 1994; Buckmaster and Schwartzkroin, 1995b; Scharfman, 1995). We did not find that passive membrane parameters and repetitive firing properties correlated with axon distribution. For example, of seven IML cells, three were nonadapting, two were normally adapting, and two were strongly adapting. Other investigators have also found variable electrophysiology in interneurons with similar morphology. Buhl et al. (1994) measured SFA in 10 axo–axonic cells during 500 msec depolarizing current injections and found one that actually increased its firing rate and nine others adapted with reductions of firing rate varying from a mere 2.5% to a striking 81%. The four most strongly adapting axo–axonic cells initially increased firing rate before the onset of accommodation and had an obvious depolarizing hump in the initial depolarization resembling the depolarizing hump in our strongly adapting cells.Scharfman (1995) also found striking variation in spike parameters and SFA among pyramidal interneurons at the D/H border.

Dendritic morphology of interneurons with similar axonal arborization can also vary significantly. Although the OML interneurons in this study are similar to the HIPP cell described by Han et al. (1993), there are important differences as well. The sparsely spinous dendrites of the HIPP cell were restricted to the hilus, and therefore this cell received no direct afferent input from the perforant path. The aspinous dendrites of our OML cells clearly arborized not only in the hilus, but in the ML also, including its outer two thirds, and could therefore receive strong input from the perforant path.

Inherent plasticity of electrophysiological properties could underlie the diverse behavior of these interneurons. SFA is probably a plastic property, and interneurons exhibiting SFA and sAHPs could be converted to cells with much less SFA and no sAHPs by neuromodulators such as norepinephrine (Madison and Nicoll, 1986) or cholinergic agonists (Lancaster and Nicoll, 1987; Storm, 1990; Zhang and McBain, 1995a). The firing properties of interneurons could reflect exposure to endogenous neuromodulators that might vary with conditions of the slice and innervation of the interneuron.

Even though we did not find correlation of axon distribution and electrophysiological properties in these interneurons, others have reported clear examples of electrophysiological anatomical correlations in interneurons in different areas. Lacaille and Schwartzkroin (1988)have described wide action potentials, anodal break excitation, and distinct firing modes of stratum lacunosum–moleculare interneurons of CA1 distinguishing them from basket and oriens/alveus CA1 interneurons.Kawaguchi and Hama (1988) reported that basket cell interneurons located in stratum pyramidale of CA1 had narrow spikes, no alteration in spike width during repetitive firing, and no SFA, whereas interneurons between the stratum radiatum and lacunosum had wider spikes and SFA. Buhl et al. (1996), comparing basket cells to bistratified cells in CA1, found that basket cells had less polarized resting potentials, lower input resistance, and shorter time constants than bistratified cells, but also found, as did we, that repetitive firing properties were quite variable even within the two groups. The dentate GCL cells we studied may have had distinctive properties, but the sample was very small and no differences reached significance. Our GCL cells had the most depolarized membrane potentials of the four interneuron morphological classes and the highest initial firing rates and did not show any spike broadening during a train; two of three were nonadapting.

Passive membrane properties of D/H border interneurons

The passive membrane properties of these D/H border cells are comparable to other studies using whole-cell recordings.R_N values of 198–252 MΩ compare well with an average of 240 mΩ for CA1 basket cells (Thurbon et al., 1994), although CA1 interneurons located near the stratum lacunosum moleculare and radiatum border have been reported to have higherR_N values averaging 352 MΩ (Williams et al., 1994).

Our physiologically determined L values for the interneurons were greater than those of granule cells, which seemed electrotonically short in comparison with the interneurons. Similarly, Soltesz and Mody (1994) noted that spiny hilar neurons were longer electrotonically than granule cells. Thurbon et al. (1994) also concluded that the physical compactness suggested by the dimensions of the processes of CA1 basket cells was not matched by electrotonic compactness. This suggests that synaptic currents in interneurons may undergo more electrotonic filtering than in granule cells. This is somewhat of a paradox, however, because both aspiny hilar neurons and D/H border interneurons have frequent and rapidly rising spontaneous EPSCs (Livsey and Vicini, 1992; Kneisler and Dingledine, 1995), suggesting that many synaptic inputs actually have minimal filtering to reach the soma. One property augmenting EPSPs seen in interneurons may be a greater density of postsynaptic excitatory amino acid receptors (Baude et al., 1995).

Action potential morphology and spike frequency adaptation

A shorter duration of spikes in “fast spiking” interneurons has been reported previously (Schwartzkroin and Mathers, 1978;McCormick et al., 1985; Kawaguchi and Hama, 1987b; Scharfman, 1992,1995) and our findings agree, because our nonadapting interneurons had shorter spikes than normally adapting interneurons.

A striking characteristic of adapting neurons was the progressive broadening and slowed repolarization of spikes. Progressive inactivation of a potassium conductance contributing to spike repolarization (Warman et al., 1994) could explain this. Both the transient potassium current and calcium-activated potassium currents have been found to contribute to repolarization of spikes in limbic system neurons (Zbicz and Weight, 1985; Storm, 1987, 1990). Recently,Zhang and McBain (1995a,b) reported that spike repolarization in area CA1 interneurons in stratum oriens–alveus involved three different potassium conductances: a transient potassium current (I_A), a sustained potassium current (I_K), and a calcium-activated potassium current (I_C). We suggest that the differences in spike broadening between nonadapting and adapting cells reflect differences in potassium currents causing repolarization, but comparative voltage-clamp studies will be needed to test this hypothesis. One possibility is that the deeper fAHP in nonadapting cells enables more effective de-inactivation of I_A, thus reducing spike broadening. Perhaps the larger fAHPs of nonadapting cells are attributable to larger I_C values, because the fAHP may be generated by I_C, which also plays a major role in spike repolarization (Zbicz and Weight, 1985; Storm, 1987; Warman et al., 1994; Ma and Koester, 1995). The functional relevance of spike broadening is unclear, although spike broadening in interneurons may augment GABA and neuropeptide release (Gainer et al., 1986; Erspamer et al., 1989; Augustine, 1990; Jackson et al., 1991; Ma and Koester, 1995).

In this study we found a correlation between SFA and the sAHP. This correlation is expected, because previous studies in pyramidal cells have shown that the sAHP plays an important role in SFA (Hotson and Prince, 1980; Madison and Nicoll, 1986; Lancaster and Nicoll, 1987;Storm, 1990; Sacchi et al., 1995). The larger sAHPs of adapting interneurons could have been linked to the spike broadening also seen in these cells, because wider spikes would admit more calcium, thereby causing larger calcium-activated sAHPs.

The four strongly adapting cells displayed depolarizing humps that augmented early firing frequency. Buhl et al. (1994) found similar depolarizing humps in a few strongly adapting axo–axonic cells in CA1 with prominent sAHPs analogous to our strongly adapting cells. We suggest that these properties are found not only in axo–axonic cells, but also in IML, TML, and GCL cells.

Conclusions

We conclude that there is a striking diversity in interneuron morphology and elementary electrophysiological responses. Even when these cells of the dentate are classified by axonal distribution patterns, there remains clear and important differences between the individual cells in each group. Our impression is that each interneuron may have a unique personality formed by its particular combination of morphological and electrophysiological properties. Furthermore, these properties are probably not fixed but would be expected to vary, depending on the local effects of neuromodulators. This tremendous diversity suggests that each interneuron may have a slightly different manner of relaying inhibitory influences to the many principal cells that it innervates.