Linearity and Normalization in Simple Cells of the Macaque Primary Visual Cortex

Abstract

Simple cells in the primary visual cortex often appear to compute a weighted sum of the light intensity distribution of the visual stimuli that fall on their receptive fields. A linear model of these cells has the advantage of simplicity and captures a number of basic aspects of cell function. It, however, fails to account for important response nonlinearities, such as the decrease in response gain and latency observed at high contrasts and the effects of masking by stimuli that fail to elicit responses when presented alone. To account for these nonlinearities we have proposed a normalization model, which extends the linear model to include mutual shunting inhibition among a large number of cortical cells. Shunting inhibition is divisive, and its effect in the model is to normalize the linear responses by a measure of stimulus energy. To test this model we performed extracellular recordings of simple cells in the primary visual cortex of anesthetized macaques. We presented large stimulus sets consisting of (1) drifting gratings of various orientations and spatiotemporal frequencies; (2) plaids composed of two drifting gratings; and (3) gratings masked by full-screen spatiotemporal white noise. We derived expressions for the model predictions and fitted them to the physiological data. Our results support the normalization model, which accounts for both the linear and the nonlinear properties of the cells. An alternative model, in which the linear responses are subject to a compressive nonlinearity, did not perform nearly as well.

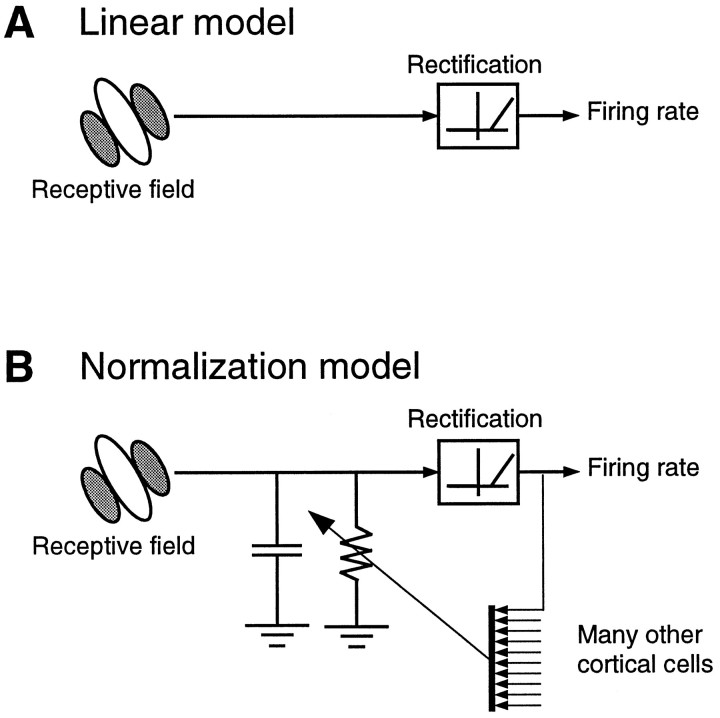
A longstanding view of simple cells in the primary visual cortex is that they compute a weighted sum of the light intensities falling on their receptive field (Hubel and Wiesel, 1962; Movshon et al., 1978a; Carandini et al., 1997b). Thislinear model is depicted in Figure1A and is usually taken to include a rectification (thresholding) stage to account for the transformation of intracellular signals into firing rates.

Fig. 1.

Two models of simple cell function. A, The linear model, composed of a linear stage(receptive field) and a rectification stage. The linear stage performs a weighted sum of the light intensities over local space and recent time. This sum is converted into a positive firing rate by the rectification stage. Rectification is a nonlinearity, so the “linear model” is not entirely linear. B, Thenormalization model extends the linear model by adding a divisive stage. The linear stage feeds into a circuit composed of a resistor and a capacitor in parallel (RC circuit). The conductance of the resistor grows with the pooled output of a large number of cortical cells. This effectively divides the output of the linear stage.

Although many aspects of simple cell responses are consistent with the linear model, there also are important violations of linearity. For example, scaling the contrast of a stimulus would identically scale the responses of a linear cell. At high contrasts, however, the responses of simple cells show clear saturation (Maffei and Fiorentini, 1973). Moreover, simple cells are subject to cross-orientation inhibition; the responses to an optimally oriented stimulus can be diminished by superimposing an orthogonal stimulus that is ineffective in driving the cell when presented alone (Morrone et al., 1982; Bonds, 1989; Bauman and Bonds, 1991).

According to a view that has emerged in recent years, the nonlinearities of simple cells could be explained by extending the linear model to include a gain control stage (Albrecht and Geisler, 1991; Heeger, 1991, 1992b, 1993; DeAngelis et al., 1992; Carandini and Heeger, 1994; Nestares and Heeger, 1997; Tolhurst and Heeger, 1997a,b). In particular, one of us (Heeger, 1991, 1992b) proposed anormalization model (Fig. 1B), in which the linear response of every cell is divided (or “normalized”) by a number that grows with the activity of a large number of cortical cells, the normalization pool. The normalization model attributes the selectivity of a cell to the initial linear stage and its nonlinear behavior to the division stage. For example, the model predicts response saturation because the divisive suppression increases with stimulus contrast, and the model predicts cross-orientation inhibition because the normalization pool includes neurons with a wide variety of tuning properties, many of which respond to orthogonal gratings.

Previously, we have suggested a possible biophysical implementation of the normalization model (Fig. 1B) (Carandini and Heeger, 1994). The cell membrane is modeled as anRC circuit, composed of a resistor and a capacitor in parallel. The linear stage injects synaptic current into the cell, and normalization operates by controlling the conductance of the resistor, i.e., the membrane conductance. The cells in the normalization pool effectively inhibit each other by increasing the membrane conductance of each other. This shunting inhibition controls the gain of the transformation of input current to output membrane potential. A rectification stage converts the latter into a firing rate.

To test this model against large data sets obtained in monkey primary visual cortex, we recorded the responses of simple cells in area V1 of paralyzed, anesthetized macaques, while presenting a variety of visual stimuli. These stimuli included drifting gratings, plaids composed of two drifting gratings, and drifting gratings superimposed on full-screen spatiotemporal white noise. The gratings had a wide range of contrasts, temporal frequencies, spatial frequencies, and orientations. We derived equations for the model responses to such stimuli, and we found that these equations provided good fits to the neural responses.

Portions of this work have been presented briefly elsewhere (Carandini and Heeger, 1994, 1995).

MATERIALS AND METHODS

Experiments were performed on five cynomolgus macaque monkeys (Macaca fascicularis) and four pigtail macaque monkeys (M. nemestrina) ranging in weight from 1.5 to 4 kg.

Preparation and maintenance

Animals were initially anesthetized with ketamine HCl (10 mg/kg) and premedicated with atropine sulfate (0.05 mg/kg) and acepromazine maleate (0.1 mg/kg). Anesthesia continued on 1.5–2.0% halothane in a 98% O₂–2% CO₂ mixture while the initial surgery was performed. Indwelling catheters were introduced into the saphenous veins of each hindlimb, and a tracheotomy was performed.

The animal was then mounted in a stereotaxic instrument, and halothane anesthesia was replaced by a continuous infusion of sufentanil citrate (typically 4–6 μg·kg⁻¹·hr⁻¹, beginning with a loading dose of 4 μg/kg). EEG, ECG, and arterial blood pressure were monitored continuously, and any signs of arousal were corrected by modifying the rate of anesthetic infusion. The monkey was artificially respirated with a mixture of O₂, N₂O, and CO₂ adjusted so that end-tidal CO₂ was maintained at 3.8–4.0%. Rectal temperature was kept near 37°C with a heating pad.

A small craniotomy was performed, usually 9–10 mm lateral to the midline and 3–4 mm posterior to the lunate sulcus. This location often yielded two encounters with the primary visual cortex, with eccentricities first at ∼2–5° and then at ∼8–15°. A small slit in the dura was made, and a vertical hydraulic microdrive containing a glass-coated tungsten microelectrode (Merrill and Ainsworth, 1972) in a guide tube was positioned. The craniotomy was covered with a chamber containing 4% agar in sterile saline solution.

On completion of surgery, animals were paralyzed to minimize eye movements. Paralysis was maintained with an infusion of vecuronium bromide (Norcuron, 0.1 mg·kg⁻¹·hr⁻¹) in lactated Ringer’s solution with dextrose (5.4 ml/hr). The pupils were dilated and accommodation paralyzed with topical atropine. The corneas were protected with zero power gas-permeable contact lenses; supplementary lenses were chosen to focus the eyes on a tangent screen plotting table set up at a distance of 57 in. To maintain the animal in good physiological condition during experiments (typically 72–96 hr), intravenous supplementation of 2.5% dextrose/lactated Ringer’s was given at 5–15 ml/hr. Animals received daily injections of a broad-spectrum antibiotic (Bicillin) as well as an anti-inflammatory agent (dexamethasone) to prevent cerebral edema.

Stimuli

Stimuli were generated by a Truevision ATVista board operating at a resolution of 582 × 752 and a frame rate of 106 Hz, the output of which was directed to a Nanao T560i monitor (mean luminance, 72 cd/m², subtending 10–25° of visual angle). Nonlinearities in the relation between applied voltage and phosphor luminance were compensated by appropriate look-up tables. Stimulus strength is measured in units of contrast, defined as the difference between the highest and lowest intensities, divided by the sum of the two.

Drifting luminance-modulated sinusoidal gratings were presented alone or superimposed on another grating or on a noise background. Superposition was obtained by interleaving, i.e., by presenting the two components in alternate frames. When two gratings were presented together they had the same temporal frequency and differed in orientation and/or spatial frequency. Their contrast could be varied independently. The noise background was composed of square pixels, the size of which was chosen for each cell to be approximately one-fourth of the spatial period of the optimal grating. Occasionally we used one-dimensional noise (bars rather than squares). The intensity of each square was randomly refreshed at 13.4 or 26.8 Hz and assumed one of two possible values.

All the stimuli had the same mean luminance. The grating and plaid stimuli were vignetted by a square window, the size of which was chosen to elicit the maximal responses. The noise masks occupied the whole screen. In their absence the surrounding field was uniform.

Experiments. Experiments consisted of two to nine consecutive blocks of stimuli. Each block consisted of a random permutation of 5–90 stimuli. Randomization was adopted to minimize the effects of adaptation and other nonstationarities. The stimuli had equal duration (generally 5–10 sec) and were separated by uniform field presentations lasting about 4 sec.

Experimental protocol. Receptive fields were initially mapped by hand on a tangent screen. When the activity of a single neuron was isolated, we established the dominant eye of the neuron and occluded the other eye. We then positioned the receptive field on the face of the monitor, and quantitative experiments proceeded under computer control.

To characterize each cell we performed the following sequence of measurements using single gratings: (1) orientation and direction tuning; (2) spatial frequency tuning; (3) temporal frequency tuning; and (4) stimulus size tuning. Each of these measurements was performed at the optimal values of the parameters as obtained from the previous measurements. Cells were classified as simple or complex on the basis of the frequency component of their response to the drifting grating eliciting the maximum number of spikes, as classified by Skottun et al. (1991). If the cell was simple we proceeded to the core experiments in this study. These were of three types:

(1) Grating matrix experiments, consisting of drifting sinusoidal stimuli having 5–10 different contrasts, two to four different temporal frequencies, and two to four different orientations or spatial frequencies. A typical experiment would involve three orientations or spatial frequencies, three temporal frequencies, and five contrasts, yielding a total of 45 stimuli.

(2) Plaid experiments, consisting of sums of two gratings with contrasts that were independently varied. Often the two directions were opposite, and the “plaid” was a counterphase flickering grating. A typical experiment would involve two orthogonal gratings with contrasts that assumed five possible values, yielding a total of 25 different stimuli.

(3) Noise-masking experiments, in which the contrast response to drifting gratings was measured in the presence of noise at different contrasts. A typical experiment would involve nine grating contrasts and two noise contrasts (0 and 0.5), yielding a total of 18 different stimuli.

Data analysis

Amplified and bandpass-filtered signals from the microelectrode were fed into a hardware window discriminator. A computer interface (Cambridge Electronic Design 1401 Plus) collected the pulses triggered by each action potential and the synchronization signals from the video graphics board.

Response measure. Our measure of cell response is thefirst harmonic r of the spike trains, a complex number indicating the amplitude and phase of the best-fitting sinusoid having the same temporal frequency as the stimulus. This number is obtained from the spike train by computing r = (1/D)Σ_k cos (2πft_k) + i sin (2πft_k) , where D is the stimulus duration, f is the temporal frequency of the stimulus, and the t_k are the times of the individual spikes. The amplitude of the first harmonic has units of spikes per second. The responses r obtained in an experiment constitute a matrix r = {r_s,b} , where the subscripts indicate the s th stimulus presented in the b th stimulus block. We denote the mean across blocks of the responses as the vector $\overline{r}$ = {r_s} . For example, in an experiment in which three blocks of 25 different stimuli were run, the matrix r would contain 75 elements, and the vector$\overline{r}$ would contain 25 elements.

Correction for eye movements. Inspection of the spike rasters often revealed a few discrete misalignments across stimulus blocks in the responses to individual stimuli, which are best explained by the presence of small eye movements. For drifting grating stimuli the sole effect of these eye movements would be a shift in response timing. We reduced this effect by shifting in time all the responses in each block by an amount chosen to minimize ς_s², the variance across blocks of the responses. Because all the responses in a block are translated by the same amount, this method would completely remove the effect of the movements only if they occurred exactly between blocks. In all other cases it is just an approximation that reduces the variance of the data. No attempt was made to correct the effect of possible eye movements on the responses to plaids or to gratings in the presence of noise.

Estimation of the variance. The number of blocks in our experiments (two to nine) was not sufficient to obtain reliable estimates of the variance ς_s² of the responses to each stimulus s . For this reason we estimated the dependence of ς_s² on ‖r_s‖ , the amplitude of the mean responses. As a functional form for this dependence we chose the simple relation ς_s² = α ‖r_s‖^β, where α and β are free parameters. This expression provided very good fits to the data. In the fits, the scale factor α was on average 2.11 ± 0.18, and the exponent β was on average 1.18 ± 0.02, consistent with previous findings that the variance of the responses of V1 neurons is proportional to their mean (Dean, 1981b; Tolhurst et al., 1983;Bradley et al., 1987; Vogels et al., 1989).

Model fits. The models discussed in Results were fit to the responses to all stimuli in an experiment. Different experiments were fitted independently and thus yielded different sets of parameters. To fit the predictions of a model m = {m_s} to the data we performed a weighted least squares fit; i.e., we searched for the parametersa that minimized the error function

$$\text{Error}(\mathbf{\text{a}})=\sum _{\text{s}}\Vert m_{\text{s}}(\mathbf{\text{a}})-r_{\text{s}}{\Vert }^2/{\varsigma }_{\text{s}}^2,$$

where the ς_s² are the estimated variances. To avoid giving too much importance to data points of low amplitude, when fitting the models of the visual responses we took all the ς_s² < 1 to be equal to 1.

Percentage of the variance. To gain an intuitive assessment of the quality of the fits provided by a model, we computed the percentage of the variance across stimuli for which the model accounted. To define this measure it is useful to consider the (mean square) distance between two sets of responses x = {x_s} and y = {y_s} :

$$d(\mathbf{\text{x}},\mathbf{\text{y}})=1/N \sum _{\text{s}}\Vert x_{\text{s}}-y_{\text{s}}{\Vert }^2,$$

where the sum is over the stimuli s , and N is the number of stimuli. The percentage of the variance accounted for by the model may then be expressed as:

$$\%\text{variance}=100\ast [1-d(\mathbf{\text{m}},\overline{\mathbf{\text{r}}})/d(\overline{\mathbf{\text{r}}},\stackrel{̿}{\mathbf{\text{r}}})],$$

where $\overline{\overline{r}}$ is the response mean computed across stimuli and across blocks. In this expression, the numerator is the distance between the model predictions and the mean cell responses; the denominator is the variance across stimuli of the mean cell responses. For example, if the model predicts the mean responses exactly, then it accounts for 100% of the variance. More realistically, if the mean error between the model predictions and the responses is d (m, $\overline{r}$) = 10 spikes/sec, and the responses in the data set have very different amplitudes and/or phases, so that their variance is large, say d ($\overline{r}$,$\overline{\overline{r}}$) = 100 spikes/sec, then the model accounts for 90% of the variance in the data.

Bootstrap test. Although the percentage of the variance is an intuitive measure of the quality of the fits, it has the disadvantage of taking into account only the variability across stimuli and not the variability across blocks. If a cell were very noisy, our experiments would yield bad estimates of its mean responses r_s; in this case the model would account for a small percentage of the variance in the data even if it reflected the exact physical reality underlying the responses. To test the quality of the model predictions taking into account all the statistical properties of the data, we performed a bootstrap hypothesis test (Efron and Tibshirani, 1991). The advantage of bootstrapping is that it does not assume that the response variability follows a particular (e.g., Gaussian) distribution.

We tested whether we could reject the null hypothesis that the mean of the probability distribution underlying the neural responses was identical to the predictions of the model. Letr_b be the vector of responses obtained in the b -th block of stimuli. If for example an experiment involved 25 different stimuli and was repeated four times, there would be four vectors of responses, r₁,r₂, r₃, andr₄, and each would contain 25 elements. Let m be the prediction of the model obtained by fitting all the r_b. The null hypothesis states that the mean μ_r of the probability distribution from which ther_b are drawn is identical to the prediction of the model:

$$H_0:{\mu }_{\text{r}}=\mathbf{\text{m}}.$$

As a test statistic we chose the distance between the model predictions and the empirical average of the responses:

$$t=d(\mathbf{\text{m}},\overline{\mathbf{\text{r}}}).$$

Having observed a value t^obs by evaluating the test statistic on the actual experimental data, we calculated the probability of observing at least that large a value if the null hypothesis were true. This probability is the achieved significance level (ASL) of the test:

$$ASL=\text{Prob}\{t\ge t^{\text{obs}}\Vert H_0\}.$$

The smaller the ASL, the stronger the evidence against H₀.

To compute the ASL with the bootstrap method, we converted our data setr into one with an empirical distribution function that obeyed H₀. This was simply done by shifting the data so that the mean responses were exactly equal to the model predictions,r̃ = r − $\overline{r}$ +m (Efron and Tibshirani, 1993). We then computed the bootstrap estimate of the ASL by repeating the following steps 1000 times: (1) Draw a sample data set r* with replacement fromr̃. For example, if the experiment was repeated four times, a possible draw would be r* = {r̃₄r̃₁r̃₂r̃₂}; another one could be r* = {r̃₂r̃₁r̃₂r̃₃}, and so on. (2) Compute the test statistic on the sample, t* = d(m, $\overline{r}$* ) .

The bootstrap estimate of the achieved significance level of the test is equal to the percentage of samples for which the t * values are larger than the observed value t^obs.

MODEL

The normalization model is depicted in Figure1B. To keep the model mathematically tractable, we adopt a number of simplifications. To begin, we define thedriving current of a simple cell to be the current that would be measured by clamping the voltage of the cell at rest. Then we assume that (1) the relation between the visual stimuli and the driving current is linear; (2) the cell membrane is a single passive compartment; (3) the firing rate is a rectified copy of the membrane potential; (4) cells inhibit each other (possibly through inhibitory interneurons) by increasing the membrane conductance of each other; and (5) the pool of cells that inhibit each other contains cells tuned to a wide variety of stimulus attributes.

The linear stage. As a visual stimulus is projected on the retina it can be described by its light distribution, l(x,y,t) , which varies in the two spatial dimensions x,y and in time t . This representation ignores the color of the stimulus and assumes monocular viewing. The light distributions of the stimuli used in this study modulated about a fixed mean $\overline{l}$. In these conditions the output of the retina is to a first approximation proportional to the local contrast, c(x,y,t) = [l(x,y,t) − $\overline{l}$]/ $\overline{l}$ (Shapley and Enroth-Cugell, 1984). We will use the term contrast and the symbol c (without arguments) to denote the maximal value of the local contrast c(x,y,t) . A uniform field has zero contrast, whereas a grating modulating between zero and twice its mean intensity has unit contrast.

We consider the driving current in simple cells to be linearly related to the output of the retina and thus to the local contrast. The driving current I_d(t) is obtained by weighting the local stimulus contrast c(x,y,t) at each location and time by the value of the receptive field W of the cell at that location and at that time, and by algebraically summing the results:

$$I_{\text{d}}(t)=\iiint W(x,y,T)c(x,y,t-T)\text{dx dy dT}.$$ Equation 1

This linear equation is at best an approximation. Possible biophysical conditions that would lead to it being exact were suggested in a previous study (Carandini and Heeger, 1994), and are summarized in Discussion.

In this study, the driving current I_d (and thus the receptive field W ) will be estimated rather than measured directly. Direct measurement of I_dwould require intracellular in vivo voltage-clamp experiments.

RC circuit. We adopt an extremely simplified biophysical model of a cell membrane: a circuit composed of a resistor and a capacitor arranged in parallel (RC circuit). According to this model, the membrane potential V(t) obeys the following equation:

$$\text{CdV}/\text{dt}+\text{gV}=I_{\text{d}},$$ Equation 2

where C is the membrane capacitance, g(t) is the total membrane conductance, and I_d(t) is the driving current. In the absence of visual stimuli the driving current is zero, and the membrane potential is driven to its resting value, which we have taken to be zero.

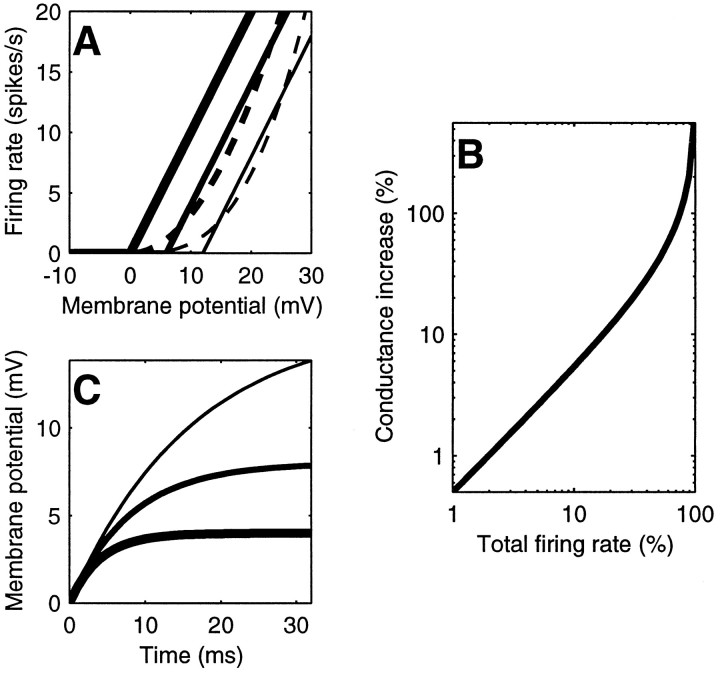
Rectification. As a first approximation, the transformation from the membrane potential V to the spike rate R can be modeled by rectification (Movshon et al., 1978b;Jagadeesh et al., 1992; Carandini et al., 1996). Rectification is a function that is zero for membrane potentials below a threshold, V_thresh, and grows linearly: R(t) ∝ max (0, V(t) − V_thresh) . This function is depicted for three different values of the threshold V_thresh by the straight lines in Figure 2A.

Fig. 2.

Interrelations and effects of the principal variables in the normalization model. A, Relation between membrane potential V and firing rate R . For simplicity in this study the resting potential is taken to be V = 0. The thick, intermediate, andthin lines depict rectification with thresholds V_thresh = 0, 6, and 12 mV, respectively. Thedashed curves indicate approximations to rectification obtained with power functions, with exponents n = 2 (thick dashes) and n = 3 (thin dashes). B, Relation between pool activity and membrane conductance. The abscissa plots the overall response of the pool, k Σ R ; the ordinate plots the increase in membrane conductance g/g₀ − 1 (Eq. 4).C, Effects of conductance on the size and time course of the membrane potential responses. The curves are the membrane potential responses to a current step with onset at time zero, for three different values of the conductance g . As the conductance doubles (thin to thick curves), it reduces both the gain and the time constant of the cell.

Rectification is however not very easily handled in mathematical derivations. We thus approximate rectification (V_thresh > 0) with half-rectification (V_thresh = 0) followed by elevation to the power n :

$$R\propto max(0,V{)}^n.$$ Equation 3

The quality of this approximation is shown by the dashed curves in Figure 2A. The value of the exponent n grows with the distance of the threshold V_thresh from the resting potential V_rest. If the threshold is very close to rest, then n ≈ 1 (“half-rectification”). If the threshold is a bit above rest, e.g., 6 mV higher, then n ≈ 2 (“half-squaring”). If the threshold is far above rest, then n ≈ 3 or more.

Conductance and cortical activity. We now make the central assumption that cells belong to a normalization pool, the members of which inhibit each other by increasing the conductance g of each other. This form of inhibition is known asshunting inhibition and unless all the neurons in the pool are inhibitory would require the presence of inhibitory interneurons.

The particular function that we choose to relate the conductance g and the overall activity of the pool Σ R is illustrated in Figure 2B. Its mathematical expression is

$$g=g_0/\sqrt{1-k\sum R},$$ Equation 4

where the parameter k determines the effectiveness of the normalization pool. This function is completely ad hocand is not currently supported by physiological evidence. Our reasons for choosing it are evident in , in which we derive closed form equations for the responses of the model.

The membrane conductance g affects both the size and the time course of the responses. Figure 2C shows the responses of the membrane to a current step for three values of the conductance g . If the conductance is very small, the response is slow, and there is high gain (that is, the voltage response to a given current is high). If the conductance g is very large (the membrane is very leaky), it has small gain and is fast in charging and discharging the capacitor.

The conductance of each cell is minimal in the absence of any visual stimulus, because all of the cells in the normalization pool are silent. The conductances are larger for a visual stimulus that is effective in driving the cells in the pool. This decreases the gain and the time constant of the cells in the pool so that they are more responsive and better able to follow the fine temporal changes of the stimulus.

The normalization pool. Our final assumption regards the composition of the normalization pool. We assume that the cells in the pool are tuned to all stimulus orientations and directions and to a broad range of spatial and temporal frequencies.

Solution of the model. The variables in the model depend on each other in a circular way: (1) the firing rate R of each cell depends on its membrane potential V (Eq. 3; Fig.2A); (2) the membrane potential V of each cell depends on its driving current I_d and on its conductance g (Eq. 2); and (3) the conductance g of each cell depends on Σ R , the total firing rate of the cells in the normalization pool (Eq. 4; Fig.2B). This arrangement results in negative feedback, because increases in the overall response Σ R increase the conductance g , which in turn reduces the overall response Σ R . This guarantees that the conductance g remains finite (Σ R < 1/k in Eq. 4).

The model is a nonlinear neural network (Grossberg, 1988) and is in general quite complicated, because both the driving current and the conductance vary over time. Nevertheless, the model was designed so that for the visual stimuli used in this study—drifting sine gratings, plaids, and noise—we can derive approximate closed form equations for its responses. These equations, together with their derivation, are detailed in .

RESULTS

We report here on 149 data sets obtained from a total of 54 cells that were clearly identified as simple and were held long enough to be tested with at least two blocks of one of the core experiments in our protocol. In particular, we report on 51 grating matrix experiments from 34 cells, 76 plaid experiments from 27 cells, and 22 noise-masking experiments from 17 cells.

The cells in the sample exhibited a broad spectrum of tuning properties. The orientation tuning of the cells ranged from 14° to 124° half-width, with one-third of the cells showing a tuning sharper than 24° and one-third broader than 51°. The directional index of the cells (DI; Reid et al., 1987) ranged over the whole spectrum from 0 to 1. Direction selectivity was prominent (DI > 0.6) in about one-third of the cells.

Responses to gratings

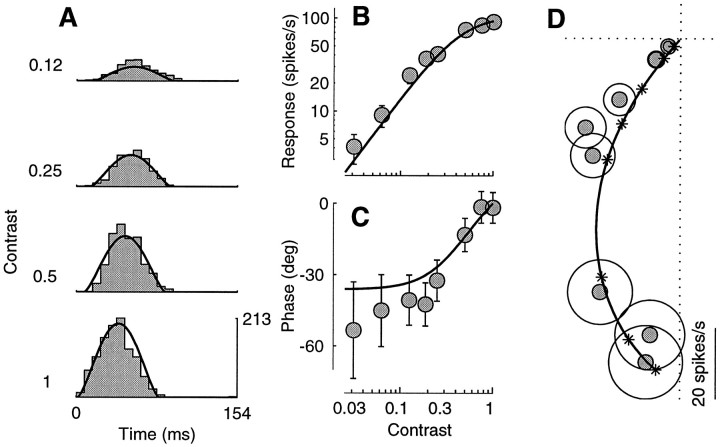
Figure 3A shows the period histograms of the responses of a typical simple cell to drifting sinusoidal gratings with four different stimulus contrasts. Consistent with the linear model, the responses look like rectified sinusoids.

Fig. 3.

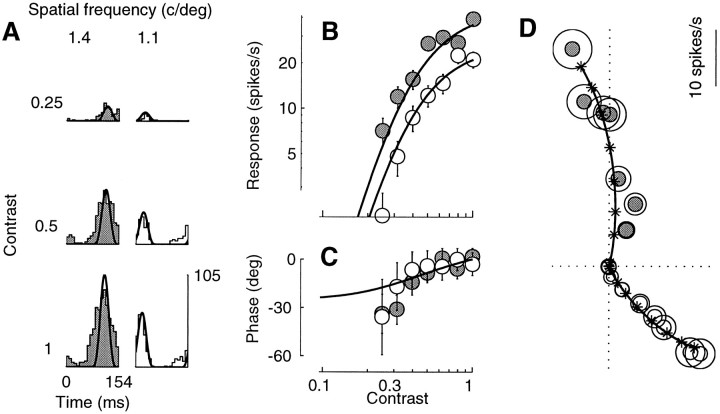
Responses to drifting sine gratings of different contrasts. The curves are fits of the normalization model. The fits were performed on a larger data set, which included the responses to 72 different drifting gratings (8 contrasts, 3 orientations, and 3 temporal frequencies). A, Period histograms of the responses to four different contrasts. Scale bar in spikes per second. B, C, Response amplitude and phase as a function of contrast, computed from the first harmonic of the spike trains. D, Polar plot of the responses in B andC. Every point in the plot corresponds to a sinusoid with an amplitude that is given by the distance from the origin, and the phase of which is given by the angle with the horizontal axis. As the contrast increases the responses get larger (far from the origin), and their phases advance (they turn counterclockwise). Asterisks indicate the predictions of the normalization model at the different stimulus contrasts.Circles have radius 1 SEM (N = 3) computed from the estimated variance. Error bars in B andC are ±1 SEM, computed from circles inD. Cell 392l008 [directional index (DI) = 0.1; preferred spatial frequency (SF) = 0.9 cycles/°, stimulus size (SZ) = 4.5°], experiment 4. Parameters: τ₀ = 37 msec; τ₁= 9 msec; n = 1.34.

Dependence on contrast

There are subtle aspects of the responses that are not consistent with a strictly linear model. One is response saturation(Maffei and Fiorentini, 1973; Dean, 1981a; Albrecht and Hamilton, 1982;Ohzawa et al., 1982; Li and Creutzfeldt, 1984; Sclar et al., 1990;Bonds, 1991; Carandini and Heeger, 1994). For a linear neuron, scaling stimulus contrast by a certain amount would scale the responses by the same amount. The responses of the cell in Figure 3, instead, increase only marginally as the contrast doubles from 0.5 to 1. Another nonlinearity is reflected in the latency of the responses. For a linear cell response latency would be unaffected by stimulus contrast. Simple cells, instead, display phase advance (Dean and Tolhurst, 1986; Carandini and Heeger, 1994; Albrecht, 1995); i.e., they respond sooner to high-contrast stimuli than to low-contrast stimuli. For example, the cell in Figure 3 responds ∼20 msec sooner to the stimulus with unit contrast than to the stimulus with 0.12 contrast.

These effects on response size and latency are reflected in the amplitude and phase of the first harmonic of the responses (Fig.3B,C). For contrasts <0.2 the amplitudes (Fig.3B) grow roughly linearly with contrast (the slope in double logarithmic coordinates is close to 1), and the phases (Fig.3C) stay substantially constant. As the contrast increases, the amplitudes saturate and the phases advance.

Figure 3D replots the data in the polar plane where response amplitude is represented as distance from the origin, and response phase is represented as the angle with the horizontal axis. As the contrast increases the data points get farther from the origin (response amplitude increases), and they turn counterclockwise (response phase advances).

The predictions of the normalization model are characterized by two equations, one for response amplitude and one for response phase. The best fit model parameters were determined by simultaneously fitting both the amplitude and phase of the responses. The model captures the saturation in response amplitude (Fig. 3B) because it postulates that increasing contrast increases the activity of the normalization pool, which increases the membrane conductance, and thus decreases the gain of the membrane. The model captures the advance in response phase, because the increase in membrane conductance decreases the time constant, so at high contrasts the membrane introduces shorter delays than at low contrasts. The fits provided by the normalization model are substantially more accurate than those provided by the linear model; according to the linear model the data in Figure 3Bshould lie on a diagonal line (no amplitude saturation), and the data in Figure 3C should lie on a horizontal line (no phase advance).

The equations for response amplitude and phase predicted by the model are derived in . We present here the equation for response amplitude, because it helps further illustrate the behavior of the model. According to the model, the amplitude of the responses R of a simple cell to a grating of contrast c and temporal frequency f is:

$$\text{amplitude}(R)={\left[\text{amplitude}(L)\frac{c}{\sqrt{\varsigma (f{)}^2+c^2}}\right]}^n,$$ Equation 5

where the quantities L, ς(f) , and n are determined, respectively, by the linear, normalization, and rectification stages of the model (Fig.1B). L is the response of the linear receptive field of the cell to the grating at unit contrast (Eq. 1). The normalization stage divides this quantity by $\sqrt{\varsigma (\text{f}{)}^2+{\text{c}}^2}$, where ς(f) grows with the temporal frequency f of the stimuli. Finally, n is the exponent of the rectification stage (Eq. 3; Fig. 2A).

The dependence of response amplitude on stimulus contrast is quite simple; at low contrasts, c ≪ ς(f) , the denominator is approximately constant, and the responses grow as cⁿ. At high contrasts, instead, the c in the denominator has a strong effect, and the responses saturate. Equation 5 is similar to a hyperbolic ratio, which was empirically found to provide good fits to the amplitude of the contrast responses of V1 cells (Albrecht and Hamilton, 1982; Sclar et al., 1990). Indeed, our ad hoc choice of the dependence of conductance on the activity of the normalization pool (Eq. 4) was made with this expression in mind.

Different orientations

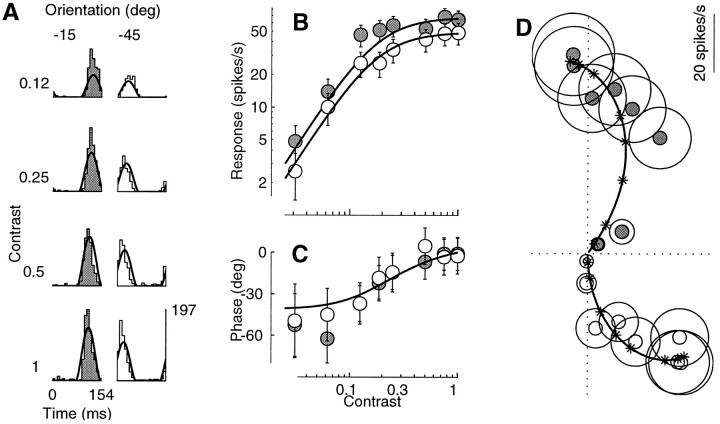
Figure 4 shows the contrast responses of a simple cell to two drifting gratings differing in their orientation. As shown in Figure 4A, the responses elicited by the grating drifting at −15° (left column) were ∼40% larger than those elicited by the grating drifting at −45°. This proportion remained substantially constant in the face of prominent saturation above a contrast of 0.25.

Fig. 4.

Responses to drifting sine gratings at two different orientations, −15° (gray) and −45° (white). Fits of the normalization model (curves) were performed on a larger data set than shown, which included 72 stimulus conditions (8 contrasts, 3 orientations, and 3 temporal frequencies). A, Period histograms. Rowscorrespond to different contrasts, columns to different orientations. B, C, Response amplitude and phase as a function of contrast. To facilitate comparison in C the responses to each grating were shifted vertically so that the values predicted by the model would overlap. D, Polar plot of the responses in B and C. Cell 392l009 (DI = 0.5; SF = 0.4; SZ = 2.2), experiment 8; N = 3. Parameters: τ₀ = 28 msec; τ₁ = 3 msec;n = 1.6.

This property can be observed more precisely in Fig.4B. The contrast responses obtained at the two different orientations are vertical shifts of each other on a logarithmic response scale, implying that the ratio of the responses to different orientations was constant, irrespective of the stimulus contrast. Another way to describe this behavior is to say that the orientation tuning scaled with contrast, a property that has been repeatedly observed for both orientation tuning and spatial frequency tuning (Movshon et al., 1978c; Albrecht and Hamilton, 1982; Sclar and Freeman, 1982; Li and Creutzfeldt, 1984; Skottun et al., 1987).

As with response saturation, phase advance was controlled by the contrast of the stimulus per se, rather than by the firing rate of the cell. Even though the absolute phases of the responses to the two gratings differed by about 180° (Fig. 4D) the relative timing of the responses (difference in response phase) was independent of stimulus contrast. This is illustrated in Fig.4C, where the phases of the responses to each grating were shifted vertically so that the fits provided by the normalization model would overlap.

The curves predicted by the normalization model provided good fits to the data in Figure 4. Because saturation and phase advance depend on the stimulus contrast, and not on the size of the responses elicited in a cell, their presence is not simply the result of nonlinearities in the spike-encoding mechanism or in other attributes of a single cell. Rather, their presence indicates the existence of a contrast gain control mechanism in the visual cortex such as that described by the normalization model.

In fact, the model mandates the orientation invariances in the contrast responses, both in amplitude and in phase. In the expression for the response amplitude (Eq. 5), stimulus contrast and stimulus orientation are separable. The expression can be seen as the product of two factors, [amplitude (L) ]ⁿ and (c/ $\sqrt{\varsigma (\text{f}{)}^2+{\text{c}}^2}$)ⁿ. The first factor depends on L , the response of the linear receptive field of the cell to the grating at unit contrast, so it depends on orientation but not on contrast. The second factor depends only on the contrast c and on the temporal frequency f of the grating. For a fixed temporal frequency the shape of the contrast responses is entirely controlled by this second factor, which is independent of stimulus orientation. A similar argument can be made for the phase responses predicted by the model: the expression for response phase (, Eq. 13) is the sum of two terms, one that depends on stimulus orientation but not on contrast, and one that depends on stimulus contrast but not on orientation.

Different spatial frequencies

Changing the spatial frequency of a grating had the same effect on the contrast responses as changing orientation; response amplitude was shifted vertically on a logarithmic scale, and response phase was shifted vertically on a linear scale. Figure5 shows an example in which the responses elicited by the 1.4 cycles/degree grating (Fig. 5A, left column) were ∼70% larger than those elicited by the 1.1 cycles/degree grating (right column). This proportion held substantially constant in the face of response saturation. The fits of the normalization model (continuous curves) capture all these properties of the responses. Indeed, the very same argument about separability in the model responses of contrast and orientation can be made for contrast and spatial frequency.

Fig. 5.

Contrast responses for gratings with two different spatial frequencies: 1.4 (gray) and 1.1 (white) cycles/degree. Fits of the normalization model (curves) were performed on a larger data set than shown, which included 40 stimulus conditions (10 contrasts, 2 spatial frequencies, and 2 temporal frequencies). Contrasts <0.12 elicited <1 spike/sec. A, Period histograms. Rows correspond to different contrasts, columns to different spatial frequencies. B, C, Response amplitude and phase as a function of contrast. Responses to each grating in C were shifted vertically so that their values predicted by the model would overlap. D, Polar plot of the responses in B andC. Cell 382l019 (DI = 0.8; SF = 1.4; SZ = 1.9), experiment 5; N = 6. Parameters: τ₀= 18 msec; τ₁ = 8 msec; n = 4.

Different temporal frequencies

Changes in the stimulus temporal frequency had very different effects from changes in orientation or spatial frequency. In particular the above-mentioned invariances of the contrast responses did not hold for stimuli differing in temporal frequency. Rather, we found that increasing the temporal frequency increased the contrast at which the responses saturated and decreased the total phase advance. Similar results (for the amplitude of the responses) were obtained in the cat by Holub and Morton-Gibson (1981) and in the monkey by Hawken and collaborators (1992; also see Albrecht, 1995, ).

Figure 6 illustrates these phenomena. At low temporal frequencies the responses saturated at low contrasts (Fig.6A, left columns), but at high temporal frequencies they did not show much saturation (right columns). This behavior can be better observed in an amplitude plot (Fig.6B); the contrast responses differ in their horizontal position, so they could not be superimposed by a vertical shift, as was the case with the contrast responses to different orientations or spatial frequencies.

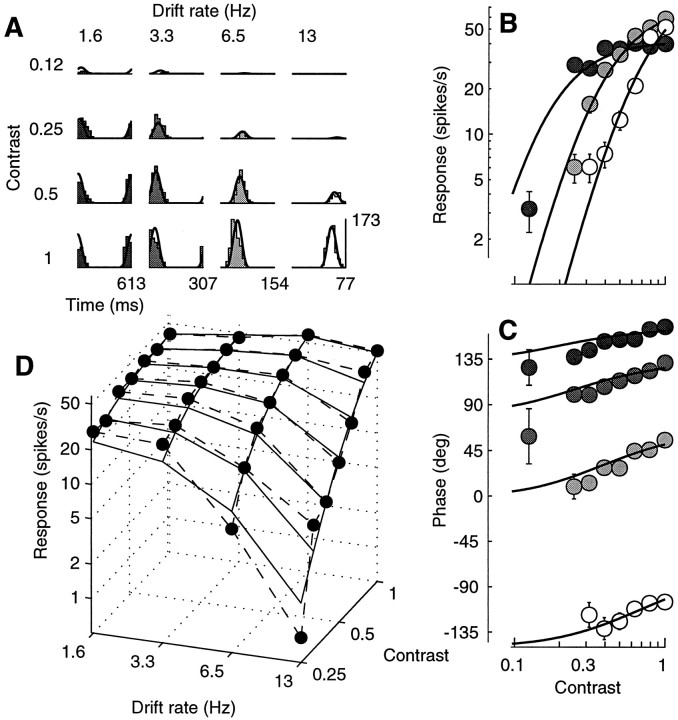
Fig. 6.

Dependence of the contrast responses on temporal frequency. Curves are predictions of normalization model.A, Period histograms. Rows correspond to different contrasts, columns to different temporal frequencies. B, Response amplitude as a function of contrast. The 3.3 Hz data were very close to the 1.6 Hz data and were omitted to avoid clutter. C, Response phase as a function of contrast. Gray levels indicate the temporal frequency as inA. D, Response amplitude as a function of temporal frequency and contrast. Dashed lines connect actual data (dots); continuous lines indicate fits of the model. Fits were performed on a larger data set than shown, which included 64 stimulus conditions (8 contrasts, 4 temporal frequencies, and 2 orientations). Cell 382l021 (DI = 0.1; SF = 1.4; SZ = 7.5), experiment 5; N = 3. Parameters: τ₀ = 66 msec; τ₁ = 8 msec;n = 4.

The effect of temporal frequency on the contrast responses can be rephrased in terms of the effect of contrast on the temporal frequency tuning. Increasing stimulus contrast increased the responsivity of the cells to the high temporal frequencies. This phenomenon is most visible in Figure 6D, which can be seen as a set of temporal frequency curves measured at different contrasts. Although at low contrasts the cell was essentially low-pass, at high contrasts the cell was mildly bandpass, with the 6.5 Hz stimulus eliciting 46% stronger responses than the 1.6 Hz stimulus. From the quality of the fits it is clear that the normalization model captures this behavior. The linear model, on the other hand, predicts that increasing the contrast should just scale the responses, with no effect on the temporal frequency tuning.

The effect of contrast on the temporal frequency tuning of the normalization model can be understood by observing the effects of changing the conductance on the temporal frequency tuning of an RC circuit (Fig. 7). Increases in conductance reduce the gain of the membrane more at low frequencies than at high frequencies, substantially increasing the cutoff frequency of the membrane. Because the conductance grows with stimulus contrast, at low contrasts the cutoff frequency of the membrane is low, and the low-pass character of the membrane dominates the responses. At higher contrasts the cut-off frequency of the membrane is higher, and the tuning of the responses is determined by the linear receptive field providing input to the membrane. In the case of the cell in Fig. 6, the fits of the model indicate that the tuning of the linear receptive field was bandpass.

Fig. 7.

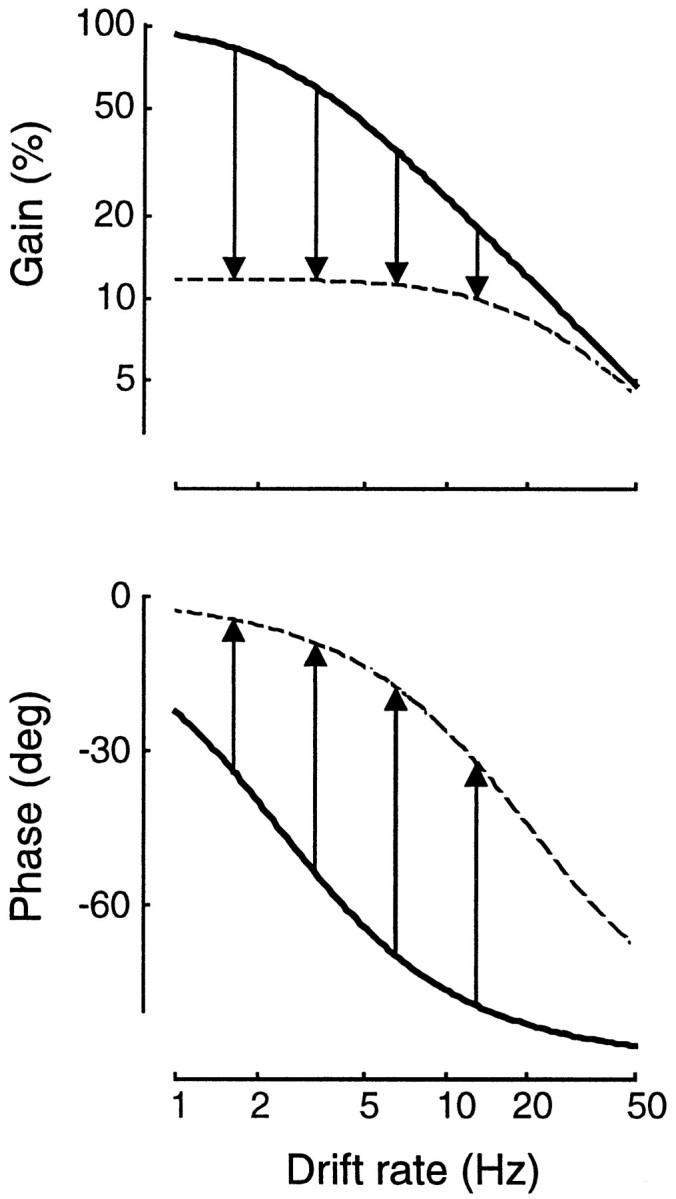
Effects of changing the conductance g = 1/R in an RC circuit. Circuit parameters, and their dependence on contrast, are estimated from the experiment in Figure 6.Continuous curves show the transfer function at rest (low conductance); dashed curves show the transfer function at unit contrast (high conductance). Arrows indicate decrease in gain (top) and phase advance (bottom) at four temporal frequencies (1.6, 3.3, 6.5, and 13 Hz).

Figure 7 also illustrates an example of how phase advances in an RC circuit with increased conductance. The vertical arrows in the bottom panel of Figure 7 indicate the total phase advance predicted by the model at the four temporal frequencies tested in the experiment of Figure 6. The best fit model parameters predict that phase advance between zero and unit contrast is largest for the 6.5 Hz stimulus (51.9°), marginally smaller for the 3.3 and 13 Hz stimuli (44.4° and 46.9°), and smaller still for the 1.6 Hz stimulus (29.5°). The expression for the total phase advance predicted by the model is:

$$\text{phase advance}=\text{arctan}(2\pi f{\tau }_0)-\text{arctan}(2\pi f{\tau }_1),$$ Equation 6

where f is the stimulus temporal frequency, and τ₀ and τ₁ are, respectively, the time constant of the membrane at 0 and at unit contrast. The maximal phase advance is achieved at a frequency equal to 1/(2π $\sqrt{{\tau }_0{\tau }_1}$).

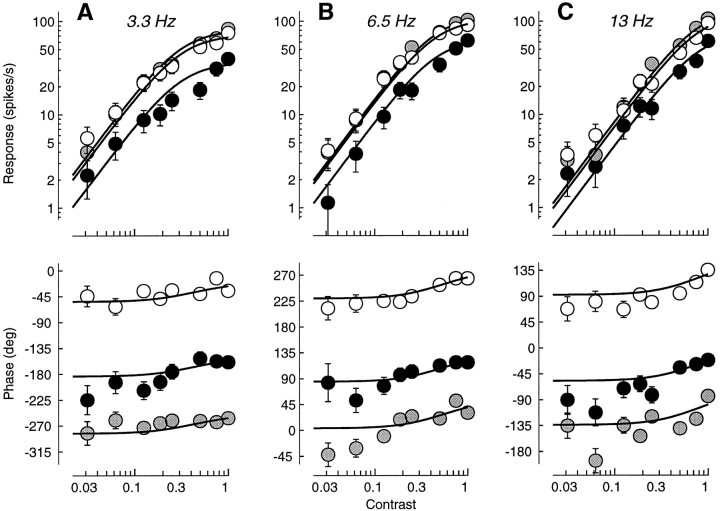
The data in Figure 8 exemplify the dependence of phase advance on temporal frequency. For this cell the best fit model parameters predict that the phase advance should be minimal (11.3°) at 1.6 Hz and increase with temporal frequency: 20.77° at 3.3 Hz, 31.8° at 6.5 Hz, and 35.7° at 13 Hz. The data clearly confirm this trend, which was typical of our sample. Indeed, most of the figures in this study display data acquired with temporal frequencies of ∼6 Hz. We wanted to provide examples of contrast responses showing clear saturation and clear phase advance. As predicted by the model, we found that temporal frequencies <3 Hz yielded strong saturation but little phase advance, whereas temporal frequencies much >6 Hz showed large phase advances but little saturation.

Fig. 8.

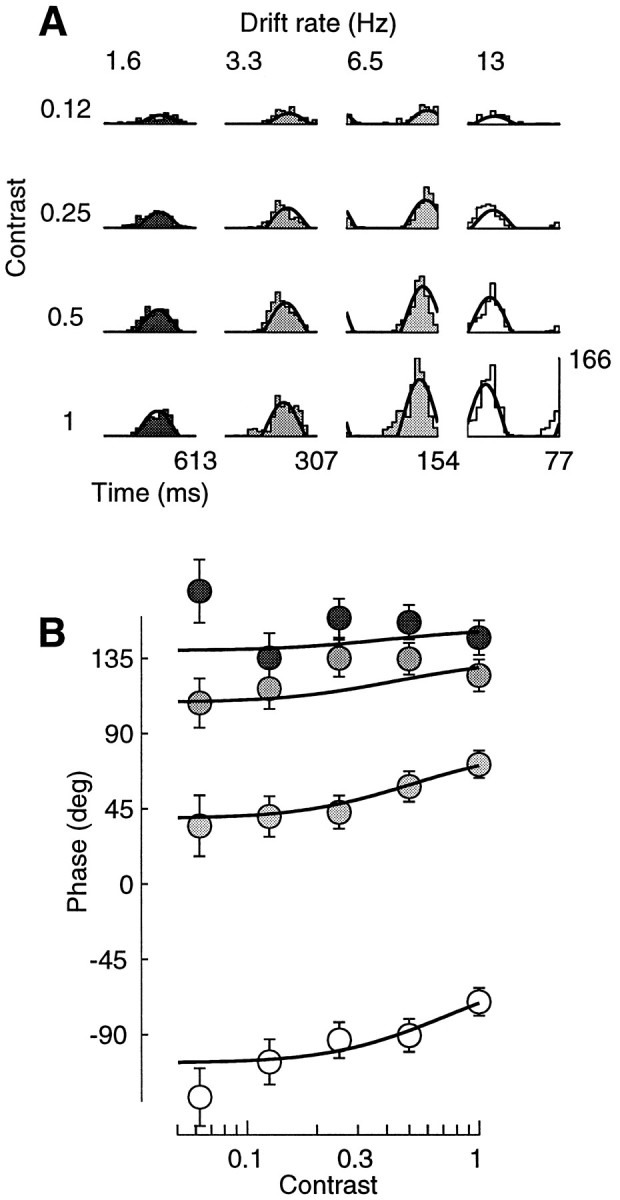
Phase advance and temporal frequency.Curves are predictions of normalization model. A, Period histograms. Rows correspond to different contrasts,columns to different temporal frequencies. B, Response phase as a function of contrast. Gray levelsindicate the temporal frequency as in A. Fits were performed on a larger data set than shown, which included 60 stimulus conditions (5 contrasts, 4 temporal frequencies, and 3 spatial frequencies). Cell 392l008 (same as Fig. 3), experiment 7; N = 3. Parameters: τ₀ = 27 msec; τ₁ = 7 msec;n = 1.2.

The increase in phase advance with increasing temporal frequency can also be seen as a decrease in integration time, the slope of a line fitted to a phase versus temporal frequency plot of the data. A similar phenomenon—together with dramatic changes in the temporal frequency tuning of the cells—was observed in cat by Reid et al. (1992) using broad-band high-energy stimuli. The authors of that study pointed out that these behaviors could be explained by changes in the membrane conductance of cortical cells. The normalization mechanism that we propose works exactly that way, and indeed we have shown that it predicts effects similar to those observed by Reid and collaborators (Carandini and Heeger, 1993).

An entire data set

The curves predicted by the model illustrated in the preceding figures were the result of fits to entire data sets, not just to the data appearing in the figures. For example, the responses in Figure 3were obtained in a grating matrix experiment that included 72 different drifting gratings, with eight different contrasts, three different orientations, and three different temporal frequencies. The full set of responses to these stimuli are shown in Figure9. This example illustrates the principal properties of the contrast responses; changing orientation shifts the amplitude responses vertically on a logarithmic scale and the phase responses vertically on a linear scale. Amplitude saturation is more prominent at low temporal frequencies; phase advance is more prominent at higher temporal frequencies.

Fig. 9.

An entire grating matrix data set. The cell was tested with three different temporal frequencies (A, 3.3 Hz;B, 6.6 Hz; C, 13 Hz), three different orientations (white, 120°; gray, 80°;black, 40°), and nine different contrasts. Some period histograms for these responses are shown in Figure 3A. The shapes of the 18 curves are determined by only 3 parameters: τ₀ = 37 msec; τ₁ = 9 msec;n = 1.34. Eighteen additional parameters determine the vertical positions of the eighteen curves. Cell 392l008, experiment 4;N = 3.  

The 18 curves predicted by the normalization model (9 for amplitude and 9 for phase) provide satisfactory fits to the data. Whereas the vertical position of each curve depends on the linear stage of the model, the shape of all the curves (including their horizontal position) depends on the normalization and rectification stages. In particular, the vertical position of each curve is determined by one parameter, corresponding to the amplitude or phase of the response of the linear stage to each grating at full contrast. The shape and horizontal position of all the curves, instead, are determined by a total of three parameters. The first two are the time constants τ₀ and τ₁ of the membrane at rest and at full contrast; these characterize the normalization stage and [by determining ς(f) ] control the horizontal position of the amplitude curves and the steepness of the phase curves. The third parameter is the exponent n , which characterizes the rectification stage. It controls the steepness of the amplitude curves below saturation, and has no effect on the phase curves.

Responses to plaids

We now consider the responses to a wider set of visual stimuli: plaids composed of two drifting gratings having the same temporal frequency. The gratings differed in orientation and/or in spatial frequency, and their contrasts c₁ and c₂ assumed a variety of different values.

Cells in the cat primary visual cortex display a phenomenon known as “cross-orientation inhibition” (Morrone et al., 1982; Bonds, 1989;Gizzi et al., 1990), in which the responses to optimal stimuli are inhibited by the presence of stimuli of nonoptimal orientation, which would elicit negligible responses if presented alone. More generally, there are numerous reports of conditions in which cells in the cat visual cortex are inhibited by stimuli that elicit no response when presented alone. This inhibition has been found to be independent of direction of motion, largely independent of orientation, and broadly tuned for spatial and temporal frequency (Bishop et al., 1973; Dean et al., 1980; Burr et al., 1981; Hammond and MacKay, 1981; Morrone et al., 1982; De Valois and Tootell, 1983; Kaji and Kawabata, 1985; Gulyas et al., 1987; Bonds, 1989; Nelson, 1991; DeAngelis et al., 1992; Geisler and Albrecht, 1992). Cross-orientation inhibition can be elicited with one grating in each eye, although suppression with both gratings in the same eye is typically stronger (Ferster, 1981; Ohzawa and Freeman, 1986a,b; Freeman et al., 1987; DeAngelis et al., 1992; Sengpiel and Blakemore, 1994; Sengpiel et al., 1995; Walker et al., 1996).

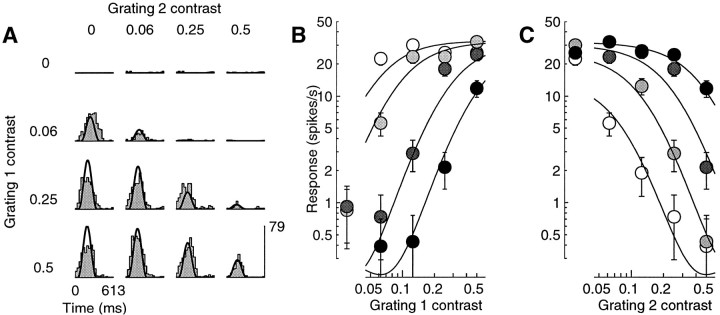
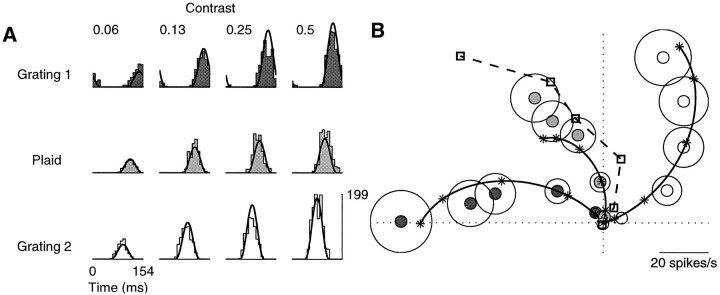
Our results indicate that cross-orientation inhibition is present in most cells of the monkey primary visual cortex. An example of this is shown in Figure 10, which shows the responses of a simple cell to a plaid with components that drifted in orthogonal directions. Although one of the gratings (grating 1) was quite effective in driving the cell (Fig. 10A, left column), the other (grating 2) elicited almost no spikes when presented alone (top row). Its presence, however, clearly suppressed the responses to the first grating. The inhibitory effect of the second grating can be observed more precisely in Figure10B, which shows the contrast responses of the cell for four different contrasts of grating 2. As observed by Bonds (1989)in the cat, the presence of the second grating shifts the contrast response to the right on a logarithmic scale. This shift to the right would not be explained by the linear model; if cross-orientation inhibition were attributable to a linear interaction between two (possibly subthreshold) linear responses, it would subtract from the responses a fixed quantity. The responses to the first grating would saturate at the same contrast, irrespective of the contrast of the second grating. As shown in Figure 10, this is not the case.

Fig. 10.

Masking by an orthogonal grating. Responses to a plaid experiment in which one component was nearly optimally oriented (grating 1), and the other was orthogonal and ineffective in driving the cell when presented alone (grating 2). Curves are fits of the normalization model. A, Period histograms for different contrasts of the components. Rows, Different contrasts of grating 1 (c₁) .Columns, Different contrasts of grating 2 (c₂) . As c₂ was increased, the responses decreased in size (cross-orientation inhibition). B, Response amplitude as a function of c₁, for different values of c₂ (white to black: 0.06, 0.12, 0.25, and 0.5). As c₂ increased, the contrast responses shifted to the right; more and more contrast of grating 1 was needed to maintain a set level of firing. C, Same data, plotted as a function of c₂, for different values of c₁ (white toblack: 0, 0.06, 0.25, and 0.5). Cell 392l024 (DI = 0.4; SF = 0.1; SZ = 6.8), experiment 9; N = 3. Parameters: τ₀ = 158 msec; τ₁ = 5 msec;n = 2.3.

The shift to the right of the contrast responses corresponds to an effective scaling of stimulus contrast. This is the behavior predicted by the normalization model (Heeger, 1992b), which, as illustrated by the curves in Figure 10, provided good fits to our plaid data. Approximate equations for the amplitude and phase of the responses of the model to plaids are derived in . The expression for response amplitude is:

$$\text{amplitude}(R)\propto {\left[\frac{\text{amplitude}(c_1{L}_1(t)+c_2{L}_2(t))}{\sqrt{\varsigma (f{)}^2+c_1^2+c_2^2}}\right]}^n,$$ Equation 7

where c₁ and c₂ are the contrasts of the two gratings, L₁(t) and L₂(t) are the responses of the linear receptive field to the individual gratings at unit contrast, and the remaining symbols have the same meaning as in the expression for the response to individual gratings (Eq. 5). Since the receptive field of the cell is linear, its response to the plaid is just a linear combination of its responses to the individual gratings, c₁L₁(t) + c₂L₂(t) . The normalization stage divides that by approximately $\sqrt{\varsigma (\text{f}{)}^2+{\text{c}}_1^2+{\text{c}}_2^2}$ (see ). If, as in Figure 10, grating 2 alone does not elicit any response (L₂ ≈ 0) , then the effect of an increase of c₂ in the denominator is to shift the contrast response to the right on the log contrast axis (Heeger, 1992b).

The pure rightward shift of the contrast responses occurs only when the cell is completely unresponsive to the masking grating. When each grating in the plaid elicits (even minimal) responses when presented alone, their combined effect is more complicated. In this case the sinusoidal responses of the linear receptive field to the individual gratings are added together before the normalization stage. Depending on their relative phase they can add constructively or destructively. An example of this is shown in Figure11. The top and bottom rows in Figure 11A show the period histograms of the responses of a cell to two gratings of different spatial frequency. Both gratings elicited strong responses, with phases differing by approximately 90°. The responses to the “plaids” obtained by summing the gratings are shown in the middle row.

Fig. 11.

Responses to the sum of two equally effective stimuli. Components differed in spatial frequency. Continuous curves are fits of the normalization model. A, Period histograms for four different contrasts. Dark gray, Responses to grating 1 (1.2 cycles/degree). White, Responses to grating 2 (0.6 cycles/degree). Light gray, Responses to the sums of the stimuli in the top and bottom rows. B, Polar plot of the first harmonic responses.Squares indicate the vectorial sums of the responses to the individual gratings (dark gray and white data points). The actual responses to the plaid were smaller (closer to the origin) and occurred slightly sooner (counterclockwise) than this linear prediction. Cell 385r037 (DI = 0.9; SF = 0.8; SZ = 1.7), experiment 05; N = 4. Parameters: τ₀ = 45 msec; τ₁ = 2 msec;n = 2.44.

The sum of sinusoids is best understood in a polar plot (Fig.11B), in which every sinusoid corresponds to a vector, and the sum of sinusoids is just a sum of vectors. Thedark gray data points are the responses to grating 1; thewhite data points are the responses to grating 2. Thelight gray data points are the responses to the plaid obtained by superimposing the two gratings. The squaresindicate the linear predictions for the plaid responses obtained by summing (vectorially) the responses to the individual gratings. The actual plaid responses show more saturation (they remain closer to the origin) than these linear predictions. They also occur earlier (their angle with the horizontal axis is larger) than the linear predictions. Although not perfect, the fits of the normalization model (continuous curves) capture both phenomena. This is because the local stimulus energy of the plaid is greater than that of the individual gratings. In the model this results in higher membrane conductance, which causes a decrease in gain and time constant.

Figure 12 illustrates another example of plaid responses. In this case two orthogonal gratings were able to drive the cell. Grating 2 was not as effective as grating 1, but it did elicit some spikes when presented alone. The dependence of the responses on the contrasts of the gratings is complicated: depending on the contrast of grating 1, increasing the contrast of grating 2 either enhanced or suppressed the responses. This behavior would be hard to explain at the level of a single cell. Instead, as shown by the continuous curves fit to the responses, it is precisely predicted by the normalization model. The contrasts of the two gratings, c₁ and c₂, appear both in the numerator and in the denominator of Equation 7. Increasing one of the two can result either in an enhancement or in a reduction in the response, depending on the amplitudes and phases of the underlying linear responses L₁ and L₂.

Fig. 12.

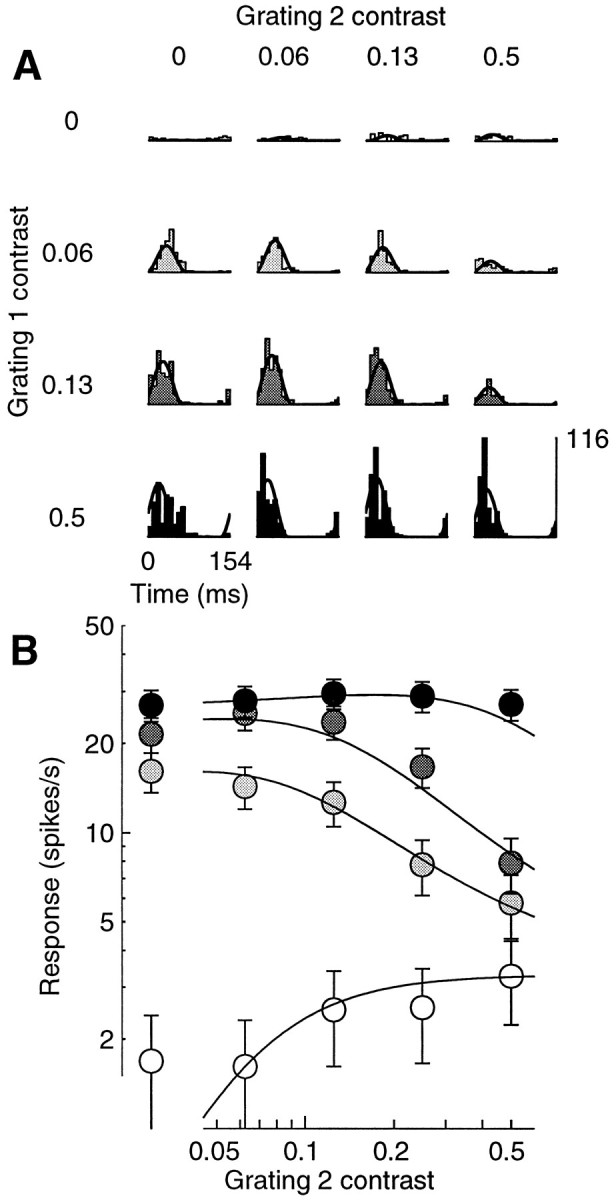
Masking with a grating that is effective in driving the cell. Responses to a plaid experiment in which one component was nearly optimally oriented (grating 1), and the other was orthogonal but still elicited some response when presented alone (grating 2). A, Period histograms for different contrasts of the components. Rows, Different contrasts of grating 1 (c₁) .Columns, Different contrasts of grating 2 (c₂) . When presented alone, grating 1 elicited strong responses (left column), grating 2 weak responses (top row). B, Response amplitude as a function of c₂, for different values of c₁ (white to black: 0, 0.06, 0.12, and 0.5). Increasing c₂ increased the size of the responses when grating 1 was absent; it inhibited the responses for intermediate contrasts of grating 1, and it had little effect for high contrasts of grating 1. Cell 392r013 (DI = 0.9; SF = 0.4; SZ = 3.4), experiment 12; N = 3. Parameters: τ₀ = 136 msec; τ₁ = 1.4 msec;n = 2.22.

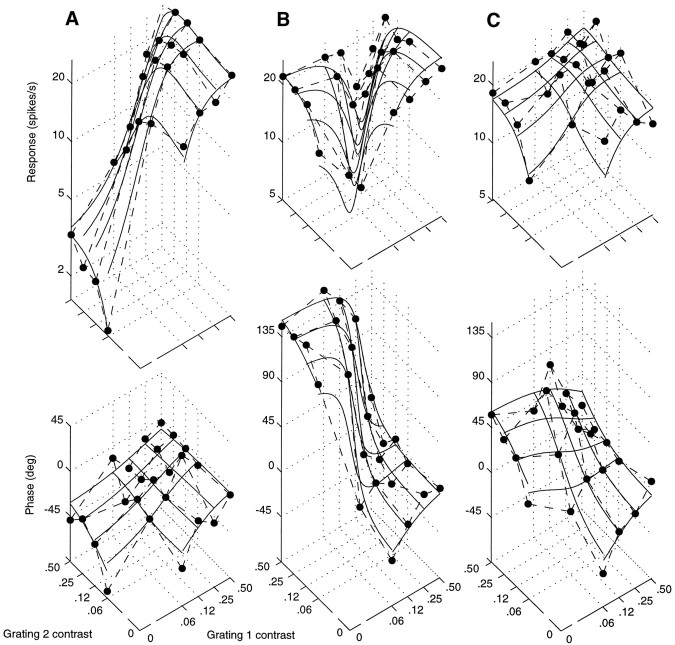
Figure 13 illustrates the responses of the same cell to different plaids. The top panel in Figure13A replots the amplitude data of Figure 12, and thebottom panel shows the corresponding phase data, illustrating that increasing the contrast of either grating resulted in phase advance. In Figure 13A grating 2 drifted at 90° with respect to grating 1, and it elicited responses that were smaller by about a factor of five. When grating 2 was replaced by one drifting at 30° with respect to grating 1, it elicited responses that were only marginally smaller than those to grating 1 (Fig. 13B, top panel). The phases of the responses to the two individual gratings were almost opposite (Fig. 13B, bottom panel), ∼0° for grating 1 and ∼135° for grating 2. As a result the two stimuli interacted destructively, as witnessed by the dip in the diagonal region of the top panel in Figure13B. In that region increasing the contrast of any of the two gratings reduced the amplitude of the responses. The model clearly captures this phenomenon, which is principally attributable to its linear stage. When the spatial phase of grating 2 was changed by 90° (Fig. 13C), this phenomenon disappeared. Now increasing the contrast of either grating increased the size of the responses.

Fig. 13.

Amplitude (top) and phase (bottom) of the responses of a cell to three different plaids, for different contrasts c₁ and c₂ of the two components. Circlesconnected by dashed lines are actual responses;continuous curves are fits of the normalization model. Grating 1 was the same in all three experiments. Its orientation was close to optimal. A, Grating 2 was orthogonal to grating 1.B, Grating 2 drifted 30° away from grating 1.C, Same as B, but phase of grating 2 was delayed by 90°. Cell 392r013 (same as Fig. 12), experiments 12, 9, and 8. Parameters: A, τ₀ = 40 msec; τ₁= 1.3 msec; n = 2.1; B, τ₀ = 35 msec; τ₁ = 1.4 msec; n = 1;C, τ₀ = 52 msec; τ₁ = 1.7 msec;n = 1.1.

Responses to gratings and noise

We now consider responses to gratings in the presence of noise. In the absence of a grating stimulus, the only visible effect of noise was a generally mild elevation in the mean firing rate (from 0.8 ± 0.3 to 2.0 ± 0.6 spikes/sec). When presented together with an effective grating stimulus, however, the noise provided strong inhibition. This is consistent with the predictions of the normalization model, because the presence of the noise mask increases the stimulus energy.

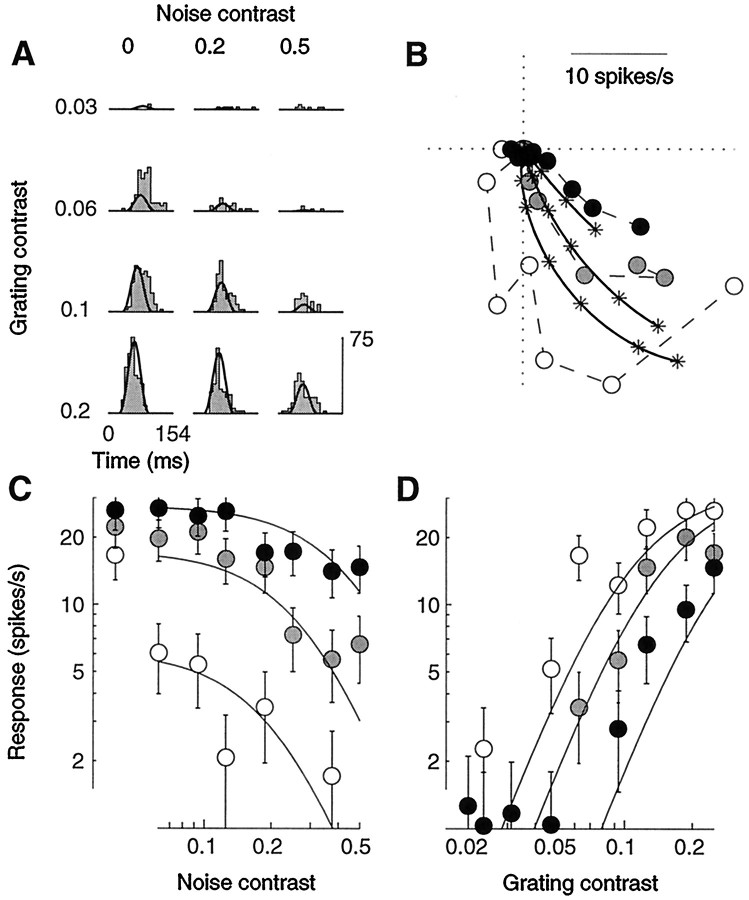
An example of our results is shown in Figure14. In the absence of a grating stimulus, the noise elicited few spikes (Fig. 14A, top row). By contrast, the cell was effectively stimulated by the drifting grating (left column). Increasing noise contrast decreased the size of the responses (Fig. 14C), shifting the contrast responses to the right (Fig. 14D). The other major effect of the noise masks was to reduce response latency. Indeed, as illustrated in Figure 14B, the highest noise contrast (black points) caused the phase to advance to its maximum, so that the grating contrast could have no further effect on response phase.

Fig. 14.

Masking with spatiotemporal white noise. An optimal drifting grating was presented together with full-screen two-dimensional flickering binary noise. Fits of the normalization model (curves) were performed on a larger data set than shown, which included 72 stimulus conditions (9 grating contrasts and 8 mask contrasts). A, Period histograms for different grating contrasts (rows) and noise contrasts (columns). When presented alone, the grating elicited strong responses (left column), the noise very weak responses (top row).B, Polar plot of the contrast responses for three different noise contrasts (white to black: 0, 0.19, and 0.5). Increasing noise contrast decreased response amplitude and advanced response phase. Error circles are omitted to avoid clutter but can be estimated from following panels. C, Response amplitude as a function of noise contrast. Grating contrasts (white to black): 0.06, 0.12, and 0.25.D, Response amplitude as a function of grating contrast, for different noise contrasts. Gray levels as in B. Cell 394l015 (DI = 0.6; SF = 2.3; SZ = 6.8° for the stimulus, 7.8° for the mask), experiment 7. Parameters: τ₀ = 82 msec; τ₁ = 2.6 msec;n = 1.85.

As exemplified by the continuous curves in Figure 14, the normalization model provided good accounts of the effects of noise masks. To fit the noise-masking data we made the simplifying assumption that the noise would be unable to drive the linear receptive field of the cells, so that its sole effect would be to provide divisive normalization. More precisely, we used the same equations that we fit to the plaid responses, except that the first harmonic of the linear response L₂ to the noise mask was set to zero. The noise contrast c₂ then only appeared in the denominator of Equation 7. This approximation neglects the mild increase in mean firing rate caused by the noise but captures the fact that the power of the noise was spread over a large band of frequencies and was thus negligible at the frequency of the test stimulus (the first harmonic).

There is a further difference between the fits to the noise data and those to the plaid data. Whereas the two gratings in a plaid were assumed to be equally effective in driving the normalization pool, the effectiveness of the noise mask in driving the normalization pool was controlled by an independent parameter α, which scaled the mask contrast c₂. The values of α that resulted from the fits were equally spread between the boundaries 0.1 and 10. In 10 of 22 data sets they were larger than 1.0, indicating that the noise mask provided more divisive inhibition than the drifting grating.

The interpretation of this result is complicated, however, by the fact that the noise masks (but not the gratings) occupied the whole screen of the monitor, extending well beyond the receptive fields of the recorded cells. As in the cat (Blakemore and Tobin, 1972; Nelson and Frost, 1978; DeAngelis et al., 1994; Li and Li, 1994), the regions outside the receptive field of monkey V1 cells can provide strong inhibition (De Valois et al., 1985; Born and Tootell, 1991; Sillito et al., 1995; Levitt and Lund, 1997). We do not know which portion of the divisive inhibition exerted by our noise masks should be ascribed to the stimulation of these regions.

Quality of the fits

We evaluated the quality of the fits both by calculating the percentage of the variance accounted for by the model and by computing bootstrap estimates of the ASL statistic (see Materials and Methods). The results of this analysis are summarized in Table1.

Table 1.

Quality of the fits of the normalization model

Experiment	N	Percentage of the variance				Achieved significance level
		<50%	50–80%	80–90%	>90%	<2.5%	2.5–5%	5–10%	>10%
Grating matrix	51	0	4	13	34	2	2	9	38
Plaids	76	4	20	33	19	9	6	11	50
Noise masking	22	0	5	8	9	1	1	2	18
All	149	4	29	54	62	12	9	22	106

Percentage of the variance

For most data sets (166 vs 33), the normalization model accounted for >80% of the variance. The median percentage of the variance accounted for by the model was 92.9% for grating matrix data sets, 85.5% for plaid data sets, and 87.3% for noise masking data sets. These values can be assessed more intuitively by considering the quality of the fits in some of the previous figures. The model accounted for 95.7% of the variance of the grating matrix data set in Figure 9, for 89.7% and 89.8% of the variance of the plaid data sets in Figures 10 and 12, and for 87.6% of the variance of the noise mask data set in Figure 14. The data sets chosen for the figures in this study were mostly in the third quartile in terms of quality of the fits to each experiment type.

Achieved significance level

To take into account the variability of the responses in our evaluation of the model we tested the hypothesis that the mean of the probability distribution underlying the neural responses was identical to the predictions of the model. This hypothesis was tested using the bootstrap procedure described in Materials and Methods. The model passed the test at the 5% significance level for 47 of 51 grating matrix data sets, for 61 of 76 plaid data sets, and for 20 of 22 noise-masking data sets. For plaid data sets, no systematic difference in the quality of the fits was found between experiments in which the two components differed in orientation (35 data sets), those in which they differed in spatial frequency (28 data sets), and those in which they differed in both attributes (13 data sets).

Comparison with other models

We compared the quality of the fits obtained with the normalization model with those of three different models: the linear model, an elaborated normalization model, and an alternative model in which saturation is brought about by a compressive nonlinearity. Figure15 presents the results of this analysis for our plaid experiments. The abscissas plot the percentage of the variance accounted for by the normalization model, and the ordinates plot the percentage of the variance accounted for by the other models. Experiments that were better fitted by the normalization model result in data points that are below the diagonal.

Fig. 15.

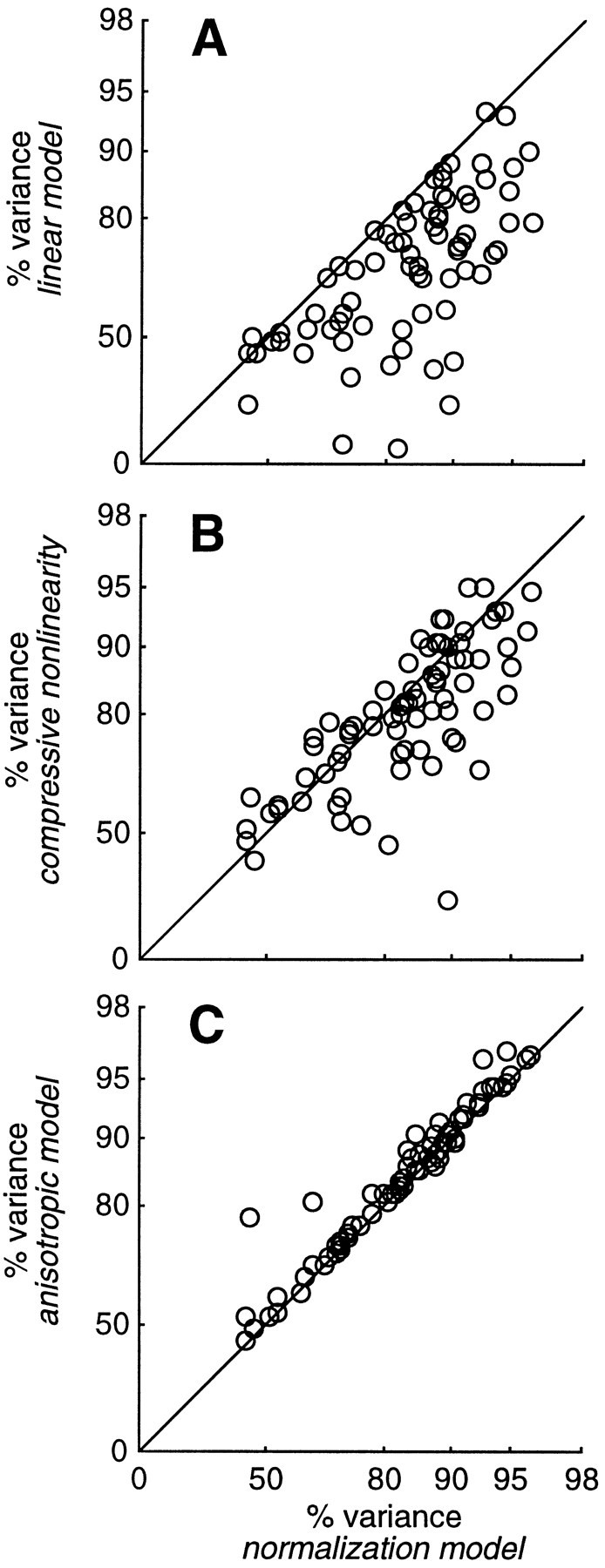
Performance of four different models, measured by the percentage of the variance accounted for in the data. Eachdata point corresponds to a plaid experiment. Theabscissas plot the performance of the normalization model, and the ordinates plot performance of three other models.A, Linear model. B, Compressive nonlinearity model. C, Anisotropic model.

Because the linear model has fewer parameters than the normalization model (five vs seven for plaid data sets), it is bound to provide worse fits. Indeed, we already know the failures of the linear model: it does not predict amplitude saturation, or phase advance, or noise masking, or any of the other nonlinearities that we have mentioned in this study. The extent of the difference in quality of the fits can be taken as a quantitative measure of the importance of the two extra parameters postulated by the normalization model. As shown in Figure15A, in most cases the normalization model provided a substantial improvement over the linear model. For plaid experiments, the median value for the percentage of the variance accounted for by the linear model was 70.5%, as opposed to 85.5% for the normalization model.

Similar results were obtained with the other two types of experiments in our protocol. For grating matrix experiments the median values of the percentage of the variance were 84.2% for the linear model and 93.0% for the normalization model. With noise-masking experiments the median values were 56.4% for the linear model and 87.3% for the normalization model.

We then considered an extension of the normalization model, ananisotropic normalization model. This model is equivalent to the normalization model except that it relaxes one of its most stringent constraints, i.e., that the normalization pool be equally responsive to a broad range of visual stimuli. It is the same model that we fitted to the noise data, and it involves the additional free parameter α, allowing for a difference in the size of the responses of the pool to the two stimulus components. The parameter α scales the contrast c₂ of the second grating in the denominator of Equation 7 and in the equation for response phase provided in . As illustrated in Figure 15C, the anisotropic model provided only a marginal improvement over the normalization model in the quality of the plaid fits. In particular, the median value for the percentage of the variance accounted for by the anisotropic model was 86.9%, only 1.3% better than the normalization model. This hardly justifies the use of its additional parameter to account for our plaid data.

Finally, we considered an alternative to the normalization model, in which the linear stage is followed by a compressive nonlinearity. Intuitively, this model postulates that gain control is proportional to the efficacy of a stimulus in driving the cell. This model could be implemented by having the initial linear stage contribute both to the driving current and to the conductance increase. More precisely, the model is defined by the same Equations 1-3 that define the normalization model, with Equation 4 replaced by g = g₀ + k amplitude (L) .

For plaid data sets, the compressive nonlinearity model can be compared on an equal footing with the normalization model, because it has the same number of free parameters. This comparison is illustrated in Figure 15B. In many cases the normalization model provided substantially better fits than the compressive nonlinearity model. For plaid data sets the median value for the percentage of the variance accounted for by the compressive nonlinearity model was 80.8%, as opposed to 85.5% for the normalization model.

Where the difference in performance between the two models was most impressive, however, is in the noise-masking data sets; for these data sets the median value for the percentage of the variance accounted for by the compressive nonlinearity model was 58.4% as opposed to 87.3% for the normalization model. The compressive nonlinearity model does not predict that noise would mask the responses of simple cells.

Model parameters and cell properties

We now examine the parameters obtained from the fits of all our data sets. Because these parameters have a biophysical interpretation, we can use them to gauge the plausibility of the mechanisms that we have postulated, rectification and shunting inhibition. We also compare the results obtained from different experiments on the same cell, and we use the model to summarize the general properties of the cells in our sample.

Exponent

The exponent n determines the gain of the transformation from membrane potentials to firing rates (Figure2A). The estimated values of this parameter were spread between 1 and 4, which was the region in which they were allowed to vary. Approximately one-fourth of the data sets yielded an n of 1, and one-fourth yielded an n of 4. The median estimated value was n = 2.37 for grating experiments, n = 2.38 for plaid experiments, and n = 2.61 for noise-masking experiments. These values should not however be assigned much confidence, as in many cases different values of the exponent yielded only minor differences in the quality of the fits (Tolhurst and Heeger, 1997b). In any event, values close to 2 are consistent with the results of Albrecht and Hamilton (1982) and Sclar et al. (1990), who fitted the amplitude of the responses with an equation similar to our Equation 5.

Time constants

The remaining two parameters of the normalization model are the membrane time constant in the absence of a visual stimulus, τ₀, and the membrane time constant in the presence of a grating of maximal contrast, τ₁. The range of time constants that we obtained by fitting all of our data sets is illustrated in Figure 16. The time constant at rest τ₀ (abscissas) was constrained to be between 1 and 1000 msec for grating matrix data sets (Fig. 16A) and between 1 and 250 msec for plaid (Fig.16B) and noise-masking (Fig. 16C) data sets. For grating matrix data sets the estimated values lie mostly between 10 and 50 msec, with a median value of 25 msec. For plaid data sets the median value was 51 msec. Noise-masking experiments yielded much higher values; if one excludes the 2 (of 22) data sets for which the estimated time constant at rest was <1 msec (that we attribute to noisy measurements), the median value of the time constant at rest was 150 msec. The ratio τ₁/τ₀ between the time constant at full contrast τ₁(ordinates) and the time constant at rest τ₀was constrained to be between 0.01 and 1 for grating matrix data sets and between 0.03 and 1 for plaid and noise-masking data sets. The estimated values of τ₁ are substantially lower than those of τ₀, with a median of 4.9 msec for grating matrix data sets, 5.4 msec for plaid data sets, and 7.5 msec for noise-masking data sets.

Fig. 16.

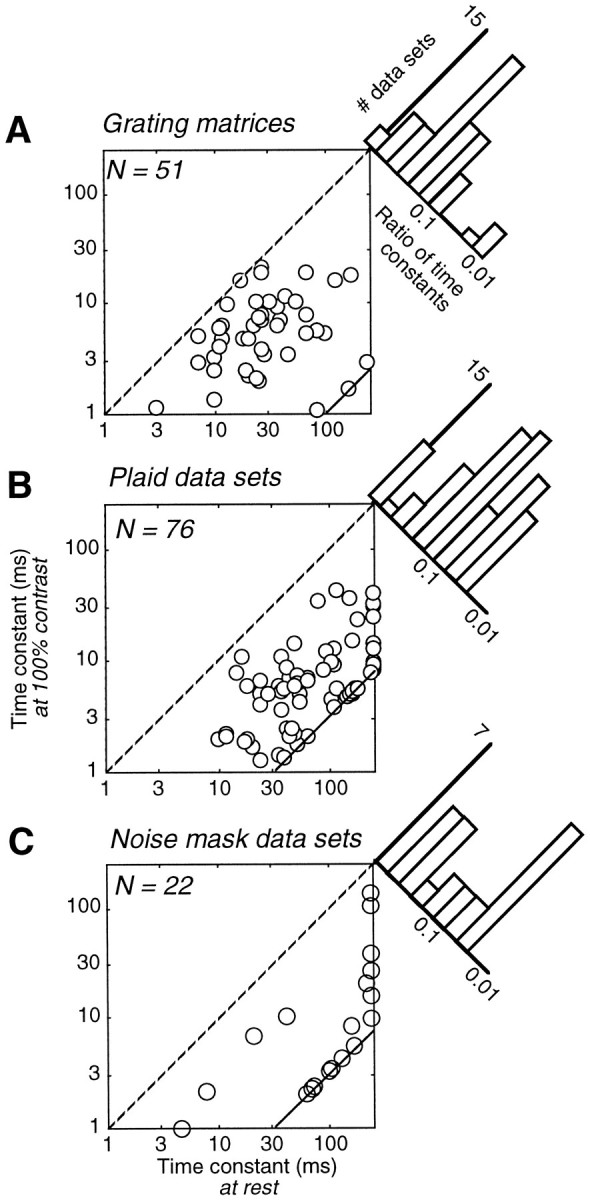
Time constants of V1 simple cells estimated by the normalization model from grating matrix data sets (A), from plaid data sets (B), and from noise masking data sets (C). Scatter diagrams plot the time constant at rest τ₀(abscissa) versus the time constant at full contrast τ₁ (ordinate). Time constants <1 msec are omitted. Dashed line indicates the identity τ₀= τ₁. Continuous lines in lower right corners indicate bounds in fitting procedure.Histograms show the distribution of ratios τ₁/τ₀. These include data sets with both time constants <1 msec that are missing from scatter diagrams.

On selected cells we performed an analysis of the dependence of the fit quality on the time constants. The percentage of the variance accounted for by the model was maximal along diagonal regions in plots of τ₀ versus τ₁, suggesting that the fits constrained the ratio τ₁/τ₀better than the individual values of the time constants.

For grating matrix data sets the ratio τ₁/τ₀ was mostly >0.1 (Fig.16A) and had a median value of 0.23, which corresponds to a fourfold increase in conductance. A value of 1 would correspond to no conductance increase, i.e., to the linear model. Plaid data sets yielded substantially smaller values for τ₁/τ₀ (Fig. 16B). The median value of this ratio in plaid data sets was 0.11, suggesting a 10-fold increase in model conductance. Noise-masking data sets (Fig.16C) yielded even more extreme values; excluding the two data sets for which τ₀ was <1 msec, the median ratio τ₁/τ₀ was 0.056, corresponding to an increase in estimated conductance by a factor of 18. A conductance increase of this extent is unlikely to be possible in real cells (see Discussion).

Variability across experiments

It is clear from Figure 16 that the three different types of experiments yielded quite different estimates of the model parameters. This could be an effect of adaptation; the responses of V1 cells are known to depend on the history of stimulation (Maffei et al., 1973; Movshon and Lennie, 1979; Ohzawa et al., 1985; Sclar et al., 1989; Carandini and Ferster, 1997b; Carandini et al., 1997a). Indeed, many cells gave different responses to a same visual stimulus in different experiments. For 60 of 69 drifting gratings that were presented in more than one experiment on a given cell, the responses elicited in different experiments were statistically different (p < 0.05, bootstrap test, 54 experiments in 23 cells). Moreover, the difference in response across experiments appeared to be consistent across contrasts, often consisting of horizontal and/or vertical shifts of the contrast response curves. An example of this is illustrated in Figure17, which shows the contrast responses of a simple cell as obtained in two consecutive grating matrix experiments.

Fig. 17.

An example of response variability across experiments. Data points represent responses of the same cell to the same stimuli in two different experiments. Stimuli were gratings drifting at 3.3 Hz. Error bars represent 1 SEM. The first experiment (black) involved a block of 40 stimuli (10 contrasts, 2 temporal frequencies, and 2 spatial frequencies;N = 6). The second experiment (white) was initiated 58 min after the first and involved a block of 90 stimuli (10 contrasts, 3 orientations, and 3 temporal frequencies;N = 5). Unit 389l019, experiments 5 and 6.

Adaptation is known to depend both on the contrast (Sclar et al., 1989) and on the type of stimulus (Movshon and Lennie, 1979; Carandini et al., 1997a) presented in the recent past. It affects the sensitivity of the cells, mostly by shifting the contrast response functions to the right in a logarithmic scale (Ohzawa et al., 1985; Sclar et al., 1989). The adaptation behavior of some cells in our sample was explicitly measured and is reported elsewhere (Poirson et al., 1995; Carandini et al., 1997a).

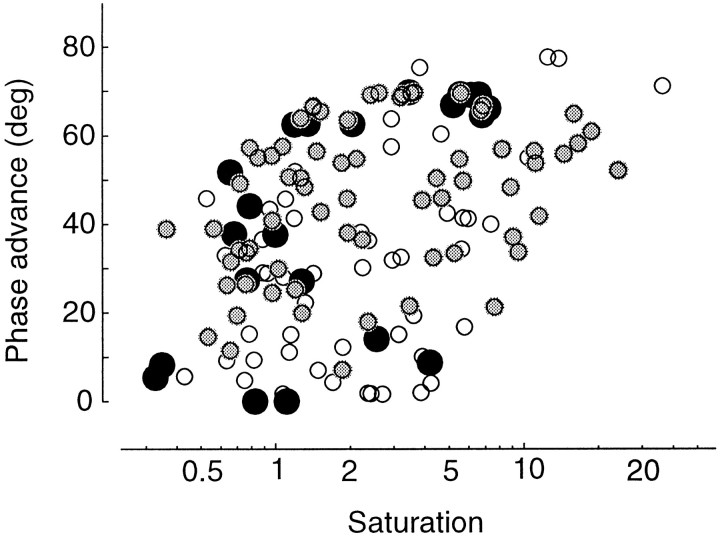
Phase advance and saturation

Given that the model provides a good fit to our data, it can be used to summarize some properties of the cells in our sample. Figure18 illustrates the relation between two characteristics of the contrast responses, both derived from the estimated (and when necessary extrapolated) responses to single gratings drifting at 6.5 Hz. On the ordinate is the total phase advance between zero and unit contrast. On theabscissa is an index of saturation between zero and unit contrast. This index is based on the semisaturation contrast c_1/2, the contrast that elicits half-maximal responses. The saturation index is defined as (1 − c_1/2)/c_1/2. It is <1 if c_1/2 >0.5 (the contrast responses do not saturate much), and >1 if c_1/2<0.5 (the contrast responses are saturated at most contrasts). In addition, because it is inversely proportional to the semisaturation contrast, the saturation index is a measure of the contrast sensitivity of the cells.

Fig. 18.

Saturation and phase advance for all the data sets in this study, estimated (at 6.5 Hz) from the fits of the normalization model. White, Grating matrix data sets.Black, Noise-masking data sets. Gray, Plaid data sets. The abscissa shows the saturation index: values of ≤1 indicate little or no saturation (see text). The ordinateshows the total phase advance between 0 and unit contrast.

Figure 18 shows that saturation and phase advance were positively correlated. For a linear cell saturation is absent, so the saturation index is <1, and phase advance is 0. Saturation and phase advance both grow with the effectiveness of the normalization stage. As a result, the position of a data point in Figure 18 is related to the linearity of the responses. Very linear responses are on the lower left, and very nonlinear (strongly normalized) responses are on the upper right.

The three types of experiments in our protocol yielded different estimates of the phase advance and saturation in the contrast responses. The contrast responses measured during grating matrix experiments (white) had lower phase advances than those measured during plaid experiments (gray). The contrast responses recorded during noise-masking experiments (black) differed from those recorded in the two other types of experiments in that they tended to have larger phase advances for any given amount of saturation. This difference may originate from the cells being in different states of adaptation after prolonged exposure to full-field spatiotemporal noise backgrounds than after prolonged exposure to spatially localized drifting gratings.

DISCUSSION

Simple cells in V1 have a limited dynamic range, a limit to how strong an output signal they can generate and, hence, a limit to the range of inputs over which they can respond differentially. As we have seen (Fig. 4B, 5A), the ratio of the responses to any two stimuli is constant, irrespective of the stimulus contrast, even in the face of response saturation. In addition, the relative timing of the responses is constant, even in the face of phase advance. These invariances, which we attribute to normalization, are critical for encoding visual information (e.g., about motion, orientation, binocular disparity, etc.) independently of contrast.

The issues of gain control and limited dynamic range are, of course, not restricted to V1 neurons. Gain control has been measured and modeled in a variety of other neural systems, including turtle photoreceptors (Baylor and Hodgkin, 1974), retinal ganglion cells (Shapley and Victor, 1978), movement detectors in the fly visual system (Reichardt et al., 1983), the vestibulo-ocular reflex (Lisberger and Sejnowski, 1992), and velocity-selective neurons in area MT of the primate cortex (Heeger et al., 1996; Simoncelli and Heeger, 1997). In particular, our model and our analyses are conceptually similar to the work of Shapley and Victor (1978). Moreover, Reichardt et al. (1983)addressed the same specific issue of retaining linearity in the presence of gain control that we encountered in this study and proposed a recurrent shunting inhibition scheme not too different from the one we have proposed. The normalization model of simple cell responses is also analogous to models of retinal adaptation and normalization (Sperling and Sondhi, 1968; Shapley and Enroth-Cugell, 1984; Grossberg and Todorovic, 1988), in which the stimulus intensity at a particular point is normalized with respect to the mean stimulus intensity.

Plausibility of the assumptions of the model

Although successful in fitting the data with very few parameters, the normalization model is based on a number of simplifications, some less plausible than others.

Linearity of the inputs

The linearity of the inputs to simple cells that we have postulated requires that the responses of lateral geniculate nucleus (LGN) neurons be linear functions of the stimulus contrast distribution. This requirement is better fulfilled by the parvocellular (P) layers of the LGN than by the magnocellular (M) layers. Evidence in this respect is available from studies of the responses of retinal ganglion cells (Benardete et al., 1992; Lee et al., 1994; Benardete and Kaplan, 1997) and of LGN cells (Derrington and Lennie, 1984; Sherman et al., 1984; Carandini et al., 1993; Movshon et al., 1994).

In particular, Movshon et al. (1994) performed noise-masking experiments in the LGN that are identical to those described in this study for V1 simple cells. An analysis of their data using the normalization model yielded the following conclusions: (1) the vast majority of P cells had substantially linear contrast responses, with no clear saturation and little phase advance (<30°); (2) the responses of P cells were only weakly affected by noise masks; contrast sensitivity was mostly unchanged, and phase advance was reduced only in the small portion of cells that did show some in the first place; (3) by contrast, M cells tended to have nonlinear contrast responses, with strong saturation and strong phase advance (mostly >45°); and (4) noise masks had strong effects on the responses of M cells; saturation dropped by a factor of 2, reflecting a large loss in contrast sensitivity, and phase advance virtually disappeared.

Altogether, these observations reinforce the view that P cells are substantially linear, and that M cells are nonlinear. The large difference in contrast saturation between M and P cells is consistent with the well established difference in contrast sensitivity between the two cell types (Kaplan and Shapley, 1982; Shapley and Perry, 1986). The difference in phase advance between M and P cells is also well established, having been mentioned by Derrington and Lennie (1984) and explicitly measured by Sherman et al. (1984). Many aspects of M cell responses (phase advance, saturation, effect of masking on sensitivity, and phase advance) suggest that their nonlinearity might be attributable to a gain control mechanism. It has been proposed (Benardete et al., 1992) that this mechanism is similar to that observed by Shapley and Victor in cat retinal X ganglion cells (Shapley and Victor, 1978; Victor, 1987).

Even though P cells constitute ∼90% of the monkey LGN (Dreher et al., 1976), many simple cells also receive M inputs (Malpeli et al., 1981). Indeed, although the two streams are segregated in layer 4C (Hubel and Wiesel, 1972; Hendrickson et al., 1978; Blasdel and Lund, 1983), they eventually combine in the upper layers (Lahica et al., 1992; Nealey and Maunsell, 1994; Yoshioka et al., 1994). In particular, for those neurons that do receive M input, the first 7–10 msec of activation may be attributable exclusively to the M signal (Maunsell and Gibson, 1992).

Could all of the nonlinearities that are present in simple cells originate from their receiving a preponderant M input? Compared with the LGN cells in the study by Movshon et al. (1994), the V1 simple cells in the present study displayed a wide range of nonlinearity, with some being as nonlinear as the most nonlinear M cells and some being as linear as the most linear P cells. In addition, simple cells typically showed less saturation than LGN cells that exhibited the same phase advance.

There is, however, evidence that the nonlinearities described in this study have a strong cortical component. Some of this evidence was obtained in the cat. Bonds (1989) reported that geniculate cells do not show any evidence of cross-orientation inhibition, and Morrone et al. (1982) found that an orthogonal contrast-modulated grating elicits frequency-doubled suppression, indicating that suppression originates in complex cells or in pools of simple cells. In addition, Reid et al. (1992) found that high-energy broad-band stimulation decreased the latency of the cortical responses to a much larger degree than would be possible for geniculate responses. Evidence for a strong gain control mechanism in monkey V1 was provided by Hawken et al. (1992, 1996), who measured temporal frequency tunings at different stimulus contrasts both in the LGN and in V1. They reported that (as observed in the cat by Orban et al., 1985) there is a significant low-pass filter between LGN and V1, and that both the gain and the time constant of that filter change with the stimulus contrast. The details of these changes are consistent with the normalization model. In particular, they found that increasing stimulus contrast increased the sensitivity of V1 cells to the high temporal frequencies, with the average high-cutoff frequency changing from 17 Hz at 8–16% contrast to 27 Hz at 64% contrast (similar to the results described in the present study; cf. Fig.6C). On the other hand, the average increase in high-cutoff frequency of LGN cells (both M and P) was negligible, suggesting that the origin of this phenomenon is cortical.

Shunting inhibition

Shunting inhibition is a widely cited proposal for how neurons might perform division (Fatt and Katz, 1953; Coombs et al., 1955; Koch and Poggio, 1987). Its defining property is that it affects only the conductance of the cell, without introducing any current when the cell is at rest. The idea that there are strong inhibitory circuits in the cortex, and that these circuits operate through shunting inhibition, arose first as a result of a seminal study by Krnjević and colleagues (Dreifuss et al., 1969). They showed that electrical stimulation of the cortical surface produced very large (up to 300%) increases in membrane conductance. Similar effects were obtained by iontophoretic application of GABA. These results were extended by Rose (1977), who observed that iontophoresing GABA over V1 cells yielded divisive effects on their visual responses.

On the other hand, intracellular in vivo studies have yielded scarce evidence for large conductance increases in V1 cells.Berman et al. (1991) measured cell conductance in the presence of drifting bar stimuli of different orientations and reported conductance increases of <20%. These results were confirmed by Ferster and Jagadeesh (1992), who measured the conductance with synaptic current rather than with injected current, and by other recent measurements (Carandini and Ferster, 1997b). More encouraging results were obtained by Allison et al. (1996), who explicitly studied the dependence of conductance on contrast and found conductance increases of up to 30%. Larger conductance increases, as large as 300%, were inferred byHirsch et al. (1995a) from the visual responses to steps of light and directly measured by Borg-Graham et al. (1996) using a voltage-clamp approach.

Is shunting inhibition really the mechanism for normalization? Our results (Figure 16) indicate that this would call for very large conductance increases associated with visual stimulation. In particular, although the conductance increases estimated from grating matrix data sets (4–500%) are large but not inconceivable (Bernander et al., 1991), those estimated from plaid and noise-masking experiments may be too large to be realistic. Our estimates of conductance increase, however, are inflated by the assumption of linearity of the inputs to simple cells. If we knew the precise balance of M and P input to our simple cells, we could ascribe some of the nonlinearities to the LGN input. Similarly, if we knew the details of active, nonlinear processing in the dendrites (e.g., calcium spikes; Hirsch et al., 1995b), we could ascribe some of the nonlinearities to dendritic integration. Knowledge of these factors would most likely allow the model to fit the simple cell responses and to require smaller, more realistic conductance increases.

Composition of the normalization pool

A question that remains largely unanswered is the precise composition of the normalization pool.

First, we have no way to tell whether the pool contains simple cells, complex cells, or both. The results of Burr et al. (1981) in the cat suggest that it could originate either in complex cells or in a number of simple cells with receptive fields that have different spatial positions or phases.

Second, we do not know whether inhibition comes from a few cells that integrate the output of the pool or from a large number of cells each of which summates the output of small portions of the pool. In the cat, the inhibitory cells that seem best placed to control the cortical gain are the basket cells, the output of which is equally distributed across different orientation columns (Kisvàrday and Eysel, 1993;Kisvàrday et al., 1994).

Third, we do not know the precise overall tuning of the inhibitory pool. In its basic formulation (Heeger, 1992b) the normalization model postulates that the suppression is independent of stimulus orientation and independent of spatiotemporal frequency over a broad range of frequencies. In the cat, this assumption of “isotropy” in the normalization pool is consistent with measurements by DeAngelis et al. (1992), who found that suppression was essentially independent of orientation. Alternate models advocate the need for frequency- and orientation-specific inhibitory mechanisms to refine selectivity. Indeed, the responses of a simple cell are often suppressed by superimposing stimuli with spatial frequencies and orientations that flank the preferred spatial frequency and orientation of the neuron (Movshon et al., 1978c; Morrone et al., 1982; De Valois and Tootell, 1983; De Valois et al., 1985; Hata et al., 1988; Bonds, 1989; Bauman and Bonds, 1991). Although this flanking suppression can be observed in some cases directly in the membrane potential of the cells (Carandini and Ferster, 1997a), in other cases it could be a distortion introduced by the spike-encoding stage. This has been shown with modeling studies by Heeger (1992b) and Nestares and Heeger (1997), who have argued that even if the normalization pool were broadly tuned, the presence of the spike-encoding stage (an accelerating static nonlinearity) would generate an apparent flanking suppression. As we have seen, our data do not allow us to reject the isotropic model in favor of one with substantial tuning in the normalization pool. Our experiments were not, however, designed to provide a strong test of the isotropy assumption, and further measurements are required in this respect.

Limitations of the model

A limitation of the model is that it is local in space. It was not designed to account for the strong surround inhibition displayed by many cortical cells (Blakemore and Tobin, 1972; DeValois et al., 1985;Born and Tootell, 1991; DeAngelis et al., 1994; Li and Li, 1994; Levitt and Lund, 1997, and references therein). Although surround suppression could in principle result from the same mechanism that provides masking, it is not clear that its nature is divisive. Indeed, there is evidence that divisive gain control is highly spatially selective (DeAngelis et al., 1992). In addition, some V1 neurons exhibit center–surround interactions that are significantly more complicated than divisive normalization; for some very specific stimulus configurations, introducing a stimulus in the surrounding field can facilitate the response of a neuron (Maffei and Fiorentini, 1976;Nelson and Frost, 1985; van Essen et al., 1989; Gilbert and Wiesel, 1990; Kapadia et al., 1995; Sillito et al., 1995; Gilbert et al., 1996). These issues are currently under investigation in our laboratory (Cavanaugh et al., 1997).

Another limitation of the model is that it is local in time; it does not take into consideration the phenomenon of adaptation. The data sets that we have fitted were all obtained by randomizing the order of presentations, in the hope of achieving an average level of adaptation. To some extent, adaptation can be framed within the context of the normalization model; it can be treated as masking by assuming that gain control has a long memory (Heeger, 1992a). It is, however, unlikely that adaptation operates through the same mechanism that provides masking. First, adaptation was shown in the cat to result from a tonic hyperpolarization (Carandini and Ferster, 1997b), which is not observed during masking (Carandini and Ferster, 1997a). Second, there are some adaptation results that cannot be explained simply by changing the gain of a cell. In particular, after long exposure to a high-contrast grating, the response to that grating is often reduced more than its response to other gratings, both in cats (Movshon and Lennie, 1979;Albrecht et al., 1984; Saul and Cynader, 1989a,b) and in monkeys (Carandini et al., 1997a).

Biophysical implementation of the model

Although the normalization model is completely described by Equations 1-4, this description lies somewhere between a biophysical one and a phenomenological one. A thorough biophysical description of the model should specify how V1 simple cells would have a linear receptive field that results in the injection of a driving current I_d without altering their conductance g , and how the activity of the normalization pool would increase the conductance g without affecting the driving current I_d.

We have recently proposed a model that meets these conditions (Carandini and Heeger, 1994). This model is based on a push–pull arrangement of feed-forward excitation and inhibition, and on feedback shunting inhibition within the normalization pool. For example, according to the model an ON subregion of a simple cell would be the result of excitation from ON-center LGN cells and inhibition from OFF-center LGN cells. Increases in conductance attributable to increased excitation would be matched by decreases in conductance attributable to decreased inhibition, and vice versa. The total conductance would depend only on a shunt conductance g_shunt that grows with the overall activity of the normalization pool, and that has an equilibrium potential exactly identical to the resting potential of the cell.

According to this view the only role of intracortical feedback is to provide shunting inhibition. This proposal differs from a number of recent recurrent models that generally consider intracortical feedback crucial in sharpening the selectivity conferred by the inputs from the lateral geniculate nucleus (Ben-Yishai et al., 1995; Douglas et al., 1995; Somers et al., 1995; Suarez et al., 1995;Maex and Orban, 1996). Although the feed-forward view is supported by recent evidence (Reid and Alonso, 1995; Ferster et al., 1996), the initial linear stage of our model should not necessarily be identified with a feed-forward arrangement. A linear receptive field could, in principle, be constructed with pure feed-forward connections, pure feedback connections, or a combination of feed-forward and feedback.

According to some of the forementioned recurrent models (Ben-Yishai et al., 1995; Somers et al., 1995) V1 cells receive a broadly tuned excitatory input from the LGN, which is substantially sharpened by intracortical excitation from similarly tuned cells and by broadly tuned intracortical inhibition. A computational analysis of these models, however, indicates that they would not account for many of the phenomena described in the present study (Carandini and Ringach, 1997). In particular, these recurrent models ascribe contrast saturation and phase advance entirely to the LGN input. In addition, these models do not account for masking by gratings and by noise, nor do they predict the associated phase advances or decreases in integration time. Finally, the recurrent models make some unlikely predictions, e.g., that the orientation tuning measured with plaids should be strikingly different from that measured with gratings (Carandini and Ringach, 1997).

On the other hand, the recurrent models may be more correct than ours in the relative importance they ascribe to geniculocortical excitation versus corticocortical excitation. A future goal for our research is to integrate the best aspects of the normalization model and of the recurrent models, perhaps by postulating a role for cortical feedback in determining the linear receptive fields of V1 simple cells.

Here we derive approximate closed-form equations for the responses of model cells to the stimuli employed in this study. The derivation is based on the assumptions stated in Equations 1-4.

Predicted responses to gratings

Consistent with results obtained in the cat and monkey (Albrecht and Hamilton, 1982; Sclar et al., 1990), we assume the average exponent for the cells in the normalization pool to be n = 2 (Heeger, 1992a). As a result, in the absence of normalization the response of each cell in the normalization pool to a drifting sine grating is a half-squared sinusoid. We call this rectified and squared linear response the “unnormalized response.” It is given by max(0, I_d)².

The receptive fields of adjacent simple cells tend to exhibit either 90° or 180° phase relationships (Palmer and Davis, 1981; Pollen and Ronner, 1981; Foster et al., 1983; Liu et al., 1992). We can thus reasonably assume the normalization pool to contain quadruples of cells with the same amplitude response but with phases 90° apart. For drifting sine grating stimuli, then, the sum of the un-normalized responses of the four units in each quadruple is constant over time and is proportional to the square of the stimulus contrast c (Adelson and Bergen, 1985). This follows directly from sin² + cos² = 1. The sum of the unnormalized responses of all the cells in the pool is thus a neural measure of local stimulus energy: Σ max(0, I_d)² ∝ c².

If the membrane conductance changes slowly, dg/dt ≈ 0 (so that V ≈ I_d/g) , it is possible to directly relate two unknowns, the overall response of the pool Σ R and the total conductance g of each cell:

$$\sum R\propto \sum max(0,V{)}^2\propto \sum max(0,I_{\text{d}}{)}^2/g^2\propto c^2/g^2.$$ Equation 8

There is another equation relating those unknowns: the definition of g (Eq. 4). It is thus easy to combine the two to eliminate Σ R and to obtain a relation between conductance and stimulus energy:

$$g=\sqrt{g_0^2+k^2{c}^2},$$ Equation 9

where this new constant k is proportional to the k in Equation 4. This relation is exact only at steady state, when the conductance g is constant in time. We have confirmed with numerical simulations that the model does reach such a steady state for drifting grating stimuli. Once in steady state the cell membrane behaves as a linear system. Stimulation with gratings of contrast c thus results in sinusoidal membrane potentials V . It is easy to show (by taking the Fourier transform of both sides of Eq. 2) that the amplitudes and phases of these sinusoids are given by:

$$\text{amplitude}(V)=\frac{\text{amplitude}(c L)}{g\sqrt{1+(2\pi f\tau {)}^2}},$$

$$\text{phase}(V)=\text{phase}(c L)-\text{atan}(2\pi f\tau ).$$ Equation 10

where τ = C/g is the membrane time constant, f is the stimulus temporal frequency (in hertz), and c L(t) is I_d(t) , the output of the initial linear stage.

Because the amplitude of the first harmonic of the n th power is proportional to the n th power of the amplitude of the first harmonic, we can rewrite the previous equations to express the first harmonic of the firing rate R :

$$\text{amplitude}(R)\propto {\left[\frac{\text{amplitude}(c L)}{g\sqrt{1+(2\pi f\tau {)}^2}}\right]}^n,$$ Equation 11

$$\text{phase}(R)=\text{phase}(V).$$

A few rearrangements yield the expressions for the first harmonic responses of the normalization model to a drifting grating that are used throughout this study:

$$\text{amplitude}(R)\propto {\left[\text{amplitude}(L)\frac{c}{\sqrt{\varsigma (f{)}^2+c^2}}\right]}^n,$$ Equation 12

$$\text{phase}(R)=\text{phase}(L)-\text{atan}\frac{2\pi f{\tau }_0}{\sqrt{1+(({\tau }_0/{\tau }_1{)}^2-1)c^2}},$$ Equation 13

where

$$\varsigma (f{)}^2=\frac{1+(2\pi f{\tau }_0{)}^2}{({\tau }_0/{\tau }_1{)}^2-1}.$$ Equation 14

The stimulus variables are the contrast c and the temporal frequency f . The model parameters are the amplitude and phase of the response L of the linear receptive field to the grating at full contrast, the time constant at rest, τ₀ = C/g₀, the time constant at full contrast, τ₁ = C/ $\sqrt{{\text{k}}^2+{\text{g}}_0^2}$, and the exponent n of the spike encoding stage.

Predicted responses to plaids

The expressions derived above for the firing rate of simple cells to drifting sinusoidal gratings can be approximately extended to stimuli composed of two gratings. We restrict our attention to the case in which the two gratings have the same temporal frequency f .

Let c₁ and c₂ be the contrasts of the two gratings. Let L₁ and L₂ (sinusoids) be the responses of the linear receptive field to the individual gratings. The driving current is just the sum of the linear responses weighted by the contrasts:

$$I_{\text{d}}(t)=c_1{L}_1(t)+c_2{L}_2(t).$$ Equation 15

The quantity Σ I_d(t)² is not in general constant in time, because it contains a component at twice the temporal frequency of the stimulus. So we must assume that the membrane conductance reflects the average firing rate of the neurons in the normalization pool. The responses may be averaged over time (e.g., with slow synapses) and/or over space (i.e., by assuming that the normalization pool is large enough that it includes neurons with different receptive field positions).

Then the conductance is approximately constant over time, and the same arguments used above may be applied to yield:

$$\text{amplitude}(R)\propto {\left[\frac{\text{amplitude}(c_1{L}_1(t)+c_2{L}_2(t))}{\sqrt{\varsigma (f{)}^2+c_1^2+c_2^2}}\right]}^n,$$ Equation 16

$$\text{phase}(R)=\text{phase}(c_1{L}_1(t)+c_2{L}_2(t))-\text{atan}\left(\frac{f{\tau }_0}{\sqrt{1+(({\tau }_0/{\tau }_1{)}^2-1)(c_1^2+c_2^2)}}\right),$$ Equation 17

where ς is defined in Equation 14.