Predicting Site-Binding Modes of Ions and Water to Nucleic Acids Using Molecular Solvation Theory

Abstract

Site binding of ions and water shapes nucleic acids folding, dynamics, and biological function, complementing the more diffuse, nonspecific “territorial” ion binding. Unlike territorial binding, prediction of site-specific binding to nucleic acids remains an unsolved challenge in computational biophysics. This work presents a new toolset based on the 3D-RISM molecular solvation theory and topological analysis that predicts cation and water site binding to nucleic acids. 3D-RISM is shown to accurately capture alkali cations and water binding to the central channel, transversal loops, and grooves of the Oxytricha nova’s telomeres’ G-quadruplex (Oxy-GQ), in agreement with high-resolution crystallographic data. To improve the computed cation occupancy along the Oxy-GQ central channel, it was necessary to refine and validate new cation−oxygen parameters using structural and thermodynamic data available for crown ethers and ion channels. This single set of parameters that describes both localized and delocalized binding to various biological systems is used to gain insight into cation occupancy along the Oxy-GQ channel under various salt conditions. The paper concludes with prospects for extending the method to predict divalent cation binding to nucleic acids. This work advances the forefront of theoretical methods able to provide predictive insight into ion atmosphere effects on nucleic acids function.

Graphical Abstract

1. INTRODUCTION

Nucleic acids are essential for how genetic information is stored, translated, regulated, and transmitted in cells,¹⁴ and, thus, a detailed understanding of their function would contribute greatly toward addressing current challenges encountered in molecular genetics, genome editing, and the treatment of disease. Crucial for nucleic acid stability is the electrostatic stabilization, provided by the ion atmosphere, of the highly negatively charged backbone, which leads to sensitivity of function to changes in ionic conditions. Understanding this sensitivity is complicated by its entanglement with nucleic acid conformational heterogeneity.^15,16 While advances have been made for 3D structural prediction of overall RNA folds,^17–19 only initial steps have been taken to develop predictive models for how nucleic acids are affected by ionic conditions that often dictate their specific biological function.^6,16

Territorial ion binding occurs through delocalized cation accumulation and anion depletion in the vicinity of the nucleic acid (including the grooves), creating a neutralizing ion atmosphere that, together with bulk solvation, provides crucial electrostatic stabilization. Even at very low salt concentrations, territorially bound ions around nucleic acids adopt organized, delocalized binding modes that extend many solvation layers (several nanometers) away from the nucleic acid surface into the bulk.^6,20 Territorial binding of ions and water can be probed experimentally using small-angle X-ray scattering or ion-counting experiments,^16,21–24 and molecular solvation models (such as explicit solvent molecular dynamics or three-dimensional reference interaction site model (3D-RISM)) have proven useful to aid in the interpretation of these experiments^6,16,20,25 and allowed benchmark tests and blind predictions to be made.^6,16,20

Alternatively, site-specific ion and water binding is localized and profoundly affects the structure and function of nucleic acids,^26,27 and hence is central to understanding the roles of these molecules in biology and nanotechnology. Long-lived or transient site bound cations are key for enabling catalytic strategies of ribozymes^28–31 and DNAzymes³² that have broad impact on the development of biosensors and new biomedical technology, as well as implications into evolutionary theories into the origins of life. Site-specific ion binding is key for maintaining nucleic acid folds, such as in the case of guanine quadruplexes (GQs), and enabling recognition of cognate ligands by some riboswitches with consequences for understanding aging, cancer, and genome function regulation. Site-bound ions mediate recognition between nucleic acid−protein interfaces or crystal contacts in the solid state and support catalysis of DNA and RNA biosynthesis, cleavage, and degradation important in biology and gene editing. Site-bound ions can mediate alternative base pairing important for nanotechnology applications such as the development of DNA wires and nanoconductors, DNA-based organic frameworks, or synthetic peptide−nucleic acid complexes.^{24,26,33–37} However, unlike in the case of territorial binding, the prediction of site binding to nucleic acids remains a major challenge for computational biophysics. Molecular dynamics (MD) simulation can be used to explore thermally accessible conformational ensembles departing from a given set of starting structures and solvent-binding modes. However, MD cannot easily predict site-specific solvent-binding modes, even for rigid nucleic acid conformational ensembles, due to sampling challenges associated with large free energy barriers for solvent exchange that lead to long residence times. MD simulations of nucleic acids thus require information about site-specific binding modes for each starting structure in order to be practically applied. Continuum solvation models such as those based on the nonlinear Poisson−Boltzmann (NLPB) equation lack the molecular-level description of solute−solvent interactions necessary to enable reliable prediction of solvent structure and site-binding occupancy.

This work develops a 3D-RISM model for prediction of site-specific monovalent ion and water binding to nucleic acids, following in the wake of success with validation of the method for territorial binding.^6,13,20,39 We study the site-specific ion and water binding in G-quadruplexes, an important class of structured nucleic acid scaffolds that form inner channels that bind cations such as Na⁺ and K⁺ in a size-specific manner and with high affinity. GQs have found a wide range of applications in both supramolecular chemistry⁴⁰ and biology, as targets for development of therapies, due to their broad regulatory roles in genome function.²

The paper departs by laying out the challenges for prediction of site-bound ions and water to nucleic acids. We next present a force field refinement approach that takes advantage of similarities between GQs and inorganic and biological ionophores; new parameters are refined against structural and thermodynamic data for crown-ethers and are subsequently validated against crystallographic data for ion channels and ion-counting measurements. With this new force field, the 3D-RISM model is shown to capture water- and cation-binding modes in GQs that are size-dependent and follow trends found in crystallographic structures; these trends are preserved when departing from GQ structures obtained using solution NMR or upon structural relaxation to solution conditions. We next demonstrate that models based on the standard NLPB approximation do not build up cation density along the GQ channel, while long MD simulations (2.4 μs) were inadequate to reach equilibrium and unable to achieve the expected experimental binding patterns on this time scale. Finally, 3D-RISM predictions for cation occupancy in the GQ central channel as a function of salt concentration are presented. Along the way, new tools are introduced for topological analysis of the 3D-RISM solvent distributions that enable quantitative comparison of site-specific binding geometry and occupation. We close by discussing the prospects of extending the current methodologies to predict site binding of divalent cations to protein−nucleic acid complexes and provide a proof-of-principle demonstration with Mg²⁺-mediated binding of DNA polymerase η to a DNA primer.

2. RESULTS AND DISCUSSION

2.1. Challenges for Predicting Site-Bound Ions and Water to Nucleic Acids.

The most straightforward rigorous computational way to study ion binding is to map ion distributions using MD simulations in explicit water and salt. While MD is moderately tractable for territorial binding,⁶ it quickly becomes limited for site binding due to the need for solution particles to cross significant free energy barriers from unbound to bound states^47,48 and to reach equilibrium with the bulk solution. This drawback is amplified by the need to consider competition between more than one solution component for the same site and to perform calculations over large ranges of ionic conditions, including variation of salt concentration (10⁻⁴−10⁻¹ M) and multiple ion composition.

Our investigation uses a methodology based on 3D-RISM^49–56 that has been introduced recently to study salt effects on nucleic acids.^6,20 3D-RISM is an integral equation theory of molecular liquids that can be used to solve for equilibrium 3D density distributions of aqueous salt solutions around molecular solutes.^49–53 3D-RISM has unique potential advantages relative to MD simulations and NLPB in that it captures complex, correlated binding modes of solvent particles and solves for particle distributions indiscriminately over a wide range of concentrations.⁵⁷ A key feature of 3D-RISM is that it treats the biomolecular system, such as a nucleic acid or protein, in equilibrium with a bulk solution at constant composition (and chemical potential), which closely mimics the experimental environment in vitro or in the cell. 3D-RISM has been validated in benchmark calculations for territorial binding^6,20 and blind tests³⁹ against ion-counting experiments^12,13 that highlight its predictive qualities, in stark contrast^6,20 with results from conventional NLPB calculations.⁵⁸ In the present work we extend the capabilities of the 3D-RISM model and develop topological analysis tools for prediction of site binding of monoalent ions and water to nucleic acids. This enables new insight to be gained on complex ion- and water-binding modes and could be used as a critical departure point for MD simulations that explore dynamical ensembles, as well in biomolecular structure refinement based on X-ray crystallographic and Cryo-EM data.

2.2. Characterization of Ion- and Water-Binding Modes Using Topological Analysis of 3D Molecular Distributions.

The raw data provided by computational methods to study salt effects on nucleic acids comes in the form of 3D distributions of ions and water. These distributions contain complex patterns of density fluctuations that require specialized topological analysis to quantify site binding of ions and water.

Mapping Binding Modes Using the Laplacian of Particle Distributions.

We identify binding modes as regions of 3D-space where particle densities are locally concentrated using a general approach for analyzing scalar fields based on the Laplacian. Application of the Laplacian operator yields a measure of the difference between the average value of a scalar function in a small neighborhood of a point and the value of the function at that point.⁵⁹ For the case of particle distributions ρ(r), in regions where the Laplacian, ∇²ρ(r), is positive the local particle density is depleted, whereas in regions with negative Laplacian the particle density is locally concentrated. This allows a mechanism to identify, isolate, and demarcate individual solvent-binding sites and quantify statistical properties for each binding mode (see Methods). Similar topological analysis approaches have been used to gain insight from molecular electron densities.⁶⁰

Mapping Density along Channels Using the Worm Projection and Tomographic Sections.

A feature of the G-quadruples and ion channel systems studied in this work is their ability to form 1D channels of curvilinearly connected binding sites. To characterize the change in density along these curves, we created a so-called worm projection using a plane perpendicular to the curve of the channel. These projections can be analyzed or visualized by tomographic sections that offer a two-dimensional snapshot of the changes in density along the channel.

2.3. Force Field Calibration and Validation Using Complexes of Bis-Crown-Ethers and Ion Channels with Na⁺ and K⁺.

In order to gain predictive insight into GQs, we sought to develop a 3D-RISM model with tuned nonbonded force field parameters that were specifically calibrated to reproduce Na⁺ and K⁺ structure and thermodynamic binding properties in complexes with bis-crown-ethers and then validated against macromolecular ion channels. Bis-crown-ethers contain two sandwiched crown-ether rings, similar to the oxygen rims composing the coordination sphere of cations in GQs (vide infra), and prefer to bind metal ions with sizes slightly larger than their cavity, as opposed to 1:1 complexes between crown ethers and cations, whose formation is favored by size matching.^61–63 For Na⁺ we consider the bis-(12-crown-4)-sodium complex, whereas for K⁺ we use the bis-(15-crown-5)-potassium complex, which has been reported to be selective for the corresponding cations⁶⁴ and for which high-resolution crystal structures exist with the cations at full occupancy (see Methods). Using the preorganized crystal structures of the complexes of the bis-crown-ether scaffolds, we adjusted the pairwise Lennard-Jones (LJ) parameters based on three criteria: (i) maximize cation occupancy within the binding locus between the two crown-ether units, (ii) minimize the deviation from the experimental cation location in the complex, and (iii) maintain a unimodal binding mode as observed experimentally. The last two criteria maintain a unimodal distribution within the binding locus, as observed crystallographically. This is needed to prevent overfitting, as for certain values of LJ parameters, the distribution within the binding pocket acquires multiple peaks as the cation size decreases and the cation prefers “to stick” to the walls of the bis-crown-ether cavity. Within these constraints, the cation occupancy in the crown-ether cavity is approximately doubled when using the updated force field (see Figure S1; a detailed description is provided in the Methods section and the SI)

The new force field was first validated in the context of territorial binding alone by computing preferential interaction parameters of NaCl or KCl in the presence of a rigid helical 24 bp DNA construct, a prototypical system that was used in our previous work^6,20 to validate 3D-RISM against existing experiments. Preferential interaction parameters (ion-counting profiles) provide a direct measure of the extent to which counterion condensation or anion depletion contributes to stabilization of nucleic acid charge. Calculations over salt concentrations ranging from 0.01 to 1 M showed no significant changes from previous calculations (up to 1% change from the total nucleic acid charge) that used the original force field (see Figure S6) and overall agreed well with recent experimental values collected at salt concentrations of up to ~0.2 M, with greater deviation observed at higher concentrations.^13,39

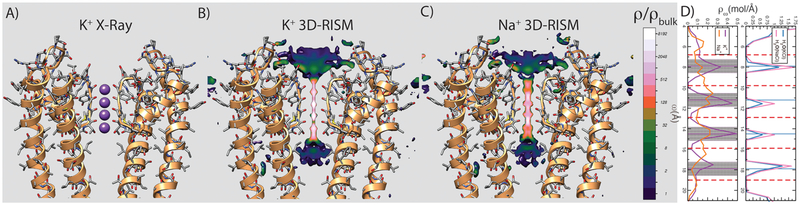
Further, we compared calculated cation and water occupancies and binding geometries with estimates from crystallographic data of KcsA ion channels.⁶⁵ Ion channels bind cations in a similar fashion to GQs using a linear series of cages of carbonyl and hydroxyl groups. The KcsA K⁺ cation channel has been well studied, and the occupancy of cations has been estimated based on the anomalous scattering signal of Tl⁺ and K⁺ that helps distinguish bound species with a similar number of electrons and helps alleviate the correlation between structure factor and occupancy during refinement.⁶⁵ The KcsA channel is composed of four identical protein units that form a selectivity filter and contains four binding sites bound by five successive planar rims; four consecutive rims are formed by backbone carbonyl oxygens belonging to the sequence Val-Gly-Tyr-Gly with one marginal rim formed by the hydroxyl oxygen of a Thr residue side chain. Each of the four binding sites is shaped as a square antiprism, similar to that of GQs. For structures crystallized in concentrations of approximately 200 mM K⁺, it was estimated that each of the four sites is half-occupied by K⁺ cations and water molecules.⁶⁵ The calibrated 3D-RISM model estimates an average occupancy of 0.46 cation and 0.50 water molecule for each site (Figure 2), in striking agreement with the crystallographic data.⁶⁵ Furthermore, the locations of the calculated density maxima of cations and water are within 0.5 Å of their crystallographic location, while the linear distributions along the channel overlap well with the distribution derived from the crystallographic refinement.⁶⁵ Further the 3D-RISM model is able to differentiate the experimentally observed Na⁺ binding site that is shifted toward each of the rims, rather than binding centrally as with K⁺.^66–68 It should be noted that a more comprehensive understanding of the KcsA channel biological function needs to factor in the cell membrane environment and atomic-scale fluctuations at room temperature,⁶⁹ while the present calculations focus on predicting the average ion density conditional to a representative channel structure captured by X-ray crystallography under nonphysiological salt conditions used for crystallization.

Figure 2.

Validation of the calibrated force field using crystallographic and thermodynamic data for cation and water binding in the selectivity filter of the KcsA ion channel. (A) Overlapping crystallographic K⁺- and water-binding loci in the selectivity filter of the KcsA ion channel are marked using violet spheres. Crystallographic data suggest that K⁺ and water molecules have approximately 50% occupancy in each locus in a background of 200 mM monovalent salt. For simplicity only two units out of four of the ion channel are shown (orange ribbons). (B) Tomographic slice along the selectivity filter through the 3D-RISM K⁺ density and (C) Na⁺ density, respectively. (D) (Left) Worm projections along the selectivity filter for K⁺ (violet solid line) and Na⁺ (orange solid line) and (right) water component of the NaCl solution (solid pink line) and KCl solution (blue solid line). The positions of the five coordinating rims of the selectivity filter are shown by red dashed lines. Crystallographic positions of K⁺ and water in the selectivity filter are marked using horizontal violet and light-blue lines, respectively. Transparent violet bars mark the width of K⁺ distribution inside (obtained from the B-factor) for each binding locus. Using the calibrated force field the average occupancy of each binding locus was estimated at approximately 46% for cations and 50% for water.

2.4. Guanine Quadruplexes as Model Systems to Study Site Binding of Ions and Water to Nucleic Acids.

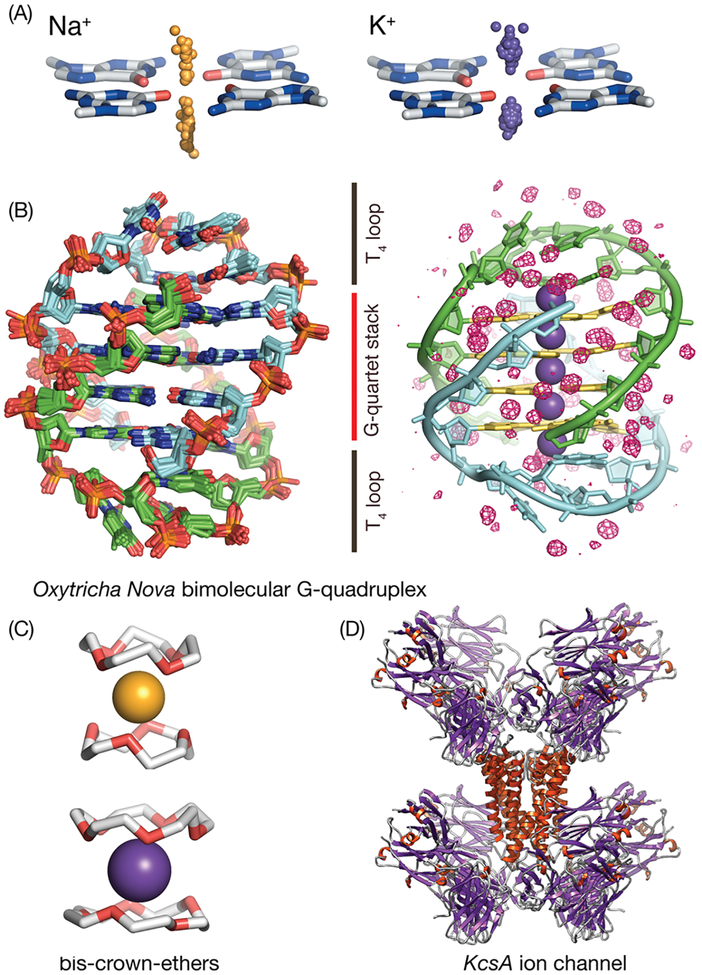
GQs are structured RNA and DNA nucleic acid motifs formed from stacked G-quartets embedded in various backbone and loop topologies that form channels known to have affinity for cations. The four guanines of each quartet are arranged in a square-planar pattern and stabilized by hydrogen bonds using adjacent Hoogsten and Watson−Crick faces (Figure 1A). Typically cations bind between stacks of G-quartets that that form coordination cages with two parallel rims of carbonyl oxygen atoms, G:O6, yielding a square antiprismatic coordination geometry.

Figure 1.

Nucleic acid quadruplexes form inner channels using stacked G-quartets within which Na⁺ and K⁺ cations are bound in a size-dependent manner. (A) K⁺ and Na⁺ adopt different binding patterns with respect to G-quartets, as shown by the distribution of Na⁺ cations (orange spheres) and K⁺ cations (right, violet spheres) with respect to a reference G-quartet obtained from all existing GQ crystal structures available in the PDB. (B) Oxy-GQ maintains the same fold in crystal and in solution and in the presence of Na⁺ or K⁺.^1,38 (B, left) Ensemble of superimposed crystallized structures of Oxy-GQ used in this work. The maximum heavy atom RMSD between its members is 0.7 Å. The two strands of Oxy-GQ are shown in green and light blue, respectively. (B, right) Solvation structure of Oxy-GQ that has an internal channel with five cation-binding sites (shown as violet spheres); K⁺ cations bind near the midpoint between G-quartets, while Na⁺ cations bind along the same channel but their positions are shifted near the G-quartets, in consensus with the trend observed for all G-quartets in the PDB. The guanine rings that form the quadruplex are highlighted in yellow. The crystallographic consensus solvation water map (isosurface red mesh) reveals tightly bound waters deeply buried within the T-loops that make direct contact with channel-bound cations and along the grooves. (C, D) The manner in which GQs bind cations bears a high degree of similarity to that of crown-ethers and ion channels. This work uses crystallographic structural and thermodynamic data on cation binding to crown ethers and ion channels to improve the underlying force-field used together with 3D-RISM and to enable quantitative predictions on the population of cations inside the GQ channel as a function of salt concentration.

Cation-binding modes and occupation in the GQ channel have been observed to be correlated with cationic size. Monovalent cations such as K⁺, NH ⁺₄, Rb⁺, and Tl⁺ have been located at the midpoint between adjacent G-quartet planes, Na⁺ has been located to bind both between consecutive G-quartet planes and within a single plane,⁷⁰ while Li⁺ is unable to bind to the central channel.^71,72 To provide a broad overview of experimentally observed Na⁺ and K⁺ binding, we have analyzed the distribution of these two cations with respect to all the G-quartets that can be extracted from crystallographic structures of GQs available in the PDB (Figure 1). On average, Na⁺ and K⁺ are located very close to the midpoint between two adjacent quartets. The Na⁺ distribution has greater variance along the normal to the quartet plane, while the variance within a plane parallel to the quartet are similar (Table 1).

Table 1.

Crystallographic Characterization of the Distribution of Na⁺ and K⁺ with Respect to a G-Quartet Plane from the PDB (See Also Figure 1 A)^a

	d (Å)	σ⊥ (Å)	σ∥ (Å)
K+	1.68	0.26	0.11
Na+	1.71	0.48	0.07

^ad is the average distance between the cation and the G-quartet plane, σ_⊥ and σ_∥ are the standard deviations along the perpendicular and parallel directions to the G-quartet plane (determined as the principal values of the distribution covariance tensor). A total of 232 G-quartets were found to directly coordinate at least one Na⁺, while 310 quartets were found coordinating K⁺.

One of the most studied GQs, Oxy-GQ, contains two segments of the telomere region of the Oxytricha nova protozoan ciliate⁷³ and and was later found to adopt the same fold in solution and in a crystal under various K⁺ and Na⁺ conditions^1,38 (Figure 1). Oxy-GQ is composed of two DNA strands with identical sequence G4T4G4, with a secondary structure resembling two interlocked hairpins; the G’s form four quartets, while the two T4 segments form loops that cross the G-quartet stack diagonally.

Available single-crystal X-ray structures of Oxy-GQ reveal several well-defined cation- and water-binding modes. In the majority of these structures Oxy-GQ displays five cationic binding modes: three of these modes are intercalated between the four G-quartets, while the other two are located on the top and bottom quartets (on the exterior of the stack) and stabilized by coordination to the T loops (T:O2 atoms) and water. A consensus conserved set of water-binding patterns is located in the grooves as well as buried near the central cations. Solution NMR data have provided evidence for at least three cationic binding modes that most likely correspond to cations intercalated between G-quartets,^74–76 as well as less tightly bound modes with shorter exchange times in the T4 loops.⁷⁷

2.5. Recapitulating the Binding of Cations in the Oxy-GQ Central Channel.

To test the ability of the new 3D-RISM model to replicate crystallographic cation- and water-binding modes, we have carried out calculations on a structural ensemble extracted from single-crystal X-ray data available for Oxy-GQ (Table S1). The largest peaks of the cation density distributions are located in the GQ channel. To illustrate this, we used a tomographic longitudinal section of the Na⁺ and K⁺ density distributions aligned along the GQ central channel (Figure 3 A). The values of the cation density along the central channel are approximately 4 orders of magnitude larger than the reference bulk concentration of 0.05 M (Figure 3). In contrast the density distribution near the phosphoryl groups reaches values of about 2 orders of magnitude larger than the bulk (approximately 5 M). The tomographic section reveals significant differences between K⁺- and Na⁺-binding modes. Potassium binding loci have an approximately spherical shape, being surrounded by regions of near-zero density. Over the same area along the tomographic section, Na⁺ density is delocalized with no significant zero-density regions and exhibits multiple maxima.

Figure 3.

Locations of cations and water around Oxy-GQ from 3D-RISM closely match crystallographic data. (A) Tomographic slice through cation (K⁺ and Na⁺) distributions where the slicing plane was aligned along the Oxy-GQ central channel and colored according to the density value. (B) Worm projections of cations (left panel) and water (right panel) along the Oxy-GQ central channel. The projected position of the crystallographic K⁺ ions resolved in the channel is marked with horizontal violet lines, while the width of the distribution taken from experimental B_iso values is shown using transparent violet bars. The position of the four G-quartets along the worm curve is marked with horizontal dashed red lines. (C) Buried cavities are predicted to be occupied by multiple species at fractional occupation, with crystallographic cation-binding pockets being partly occupied by water and vice versa. Calculations reproduce crystallographically resolved water molecules (red spheres) that coordinate directly K⁺ (violet sphere) cations and that form bridging interactions with the DNA. Water (red) and K⁺ (violet) density is represented using an isodensity mesh. (D) Overall analysis of the proximity of 3D-RISM bound waters and cations to crystallographically assigned water molecules.

The Na⁺ and K⁺ cation distributions were analyzed using a worm projection traversing the channel and extending to traverse two additional, symmetric binding sites buried in the T4 loops, yielding an elongated C-shaped path of approximately 25 Å. The curvilinear path was defined using a B-spline representation whose pivot points were chosen as the critical points of the cation density and the geometric centers of the G-quartets, and density was integrated within a tube of 3 Å radius around the path.

The worm projection (Figure 3) shows that the positions of the cation peaks match the K⁺ crystallographic positions of Oxy-GQ. Whereas K⁺ binding is unimodal, the worm projection shows Na⁺ can adopt multiple binding modes in between each quartet stack: a wider mode centered at the midpoint of the quartet stack and two tighter modes near the plane of the quartet. Further, Na⁺ has a nonzero density in the quartet plane, as opposed to K⁺, indicating a lower barrier for cation conduction across the GQ central channel. The distributions of both Na⁺ and K⁺ within the quadruplex are correlated with the distribution observed among G-quartets available in crystallographic structures in the PDB, discussed in the previous section.

To further explore the extent to which cation size affects the binding patterns and population along the GQ channel, we computed Li⁺ distributions around Oxy-GQ. Li⁺ has a smaller ionic radius than Na⁺ or K⁺, yet is known to inhibit the formation of quadruplexes.⁷² Li⁺ is unable to displace Na⁺ or K⁺ from the GQ channel, preferring to bind in the grooves⁷¹ or territorially.⁷⁸ Worm plots (Figure 3) show that the amount of bound Li⁺ along the GQ channel as well as the transversal loops is greatly reduced as compared to Na⁺ or K⁺, being compensated by a stronger water binding to the channel and loops. This behavior resonates with experimental interpretations that suggested the cation occupancy along GQ channels is controlled by the balance between steric fitness into the cavity and by the strength of interactions with other functional groups of the nucleic acid, territorial binding modes, and the bulk solution.⁷⁹

Ion and water distribution obtained from 3D-RISM can be revelatory for gaining a basic understanding of the exchange mechanism between channel binding sites and territorial binding modes, an insight that can be relevant when using GQ scaffolds for the design of molecular wires or GQ-based organic frameworks that can transport ions and be used for energy storage.^37,48,80 Both tomographic sections and worm projections can be used to trace the path of traversing the GQ channel. As shown in Figure 3A, the path is independent of the ion identity, but smaller cations such as Na⁺ and Li⁺ appear to face lower barriers then K⁺ when circulating along the GQ channel, especially since their density is finite even in each of the G-quartet planes.

2.6. Recapitulating the Binding Modes within the T4-Loops and Grooves.

In addition to ion distributions, 3D-RISM is able to compute water distributions that can be compared with consensus distributions derived from high-resolution crystallographic data. A consensus solvent distribution map was built based from on available crystallographic data by first aligning all the existing X-ray structures of Oxy-GQ to a reference structure (PDB ID 4r45) followed by mapping the position of each water molecule on a 3D grid with a normal distribution with a width derived from the crystallographic B-factor and scaled by the reported crystallographic occupancy. To quantify the proximity between water binding modes from 3D-RISM and the consensus water solvation map, we have computed the closest distance between each of the binding modes in the consensus map and those predicted by 3D-RISM. The distribution of these distances is shown in Figure 3D and shows high correlation with the distribution from crystallographic data: 35% of the computed waters modes are within 1 Å from crystallographic modes, while 80% are within 2 Å.

2.7. Effect of Structural Relaxation and Dynamical Ensembles in Solution.

While the choice of crown ethers, ion channels, and GQs was guided by their structural rigidity as a means to eliminate the need for extensive conformational sampling, we nevertheless tested to what extent the use of static structures is justified when estimating ion- and water-binding modes. First, the initial ensemble of X-ray structures was relaxed to the actual solution conditions using free energy minimization (see Methods). The relaxed ensemble showed little deviation from the crystallographically resolved structures with overall mean squared deviations of 0.8 Å, with the T4 loops showing the largest changes (Figure S4). We noted a slight increase in the cation populations in the GQ-channel as well as a nearly total depletion of water binding in the intercalated sites, which was accompanied by a stronger water accumulation in the T4 loops (Figure S5). Second, the same minimization procedure was applied to an NMR structural ensemble of Oxy-GQ¹¹ to test the extent to which structural fluctuations captured in solution can impact computed ion and water distributions. While the conformational variation of the backbone and transversal loops was larger than in the case of the crystallographic ensemble, the ion-binding patterns were maintained (see Figures S4 and S5), especially for the intercalated cation-binding sites. The marginal sites were less populated than in the case of the minimized crystallographic ensemble, possibly reflecting the observations that in solution only three major cationic binding modes exist that are likely intercalated between the G-quartets,^74–76 as well as the presence of weaker cation binding modes with shorter exchange times in the T4 loops.⁷⁷

2.8. Assessment of Other Methodologies: Standard NLPB and MD Simulation.

To test whether NLPB is able to capture site-specific binding to GQ, we carried out similar calculations at the same salt conditions as those reported here using 3D-RISM. The cation effective size used is a key parameter in NLPB calculations and controls the ability of such calculations to match experimental IC measurements or cation solvation free energies. The effective cationic radii were varied over a range from 1.0 to 3.5 Å, which encompasses values that reproduce solvation free energies of Na⁺ and K⁺ as well as values that include a solvation layer.^6,12 Worm projection (Figure S2, computed at 100 mM monovalent salt concentration) reveals that the cationic density values inside the GQ channel and the diagonal loop are negligible for cationic radii that are able to reproduce hydration free energies for Na⁺ or K⁺ while decreasing the radii results in overpopulating the binding loci in the loops as opposed to the ones in the central channel, and only at cationic radii of 1 Å can one see any density building up in the quadruplex channel. These results suggest that NLPB is not adequate to provide even qualitative insight into site-specific cation binding in GQs.

In addition, the ability of MD simulations to find binding modes of cations and water to GQs was tested using an approach developed for studying territorial ion and water binding to nucleic acids in which multiple independent simulations are launched from different configurations with ions distributed randomly.⁶ A general feature of all simulations was the significant time required to achieve equilibration by cations and water coordination along the GQ central channel, resonating with earlier observations.⁸¹ Nevertheless, by the end of each of all the eight 300 ns long trajectories, each simulation reached a metastable distinctive coordination pattern along the channel. In the case of simulations run in the presence of 0.2 M KCl, three simulations converged to a coordination pattern whereby K⁺ occupied two (out of three) intercalated binding sites with the other intercalated site being occupied by a water molecule, while in a fourth simulation K⁺ cations were located in the central intercalated binding mode and on the marginal binding sites; in this case the cation entered the quadruplex laterally, not along the channel. In the case of simulations in the presence of NaCl, the majority of simulations adopted a coordination pattern whereby two cations adopt intercalated binding modes, with one simulation having a cation located in the central intercalated site and two other cations in the marginal sites. (see Figure S3). None of the simulations were able to reach globally converged ion occupancies that were consistent with the crystallographic and 3D-RISM binding modes. This underscores the need of 3D-RISM as a tool to predict site binding that could be used to provide starting configurations for MD simulations.

2.9. Enhancing the Description of Binding with Overlapping Binding Modes.

Water density builds up in the channel of Oxy-GQ, although the integrated occupancy is lower than that for cations (Figure 3B). Additionally, overlapping cation- and water-binding modes have been observed (experimentally and using the current methodology, vide supra) in the case of water and cation binding to the selectivity filter of ion channels, where the larger size of the binding pore can accommodate water at half-occupation. Furthermore, binding within the T-loops also presents the same characteristic (Figure 3C) whereby one of the buried loci can preferentially accommodate water and cations with a lower affinity. The other buried locus is predicted to be exclusively occupied by water, similar to the crystallographic assignment. Overall, the possibility of having some of the water-binding modes identified in crystal structures occupied partially by cations is reflected in Figure 3D, which shows that 10% of the crystallographically resolved water-binding modes are within 1 Å of a 3D-RISM cation locus, while approximately 40% are within 2 Å. The ability of the 3D-RISM results to identify and describe overlapped binding modes makes it valuable for crystallographic or Cryo-EM refinement, where often particles with a similar number of electrons occupying the same location can be identified only when additional experimental information (such as anomalous scattering signal) can be detected.

2.10. Predictions for Cation Binding Isotherm to Oxy-GQ Inner Channel.

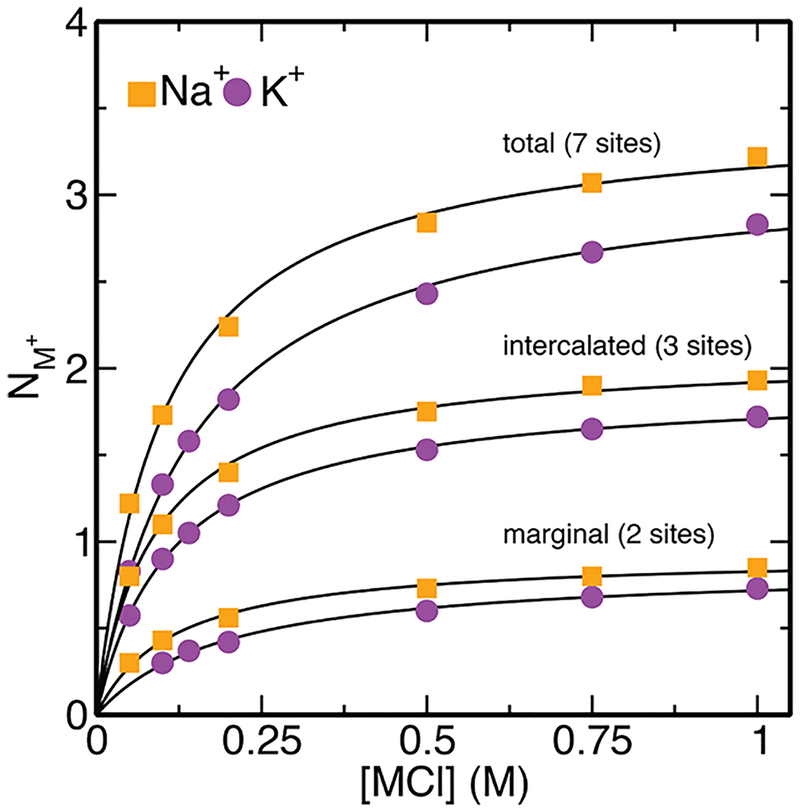
Since the 3D-RISM model developed in the present work describes well ion channels, the occupancy estimates for the GQ channel are intriguing predictions that provide new insight into these systems. The heights and occupancies of the water and cation peaks are anticorrelated along the central channel, with water having larger populations and intensities outside the quartet stack in the T4 loops and cations having a larger population in the channel. This is consistent with experimental NMR data that report only three intercalated binding modes.^74–77 The binding isotherms suggest that the occupancy saturates close to 2.5 cations for K⁺ and 2.8 cations for Na⁺, with the intercalated modes being 50% occupied at saturation (Figure 4).

Figure 4.

Predicted binding isotherm of cations within the GQ channel as a function of salt concentration (NaCl, shown in orange; KCl, shown in violet). A total of seven potential binding sites were identified for cations along the Oxy-GQ channel (see the section Recapitulating the Binding of Cations in the Oxy-GQ Central Channel), three of which are intercalated between G-quartet stacks, two that are marginal and bind with one G-quartet and Ts in the T4 loops, and two that are buried within the T4 loops. Binding isotherms are shown for the intercalated and marginal sites.

2.11. Prospects for Extending 3D-RISM to Treat Divalent Ion Site Binding to Nucleic Acids and Their Complexes.

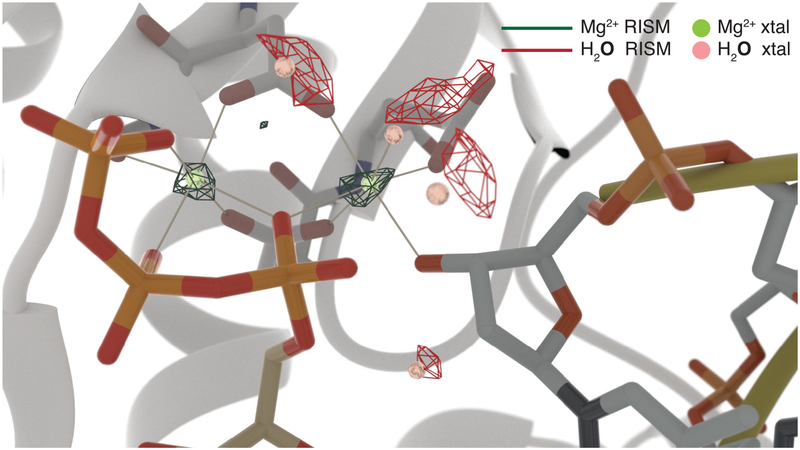
While the focus of this work was on understanding the interaction of nucleic acids with Na⁺, K⁺, and water—the most abundant cations and the most abundant component of the cell, respectively⁸³—there is great interest in the prediction of site-specific binding of divalent metal ions such as Mg²⁺ to nucleic acids due to their importance in folding^27,35 and mediating formation of complexes with proteins critical for biological processes such as storage of genetic information, transcription, translation, replication, and gene regulation.¹⁴ To provide initial support for the extensibility of our 3D-RISM tools to describe site binding of divalent cations to nucleic acid−protein complexes, we present results that explore the degree to which crystallographically resolved binding modes of Mg²⁺ and water can be reproduced for the polymerase η complex with a DNA primer, template, and nucleoside triphosphate. Figure 5 shows that the crystallographic binding locations near the catalytic active site overlap closely with those computed for Mg²⁺ and water. This includes one water that completes the octahedral coordination sphere of a Mg²⁺ cation as well another water molecule that coordinates the primer’s nucleophile O3′ oxygen that participates in the phosphodiester bond formation catalyzed by polymerase η.³⁶ This is an initial promising set of results that strengthens the prospect for developing 3D-RISM as a general method to predict site binding of divalent ions in larger nucleic acids and their complexes with proteins. Accomplishment of this goal would create a key enabling technology for prediction of site-specific divalent metal ion binding in order to generate starting states for MD simulations and for enhancing biomolecular structure refinement based on X-ray, NMR, and Cryo-EM data.

Figure 5.

Computed Mg²⁺ and water densities (shown as dark green and red isodensity meshes, respectively) versus crystallographically resolved positions (shown as light green and pink spheres) near the protein−DNA interface of the catalytic site of polymerase η (PDB ID: 3MR2⁸²). The nucleoside triphosphate is on the left (shown as sticks); the primer is on the right (shown using sticks and yellow ribbons); the protein is shown using white ribbons with only the residues that make direct contacts with Mg²⁺shown using sticks. The isodensity mesh of Mg²⁺ is 1000 times the bulk concentration value of 0.01 M, while that of water oxygens is at 5 times the water bulk concentration of 55.55 M.

3. CONCLUSIONS

The current work highlights the power of the 3D-RISM molecular solvation theory and of novel methods of topological analysis to describe, capture, and predict binding modes of tightly bound monovalent cations and water to GQs, a model system for site binding to nucleic acids. Having the ability to recalibrate and validate the underlying force field using structural and thermodynamic information from a variety of prototype ionophores allows us to create a predictive model for cation occupancy in GQ channels as a function of salt concentration. The current work opens the way for a broader application of this methodology to sharpen the structural and dynamical information obtained from X-ray crystallography, NMR, or Cryo-EM and enhance prediction of metal ion binding modes relevant for molecular dynamics simulations in solution. The current work integrates new 3D-RISM models and topological tools into a powerful computational and theoretical framework for predicting ion binding and salt effects on nucleic acids structure and function.

4. METHODS

Three-Dimensional Reference Interaction Site Model.

3D-RISM expresses the solution particle density distributions, ρ_γ(r), in terms of the total correlation functional, $h_{\gamma }\left(r\right)=\frac{{\rho }_{\gamma }\left(r\right)}{{\rho }_{\gamma }^{\text{bulk}}}-1$, and direct correlation functional, c_γ(r), which are related through a convolution: h_γ(r) = ∑_α∫c_α(r − r′) χ_αγ(r′) dr′, where χ_αγ(r) is the site−site solvent susceptibility of solvent sites α and γ and contains the bulk properties of the solvent.^{49–56,84–86} χ_αγ are precomputed using the dielectrically consistent RISM.^87,88 To arrive at a unique solution, a second relation (closure) between h and c is necessary that has a major impact on the quality of resulting thermodynamic quantities and distributions. The PSE-1,2,3,4⁸⁹ closures have been tested extensively, and it was found that PSE-3 best reproduces and predicts the closest ion-counting measurements^6,20 when compared against experiment.^12,13 Details of energy minimization using 3D-RISM, MD simulation setup, and NLPB calculations are give in the Supporting Information.^7–10

Molecular Mechanics Force Fields.

3D-RISM calculations for the nucleic acid systems used the DNA.OL15 AMBER force field,^90–92 SPC/E water model,⁹³ and alkali halide parameters.^94,95 For protein systems the ff14SB⁹⁶ force field was used; for small molecules (bis crown ethers), point charges were determined using the AM1-bcc semiempirical electronic structure method^97,98 and nonbonded parameters for secondary carbons and ether oxygens were taken from ff14SB.

Structural Data.

The crystallographic structures used for Oxy-GQ calculations are listed in Table S1.^1,3–5 The structures of the bis-crown-ethers complexed with Na⁺ and K⁺ had the CSD⁹⁹ codes FOPPOP¹⁰⁰ and CEBHAT.¹⁰¹ The structure for the KcsA ion channel calculations was taken from the PDB entry 1k4c.¹⁰² Analysis of nucleic acid motifs and identification of G-quartets were carried out using DSSR and 3DNA.^103–105

Site Binding Mapping Using Laplacian Analysis.

The derivatives of the distribution functions were taken using a spectral approach that affords a seamless usage of convolution kernels, such as Gaussian functions used to remove noise or small-scale localized variations. Since the convolution operation commutes with the differential operator, the Laplacian of convoluted density can be obtained by a single convolution operation of the density with the second derivative of the Gaussian kernel. Demarcation of the highly concentrated regions has been realized by (1) identifying the voxels with a negative value of the Laplacian and (2) grouping neighboring distribution voxels into connected components using a depth-first-search algorithm.¹⁰⁶ Connected components are groups of voxels that share an edge within the 3D-mesh that is used to represent the distribution functions obtained from 3D-RISM calculations.