Low-gradient, single-threaded rivers prior to greening of the continents

Significance

The origin of low-gradient meandering rivers—the primary conduits of water, carbon, and nutrients in present-day terrestrial landscapes—is considered coeval with Silurian-age plant evolution. It was hypothesized that pre-Silurian rivers lacked bank strength and were dominantly steep and braided, implying vastly different transport capacities of water and sediment. This idea, however, is inconsistent with the supercontinental-scale drainage of Neoproterozoic rivers, which requires unrealistically high mountains to achieve the necessary river gradients. Using geologic observations and paleohydraulic analyses, we show that pre-Silurian rivers were low-gradient, deep, and single-threaded—similar to modern meandering rivers. Results demonstrate uniformity of fluvial morphology despite a global revolution in Earth’s terrestrial biota, with ramifications for the topographic signature of life on Earth and other planets.

Abstract

The Silurian-age rise of land plants is hypothesized to have caused a global revolution in the mechanics of rivers. In the absence of vegetation-controlled bank stabilization effects, pre-Silurian rivers are thought to be characterized by shallow, multithreaded flows, and steep river gradients. This hypothesis, however, is at odds with the pancontinental scale of early Neoproterozoic river systems that would have necessitated extraordinarily high mountains if such river gradients were commonplace at continental scale, which is inconsistent with constraints on lithospheric thickness. To reconcile these observations, we generated estimates of paleogradients and morphologies of pre-Silurian rivers using a well-developed quantitative framework based on the formation of river bars and dunes. We combined data from previous work with original field measurements of the scale, texture, and structure of fluvial deposits in Proterozoic-age Torridonian Group, Scotland—a type-example of pancontinental, prevegetation fluvial systems. Results showed that these rivers were low sloping (gradients 10⁻⁵ to 10⁻⁴), relatively deep (4 to 15 m), and had morphology similar to modern, lowland rivers. Our results provide mechanistic evidence for the abundance of low gradient, single-threaded rivers in the Proterozoic eon, at a time well before the evolution and radiation of land plants—despite the absence of muddy and vegetated floodplains. Single-threaded rivers with stable floodplains appear to have been a persistent feature of our planet despite singular changes in its terrestrial biota.

Photosynthesis has profoundly influenced the processes and environments at or near the Earth’s surface, including the Great Oxygenation Event (1); it is also responsible for fundamental changes in the transport of sediment from the continents and its accumulation in basins. The colonization of terrestrial landscapes by land plants since approximately 450 Ma (2, 3) left its mark in the composition of deposits, with the pre-Silurian fluvial strata showing a distinctive lack of alluvial mudstones—a feature common in younger fluvial deposits (4). Land plants are also thought to have irreversibly changed the planform morphology of large rivers from a “sheet-braided” style to the more commonly observed sinuous, meandering mode (5–7). Pre-Silurian rivers are hypothesized to be characterized by relatively steep, shallow, unconfined flows with multiple channel threads and unstable banks (5–9). For example, existing estimates of Proterozoic fluvial gradients span 4 × 10⁻³ to 4 × 10⁻² (SI Appendix), which are two to three orders of magnitude steeper than modern continental-scale lowland rivers. These estimates are consistent with present-day observations, in which braided rivers are steeper than meandering rivers of the same water discharge (10) but raise an apparent paradox about the geodynamics of the Proterozoic Earth. Some Neoproterozoic rivers were pancontinental in size; provenance analyses indicate that major early Neoproterozoic rivers draining the Grenville orogen on the supercontinent Rodinia were >3,000 km long (11). To achieve the estimated river gradients, continents would require >12-km relief—elevations significantly larger than any modern or previously recognized ancient orogens. This would have necessitated extraordinarily thick continental lithosphere and is inconsistent with evidence that Neoproterozoic lithospheric thickness was likely similar to modern values (12).

These observations reveal a discordance between the inferred surficial environments in a prevegetation world and the geodynamical state of the Proterozoic Earth. Assemblages of tabular and laterally continuous sandstones in pre-Silurian fluvial deposits have been used to support the “sheet-braided” hypothesis (5, 13–15), in addition to experiments that required vegetation-induced bank strength to elicit meandering (16, 17), and an increase in point-bar deposits associated with meandering since Silurian time (8). However, others have argued that some pre-Silurian rivers were deep (18–20) based on channel-body dimensions similar to modern single-threaded unvegetated rivers (21, 22), raising the possibility that they also could have had low gradients. Moreover, the existence of sinuous, meandering channels in desert landscapes (21–23), extraterrestrial deposits (like those seen on Mars) (24), and experiments with muddy cohesive banks (25) implies that single-threaded rivers can exist devoid of vegetation. Despite the ongoing debate as to how land plants changed the planform morphology of rivers (26–29), little work has focused on quantitative reconstructions of pre-Silurian river gradients. Thus, the apparent paradox between putative steep pre-Silurian river gradients and the scale of ancient orogens has yet to be reconciled. In addition, by quantifying river gradients it becomes possible to compare pre-Silurian river geometries to a mechanistic theory for the onset of river braiding (30). This further provides an assessment of river planform morphology independent of the typical approach using the deposit architecture of ancient rocks that has produced differing interpretations (26–29). Ultimately, quantitative reconstructions of pre-Silurian river morphology are needed to understand the routing and storage of water, sediment, carbon, and nutrients—processes that maintain a habitable planet—on the early Earth and on extraterrestrial environments devoid of land plants.

Here, we generated estimates of the paleogradients and morphologies of pre-Silurian rivers based on a suite of quantitative, paleohydraulic relations enabled by recent advances in the understanding of processes that form river bars and dunes. This approach differs considerably from that used by previous workers who estimated steep gradients based on empirical scaling relationships of present-day rivers with the a priori assumption that pre-Silurian rivers were bedload-dominated systems that lacked cohesive bank strength (SI Appendix). That logic presumes the validity of the sheet-braided hypothesis, rather than providing a test of it. By contrast, our calculations were based on original field measurements of bar and dune deposits in the Torridonian Group, Scotland—a type-example of prevegetation fluvial system—and compilation of data from other pre-Silurian fluvial deposits worldwide. Contrary to the sheet-braided hypothesis, results provide evidence for the abundance of low-gradient, single-threaded rivers before greening of the continents.

Deposits of a Pancontinental, Prevegetation Fluvial System: The Torridonian Sandstone

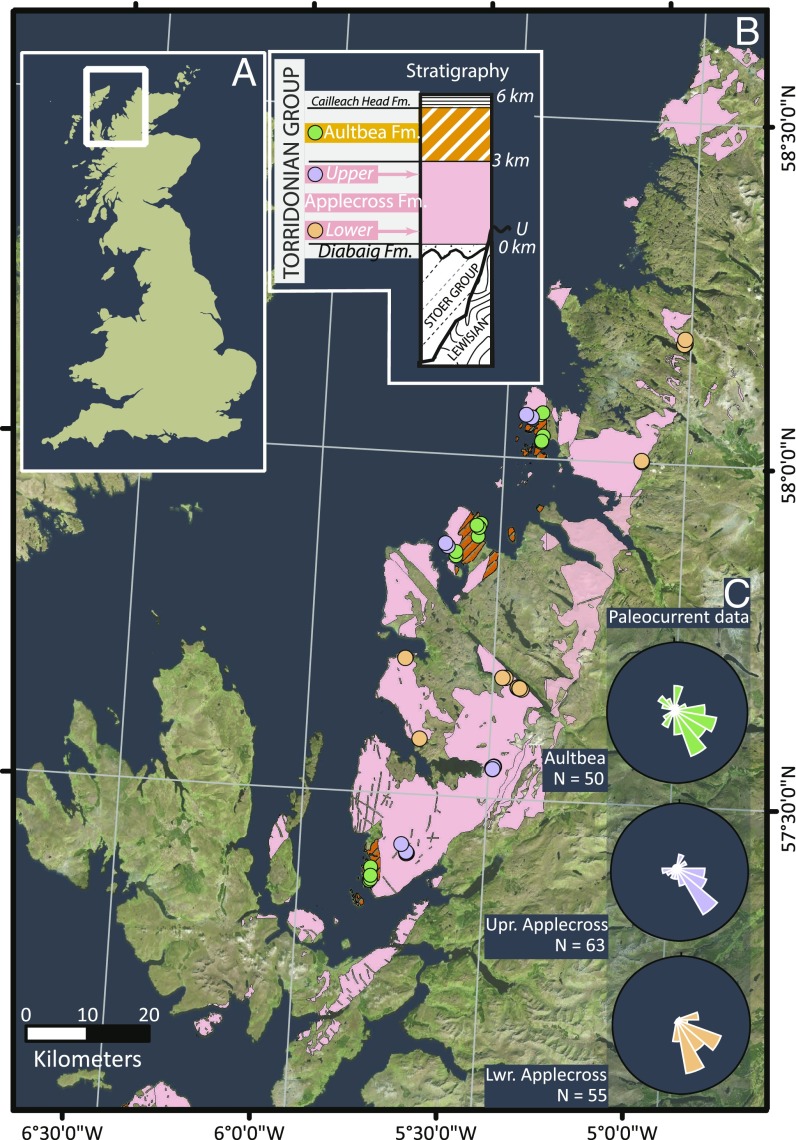
We studied the well-documented, classic fluvial sandstones in northwest Scotland known as the Torridonian Group (Fig. 1). These sedimentary rocks comprise an exceptionally and almost complete Middle to Upper Proterozoic succession of clastic, fluvial deposits, largely unmetamorphosed and undeformed, which rests unconformably on both Archean to Lower Proterozoic gneissic basement and tilted Mesoproterozoic strata of the Stoer Group (31) (Fig. 1). The >6-km-thick sedimentary succession is dominated by the ubiquity of tabular- and trough-cross bedded sandstones in its upper to middle parts. Geochronological studies have constrained the onset of Torridonian sedimentation to early Neoproterozoic time (SI Appendix). We focused our analyses on two dominant formations within the group, the Applecross Formation (approximately 3 km thick) and the conformably overlying Aultbea Formation (>2 km thick) (31) (Fig. 1). Following previous work within the Applecross Formation (32), we adopted two sampling intervals to provide a relative stratigraphic framework. These two subunits, defined by their stratigraphic height above the underlying Lewisian Gneiss, are the “Lower Applecross Formation” (LAF) (∼500 to 1,000 m) and “Upper Applecross Formation” (UAF) (∼2,000 to 3,000 m) (Fig. 1). This sampling strategy provides information averaged over similar stratigraphic thicknesses.

Fig. 1.

Location and stratigraphy of the Torridonian Group. (A) Location of exposures of Torridonian Sandstone and a simplified stratigraphic section of the Torridonian Group. (B) Detailed location of exposures of Applecross (pink) and Aultbea Formation (orange). The filled markers (light orange, LAF; purple, UAF; and green, Aultbea Formation) indicate the field localities where set thickness and grain size data were measured. (C) Rose diagram of the paleocurrent vectors for each stratigraphic sampling interval (Materials and Methods).

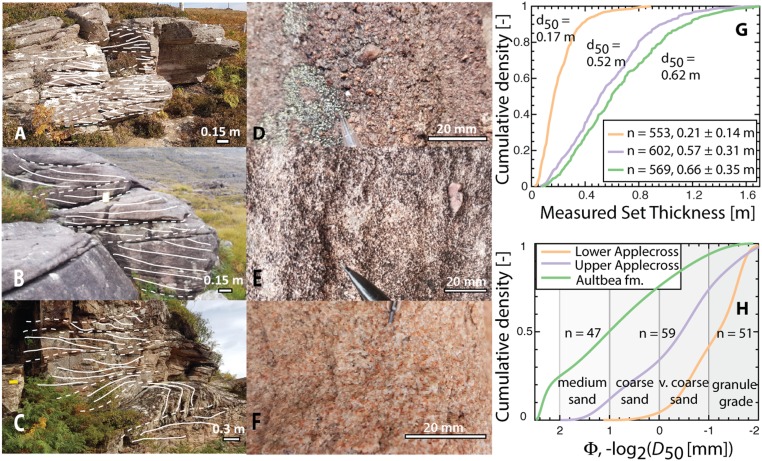
In alluvial rivers, the interactions between bed topography, sediment transport, and fluid flow result in the formation of dynamic repeating topographic features such as ripples, dunes, and bars—all called bedforms. The migration of bedforms results in the development of cross-stratification in the sedimentary record (33–35), which are primary indicators of paleoflow and sediment transport conditions. In the field, we measured 1,724 individual cross-set thicknesses across 226 individual sets, median grain size (D₅₀), and paleocurrent vectors at >150 individual sets across 51 localities, evenly distributed among our stratigraphic sampling intervals (Figs. 1 and 2 and SI Appendix, Figs. S1–S3 and Table S1). The results demonstrated a monotonic increase in set thicknesses over time, with d_m = 0.21 ± 0.14 m (mean ± 1σ), 0.56 ± 0.31 m, and 0.66 ± 0.35 m for LAF, UAF, and Aultbea Formation, respectively (Fig. 2G and SI Appendix, Fig. S4). The increase in d_m was concomitant with a decrease in D₅₀ (Fig. 2H); D₅₀ is 2.25 ± 0.75 mm (mean ± 1σ) (particle sizes of very coarse sand to granules), 1.5 ± 0.12 mm (very coarse sand), and 0.7 ± 0.5 mm (medium to coarse sand) for LAF, UAF, and Aultbea Formation, respectively. Paleocurrent vector data confirmed a dominant east-southeast paleoflow direction (31, 32), with no trend across stratigraphic intervals (Fig. 1C).

Fig. 2.

Summary of field data collected for the Torridonian Group. (A–C) Cross-stratification in the LAF, UAF, and the Aultbea Formation, respectively. The solid and dashed lines indicate cross-bedding and the interpreted erosional boundaries, respectively (Materials and Methods and SI Appendix, Figs. S1–S3). (D–F) Macro photographs showing the reduction in grain size from the LAF to the Aultbea Formation (SI Appendix, Figs. S1–S3). Cumulative distribution function of the measured set thickness (G) and median grain size (H) at individual outcrops within the stratigraphic sampling intervals.

Morphological Reconstruction of Prevegetation Rivers

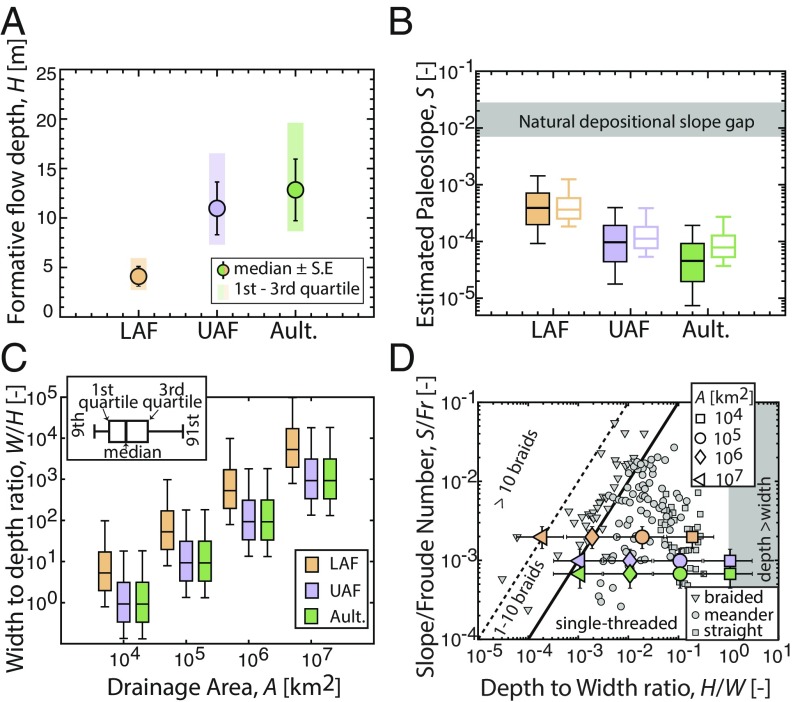
In agreement with prior studies of the Torridonian Group (31, 32), we interpreted the observed cross-stratification as fluvial dune deposits, which is supported by observations of steep cross-bed dip angles (SI Appendix, Fig. S5), typical of modern dune lee-face angles (36), and the presence of larger, rare barform deposits that represent higher-order fluvial hierarchical elements (SI Appendix, Figs. S6 and S7). Numerical and experimental studies revealed that a strong relationship exists, given by h_d = (2.9 ± 0.7)d_m, between d_m and mean bedform heights (h_d); this is well-constrained across a wide range of aggradation and migration rates of subcritically climbing bedforms (33–35). Thus, our observed increase in d_m reflects an increase in formative dune heights (Materials and Methods and SI Appendix, Figs. S8 and S9). The dune heights scale with the boundary layer thickness, which is approximated by the flow depth (H) in open-channel flows (36). An extensive field and experimental data compilation constrained the h_d-H scaling relation, given by H = 6.7h_d, with the first and third quartiles of H given by 4.4h_d and 10.1h_d, respectively (36). Using this empirical observation, the estimated median values of H for LAF, UAF, and Aultbea rivers were 4.1 ± 1 m ([2.7,6.2] m, first and third quartiles of H), 11 ± 2.7 m ([7.2,16.5] m), and 12.8 ± 3.1 m ([8.4,19.4] m), respectively (Fig. 3A and Materials and Methods). These data are inconsistent with the sheet-braided hypothesis that predicts shallow flows in Neoproterozoic rivers (5, 6) but, instead, show that deep flows characterized well-known Proterozoic rivers (18–20).

Fig. 3.

Paleohydraulic reconstruction for the Torridonian Group demonstrates that these ancient rivers were low-sloping and single-threaded. (A) Estimated formative flow depth, H, for the Applecross and Aultbea Formations (Materials and Methods and SI Appendix). (B) Estimated S from bedform stability diagrams (38) (filled boxplots) and modern scaling arguments (open boxplots) (39) (Materials and Methods). The gray shaded area denotes the natural depositional slope gap between alluvial fans and rivers (57). (C) Estimated W/H of the Torridonian rivers as a function of A (Materials and Methods and SI Appendix, Fig. S11). (D) Theoretical stability fields of fluvial planform morphology along with supporting data from modern fluvial environments (30). Reconstructed data of the Torridonian rivers for four decades of drainage area; colored markers and error bars indicate the median and the interquartile range, respectively (Materials and Methods). The solid, thick line indicates the theoretical prediction of the transition from single-threaded to braided planform morphology.

The ubiquity of cross-bedded sandstones indicates that fluvial dunes were stable and pervasive during Torridonian sedimentation. Several studies have formulated a graphical framework that establishes the hydraulic and sediment transport conditions for the stable existence of fluvial dunes (37), parameterized by the Froude number, particle Reynolds number, and Shields stress (${\tau }^{\ast }={\tau }_b/\rho R\mathit{g}{D}_{50}$, where ρ is the density of water, g is gravitational acceleration, τ_b is bed shear stress, and R = 1.65 for quartz). We used a bedform stability diagram (38) to place bounds on the range of τ* (SI Appendix, Fig. S10) and approximated τ_b assuming steady, uniform flow $\left({\tau }_b=\rho \mathit{g}HS\right)$ to estimate a distribution of paleoslope (S) values using Monte Carlo sampling (Materials and Methods). These results show that the Torridonian Group was deposited by gently sloping rivers, and S decreased from the older to the younger stratigraphic units. The estimated median value (and first and third quartiles) of S for LAF, UAF, and Aultbea rivers were 3.9 × 10⁻⁴ ([2.0 × 10⁻⁴, 7.1 × 10⁻⁴]), 9.7 × 10⁻⁵ ([4.4 × 10⁻⁵, 1.9 × 10⁻⁴]), and 4.5 × 10⁻⁵ ([2.0 × 10⁻⁵, 9.2 × 10⁻⁵]), respectively (Fig. 3B). The estimated S values for the Torridonian Group are similar to modern continental, lowland and foreland-basin rivers. To confirm this result, we constrained S independently, using an empirical relationship based on the bankfull Shields stress criteria observed in modern alluvial rivers (39). This approach yielded similar values for paleoslope, supporting the estimates derived from bedform stability diagram and implying that Proterozoic rivers had gradients similar to modern, lowland rivers (Fig. 3B).

Modern low-gradient, continental rivers are bounded by floodplains, in contrast to the sheet-braided hypothesis where floodplains would be absent. Quantifying floodplain facies in prevegetation alluvium is challenging, considering the lack of bioturbation and fossils, absence of mudstones, and limited outcrop extent (40). However, recent work has documented mature floodplain systems with bedsets >10 m in thickness throughout the Proterozoic eon (40). In the Applecross Formation, floodplain facies composed of ripple-laminated heterolithic beds, sets that thin away from the channel bank, and rare preserved channel levees have been documented (20, 40). Thus, like modern continental rivers, pre-Silurian rivers did have floodplains, but they were coarser-grained than their modern counterparts possibly due to vegetation baffling overbank flows and binding mud deposits (4, 40).

Were Prevegetation Rivers Single-Threaded or Braided?

Sheet-braided hypothesis requires large channel width-depth ratios to trigger the onset of braiding (30). We constrained the aspect ratio of Torridonian rivers by examining the water balance at both the channel and catchment scales (Materials and Methods and SI Appendix, Fig. S11). Water discharge was equated to the product of flow width (W), depth (H), and velocity (U) at a given location; it is also related to the average precipitation rate (P) and the area over which this rainfall accumulates to contribute to the streamflow (A) (Materials and Methods). Using these mass balance constraints, previous estimates of A (32, 41), and our reconstructions of H and S (Fig. 3 A and B), we found that $W/H\in \left[\mathrm{10,100}\right]\text{for}{10}^4\le \mathit{A}\le {10}^6{\text{km}}^2$(Fig. 3C), and the data reside in the stability field for single-threaded, rather than braided, rivers (Fig. 3D). UAF and Aultbea rivers could only have exceeded the threshold of 10 braided threads, as implied by the sheet-braided hypothesis, for unrealistic values of A >10⁸ km² (i.e., river lengths > Earth’s circumference) or P > 10 m/y that would be tenfold the precipitation in the modern Intertropical Convergence Zone (Materials and Methods). The predominance of >100-m lateral continuity of Applecross sandbodies (32) was previously used to support the sheet-braided hypothesis, but these dimensions are consistent with channel belts from single-threaded rivers given our estimates of channel depths and width–depth ratios.

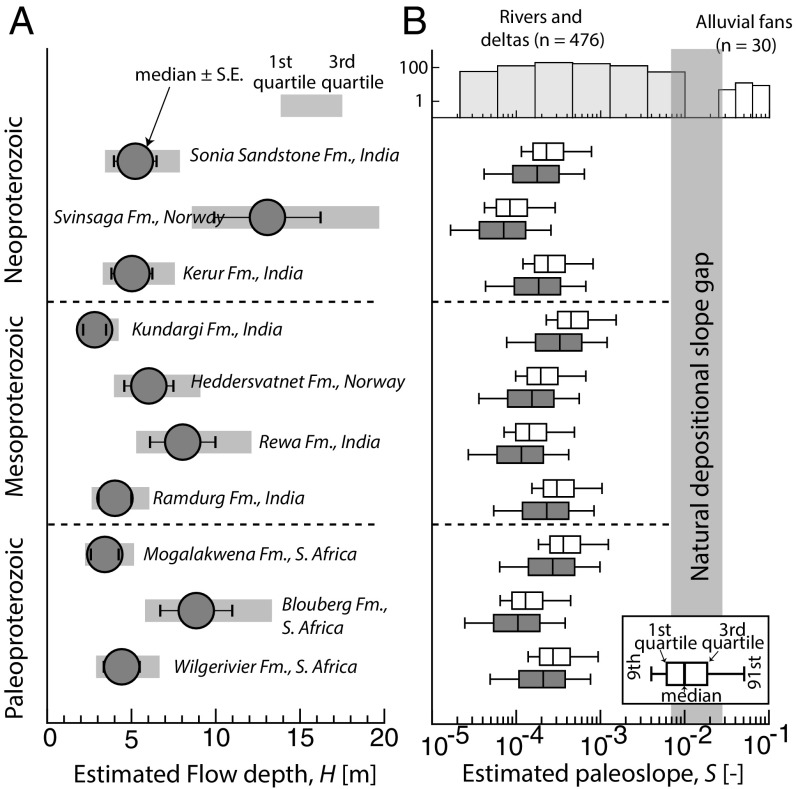
Did low-gradient, deep rivers persist throughout the Proterozoic eon? We compiled reported cross-set thickness for 10 fluvial formations throughout the Proterozoic eon (SI Appendix) and estimated H and S in a similar way as the Torridonian Group (Fig. 3 A and B). For the global compilation, H ranged from 4 to 15 m and S was on the order of 10⁻⁴ (Fig. 4), indicating that low-sloping, deep rivers persisted throughout Proterozoic time.

Fig. 4.

Estimated flow depths and paleo-fluvial gradients for a global compilation of Proterozoic rivers. (A) Formative flow depths for 10 fluvial formations throughout the Proterozoic eon (Materials and Methods and SI Appendix). (B) Estimated fluvial gradients from bedform stability diagram (filled boxplots) and modern scaling arguments (open boxplots), similar to Fig. 3B (Materials and Methods). The shaded gray area indicates the natural depositional slope gap between modern alluvial rivers and alluvial fans (57). The histogram shows a worldwide compilation of gradients for modern rivers and alluvial fans (SI Appendix).

While vegetation is hypothesized to be the primary control on bank strength that allows small width-depth ratios for post-Silurian single-threaded rivers (5, 6), other mechanisms for bank strength are needed to explain single-threaded pre-Silurian rivers. Mud and fine-grained sediments can, in principle, provide the required cohesive bank strength (23, 25); however, the mineralogy of Applecross sandstones indicates that mud was rare (31). Microbial mats and biofilms can also provide cohesion to unconsolidated sand, and microbial sedimentary structures are prevalent in the Torridonian Supergroup (42). Experimental studies demonstrated that microbially bound medium-to-coarse sand can withstand a shear stress between 0.3 and 4 Pa without significant grain movement (43). The estimated range of τ_b for the Torridonian rivers was 0.2–10 Pa (Fig. 3 A and B), suggesting that microbial stabilization of bank sediment could have sustained deep flows with relatively high τ_b during the Proterozoic eon. Regardless of the bank stabilization mechanism, our results point to the abundance of low-gradient, deep, single-threaded rivers and imply a typical degree of relief for pancontinental river systems before the evolution of plants.

Materials and Methods

Stratigraphic Correlation and Sedimentological Context.

We focused on Applecross and Aultbea Formations of the Torridonian Group (Fig. 1 and SI Appendix). The basal Diabaig Formation was not sampled, but its stratigraphic position within incised paleo-valleys in the Lewisian Gneiss, was used to evaluate the stratigraphic position of localities within the Applecross Formation. All sampling localities were located with reference to (i) British Geological Survey (Scotland) maps at 1:50,000 and 1:63,360 scale; (ii) Geological Society of London memoir (31); (iii) field sites described in ref. 32. Sites were visited in September 2016 and 2017. The Applecross Formation makes up the majority of the Torridonian Group and consists of >3 km of coarse red sandstones, pebbly in sections particularly toward the base, which are planar and trough cross-bedded. We adopted the informal subdivision of Nicholson (32) and Stewart (31), and collected data from the formation in two groupings, one toward the base and one toward the top, referred to as the LAF and UAF. The LAF overlies the distinctive Diabaig Formation; we use an interval of ∼500 to 1,000 m above the lower basal unconformity of the Lewisian to constrain this unit. The UAF refers to sediments underlying the Aultbea Formation and located ∼2,000 to 3,000 m above the base of the Torridonian Group.

At the majority of field localities, planar to trough cross-bedded sandstones, typically in coarse to very coarse sand (sometimes at granule grade in the LAF), comprise the dominant facies association and represent the migration of fluvial dunes, worked by sustained subcritical flows within active channels (SI Appendix, Figs. S1–S3). Many cross-bedded horizons can be traced for > 10 m. Mud-size sediment is generally absent. In the Aultbea Formation a further facies association consists of medium sandstones with marked soft sediment deformation, which overprints trough cross-bedding to a lesser or greater degree, and is interpreted as sediment liquefaction and/or water escape (SI Appendix, Fig. S3). Other elements of facies architecture include occasional bar forms (SI Appendix, Figs. S6 and S7) and rare channel bodies (20). Interpreted bar forms have a planar to mildly erosive base and fine upwards over length scales of several meters. They show changes in sedimentary structures from thicker, tabular or trough cross-bedding near the base, representing dunes to smaller ripple cross-beds at the bar top, where preserved. Evidence of lateral accretion consists of smaller cross-sets climbing on the bar flanks. Lateral accretion surfaces dip at angles <10° when corrected for depositional dip, markedly shallower than the trough cross-bedding (SI Appendix, Fig. S5). Cross-set thicknesses were measured at regular intervals within each set with a tape or rule from the asymptotic lower bounding surface to the erosional bounding surface at the top of the set, with a precision of ±5 mm. This method required delineation of the cross-set boundaries, which we agreed in the field before measurement. A distribution of cross-set thicknesses was obtained for each cross-set; at most localities, multiple sets were measured (SI Appendix, Table S1). In total, 553, 602, and 569 thickness measurements were made for the LAF, UAF, and Aultbea Formation, respectively. Grain size for the cross-sets was constrained from the analysis of scaled field photographs (SI Appendix, Figs. S1–S3 and Table S1). The dip and dip direction of planar cross-bedding (or the trend and plunge of the center of trough cross beds, where necessary) was used to estimate paleo-flow direction. These measurements were corrected by the dip and dip direction of the depositional bedding at each locality; the failure to correct for bedding can lead to spurious results, particularly where the dip angle of the cross-beds is less than that of the bedding.

Scaling Bedform Heights (h_d) from Cross-Set Thickness (d_m).

Previous experimental (33, 44, 45) and numerical (34) work demonstrated that h_d/d_m = 2.9 ± 0.7 for a range of aggradation and migration rates of subcritically climbing bedforms. We used this scaling relationship to estimate the formative bedform heights (SI Appendix). We used the global mean of measured set thickness within each stratigraphic interval for this estimation (Fig. 2).

Scaling Formative Flow Depths (H) from Estimated Bedform Heights (h_d).

Based on >380 field observations of h_d and H, Bradley and Venditti (36) provided a scaling relation given by:

$$H=6.7h_d.$$ [1]

The first and third quartiles of H were bound by 4.4h_d and 10.1h_d. We used these estimates for constraining H (Fig. 3A). Comparison of these estimates with other methods showed good agreement (SI Appendix, Fig. S12).

Bedform Stability and Estimation of Paleoslope.

Previous work indicated that three dimensionless numbers are needed to describe the stability of fluvial bedforms (37). River dunes exist only in subcritical flow conditions (SI Appendix), i.e., Froude number (Fr) < 1, and bedform stability is independent of Fr for subcritical flows (SI Appendix). We used the bedform stability diagram proposed by Lamb et al. (38), which parameterized flow and sediment transport conditions using Shields stress and the particle Reynolds number, Re_p (SI Appendix, Fig. S10), to bound the formative Shields stress of Torridonian rivers. We estimated Re_p for each stratigraphic interval using our measurements of D₅₀ (Fig. 2), and assumed the kinematic viscosity of water of ν = 10⁻⁶ m²/s, which corresponds to a temperature of 20 °C. The estimated ${\tau }^{\ast }$ bounds are insensitive to ν over a range of 10 to 30 °C —a temperature range consistent with the inferred subtropical, semiarid climate during Torridonian sedimentation (31).

We included the range of Shields stresses that correspond to the existence of dunes and the transitional zone between dunes and upper plane beds (SI Appendix, Fig. S10). This is a conservative approach that represents the maximum possible range of ${\tau }^{\ast }$ for stable existence of river dunes. Once ${\tau }^{\ast }$ was bound for each stratigraphic sampling interval, we approximated ${\tau }_b$ as the depth-slope product, and the paleoslope, S, is given by

$$S=\frac{R{D}_{50}{\tau }^{\ast }}{H},$$ [2]

in which R = 1.65 is the submerged specific density of sediment for quartz. We then estimated S using Monte Carlo simulations. We generated 10⁷ random samples of ${\tau }^{\ast }$ (uniformly distributed within the bounds provided by the bedform stability diagram) and 10⁷ normally distributed random samples of D₅₀ given the mean and SD of D₅₀ across multiple localities within each stratigraphic sampling interval. Finally, we generated 10⁷ random samples of H given the uncertainty in formative flow depths (36). This procedure yielded 10⁷ samples of S (Eq. 2), and we reported the median, first and third quartiles, and the ninth and 91st percentiles in Fig. 3B.

Finally, we validated the bedform stability diagram using a recent compilation of experimental and field data (46). We reduced this compilation to the range of Re_p that span observations in the Torridonian Group, which resulted in 998 experimental data points and 47 field data points. This comparison indicates that the bedform stability diagram predicts the range of formative Shields stress reasonably well (SI Appendix, Fig. S10).

Estimation of Paleoslope from Modern Scaling Arguments Based on Bankfull Shields Stress.

Models for paleoslope estimation from stratigraphic observations are based on the empirical observation that rivers organize their bankfull shear stress around a geomorphic threshold driven by the dominant transport mode of bed sediment. Based on a compilation of 541 bankfull measurements of alluvial rivers and Bayesian regression analysis, the following equation was proposed for estimating paleoslope of alluvial rivers (39):

$$\log S={\alpha }_0+{\alpha }_1\log D_{50}+{\alpha }_2\log H,$$ [3]

where α₀ = −2.08 ± 0.036 (mean ± 1σ), α₁ = 0.254 ± 0.016, and α₃ = −1.09 ± 0.044 are empirical constants, and H and D₅₀ are measured in m. We used Monte Carlo simulations to constrain S using this independent method (Fig. 3B).

Constraining the Aspect Ratio of Channels.

We estimated the aspect ratio of the Torridonian rivers by performing water balance at reach- and catchment-scale (47) and using constraints on precipitation rate, P, drainage area, A, and depth-averaged flow velocity, U. Mass balance dictates that the water discharge, Q, satisfies the following relation:

$$Q=UWH,$$ [4]

in which W is the channel width. Under normal flow assumption:

$$U=\sqrt{\frac{gHS}{C_f}},$$ [5]

where C_f is a dimensionless friction coefficient that is a function of the ratio of D₅₀ and H. Following previous work (48), we assumed $C_f\approx 0.01;$ however, using a more elaborate friction law (49) results in C_f values that range between 10⁻³ and 10⁻². Since U is inversely proportional to $\sqrt{C_f}$ (Eq. 5), we used the simplest formulation of a constant C_f because the variability in our data supersedes these differences. The estimated U using $C_f\approx 0.01$ is consistent with the bedform stability diagram expressed in terms of U and D₅₀ (SI Appendix, Fig. S10C) (50). We estimated Fr, which is required for assessment of the planform stability of rivers (Fig. 3D) (30), using $C_f\approx 0.01$ and through Monte Carlo sampling where 10⁷ random samples of H and S were generated as described previously (SI Appendix).

Water discharge can also be related to P and A through the following relation:

$$Q=cPA,$$ [6]

where $c\in \left[\mathrm{0,1}\right]$ and accounts for infiltration, evaporation, and attenuation of the rainfall pulse within a drainage basin. Combining Eqs. 4–6 and rearranging results in:

$$W=cPA\sqrt{\frac{c_f}{gS{H}^3}}.$$ [7]

In Eq. 7, sedimentological data and paleohydraulic analyses provide constraints on S, H, and C_f. Thus, W can be constrained if we can bound the values of c, P, and A, which we discuss individually next.

Constraints on Precipitation Rates.

Data from paleomagnetism studies suggest that the Applecross and Aultbea Formations were deposited in subtropical to temperate regions with paleolatitude estimates ranging from 30 to 50° S, consistent with the inferred paleoclimate from the modal feldspar and quartz content of the Applecross sandstones (31). The modern precipitation rates are greatest within 15° of the equator and the subtropical and temperate regions receive approximately five times less rainfall than the tropical regions, on average (51). The precipitation maximum within the tropics is associated with the ascending branch of the Hadley circulation (52), and the drier climates in the subtropics and temperate regions are associated with the drier descending air of the same Hadley circulation. Geologic and paleomagnetic data spanning the last 2 billion years indicate that this descending circulation is a persistent feature of the Earth’s climate (53), indicating that modern precipitation data may provide a reasonable first-order proxy for P in Eq. 7. A recent data compilation demonstrated that P is symmetric around the Earth’s equator, and the subtropical and temperate regions receive rainfall between 0.5 and 1 m/y (51).

To test the veracity of Eq. 6 and constrain c, we compiled monthly water discharge data, Q, and drainage area, A, for modern subtropical and temperate continental-scale rivers (54). Our compilation includes data from 29 rivers such as the MacKenzie, Nelson, Yukon, Mississippi, Missouri, Parana, Danube, Lena, Murray, and Indus. We then assumed $P\in \left[0.5,1\right]$ m/y, which represents the full range of observed average precipitation rates in the subtropical and temperate regions (51). Our data compilation validated Eq. 6 and constrained the value of c between 0.1 and 1 (SI Appendix, Fig. S11). Only one data point lies outside these bounds, which corresponds to the Murray River, Australia, where evapotranspiration and infiltration rate is greater than the precipitation rate. Thus, Eq. 6 with $c\in \left[0.1,1\right]$ provides an estimate of the maximum possible water discharge. This framework is valid for fluvial systems that experience either flashy or more uniform hydrographs.

Constraints on Drainage Area.

The age distributions of detrital zircons from the Applecross and Aultbea Formations were documented to be similar, suggesting that they were part of the same depositional system (55). Moreover, the conformable nature and the overall upward fining sequence of Applecross and Aultbea Formations (Fig. 2H) suggest that the UAF and Aultbea Formation were more distal parts of the same sediment routing system, compared with the LAF (31, 32). Previous researchers argued that the Torridonian Group was deposited by a late- to post-Grenvillian foreland trunk river system, near the middle of supercontinent Rodinia (31, 55). Thus, the drainage area likely increased monotonically from LAF to the Aultbea Formation. We interrogated the aspect ratio of the Torridonian rivers for A of 10⁴ to 10⁷ km² (Fig. 3C). The lower bound on A is consistent with previous estimates for LAF (32, 41), and the upper bound on A is twice the drainage area of the Amazon, the largest drainage area of present-day rivers.

Estimation of Aspect Ratio of Flows.

Similar to paleoslope estimation, we generated 10⁷ random samples of S for LAF, UAF, and Aultbea Formation using Eq. 2 and H using methods described earlier. We assumed C_f = 0.01 and generated 10⁷ random samples of P, uniformly distributed and bound by 0.5 and 1 m/y. We also generated 10⁷ random samples of c, uniformly distributed and bound by 0.1 and 1 (SI Appendix, Fig. S11). Using Eq. 7, we then evaluated W for four values of A: 10⁴, 10⁵, 10⁶, and 10⁷ km², for each stratigraphic sampling interval (Fig. 3C). Consistent with previous studies (32, 41), our independent analyses suggests that W > H for drainage areas in excess of 10⁴ and 10⁵ km² for LAF and UAF, respectively. Finally, we used Monte Carlo sampling approach to estimate S/Fr and H/W for the assessment of the planform stability of Torridonian rivers for different values of A (Fig. 3D). We did not estimate W for A > 10⁷ km². River length (L) and A in present-day rivers are related through: L = 1.4A^0.6 (56), where L and A are in miles and square miles, respectively. Using this scaling argument, A = 10⁸ km² corresponds to L ∼ 80,000 km, which is twice the Earth’s equatorial circumference. Drainage areas of 10⁴, 10⁵, 10⁶, and 10⁷ km² correspond to river lengths of ∼300 km, 1,200 km, 5,000 km, and 20,000 km, respectively.

Code and Data Availability.

All data generated or analyzed during this study are included in SI Appendix.