Using attribution to decode binding mechanism in neural network models for chemistry

Significance

Advances in machine learning have led to neural network-based methods for virtual screening, making it possible to sift through trillions of small molecules to find those that are pharmacologically important. Such methods have the potential to make chemical discoveries, but only if it is possible to untangle why models make the predictions that they do. Here we use attribution methods to investigate neural network models for small-molecule binding, and show that, while it is possible to identify pharmacophores with attribution, there is also the real possibility that a model which seems to perform perfectly instead learns spurious correlations in the underlying dataset that have nothing to do with binding chemistry. We propose an attribution-based test for determining whether a model can learn a hypothesized binding mechanism on a training set.

Abstract

Deep neural networks have achieved state-of-the-art accuracy at classifying molecules with respect to whether they bind to specific protein targets. A key breakthrough would occur if these models could reveal the fragment pharmacophores that are causally involved in binding. Extracting chemical details of binding from the networks could enable scientific discoveries about the mechanisms of drug actions. However, doing so requires shining light into the black box that is the trained neural network model, a task that has proved difficult across many domains. Here we show how the binding mechanism learned by deep neural network models can be interrogated, using a recently described attribution method. We first work with carefully constructed synthetic datasets, in which the molecular features responsible for “binding” are fully known. We find that networks that achieve perfect accuracy on held-out test datasets still learn spurious correlations, and we are able to exploit this nonrobustness to construct adversarial examples that fool the model. This makes these models unreliable for accurately revealing information about the mechanisms of protein–ligand binding. In light of our findings, we prescribe a test that checks whether a hypothesized mechanism can be learned. If the test fails, it indicates that the model must be simplified or regularized and/or that the training dataset requires augmentation.

A major stumbling block to modern drug discovery is to discover small molecules that bind selectively to a given protein target, while avoiding off-target interactions that are detrimental or toxic. The size of the small-molecule search space is enormous, making it impossible to sort through all of the possibilities, either experimentally or computationally (1). The promise of in silico screening is tantalizing, as it would allow compounds to be screened at greatly reduced cost (2). However, despite decades of computational effort to develop high-resolution simulations and other approaches, we are still not able to rely solely upon virtual screening to explore the vast space of possible protein–ligand binding interactions (3).

The development of high-throughput methods for empirically screening large libraries of small molecules against proteins has opened up an approach where machine learning methods correlate the binding activity of small molecules with their molecular structure (4). Among machine learning approaches, neural networks have demonstrated consistent gains relative to baseline models such as random forest and logistic regression (5–9). In addition to protein–ligand binding, such models have been trained to predict physical properties that are calculated using density functional theory, such as polarizability and electron density (10–12). The ultimate promise of data-driven methods is to guide molecular design: Models learned from ligands that bind to particular proteins will elucidate the mechanism and generate hypotheses of ligands that bind the required target in addition to providing improved understanding of the noncovalent interactions responsible.

The motivating question for this work is: Why do virtual screening models make the predictions they do? Despite their high accuracy, the major weakness of such data-driven approaches is the lack of causal understanding. While the model might correctly predict that a given molecule binds to a particular protein, it typically gives no indication of which molecular features were used to make this decision. Without this, it is not clear whether the model learns the mechanism of binding or spurious molecular features that correlate with binding in the dataset being studied (13–15). Such model weaknesses are not captured by traditional evaluations that measure model accuracy on held-out test sets, because these held-out sets suffer from experimental selection bias and do not contain random samples drawn at uniform from the space of all molecules.

The key issue is to assess whether state-of-the-art neural network models trained on protein–ligand binding data learn the correct binding mechanisms, despite the presence of dataset bias. To unravel this, we define a synthetic “binding logic” as a combination of molecular fragments that must be present (or absent) for binding to occur, e.g., “naphthalene and no primary amine.” We construct 16 binding logics and use each to label molecules from the Zinc12 database (16). We randomly split the dataset for each logic into test and train splits, and train models. Model attribution is used to assess whether each trained model has learned the correct binding logic.

To measure model performance on held-out sets, we report the Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC) curve (17), and refer to this as the Model AUC. We then use a recently developed attribution method (18) to verify whether each model learns its corresponding binding logic correctly. The method assigns an attribution score to each atom that reports how important the atom is to the model’s ultimate prediction. We develop a metric called the Attribution AUC that measures how well the per-atom attribution scores reflect the ground truth binding logic. The atoms within each molecule are ranked by their attribution scores, and these rankings are compared with the ground truth binary label for each atom indicating whether that atom is part of the binding logic.

The synthetic labels perfectly obey each binding logic, removing issues of experimental noise, so it is perhaps not surprising that neural network models obtain Model AUC of $\sim 1.0$ in all cases on held-out sets filtered from Zinc. Nonetheless, the Attribution AUC is often much lower than 1.0, likely due to biases in the original dataset. Zinc12 does not contain all possible molecules, so there are molecular fragments that correlate with the binding logic but are not themselves involved in binding. This dataset bias implies that there exist “adversarial molecules” that do not satisfy the defined binding logic, for which the model makes incorrect predictions. Indeed, examining the model attributions allows us to identify adversarial molecules. Hence, even in this controlled setting, the network fails to learn the binding logic. Real-world protein-binding tasks are even more complex, due to noise in the binding assay, as well as underlying binding logics that are potentially more complex.

To illustrate the practical utility of this approach, we apply this framework to ligands from the Database of Useful Decoys: Enhanced dataset (19) that bind ADRB2. We create a hypothesized logic for the binding mechanism, and create synthetic labels for the DUD-E dataset based on this logic. Although a graph convolution (GC) neural network makes perfect predictions on a held-out dataset, biases in the dataset lead us to discover molecules which the model predicts bind to ADRB2, despite not satisfying the logic. The pattern used by the model to decide binding is different from the logic we imposed. Thus, despite its seemingly perfect performance, the model is fundamentally not able to predict that molecules bind for the right reason.

Analysis Framework

To generate data with ground truth knowledge of the binding mechanism, we construct 16 synthetic binary label sets in which binding is defined to correspond to the presence and/or absence of particular logical combinations of molecular fragments. For example, ligands could be labeled positive (i.e., bind to the target protein) if they obey the binding logic “carbonyl and no phenyl.” Each binding logic is used to filter the Zinc database of molecules to yield sets of positive and negative labeled molecules. In our implementation, we specify molecular fragments using the Smiles Arbitrary Target Specification format (20), and we use RDKit (21) to match them against candidate molecules, with a custom implementation of the logical operators and, or, and not. The 16 logics used in this paper are made up of elements sampled from 10 functional groups (SI Appendix, Table S1), with up to four elements per logic joined by randomly selected operators (Table 1 and SI Appendix, Table S2).

Table 1.

Attribution AUC and Model AUCs for two held-out sets for GC networks and MPNNs trained against synthetic data labels generated according to the binding logics listed in column 1

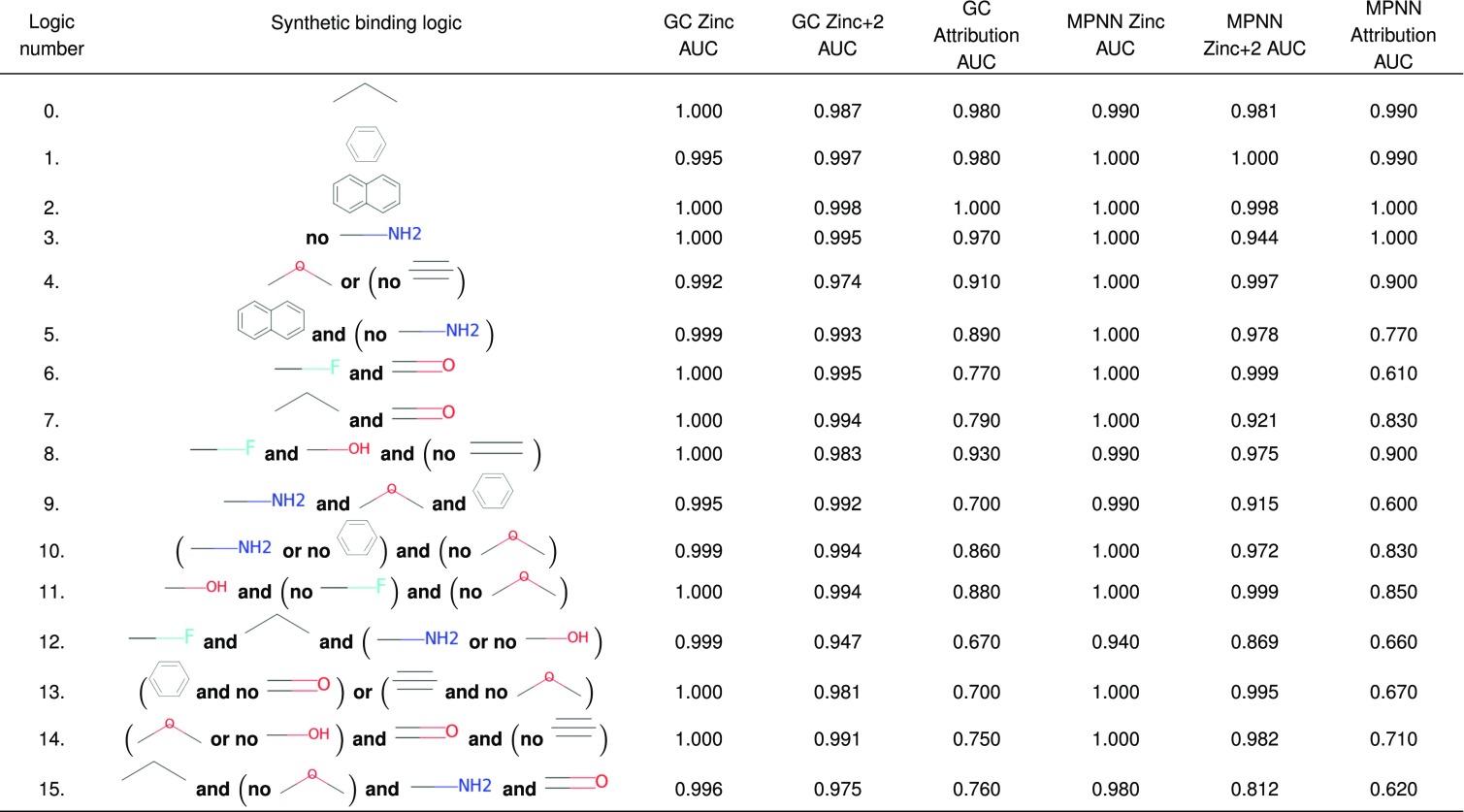See SI Appendix for more details on the binding logics and their component molecular fragments.

Dataset bias in chemistry is a well-known issue that has previously been described (13). Essentially, molecules that have been used in protein–ligand binding assays are not drawn uniformly at random from chemical space, but, instead, their selection for inclusion in a binding assay reflects the knowledge of expert chemists. These biases mean that large neural network models are at risk for overfitting to the training data. To reduce this risk, we carefully construct each dataset to be balanced, by sampling equally from all combinations of negations of the functional groups that make up each logic. In the case of just one functional group (A), this means that dataset contains equal numbers of molecules that match “A” and “∼A.” When there are two functional groups, say A and B, we have equal numbers matching “A&B,” “A&∼B,” “∼A&B,” and “∼A&∼B.” Similarly, all combinations are considered for logics with three and four functional groups. Each negation combination is represented by 1,200 molecules in the dataset, with ∼10% of each reserved for held-out model evaluation.

Model Training.

We use two models: the molecular GC model from Kearnes et al. (22) and the message passing neural network (MPNN) from Gilmer et al. (10). Both featurize each molecule using atoms and pairs of atoms. We use the same hyperparameters reported, with the exception of a minibatch size of 99 and training each to 10,000 steps, taking $\sim 1$ h on one graphics processing unit for each dataset. The model returns a binding probability for each molecule in the held-out test set, which is used to rank the molecules. Each molecule has a binary label indicating whether it binds. The ROC curve is generated by plotting the true positive rate against the false positive rate for ranking score thresholds in [0, 1]. The AUC is the area under the ROC curve: 1.0 is a perfect classifier with 100% true positives and 0% false positives, while a random classifier would receive 0.5.

Attribution Technique: Integrated Gradients.

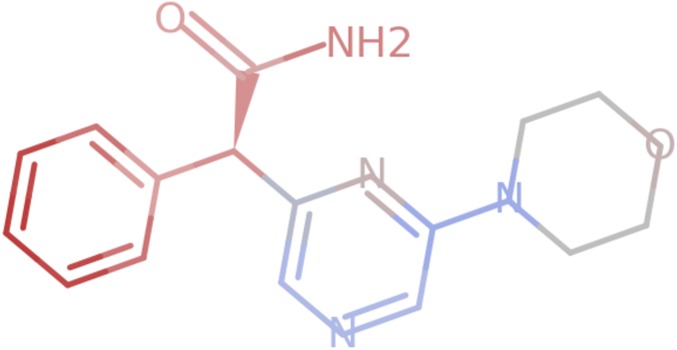
We next seek to determine whether these models have learned the binding logic used to generate the synthetic labels. Given a trained model and an input, an attribution method assigns scores to each input feature that reflect the contribution of that feature to the model prediction. Inspecting or visualizing the attribution scores reveals what features, in our case atoms and atom pairs, were most relevant to the model’s decision (Fig. 1). Formally, suppose a function $F:{\mathbb{R}}^n\to \left[\mathrm{0,1}\right]$ represents a deep network.

Fig. 1.

An example of per-atom model attributions visualized for a molecule. Each atom is colored on a scale from red to blue in proportion to its attribution score, with red being the most positive and blue being the most negative.

Definition 1: The attribution at input $x=\left(x_1,\dots ,x_n\right)\in {\mathbb{R}}^n$ is a vector $A_F\left(x\right)=\left(a_1,\dots ,a_n\right)\in {\mathbb{R}}^n$ where $a_i$ is the contribution of $x_i$ to the prediction $F\left(x\right)$.

In our case, the input $x$ is a molecule featurized into atoms and atom pairs, and $F\left(x\right)$ denotes the probability of binding to a protein target. To compute attributions to individual molecular features, we use the Integrated Gradients method (18). This method is justified by an axiomatic result showing that it is essentially the unique method satisfying certain desirable properties of an attribution method. Formal definitions, results, and comparisons to alternate attribution methods are available in ref. 18.

In this approach, attributions are defined relative to a baseline input, which serves as the counterfactual in assessing the importance of each feature. Such counterfactuals are fundamental to causal explanations (23). For attribution on images, the baseline is typically an image made of all black pixels. Here, we use an input where all atom and atom pair features are set to zero (details in SI Appendix).

The Integrated Gradient is defined as the path integral of the gradient along the linear path from the baseline $x\prime$ to the input $x$. The intuition is as follows. As we interpolate between the baseline and the input, the prediction moves along a trajectory, from uncertainty to certainty (the final probability). At each point on this trajectory, the gradient of the function $F$ with respect to the input can be used to attribute the change in probability back to the input variables. A path integral is used to aggregate the gradient along this trajectory.

Definition 2: Given an input $x$ and baseline $x\prime$, the integrated gradient along the $i\mathrm{t}\mathrm{h}$ dimension is defined as follows:

$$a_i:≔\left(x_i-x_i^{\prime }\right)\times {\int }_{\alpha =0}^1\frac{\partial F\left(x\prime +\alpha \times \left(x-x\prime \right)\right)}{\partial x_i}d\alpha ,$$ [1]

where $\frac{\partial F\left(x\right)}{\partial x_i}$ is the gradient of $F$ along the $i\mathrm{t}\mathrm{h}$ dimension at $x$.

Attribution scores are assigned to both atom and atom pair features. To simplify the analysis, we distribute the atom pair scores evenly between the atoms present in each pair. If $v_i\in A_F$ is the attribution for atom $i$, and $e_{ij}\in A_F$ is the attribution for atom pair $i,j$, then our aggregated attribution vector (indexed over $k$ atoms) $\widetilde{A_F}=\left({ã}_1,\dots ,{ã}_k\right)\in {\mathbb{R}}^k$ where

$${ã}_i=v_i+\sum _{\left(i,j\right)\in E_i}\frac{e_{ij}}{2}$$ [2]

and $E_i$ is the set of all featurized pairs that include atom $i$. Henceforth, we study these aggregated per-atom attributions for each molecule.

Attribution AUC.

Ideally, we would like the attribution scores to isolate the synthetic binding logic used to label the dataset, since this would translate to the ability to identify pharmacophores in real data. Attribution scores are typically studied by visualization using heatmaps; Fig. 1 provides a visualization of the per-atom attribution scores for a molecule. If a model learns the correct binding logic, we would expect the attribution scores to be larger in magnitude for atoms involved in the binding logic and small elsewhere.

Fig. 2 illustrates the attributions calculated for a molecule using the model trained on logic 1, which requires a phenyl group. A positive attribution score (red) indicates that this atom increases “protein binding” ability, according to the trained model, whereas a negative attribution score (blue) indicates that the model thinks that this atom hurts binding.

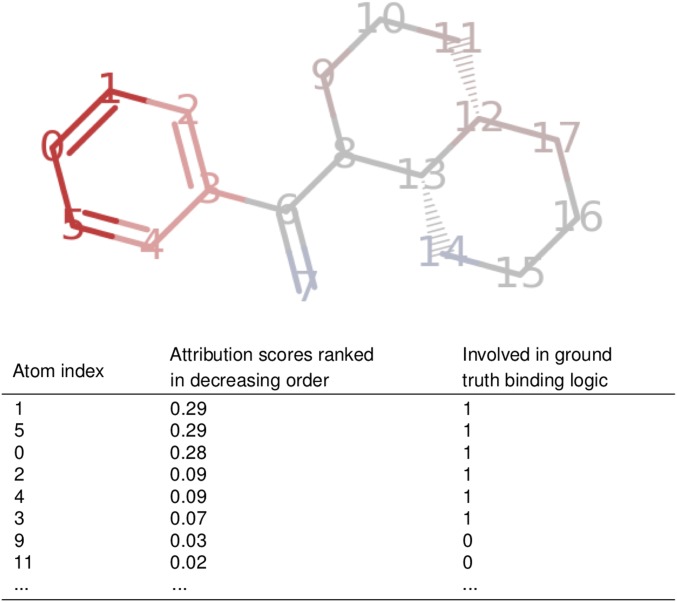
Fig. 2.

(Top) Visualization of Integrated Gradients on a “binding” molecule for logic 1 (must contain a phenyl group). (Bottom) The top eight atoms ranked by attribution score in descending order. This molecule would receive an Attribution AUC of 1.0 for these attributions, because all atoms involved the binding logic (indicated by 1 in the second column) have larger scores than all other atoms (marked 0 in second column).

Our goal is to evaluate how faithfully these scores reflect the binding logic used to label the dataset. To that end we develop a metric called the Attribution AUC that measures how well the per-atom attribution scores reflect the ground truth binding logic. We handle fragments required to be present for binding to occur separately from those required to be absent. If a binding logic contains fragments required to be present, we assign each fragment atom the label 1, and all other atoms the label 0. We then use these labels and the attribution scores to compute the Present-Attribution-AUC. If a logic contains fragments required to be absent, the process is analogous, except that we first multiply all attribution scores by −1.0 to reverse their ranking before calculating the Absent-Attribution-AUC. The final Attribution AUC for the molecule is simply the average of its Present-Attribution-AUC and its Absent-Attribution-AUC. This same process is applied regardless of which synthetic “binding” label the molecule carries. We report the average Attribution AUC across all molecules in the held-out set for each dataset. The Attribution AUC is entirely distinct from the Model AUC, which measures model performance on held-out data.

For some molecules and binding logics, there is more than one correct set of ground truth labels. Consider disjunctive binding logics (that contain an “or” operator), e.g., “phenyl or alkyne or alcohol.” The model can satisfy the binding logic by detecting phenyl alone or alkyne alone, or alcohol alone, or any pair of the fragments, or all three together. Each case results in different sets of ground truth labels. A similar multiplicity of possible ground truth labels arises when a molecule exhibits multiple occurrences of a fragment in the binding logic (e.g., if a molecule has two phenyl groups). Because all these label sets are correct, we enumerate them and report the maximum Attribution AUC found among them. Formally, for a set $S$ of molecular fragments in a disjunctive binding logic or present multiple times in the molecule, we enumerate the set of all $k$ combinations $\left(\genfrac{}{}{0ex}{}{S}{k}\right)$ ($1\le k\le \left|S\right|$) of molecular fragments. Each $k$ combination has a ground truth labeling where atoms in its molecular fragment(s) receive a 1 label, while others are labeled 0. We report the maximum Attribution AUC found.

Zinc+2 Test Set.

We also report the Model AUC for a “Zinc+2” holdout set, generated from the Zinc holdout set by iterating through molecules and adding or removing an atom or bond to each in nearly every valence-valid way as in ref. 24. This process is then repeated, resulting in a set of molecules each a molecular graph edit distance $\le 2$ from the Zinc holdout set, and about 5,000 times larger, for each logic.

Results

Table 1 lists the results obtained for networks trained using data with synthetic labels that reflect the binding logics listed. The Zinc Model AUC is near-perfect (1.0) for each of the binding logics, indicating that the trained models can correctly classify the molecules in the held-out test sets. Furthermore, the Attribution AUC is significantly lower than 1.0 for several logics. For instance, for binding logic 9, the GC Attribution AUC is only 0.7, while the Zinc Model AUC is 0.995. We note that the Attribution AUC declines as the logics become more complicated and include larger numbers of functional groups. The MPNN models exhibit a similar pattern. We now discuss further implications of these findings.

Attacks Guided by Attributions.

The combination of near-perfect model performance and low Attribution AUCs indicates either: 1) a weakness of the attribution technique or 2) failure of the model to learn the ground truth binding logics. We distinguish these cases by investigating individual molecules that were correctly classified but have low Attribution AUCs. Guided by patterns across multiple molecules where the attributions were misplaced with respect to the ground truth binding logic, we discovered small perturbations of each molecule which caused the class predicted by the model to be incorrect. By manually inspecting a few perturbations for a few misattributed molecules, we found at least one perturbation attack for every logic that did not have a high Attribution AUC, leading us to conclude that the model did not learn the correct binding logic. These results clarify that the Zinc held-out sets are still underrepresentative, despite their careful balancing, discussed above.

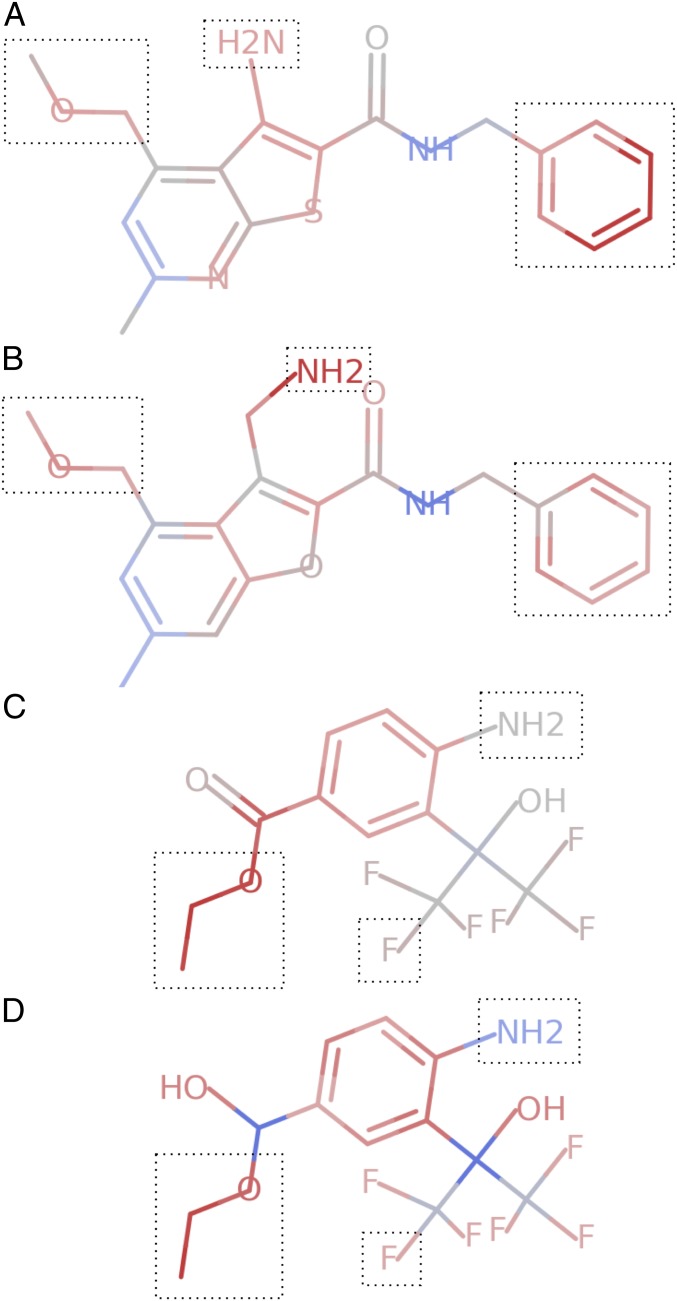
Here, we describe a few of the perturbation attacks that we found. Binding logic 9 requires the presence of “a primary amine and an ether and a phenyl.” One example from Zinc that satisfies this logic is shown in Fig. 3A. This molecule is correctly classified as positive (i.e., binding) by the model with a probability of 0.97; however, as seen in the figure, it has misplaced attributions on several atoms in the ring structures on the left. We perturb those atoms and separate the primary amine from them with an additional carbon, resulting in the molecule shown in Fig. 3B. The model gives this perturbed molecule a predicted score of 0.20, a negative class prediction, despite the fact that the molecule still fully satisfies the same binding logic that the model was trained against.

Fig. 3.

Visualizations of attribution scores, calculated using Integrated Gradients. (A) Attribution scores for a molecule from the logic 9 held-out set that obeys the binding logic. (B) A minor perturbation of the above molecule, guided by errors in the attributions shown in A, which gets misclassified by the model. (C) Attribution scores for a molecule from the logic 12 held-out set that obeys the binding logic. (D) A minor perturbation of the above molecule which still obeys the logic, but is misclassified by the model. Dotted boxes are added around the fragments whose presence defines the molecules as members of the positive class.

Binding logic 12 requires that a molecule satisfy the “absence of an alcohol or presence of a primary amine, along with an unbranching alkane and a fluoride group.” One example from Zinc that satisfies this logic is shown in Fig. 3C. It is correctly classified as positive by the model with a prediction of 0.97; however, it has misplaced attributions on the carbon atom in the carbonyl group on the left. Guided by these attributions, we perturb that carbonyl, converting it to a single bond, resulting in the molecule in Fig. 3D. The model gives this perturbed molecule a predicted score of 0.018, a negative class prediction, despite the fact that the molecule still satisfies the ground truth binding logic.

Zinc+2 Holdout Set.

To further probe the ability of the model to generalize, and the role played by dataset bias, we also report Model AUCs for each logic measured on the “Zinc+2” holdout sets described above. These sets are a factor of 5,000 larger than the Zinc holdout sets, and contain many of the perturbations that led to adversarial attacks. The Zinc+2 Model AUCs are almost uniformly lower than the Zinc Model AUCs, reflecting the more stringent nature of this test. In some logics (e.g., number 13), the Zinc+2 Model AUC is substantially lower, indicating dataset bias in the Zinc holdout for these models. In most logics, the Zinc+2 Model AUC is slightly lower, and we interpret this as evidence for some degree of bias in the Zinc datasets. We conclude that, even when adversarial examples are rare, finding them is easy by following misattributions. Furthermore, if only the Model AUC on the Zinc holdout set is considered—as in common practice—the MPNN and GC models perform similarly on 15 of the 16 datasets. However, our Zinc+2 sets reveal that they do not generalize with the same fidelity.

A Pharmacological Hypothesis.

These results indicate that the attribution can be more trustworthy than the model: Even if the model achieves a high Model AUC, a low Attribution AUC appears to indicate that there exist molecules that do not satisfy the binding logic but are predicted to bind by the model. This occurs because of biases in the underlying dataset learned by the model.

The same concern applies to real protein binding datasets. Our results suggest a simple test that can be performed to test an existing hypothesis about the pharmacophore(s) that control binding. First, the hypothesis is codified as a “binding logic,” which is used to create a set of synthetic labels. Next, these synthetic labels are used to train a neural network and analyze its attributions and Attribution AUC. A good Attribution AUC, with attribution to the correct functional groups, suggests that the combination of dataset and trained neural network is able to generalize. However, a poor Attribution AUC or consistent unexpected attribution artifacts would suggest a need for model simplification and regularization, and/or dataset augmentation.

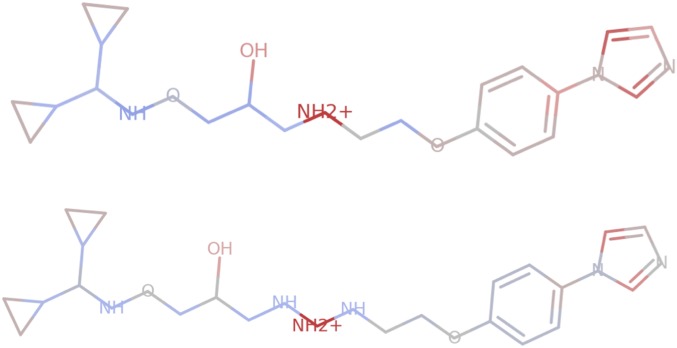
We follow this protocol using data for binding to the protein ADRB2 from the DUD-E dataset (19). One hypothesis for a pharmacophore is a benzene ring with a two-carbon chain connected to an ionized secondary amine. This results in a dataset with 934 positives and 14,290 negatives, of which ∼10% are reserved as a held-out set by ID hash. We trained a graph convolution model (see details in SI Appendix), and achieved a Model AUC on the held-out set of 1.0. However, its Attribution AUC is extremely low, at only 0.11. Visualizations of the attributions show the attribution only consistently highlights the NH2+ group. This means that attacks (e.g., Fig. 4) are easily discovered using this insight.

Fig. 4.

Visualizations of Integrated Gradients attributions. (Top) An example “binder” from the synthetic ADRB2 dataset, correctly predicted as a positive with prediction 0.999. (Bottom) A minor perturbation of the above molecule which should be a negative but gets misclassified as still a positive with prediction 0.995.

Discussion

There is growing concern about the nonrobustness of machine learning models, and much recent research has been devoted to finding ways to assess and improve model robustness (13–15, 25. A common source of nonrobustness is bias in the training dataset (13, 25, 27, 30). An approach to identifying such bias is to examine attributions of the model’s predictions, and determine whether too much attribution falls on noncausal features or too little falls on causal features (25); both are undesirable and indicate bias in the training dataset that the model erroneously learned.

The central challenge in applying this approach to virtual screening models is that, a priori, we know neither the internal logic of the model nor the logic of protein binding. Thus, we have no reference for assessing the attributions. To resolve this, we introduce the idea of evaluating hypotheses for binding logics by setting up a synthetic machine learning task. We use the hypothesized logic to relabel molecules used in the original study, and train a model to predict these labels. If attributions fail to isolate the hypothesized logic on this synthetic problem, it signals that there exist biases in the training dataset that fool the model into learning the wrong logic. Such bias would also likely affect the model’s behavior on the original task.

To quantitatively assess attributions, we introduce the Attribution AUC metric, measuring how well the attributions isolate a given binding logic. It is not a measure of the “correctness” of the attributions. The mandate for an attribution method is to be faithful to the model’s behavior, and not the behavior expected by the human analyst (18). In this work, we take the faithfulness of the attributions obtained using Integrated Gradients as a given. For our synthetic task, we find the attributions to be very useful in identifying biases in the model’s behavior, and we were able to successfully translate such biases into perturbation attacks against the model. These attacks perturb those bonds and atoms with unexpected attributions, and their success confirms the faithfulness of the attributions. The attacks expose flaws in the model’s behavior despite the model having perfect accuracy on a held-out test set. This reiterates the risk of solely relying on held-out test sets to assess model behavior.

Finally, we acknowledge that attributions as a tool offer a very reductive view of the internal logic of the model. They are analogous to a first-order approximation of a complex nonlinear function. They fail to capture higher-order effects such as how various input features interact during the computation of the model’s prediction. Such interactions between atom and bond features are certainly at play in virtual screening models. Further research must be carried out to reveal such feature interactions.

Thoughts for Practitioners.

The recent machine learning revolution has led to great excitement regarding the use of neural networks in chemistry. Given a large dataset of molecules and quantitative measurements of their properties, a neural network can learn/regress the relationship between features of the molecules and their measured properties. The resulting model can have the power to predict properties of molecules in a held-out test set, and, indeed, can be used to find other molecules with these properties. Despite this promise, an abundance of caution is warranted: It is dangerous to trust a model whose predictions one does not understand. A serious issue with neural networks is that, although a held-out test set may suggest that the model has learned to predict perfectly, there is no guarantee that the predictions are made for the right reason. Biases in the training set can easily cause errors in the model’s logic. The solution to this conundrum is to take the model seriously: Analyze it, ask it why it makes the predictions that it does, and avoid relying solely on aggregate accuracy metrics. The attribution-guided approach described in this paper for evaluating learning of hypothesized binding logics may provide a useful starting point.