Role of Monkey Nucleus Reticularis Tegmenti Pontis in the Stabilization of Listing’s Plane

Abstract

An important problem in motor control is how the nervous system deals with redundant degrees of freedom. It has been well documented that voluntary eye movements are constrained to a plane by Listing’s law. Recent evidence has indicated that Listing’s law is implemented downstream from the motor superior colliculus (SC), but controversy exists whether this synergy results from a neural control mechanism or from passive mechanical properties of the oculomotor plant. To address this problem, we have investigated the role of the caudal nucleus reticularis tegmenti pontis (cNRTP), which is functionally positioned inbetween the SC and cerebellar vermis, in the three-dimensional (3-D) control of saccades. In three rhesus monkeys, 3-D eye movements were measured while recording from single units in the cNRTP. In contrast to the SC, movement fields of cNRTP cells were best described by 3-D eye displacement vectors. We also performed electrical microstimulation with the eyes starting from a large range of initial eye positions. Evoked movements were always ipsilaterally directed but were often endowed with a fixed torsional component in either the positive or the negative direction. In two monkeys, small amounts of muscimol were unilaterally injected into the cNRTP. The results of these experiments strongly suggest that the cNRTP contributes to the stabilization of Listing’s plane against torsional errors of the saccadic system. It is concluded, therefore, that the saccadic burst generator is 3-D, and that Listing’s law is at least partially implemented by a neural control strategy.

Directing the line of sight toward a visual target is a redundant motor task because it leaves unspecified the amount of torsion about the visual axis. However, it was already observed by Helmholtz (1867) that, with the head upright and at rest, and the eyes not converging, the three degrees of freedom for static conjugate eye orientation are reduced to two by Listing’s law, which restricts the rotation axis of eye position to a plane with zero torsion. More recently, it has been shown that the same mechanism also holds dynamically for both saccadic and smooth pursuit eye movements (Tweed and Vilis, 1988; Haslwanter et al., 1991). In addition, we have provided neurophysiological evidence that Listing’s law is implemented downstream from, or parallel to, the deep layers of the motor superior colliculus (SC) (Van Opstal et al., 1991; Hepp et al., 1993).

It has been hypothesized that the implementation of Listing’s law requires that the eye angular velocity axis retains three degrees of freedom, by combining both eye displacement and eye position signals (Tweed and Vilis, 1988; Haustein, 1989; Van Opstal, 1993) (see also Materials and Methods). In addition, the oculomotor system should be able to detect, and correct for, torsional errors (Hepp, 1995).

There is controversy over whether Listing’s law is attributable to a neural control strategy (Nakayama, 1975), in which case the three coordinates of the ocular rotation axis are specified by the saccadic commands (Tweed and Vilis, 1987; Crawford and Vilis, 1991; Tweed et al., 1994). Possibly, the cerebellum could be involved in this process (Hepp et al., 1993). Alternatively, a decisive factor responsible for Listing’s law could reside in passive mechanical properties (Schnabolk and Raphan, 1994; Demer et al., 1995; Straumann et al., 1995). In that case, the neural controller specifies a two-dimensional (2-D) eye displacement in Listing’s plane, which is transformed into the 3-D angular velocity vector through mechanical interactions at the level of the oculomotor plant. Both mechanisms, of course, can work together.

In the present study, we have investigated the involvement of the caudal part of the monkey nucleus reticularis tegmenti pontis (cNRTP) in the control of saccadic eye movements in three dimensions. The cNRTP is functionally positioned between the motor SC and the cerebellar vermis (CV) (Harting, 1978; Brodal, 1980; Gerrits and Voogd, 1986). Cells in the cNRTP have saccade-related movement fields that, when measured in two dimensions, resemble those of the motor SC (Crandall and Keller, 1985). Electrical microstimulation was reported to yield saccadic gaze shifts that depend on initial eye position (Yamada et al., 1992).

We hypothesized that, because the relevant eye displacement and position signals appear to be present at this level, a disruption of normal cNRTP function might disturb the coordination of saccades in three dimensions. To that end, we recorded single-unit activity, applied electrical microstimulation, and inactivated the cNRTP with muscimol.

Our results provide strong evidence that the cNRTP is part of a pathway that corrects for torsional displacements from Listing’s plane, and, therefore, that Listing’s law is implemented as a neural strategy.

A brief account of the behavioral and neurophysiological results has appeared elsewhere (Van Opstal et al., 1996a,b).

MATERIALS AND METHODS

General procedures

Three adult rhesus monkeys (Macaca mulatta) participated in these experiments. All surgical procedures and experimental protocols have been described in detail in recent papers from this laboratory (Van Opstal et al., 1991, 1995; Hepp et al., 1993). They followed the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and protocols were approved by the Veterinary Office of the Canton of Zürich.

In short, after an initial training period in which the monkey learned, against liquid reward, to follow accurately a small red laser spot with saccadic eye movements, two operations were carried out. In the first operation, the recording chamber (16 mm diameter) was implanted in stereotaxic coordinates over a trephine hole. In addition, bolts were implanted in the skull for rigid attachment of the head during the experiments.

In a second operation, a special dual-search coil designed for recording 3-D eye position was implanted on either the right (monkey CR) or the left (monkeys AL and NE) eye. Manufacturing of the coils and surgical procedures have been described by Hess (1990).

Eye movements were recorded with the monkey’s head in the center of two alternating magnetic fields (20 kHz) in phase and spatial quadrature (Skalar Instruments, Delft, The Netherlands).

Experimental paradigms

Single-unit recording. During single-unit recordings, with varnished tungsten microelectrodes, the monkey made voluntary saccades in the light in all directions and amplitudes, from a large range of initial eye positions. In a previous paper, we documented that this paradigm yields an approximately Gaussian distribution of eye displacement vectors (with a typical standard deviation for horizontal and vertical components of 14 deg), which are homogeneously distributed over a ±30 deg oculomotor range (Van Opstal et al., 1995). To extend the oculomotor range to three dimensions (with torsional excursions of up to ±15 deg), whole-body rotations were performed in the light around five different axes (horizontal, vertical, torsional, and along the two axes perpendicular to the vertical semicircular canals). For further details, see Hepp et al. (1993).

Electrical microstimulation. The recording electrode was also used for electrical microstimulation of the cNRTP, carried out at the different depths where presaccadic cells had been encountered earlier. The default stimulation train had a duration of 70 msec and consisted of negative pulses (pulse width 0.25 msec; guide tube as common ground) delivered at a frequency of 330 Hz. The typical current strength ranged from 15 to 50 μA. On various occasions, we increased the duration of the stimulation train to 140, 280, or 420 msec. The monkey made voluntary eye movements in the light while stimulus trains were delivered at 2 sec intervals. No vestibular stimulation was applied in these experiments.

Reversible inactivation. In three unilateral reversible inactivation experiments, we applied small amounts of muscimol at locations in either the left or the right cNRTP, where saccade-related burst activity had been recorded on the same day and electrical stimulation had yielded rapid gaze shifts at low stimulus intensities. The recording electrode was removed while the guide tube remained in place. A Hamilton syringe with an outer diameter of 0.5 mm was then inserted. In monkey CR, two muscimol injections were made: 300 nl, 0.1% into the left cNRTP, and 700 nl, 0.1% into the right cNRTP. In monkey AL, a 700 nl, 0.5% injection was placed into the left cNRTP.

After the injection, behavioral testing was carried out for at least 1 hr, and the data described in this paper were taken during the first 25 min after the injection. There were no obvious side effects caused by spreading of the muscimol into other oculomotor areas at that time. Oculomotor testing at the next day showed no deficits.

Data representation

The calibration procedures of the dual-search coil signals, allowing for an absolute measure of the orientation of the eye at an accuracy of 0.5 deg or less for all three components over the full oculomotor range, have been described in detail by Hess et al. (1992). The theoretical considerations underlying the representation of eye movements in three dimensions have been described fully by Hepp et al. (1993) and Van Opstal (1993). Here, we will restrict our description to a brief account of the main concepts.

It has become customary to represent 3-D eye position by a so-called rotation vector:

$$\vec{r}=tan(\rho /2)\widehat{n},$$ Equation 1

with n̂ a unit vector and ρ the angle of rotation about n̂ from the primary position (defined byr⃗ = 0⃗). A right-handed, head-fixed cartesian coordinate system is adopted, in which the (r_x, r_y, r_z) components represent the torsional, vertical, and horizontal components of the rotation vector, respectively. Units are expressed in half-radians (from Eq. 1 it follows, e.g., thatr_z = 0.1 rad/2 corresponds roughly to ρ_z ≈ 10 deg). In this primary frame of reference, Listing’s law takes the simple form (Tweed and Vilis, 1988;Van Opstal et al., 1991; Hess et al., 1992; Hepp et al., 1993):

$$r_x=0.$$ Equation 2

Thus, in this representation, eye position vectors (Eq. 1) are restricted to the (y,z)-plane, which is called Listing’s plane.

Straight saccades in Listing’s plane, between initial (A) and final (B) eye position, can be characterized by the 2-D eyedisplacement vector:

$${\vec{d}}_{BA}={\vec{r}}_B-{\vec{r}}_A$$ Equation 3

or, equivalently, by 3-D eye motor error, which is parallel to the eye angular velocity vector:

$${\vec{q}}_{BA}\approx {\vec{d}}_{BA}+{\vec{r}}_A\times {\vec{d}}_{BA}$$ Equation 4

[see Hepp et al. (1993) and Van Opstal (1993) for a full account of this distinction]. Note that, whereas the eye displacement vector lies in Listing’s plane, the eye motor error vector depends in a nonlinear way on initial eye position,r⃗_A, and, in general, has a torsional component: q_BA^x ≠ 0 (Eq. 4; Tweed and Vilis, 1988; Haustein, 1989; Van Opstal, 1993).

Data analysis

Details on the procedures of the principal analysis of the 3-D eye movements (such as calibration and saccade detection) are described in Hepp et al. (1993) and Van Opstal et al. (1995). Here, only a detailed account is given of the analysis of the cell data.

As will become clear in Results, the typical tuning of cNRTP units to saccade direction is broader than for collicular burst neurons (see also Crandall and Keller, 1985), whereas the tuning to saccade amplitude is either confined to a restricted range (“vectorial burst neurons”; similar to collicular units) or monotonic (“directional burst cells”).

Our main objective of the recording study, however, was to quantify thedirectional tuning of a cell in three dimensions, regardless of its precise tuning properties to saccade amplitude. As is illustrated in Figure 1 (described below), this requires the determination of two angles for saccades of optimal amplitudes. To that end, we have adopted the following procedure:

Fig. 1.

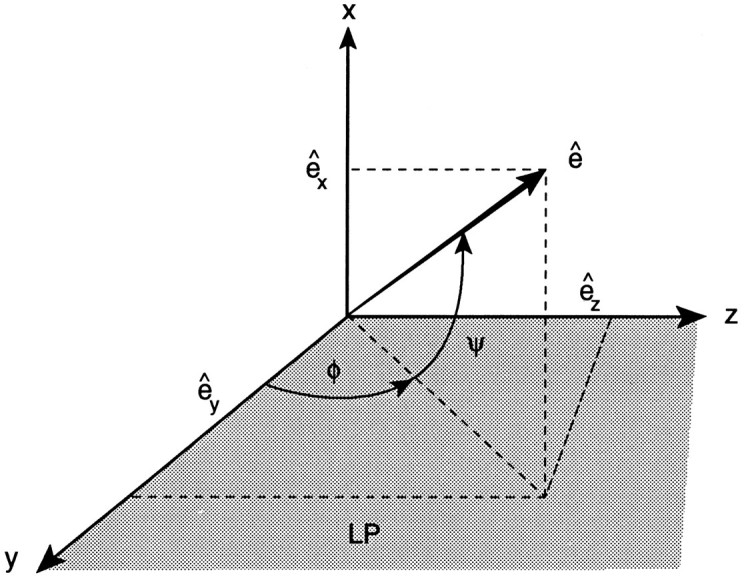
Coordinate system used to describe the tuning of cNRTP neurons to saccades in three dimensions. The normalized optimal tuning vector, ê = (ê_x,ê_y, ê_z), which is found by fitting Eq. 6 to the data, is parametrized by polar angles φ (angle with positive y-axis in Listing’s plane; LP, shaded area) and ψ (torsional polar angle with LP).

(1) Cell activity, $\overline{F}$, was quantified by the mean firing rate from 20 msec before saccade onset to 20 msec before saccade offset.

(2) The optimal range of saccade amplitudes for a given cell was first determined by means of the weighted center of gravity of the cell’s activity:

$$\vec{c}=\sum _i{\vec{F}}^i·{\vec{d}}^i/\sum _i{\vec{F}}^i,$$ Equation 5

with d⃗ⁱ the eye displacement vector (Eq. 3) of saccade i. When a cell is tuned for specific eye displacement vectors, and with saccades evenly distributed over the oculomotor range (see above), c⃗ will provide a good first approximation for the center of the movement field. Also, when the cell has a saturating monotonic sensitivity for saccade amplitude, the amplitude of c⃗ will fall in the optimal (large) amplitude range. Because the movement fields are broadly tuned, optimal saccade amplitudes were selected for the range between 70 and 130% of the amplitude of c⃗. To eliminate the variability in saccade amplitudes, all selected saccade vectors were then normalized:d̂ = d⃗/d (units ofd̂ are dimensionless). We have verified that the amplitude normalization had no qualitative effect on the results of the fit procedure described below.

(3) The optimal direction of the saccadic displacement vector in three dimensions for a given single unit, e⃗(Fig. 1), was obtained by fitting the data to the following equation:

$${\overline{F}}_p=F·(1+\vec{e}·\widehat{d}),$$ Equation 6

where F̄_p is the predicted mean firing rate (in Hz) for normalized saccade d̂, the free parameter F is in Hz, and the units of the tuning vector,e⃗ (three components), are dimensionless. Note that Eq. 6 assumes a cosine tuning characteristic for cNRTP neurons. Although it provides only a first-order description, we obtained sufficiently high correlations between measured and predicted activity to justify such an approximation and not to investigate (ad hoc) higher-order models with more parameters (see Results, Table 1).

Table 1.

Summary of NRTP 3-D movement fields

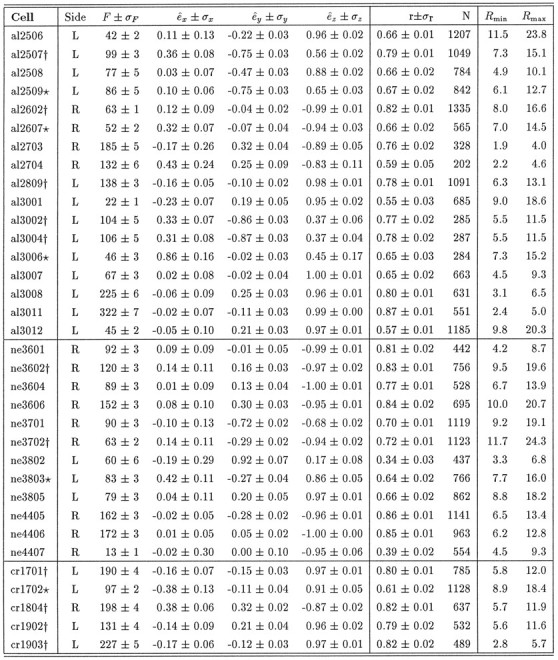
Fit results of Eq. 6 for all 34 cNRTP burst neurons. Fis the mean firing rate (in Hz), (ê_x,ê_y, ê_z) are the (dimensionless) components of the normalized eye displacement tuning vector, ê. ς_i is the standard deviation of parameter i and was obtained by bootstrapping the fit 75 times (see Efron and Tibshirani, 1991). r is the correlation coefficient between fit and data, and N is the number of saccades, selected on the basis of an optimal amplitude criterion (see Materials and Methods). R_min andR_max are the minimum and maximum saccade amplitudes (in deg), selected for each cell. L,R = left/right recording side.

F1_152: , Significant torsional component, r ≥ 0.7;

F1_150: , significant torsional component, 0.6 ≤ r ≤ 0.7. In 20/34 cells the correlation exceeded 0.7, and in 11/20 the torsional component differed significantly from zero. In 11/34 neurons correlations are higher than 0.8, out of which 5 have a torsional on-direction. For 9/34 cells 0.6 ≤ r ≤ 0.7, and in 5 torsion was unequal to zero. For 5/34 cellsr < 0.6, and in 2 of these a significant torsion was obtained. Also, from the 10 directional burst neurons, 4 were torsional. Thus, regardless of the criteria applied, in roughly half of the cells (18/34) the obtained torsional component was significant.

(4) Finally, we parametrized the 3-D on-direction of the cell’s movement field from the normalized tuning vector, ê = e⃗/e, by the two polar angles shown in Figure 1: φ (in deg) is the angle of the vector’s projection in Listing’s plane with the positive y-axis (Listing’s polar angle), and ψ (deg) is the angle of the tuning vector with Listing’s plane (torsional polar angle):

$$\phi =\text{acos}\left(\frac{{\widehat{e}}_y}{\sqrt{({\widehat{e}}_y{)}^2+({\widehat{e}}_z{)}^2}}\right) \text{and} \psi =\text{asin}({\widehat{e}}_x)$$ Equation 7

(0 ≤ φ < 360 deg; −90 ≤ φ ≤ 90 deg). For example, φ = 0 deg represents a downward on-direction, and φ = 90 deg is leftward. When ψ = 0 deg, a cell is tuned in Listing’s plane, whereas ψ = 90 deg would describe a purely torsional cell with a clockwise on-direction. Note that the polar angles (expressed in deg) should not be confused with the cartesian components of the eye displacement vector (expressed in half-radians, see above).

(5) The confidence limits of the four fitted parameters, {F, e_x, e_y, e_z}, were obtained by bootstrapping (Efron and Tibshirani, 1991; Press et al., 1992) (see also Van Opstal et al., 1995). If e_x differed significantly from zero (p < 0.05), the unit’s movement field was judged to have a significant torsional on-direction.

(6) Finally, we have also checked whether the cNRTP activity was systematically influenced by changes in initial eye position (Crandall and Keller, 1985) by extending the movement field description of Eq. 6 to:

$${\overline{F}}_p=F·(1+\vec{e}·\widehat{d}+\vec{f}·{\vec{r}}_{\text{on}}),$$ Equation 8

where f⃗ = (f_y, f_z) is a cell’s eye position tuning vector [units in (rad/2)⁻¹] and r⃗_on is the onset position of the eye in Listing’s plane. This so-called linear gainfield description has also been used to characterize the eye position sensitivity of SC neurons (Van Opstal et al., 1995).

Histology

During the recording sessions, the oculomotor nucleus (NIII) provided a reliable landmark for the subsequent localization of the cNRTP. Typically, ∼4–5 mm below NIII, presaccadic activity, indicative for the cNRTP (Crandall and Keller, 1985), was first encountered. Toward the final experiments, small electrolytic lesions were made at the recording sites in the three monkeys. These lesions were histologically verified in or near the cNRTP. Figure2 shows the site of the electrolytic lesion in the right NRTP of monkey CR.

Fig. 2.

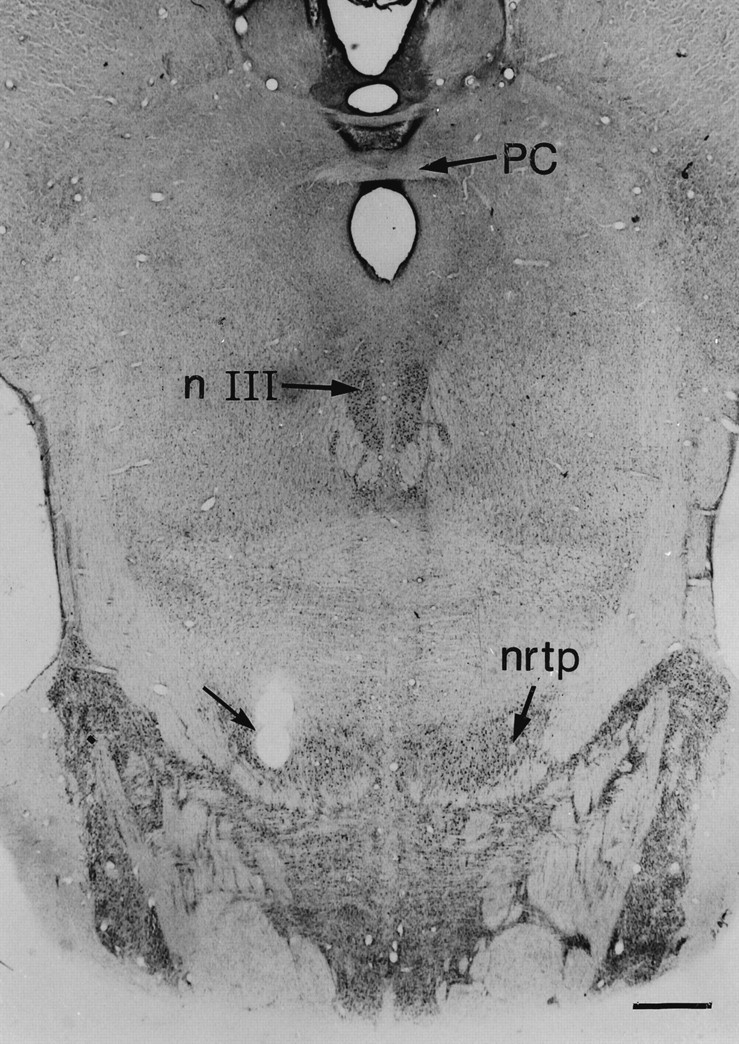
Electrolytic lesion in the right NRTP of monkey CR. Site of the lesion is indicated by the arrow. PC, Posterior commisure; NIII, oculomotor nucleus;nrtp, nucleus reticularis tegmenti pontis. Scale bar, 1.0 mm.

RESULTS

Single-unit recording

In line with earlier findings (Crandall and Keller, 1985), we observed that the tuning characteristics of cells in the cNRTP for saccades near Listing’s plane [i.e., eye movements for whichd_x (Eq. 3) is close to zero] roughly resemble those of the motor SC. Although broader tuning was obtained than for SC neurons, most cells had a circumscribed (vectorial) movement field (24/34). However, a substantial fraction of the cells were tuned for saccade direction only, with firing rate increasing monotonically as a function of amplitude (10/34).

To investigate the 3-D structure of the cNRTP movement fields, saccades elicited by vestibular stimuli (having three degrees of freedom) were pooled with the spontaneous eye movements in the light. To check the consistency of our 3-D analysis, both qualitative and quantitative plots were made from these recordings.

Qualitative analysis

In our qualitative 3-D movement field plots (such as in Fig.3), we selected saccades with comparable, near-optimal amplitudes according to the procedure described in Materials and Methods. The 3-D direction of saccade displacement vectors was then parametrized by the two polar angles (φ, ψ) by applying Eq. 7, and the average firing rate was computed for all saccades belonging to a particular 10 × 10 deg direction bin (no overlap of bins; no interpolation between bins). Two examples of the resulting 3-D tuning surfaces of cNRTP burst neurons are shown in Figure 3. Note that, for both neurons, activity increases in a systematic way with ψ for saccades in a particular optimal Listing direction, φ.

Fig. 3.

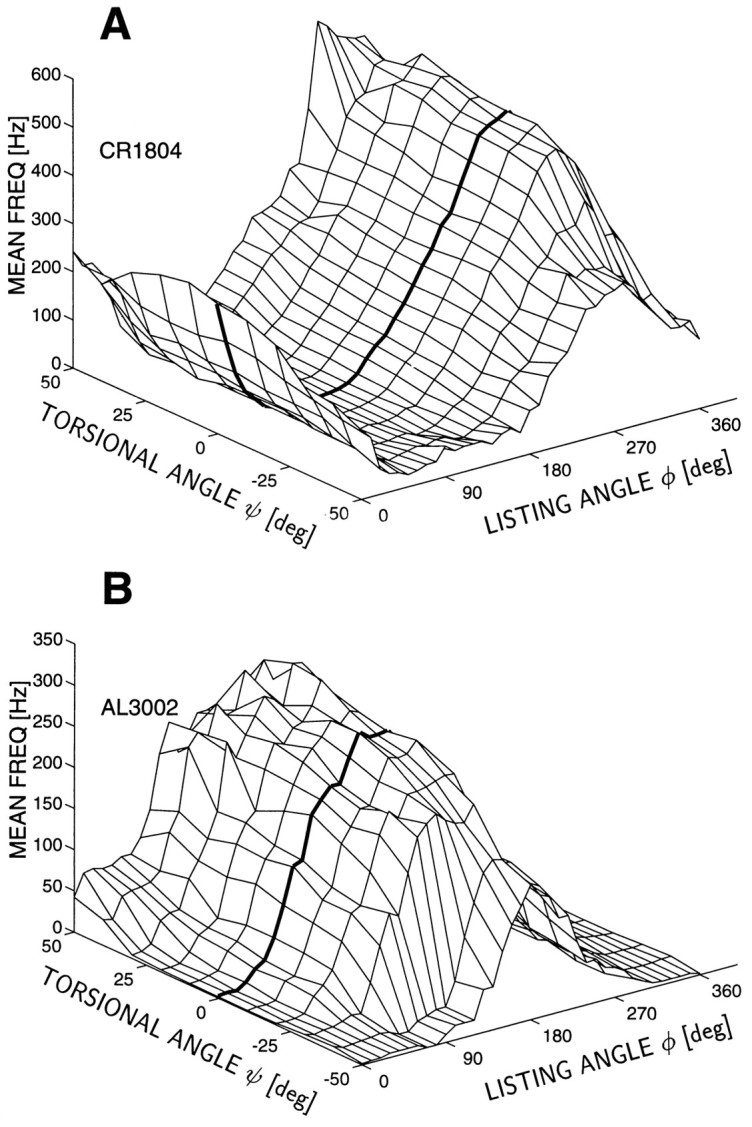
Movement field in three dimensions of two cNRTP units [CR1804 (A) and AL3002(B)] recorded in two of the monkeys for saccades with near-optimal amplitudes (see Materials and Methods and Table 1). The tuning characteristic of the cells is plotted as a function of the 3-D direction of normalized saccade vectors parametrized by the polar angles φ and ψ (see Fig. 1). The thick line corresponds to the activity of the neuron for saccades in Listing’s plane (ψ = 0). Note that for both neurons, firing rate systematically increases in the positive torsional direction. The optimal 3-D saccade displacement vectors for these cells are given in Table 1.

Quantitative analysis

In our quantitative 3-D analysis of the cells, we took as a first approximation a cosine-tuning characteristic to 3-D saccade displacement vectors for all saccades with selected near-optimal amplitudes (Eq. 6; see Materials and Methods). In Figure4A, the quality of the prediction provided by this simple model is illustrated for cell CR1804 (same cell as Fig. 3A). Note the high correlation between fit and data. The results of the fit analysis for all recorded cells are shown in Figure 4B. Bootstrapping showed that a large proportion of our sample of neurons had 3-D on-directions, with a significant torsional component (∣e_x∣ > 0;p < 0.05). From the 20 neurons for which the correlation between fit and data exceeded 0.7, 11 had a significant torsional component (see also legend to Table 1). Interestingly, positive as well as negative torsional components were obtained from both sides (Fig. 4B, Table 1). The optimal tuning parameters of the cells, as well as the obtained correlations, are given in Table 1.

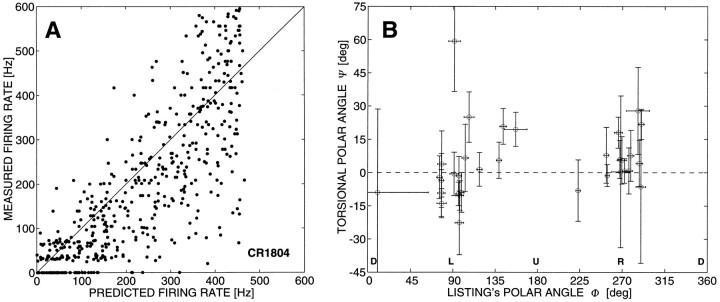
Fig. 4.

A, Result of fitting Eq. 6 to the data of cell CR1804 (see Fig. 3A and Table 1) by comparing predicted versus measured firing rate. A perfect fit would require the data to lie on the diagonal line. The correlation between predicted and measured firing rate is r = 0.82 (N = 637). Saccade amplitudes were selected between 5.7 and 11.9 deg (see Eq. 5). B, Result for all cells, in which optimal tuning directions are plotted as (φ, ψ) angles. Standard deviations were computed by bootstrapping Eq. 6 (see Materials and Methods). Note that a substantial portion of the neurons have a significant torsional on-direction (ψ ≠ 0; see also Table 1).

Electrical stimulation

Electrical stimulation was performed in 11 recording tracks at 59 different sites within the cNRTP of all three monkeys. At a majority of sites, evoked gaze shifts had onset latencies in the range from 12 to 18 msec, which excludes backfiring of the motor SC as an explanation for the observed movements (minimum latency 20 msec).

At most stimulation sites, evoked eye movement amplitude and direction systematically depended on the initial eye position (e.g., Fig.5A,C). The movements always had an ipsi-horizontal component, often in oblique directions, and remained close to Listing’s plane at 30% of the stimulation sites. At a majority of sites, however, a small torsional displacement was apparent in the evoked gaze shifts. In these cases, neither the sign nor the size of the evoked torsional displacement was systematically related to initial eye position. In all experiments, the torsional position of the eye was maintained after the stimulation ceased (see below).

Fig. 5.

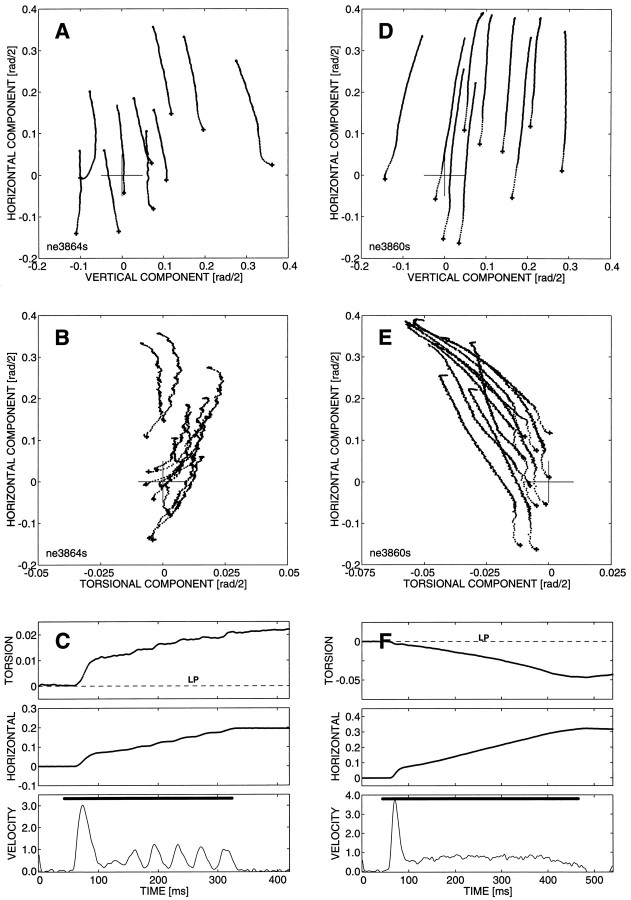
Results of electrical microstimulation at two different depths in the left cNRTP of monkey NE. Stimulation parameters: current strength, 50 μA; frequency, 330 Hz; train duration, 70 msec. Evoked eye movements were leftward, and at both sites movement direction and amplitude varied with initial eye position. A, C, Projection of the eye movement trajectories in Listing’s plane [the (y, z) plane];B and D present the same data in the (x, z) plane (see Tweed and Vilis, 1988; Van Opstal et al., 1991; Hepp et al., 1993). Note different scales. Top panels show data obtained at site 1, and the bottom panels represent site 2, which was located 500 μm deeper along the same penetration. Note that evoked eye movements at both sites have a substantial torsional displacement (B, D). However, the sign of the torsional movements is opposite for the two sites: movements at site 1 had a negative torsional displacement, whereas the gaze shifts evoked at site 2 had positive torsion. The size of the torsional displacement was independent of initial eye position (site 1: offset −0.006 rad/2; slope 0.009; r = 0.33;N = 42; p = 0.03; site 2: offset +0.013 rad/2; slope 0.013; r = 0.26; N = 42;p = 0.10) [see Van Opstal et al. (1991) and Hepp et al. (1993) for details on this procedure]. Note also the small negative torsional offset at the first stimulation site, which is absent at the second site.

During four penetrations (at least one in each monkey) the direction of the torsional displacement varied systematically with the depth of the electrode within the cNRTP. In Figure 5, the results of such a penetration (monkey NE) are shown for electrically evoked saccades from two different depths. In this example, the direction of evoked torsional eye displacements changed continuously from negative (Fig.5B) to positive values (Fig. 5D) as the electrode was advanced 500 μm.

Linear regression on the evoked torsional eye displacement as a function of initial eye position resulted in insignificant relations for the majority of cases (see legend to Fig. 5). Prolonged stimulation (train durations 140, 280, or 420 msec) typically evoked a “staircase” of multiple rapid eye movements having the same direction as, but smaller amplitudes than, the first evoked response. If a torsional component was evoked in the first movement, the subsequent movements of the staircase were also endowed with such a torsional displacement. This property is illustrated in Figure6A–C, where 10 movement trajectories, evoked at the same site as the data in Figure 5, C andD, are presented. At other sites, however, an evoked rapid eye movement was combined with a smooth oblique eye movement, also in the same 3-D direction as the primary gaze shift. Examples of such movements are given in Figure 6D–F (obtained from the same site as Fig. 5A,B). Again, the torsional directions for the two sites are quite different, although both stimulations were performed within the same penetration.

Fig. 6.

Effects of prolonged electrical stimulation in the cNRTP. Data from monkey NE, same stimulation sites as in Figure 5.Left column shows stimulation at site 2; train duration 280 msec. Right column shows stimulation at site 1; train duration 420 msec. The top two rows show 10 typical eye movement trajectories from each site presented in the (y, z)-plane (top) and (x, z)-plane (center). The bottom row shows the detailed position and track velocity signals (r˙ =  $\sqrt{{\dot{\text{r}}}_{\text{x}}^2+{\dot{\text{r}}}_{\text{y}}^2+{\dot{\text{r}}}_{\text{z}}^2}$) for one of the traces. Note that stimulation at site 1 produced a staircase of small gaze displacements (5–6) into roughly the same 3-D direction as the initial, larger movement (onset latency: 17 msec). The evoked torsional displacement accumulates during the stimulation (no intermediate reset) and reaches almost 3 deg in the positive direction. Stimulation at site 2 produced an initial rapid gaze shift (latency: 16 msec), followed by a smooth, constant-velocity movement into the same direction. The torsional displacement is negative throughout and reaches almost 5 deg. Thick lines in the bottom panels correspond to the timing of the stimulus train. Units:top two rows, rad/2; bottom row, rad/2 sec⁻¹.

We noted that when electrical stimulation had brought the eye out of Listing’s plane, the first spontaneous saccade after the electrical stimulus tended to bring the eye back into Listing’s plane by a rapid torsional reset component. This torsional displacement was tightly synchronized with the horizontal and vertical movement components. In Figure 7A, a number of typical torsional traces of such spontaneous poststimulation saccades have been superimposed (data from the same site as Fig. 5C,D). After the electrically induced positive torsional eye displacement, the subsequent spontaneous saccade evoked a negative torsional displacement such that eye position after the correction remained close to Listing’s plane. Figure 7B shows, for all saccades of that particular stimulation experiment, that there is a tight relation between the size of the torsional onset position and the size of the torsional reset component. This feature is illustrated even more dramatically in Figure 7C, where we have also included stimulation data from the same tract with much larger torsional onset positions in both the negative (see Fig. 6E) and the positive (Fig. 6B) directions. The torsional reset component of the first spontaneous saccade after stimulation offset compensates very precisely for the induced torsion. It is important to note that the large torsional components of the spontaneous saccades were generated without any vestibular or otolith stimulation.

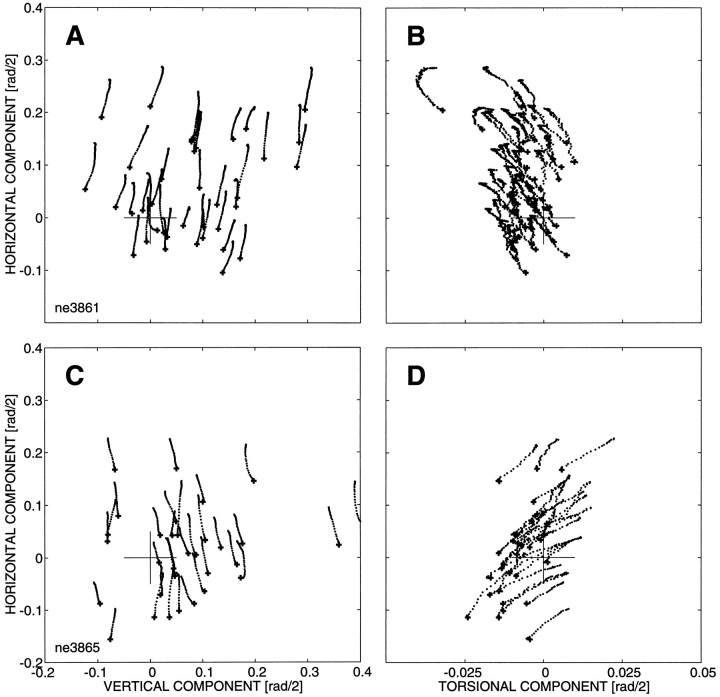
Fig. 7.

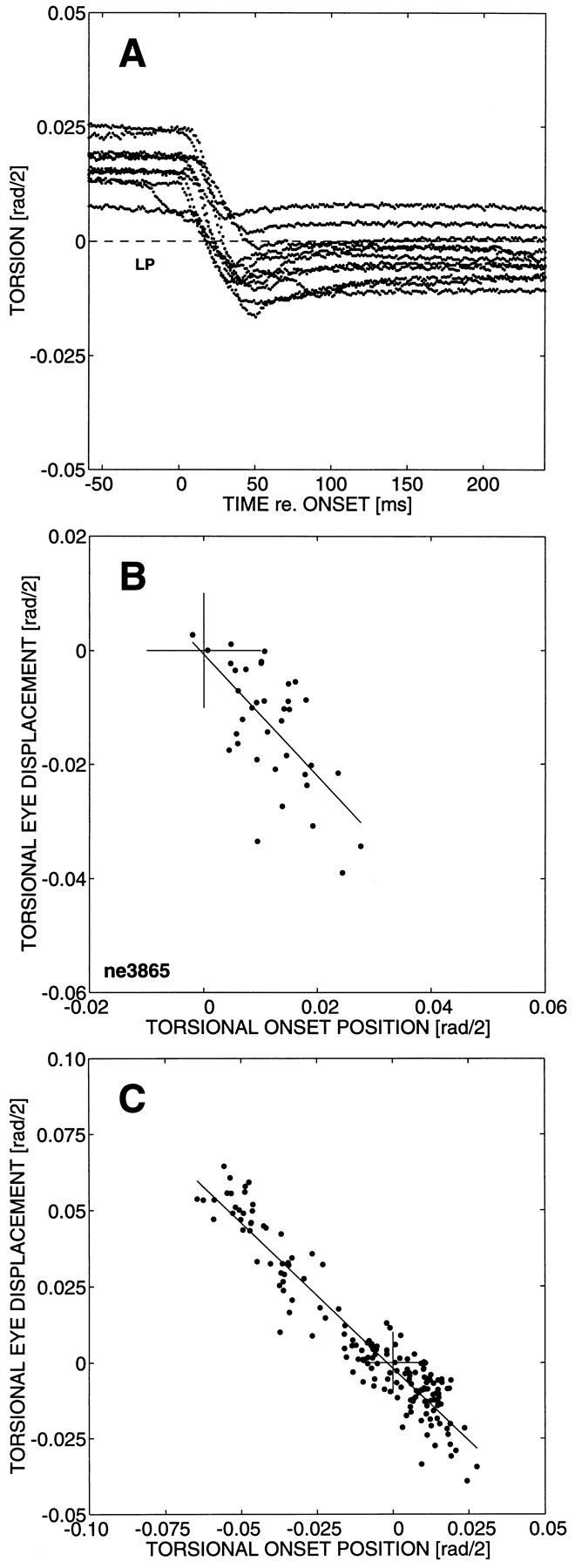
Torsional resets of spontaneous saccades after the offset of the electrical stimulus train. A, Electrical stimulation at site NE3865 (see Fig. 5D) had brought the eye out of Listing’s plane into the positive torsional direction (up to ∼2.5 deg). The first spontaneous saccade after the stimulus train had stopped (saccade onsets aligned with time = 0 msec) brings the eye immediately back to a narrow band surrounding Listing’s plane.B, The torsional displacement of the first spontaneous saccade after stimulation compensates well for the onset position of the torsional component. Linear regression yielded a slope of −1.07 (r = −0.65; N = 67). C, Including the data of Figure 6, the range of torsional onset positions has been dramatically expanded. The torsional reset of the spontaneous saccades immediately after stimulation is almost perfect: slope of the regression line −0.95 (r = −0.96; N = 167).

Unilateral injections

In monkey, with the head stationary, the torsional scatter around Listing’s plane is usually quite small. The typical standard deviation of torsional eye position components is ∼0.005 rad/2 (i.e., 0.6 deg), which should be compared to a torsional oculomotor range of ±0.15 rad/2 (or ±15 deg) during dynamic vestibular roll stimulation (Suzuki et al., 1995). However, we noted that even in the absence of head movement, the eyes do not always remain exactly in Listing’s plane during spontaneous saccadic eye movements. Close inspection of the data revealed occasional violations of Listing’s law (torsional “errors”) up to ∼1.5 deg (see, e.g., Fig.8A). These violations, which appeared to be in random directions, were not systematically related to the amplitude and direction of the saccade or to specific initial eye positions within the oculomotor range. In those instances, the small torsional displacement of the eye is tightly synchronized with the horizontal and vertical saccade components, suggesting a shared burst controller for the three saccade components. Between saccades, the eye stayed at the newly obtained torsional level, often for as long as 800 msec (not shown here, but see Van Opstal et al., 1996a), and did not drift back passively into Listing’s plane. Just as was observed for the electrically induced torsion (see above), the self-induced deviation from Listing’s plane was usually reset by the next saccadic eye movement (Fig. 8A), and not by a smooth backwards drift.

Fig. 8.

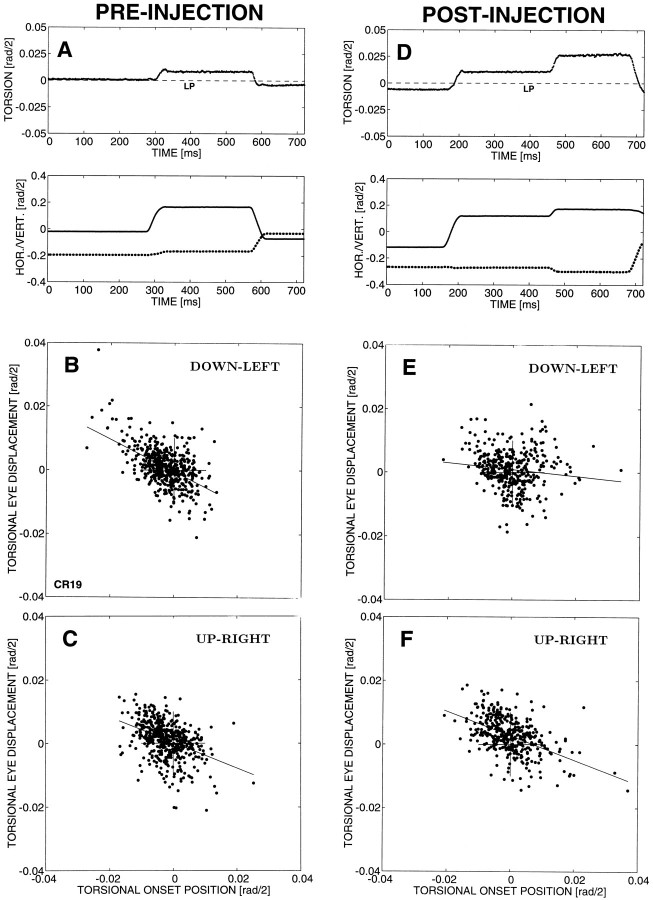
Results of a 300 nl, 0.1% muscimol injection in the left cNRTP of monkey CR. Left panels show the properties of saccades in three dimensions before the injection, whereasright panels are the results obtained within the first 25 min after the injection. A, Example of a torsional reset movement (top panel) that keeps eye position near Listing’s plane (dashed line, LP), despite occasional imperfections of the 3-D saccade generator. Two consecutive saccades are shown [bottom panel: horizontal (dotted) and vertical (continuous) eye position]. Note different scales. In this example, the first saccade brings the eye to ∼1 deg in the positive torsional direction. This torsional position is maintained until the second saccade resets the eye towards Listing’s plane.B, The torsional displacement component,d_x, for all saccades with left- and downward components are plotted as a function of initial torsional eye position, r_x. Note that there is a strong negative correlation (r = −0.51;N = 506), indicating that the saccadic system actively resets the eye toward LP. The slope of the linear regression line is −0.54. C, Similar analysis for saccades with right- and upward components (r = −0.41; N = 505; slope = −0.40). D, After the injection, torsional eye positions are not always followed by a reset to LP, but may even increase substantially, as in this example, in which a downward saccade (at 170 msec) overshoots Listing’s plane by >1 deg, and the subsequent small right- and downward saccade (at 460 msec) brings the eye to almost 3 deg into the positive torsional direction. Such a sequence of events was never obtained in the preinjection data.E, Saccades with a left- and downward component appear to have a clear deficit with respect to the preinjection data inB (r = −0.12; N = 377; slope = −0.11). Large torsional “errors” are no longer reliably followed by a systematic reset to LP. F, No deficit is obtained, however, for saccades with a right- and upward componentr = −0.49; N = 384; slope = −0.38) or for saccades in the remaining two quadrants (data not shown; see Table 2). Note that in both E and F the torsional onset positions are extended into the positive direction.

In Figure 8, B and C, the data obtained for a large number of voluntary saccades in the light of monkey CR, before a small injection of muscimol in the right cNRTP, are shown in the format of Figure 7, B and C, for saccades, having directions confined to the first (Fig. 8B; 0 ≤ φ ≤ 90 deg, i.e., left- and downward saccades) and third (Fig.8C; 180 ≤ φ ≤ 270 deg; right- and upward) movement quadrants. Note, that these saccades had positive as well as negative torsional reset components and that the torsional direction was not related to horizontal/vertical eye position within the oculomotor range.

For all three monkeys, we obtained a significant negative correlation between the torsional onset position of the saccade (r_A^x, caused by a self-induced torsional “error”) and the torsional component of the ensuing saccadic displacement vector (d_AB^x; see Table2). This relation was strongest when the torsional component exceeded ∼1 deg, suggesting a tolerance (“dead zone”) of the saccadic system to small violations of Listing’s law (see also Fig. 7A and legend to Fig. 8).

Table 2.

Summary of muscimol results

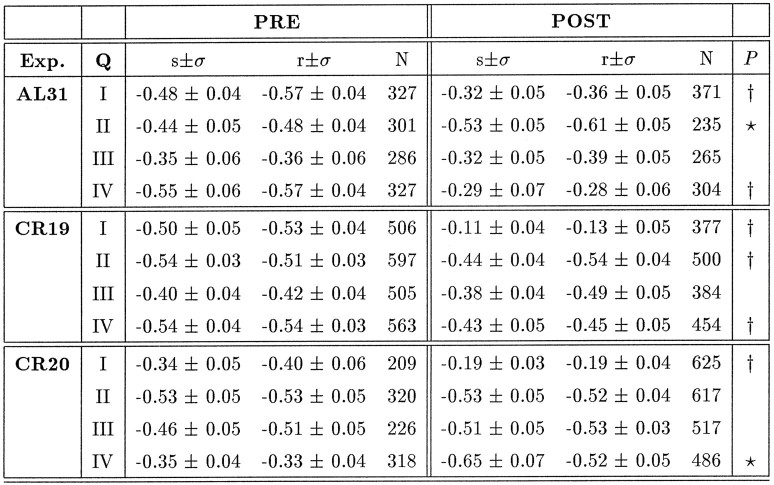
Summary of the results of the three muscimol experiments in monkeys AL and CR. Column Q identifies the saccade vector quadrant (e.g., I: 0 ≤ φ ≤ 90 deg, etc.). Preinjection and postinjection data are quantified by the relation between the initial torsional eye position,r_A^x, and the subsequent torsional displacement of the saccade,d_AB^x. The slope of this relation, s (dimensionless), is given in the left column, the correlation coefficient, r, in the center column, and the number of data points, N, in the right column. Offsets were indistinguishable from zero in all cases. Standard deviations were obtained by bootstrapping the data 100 times. P indicates whether the pre- and postinjection data are significantly different from each other.

F2_152: , Significantly lower slope (P < 0.0001);

F2_150: , significantly higher slope. We have also analyzed the data by including a “dead zone” of 0.6 deg, which excluded torsional onset positions within a range roughly equal to the standard deviation of a normal Listing’s plane. In that case, correlation coefficients increased dramatically, and the lesion effects were even more prominent. For example, for the data presented in Figure 8 (quadrants I and III of experiment CR19), we found:

Prelesion: QI: s = −0.54 (r = −0.63,N = 163); QIII: s = −0.39 (r = −0.53, N = 171);

Postlesion: QI: s = −0.09 (r = −0.17,N = 138); QIII: s = −0.35 (r = −0.62, N = 138).

However, after a unilateral muscimol injection a saccade-direction-specific deficit in this torsional reset mechanism was obtained in all three cases. Typically, a torsional reset after a violation of Listing’s law was absent for those saccades. Sometimes, the eye would move even further out of Listing’s plane at the next saccade (occasionally up to 5 deg) and then stay there until a saccade would reset it (see, e.g., Fig. 8D). These patterns were never observed in the preinjection data. For the particular injection shown in Figure 8 (CR19, right side), saccades with a left- and downward component (0 ≤ φ ≤ 90 deg) had a deficit in their torsional reset (Fig. 8E), whereas saccades directed into the other three quadrants did not. In Figure8F, saccades in the opposite direction (180 ≤ φ ≤ 270 deg) are shown for comparison.

Similar effects were obtained for the other two injection experiments in monkeys CR and AL. The largest effects were obtained in monkey AL, in which a larger amount of muscimol was injected. The results are summarized in Table 2. Significance of a difference between pre- and postinjection data distributions was assessed by a 2-D Kolmogorov–Smirnov test (Press et al., 1992).

Note, that the correlations in Figure 8, B andC, and Table 2 are much lower than for the stimulation data shown in Figure 7. This apparent discrepancy has two causes. First, the torsional range of the spontaneous eye movements in the light is almost an order of magnitude smaller than when evoked by electrical stimulation in the cNRTP (Fig. 7C); a majority of data points cluster within a 1 deg error zone, which is close to the tolerance level of the saccadic system to violations of Listing’s law (e.g., Fig. 7A). Second, in Figure 8, the torsional resets are there because the saccadic system has made errors. However, these errors are, of course, also included in the spontaneous eye movement data set.

DISCUSSION

The results of our study support the hypothesis that the saccade burst generator is 3-D, also in the absence of vestibular stimulation, and that the cNRTP plays an important role in stabilizing Listing’s plane against torsional errors of the saccadic system. Based on these data, we conclude that Listing’s law has a major neural control component, and cannot be explained by a 2-D burst generator in combination with passive mechanical interactions at the level of the oculomotor plant.

Cell recordings

The movement field types, i.e., vectorial versus directional burst cells, agree well with the recordings of Crandall and Keller (1985). Here, we describe two novel aspects. First, a large proportion of cells have a 3-D on-direction. This finding contrasts with recordings from the motor SC (Hepp et al., 1993), which provides a major afferent input to the cNRTP (Harting, 1978). By applying the movement field description of Eq. 6 to our sample of 57 SC neurons, only two cells had a significant torsional component (data not shown). Note that Eq. 6 resulted in a rather poor model of SC activity. This is mainly because the SC neurons are more sharply tuned to saccade direction than the cosine characteristic of this simple model.

None of the cNRTP cells tested had a significant eye position sensitivity (Eq. 8), which also contrasts with recent findings from the motor SC. There, the peak activity of ∼50% of the neurons was modulated by eye position (Van Opstal et al., 1995).

Second, both positive and negative torsional components were obtained from recordings on both sides in the cNRTP. This result differs from studies of the vertical/torsional saccadic burst generator in the rostral interstitial nucleus of the medial longitudinal fasciculus (riMLF), a second major output station of the motor SC, where torsional on-directions are always positive on the right side and negative on the left side (Vilis et al., 1989; Crawford and Vilis, 1992; Suzuki et al., 1995).

Electrical stimulation

The initial rapid eye movements were saccadic gaze shifts that belonged to the same main sequence as normal spontaneous saccades. Amplitudes of the evoked movements, however, were typically <15 deg. Often, a weak eye position dependence of the amplitude and direction of stimulation-evoked gaze shifts was observed (Yamada et al., 1992). However, this finding could not be related to the activity of the cells (see above).

During longer stimulation trains, the evoked movements displayed two different patterns (Fig. 6). The first pattern, a rapid succession of small saccades in the same direction as the principal gaze shift, is also observed during prolonged SC stimulation, albeit without a displacement in the torsional direction. Smooth constant-velocity movements, however, have never been observed during stimulation of monkey SC. While stimulating, evoked torsion was not reset to Listing’s plane, but accumulated until the stimulus train was stopped. Again, the eye stayed at the new torsional level until a spontaneous saccade would reset it.

The bilateral representation of evoked torsional eye displacements (Figs. 5, 6), observed in all three monkeys, differs markedly from stimulating the motor SC, where no significant torsional components are obtained (Van Opstal et al., 1991) [see also Hepp et al. (1993), their Fig. 5]. We cannot exclude the possibility that the short latencies observed could be due to the stimulation of fibers projecting into the paramedian pontine reticular formation (PPRF) and riMLF. As in the cNRTP, the riMLF-induced ocular torsion accumulates during stimulation and is held at its new level until it is reset by the next spontaneous saccade [Henn et al. (1992), their Fig. 2]. On the other hand, electrical stimulation in the riMLF yields exclusively ipsitorsional eye displacements. The mixture of evoked saccadic and smooth movements at nearby stimulation sites (Fig. 6) suggests that local cell populations may be organized in functional “patches.” The precise organization of these patches, however, remains to be determined.

Behavior

In normal monkeys, Listing’s law is accurately obeyed, with a typical thickness of Listing’s plane of only 0.6 deg (i.e., 0.005 rad/2). Nevertheless, the saccadic system induces occasional torsional errors. In all monkeys tested so far (N = 10), however, torsional errors were consistently reset by the next saccade, rather than by a passive torsional drift into Listing’s plane (Van Opstal et al., 1996a).

Local inactivation

The unilateral muscimol injections in the cNRTP show that the error-correcting mechanism may be selectively disrupted. Remarkably, the deficit in the resetting process appeared to be saccade-direction-specific. Neither the sign of the torsional reset deficit nor the direction of the deficient eye movements could be predicted by the laterality of the injection (see Results). This observation is in line with the electrical stimulation data and single-unit recordings, indicating that both ipsi- and contratorsional eye displacements are represented in this region.

Relation to other studies

We do not believe that our results are related to a role of the cNRTP in the control of vergence eye movements (Gamlin and Mitchell, 1993), because (1) the monkeys made spontaneous saccades in the light during which no nearby visual stimuli were provided, and (2) if the torsional components after electrical stimulation were vergence-related, a linear elevation dependence of eye torsion would be expected (Mok et al., 1992; Van Rijn and Van den Berg, 1992; Minken and Van Gisbergen, 1994). Such systematic relations were not obtained (e.g., Figs. 5, 6).

An interesting question is whether the torsional reset displacements require the involvement of the cerebellar vermis (Harting, 1977;Brodal, 1980; Gerrits and Voogd, 1986), or whether a direct projection of the cNRTP to the rostral part of the PPRF may be responsible for this signal. The rPPRF contains saccadic burst neurons with direction-specific movement fields (Hepp and Henn, 1983), quite similar to the cNRTP neurons. At present, it is unknown whether the rPPRF movement fields also have 3-D on-directions. It also remains to be tested whether the torsional deficits after muscimol injections in the cNRTP are caused by disrupting a putative cNRTP-brainstem pathway, or whether it is due to the absence of a contribution from the cerebellum.

3-D neural code in cNRTP

Our data further suggest that the cNRTP is not involved in the generation of an eye angular velocity signal because the required dependence on eye position (Eq. 4) was lacking for all three types of neurophysiological experiments: Movement fields were not consistently modulated by initial eye position, and the violations of Listing’s law, induced by either electrical stimulation or reversible inactivation, were independent of eye position. Therefore, we conjecture that cNRTP cells encode a 3-D eye displacementsignal, d⃗ (see Materials and Methods, Eq. 3). Such an encoding would be in line with the hypothesis that the cNRTP plays a role in torsional error correction, which requires that a given torsional eye displacement can be generated irrespective of both the initial eye position and the direction of the upcoming saccade displacement vector.

It should be noted that at present it is not clear whether the oculomotor plant needs a signal proportional to eye angular velocity in order to comply with Listing’s law. Although saccadic eye movements are well described by a fixed-axis rotation (Tweed and Vilis, 1988), the neural controller may carry a complex code that needs to compensate for eye position-dependent orbital effects (Hepp, 1990, 1995). In addition, recordings from both the riMLF and the oculomotor nucleus so far indicate that saccade-related burst activity is better correlated with the rate-of-change of 3-D eye position, $\dot{r},$than with eye angular velocity, ω⃗ (our unpublished observations).

Conceptual scheme of 3-D saccade generation

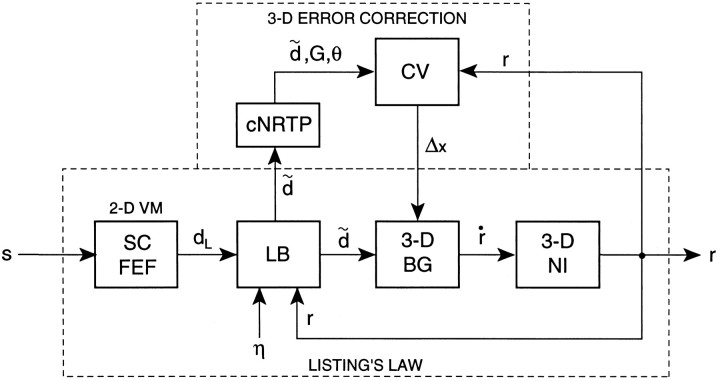
Figure 9 shows a conceptual model of 3-D saccade generation that could account for the observed properties of the cNRTP. In this scheme, the visuomotor system, incorporating both the motor SC and the cortical frontal eye fields (FEF), encodes desired saccades as 2-D eye displacements in Listing’s plane (Van Opstal et al., 1991;Hepp et al., 1993). The main focus of the model is on the control of ocular torsion. The two mechanisms underlying Listing’s law are embodied by independent, parallel pathways. The feedforward path (SC/FEF–brainstem–plant) is proposed to impose Listing’s law by transmitting a kinematically correct signal to the oculomotor plant through the operation of Listing’s Box (LB). Note that LB is situated downstream from the SC/FEF output. This process is assumed to be endowed with (torsional) noise (η) that is interpreted by the saccadic system as an error with respect to Listing’s plane. A parallel pathway (involving SC/FEF–cNRTP–Vermis) ensures that this torsional error is reset at the next saccade, provided a threshold θ (∼0.6 deg) is exceeded. Note, that the Vermis (CV) receives the torsional position signal from a 3-D position integrator (Henn et al., 1992). The cNRTP is proposed to set the gain (G) and the threshold (θ) of the torsional correction pathway. In this way, local inactivation within the cNRTP yields a decrease of the torsional reset gain, as well as an increase of torsional position errors (Fig. 8). Simulations indicate that the data of this study can be reproduced by this simple model (Van Opstal et al., 1996a).

Fig. 9.

Conceptual model of 3-D saccade generation. Listing’s law results from the operation of two separate pathways: the direct visuomotor pathway implements Listing’s law on the basis of crude commands. Retinal error, s, is mapped onto a desired eye displacement in Listing’s plane, d_L = (d_y, d_z), by the initial processing stages of the visuomotor system [VM, comprising superior colliculus (SC) as well as frontal eye fields (FEF)]. Listing’s Box (LB) transforms the 2-D visuomotor signal into a 3-D ocular rotation signal by combining the nonideal displacement command with initial eye position. The latter is generated by the 3-D neural integrator (NI). There are several ways of combining these signals (see text), but in this scheme LB generates a 3-D desired eye displacement signal in Listing’s plane, d = (0, d_y, d_z). However, noise, η, enters the system at this stage: d̃ = d + η. As a result, the 3-D burst generator (BG) issues an eye velocity command (r˙) to the neural integrator and the oculomotor neurons that may be endowed with small saccadic deviations from Listing’s plane. The cNRTP–cerebellar pathway is involved in torsional error correction. To that end, the cerebellar vermis (CV) receives the crude 3-D displacement command from LB, d̃, as well as the current 3-D eye position signal. The torsional component of eye position, r_x, is reset whenever the torsional position exceeds a threshold, θ, by updating the input for the 3-D BG at the upcoming saccade: Δx = −G · (r_x − d̃_x). Here, G is a gain that depends on the integrity of the cNRTP (see Discussion).