A Framework for Biomechanics Simulations Using Four-Chamber Cardiac Models

Abstract

Computational cardiac models have been extensively used to study different cardiac biomechanics; specifically, finite-element analysis has been one of the tools used to study the internal stresses and strains in the cardiac wall during the cardiac cycle. Cubic-Hermite finite element meshes have been used for simulating cardiac biomechanics due to their convergence characteristics and their ability to capture smooth geometries compactly–fewer elements are needed to build the cardiac geometry–compared to linear tetrahedral meshes. Such meshes have previously been used only with simple ventricular geometries with non-physiological boundary conditions due to challenges associated with creating cubic-Hermite meshes of the complex heart geometry. However, it is critical to accurately capture the different geometric characteristics of the heart and apply physiologically equivalent boundary conditions to replicate the in vivo heart motion. In this work, we created a four-chamber cardiac model utilizing cubic-Hermite elements and simulated a full cardiac cycle by coupling the 3D finite element model with a lumped circulation model. The myocardial fiber-orientations were interpolated within the mesh using the Log-Euclidean method to overcome the singularity associated with interpolation of orthogonal matrices. Physiologically equivalent rigid body constraints were applied to the nodes along the valve plane and the accuracy of the resulting simulations were validated using open source clinical data. We then simulated a complete cardiac cycle of a healthy heart and a heart with acute myocardial infarction. We compared the pumping functionality of the heart for both cases by calculating the ventricular work. We observed a 20% reduction in acute work done by the heart immediately after myocardial infarction. The myocardial wall displacements obtained from the four-chamber model are comparable to actual patient data, without requiring complicated non-physiological boundary conditions usually required in truncated ventricular heart models.

1. Introduction

Computational models of cardiac biomechanics can improve the fundamental understanding of the cardiovascular system by providing access to different quantities of interest that cannot be directly measured or require invasive procedures. Computational models have been used to study normal cardiac physiology (Kerckhoffs et al., 2007) and pathological conditions such as heart failure (Kerckhoffs et al., 2010; Niederer et al., 2011), myocardial infarction (Wang et al., 2011), etc. Most existing computational biomechanics cardiac models focus only on specific regions of the heart such as the left ventricle or both ventricles without explicitly modeling the atria. The complex and irregular geometry of the left and right atria of the heart have restricted most modeling and simulation to ventricular models. Excluding parts of the heart geometry necessitates the use of non-physiological boundary conditions that require extensive and tedious tuning to match the simulated cardiac motion with patient data. Advances in non-invasive imaging technology have made it feasible to generate patient-specific ventricular models (Aguado-Sierra et al., 2011; Krishnamurthy et al., 2013a), but it remains difficult to create high-quality meshes that include anatomic features such as valve annuli or atria automatically. A four-chamber cardiac model will enable the use of a wide variety of physiologically equivalent boundary conditions for each specific patient that can optimally match the cardiac motion with patient data.

Cubic-Hermite finite element interpolation schemes have been popular in cardiac modeling because of their convergence properties in finite element simulations of ventricular biomechanics (Costa et al., 1996). However, construction of cubic-Hermite geometric meshes have been limited to ventricular geometries below the valve plane due to difficulties in handling complex topologies of the atria and great veins (Figure 1). Recently, Land & Niederer (2018) extended their biventricular geometry which was built initially using cubic-Hermite elements to a four-chamber model using the tetrahedral finite elements to overcome the more complex topology associated with atria and studied the effects of atrial contraction on whole organ function. By applying different types of boundary conditions they showed that ventricular pressure-volume curves do not change significantly. Krishnamurthy et al. (2016) made use of cubic-Hermite meshes with extraordinary nodes to model the complex geometry of the heart with valve annuli and perform biomechanics simulations. Here we extend the same extraordinary node concept to construct a four-chamber cubic-Hermite finite element model and perform full-beat simulations.

Figure 1:

Topologically complex four-chamber model and a four-chamber model with valve annuli at the end-diastolic and end-systolic states of the cardiac cycle. The left ventricle is shown on the right side due to better informative cut-section view

Modeling the local fiber architecture of the heart muscles is a challenge, since it can be computationally expensive or inaccurate depending on the interpolation method used. In addition, the fiber architecture of the atria is not that extensively studied as the ventricles (Gonzales et al., 2013). Detailed histological studies and diffusion tensor imaging of the ventricles show that the heart muscle fibers rotate 120° from the epicardial to the endocardial surface (Wong & Kuhl, 2014) and this rotation can be reasonably considered similar for a large group of individuals (Lombaert et al., 2011). On the other hand, there seems to be not much variation in the fiber direction through the atrial wall due to its thin structure. Among all the fiber mapping methods, using a coordinate-frame interpolation scheme with the log-Euclidean transformation guarantees smooth interpolation accounting for the the shape and size of the cardiac geometry (Krishnamurthy et al., 2013a). In this work, we make use of the cubic-Hermite mesh topology to orient the fibers in the atria and use the log-Euclidean transformation to interpolate the fibers in the ventricles.

Simulating a complete cardiac cycle requires the correct chamber pressures to be applied to the four chambers. To perform this, the 3D finite element model needs to be coupled with a circulatory model that includes both pulmonary and systemic circulations (Kerckhoffs et al., 2006). Traditionally, the circulatory system is modeled using a set of lumped-parameter Windkessel models. We make use of the CircAdapt circulation model (Arts et al., 2005) to model the circulation and couple it with the ventricles of our finite element model.

Myocardial infarction is a leading cause of heart failure that occurs due to blood blockage to some regions of the heart, causing damage to the heart muscles. Cardiac motion can be used as a diagnostic tool to identify the effects of myocardial infarction. Cardiac simulation can help understand the acute effect of myocardial infarction on the cardiac motion. However, correctly replicating the motion of the heart after myocardial infarction requires corresponding changes to the active muscle properties in the infarcted region and modeling the effect of atrial structures of the heart on the deformations. In this work, we show that using a four-chamber model can help in assessing the acute impact of the myocardial infarction on the cardiac motion.

2. Methods

2.1. Geometric Modeling of the Four-Chamber Heart

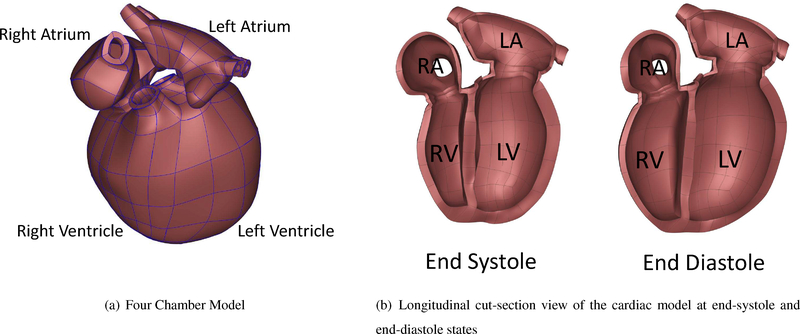
We built the 3D atlas mesh for the current work based on a previously constructed 3D biventricular mesh model (Zhang et al., 2012) and a biatrial model (Gonzales et al., 2013), both of which are publicly available. The atria were attached to biventricular model manually by connecting the nodes along the valve annuli. This atlas mesh was then modified using the data from literature for healthy humans. The atlas mesh was imported as a 3D obj format in Blender. Using the imported mesh in Blender the ventricular and atrial walls were adjusted by moving cubic-Hermite mesh nodes. However, we had to manually subdivide some elements, since creating a perfectly matched cubic-Hermite mesh including all four chambers leads to skewed elements around the valve annuli. Skewed elements might cause divergence during the finite element analysis, therefore, we manually inserted newer elements without deviating too much from the actual geometry. The data from literature including the average unloaded volume of the human left and right ventricles Hudsmith et al. (2005) were used to adjust the cardiac size after the geometry building process. The unloaded volumes are 47ml and 49ml for the RV and LV, respectively. The number of nodes, elements, and the degrees of freedom are tabulated in Table 1.

Table 1:

Comparison between the present work and Augustin et al. (2016) of a four-chamber cardiac finite element model.

	element type	# nodes	# elements	# DOF
Present work	cubic-Hermite	968	480	30720
Augustin et al. (2016)	tetrahedral	-	184.6 × 106	95.9 × 106

The model includes both the left and the right ventricles, orifices and valve annuli, and both the left and the right atria in a regular human heart. The model dimensions including the volume of both ventricles, the volume of both atria, and wall (myocardium) thickness were taken from available literature. As stated earlier, The finite element mesh of the cardiac model was generated with an open-source 3D computer graphics software, ”Blender”, similar to the methods described by Krishnamurthy et al. (2015). Utilizing these user-defined tools makes geometry editing more efficient as complex repeated functions is automated and performed simultaneously. Compared to past methods of defining geometry from patient data, which relied heavily on manually and meticulously placing individual nodes on cross-sectional cardiac images, this new method and tool-set has drastically cut down on model build time.

After generating the geometric mesh of the heart, we have to determine an unloaded reference state (the state at which the ventricle cavity pressure in a passive state is zero) to accurately compute the stresses. Dimensional data obtained from clinical images in vivo are not in the unloaded state due to continuous heart motion (Alastrue et al., 2008). Many researchers have tried to consider the end-systolic (Walker et al., 2005) or mid-diastolic (Sermesant & Razavi, 2010) geometry as the unloaded state, but it was shown later that the unloaded state deviates from both these states (Klotz et al., 2006). The method developed by Rajagopal et al. (2006) can be used to estimate the reference state for a wide variety of problems by using inverse methods. We had previously applied this method to compute the unloaded state for biventricular models (Krishnamurthy et al., 2013a) from the measured end-diastolic geometry, pressure, and passive material properties through an iterative method. However, in our case, we do not have a patient-specific geometry at the end diastolic state to apply this method. Hence, we make use of the empirical formula provided by Klotz et al. (2006), which correlates the unloaded left-ventricular volume to the end-diastolic volume and pressure, to rescale the ventricular geometry to the correct volume. We also keep the ventricular wall volume constant to account for the incompressibility in the simulations.

2.2. Modeling Fiber Orientation

Modeling the fiber architecture of both the ventricles and the atria is important for accurately capturing the cardiac deformations. Krishnamurthy et al. (2013a) used the diffusion tensor D, which is a 3 × 3 symmetric, positive-definite, covariance matrix representing the local voxel-averaged distribution of the diffusion of water molecules to define the local fiber coordinate system. By applying a coordinate-frame interpolation, they were able to guarantee a smooth interpolation of the fiber direction especially around extraordinary vertices (Krishnamurthy et al., 2016). However, it has been shown that the fiber orientation in the ventricles vary from −60° to +60° with respect to the circumferential direction. In addition, a recent statistical analysis (Lombaert et al., 2012) of fiber architecture variation in a population of human hearts has revealed that fiber orientations are well preserved between individuals. Unlike ventricles, the thin structure of the atrial wall makes it difficult to measure its fiber angles. Therefore, a fixed fiber angle for the whole atria was used in previous works, which is based qualitatively on published diagrams of atrial fiber tracts (Krueger et al., 2011; Gonzales et al., 2013). The significant changes in the ventricles’ fiber angles in the transmural direction necessitate an interpolation method to model the fiber orientations accurately and smoothly.

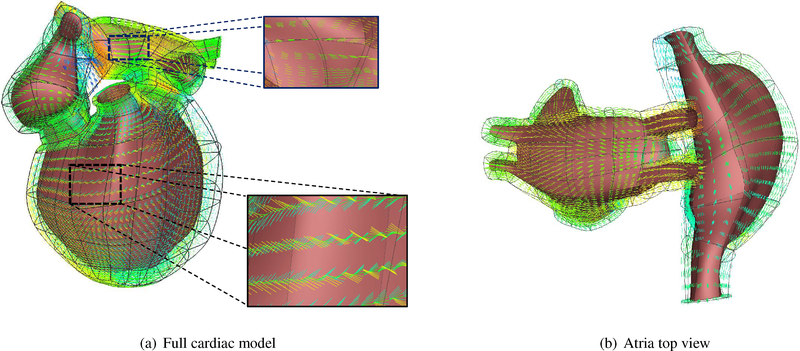
In this work, we make use of a coordinate-frame interpolation scheme that uses the log-Euclidean transformation (see Appendix C for details). This method provides a simple way to specify the cardiac fiber orientations in complex cardiac models. We calculate the orthogonal matrix F_endo by calculating the circumferential, radial, and transverse direction and rotating it by +60° with respect to the circumferential direction and assigned to the endocardial nodes. Similarly the F_epi is calculated and assigned to the epicardial nodes. The circumferential, radial, and transverse direction are explicitly calculated from the mesh, since the cubic Hermite elements are oriented along these directions in our model. The log-Euclidean interpolation is then used to calculate the fiber orientations at any position inside the cardiac wall. As can be seen in Figure 2(a), the fiber orientations gradually rotates from +60° at the endocardium with respect to the circumferential direction to −60° at the epicardium. On the other hand, we make use of the cubic-Hermite mesh topology to define the fibers in the atria (Figure 2(b)) which are transmurally constant.

Figure 2:

Fiber orientation from +60° (at endocardium) with respect to the circumferential direction to −60° (at epicardium) at ventricular region; the Atrial fiber angle is kept at zero everywhere, following the cubic-Hermite mesh topology.

2.3. Simulation of Full Cardiac Cycle

A complete cardiac cycle was simulated by coupling the finite element mesh of a two-chamber human cardiac model with a lumped-parameter closed-loop circulation model using the methods described in Kerckhoffs et al. (2007). The pulmonary and systemic circulations are each modeled as two lumped Windkessel compartments in series. The model couples both the 3D ventricular finite element model and the lumped-parameter model with the assumption of constant blood volume inside the cardiovascular system. Convergence is achieved if the difference between the calculated ventricular volumes obtained from both models at each time step lies within a tolerance range (10⁻⁴).

We make use of the model developed by Holzapfel & Ogden (2009) to model the passive material properties of the cardiac tissue. The strain energy in this model is given by

$$\psi =\frac{a}{2b}{e}^{b\left(I_1-3\right)}+\frac{a_f}{2b_f}\left(e^{b_f{\left(l_{4f}-1\right)}^2}-1\right).$$ (1)

In Equation 1, I₁ corresponds to the first invariant of the right Cauchy-Green strain tensor, I_4f corresponds to the components of the right Cauchy-Green strain tensor in the fiber direction. The parameter values used for the simulations in this paper are listed in Table 2.

Table 2:

Passive parameters of the Ogden-Holzapfel models

	a (kPa)	b	af (kPa)	bf
present work	0.684 (LV,RV) 1.368 (LA,RA)	9.726	0.51 (LV,RV) 1.02 (LA,RA)	15.779
(Krishnamurthy et al., 2013b)	0.684	9.726	0.51	15.779
(Holzapfel & Ogden, 2009)	2.28	9.726	1.685	15.779

Javani et al. (2016) studied the passive mechanical properties of a healthy ovine heart using a planar biaxial stretching system. They showed that the stress-strain response of all four different chambers’ specimens is nonlinear both in fiber and cross-fiber directions. Considering the Fung strain energy function to fit the material coefficients, they obtained stiffer behavior for atria compared to the ventricles (up to 1.5x). In the present work, we assumed that both the left and the right atria behave stiffer than ventricles (two times stiffer) by increasing the coefficients of the corresponding strain energy function (a_f & b_f ) in Equation 1.

The active contraction model developed by Lumens et al. (2009) is used to model the muscle contraction. This active contraction is defined as a function of sarcomere length (L_s) and mechanical activation (C) by

$${\sigma }_{f,act}={\sigma }_{act}.C.\left(L_{sc}-L_{sc0}\right).\frac{L_s-L_{sc}}{L_{se,iso}}.$$ (2)

The details of the active contraction stress can be found in Lumens et al. (2009) and it is defined as a 1-D model. Assuming no sheer stresses during contraction, this mid-wall tension is converted to a 3 dimensional transversely isotropic active stress with the transverse component being 30% of the fiber direction active stress (Guccione et al., 1991) as follows

$${\mathbf{T}}_{active}=\left[\begin{array}{ccc}{\sigma }_{f,act}& 0& 0\\ 0& 0.3\times {\sigma }_{f,act}& 0\\ 0& 0& 0.3\times {\sigma }_{f,act}\end{array}\right].$$ (3)

The T_active component in Equation 3 is added to the passive stress matrix calculated from the strain energy. The combined stress equation is then used to solve for the deformed geometry that will be in equilibrium with the externally applied pressure boundary conditions on the cardiac walls.

In this work, we consider the time dependent variation of the atrial pressures, deformation, and contraction. The electrical signal generated in the sinoatrial node travels through the atria causing the atrial muscles contract first while the ventricles contract 120 ms later in a normal human heart. In the present work, we applied the timing difference in atrial and ventricular contraction by modifying the corresponding active tension’s starting time (Equation 2). This modification in active tension for ventricular and atrial chambers let the atria contract 120 ms in advance of ventricular contraction. All regions of the ventricles were contracted simultaneously.

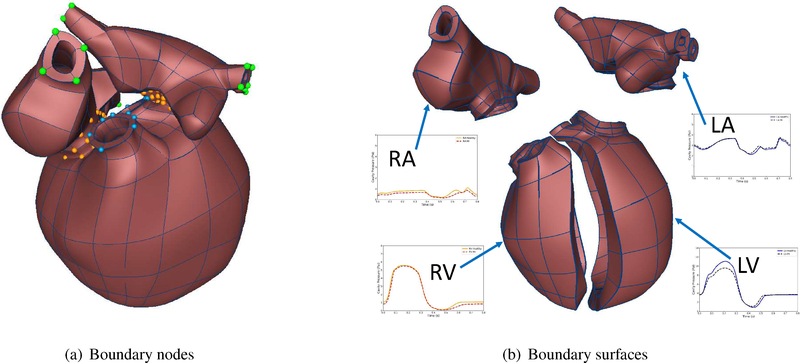
The circulation model is coupled to the two-chambers of the four-chamber model, since this coupling has to conserve the volume of the ventricles due to the presence of valves. We ran the simulation for seven full beat cycles, which was enough to achieve steady state for the cardiac simulations. The circulation model outputs the atrial pressure as well as the ventricular pressure values, which are used as pressure boundary conditions to achieve the deformation of the four-chamber cardiac model for the full beat cycle. Owing to the complex geometry of a four-chamber cardiac model, the necessary and proper boundary conditions need to be carefully applied to replicate the deformation of the heart. In our model, both Mitral and Tricuspid valves (displayed in orange color in Figure 3(a)) were fixed along the x-axis (vertical direction) while they can move freely in other directions (y-axis and z-axis). Moreover, the first and second-cross derivatives with respect to y and z directions were set to zero to prevent any non-planar deformation near the valves. The Pulmonary artery and Aorta (displayed in blue color in Figure 3(a)) are only fixed in y and z directions while they can move freely along the x-axis (vertical direction). The first and second derivatives with respect to y and z directions are set to zero to avoid any non-planar deformations. The venae cavae and pulmonary veins are fixed in three directions without applying any first or second order derivatives (green colored nodes). The Neumann pressure boundary conditions were applied on the inner surfaces of all the four chambers as shown in Figure 3(b). These boundary conditions prevent any rigid body motion of the heart while not constraining any other specific region, making them equivalent to the in vivo rigid body constraints.

Figure 3:

Boundary conditions.

2.4. Simulation with Myocardial Infarction

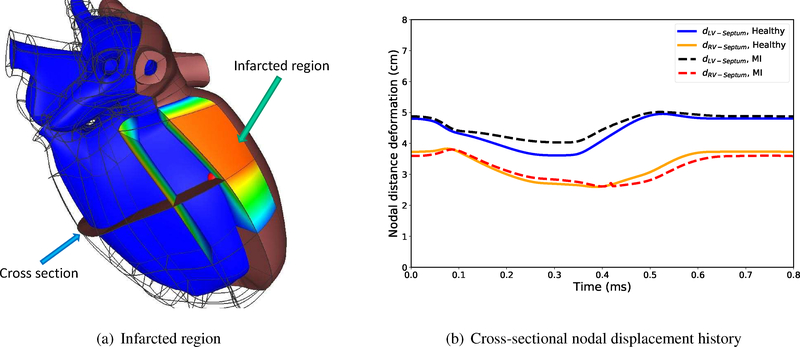
We studied a heart with an infarcted region (Figure 5(a)) to investigate the acute effects of MI on the ventricular efficiency and the corresponding acute P-V loop. The volumetric ratio of the infarcted region compared to the left ventricular wall volume is about 15%. MI leads to the stiffening (chronic effects) of the myocardium in the infarcted region along with reduction in its contractility (acute effects). We modeled the acute tissue damage by keeping the muscle stiffness same as the healthy heart, while reducing the contractility σ_act in Equation 2 down to ten times less than a healthy heart (Genet et al., 2015).

Figure 5:

Heart with myocardial infarction.

3. Results

3.1. Validation of Cardiac Motion

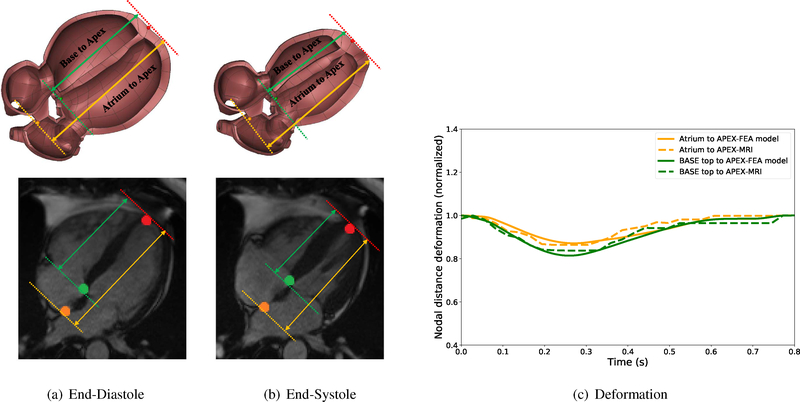
The validity of the proposed rigid body constraints to replicate the correct normal cardiac motion can be examined by comparing the normalized apex-base and apex-atrium distances (with respect to their corresponding maximum values) obtained from our simulation with open-source MRI data provided by Kaggle Second Annual Data Science Bowl (2015). The comparison between the model and the clinical data over the complete cardiac cycle (Figure 4(c)) shows that simulation results closely match the clinical data (Error RMS _apex−base = 1.5%, RMS _{atrium−apex} = 1.7%).

Figure 4:

Cut-section view of the cardiac model and open-source clinical data (Kaggle Second Annual Data Science Bowl (2015)) at end-diastole and end-systole states. Comparison between the normalized apex-base and atrium-apex with clinical data in a cardiac cycle, RMS _apex−base = 1.5%, RMS _{atrium−apex} = 1.7%

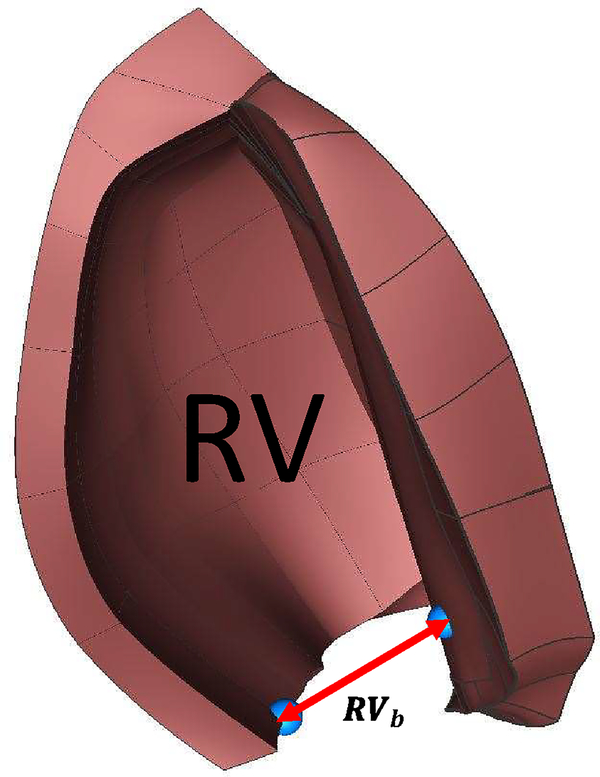
Moreover, Kou et al. (2014) performed a comprehensive echocardiographic examination of 734 healthy volunteers to provide normal reference ranges for cardiac chambers size during a full-beat cycle. The comparison between the ratio of the right ventricle basal linear dimension (RV_b) at the end-diastole and end-systole obtained from the present work (1.62) is within the range of values reported by Kou et al. (2014) (1.45±0.13). (Table E.4 and Figure E.9)

3.2. Comparison of PV-Loops and Cardiac Motion

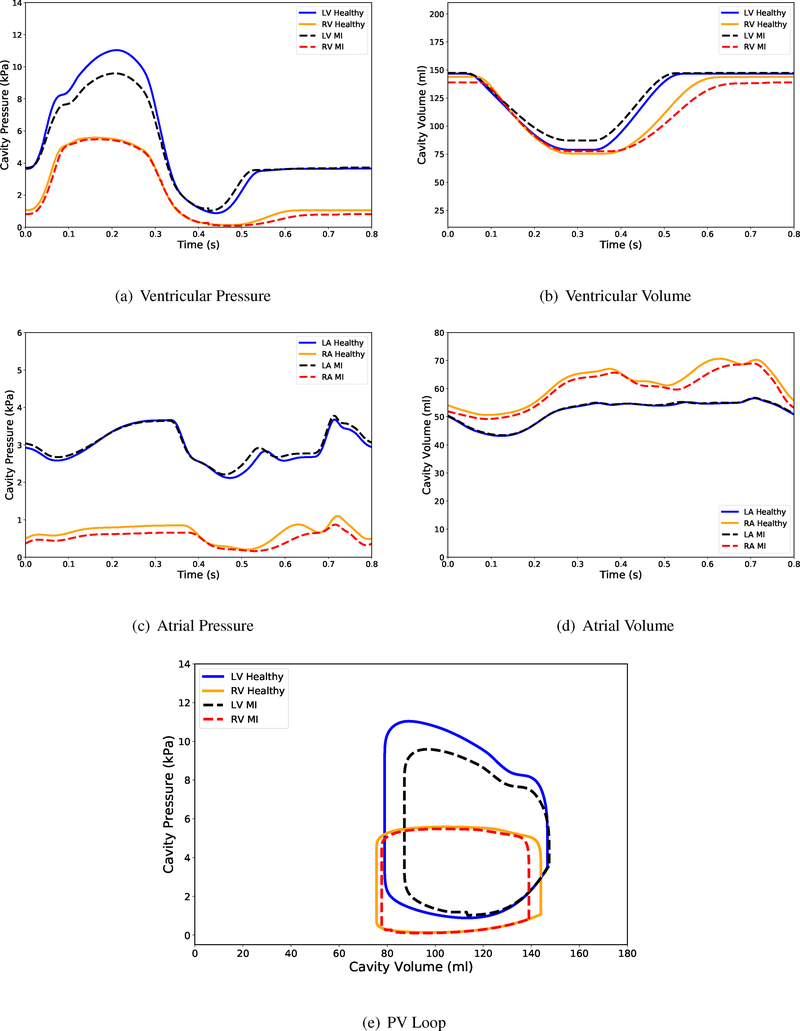
The comparison between the PV-loop of a healthy heart and the heart with MI shows that there is a significant reduction in the acute left ventricular peak pressure (≈13%, Figures 6(a) and 6(e)) while there is not that much change in the right ventricular peak pressure (< 2%). This is because the MI is confined to the left ventricular walls. Both the left and the right ventricular volumes are larger at end-systole for a heart with MI compared to the healthy heart, since an acute myocardial infarction reduces local contractility (in this case, the left ventricle) (Figure 6(b)). However even though the myocardial infarction is localized to the left ventricular wall, the right ventricular PV-loop would still be affected due to constant blood volume in the circulation system. In addition, as Figure 6(c) shows, the right atrial pressure history of the heart with MI is slightly lower than the one corresponding to the healthy heart.

Figure 6:

Pressure and volume time-course output from the full beat simulation of the four-chamber heart model. Figure 6(e) shows the simulated pressure-volume loops for the left and the right ventricles of a healthy heart and a heart with MI.

The decrease in pumping ability due to MI is calculated by the area enclosed inside the PV-loop (Figure 6(e)) for both ventricular chambers. As stated earlier, the acute MI causes the loss of contractility for the left ventricle (local effects). Since we modeled only the acute effects, we did not assume any material stiffness change for the infarcted region. The right ventricle fills up to less volume at end-diastole for MI compared to the healthy heart. This can be explained by the fact that the constant blood volume inside the circulatory system necessities this loss in filling for the right ventricle. Due to the less active cardiac cells in the heart with MI, its pumping ability is reduced by 20% compared to the healthy heart (16% reduction from left ventricle and 4% from the right ventricle, see Table 3).

Table 3:

Characteristics of the healthy heart and the heart with MI.

	LV Work	RV Work	Peak Pressure	Lowest Pressure
Healthy Heart	557 (kPa.ml)	345 (kPa.ml)	11.04 (kPa)	5.58 (kPa)
Heart with MI	414 (kPa.ml)	309 (kPa.ml)	9.59 (kPa)	5.47 (kPa)

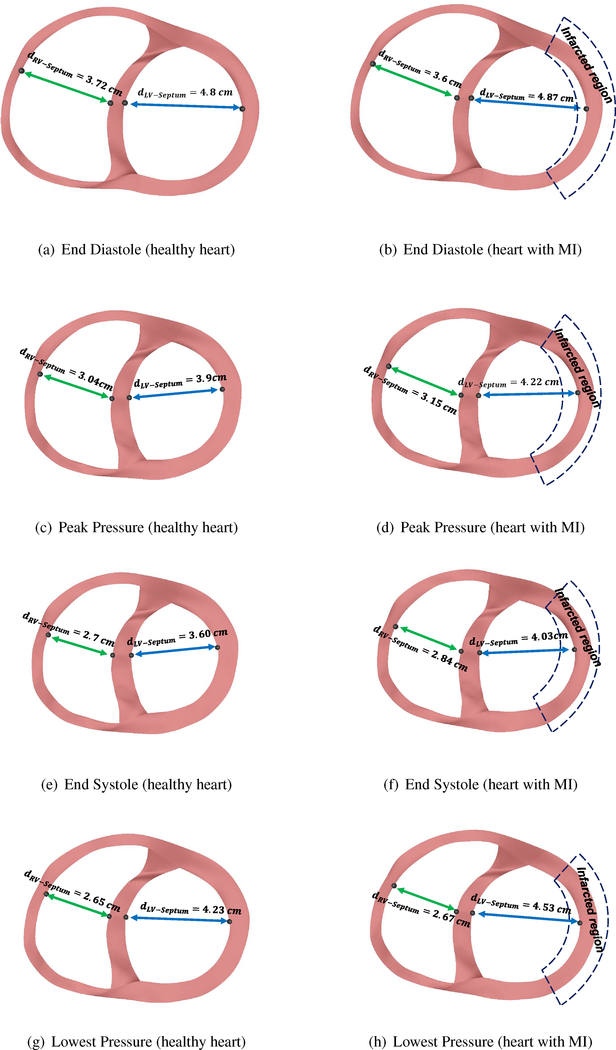
The changes in the left and the right ventricles’ deformation in the heart with MI and the healthy heart at different states of the cardiac cycle is shown in Figure 7. The left column shows the cross-sectional views of a healthy heart while the right column shows the heart with MI. The nodal distance between the septum and the left and the right ventricular free wall, denoted by d_LV−Septum and d_RV−Septum, can be used to determine the effects of MI on the local ventricular deformation. As can be seen, the LV in a heart with MI fills as much as a healthy heart (Figures 7(b)–7(a)) at end-diastole, while at peak pressure and the end-systolic state, it shows less contraction (Figures 7(d)–7(c)) due to the weaker contractility of the heart with MI. At lower pressure (Figures 7(h)–7(g)), this difference is negligible compared to the other cardiac state. On the other hand, the RV in a heart with MI expands less than the healthy heart at end-diastolic states. In addition, as a consequence, the RV also loses some of its contractility due to the Frank-Starling mechanism.

Figure 7:

Cross-section views of the infarcted region at different cardiac cycle for healthy heart and the heart with MI.

Figure 5(b) shows the history of d_LV−Septum and d_RV−Septum in the cardiac cycle. As can be seen the differences in d_LV−Septum between a heart with MI and a healthy heart is more significant when the heart is contracting while the right ventricle shows greater deviation from the healthy heart during isovolumic contraction after the end-diastolic state. This shows that losing the contractility is more critical for the LV at end-systolic state while the effects are more prominent on the RV after the end-diastolic state.

4. Discussion

The heart’s complex geometry requires the implementation of very fine meshes on regions of high curvature, which makes simulations numerically expensive with linear elements. For instance, Augustin et al. (2016) presented an accurate high-resolution model of the human heart electromechanics by using up to 184.6 million tetrahedral elements to solve the nonlinear governing equations. However, the use of cubic-Hermite elements in our study helps us to use fewer number of elements to capture the complex geometry. In addition, the mesh element sizes that we have employed for our four-chamber model are refined enough to obtain converged mesh displacements and chamber volumes (see Appendix F for mesh size comparison and convergence of cubic-Hermite elements for biomechanics). We had previously reported that cubic-Hermite meshes require fewer Newton-Raphson iterations to converge even in the presence of extraordinary nodes (Krishnamurthy et al., 2015). Recent comprehensive work done by Vincent et al. (2015) compares the convergence behavior of different interpolation methods for finite element simulations on a cardiac monodomain equations for electrophysiology. These convergence analysis results show that cubic-Hermite meshes can accurately capture the biomechanics of a cardiac geometry with fewer elements.

Fritz et al. (2014) built a four-chamber cardiac model from MRI data of a healthy middle age volunteer to study the interaction between the ventricles, the atria, and the pericardium in a full-beat cycle. By developing a contact handling algorithm, they were able to solve the contact between the epicardium and the pericardium. The apex, the openings of the pulmonary vein, and both the inferior and the superior venae cavae, were fixed in their model as well as the outer surface of the mesh of the surrounding tissue. They found out that, after including the pericardium, the contour of the outer surface of the heart of varied only minimally, although the ventricles as well as the atria were significantly deformed. In this study, we have not included the effect of pericardium directly. One possible way this can be included in our model is to apply a direct pressure to the outer faces of the elements that can simulate the effect of the pericardium. However, even without this effect included, we found that the apex-base displacement in our model matches commonly observed values reported in literature. In addition, we post processed our deformation results to fix the apex instead of the valve plane (please see included full beat video, Appendix D). The resulting deformation matches observed cardiac deformation in the chest cavity.

We have presented a four-chamber cardiac model utilizing cubic-Hermite elements and simulated a full cardiac cycle by coupling the 3D finite element model with a lumped-parameter circulation model. The G¹ continuity of the finite-element fields in the neighborhood of extraordinary nodes were maintained using an ensemble coordinate system with a linear global-to-local transformation. The myocardial fiber orientations were interpolated within the mesh using the Log-Euclidean transformation to overcome the singularity associated with interpolation of orthogonal matrices. Physiologically equivalent rigid body constraints were applied to the nodes along the valve plane. We simulated a complete cardiac cycle of a healthy heart using this four-chamber model. Accurately modeling the geometric structures of the heart allows the application of practical and physiologically equivalent rigid body constraints. These, in turn, allows the model to replicate the deformations of the different regions of the heart. The resulting deformations were validated using open-source cardiac motion data from literature. Our four-chamber model has the capability to match patient-specific cardiac deformations, thereby improving the state-of-the-art of patient specific cardiac modeling.

Appendix A. Additional Discussion

In this paper, we make use of a cubic-Hermite mesh with extraordinary nodes to construct a four-chamber cardiac model. We then demonstrate the versatility of the model to perform biomechanics simulations by simulating a full beat cycle of a ”healthy” and an ”infarcted” heart. The main contributions of the paper include:

• Constructing a four-chamber cardiac model using higher order cubic-Hermite meshes with extraordinary nodes.

• Accurately modeling the fiber architecture in a four-chamber cardiac model, including the atria.

• Performing full beat biomechanics simulations of four-chamber cardiac models using physiologically equivalent rigid body constraints.

• Investigating the effects of acute myocardial infarction on the local deformation in a four-chamber cardiac model and the ventricular pumping ability.

We compared the deformation of a four-chamber heart with acute myocardial infarction with an healthy heart. The tissue damage due to myocardial infarction is modeled using a reduced contractility in the infarcted region (no chronic effects of MI). We compared the acute pumping function of the heart for both cases by calculating the work done by the ventricles (area enclosed inside the left and the right ventricular Pressure-Volume (P-V) loop). We observed a 20% reduction in work done by the heart immediately after myocardial infarction. The comparison between the displacement of the infarcted region and the corresponding region in a healthy heart shows that the heart with MI loses its ability to contract depending on the location and strength of the infarcted region.

There are several improvements that can be made to our model to make it more accurate. We are planning to improve our model by incorporating the following model details.

• Improving the current muscle contraction by applying a biophysically accurate human contraction model (for example, Land et al. (2017)) and incorporating the spatial delay in contraction from apex to base of the ventricles.

• Improving the accuracy of the results by considering the pericardium pressure as an additional boundary condition (Pfaller et al., 2019).

Incorporating these elements will enable our four-chamber model to match patient-specific deformations.

Figure B.8:

Four-chamber cardiac model cubic-Hermite meshes build in Blender from the original mesh to the two-level subdivided mesh.

Appendix B. Blender 3D model

The necessary derivatives for presenting a smooth geometry were also obtained using a Blender plug-in. This plug-in has an array of functions, one of which is able to perform subdivision of the domain and calculate the nodal derivatives. Blender is an open-source software which users can add their own written plug-in as a Python script, which improves functionality for work with complex geometries.

Due to the complex curvature and geometry of the human heart, extraordinary nodes are introduced in the finite element mesh in order to maintain smoothness and to capture specific details. At ordinary vertices, arc-length and G¹ continuity is enforced as described by Gonzales et al. (2013). At extraordinary nodes, however, continuity is maintained via new coordinate frames called ensemble coordinates, coupled with a local-to-global map transforming global ensemble derivatives into local element derivatives using a method also described by Gonzales et al. (2013). Estimation of the local element derivatives are obtained from nodes after subdividing the mesh twice to enforce C⁰ continuity.

Figure B.8 shows the original model followed by two level subdivision to calculate the first, second, and cross derivatives at each vertex. As can be seen, after the second level of subdivision a smooth geometry can be obtained while guaranteeing the G¹ continuity on every node including ordinary and extraordinary nodes.

Appendix C. Fiber Interpolation

In this section, we briefly describe a coordinate-frame interpolation scheme that uses the log-Euclidean transformation ensuring the preservation of the shape and size of the geometry.

The fiber coordinate frame corresponds to the fiber and cross-fiber orientations at each node is represented using a 3×3 orthogonal matrix, F whose columns represent the vectors along the three orthogonal coordinate directions. The first step is converting matrix F to log-Euclidean space by taking the matrix logarithm. However, a real matrix has a real logarithm if and only if it is invertible and each Jordan block belonging to a negative eigenvalue occurs an even number of times, otherwise it has only non-real logarithms (Culver, 1966). The necessary conditions can be satisfied by constructing a synthetic symmetric matrix, T whose eigenvalues are synthetic but unique and positive, as shown below,

$$\mathbf{T}=\mathbf{F}\left[\begin{array}{ccc}{d}_{11}& 0& 0\\ 0& d_{22}& 0\\ 0& 0& d_{33}\end{array}\right]{\mathbf{F}}^T$$ (C.1)

In Equation C.1, the values of d₁₁, d₂₂, and d₃₃ are chosen to be unique, positive, and in sorted order (d₁₁ < d₂₂ < d₃₃, (5,10,20), for instance). The matrix T is then transformed to L by the matrix logarithm: L=log(T) while the symmetry and positive-definiteness of L is preserved. The calculated matrix logarithm is then used to interpolate the coordinate frame within an element. It is worth mentioning that the matrix logarithm of a positive definite matrix is symmetric with only six independent components. The same basis functions are also used to estimate the matrix L’s components interpolation, similar to scalar quantities in Euclidean space. We also take advantage of the local-to-global mapping to interpolate the six independent components of logarithm matrix in the presence of extraordinary nodes. At any arbitrary point within the element, the coordinate frame can then be obtained by calculating the matrix exponential of the interpolated L_e,

$${\mathbf{T}}_e=e^{\left({\mathbf{L}}_e\right)}$$ (C.2)

and then computing the eigenvectors, v_i (i=1,2,3) of the resulting matrix and sorting them according to the eigenvalues of T_e. Sorting is necessary to keep the order of vectors in the coordinate frame unchanged. Since the eigenvalues are only used for sorting the eigenvectors, there are no stability issues during interpolation as long as they are positive and unique.

Appendix D. Supplemental Videos

We have included a movie which shows the deformation of the four-chamber cardiac model in a full-beat cycle after transferring the fixed boundary conditions to the apex instead of the base. The deformations shown here closely matches the in vivo heart deformations. This shows that the boundary conditions that we applied are physiologically equivalent to the in vivo rigid body constraints.

We have also included another movie which shows the deformation of the four-chamber cardiac model in a full-beat cycle for both the healthy heart and the heart with myocardial infarction. As can be seen, the heart with myocardial infarction shows less contractility compared to the healthy heart.

Appendix E. Validation of Cardiac Motion

This section shows some additional validation of the cardiac motion. Figure E.9 shows the comparison in the RV dimension in the same orientation as Figure 4 from Kou et al. (2014).

Figure E.9:

Right ventricle’s basal linear dimension. The orientation of the model corresponds to Figure 3 in Kou et al. (2014).

Table E.4:

The comparison between the ratio of the right ventricle basal linear dimension (RV_b) at the end-diastole and end-systole obtained from the present work and Kou et al. (2014).

	Present Work	Kou et al. (2014)
$\frac{R{V}_b(end-diastole)}{R{V}_b(end-systole)}$	1.62	1.45 ± 0.13

Appendix F. Convergence Study

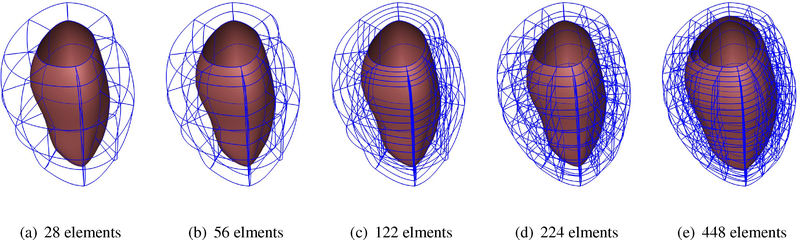
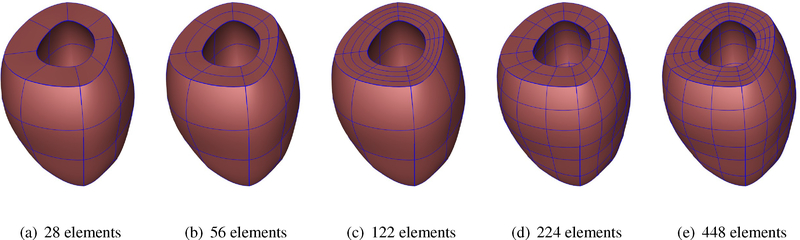
We performed a mesh refinement convergence study of the cubic-Hermite models with extraordiary nodes. For this purpose, we created five different geometries of a single left ventricular model and inflated them to the end-diastolic pressure and compared the ventricular volumes and the apex-base distances at different pressure steps. Figure F.11 shows the ventricular geometry with increasing refinement from left to right in either the radial, circumferential, or both directions.

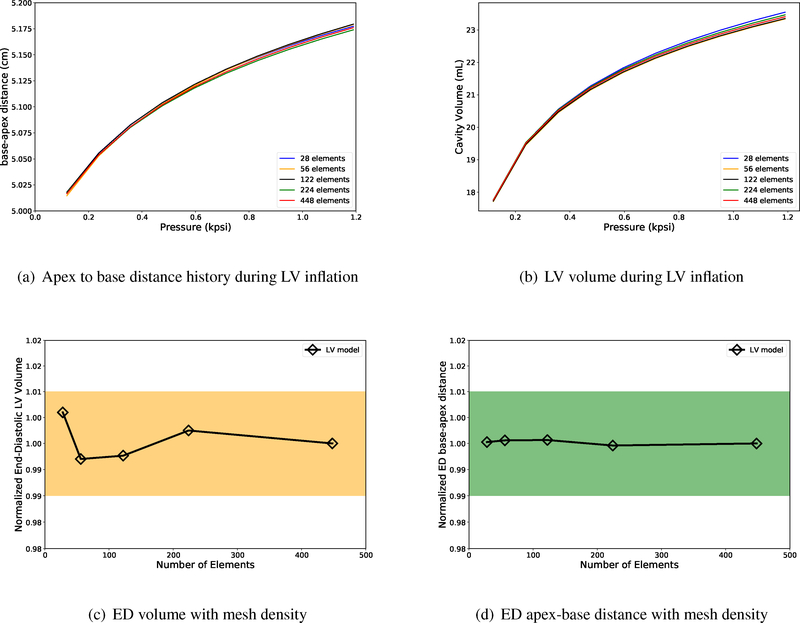
As can be seen in Figures 12(a)–12(b), there is not a significant change in the nodal deformations or the volume history with the increase in number of elements. We achieve an acceptable tolerance (for example, 0.016 mm for nodal displacement, comparable to 0.5 mm spatial resolution of the CT images with fewer mesh elements with cubic-Hermite elements. Moreover, Figure 12(c) shows that the LV end-diastolic volume obtained using different mesh densities lie within 1% (orange rectangle) of the value obtained using the finest mesh, while the end-diastolic apexbase distance shows even smaller deviation (< 0.5%). Table F.5 contains some properties that corresspond to the size of each mesh, including the minimum and the maximum element size (volume, in ml), plus their corresponding ratios with respect to the model’s total volume. As can be seen, Max_{elm vol}/tot_vol value for the current four-chamber model is approximately similar to the LV model with 122 elements. As we showed in Figure F.12, mesh-independent results can be achieved by the LV model with even fewer cubic-Hermite elements. Therefore, we conclude that the current four-chamber model mesh resolution is adequate to obtain displacement and volume results that are within a reasonable tolerance value (! 1%).

Figure F.10:

Wireframe renderings of the unloaded left ventricular models with increasing refinement.

Figure F.11:

Unloaded left ventricular models with increasing refinement.

Appendix G. Additional Related Work

In this section, we provide additional references for related work on cardiac modeling and simulations.

Most previous cardiac models using high-order meshes have been restricted to geometries described by a single set of parametric coordinates that are topologically equivalent to a cylinder (Vetter & McCulloch, 1998). However, such meshes require special boundary conditions at the cardiac apex to enable multiple overlapping nodes or sector elements (Bradley et al., 1997) to close the mesh. The restriction of using a single set of parametric coordinates enables enforcing continuity across element edges easier, but introduces element distortions. In the present work, we make use of cubic-Hermite functions using hexahedral elements to simulate the full beat cycle of a four-chamber healthy heart and a heart with myocardial infarction. Structured grids with hex or quad meshes (either regular or curvilinear) can be implemented using compact meshes and usually execute faster than algorithms that support unstructured grids (Bourdin et al., 2007). Our method requires fewer elements and results in a smaller stiffness matrix, leading to faster solution while preserving a reasonable level of accuracy.

Figure F.12:

Mesh independence study of a single LV model. Both the chamber volume and the apex to base distance are within 1% of the values computed using the finest mesh.

Table F.5:

Mesh size metrics of the different cardiac models.

	LV Model (28 elms)	LV Model (56 elms)	LV Model (122 elms)	LV Model (244 elms)	LV Model (488 elms)	Four-Chamber Model (480 elms)
Minelm vol (ml)	0.61	0.23	0.09	0.048	0.021	0.017
Maxelm vol (ml)	1.94	1.23	0.65	0.30	0.165	3.96
totvol (ml)	33.47	33.45	33.45	32.12	32.12	187.59
Minelm vol/totvol	0.02	7 × 10−3	3 × 10−3	9 × 10−3	6 × 10−4	9 × 10−5
Maxelm vol/totvol	0.06	0.037	0.019	0.01	0.005	0.021

The popularity of cubic-Hermite meshes in isogeometric finite element analysis and computer graphics have grown up significantly in recent years due to its compactness and convergence advantages. They have shown to have better convergence properties compared to linear hexahedral and tetrahedral elements in cardiac electrophysiology simulations (Vincent et al., 2015). Although cubic-Bezier curves are widely used to create smooth curves, cubic-Hermite representation makes it possible to store all degrees of freedoms (DOF) at the element corners without any additional information stored in the element edges or body nodes. The complex geometries associated with biomechanics modeling of the heart necessitate the construction of cubic-Hermite surfaces which share at least a common tangent plane (G¹ continuity) along their boundaries (Farin, 1982, 1986). A number of researchers have worked to propose the necessary and sufficient conditions for G¹ continuity of rational surfaces. Liu & Hoschek (1989) were among the first who studied and proposed the necessary and sufficient conditions of G¹ continuity condition for all four possible combinations of rectangular and triangular Bezier patches. Later DeRose (1990) improved their work and derived the necessary and sufficient conditions for G¹ continuity for cubic-Bezier patches which did not possess a large number of indeterminate parameters (Liu & Hoschek, 1989). Finally, Du & Schmitt (1990) extended the geometric continuities between adjacent patches and presented new alternative approaches for modeling free-form G¹ continuous surfaces including extraordinary nodes.

As a recently developed computational method, isogeometric analysis was first introduced and developed by Hughes et al. (2005) and uses the basic functions from NURBS to analyze a wide variety of mathematical problems including finite element analysis. Nielsen et al. (1991) developed a mathematical model of a canine cardiac architecture using the cubic-Hermite basis functions on a prolate spheroidal coordinate system. Since their model considered only the left and the right ventricles with myocardial fiber orientations, extraordinary nodes were not required. This work extends their cubic-Hermite finite element analysis to model the full geometry of a human heart by considering the atria in addition to the ventricles. The complexity of the geometry necessitates the use of extraordinary nodes (nodes which are shared between three or more than four elements in two dimensions), which must be treated separately to maintain continuity between the different patches of NURBS surfaces. Gonzales et al. (2013) developed a general framework to construct the bicubic and tricubic Hermite basis function to model the human atria with extraordinary nodes. This work is the extension of their model by simulating the inflation and full beat cycle of the human heart which was first introduced by Krishnamurthy et al. (2016) for isogeometric cardiac modeling. Moreover, they investigated the numerical error in their simulation in the presence of extraordinary nodes and found that a faster convergence can still be achieved.

Unlike Lagrange basis functions which only maintain the C⁰ continuity at adjacent elements, cubic-Hermite functions can also preserve the C¹ continuity for regular nodes (non-extraordinary nodes). Moreover, better convergence properties of cubic-Hermite elements compared to other types of elements such as linear hexahedral or tetrahedral elements, make it more appropriate and compatible for biomechanics simulations (Bradley et al., 1997; McLeod, 1977). Several researchers have studied the convergence of numerical electrophysiology solutions (Rogers & McCulloch, 1994; Bernus et al., 2002; Pathmanathan et al., 2012). Recent comprehensive work done by Vincent et al. (2015) compares the convergence behavior of different interpolation methods for finite element simulations on a cardiac monodomain equations for electrophysiology. They investigated linear Lagrange, cubic Hermite, and cubic Hermite-style serendipity meshes in their study and found that high-order methods with fewer degrees of freedom and longer element edge lengths converge better than conventional linear elements. They also introduced a dimensionless number to determine the solution convergence not only dependent on element size, but on the ratio of the discretization length to the characteristic length of the monodomain equation.

Subdivision is a powerful technique in computer graphics and surface modeling and can create reasonably smooth surfaces from relatively simple meshes. Two main subdivision categories can be classified as interpolating and approximating depending on if they are required to interpolate the position of the vertices in the original mesh or not. Catmull & Clark (1978) and Doo & Sabin (1978) were among the well-known researchers who first developed and derived the approximating subdivision methods by generalizing bi-cubic and bi-quadratic B-spline to generate surfaces with C² continuity except at extraordinary vertices where they are C¹ continuous. As stated earlier, a full model of the human heart including both atria and ventricles necessitates the use of extraordinary vertices. Therefore we use the subdivision scheme used by Gonzales et al. (2013), the Li-Kobbetl subdivision scheme (Li et al., 2005) to approximate the derivatives in the presence of extraordinary nodes. In order to have a natural adaptive mesh refinement, this method only adds ordinary vertices to the refined mesh while the number of extraordinary vertices remain unaltered.

Non-invasive clinical imaging techniques have become the standard means for diagnosing cardiac function, viability, and heart failure (Petitjean & Dacher, 2011; Ringenberg et al., 2014). These techniques can be classified into three common categories: cardiac ultrasound (echocardiography), computed tomography (CT), and magnetic resonance imaging (MRI). Echocardiography, being less expensive and radiation free, makes it an acceptable modality for patient-specific cardiac modeling over CT or MRI. In addition, the lower resolution of ultrasound images results in a geometric model with fewer degrees of freedom (DOFs) (Aguado-Sierra et al., 2011).

There have been many researches to model the distribution of fiber orientation within the cardiac wall (Zhukov & Barr, 2003; Rijcken et al., 1999; Gasser & Forsell, 2011; Robb & Robb, 1942; Freeman et al., 1985). Since the availability of the in vivo human hearts except for transplantation surgeries is limited, Lombaert et al. (2011) studied more than ten ex vivo human hearts from DT-MRI. Their studies showed that the fiber orientation can be considered reasonably the same for a large group of humans, however the apex shows a higher deviation. Postmortem radiography and histological techniques show that fibers rotate around 120° from the epicardial (outside) surface to the endocardial (inside) surface with the fiber angle increasing linearly from −60° to 60° with respect to the circumferential direction. Other values were also reported for the fiber rotation such as 105.7±14.9° by Smith et al. (2008) in which they use nondestructive optical determination to overcome the limitation of histological sectioning (which might damage the tissue) and diffusive tensor imaging (which is comparatively expensive). Numerous methods have been proposed (Toussaint et al., 2013; Wong & Kuhl, 2014; Gonzales et al., 2013) to overcome the complexity of creating the fiber orientation map for computational analyses, especially the interpolation of fiber angles in meshes with extraordinary vertices. Interpolation of tensor fields in normal Euclidean space may result in null or non-positive-definite interpolated tensors (Fillard et al., 2006). On the other hand, affine invariant Reimannian framework is an alternative method that can alleviate these problems but is not computationally efficient (Pennec et al., 2006). In the present work we make use of Log-Euclidean (LE) framework (Arsigny et al., 2005), which is simpler to implement and preserves the orthogonality of the interpolated coordinate frame (Arsigny et al., 2005; Krishnamurthy et al., 2016).

Identifying the myocardial material properties is still an active ongoing research topic (Remme et al., 2004; Sommer et al., 2015). Although the myocardial tissue appears to be viscoelastic (Taber, 1995), the short cardiac cycle time scale compared to the tissue relaxation time makes it less significant to be simulated as a viscoelastic material. Holzapfel & Ogden (2009) did a comprehensive study on morphology and structure of the myocardium and introduced a new constitutive model for passive myocardium. Unlike previous models which were based on linear isotropic elasticity, the model developed by Holzapfel & Ogden (2009) is a transversely-isotropic form of the conventional Fung-type constitutive models (Holmes et al., 2000). In this model, the anisotropy in the fiber and cross-fiber directions of the myocardium is modeled using a separate exponential term with different exponents.

Myocardial infarction (MI), also known as heart attack is a leading cause of heart failure which increases with age, lower physical activity, and socioeconomic status (Perk et al., 2012). MI occurs due to the blood blockage caused by buildup of plaque in coronary arteries leading in the lack of oxygen and nutrients supplies to left ventricle (Sáez & Kuhl, 2016). MI is critical and can damage the heart muscles if it is not treated immediately. Angioplasty and clot-busting medicine are among the most common treatments to minimize or prevent the damage caused by MI. The infarcted regions lose their contractility and become stiffer, therefore, unable to keep their contribution in conducting the electrical signal and the pumping ability. P-V loop analysis has been shown to be an appropriate method to quantitatively evaluate the underlying degradation in cardiac function after MI (Shioura et al., 2007).