A Driving-Force Predictor for Estimating Pathway Activation in Patient-Specific Models of Deep Brain Stimulation

Abstract

Objective:

Detailed biophysical modeling of deep brain stimulation (DBS) provides a theoretical approach to quantify the cellular response to the applied electric field. However, the most accurate models for performing such analyses, patient-specific field-cable (FC) pathway-activation models (PAMs), are so technically demanding to implement that their use in clinical research is greatly limited. Predictive algorithms can simplify PAM calculations, but they generally fail to reproduce the output of FC models when evaluated over a wide range of clinically relevant stimulation parameters. Therefore, we set out to develop a novel driving-force (DF) predictive algorithm (DF-Howell), customized to the study of DBS, which can better match FC results.

Methods:

We developed the DF-Howell algorithm and compared its predictions to FC PAM results, as well as to the DF-Peterson algorithm, which is currently the most accurate and generalizable DF-based method. Comparison of the various methods was quantified within the context of subthalamic DBS using activation thresholds of axons representing the internal capsule, hyperdirect pathway, and cerebellothalamic tract for various combinations of fiber diameters, stimulus pulse widths, and electrode contact configurations.

Results:

The DF-Howell predictor estimated activation of the three axonal pathways with less than a 6.2 % mean error with respect to the FC PAM for all 21 cases tested. In 15 of the 21 cases, DF-Howell outperformed DF-Peterson in estimating pathway activation, reducing mean-errors up to 22.5 %.

Conclusions:

DF-Howell represents an accurate predictor for estimating axonal pathway activation in patient-specific DBS models, but errors still exist relative to FC PAM calculations. Nonetheless, the tractability of DF algorithms helps reduce the technical barriers for performing accurate biophysical modeling in clinical DBS research studies.

INTRODUCTION

Computational models represent useful tools to understand and improve deep brain stimulation (DBS), as they allow for noninvasive quantitative characterization of the theoretical response of neurons to a wide range of stimulation settings ¹. When coupled with medical imaging data, patient-specific DBS models provide opportunities for correlating neural activation predictions with clinical outcomes ^2,3. However, the utility and validity of such analyses are dependent upon the selection of the appropriate modeling methodology to simulate the underlying biology with sufficient technical sophistication. For example, models used to dissect the neurophysiological mechanisms of DBS currently differ from models used for clinical DBS analyses, where speed and simplicity are valued over scientific accuracy ⁴. However, as clinical DBS software tools evolve, it may become possible for their technical capabilities to better coincide with scientific DBS models. One opportunity for that kind of evolution is in DBS models that attempt to simulate the response of specific axonal pathways to stimulation.

While not without their own limitations, field-cable (FC) pathway-activation models (PAMs) are the current “gold standard” for simulating neural responses to electrical stimulation ⁵. FC PAMs explicitly integrate two main components: 1) a volume conductor model of the head, which simulates the electric field generated by the electrode, and 2) multi-compartment cable models that simulate the electrical response of axons and/or neurons in the presence of the applied electric field. Patient-specific FC PAMs are capable of making detailed quantitative predictions ^6,7 and can explicitly account for many of the key modeling parameters relevant to DBS ^7,8. Nonetheless, the technical expertise and computational resources required to implement them are prohibitive for common use by non-expert users. As such, simplified predictors of FC PAM results became a necessity for most clinically focused analyses of DBS with patient-specific models.

The volume of tissue activated (VTA) is the most widely utilized simplified predictor in clinical DBS research studies ^9–12. VTA predictors have been used to retrospectively identify therapeutic regions for stimulation ^13,14 and prospectively define surgical targets and stimulation parameters that improve clinical outcomes ^15,16. However, the simplifying assumptions in VTAs greatly limits their accuracy in estimating neural responses for a wide variety of axonal trajectories, stimulation parameter settings, and electrode configurations ⁴.0

Driving-force (DF) predictors represent a more advanced class of predictive algorithms that are more accurate than VTAs in approximating neural activation thresholds ⁴. In general, DF predictors use the steady-state polarization response of passive/linear cable models to an applied stimulus to estimate activation thresholds of the nonlinear model ^17–19. DF predictors are especially well-suited to research applications attempting to integrate DBS models with tractography, or axonal pathways representations. This is because DF predictors explicitly account for the complex DBS electric field, as well as the anatomical trajectory of the axon, when attempting to predict activation. As such, DF predictors may represent a useful technological advance in the scientific evolution of clinical DBS software tools. Therefore, the goal of this project was to develop a novel DBS-specific DF-based predictor we call DF-Howell.

METHODS

We used the most detailed patient-specific foundation for DBS modeling currently available to establish a standard for estimating pathway activation ². We refer to this foundational model as the patient-specific FC PAM. Outputs from the FC PAM were then compared to two DF PAMs, DF-Howell (see below) or DF-Peterson ¹⁹, which are predictors of neural activation.

This study focused on analysis of subthalamic DBS. Within the subthalamic region there are many different axonal pathways that are likely capable of generating behavioral effects when stimulated. We choose to analyze three different pathways: 1) internal capsule fibers of passage, 2) hyperdirect pathway, and 3) cerebellothalamic tract. These pathways were chosen because their modulation has been implicated in either therapeutic or non-therapeutic effects of DBS. Activation of the internal capsule is commonly associated with motor contraction side effects of subthalamic DBS ²⁰. Stimulation of the hyperdirect pathway is thought to be a major contributor to the therapeutic effects of subthalamic DBS ²¹. Stimulation of the cerebellothalamic tract is considered therapeutic for the control of tremor ²², but has also been implicated in the generation of dysarthria ²³.

Field-cable pathway-activation model

The technical details and methodology for constructing the patient-specific FC PAM of subthalamic DBS are described in our prior work ^2,4. The details of image processing and streamline reconstruction (Figure 1) are found in a previous work ⁴. The construction and analysis of the models and algorithms is summarized below.

Figure 1.

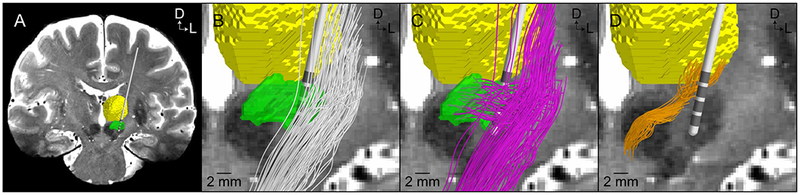
Reconstruction of axonal pathways in the subthalamic region with diffusion-weighted imaging-based tractography. A) Coronal view of the model anatomy (green volume – subthalamic nucleus; yellow volume – thalamus). B) Internal capsule fibers of passage (white streamlines). (B) Hyperdirect pathway axons exhibiting a collateral that terminates within the subthalamic nucleus (pink streamlines). (C) Cerebellothalamic tract axons (orange streamlines). Reprinted from Gunalan et al. (2018) with permission from Elsevier.

Volume conductor

The volume conductor of the head consisted of three domains: 1) a domain of encapsulation tissue, which was a 0.5 mm thick uniform layer surrounding the Medtronic 3389 DBS lead, 2) a domain of brain tissue, and 3) a non-brain domain delineated by the outer boundaries of the brain and the scalp. We constructed a conductivity tensor field for the entire head volume in the patient’s T1W space ²⁴. Voxels were categorized into 1 of 11 different types of tissues (Figure 2A), each with its own corresponding effective conductivity ². Within the brain volume, FSL’s dtifit tool was used to fit a single tensor to the signal in each voxel of the patient’s DW image, and the tensors in DW space were warped to T1W space. We then used the load preservation approach ²⁴ to define a conductivity tensor in each voxel from the respective isotropic conductivity, and eigenvalues and eigenvectors of the fitted diffusion tensor. Diffusion tensor data was only used within the boundaries of the patient’s brain (i.e. domain 2); therefore, conductivity tensors within the brain were anisotropic, whereas the tensors outside the brain (i.e. in domain 3) were isotropic.

Figure 2.

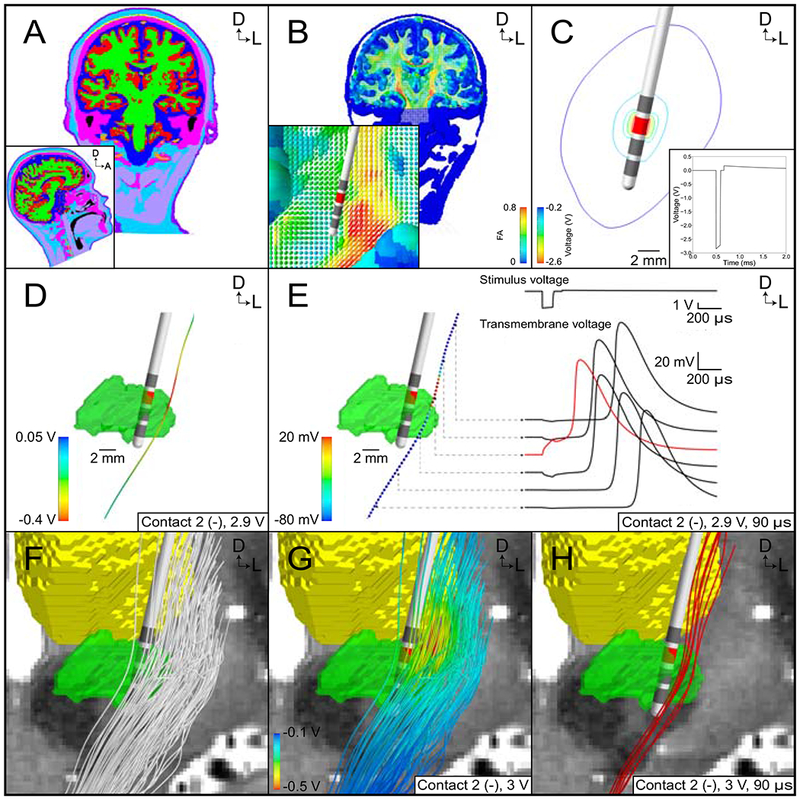
Patient-specific field-cable pathway activation model (FC PAM) in the context of subthalamic deep brain stimulation (DBS). (A) Tissue-type segmentation of the head. (B) Conductivity tensor field based on the tissue-type segmentation and patient-specific diffusion-weighted images. (C) Isocontours of the extracellular potentials generated by contact 2 for a stimulus amplitude of 3 volts. Inset shows the waveform generated by contact 2 at the electrode-tissue interface for a stimulus pulse width of 90 μs. (D) Extracellular potentials along an internal capsule axon. (E) Propagation of an action potential along an internal capsule axon in response to a suprathreshold stimulus. (F) Representative population of 100 internal capsule fibers of passage. (G) Extracellular potentials along 100 internal capsule fibers of passage for a stimulus amplitude of 3 volts. (H) Internal capsule axons activated by stimulation (red). Reprinted from Gunalan et al. (2018) with permission from Elsevier.

We used COMSOL (version 5.1) to construct tetrahedral meshes for the head model. The mesh had an especially high nodal density within a 30-mm cubic region surrounding the tip of the modeled DBS lead. Elements within the encapsulation tissue were assigned an isotropic conductivity of 0.07 S/m, which falls within the range of previously reported values ²⁵, was chosen so that the load of the modeled head matched that measured from the patient by the Medtronic programming device ². Elements in domains 2 and 3, the brain and non-brain domains, respectively, were assigned conductivity tensors based on their proximity to the nearest neighbor in the tensor field defined by the structured rectangular grid in the patient’s T1W space. The complete head model consisted of 1,429,416 total tetrahedral elements and 6,524,354 nodes in the finite element mesh.

Dirichlet boundary conditions were chosen to model either a monopolar (C2⁻ / IPG⁺), bipolar (C2⁻ / C3⁺), or tripolar (C2⁻ / C1⁺, C3⁺) electrode configuration. Inactive contacts were treated as ideal conductors and modeled using boundary conditions that specified two conditions, per contact: all potentials within the contact were equal in value, and the net current flow through the surface of the contact was 0 A. Neumann boundary conditions of 0 A/mm² were used to model the electrode shaft and scalp surface (minus the neck) as perfect insulators. Because we did not model the patient’s torso and IPG, the monopolar configuration was approximated by specifying the base of the neck as ground, or 0 V; whereas in the other two configurations, the base of the neck was insulated.

The potential field ($\Phi$) in the volume conductor at the onset of the stimulus was calculated by using the finite element method (FEM) to solve numerically Laplace’s equation for conductive media:

$$\nabla \cdot (\Sigma \cdot \nabla \Phi )=0$$ (1)

, where Σ is tensor conductivity field. The variation of the potentials over time was approximated by multiplying the above solution with a time-varying waveform derived from an equivalent circuit model of the implanted DBS system ⁸.

Cable model of axons

Multi-compartment cable models of axons were constructed and solved in the NEURON simulation environment (version 7.3). We started with the MRG axon model ²⁶ and modified some of the geometrical parameters to better reflect axons of the central nervous system ²⁴. We defined the diameter of the hyperdirect collateral as a fraction (1/3.1) of the diameter of the corticofugal axon ^27,28. We used the streamlines generated from tractography to define the axonal trajectories of the cable models.

We reconstructed three pathways, each consisting of 1000 axons, that coursed through the subthalamic region: internal capsule fibers of passage (IC), hyperdirect pathway (HDP), and cerebellothalamic tract (CbTT) (Figure 1). Given the position of each axon model relative to the DBS electrode, we interpolated an extracellular potential from the volume conductor electric field model at the coordinates of the center of each compartment in the cable models. During the stimulus pulse, those extracellular potentials were applied to the axon model via the extracellular mechanism in NEURON ^2,5 (Figure 2). The cable equation was then solved using NEURON’s default solver, Backward Euler, with a time step of 1 μs. Further refinement of the time step changed the stimulation thresholds by less than 1.2 %. For a given electrode configuration and stimulus pulse width, we used a binary search algorithm to determine the threshold stimulus amplitude for the generation of action potentials to within 0.01 V. An axon was considered activated when it responded “one-to-one” with the stimulus frequency.

Driving Force Models

DF-Howell

We used a simplified model of a DBS lead in a box, or LIB model, to generate training data for DF-Howell. The LIB model consisted of a 2D axisymmetric volume conductor model with populations of perfectly straight axons oriented parallel to the long axis of the lead, the Model 3389 electrode array (Medtronic, Minneapolis, MN), which has four cylindrical contacts, 1.5 mm in height, 0.635 mm in radius, and an edge-to-edge spacing of 0.5 mm lead (Figure 3A). The lead was surrounded by a 0.5 mm-thick encapsulation tissue (σ_scar = 0.07 S/m), which itself was surrounded by a 60 mm x 60 mm axisymmetric bulk tissue medium (σ_tissue = 0.2 S/m). Perfectly straight axons were seeded at ten different distances with respect to the surface of the lead: 0.5 mm and 1–9 mm in increments of 1 mm. Axons were modeled using 20 fiber diameters: 1.5–6 μm in increments of 0.5 μm, 6.5 μm, and 7–15 μm in increments of 1 μm. And, axons were stimulated using ten different pulse widths (30–150 μs in increments of 30 μs, 200 μs, 250 μs, 300 μs, 400 μs, and 500 μs) and three different electrode configurations (monopolar = C2− / IPG+, bipolar = C2− / C3+, and tripolar = C1+ / C2− / C3+). Therefore, we calculated 2000 activation thresholds (V_th) for each electrode configuration (10 distances, 20 fiber diameters, 10 pulse widths). We refer to the monopolar, bipolar, and tripolar electrode configurations as Cases 1, 2, and 3, respectively, for classification (see below).

Figure 3.

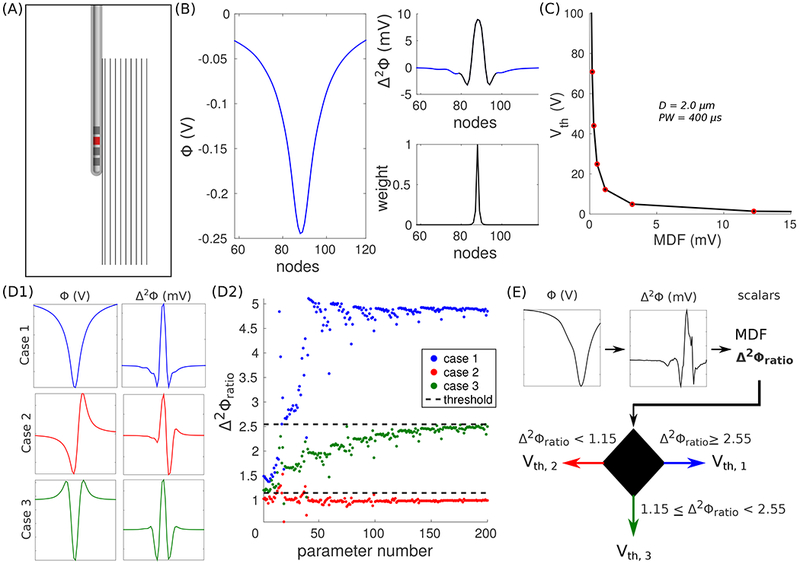
DF-Howell. (A) Axisymmetric volume conductor model of Medtronic’s Model 3389 lead-in-a-box. Ten axons are oriented parallel to the long axis of the shaft. The lead is programmed in a monopolar cathodic configuration (C2−, red contact). The model is not drawn to scale. (B) Extracellular potentials (Φ, left) across an axon 1 mm from the surface of the lead. The modified driving force (MDF) is the inner dot product between the second difference of the potentials (Δ²Φ, top-right) and a set of weights (bottom-right). The black line in the top-right panel denotes where the weights are non-zero. (C) Activation thresholds (V_th) estimated with the models as a function of MDF. (D1) Φ and Δ²Φ for three different electrode configurations: Case 1 (C2− / IPG+, top), Case 2 (C2− / C3+, middle), and Case 3 (C2− / C1+, C3+, bottom). (D2) Δ²Φ_ratio for all combinations of distance and fiber diameter. Δ²Φ_ratio = Δ²Φ_max / Δ²Φ_min. The dashed lines denote decision boundaries that best separate the ratios between Cases 1 and 3, and Cases 2 and 3. (E) DF-Howell algorithm: V_th of a random axon in the cerebellothalamic tract (CbTT) is estimated using its MDF and Δ²Φ_ratio.

We used the modified driving force (MDF) ¹⁷ to reduce the vector of extracellular potentials driving the polarization of the axonal membrane to a single scalar; therefore, each activation threshold was associated with one input. MDF is the inner dot product between the second spatial difference (Δ²Φ) of the extracellular potentials (Φ) at the nodes of Ranvier (NoRs) and a set of decaying weights (w) that is centered with respect to the NoR where (Figure 3B)

$${\Delta }_k^2\Phi ={\Phi }_{k-1}-2{\Phi }_k+{\Phi }_{k+1}$$ (2)

is maximal. Therefore,

$$MDF=\sum _{k=-(n_{node}-1)/2}^{(n_{node}-1)/2}{w}_k{\Delta }_k^2\Phi$$ (3)

, where n_node is the number of nodes, and

$$w_k=\frac{\mathit{max}(V_{m,k})}{\mathit{max}(V_{m,k=0}{)}_{⬚}}$$ (4)

, where k = 0 denotes the NoR where Equation 2 is maximal, and V_m is the transmembrane voltage. Weights were calculated in two steps. First, all nonlinear resistances representing ion channels were removed and replaced with a constant conductances (1 S/cm²) in series with the battery representing the resting membrane voltage. Second, we calculated the maximum V_m at the center NoR (or k = 0) while an intracellular rectangular pulse of current was applied at the k_th NoR. The intracellular pulse was 100 μs in duration and 1 nA in amplitude. Steps one and two were repeated for all nodes.

For each combination of pulse width, fiber diameter, and electrode configuration, the input-output (MDF-V_th) relationship was approximated using the following rational, nonlinear expression (Figure 3C):

$$V_{th}=a_0+a_{1}MD{F}^{\alpha }$$ (5)

where a₀ and a₁ are constants that minimize the sum square residuals for a given α. Note: although a₀, a₁, and α vary depending on the pulse width, fiber diameter, and electrode configuration; we omit the three sub-indices for the above constants in Equation 5 without loss of generality. We used a brute force approach to find the optimal α (to a precision of 0.01) that maximized the coefficient of determination, or R²; the optimal α always fell between −0.01 and −4. Expressions were fit only to V_th < 20 V, unless there were less than five values, in which case additional values were added so that five or more points were used to fit Equation 5.

The profiles of Φ and Δ²Φ for a given electrode configuration are stereotypical in a homogeneous, isotropic medium with straight axons (Figure 3D1), such as the LIB model. However, the same is not true in a patient-specific FC PAM (Figures 1 and 2), where complex electrical properties and non-straight axonal trajectories can produce, for example, Δ²Φ with a monopolar configuration that more closely resembles a bipolar configuration in terms of the relative sizes of adjacent depolarizing and hyperpolarizing lobes/regions (e.g., see Figure 3E). Therefore, we used a 1D classifier to account for different profiles of Φ and Δ²Φ in the patient-specific FC PAM. To determine cutoffs for classification, we calculated the Δ²Φ_ratio = Δ²Φ_max / Δ²Φ_min for all combinations of distance and fiber diameter in the LIB model, and we determined which two constants best separated Δ²Φ_ratio for the three different training cases (Figure 3D2).

DF-Howell was implemented using the following steps for each axon. The coordinates of the nodes of Ranvier were determined, and then the Φ for the given DBS settings were defined at those coordinates using the patient-specific volume conductor. From the Φ, we calculated Δ²Φ, both vector quantities, and from Δ²Φ, we calculated MDF and Δ²Φ_ratio, the scalar metrics. We used Δ²Φ_ratio to determine which training case to use, Case 1, 2, or 3 (Figure 3E); and MDF was used to estimate V_th with the appropriate fitted expression (i.e., Equation 5).

DF-Peterson

We also analyzed the DF-based predictor proposed by Peterson et al. ¹⁹, which we term DF-Peterson. This algorithm is the most recent iteration of a DF-type predictor available in the literature and is more accurate than VTA-type predictors ⁴. Although DF-Howell and DF-Peterson both use MDF as a regressor to estimate activation thresholds of the MRG axon model, there are a few notable differences. First, DF-Peterson uses both MDF and the maximum absolute value of Φ to estimate V_th. Second, DF-Peterson was parameterized using artificial potentials as opposed to potentials generated in a simplified volume conductor model, although the artificial potentials did resemble the voltage distribution of a monopolar electrode configuration. And third, DF-Peterson is a lookup table as opposed to a set of analytic expressions. More details on the construction of DF-Peterson can be found in the work by Peterson et al. ¹⁹.

We used the lookup tables provided by Peterson et al. ¹⁹ to estimate V_th. If specific combinations of fiber diameter and pulse width were unavailable, we used bilinear interpolation to estimate the relationship between MDF, |Φ|_max, and V_th. For axons with collaterals, we calculated the MDF of the body and collateral separately, and the larger MDF (and |Φ|_max) was used to estimate V_th. See the work of Gunalan et a. ⁴ for more details on how we used DF-Peterson to estimate pathway-activation in a patient-specific DBS model.

Analyses

DF- and VTA- type algorithms are derived from relatively simple FC PAMs for practical reasons and because one can clearly delineate relationships between input parameters and the stimulation thresholds in a low dimensional space. To determine how generalizable the estimates of DF-Howell and DF-Peterson are over a broad space of clinically relevant parameters, we prospectively tested the predictors against various data sets from a de novo, patient-specific FC PAM (Figure 2). We considered considerable variation in axonal trajectories and morphologies (three different pathways), distances (1-10 mm), stimulus pulse widths (30-500 μs), fiber diameters (2-10 μm), stimulus amplitudes (1-10 V), and electrode configurations (mono-, bi-, and tri-polar). More specifically, test cases included a small (2 μm), medium (5.7 μm), and large (10 μm) fiber diameter; a small (30 μs), medium (90 μs), and large pulse width (450 μs); and a monopolar (C2⁻ / IPG⁺), bipolar (C2⁻ / C3⁺), and tripolar (C1⁺ / C2⁻ / C3⁺) electrode configuration. No attempts were made to make the test data similar or uniform to the training data.

Unless specified otherwise, errors are the difference between the output of the DF PAM and that of the patient-specific FC PAM. Outputs of interest were V_th and the percent activation of a given pathway at the specified DBS parameter settings. We evaluated the percent activation between 0 and 10 V, in increments of 0.1 V, for pathway-activation values below 100 %.

RESULTS

Approximating the training data set

DF-Howell approximated the majority (> 95 %) of activation thresholds of the training data to within a precision of approximately + 0.25 V (Figure 4). The median absolute error across all combinations of input parameters was 0.04 V, and we observed no bias with fiber diameter, stimulus pulse width, or stimulus amplitude. When Equation 5 was fitted to V_th ≤ 20 V, V_th were overestimated above 20 V (Figure 4A). Laxing this restriction reduced errors for V_th > 20 V but at the expense of marked increases in error at smaller fibers diameters and longer pulse width (results not shown).

Figure 4.

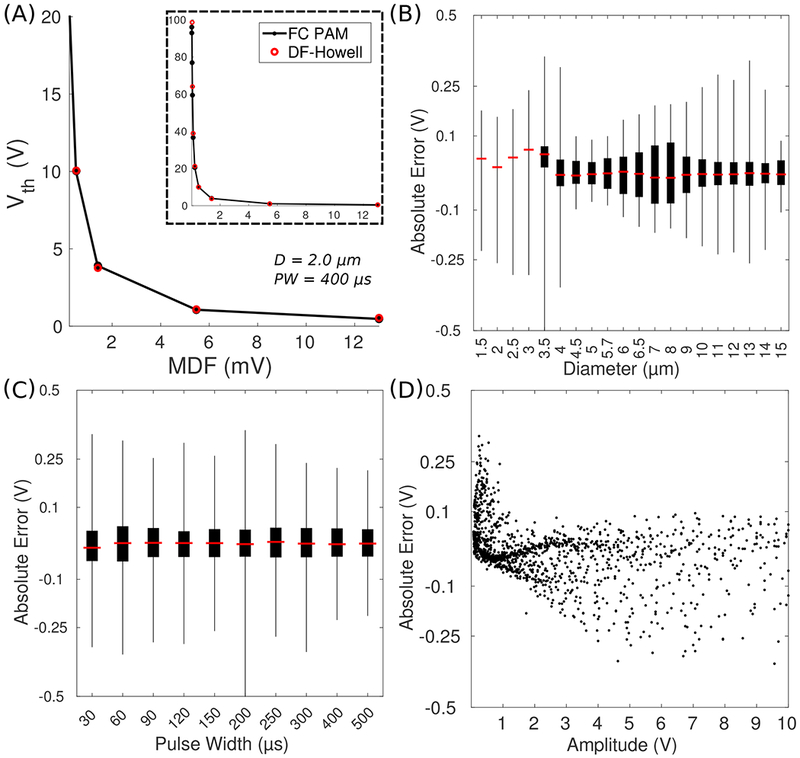
DF-Howell training. (A) Activation thresholds (V_th) as a function of the modified driving force (MDF) for a given combination of fiber diameter (D) and pulse width (PW). Inset: y-axis extended to 100 V. FC = field-cable, PAM = pathway-activation model, DF = driving force. (B) Error of V_th versus fiber diameter. Box plot whiskers represent minimum and maximum of all data. (C) Error of V_th versus pulse width. (D) Error of V_th versus the amplitude of the applied voltage.

Approximating pathway recruitment

We analyzed the recruitment of the axonal pathways to determine to what degree of accuracy the two DF PAMs could reproduce the output of the FC PAM. We quantified mean errors between the FC and respective DF PAM for the amplitude range of 0.1 V to 10 V. Across the range of fiber diameters tested (monopolar configuration, 90 μs), DF-Howell outperformed DF-Peterson in the majority of the cases (Figure 5). Although DF-Peterson outperformed DF-Howell at 5.7 μm, the magnitude of the mean errors was below 6.2 %. Both predictors did the worst with a large fiber diameter: for example, the mean errors for DF-Peterson and DF-Howell for IC, with 10 μm diameter axons, were 24 % and 1.5 %, respectively. Across the pulse widths tested (monopolar configuration, 5.7 μm), DF-Howell also outperformed DF-Peterson (Figure 6), with DF-Peterson doing appreciably worse than DF-Howell at small and large pulse widths. However, neither predictor was able to recapitulate the output of the patient-specific FC PAM to within an accuracy of 5 % across all combinations pulse width, amplitude, and fiber diameter.

Figure 5.

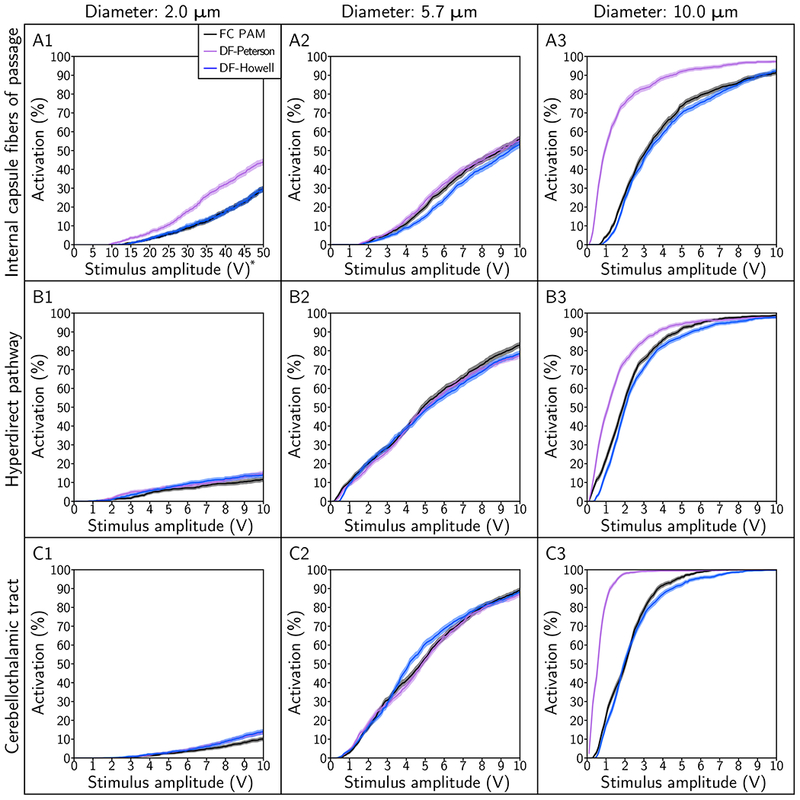
Pathway recruitment curves for fiber diameters of 2.0 μm, 5.7 μm, and 10.0 μm. The pathways modeled include the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract. The stimulus pulse width was 90 μs and electrode configuration was contact 2 (−), case (+).

Figure 6.

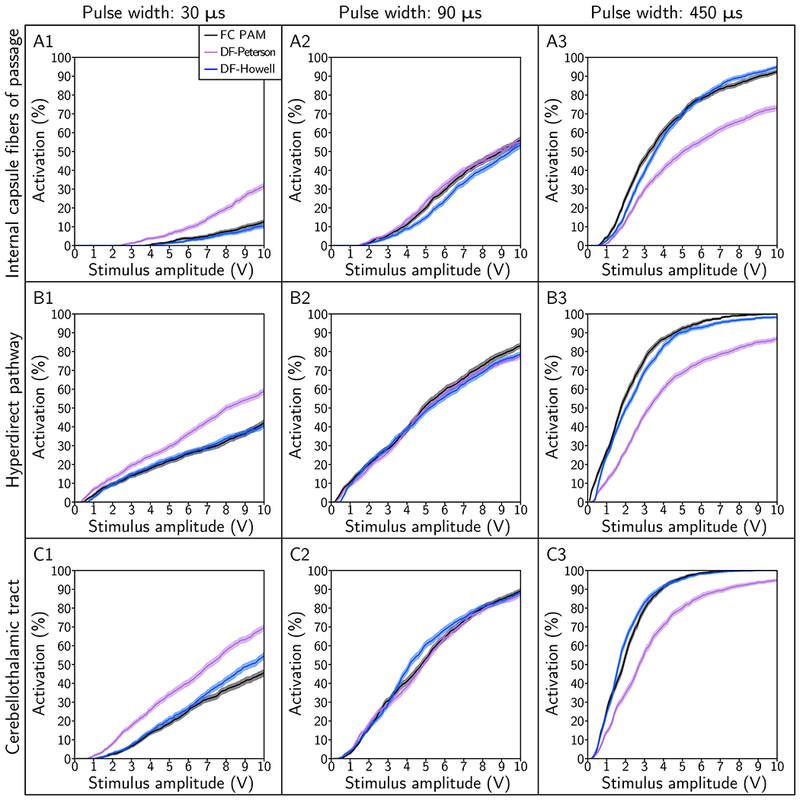
Pathway recruitment curves for stimulus pulse widths of 30 μs, 90 μs, and 450 μs. The pathways modeled include the: (A) internal capsule fibers of passage, (B) hyperdirect pathway, and (C) cerebellothalamic tract. The electrode configuration was contact 2 (−), case (+) and fiber diameter was 5.7 μm.

DF-Howell was able to predict pathway recruitment to within a mean error of + 5 % for all but one of the multipolar cases tested, and the performance of DF-Howell was improved by removing the classifier and using Cases 2 and 3 to estimate activation for the bipolar and tripolar configurations, respectively (see Supplemental Material). However, this improvement in performance came at the expense of a degradation in performance for the monopolar cases. In contrast, DF-Peterson was only reasonably accurate for half of the cases (Figure 7). It’s also worth noting that errors were largest for both predictors when estimating recruitment of the hyperdirect pathway with a tripolar electrode configuration. Action potentials in this pathway initiated at branch points in 60-72 % of the axons depending on the fiber diameter and stimulus settings; and when axons with branch activation were ignored, errors for both predictors were within + 1 % (results not shown). Thus, branch points and terminals (see Supplemental Material) should be considered as a limiting factor in the predictive accuracy of DF-type algorithms.

Figure 7.

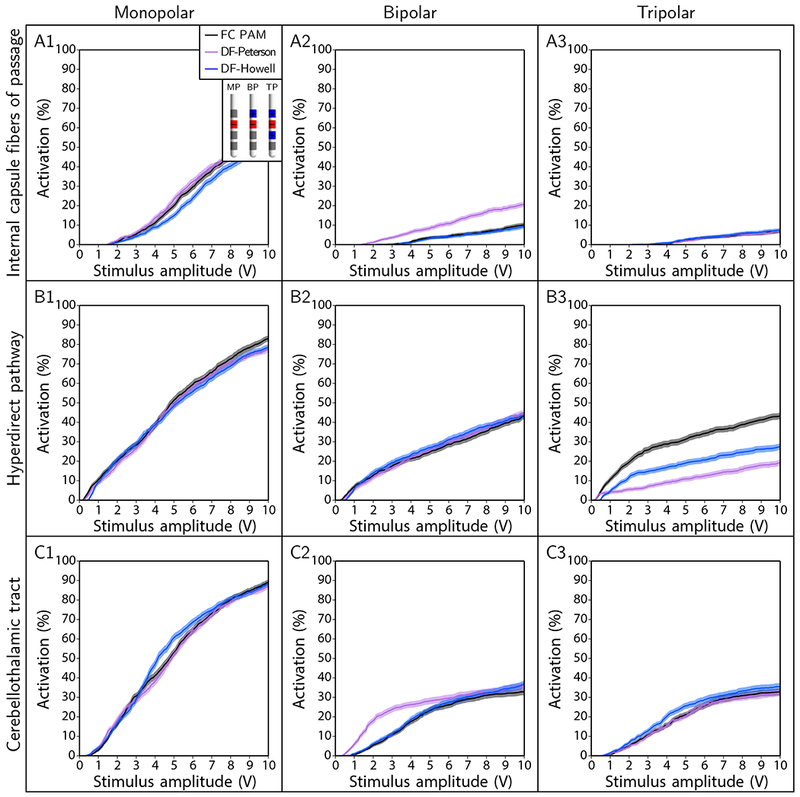
Pathway recruitment curves for electrode configurations of monopolar (MP; contact 2 [-], case [+]), bipolar (BP; contact 2 [-], contact 3 [+]), and tripolar (TP; contact 1 [+], contact 2 [-], contact 3 [+]). The axonal pathway was the cerebellothalamic tract, stimulus pulse width was 90 μs, and fiber diameter was 5.7 μm.

DISCUSSION

The goal of this study was to develop and evaluate a novel DF predictor customized to the study of clinical DBS PAMs. The results demonstrate that DF predictors generate reasonable estimates of pathway activation for clinically relevant stimulus parameters. DF-Howell outperformed DF-Peterson in a majority (15 of 21) of the cases, and in situations where DF-Howell performed worse, mean absolute errors were relatively small (i.e., < 6.2 %). Because DF-based predictors substantially reduce the computational demands and technical expertise required for DBS modeling, relative to FC models, they may prove useful in reducing technical barriers for adopting quantitatively accurate patient-specific PAMs into clinical DBS research.

Pathway-activation models

Numerous open-source software tools have been developed to help facilitate the implementation of a variety of simplistic PAM methods into clinical workflows using VTAs ^29–32. In DBS therapies where the targets are large white-matter fiber tracts, VTA PAMs can help position the lead within the confluence of candidate targets, potentially improving clinical outcomes ¹⁶. However, VTA-based estimates on the extent of activation are prone to errors that can be several millimeters ⁴. Therefore, to help minimize the potential for confounding errors in connectomic DBS analyses, we advise that future versions of DBS software tools evolve to integrate DF-based algorithms. While patient-specific FC PAMs require weeks to months to build and solve, DF PAMs can simulate those results in a very small fraction of that time (i.e. seconds to minutes depending upon the number of axons being evaluated). As such, DF PAMs can enable high-powered analyses of large patient cohorts, or interactive evaluation of individual subjects, with quantitatively accurate estimates of pathway activation.

DF-based algorithms have long offered a tractable alternative to cable-based models when estimating pathway recruitment ¹⁷. DF predictors can be parameterized using data from a simplified FC model with straight axons (Figure 3A), or even simpler, a point-source electrode in an infinite medium ¹⁹. Moreover, DF predictors provide reasonable estimates of pathway recruitment for clinically-relevant parameters (Figures 5–7), and they are versatile. If the distribution of electric potentials is altered due to changes in the configuration of active contacts on the electrode, a DF predictor does not need to be re-parameterized because the spatial characteristics of the applied electric fields, or MDF, accounts for these changes. In regards to computational savings, both DF-based algorithms had compute times on the order of seconds for all cases tested. For comparison, based on our own compute times on a modern piece of hardware (e.g., 2.4 GHz, 4 cores, 8 Gb memory, etc.), we estimate it would take approximately one week to calculate serially 1000 activation thresholds in NEURON, and with a compute cluster under typical loads, compute times can only be reduced to one or more hours.

DF-based algorithms are not as simple to implement as VTA-based algorithms. While DF algorithms do simplify the process of simulating neural responses, they are only a one-step reduction from an FC model. VTA algorithms represent a two-step reduction, as that they obviate the need for both electric field models and neural cable models ³³. This additional simplification makes VTA-based algorithms very easy to use, but at the cost of a substantial decline in the accuracy of the model predictions ⁴. We have found that calculation of the electric potentials is crucial for accurate neural activation estimates and those details are important when attempting to perform connectomic DBS analyses. Therefore, we propose that DF-based algorithms should replace VTAs in scientific research. To help facilitate that transition, we propose the use of DBS electric field simulations derived from an atlas head model ^34,35 or a bank of predefined solutions from a relatively simplified volume conductor ^36,37. Then these electric field solutions can be managed/accessed by hosting them on the back-end of a web-based platform (e.g., CranialCloud, ³⁸), which works in concert with a connectomic DBS software tool. Such a strategy could improve the accuracy of DBS PAM analyses, while maintaining a low degree of technical expertise required from the user.

Sources of error with DF-based predictors

Simple FC models with ideal electrical properties and a homogeneous population of neural elements, like the LIB model, have relatively simple input-output relationships (Figure 3). However, more generally, populations of neurons and axons are heterogeneous with different morphologies. In addition, the polarization of the neural membrane depends on many factors, including the spatiotemporal aspects of the applied extracellular potentials, which depend on a multitude of model parameters. As such, scalar metrics, like MDF, do not fully capture the nonlinear dynamics of the cable equation, especially in patient-specific models, where the electrical properties and axonal geometries are inherently variable. Between non-ideal electrical properties and axonal geometries, the latter was more limiting in accurately predicting stimulation thresholds in our analyses.

We found that the high variability in predictions of V_th was due to the inherent limitations in using MDF as a proxy for excitation, especially for axonal pathways with non-straight trajectories (Figure 8). For example, incorporating patient-specific conductivities changed the shape of Δ²Φ along perfectly straight axons aligned to the DBS electrode (Figure 8A), but the predicted V_th’s were very similar to that of the FC PAM. With non-straight trajectories, the errors in V_th were relatively large, despite the pathways residing in an ideal, homogeneous, isotropic medium (Figure 8B). Pathways, such as the internal capsule and cerebellothalamic tract, were previously considered to be relatively straight near the active contact, justifying the use straight axons to construct predictive algorithms. However, even mild tortuosities in the internal capsule, which contain some of the straightest axons in the brain, can preclude accurate estimates of V_th, and errors will likely be greater for more complex, tortuous pathways.

Figure 8.

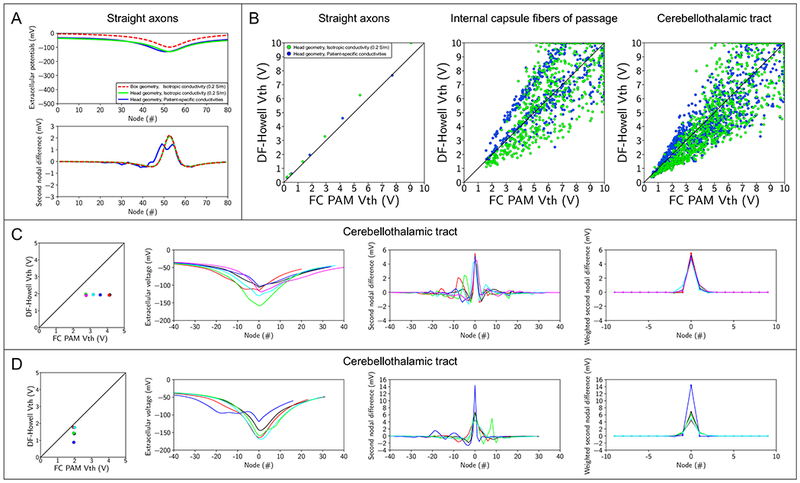
Sources of error with driving force-based predictors. (A) A straight axon aligned to the DBS electrode with an electrode-to-axon distance of 3mm. Extracellular potentials (top) and second nodal differences of extracellular potentials (bottom) along the straight axon. The straight axon was modeled within the following volume conductors: axisymmetric box with an isotropic tissue conductivity (red), patient-specific head boundaries with an isotropic tissue conductivity (green), and patient-specific head boundaries with tissue conductivities derived from the patient-specific diffusion-weighted images. (B) Activation thresholds generated with the FC and DF-Howell PAMs. Activated thresholds were calculated for straight axons aligned to the DBS electrode (left), internal capsule fibers of passage (middle), and the cerebellothalamic tract (right). The tissue conductivities were either isotropic (green) or derived from the patient-specific diffusion-weighted images (blue). (C) Cerebellothalamic axons with DF-Howell MDF values between 5.7 mV and 6 mV, which equates to activation thresholds (V_th) between 1.9 V and 2 V. Axons are those classified as Case 1. Colors correspond to different axons. (D) Cerebellothalamic axons with FC PAM V_th values between 1.9 V and 2 V. Axons are those classified as Case 1. Colors correspond to different axons.

MDF is also prone to ambiguity because it reduces the force driving the polarization of the neural membrane, i.e., Δ²Φ, to a single scalar, producing situations where different profiles of Δ²Φ yield the same V_th, despite the FC PAM predicting otherwise (Figure 8C). Additionally, in some cases, the relationship between the MDF and V_th is sensitive to changes in Δ²Φ in close proximity to the putative node of excitation, leading to situations where V_th can vary greatly despite little to no change in MDF (Figure 8D). Nonetheless, despite the aforementioned limitations of MDF, if overt bias in V_th is minimized, DF-based predictors can give reasonable estimates of overall pathway recruitment (Figures 5–7).

Bias in estimates of V_th generated by DF-based predictors can be explained by overfitting (see Supporting Information). For example, DF-Peterson had a low variance and high bias, whereas the opposite was true for DF-Howell (Figure S1). Both algorithms use MDF, but only DF-Peterson uses an additional regressor, |Φ|_max, which, when added to DF-Howell, lowered the variance at the cost of a marked bias, as seen in DF-Peterson (Figures S1 and S2). In the bivariate case, bias can be minimized by retrospectively fitting Equation S1 to the patient-specific thresholds, but eliminating bias retrospectively is reactive as opposed to predictive, thereby diminishing the utility of the predictor.

Recruitment dynamics at termini ³⁹ and branch points ⁴⁰, which we refer to as end- and branch-activation, respectively, can, if not accounted for, also limit the accuracy of DF-type predictors; and both these dynamics were observed with activation of the hyperdirect pathway. Branch-activation affected the accuracy of both DF-type predictors, albeit only for a single, tripolar electrode configuration, and although we minimized end-activation by substituting terminal nodes of Ranvier with passive patches of membrane, hyperdirect collaterals may be more excitable than previously thought for anodic electrode configurations, if the nodes are treated as “active” (see Supporting Information), which is consistent with a larger therapeutic window for anodic stimulation compared to cathodic stimulation ⁴¹. We accurately estimated the recruitment of the hyperdirect pathway, even when end-activation occurred, by adding the driving force at the collateral termini in the calculation of MDF (Figure S3), but a simple modification of MDF at branch points is generally infeasible due to asymmetric topologies and variable geometries that preclude reducing the driving force to a single scalar term. With the said, we caution against overextending the use of current DF-type predictors to complex axonal morphologies, and more sophisticated DF-type predictors and/or alternative strategies are recommended for these complex cases.

Ultimately, an ideal predictor would minimize both bias and variance in its estimates of V_th, but based on our findings, we posit that such a predictor is not possible in two or less dimensions. Because of the inherent variability in the electrical properties of the conductive medium and geometry of neural elements in patient-specific FC models, an empirical relationship between the input parameters and V_th may be better resolved in higher dimensions with a machine learning approach. DF-based predictors use a static set of weights based on the underlying physics, and Δ²Φ, to estimate neural excitability. With a machine learning approach, the inputs could be vectors of Φ or Δ²Φ sampled across multiple pathways in an FC model, and the optimal transformation and weighting of the inputs could be determined using an elastic net or a radial basis function network. Possibly the end justifies the means, but there are also negatives to a machine learning approach, one of which is that machine learning forgoes a direct connection to biophysical first principles, which is explicitly tangible with the MDF.

Study limitations

The predictive algorithms analyzed in this study estimate the stimulation thresholds predicted by FC PAMs. Thus, the biological accuracy of these predictions is limited to that of the parent model from which they are derived. The patient-specific FC PAM evaluated in this work is the most detailed FC PAM built to date, accounting for patient-specific anatomy and electrical properties, as well as realistic axonal pathways and neural membrane dynamics ². However, while the individual components of FC PAMs can be validated and constrained by experimental data ^26,42, defining the predictive power of these models for clinical measurements still requires experimental validation. Electromyography ⁴³, electroencephalography ²¹, electrocorticography ⁴⁴, and subthalamic evoked potentials ⁴⁵ all present excellent opportunities to test the predictions of PAMs.

The parameter spaced reviewed in this study spanned the range of clinically-relevant parameters in DBS, and we used representative axonal geometries in the subthalamic region. However, we did not present results for different DBS electrode designs, brain regions, and neuron models. The MDF accounts for changes in the spatial characteristics of the applied extracellular potentials, so by design, DF-based predictors are presumably insensitive to changes in the electrode configuration and position ¹⁹. However, for different neuron models and modes of stimulation, such as constant-current stimulation, DF-Howell should be re-fit to account for changes in the modeled system, which the MDF does not directly capture.

Our analysis was limited to relatively simple axonal morphologies that were reconstructed using tractography. As such, the long list of caveats and limitations associated with tractography apply to our pathway representations ⁴⁶. In addition, we only evaluated three of the many different axonal pathways within the subthalamic region. Nonetheless, our goal was to demonstrate the general method, and we found that DF-Howell was reasonably accurate in estimating pathway recruitment of a tortuous pathway (i.e. the cerebellothalamic tract) as well as a pathway with a single collateral (i.e. the hyperdirect pathway). However, as discussed above, it should be noted that stimulation of neurons with dendritic and axonal arborizations is likely more complex ^47,48. Moreover, we ignored the morphology of the terminus of the axon, which also impacts its excitability ³⁹. Future studies are needed to explore the effect of such axonal complexities on the accuracy of DF-based predictors.

CONCLUSIONS

Patient-specific DBS models represent powerful research tools that can be used to simulate the neural response to applied electrical stimuli. In this study, we developed a DF-based algorithm that can provide reasonably accurate estimates of pathway-activation for a wide range of clinically-relevant DBS settings and fiber diameters found within the brain. The compute times of these algorithms is orders of magnitude below that of nonlinear cable models, permitting near real-time evaluation of stimulation parameter or electrode contact configuration changes. As such, DF-based predictors may prove useful in reducing the technical barriers for implementing quantitatively accurate computational models of DBS in clinical research studies.