A New Multi-Atlas Registration Framework for Multimodal Pathological Images Using Conventional Monomodal Normal Atlases

Abstract

Using multi-atlas registration (MAR), information carried by atlases can be transferred onto a new input image for the tasks of region of interest (ROI) segmentation, anatomical landmark detection, and so on. Conventional atlases used in MAR methods are monomodal and contain only normal anatomical structures. Therefore, the majority of MAR methods cannot handle input multimodal pathological images, which are often collected in routine image-based diagnosis. This is because registering monomodal atlases with normal appearances to multimodal pathological images involves two major problems: (1) missing imaging modalities in the monomodal atlases, and (2) influence from pathological regions. In this paper, we propose a new MAR framework to tackle these problems. In this framework, a deep learning based image synthesizers are applied for synthesizing multimodal normal atlases from conventional monomodal normal atlases. To reduce the influence from pathological regions, we further propose a multimodal low-rank approach to recover multimodal normal-looking images from multimodal pathological images. Finally, the multimodal normal atlases can be registered to the recovered multimodal images in a multi-channel way. We evaluate our MAR framework via brain ROI segmentation of multimodal tumor brain images. Due to the utilization of multimodal information and the reduced influence from pathological regions, experimental results show that registration based on our method is more accurate and robust, leading to significantly improved brain ROI segmentation compared with state-of-the-art methods.

I. Introduction

USING multi-atlas registration (MAR), information carried by atlases can be transferred onto a new input image for tasks such as segmentation [1]–[3], landmark detection [4], and surgical planning [5]. Atlases adopted in MAR methods are generally obtained from monomodal normal images (e.g., T1-weighted MR images of normal brains) [6]–[9]. Thus, the majority of MAR methods cannot be applied to multimodal pathological images. This is because registering monomodal normal atlases to multimodal pathological images involves two major problems: (1) missing imaging modalities in the monomodal atlases, and (2) influence from pathological regions because of lacking correspondence between pathological and normal regions. However, multimodal pathological images are often collected in routine image-based diagnosis. For example, T1-weighted, T1 contrast-enhanced (T1c), T2-weighted and FLAIR MR images are usually acquired for patients with brain tumors.

One way to deal with the problem of missing imaging modalities is by discarding the modalities that are not available in the monomodal atlases, but at the cost of losing useful information. An alternative is to use cross-modal similarity metrics such as mutual information (MI) [10] and normalized mutual information (NMI) [11] for cross-modality registration. However, unlike monomodal similarity metrics, such as the mean squared difference of image intensity, local anatomical similarity cannot be directly or efficiently calculated with MI or NMI [12].

To reduce the influence from pathological regions, Brett et al. [13], [14] proposed a cost function masking (CFM) strategy to exclude pathological regions from registration, and registration is driven only by normal regions. Gooya et al. [15], [16] synthesized pathological regions (i.e., tumors) in a normal brain atlas to make the brain atlas similar to the input tumor brain image, facilitating subsequent registration. Liu et al. [17], [18] used a method called Low-Rank plus Sparse matrix Decomposition (LRSD) [19] to recover normal-looking brain image from the input tumor brain image. Then typical image registration methods [20]–[24] can be used to register normal brain atlases to the recovered normal-looking image.

In this paper, we propose a new MAR framework to solve the two aforementioned problems in traditional MAR methods, which have not been well addressed in the literature. Our MAR framework can handle multimodal pathological images based on conventional monomodal normal atlases. In our framework, deep learning based image synthesizers are introduced to produce multimodal normal atlases from conventional monomodal normal atlases. Then based on the resulting multimodal normal atlases, a multimodal low-rank method is further proposed to recover a multimodal normal-looking image from the input multimodal pathological image. Finally, the multimodal normal atlases are registered to the recovered multimodal image in a multi-channel way, where each channel operates one modality guided by monomodal image similarity metric. In our MAR framework, the multimodal low-rank recovery and the multi-channel registration are iteratively refined until convergence. We demonstrate the effectiveness of our MAR framework via segmentation of brain region of interest (ROI) in multimodal tumor brain images. The experimental results indicate that segmentation is significantly improved compared with state-of-the-art methods.

II. Methods

Since brain tumor is a common brain disease, and multimodal MR tumor brain images are usually captured for patients with suspicious brain cancer syndromes, our MAR framework is formulated for multimodal MR tumor brain images. By default, each multimodal MR tumor brain image has four modalities: T1, T1c, T2 and FLAIR, denoted as $\mathcal{T}=\{{\mathcal{T}}_{\text{T}1},{\mathcal{T}}_{\text{T}1\text{c}},{\mathcal{T}}_{\text{T}2},{\mathcal{T}}_{\text{FLAIR}}\}$. The monomodal brain atlases adopted in our framework are N T1-weighted MR normal brain images, denoted as ${\mathcal{A}}_{i,\text{T}1}$, i = 1, ..., N. An overview of our framework is shown in Fig. 1.

Fig. 1.

Overview of our multi-atlas registration framework for multimodal pathological brain images.

Our MAR framework consists of three main components. The first component contains CycleGAN [25] based image synthesizers, which synthesize the brain atlases of missing modalities, i.e., ${\mathcal{A}}_{i,\text{T}1\text{c}}$, ${\mathcal{A}}_{i,\text{T}2}$ and ${\mathcal{A}}_{i,\text{FLAIR}}$, from ${\mathcal{A}}_{i,\text{T}1}$, i = 1, ..., N, resulting in the multimodal brain atlases ${\mathcal{A}}_i=\left\{{\mathcal{A}}_{i,\text{T}1},{\mathcal{A}}_{i,\text{T}1\text{c}},{\mathcal{A}}_{i,\text{T}2},{\mathcal{A}}_{i,\text{FLAIR}}\right\}$, i = 1, ..., N. This component is needed to be executed only once. The second component uses a low-rank method called multimodal SCOLOR (Spatially COnstrained LOw-Rank), which is an improvement of our previously proposed method [26], to recover multimodal normal-looking image $\hat{\mathcal{T}}=\{{\hat{\mathcal{T}}}_{\text{T}1},{\hat{\mathcal{T}}}_{\text{T}1\text{c}},{\hat{\mathcal{T}}}_{\text{T}2},{\hat{\mathcal{T}}}_{\text{FLAIR}}\}$ from the input multimodal tumor brain images $\mathcal{T}$ based on the information provided by ${\mathcal{A}}_i$, i = 1, ..., N. The third component involves multi-channel image registration of the multimodal brain atlases ${\mathcal{A}}_i$, i = 1, ..., N to the recovered multimodal image $\hat{\mathcal{T}}$, where each channel operates one modality using monomodal image similarity metric. The multimodal SCOLOR based image recovery and the multi-channel image registration components are iteratively proceeded to refine the image recovery and registration results until convergence (illustrated by the two blue arrows in Fig. 1). Details on each component are presented next.

A. CycleGAN based image synthesizers

We use CycleGAN [25] to get multimodal brain atlases by synthesizing missing modalities from available monomodal brain atlases. CycleGAN is a special kind of generative adversarial network (GAN). Conventional GAN [27] consists of a generator G : X ⟼ Y which is responsible for synthesizing image y ∈ Y from image x ∈ X and a discriminator D which is responsible for discriminating the synthesized images G(x), x ∈ X, from the images in Y. G is typically a fully convolutional network (FCN) [28], and D is a convolutional neural network (CNN) [29]. Given a set of training data X = {x₁, ..., x_M} (from the reference modality) and Y = {y₁, ..., y_M} (from the desired modality), the objective function of GAN is

$$\begin{gathered} {\mathcal{L}}_{\text{GAN}}(G,D,X,Y)=\underset{G}{\min }\underset{D}{\max }({\mathbb{E}}_{y_i\in Y}\left(\log \left(D\left(y_i\right)\right)\right) \\ +{\mathbb{E}}_{x_i\in X}\left(\log \left(1-D\left(G\left(x_i\right)\right)\right)\right)). \end{gathered}$$ (1)

To minimize (1), G should produce synthetic images G(x) that cannot be discriminated by D from images in Y. On the other hand, D tries to reject all synthetic images produced by G, i.e., D(G(x)) = 0. The optimization process consists of two steps. In the first step, the discriminator D is updated by stochastic gradient ascent

$$\nabla \frac{1}{M}\sum _{i=1}^M\left(\log \left(D\left(y_i\right)\right)+\log \left(1-D\left(G\left(x_i\right)\right)\right)\right).$$ (2)

In the second step, the generator G is updated by stochastic gradient descent

$$\nabla \frac{1}{M}\sum _{i=1}^M\left(\log \left(1-D\left(G\left(x_i\right)\right)\right)\right).$$ (3)

These two steps are iterated until convergence, i.e., the discriminator D cannot differentiate the synthetic images G(x) from the images in Y. GAN requires paired training data to make G(x_i) have consistent image content with x_i. However, paired normal brain images of different modalities are usually unavailable. Therefore, we use CycleGAN, which only require unpaired training data. The CycleGAN can be regarded as a combination of two GANs. Given a set of unpaired training data $\tilde{X}=\left\{{\tilde{x}}_1,\dots ,{\tilde{x}}_M\right\}$ of the reference modality and $\tilde{Y}=\left\{{\tilde{y}}_1,\dots ,{\tilde{y}}_M\right\}$ of the desired modality, One GAN (G₁ and D₁) is created for $\tilde{X}\mapsto \tilde{Y}$, and the other GAN (G₂ and D₂) is created for $\tilde{Y}\mapsto \tilde{X}$. The objective function of CycleGAN is defined as

$$\begin{gathered} {\mathcal{L}}_{\text{CycGAN}}(G_1,G_2,D_1,D_2,\tilde{X},\tilde{Y})=\underset{G_1,G_2}{\min }\underset{D_1,D_2}{\max }( \\ {\mathcal{L}}_{\text{GAN}}(G_1,D_1,\tilde{X},\tilde{Y}) \\ +{\mathcal{L}}_{\text{GAN}}(G_2,D_2,\tilde{Y},\tilde{X}) \\ +{\mathcal{L}}_{\text{cyc}}(G_1,G_2)) \end{gathered}$$ (4)

where ${\mathcal{L}}_{\text{GAN}}(G_1,D_1,\tilde{X},\tilde{Y})$ and ${\mathcal{L}}_{\text{GAN}}(G_2,D_2,\tilde{Y},\tilde{X})$ are two GANs defined in (1), λ is a weighting factor, and ${\mathcal{L}}_{\text{cyc}}\left(G_1,G_2\right)$ is the cycle consistency loss which is defined as

$$\begin{gathered} {\mathcal{L}}_{\text{cyc}}\left(G_1,G_2\right)={\mathbb{E}}_{{\tilde{y}}_i\in \tilde{Y}}\left({\Vert G_1\left(G_2\left({\tilde{y}}_i\right)\right)-{\tilde{y}}_i\Vert }_1\right) \\ +{\mathbb{E}}_{{\tilde{x}}_i\in \tilde{X}}\left({\Vert G_2\left(G_1\left({\tilde{x}}_i\right)\right)-{\tilde{x}}_i\Vert }_1\right). \end{gathered}$$ (5)

The cycle consistency loss encourages $G_1\left(G_2\left({\tilde{y}}_i\right)\right)={\tilde{y}}_i$ and $G_2\left(G_1\left({\tilde{x}}_i\right)\right)={\tilde{x}}_i$, therefore it prevents images in $\tilde{X}$ from mapping to random images in $\tilde{Y}$.

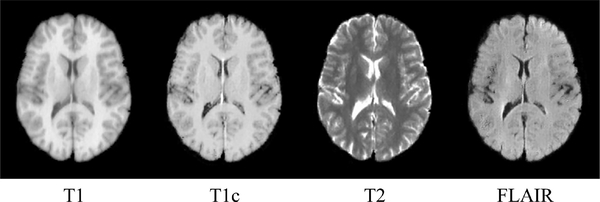
We construct three CycleGAN image synthesizers, each of which is used to synthesize the brain atlases of one of the three missing modalities (i.e., T1c, T2 and FLAIR) from available T1-weighted brain atlases. Three training datasets, each containing images from the available modality (i.e., T1) and one of the desired modalities (i.e., one of T1c, T2 and FLAIR) are used to train the image synthesizers. Ideally, these training datasets should be collected from normal brain images. However, normal MR brain images with all four modalities are rare. For example, the T1c modality is only used for tumor cases. Therefore, we create these three training image datasets based on a tumor brain image dataset called BRATS2015 [30]. In BRATS2015, the multimodal MR image of each subject has T1, T1c, T2 and FLAIR modalities. For each modality, 1000 image slice sections containing only normal brain regions, are extracted from 100 subjects in BRATS2015. Each image slice section has three consecutive 2D image slices in an MR image. Based on the resulting four sets of image slice sections, the three training datasets, i.e., (T1, T1c), (T1, T2) and (T1, FLAIR), can be created and used to train each CycleGAN based image synthesizer. In the testing stage, for each T1-weighted MR normal brain atlas ${\mathcal{A}}_{i,\text{T}1}$, i = 1, ..., N, every image slice section in ${\mathcal{A}}_{i,\text{T}1}$ is proceeded by the three CycleGAN based image synthesizers to produce synthetic image slice sections of respective modalities. Then center slices of the resulting synthetic image slice sections of each modality are stacked into the final synthetic brain atlas of the corresponding modality. In this way, the multimodal brain atlases of four modalities ${\mathcal{A}}_i=\left\{{\mathcal{A}}_{i,\text{T}1},{\mathcal{A}}_{i,\text{T}1\text{c}},{\mathcal{A}}_{i,\text{T}2},{\mathcal{A}}_{i,\text{FLAIR}}\right\}$, i = 1, ... , N can be obtained. Fig. 2 shows an example of a multimodal brain atlas, which has T1, T1c, T2 and FLAIR modalities. It is worth noting that, except the T1 modality which is real, the other modalities are synthetic.

Fig. 2.

Example of a multimodal brain atlas of T1, T1c, T2 and FLAIR modalities. The T1 modality is real, and other modalities are produced by the CycleGAN based image synthesizers. A 2D slice at the same level is used to represent the brain atlas of each modality.

B. Multimodal SCOLOR based image recovery

We represent a set of MR brain images of the same modality as a matrix $\mathit{I}=\left[I_1,\dots ,I_W\right]\in {ℝ}^{H\times W}$ with each image in a column. W is the number of images, and H is the number of voxels in each image. Conventional low-rank methods, e.g., Low-Rank plus Sparse matrix Decomposition (LRSD) [19], can recover a low-rank matrix $\hat{\mathit{I}}=[{\hat{I}}_1,\dots ,{\hat{I}}_W]\in {ℝ}^{H\times W}$ from I by minimizing the following function:

$$\underset{\hat{\mathit{I}}}{\min }(\Vert \mathit{I}-\hat{\mathit{I}}{\Vert }_1+\lambda \Vert \hat{\mathit{I}}{\Vert }_{*}).$$ (6)

The first term of (6) is the residual error constraint, which is a L1 norm of residual error $\mathit{I}-\hat{\mathit{I}}$, encouraging $\hat{\mathit{I}}$ to be close to I. The second term is the low-rank constraint, which is a nuclear norm of $\hat{\mathit{I}}$, preventing $\hat{\mathit{I}}$ having large rank. If images in I contain tumor regions, the rank of I will be larger than the case that I is comprised of normal brain images. This is because tumors usually have inconsistent image appearances and locations. Therefore, tumor regions in I are recovered by normal-looking brain regions in $\hat{\mathit{I}}$ to make $\hat{\mathit{I}}$ satisfy the low-rank constraint. In this way, if an MR brain image I_i ∈ I contains tumors, ${\hat{I}}_i\in \hat{\mathit{I}}$ is its corresponding recovered image of normal-looking brain. To achieve effective recovery of tumor regions, the residual error constraint has to be relaxed to allow large difference between I and $\hat{\mathit{I}}$, i.e., large residual error $\mathit{I}-\hat{\mathit{I}}$. Since the residual error constraint is equally imposed on the whole images in I regardless of tumor regions or normal brain regions, effective recovery of tumor regions is always at the cost of seriously distorted normal brain regions in recovered images.

To effectively recover tumor regions and avoid introducing distortion to normal brain regions in the recovered image, in our previous study, we proposed a low-rank method called spatially constrained low-rank (SCOLOR) [26] for image recovery. Unlike conventional low-rank methods, a tumor mask is introduced to impose different residual error constraints on tumor regions and normal brain regions. Specifically, weak residual error constraint is imposed on tumor regions for effective recovery, whereas strong residual error constraint is imposed on normal brain regions for good preservation. The objective function of SCOLOR is

$$\begin{gathered} \underset{\hat{\mathit{I}},\mathit{C}}{\min }\Vert (\mathbf{1}-\mathit{C})\odot (\mathit{I}-\hat{\mathit{I}}){\Vert }_F^2+\lambda \Vert \hat{\mathit{I}}{\Vert }_{*} \\ +\alpha \sum _{1\le h\le H \\ 1\le w\le W}{\mathit{P}}_{hw}\cdot {\mathit{C}}_{hw} \\ +\beta \sum _{1\le h,k\le H \\ 1\le w\le W}{\mathit{W}}_{hw,kw}\left|{\mathit{C}}_{hw}-{\mathit{C}}_{kw}\right| \end{gathered}$$ (7)

where $\mathbf{1}\in {ℝ}^{H\times W}$, 1_hw = 1,1 ≤ h ≤ H, 1 ≤ w ≤ W, $\mathit{C}\in {ℝ}^{H\times W}$ is the tumor mask whose elements C_hw are equal to 0 (normal brain regions) or 1 (tumor regions). Therefore, only the residual error of normal brain regions is restricted by the first item (Frobenius norm). The second item is the nuclear norm which is the same as the conventional low-rank methods, e.g., LRSD. The third and fourth items are constraint and regularization terms for the tumor mask C. Specifically, $\mathit{P}\in {ℝ}^{H\times W}$ in the constraint term is the probability map of normal brain regions, and it has large values in normal brain regions and small values in tumor regions. C is constrained by P, which will be discussed later. $\mathit{W}\in {ℝ}^{(H\times W)\times (H\times W)}$ is an adjacent matrix, and its element W_hw,kw = 1 means C_hw and C_kw are adjacent to each other, otherwise W_hw,kw = 0. So the regularization term encourages adjacent elements in C have the same label (i.e., 1 or 0). In this paper, for each element in C, its adjacent elements are set to be within its 1 voxel radius (i.e., 26-voxel neighborhood) in the same image (3D space), which corresponds to the same column of C. Optimization of (7) is composed of two steps. In the first step, $\hat{\mathit{I}}$ is updated with fixed tumor mask C, then (7) becomes

$$\underset{\hat{\mathit{I}}}{\min }\Vert (\mathbf{1}-\mathit{C})\odot (\mathit{I}-\hat{\mathit{I}}){\Vert }_F^2+\lambda \Vert \hat{\mathit{I}}{\Vert }_{*}.$$ (8)

(8) is a matrix completion problem which can be solved by soft impute method [31]. Based on the result of (8), the probability map of normal brain region P can be obtained by

$$\begin{gathered} {\mathit{P}}_{hw}=\frac{1}{W-1}\sum _{1\le l\le W \\ l\ne w}{e}^{-\frac{{(r_{hw}(|\mathit{I}-\hat{\mathit{I}}|)-r_{hl}(|\mathit{I}-\hat{\mathit{I}}|))}^2}{2}} \end{gathered}$$ (9)

where $r_{hw}(|\mathit{I}-\hat{\mathit{I}}|)$ is the average absolute residual error in 3×3×3 image patch centered at the h^th voxel (i.e., row) in the w^th image (i.e., column) of absolute residual error $|\mathit{I}-\hat{\mathit{I}}|$. It is worth noting that both $r_{hw}(|\mathit{I}-\hat{\mathit{I}}|)$ and $r_{hl}(|\mathit{I}-\hat{\mathit{I}}|)$ are calculated in 3D image space where each column of $|\mathit{I}-\hat{\mathit{I}}|$ is reformed as a 3D image. The definition of P is based on the observation that tumor regions usually have inconsistent positions and big values in $|\mathit{I}-\hat{\mathit{I}}|$, while normal brain regions usually have consistent positions and small values in $|\mathit{I}-\hat{\mathit{I}}|$. Therefore, the value of P is larger in normal brain regions than in tumor regions. In the second step, C is updated with fixed $\hat{\mathit{I}}$, then (7) can be rewritten as

$$\begin{gathered} \underset{\mathit{C}}{\min }\sum _{1\le h\le H \\ l\le w\le W}(\alpha {\mathit{P}}_{hw}-{({\mathit{I}}_{hw}-{\hat{\mathit{I}}}_{hw})}^2){\mathit{C}}_{hw} \\ +\beta \sum _{1\le h,k\le H \\ l\le w\le W}{\mathit{W}}_{hw,kw}\left|{\mathit{C}}_{hw}-{\mathit{C}}_{kw}\right|+ϵ \end{gathered}$$ (10)

where ϵ is a constant. Element in C, i.e., C_hw, tends to be 0 (normal brain regions) when P_hw is larger and 1 (tumor regions) when P_hw is smaller. This is because large P_hw indicates normal brain region, and the corresponding square residual error ${({\mathit{I}}_{hw}-{\hat{\mathit{I}}}_{hw})}^2$ is usually small. In this way, the first item of (10), i.e., $(\alpha {\mathit{P}}_{hw}-{({\mathit{I}}_{hw}-{\hat{\mathit{I}}}_{hw})}^2)$, is of high probability to be positive, which encourages C_hw to be 0. While small P_hw means tumor region, whose corresponding square residual error is usually large, making the first item of (10) be negative. So C_hw is encouraged to be 1. (10) is in the form of Markov random field and can be solve by graph cut method [32]. These two steps are iterated until convergence, for obtaining recovered images $\hat{\mathit{I}}$. It is worth noting that, in the first iteration, all elements in C are set to 0. Therefore, SCOLOR is identical to conventional low-rank methods. As the iteration goes, C is refined based on the square residual error from previous iteration. Since the objective function of SCOLOR (7) decreases in each step and has a low bound, the convergence of SCOLOR is always guaranteed.

Original SCOLOR proposed in [26] accepts monomodal images only. In this paper, we improve the original SCOLOR to make it work in the context of multimodal images. The new SCOLOR is denoted as multimodal SCOLOR. In our MAR framework, the multimodal SCOLOR is responsible for recovering the multimodal normal-looking image $\hat{\mathcal{T}}=\{{\hat{\mathcal{T}}}_{\text{T}1},{\hat{\mathcal{T}}}_{\text{T}1\text{c}},{\hat{\mathcal{T}}}_{\text{T}2},{\hat{\mathcal{T}}}_{\text{FLAIR}}\}$ from the input multimodal tumor brain image $\mathcal{T}=\{{\mathcal{T}}_{\text{T}1},{\mathcal{T}}_{\text{T}1\text{c}},{\mathcal{T}}_{\text{T}2},{\mathcal{T}}_{\text{FLAIR}}\}$ based on the information of multimodal brain atlases ${\mathcal{A}}_i=\left\{{\mathcal{A}}_{i,\text{T}1},{\mathcal{A}}_{i,\text{T}1\text{c}},{\mathcal{A}}_{i,\text{T}2},{\mathcal{A}}_{i,\text{FLAIR}}\right\}$, i = 1, ..., N. Specifically, the objective function of the multimodal SCOLOR is defined as

$$\begin{gathered} \underset{{\hat{\mathit{I}}}_{\text{mod}},\mathit{C}}{\min }\frac{1}{\left|\mathrm{mod}\right|}\sum _{\text{mod}}({\Vert (\mathbf{1}-\mathit{C})\odot ({\mathit{I}}_{\text{mod}}-{\hat{\mathit{I}}}_{\text{mod}})\Vert }_F^2+\lambda {\Vert {\hat{\mathit{I}}}_{\text{mod}}\Vert }_{*}) \\ +\alpha \sum _{1\le h\le H \\ 1\le w\le W}{\mathit{P}}_{hw}^{\prime }\cdot {\mathit{C}}_{hw} \\ +\beta \sum _{1\le h,k\le H \\ 1\le w\le W}{\mathit{W}}_{hw,kw}\left|{\mathit{C}}_{hw}-{\mathit{C}}_{kw}\right| \end{gathered}$$ (11)

where input matrices ${\mathit{I}}_{\text{mod}}=\left[{\mathcal{T}}_{\text{mod}},{\mathcal{A}}_{1,\text{mod}},\dots ,{\mathcal{A}}_{N,\text{mod}}\right]\in {ℝ}^{H\times (N+1)}$, mod ∈ {T1, T1c, T2, FLAIR}, |mod| is the number of possible modalities, and here |mod| = 4. Similar to the original SCOLOR defined in (7), optimization of (11) consists of two steps: one is the matrix completion problem which can be solved by soft impute method

$$\underset{{\hat{\mathit{I}}}_{\mathrm{mod}}}{\min }\frac{1}{\left|\mathrm{mod}\right|}\sum _{\text{mod}}({\Vert (\mathbf{1}-\mathit{C})\odot ({\mathit{I}}_{\text{mod}}-{\hat{\mathit{I}}}_{\text{mod}})\Vert }_F^2+\lambda {\Vert {\hat{\mathit{I}}}_{\mathrm{mod}}\Vert }_{*}),$$ (12)

and the other is the graph cut problem

$$\begin{gathered} \underset{\mathit{C}}{\min }(\sum _{1\le h\le H \\ l\le w\le N+1}(\alpha {\mathit{P}}_{hw}^{\prime }-\frac{1}{\left|\text{mod}\right|}\sum _{\text{mod}}{({\mathit{I}}_{hw,\text{mod}}-{\hat{\mathit{I}}}_{hw,\text{mod}})}^2){\mathit{C}}_{hw} \\ +\beta \sum _{1\le h,k\le H \\ l\le w\le N+1}{\mathit{W}}_{hw,kw}\left|{\mathit{C}}_{hw}-{\mathit{C}}_{kw}\right|+ϵ) \end{gathered}$$ (13)

where I_hw,mod and ${\hat{\mathit{I}}}_{hw,\text{mod}}$ are values at the hth row and wth column of the input matrix and the low-rank matrix of each modality, respectively. P′ is the probability map of normal brain region, which is defined by

$$\begin{gathered} {\mathit{P}}_{hw}^{\prime }=\frac{1}{W-1}\sum _{1\le l\le W \\ l\ne w}{e}^{-\frac{{\sum }_{\text{mod}}{(r_{hw}(\left|{\mathit{I}}_{\mathrm{mod}}-{\hat{\mathit{I}}}_{\text{mod}}\right|)-r_{hl}(\left|{\mathit{I}}_{\text{mod}}-{\hat{\mathit{I}}}_{\text{mod}}\right|))}^2}{2\left|\mathrm{mod}\right|}}. \end{gathered}$$ (14)

The two steps of the multimodal SCOLOR are iterated until convergence, and each modality in the recovered multimodal normal-looking image $\hat{\mathcal{T}}=\{{\hat{\mathcal{T}}}_{\text{T}1},{\hat{\mathcal{T}}}_{\text{T}1\text{c}},{\hat{\mathcal{T}}}_{\text{T}2},{\hat{\mathcal{T}}}_{\text{FLAIR}}\}$ is at the first column of the corresponding low-rank matrix ${\hat{\mathit{I}}}_{\text{mod}}=[{\hat{\mathcal{T}}}_{\text{mod}},{\hat{\mathcal{A}}}_{1,\text{mod}},\dots ,{\hat{\mathcal{A}}}_{N,\mathrm{mod}}]$, mod ∈ {T1, T1c, T2, FLAIR}. It is worth noting that, the first column of I_mod is the tumor brain image, and the rest columns are normal brain atlases. Thus, only the first column of C is needed to be calculated using (13), and the values for the rest columns of C are all 0, i.e., normal brain regions.

The core of SCOLOR is the tumor mask C, by which tumor regions can be effectively recovered without distorting normal brain regions in the recovered image. In essence, the accuracy of the tumor mask heavily depends on the intensity difference between tumor regions and normal brain regions in the input images. If tumor regions have discriminative image intensity from normal brain regions, ${({\mathit{I}}_{hw}-{\hat{\mathit{I}}}_{hw})}^2$ in (10) and $\frac{1}{|\mathrm{mod}|}{\sum }_{\mathrm{mod}}{({\mathit{I}}_{hw,\mathrm{mod}}-{\hat{\mathit{I}}}_{hw,\mathrm{mod}})}^2$, mod ∈ {T1, T1c, T2, FLAIR} in (13) will be large, making C_hw be prone to 1 (tumor regions). Comparing with (10) proposed in original SCOLOR, which is based on mono-modality, (13) utilizes multi-modality to calculate the tumor mask. Usually, tumor regions can be more easily discriminated from normal brain regions using multi-modality than mono-modality. Therefore, the resulting tumor mask calculated based on multi-modality could be more accurate and reliable than that using mono-modality. With improved tumor mask, tumor regions can be more effectively recovered and normal brain regions can be better preserved in the resulting recovered images.

C. Multi-channel image registration

At this stage, we have the multimodal brain atlases ${\mathcal{A}}_i=\left\{{\mathcal{A}}_{i,\text{T}1},{\mathcal{A}}_{i,\text{T}1\text{c}},{\mathcal{A}}_{i,\text{T}2},{\mathcal{A}}_{i,\text{FLAIR}}\right\}$, i = 1, ..., N from the Cycle-GAN based image synthesizers and the recovered multimodal image of normal-looking brain $\hat{\mathcal{T}}=\{{\hat{\mathcal{T}}}_{\text{T}1},{\hat{\mathcal{T}}}_{\text{T}1\text{c}},{\hat{\mathcal{T}}}_{\text{T}2},{\hat{\mathcal{T}}}_{\text{FLAIR}}\}$ from the multimodal SCOLOR based image recovery. Thus, each atlas ${\mathcal{A}}_i$ can be registered to $\hat{\mathcal{T}}$ in a multi-channel way, where each channel operates one modality. We choose SyN [20] to do multi-channel registration, which uses the monomodal similarity metric mean squared difference (MSD). The objective function of the multi-channel SyN is

$$\begin{gathered} \underset{d_{{\mathcal{A}}_i\to \hat{\mathcal{T}}}}{\min }(\sum _{\text{mod}\in \{\text{T}1,\text{T}1\text{c}, \\ \text{T}2,\text{FLAIR}\}}\frac{1}{H}\sum _{x\in \mathrm{\Omega }}({\hat{\mathcal{T}}}_{\text{mod}}(x) \\ -{\mathcal{A}}_{i,\mathrm{mod}}\circ d_{{\mathcal{A}}_i\to \hat{\mathcal{T}}}(x){)}^2) \end{gathered}$$ (15)

where $d_{{\mathcal{A}}_i\to \hat{\mathcal{T}}}$ is the deformation field warping ${\mathcal{A}}_i$ to $\hat{\mathcal{T}}$, Ω is the whole image, and H is the number of voxels in an image.

In our MAR framework, the multimodal SCOLOR based image recovery and the multi-channel image registration components are iteratively proceeded to mutually refine their results until convergence. Specifically, in the t^th iteration, the original multimodal brain atlases ${\mathcal{A}}_i$, i = 1, ..., N are warped using the deformation fields $d_{{\mathcal{A}}_i\to {\hat{\mathcal{T}}}^{t-1}}$, i = 1..., N produced by the multi-channel image registration in the previous iteration, i.e., ${\mathcal{A}}_i\circ d_{{\mathcal{A}}_i\to {\hat{\mathcal{T}}}^{t-1}}$, $i=1,\dots ,N({\hat{\mathcal{T}}}^{t-1}$ is the recovered multimodal image in the previous iteration). The warped multimodal brain atlases and the original input multimodal tumor brain image $\mathcal{T}=\left\{{\mathcal{T}}_{\text{T}1},{\mathcal{T}}_{\text{T}1\text{c}},{\mathcal{T}}_{\text{T}2},{\mathcal{T}}_{\text{FLAIR}}\right\}$ can then be combined into new input matrices ${\mathit{I}}_{\text{mod}}^t=$ $[{\mathcal{T}}_{\text{mod}},{\mathcal{A}}_{1,\mathrm{mod}}\circ d_{{\mathcal{A}}_1\to {\hat{\mathcal{T}}}^{t-1}},\dots ,{\mathcal{A}}_{N,\mathrm{mod}}\circ d_{{\mathcal{A}}_N\to {\hat{\mathcal{T}}}^{t-1}}]$, mod ∈ {T1, T1c, T2, FLAIR}, which are proceeded by the multimodal SCOLOR based image recovery to get the new recovered multimodal image ${\hat{\mathcal{T}}}^t$. Then the original multimodal brain atlases ${\mathcal{A}}_i$, i = 1, ..., N are registered to the new recovered multimodal image ${\hat{\mathcal{T}}}^t$ by the multi-channel image registration. The resulting deformation fields $d_{{\mathcal{A}}_i\to {\hat{\mathcal{T}}}^t}$, i = 1..., N are used to warp the original multimodal brain atlases ${\mathcal{A}}_i$, i = 1, ..., N again for the next iteration.

It is worth noting that in the first iteration (t=1), the multimodal brain atlases in ${\mathit{I}}_{\text{mod}}^t$ are aligned to the input multimodal tumor brain image $\mathcal{T}$ by affine transformation on T1 modality, i.e., ${\mathit{I}}_{\text{mod}}^t=[{\mathcal{T}}_{\text{mod}},{\mathcal{A}}_{1,\text{mod}}\circ d_{{\mathcal{A}}_{1,\text{T}1}\mapsto {\mathcal{T}}_{\text{T}1}},\dots ,{\mathcal{A}}_{N,\text{mod}}\circ d_{{\mathcal{A}}_{N,\text{T}1}\mapsto {\mathcal{T}}_{\text{T}1}}]$, mod ∈ {T1, T1c, T2, FLAIR}, where $d_{{\mathcal{A}}_{i,\text{T}1}\mapsto {\mathcal{T}}_{\text{T}1}}$, i = 1, ..., N means the affine transformation from ${\mathcal{A}}_{i,\text{T}1}$ to ${\mathcal{T}}_{\text{T}1}$. It is clear that images cannot be well aligned using affine transformation only. Therefore large modification in ${\mathit{I}}_{\text{mod}}^t$ is needed in the multimodal SCOLOR based image recovery to meet the low rank criterion, which results in a relatively low quality recovered multimodal image ${\hat{\mathcal{T}}}^t$. Such kind of ${\hat{\mathcal{T}}}^t$ could also make the subsequent multi-channel image registration inconvenience. As the iteration goes, images in ${\mathit{I}}_{\text{mod}}^t$ get well aligned. Therefore, little modification in ${\mathit{I}}_{\text{mod}}^t$ is required to make ${\hat{\mathit{I}}}_{\text{mod}}^t$ satisfy the low-rank criterion, making the recovered multimodal image ${\hat{\mathcal{T}}}^t$ has more consistent normal brain regions with $\mathcal{T}$ in each modality. In turn, with improved recovered multimodal image ${\hat{\mathcal{T}}}^t$, images in ${\mathit{I}}_{\text{mod}}^t$ can get further aligned. The iteration stops when ${\hat{\mathcal{T}}}^t$ is stable or changes little.

III. Results

We evaluate our MAR framework via multi-atlas segmentation (MAS) of brain ROI of multimodal tumor brain images. Specifically, a label fusion stage is added after our MAR framework to get the final segmentation result from registered atlases for each input image. The accuracy of the final segmentation result mainly depends on the registration quality between the atlases and the input image. Both synthetic and real multimodal tumor brain images are used to evaluate our method. Each multimodal tumor brain image contains four modalities: T1, T1c, T2 and FLAIR. In addition, other four different MAS methods, which use different MAR frameworks, are also tested. Particularly, the first MAS method uses conventional MAR framework, which registers each brain atlas to the input image by typical image registration methods, hence it can only handle normal brain images, and we denote it as ORI+MAS. The second MAS is based on the MAR framework which adopts a well-known strategy called cost function masking (CFM) [13] for registering normal brain atlases to pathological brain images, and we denoted it as CFM+MAS. The third one integrates a conventional low-rank method i.e., LRSD (defined in (6)) to handle registration of tumor brain images, and we denote it as LRSD+MAS. The last one is similar as LRSD+MAS except that the low-rank method is SCOLOR (defined in (7)) instead of LRSD, and we denoted it as SCOLOR+MAS. LRSD+MAS and SCOLOR+MAS have similar processing flow as our method, where image recovery and registration of normal brain atlases to the recovered image are iterated until convergence. The difference is that our method works with multimodal images while monomodal images are used in LRSD+MAS and SCOLOR+MAS. Note that, these four MAS methods can only handle monomodal brain images which have the same modality as the adopted brain atlases. For CFM+MAS, the tumor mask used in original CFM is delineated manually, but for the sake of fairness, the tumor mask used in CFM+MAS is the same as the tumor mask calculated in SCOLOR+MAS. The brain atlases used in all methods under comparison are T1-weighted MR normal brain images from LPBA40 [33], and each brain atlas carries 54 manually labeled brain ROIs. Therefore, except our method, ORI+MAS, CFM+MAS, LRSD+MAS and SCOLOR+MAS can only use T1 modality of the multimodal tumor brain images. The registration algorithm used in our method is multi-channel SyN, and the other four MAS methods under comparison use single-channel SyN. All the MAS methods under comparison adopt joint label fusion [9] to do the label fusion. Table I gives the summary of all MAS methods under comparison. The multimodal tumor brain images are preprocessed by affine transformation [34] with reference to MNI152 [35] of 182×218×182 voxels (1×1×1 mm³ voxel) and histogram matching [36] with reference to a multimodal brain atlas used in our method (i.e., generated by the Cycle-GAN based image synthesizers).

Table I.

List of all methods under comparision in the experiment.

Method name	Atlas modality	Input modality	Tumor strategy	Registration	Iterative process	Label fusion
ORI+MAS	monomodal (T1)	monomodal (T1)	not applied	SyN (single channel)	no	joint label fusion
CFM+MAS	monomodal (T1)	monomodal (T1)	cost function masking	SyN (single channel)	no	joint label fusion
LRSD+MAS	monomodal (T1)	monomodal (T1)	low-rank recovery (LRSD)	SyN (single channel)	yes	joint label fusion
SCOLOR+MAS	monomodal (T1)	monomodal (T1)	low-rank recovery (SCOLOR)	SyN (single channel)	yes	joint label fusion
Our method	monomodal (T1)	multimodal (T1,T1c,T2, FLAIR)	low-rank recovery (multimodal SCOLOR)	SyN (multi-channel)	yes	joint label fusion

A. Parameter tuning

Like most low-rank based methods [17], [26], [37], [38], in LRSD+MAS, SCOLOR+MAS and our method, the parameter λ, which is used to balance the residual error constraint and the low-rank constraint, is heuristically determined in the experiment. Actually, the recovered images are relatively insensitive to λ, and the final segmentation results of our method keep a relatively consistent quality within a large range of λ. Particularly, for all the testing images including synthetic and real tumor brain images, λ is set to 800 in LRSD+MAS and 40 in SCOLOR+MAS and our method. In section III-D, we will show the impact of λ on the final segmentation results of SCOLOR+MAS and our method. Parameters α and β in SCOLOR (see (10)) and multimodal SCOLOR (see (13)) are used to control the balance between the constraint and the regularization terms of the tumor mask C. In the experiment, we set α = 0.08 and β = 1 for SCOLOR in SCOLOR+MAS, and α = 0.1 and β = 1 for multimodal SCOLOR in our method. In section III-E, we will show the impact of α and β on the resulting tumor mask C in SCOLOR+MAS and our method.

B. Evaluation of synthetic tumor brain images

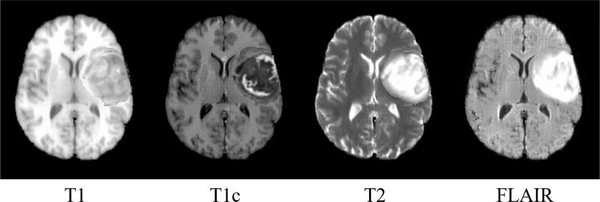
The synthetic multimodal tumor brain images are produced based on LPBA40 image dataset which consists of 40 T1-weighted MR normal brain images of different subjects. For each test, one image from LPBA40 is selected to make the synthetic multimodal tumor brain image, and the rest are used as the available monomodal brain atlases. Specifically, a synthetic multimodal normal brain image is first produced from the selected image by CycleGAN based image synthesizers. Then tumor(s) in a real multimodal tumor brain image, which is randomly selelcted from BRATS2015 [30], are inserted into the synthetic multimodal normal brain image. The mass effect of the inserted tumor(s) is also considered. Particularly, since images are aligned with MNI152 by affine transformation in the preprocessing stage, tumor regions in the real multimodal tumor brain image are directly used to replace the image contents at the same location of the synthetic multimodal normal brain image. The mass effect of the inserted tumor(s) to the surrounding normal tissues is simulated by adding deformation fields at the boundaries of the inserted tumor(s) (with perpendicular direction to the tumor boundaries and diffused by a Gaussian kernel with σ = 3.0) to deform the surrounding normal tissues. The magnitude of the resulting deformation vectors at the boundary of the inserted tumor(s) is around 3 mm. An example of a synthetic multimodal tumor brain image is shown in Fig. 3.

Fig. 3.

An example of a synthetic multimodal tumor brain image.

Totally, 40 synthetic multimodal tumor brain images, each of which contains tumor(s) from different real multimodal tumor brain image in BRATS2015, are made and tested in our experiment. Details of the 40 synthetic multimodal tumor brain images are listed in the supplement. Since we have the ground truth of tumor-free image and the corresponding 54 manually labeled brain ROIs for each synthetic multimodal tumor brain image, recovery quality (for LRSD+MAS, SCOLOR+MAS and our method) and segmentation accuracy are evaluated. The recovery quality is quantified by recovery error ratio which is defined as

$$E_{rc}\text{=}\frac{{\sum }_{x\in \mathrm{\Omega }}\left|{\hat{\mathcal{T}}}_{\text{mod}}(x)-{\mathcal{G}}_{\mathrm{mod}}(x)\right|}{{\sum }_{x\in \mathrm{\Omega }}\left|{\mathcal{G}}_{\mathrm{mod}}(x)\right|},$$ (16)

where Ω stands for the whole image, ${\hat{\mathcal{T}}}_{\mathrm{mod}}(x)$ and ${\mathcal{G}}_{\mathrm{mod}}(x)$ are image intensities at position x in the recovered image and the ground truth of tumor-free image of certain modality, respectively. Since the real tumor-free images are T1-weighted MR images, and only T1-weighted recovered images can be produced by LRSD+MAS and SCOLOR+MAS, the recovery error ratio is evaluated using T1 modality, i.e., mod = T1.

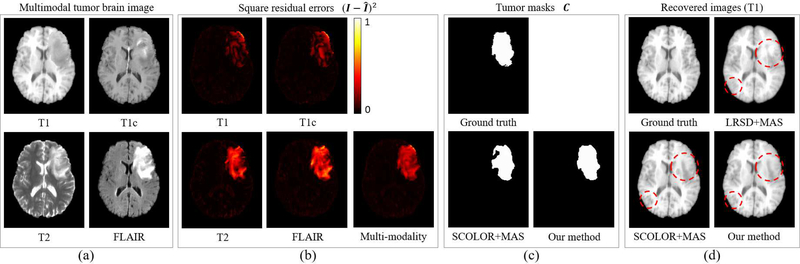
Fig. 4 shows some recovered images in LRSD+MAS, SCOLOR+MAS and our method. Specifically, Fig. 4 (a) shows an input synthetic multimodal tumor brain image. The square residual errors of each modality using SCOLOR, i.e., ${({\mathit{I}}_{\text{mod}}-{\hat{\mathit{I}}}_{\text{mod}})}^2$, and multi-modality using multimodal SCOLOR, i.e., $\frac{{\sum }_{\text{mod}}{({\mathit{I}}_{\text{mod}}-{\hat{\mathit{I}}}_{\text{mod}})}^2}{|\mathrm{mod}|}$, mod ∈ {T1, T1c, T2, FLAIR}, are shown in Fig. 4 (b). The resulting tumor masks are presented in Fig. 4 (c). Since the tumor mask C of multimodal SCOLOR in our method is calculated based on the square residual error of multi-modality, the resulting tumor mask is much closer to the ground truth than SCOLOR in SCOLOR+MAS which is based on the square residual error of T1 modality. Consequently, the recovered image of our method contains more effectively recovered tumor regions and better preserved normal brain regions than both LRSD+MAS and SCOLOR+MAS, especially in the regions marked by red circles in Fig. 4 (d).

Fig. 4.

(a) Example of input synthetic multimodal tumor brain image; (b) The square residual errors of each modality using SCOLOR and multi-modality using multimodal SCOLOR; (c) The tumor masks calculated by SCOLOR in SCOLOR+MAS and multimodal SCOLOR in our method. Since the multimodal SCOLOR utilizes multimodal information, the tumor mask is much closer to the ground truth than SCOLOR which is based on T1-weighted MR images only; (d) The recovered image of our method contains more effectively recovered tumor regions and better preserved normal brain regions than LRSD+MAS and SCOLOR+MAS, especially in the regions marked by red circles.

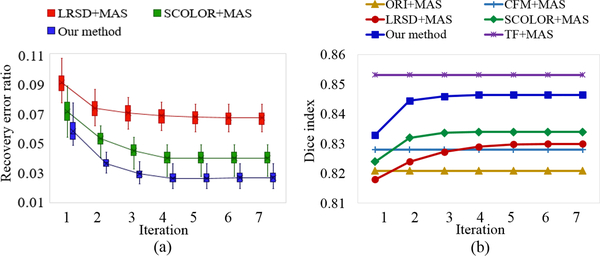
Details of the evaluation result of recovery error ratio using LRSD+MAS, SCOLOR+MAS and our method are shown in Fig. 5 (a). The recovery error ratios of the three methods decrease after each iteration. This is because as atlases and synthetic tumor brain images get well aligned after each iteration, less modification in the input image matrix is required to make the resulting recovered images satisfy the low-rank constraint. Due to the tumor mask in SCOLOR and multimodal SCOLOR, normal brain regions are well preserved, making the recovered images of SCOLOR+MAS and our method closer to their ground truth tumor-free images than LRSD+MAS. In contrast, normal brain regions are usually distorted in the recovered images using LRSD. Therefore, recovery error ratios of SCOLOR+MAS and our method are smaller than LRSD+MAS after each iteration. Since the multimodal SCOLOR used in our method works with multimodality where complementary information of tumor regions of different modalities is used, the tumor mask calculated in the multimodal SCOLOR is more accurate than the SCOLOR used in SCOLOR+MAS. Furthermore, as different modalities may contain exclusive features of the same anatomical structure, images could be better registered in multi-channel way than single-channel way. As a result, the recovery error ratio of our method is the smallest. For each synthetic brain tumor image, LRSD+MAS needs less than 7 iteration to reach to convergence, while less than 4 iterations are required for SCOLOR+MAS and our method.

Fig. 5.

(a) Recovery error ratios of 40 synthetic tumor brain images after each iteration of LRSD+MAS, SCOLOR+MAS and our method; (b) Average of 40 whole-brain Dice indices of segmented synthetic tumor brain images after each iteration using ORI+MAS, CFM+MAS, LRSD+MAS, SCOLOR+MAS, our method and TF+MAS. TF+MAS applies the same MAS method as ORI+MAS to segment original tumor-free images in LPBA40. ORI+MAS, CFM+MAS and TF+MAS have no iterative process, so their average Dice indices after each iteration are constant.

Segmentation results are evaluated by calculating the Dice index [39] of the whole brain (54 brain ROIs) between each segmented result and the corresponding ground truth, which is defined as

$$\sum _{i=1}^{54}\frac{V_i^{\text{GT}}}{V^{\text{GT}}}\cdot \frac{2\left|{\mathrm{\Omega }}_i^{\text{seg}}\cap {\mathrm{\Omega }}_i^{\text{GT}}\right|}{\left|{\mathrm{\Omega }}_i^{\text{seg}}\right|+\left|{\mathrm{\Omega }}_i^{\text{GT}}\right|},$$ (17)

where V^GT and $V_i^{\text{GT}}$ are the volume (number of voxel) of the whole brain and the i^th brain ROI in the ground truth, respectively. ${\mathrm{\Omega }}_i^{\text{seg}}$ and ${\mathrm{\Omega }}_i^{\text{GT}}$ are the segmented i^th brain ROI and its corresponding ground truth, respectively. Fig. 5 (b) shows the average of 40 whole-brain Dice indices of segmented synthetic tumor brain images using ORI+MAS, CFM+MAS, LRSD+MAS, SCOLOR+MAS, and our method after each iteration. Moreover, original tumor-free images of LPBA40 are also tested using the same MAS method as ORI+MAS, which is denoted as TF+MAS in Fig. 5 (b). Obviously, TF+MAS achieves the highest average whole-brain Dice index of all methods under comparison. Because of distorted normal brain regions in recovered images using LRSD, the average whole-brain Dice index after the first iteration of LRSD+MAS is even lower than ORI+MAS. But as the iteration goes in LRSD+MAS, atlases get aligned with input tumor brain images, which improve both the recovered images and the registration results, eventually outperforming ORI+MAS after the second iteration. The averages and standard deviations of the 40 whole-brain Dice indices after the final iteration of all methods under comparison are ORI+MAS (0.821±0.015), CFM+MAS (0.828±0.017), LRSD+MAS (0.83±0.018), SCOLOR+MAS (0.834±0.017), our method (0.847±0.012) and TF+MAS (0.853±0.01). The Wilcoxon signed rank test [40] is adopted to do statistical significance test over the 40 whole-brain Dice indices after the final iteration of ORI+MAS, CFM+MAS, LRSD+MAS, SCOLOR+MAS and our method. The p values between our method and other four methods are all 3.569×10⁻⁸, indicating that our method is better than the other four methods with statistical significance.

C. Evaluation of real tumor brain images

Totally, 50 real multimodal tumor brain images of different subjects are randomly selected from BRATS2015 as testing images. Details of the 50 real multimodal tumor brain images are listed in the supplement. 40 T1-weighted MR normal brain images from LPBA40 are used as brain atlases in all methods under comparison. For each testing image, LRSD+MAS requires no more than 6 iterations to reach to convergence, whereas SCOLOR+MAS and our method need no more than 4 iterations. Due to the lack of tumor-free images, recovery error ratio cannot be calculated, and the recovery quality is evaluated by visual inspection. Benefiting from multimodal SCOLOR, the recovered images in our method have better visual quality than LRSD+MAS and SCOLOR+MAS. Fig. 6 shows an example of a real multimodal tumor brain image and its corresponding recovered T1-weighted MR images using LRSD+MAS, SCOLOR+MAS and our method after the final iteration. It is clear that, in the square residual error using multimodal SCOLOR, high value elements cover most of the tumor regions than the square residual error of each modality using SCOLOR (see Fig. 6 (b)). Therefore, as Fig. 6 (c) shows, the tumor mask calculated by multimodal SCOLOR in our method (based on the square residual error of multi-modality) is much closer to the ground truth than SCOLOR in SCOLOR+MAS (based on the square residual error of T1 modality). As a result, the recovered image of our method contains more effectively recovered tumor regions and better preserved normal brain regions than LRSD+MAS and SCOLOR+MAS, especially in the regions marked by red circles in Fig. 6 (d).

Fig. 6.

(a) Example of input real multimodal tumor brain image; (b) The square residual errors of each modality using SCOLOR and multi-modality using multimodal SCOLOR; (c) The tumor masks calculated by SCOLOR in SCOLOR+MAS (based on the square residual error of T1 modality) and multimodal SCOLOR in our method (based on the square residual error of multi-modality); (d) The recovered image of our method contains more effectively recovered tumor regions and better preserved normal brain regions than LRSD+MAS and SCOLOR+MAS, especially in the regions marked by red circles.

Segmentation results are evaluated by calculating Dice indices of grey matter (GM), whiter matter (WM), and cerebrospinal fluid (CSF) between the segmented result of each method and the ground truth. Specifically, we use SPM12 [41] to coarsely segment GM, WM and CSF from the 50 tumor brain images and the 40 brain atlases. Then these segmented results are further revised by an expert and regarded as the ground truth. Fig. 7 shows the Dice indices of GM, WM and CSF of the segmentation results using ORI+MAS, CFM+MAS, LRSD+MAS, SCOLOR+MAS and our method after each iteration. It is worth noting that tumor regions are ignored in the calculation of Dice index. Our method outperforms other methods in GM, WM and CSF after each iteration. LRSD+MAS gets the lowest Dice indices of GM, WM, and CSF after the beginning iterations because of distorted normal brain regions in the recovered images.

Fig. 7.

Average Dice indices of segmented GM, WM, and CSF of 50 real MR tumor brain images using ORI+MAS, CFM+MAS, LRSD+MAS, SCOLOR+MAS, and our method after each iteration.

Table II shows average Dice indices and standard deviations of GM, WM, and CSF of the final segmentation results using ORI+MAS, CFM+MAS, LRSD+MAS, SCOLOR+MAS, and our method. Statistical significance test is perform over these evaluation results (50 Dice indices of GM, WM, and CSF for each method) using Wilcoxon signed rank test. Our method outperforms all the other methods in GM, WM and CSF with statistical significance (p < 0.05).

Table II.

Average Dice index and standard deviation of the final sigmentation result obtained by each method under comparision.

	GM	WM	CSF
ORI+MAS	0.639±0.050	0.698±0.040	0.566±0.053
CFM+MAS	0.657±0.045	0.712±0.034	0.571±0.047
LRSD+MAS	0.657±0.038	0.711±0.036	0.573±0.038
SCOLOR+MAS	0.669±0.044	0.719±0.036	0.580±0.046
Our method	0.701±0.035*	0.748±0.030*	0.593±0.041*

Asterisk indicates the evaluation result is better than the other four methods with statistical significance (P<0.05 in Wilcoxon signed rank test).

D. Impact of λ on the segmentation result

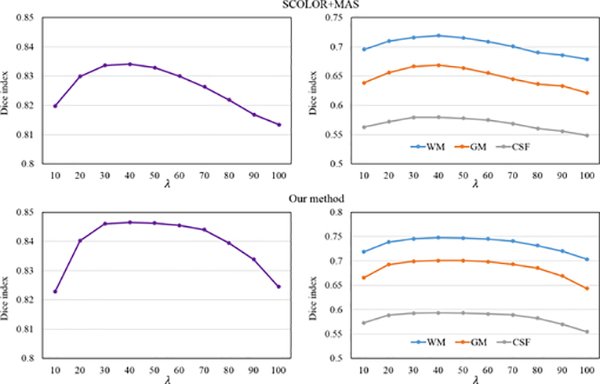
The 40 synthetic and 50 real tumor brain images are used to evaluate the impact of the parameter λ in SCOLOR and multimodal SCOLOR on the segmentation result of SCOLOR+MAS and our method. Specifically, we test SCOLOR+MAS and our method using λ from 10 to 100 with step size of 10. For each λ, we calculate the Dice indices of the corresponding segmentation results of SCOLOR+MAS and our method. Fig. 8 shows the evaluation result. It is clear to see that as the λ increases, the Dice indices of segmentation results using both SCOLOR+MAS and our method are first increased because of the recovered tumor regions and then decreased because of the distorted normal brain regions using large λ, i.e., over strength low-rank constraint. The segmentation results of both SCOLOR+MAS and our method are good and stable using λ from 30 to 60. Furthermore, since multimodal SCOLOR and multi-channel registration are used in our method, the segmentation result of our method is more stable than SCOLOR+MAS. For example, the largest differences of the average whole-brain Dice index of segmented 40 synthetic tumor brain images using λ within the range of 30–60 are 0.004 (SCOLOR+MAS) and 0.001 (our method), and the largest differences of the average Dice indices of GM, WM, and CSF of segmented 50 real tumor brain images using λ within the range of 30–60 are 0.01, 0.013, and 0.005 (SCOLOR+MAS), and 0.002, 0.003, and 0.002 (our method). Therefore, we set λ to 40 for SCOLOR+MAS and our method in the experiment as mentioned before.

Fig. 8.

Average whole-brain Dice indices of 40 segmented synthetic tumor brain images (left) and average Dice indices of GM, WM and CSF of 50 real tumor brain images (right) using different λ in SCOLOR+MAS (top) and our method (bottom).

E. Impact of α and β on tumor mask

For both SCOLOR used in SCOLOR+MAS and multimodal SCOLOR used in our method, the tumor mask C, which is used to discriminate tumor regions and normal brain regions, plays an important role. For tumor regions defined in C (values of corresponding elements in C are 1), strong recovery is performed, while relatively weak recovery is used for normal brain region defined by C (values of corresponding elements in C are 0). Therefore, with accurate tumor mask, recovered images of effectively recovered tumor regions and well preserved normal brain regions can be produced. According to the objective functions of C, i.e., (10) (SCOLOR) and (13) (multimodal SCOLOR), the result of tumor mask C is influenced by parameters α and β which control the strength of the constraint and regularization terms imposed on C. In our experiment, we evaluate the impact of α and β on the resulting tumor mask C after the final iteration of SCOLOR+MAS and our method. Particularly, we evaluate the resulting tumor masks for the 90 tumor brain images (40 synthetic and 50 real tumor brain images) using different value of α and β. For each tumor brain image, its corresponding manually segmented tumor regions are available and used as the ground truth. We change α and β separately and calculate the average Recall and Precision [42] of the resulting tumor masks according to the ground truth. Evaluation result is shown in Fig. 9. High Recall means most of tumor regions are correctly defined in the tumor mask, and tumor regions can be effectively recovered. High Precision means most tumor regions defined by the tumor mask are correct, and normal brain regions can be well preserved in the recovered image. As shown in Fig. 9 left, when α becomes bigger, Recall is decreased and Precision is increased. Similar results can be observed when β becomes bigger as shown in Fig. 9 right, except that Recall and Precision are relatively more stable within a large range of β than that of α. It is clear that high Recall and Precision of the resulting tumor masks could produce good recovered images, which could enhance the subsequent image registration as well as the final segmentation result. Therefore, a trade-off between Recall and Precision has to be made. In our experiment, we found that for recovered images, ineffectively recovered tumor regions could degrades the registration quality and the final segmentation result more than low-rank distorted normal brain regions of comparable region size. So as α or β increase, the registration quality and the final segmentation result would be first improved as the shrunken low-rank distorted normal brain regions, which are much larger than the real tumor regions at the beginning (i.e., high Recall and low Precision). Then as the low-rank distorted normal brain regions shrink to a comparable size as the ineffectively recovered tumor regions (i.e., similar Recall and Precision), the registration quality and the final segmentation result would be degraded. So as aforementioned, in the experiment, α is set to 0.08 (SCOLOR+MAS) and 0.1 (our method), and β is set to 1 for both SCOLOR+MAS and our method. The corresponding average Recall and Precision of the 90 tumor images after the final iteration of SCOLOR+MAS and our method are (0.701, 0.670) and (0.833, 0.785), respectively. It is clear that, the average Recall and Precision of our method are higher than SCOLOR+MAS. This is because tumor regions are more discriminative using information from multimodal images than monomodal images. Table III shows the average Recall, Precision and Dice index of the tumor masks of 40 synthetic and 50 real brain images after the final iteration of SCOLOR+MAS and our method in detail.

Fig. 9.

Average Recall (left) and Precision (right) of resulting tumor masks after the final iteration of SCOLOR+MAS (top) and our method (bottom) using different α and β.

Table III.

Evaluation result of tumor masks calculated by SCOLOR in SCOLOR+MAS (S) and multimodal SCOLOR in our method (O).

	Recall	Precision	Dice
Synthetic tumor brain images	0.73±0.07 (S)	0.70±0.17 (S)	0.70±0.10 (S)
	0.90±0.05* (O)	0.83±0.12* (O)	0.86±0.08* (O)
Real tumor brain images	0.68±0.12 (S)	0.65±0.18 (S)	0.64±0.10 (S)
	0.78±0.10* (O)	0.75±0.13* (O)	0.76±0.10* (O)

Asterisk means statistical significance (P<0.05 in Wilcoxon signed rank test).

IV. Conclusion

We proposed a new multi-atlas registration (MAR) framework for input multimodal pathological images using conventional monomodal normal atlases. Our framework systematically solved two challenging problems in existing MAR methods: one is the missing modality in monomodal normal atlases, and the other is the registration of normal atlases to pathological images. Specifically, by using deep learning (CycleGAN) based image synthesizers, desired modalities can be produced from available monomodal normal atlases. With the proposed multimodal SCOLOR based image recovery, influence of pathological regions in registration can be effectively reduced. Finally, information of multimodal atlases and recovered images is fully utilized by multi-channel image registration. In our experiment, synthetic and real tumor brain images were used to evaluate our method. Our method showed better performance than state-of-the-art methods in terms of both image recovery quality and segmentation accuracy (i.e., registration accuracy between atlases and input images).

Theoretically, input images of any possible number and types of modalities can be handled by our framework using conventional monomodal normal atlases. Moreover, images containing pathological regions which have similar properties as the brain tumor (e.g., relatively large region, inconsistent location across subjects and different image appearance from normal regions) can be proceeded by our framework.