Mechanical stimuli in the local in vivo environment in bone: Computational approaches linking organ-scale loads to cellular signals

Abstract

Purpose of Review

Connecting organ-scale loads to cellular signals in their local in vivo environment is a current challenge in the field of bone (re)modelling. Understanding this critical missing link would greatly improve our ability to anticipate mechanotransduction during different modes of stimuli, and the resultant cellular responses. This review characterises computational approaches that could enable coupling links across the multiple scales of bone.

Recent Findings

Current approaches using strain and fluid shear stress concepts have begun to link organ-scale loads to cellular signals, however these approaches fail to capture localised microstructural heterogeneities. Furthermore, models that incorporate downstream communication from osteocytes to osteoclasts, bone-lining cells and osteoblasts, will help improve the understanding of (re)modelling activities. Incorporating this potentially key information in the local in vivo environment will aid in developing multiscale models of mechanotransduction that can predict or help describe resultant biological events related to bone (re)modelling.

Summary

Progress towards multiscale determination of the cell mechanical environment from organ-scale loads remains elusive. Construction of organ-, tissue- and cell-scale computational models that include localised environmental variation, strain amplification, and intercellular communication mechanisms will ultimately help couple the hierarchal levels of bone.

Introduction

Within the last few decades, significant advances in imaging and computational technologies have allowed new insights into biomedical phenomena. However, our ability to utilize these tools has struggled to keep pace with their rapidly expanding capabilities. In the field of bone biomechanics, this is evident in our lack of understanding how organ-scale loads translate to biochemical responses via cellular mechanotransduction. Such information would help to gain deeper insight into how cells respond to loading modalities, leading to computationally driven understanding of, and therapies for, skeletal diseases such as osteoporosis (1). This review discusses how the transmission of in vivo mechanical stimuli across multiple scales can be greatly improved by using computational methods, often in conjunction with other well-established approaches. The aim is to define a computationally driven framework for translating organ-scale loads into relevant cell-scale responses, which would ultimately increase our understanding of the in vivo mechanosensitive aspects and mechanisms of bone (re)modelling, and its importance in the pathophysiology of bone.

Existing Tools, Techniques and Concepts

The knowledge of bone systems biomechanics is not new, though translating this into substantial improvements in bone health is yet to be realised. The theory of load driven bone (re)modelling was first postulated over a century ago (2, 3), however, only with the development of powerful in vivo imaging techniques, such as micro-computed tomography (micro-CT), has detailed time-lapsed microscale observation of bone (re)modelling for both formation and resorption been possible (4, 5). Concurrently, advances in computational power has driven the development of predictive models of mechanical loading within bone tissue (6–8). Coupling these technologies has revealed great insights into dynamic bone (re)modelling via comparisons between mechanical loading and structural changes in bone tissue (6, 9–11). As these imaging and computational modelling methods have matured, they have become accurate enough to inform techniques such as laser capture microdissection to investigate individual cells within the bone tissue, and to perform “mechanomic” analysis, reconciling genetic responses to mechanical stimuli (12, 13) of the acquired cells (14, 15). The extraction of small populations of cells (16) and the assessment of their molecular and genetic profiles (17) has been combined with computational predictions of mechanical loads within the local in vivo environment (LivE) of these cells (17), advancing our understanding of how organ-scale loads influence individual cells and the resultant (re)modelling behaviour. Understanding the mechanical environment in which these cell populations reside is a key link in the chain towards understanding the governing mechanisms between mechanical loads and (re)modelling of bone.

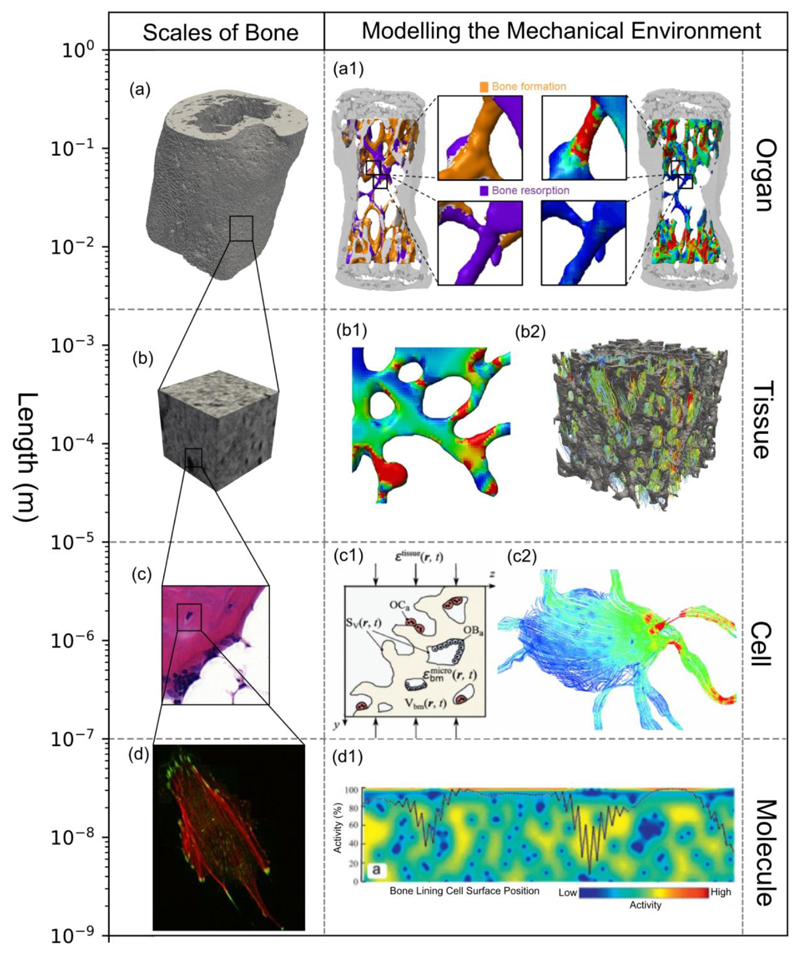
Within bone, the organ, tissue and cell scales are linked via complex macro- and micro-structural geometries. The hierarchical structure of bone can be subdivided into four scales: the organ scale, comprising the whole bone; the tissue scale, consisting of cortical and trabecular structures; the cell scale, which also includes microstructural features such as osteons, lamellae plates, lacunae and canaliculi (18); and the molecular scale, consisting of ions (19) and proteins such as signalling molecules, receptor and ligands (20). At the larger scales, mechanical supporting roles are evident from the flaring of proximal condyles in bone, to the changing density and thickness of trabecular struts. However, at the cell-scale and beyond, the functionality is less obvious. These scales and their respective computational approaches can be seen in Figure 1. This environment extends into the bone marrow, where many of the mechanosensitive cells reside, such as osteoblasts, osteoclasts, bone lining cells and mesenchymal and hemapoetic stem cells. Accurately imaging and modelling the multiscale structures of bone is fundamental to predicting multiscale mechanotransduction. Capturing these features using in vivo imaging and converting the organ and tissue scale geometries into a computational model is well established (4, 5). However, in vivo imaging beyond the cell-scale poses a significant challenge. Technologies such as confocal microscopy (21), synchrotron radiation computed tomography (22) and ultra-high-resolution computed tomography (23) have been applied ex vivo to attempt to capture the microstructural geometry. With these methods, several authors (22, 24) have performed comprehensive analyses of osteocyte networks and individual lacunae, assessing typical densities and distributions (22, 23), as well as studies on strain amplification on individual lacunae-canaliculi structures (21). Even with the multitude of tools and techniques available to gather information, they are often single-scale focused, and seem to struggle coupling the hierarchies of bone.

Figure 1. Capturing the mechanical environment over different scales has been performed using many approaches.

(a) Organ scale, (b) Tissue scale, (c) Cell scale, and (d) Molecular scale (69) have been captured by (a1 – c2). Micro-FE models such as (a1) Schulte et al. (63) and (b1) Lambers et al. (61) have been applied at organ level to calculate the tissue level mechanical environment. Within the tissue level, localised tissue boundary conditions can be used to calculate a reduced tissue scale bone marrow environment, such as (b2) investigated by Metzger et al. (71). The RVE (c1) concept can be applied to link organ-scale loads to a BMU type environment such as that by Lerebours et al. (52) Boundary conditions from the lower end of the tissue scale can be applied to determine fluid flow stresses on the cell, as seen by Vaughan et al. (43) in (c2). In the molecular scale, stretch, primary cilia deformation and signalling between osteocytes and other mechanosensitive cells can be simulated; an example of this is the model by Jahani et al. (80) studying the osteocyte – bone lining cell signalling pathways (d1). a1 reproduced in adherence with the CC BY licence applied by PLOS One, b1, b2, d1 reproduced with permission from Elsevier and c1,c2, d reproduced with permission from Springer.

Bridging the Multiple Scales with Computational Models

Organ and Tissue-Scale Load Determination

Micro-finite element analysis (micro-FE) has become a standard for organ and tissue-scale load calculations in bone. It has been extensively used for in vivo studies to compare and correlate strain with bone resorption, formation and quiescence (8, 10, 25–29). Such models are created with a mesh generated by direct conversion of micro-CT voxels into hexahedral elements, and solved using well-established micro-FE principles (30). In contrast to traditional FE approaches, this micro-FE approach provides simple meshing, and a unified approach to solving large-sacle problems. The resolution of these models is governed by the resolution of the scanner settings, which typically ranges from 10 to 80 micrometres in vivo (4), where the very high resolution images provide voxels in the same size range as osteocytes and osteoblasts, but substantially less than osteoclasts. Primarily these models are elastic, isotropic, and homogenous, omitting ultrastructural details. Further simplification includes modelling of cyclic and dynamic organ-scale boundary conditions as static loads (10, 29), shown still capable of capturing (re)modelling behaviour (31). Schulte at al. (10) and Lambers et al. (26) applied the micro-CT to micro-FE approach to determine the mechanical environment and its effect on bone (re)modelling in mouse tail vertebrae under normal (10, 26), ovarectomised (10) and aging conditions (26). For both studies, strain energy density (SED) was calculated for each voxel in the vertebrae, with this SED-voxel value representing the mechanical stimuli present at the bone surface. This allowed for correlation of SED values to in vivo formation or resorption at that same voxel. Cresswell et al. (23, 29) applied a similar approach to calculate the mechanical in vivo environment during (re)modelling in rat vertebrae. Micro-CT images of rat vertebrae were converted to micro-FE appropriate hexahedral element using custom software and solved using ABAQUS (29) or a custom solver (23). Similarly, the SED, maximum principle strain and von Mises stress for each element represented the local mechanical in vivo environment. Using florescent markers of bone formation, they correlated high bone formation with high SED values. In a study in which young and adult mouse tibia were subjected to extraphysiological loads, Willie et al. (9) converted micro-CT images to tetrahedral elements which were then solved using ABAQUS via conventional finite element analysis (FEA). Age related and location related material properties were implemented, and maximum and minimum strain were used to assess the local mechanical in vivo environment. Here, both groups had increased anabolic response, though they observed a delayed and reduced response to stimuli in the aged mice versus the young mice. Such studies demonstrate that these computational models can provide a mechanical context for complimentary experimental data.

Another common approach is the use of poroelastic models, instead of linear elastic models, to calculate the mechanical environment. Kameo et al. (6, 32) applied a voxel-based micro-FE poroelastic model for a fluid shear stress based approach to predict (re)modelling of trabeculae under both bending and uniaxial loads. A uniform and isotropic poroelastic model was used on a cube of randomly arranged trabeculae with a bone volume ratio of 0.4. Over a simulation period 30 days, an increasing load was used to induce fluid shear stress, which was used as a measure of the local mechanical environment. The initially randomly arranged trabecular rearranged in the loading direction, with an increase in mean equivalent stress and SED observed when comparing the initial state to the end state of the (re)modelling simulation. However, a significant reduction in the standard deviation of the SED and mean equivalent stress was also observed, confirming their hypothesis that (re)modelling leads to homogenization of tissue strains. Conventional FEA has also been used to provide a mechanical environment for (re)modelling. Pereira et al. (33) also applied a poroelastic model to simulate (re)modelling in a loaded mouse tibia, in which micro-CT images were acquired from mouse tibia and then converted to a triangular volume mesh, and solved dynamically using a commercial solver. The bone was modelled as a poroelastic material, with isotropic elastic parameters and an anisotropic permeability, where the highest permeability was assumed to lie in line with the primary direction of the lacunacanalicular structures. The combination of both fluid and solid phases into a single non-poroelastic model, was investigated by Tiwari et al. (34), where a (re)modelling simulation was driven by a combination of both strain based measures (compressive and tensile strain and tensile shear) as well as fluid shear stresses. The mechanical environment was calculated via FEA, and this prediction accuracy of (re)modelling was assessed based on six variations of mechanical parameters in a mouse tibia. Strains were calculated with FEA and the tibia was idealised as a homogeneous, isotropic cantilevered beam. Their model showed that highest prediction accuracy occurred upon combination of all types of strain and fluid shear stress.

When approaching the mechanical environment outside the mineralised bone tissue, the bone marrow and the fluid structure interface pose a challenge in determining the mechanical environment surrounding non-osteocyte cells. Webster et al. (35) applied voxel-based micro-FE to determine SED within the bone marrow of a murine vertebrae, illustrating the importance of the mechanical environment of bone marrow on osteoblast and osteoclast activity. In this study, bone marrow was modelled as a linear elastic solid, and they reported that newly formed bone correlated best with the SED gradient of the marrow. Metzger et al. (36, 37) investigated the mechanical environment of bone marrow using conventional FEA and fluid-structure interaction. Within a region of 3x3x3mm cubic regions of human trabecular bone, they investigated the effect of constitutive model choice on the mechanical environment within the bone marrow, comparing linear-elastic solid, neo-hookean solid, viscoelastic solid and a power law fluid constitutive models. They observed differences of up to 25% in mean shear stress between the constitutive models, indicating the importance of constitutive model selection. Additionally, significant heterogeneities in spatial shear stress distributions were noted.

Approaches other than FEA have also been applied to determine the mechanical environment on a tissue scale. In studies working towards coupling (re)modelling biology with mechanics, Lerebours et al. (38) and Scheiner et al. (11, 39) applied representative volume element (RVE) concepts, beam theory and continuum micromechanics theory, under assumptions of pure normal and bending force, to a femur mid-shaft. Both studies argue that this analytical approach, adopted from Hellmich et al. (40), provides a preferable alternative to the conventional micro-FE approach. With this approach, Lerebours et al. (38) investigated site-specific bone loss due to mechanical disuse in a multiscale model combining organ, tissue and cell scale simulation. This approach allowed the combination of tissue and vascular phases into a singular model with an analytical solution and predicted SED for a given RVE, which was coupled with a bone-(re)modelling algorithm. Within the beam theory assumptions lies a challenge for this type of approach. It is assumed that no shear forces or torsional loads are present, and the material cross-section need to remain plane and un-deflected relative to the bone’s neutral axis. Lerebours et al. (38) claim these assumptions hold true primarily at the femur mid-shaft under small deformations, however expanding this model to other sections, geometries or anatomical location would require validation that these assumptions hold true for each location.

Due to the scale and availability of techniques to gather information at the organ and tissue scale, bridging of these levels using fundamental concepts has been demonstrated. Expanding and integrating this with smaller scales becomes the next challenge.

Tissue to Cell

One aspect that would help linking these hierarchical scales is differentiating between the modes of cellular mechanotransduction. Strain experienced by a cell arises primarily from matrix deformation strain and fluid flow strain (20). However, at least with osteocytes, these mechanisms are coupled to some degree (35); volumetric tissue deformation surrounding an osteocyte causes interstitial fluid flow, inducing a pressure gradient within the lacunar-canalicular network (41). Correctly capturing the mechanical environment at a cellular level requires incorporating ultrastructural features and their relation to the mechanisms of cell mechanotransduction. In the immediate cell environment, the effect of the ECM, the pericellular matrix (PCM) and microstructural features such as Volkmann canals and lamellar layers influence strain transmission from tissue level to the cell. This was first shown by Anderson and Tate (42), who modelled fluid flow on osteocytes processes. Using computational fluid dynamics, localised stress spikes of up to 5x were found on geometries constructed from transmitted electron micrographs (TEM), compared with idealised geometries. Investigating localised structural deformation, Verbruggen et al. (21) constructed geometries of osteocytes and their ECM and PCM from confocal microscopic images, comparing this to FE-based strain results based on idealised geometries. For simulations of physiological tissues strains of 500 to 3000 microstrain, they reported that both the ECM and PCM increased strain transfer to the osteocyte. Specifically, the PCM decreased peak strain transferred but increased the overall transmission of strain to the osteocyte. This suggests that real geometries, consisting of an osteocyte surrounded by ECM and PCM, amplify average strain by 3 - 4 times that of idealised geometries without an ECM or PCM network, reaching maximum strains of more than 10’000 microstrain. In a further extension of this work using fluid-structure interaction modelling, Verbruggen et al. (43) introduced fluid in the PCM, between the ECM and the cell. This fluid-structural coupling was analysed using ANSYS CFX and Structural finite element solver, and solved using a staggered iteration approach. All solid structures were linear, elastic and isotropic, while the interstitial fluid was modelled as a laminar flow, with fluid properties of salt water. They reported that the highest stress levels occurred not in the cell body itself, but within the surrounding canaliculi. As such, compared with idealised canaliculi, real canaliculi caused an amplification of stimuli by 2 - 3 times. Vaughan et al. (7) also showed similar strain amplification when modelling inhomogeneities in the microstructure around osteocytes, by incorporating Volkmann and Haversian canals into an osteon. Osteocytes around the Volkmann canals experienced strain up to 9 times the generalised applied strain, while osteocytes in the region of lamella rings around the osteon experienced greater strain amplification as their primary axis angle relative to the rings increased. This amplification aligns well with several in vitro studies, which report that osteocytes require a stimulation of 5’000 to 10’000 microstrain to elicit a biological response (44), as well as similar results from computational approaches performed by Bonivtch et al. (45), Wang et al. (46) and Kamioka et al. (47). Estimating the mechanical loads transferred from the tissue scale to the cell scale is achievable with such computational approaches, albeit without in vivo reference, and becomes even more challenging beyond this scale.

Cell and Beyond

While intracellular mechanics models exist, it is questionable whether multiscale models incorporating intracellular complexity would increase accuracy, or only increase computational burden. Hence, at this stage, it may be more beneficial to incorporate these mechanisms outside of the models. Indeed, several mechanisms transduce mechanical stimuli that ultimately lead to the production of molecules orchestrating the (re)modelling behaviour between all involved cells. Extracellular matrix (ECM)-integrin-cytoskeleton connections, such as focal adhesions, sense and process ECM strain and fluid shear stress, transferring these signals across transmembrane integrin proteins to the actin cytoskeleton (48). Proteins, including myosin II motors, actin filaments, and actin crosslinkers, link the cell’s membrane via anchoring proteins such as α-actinin or filamin, that sense dilation versus shear cell deformations, respectively (49). Fluid flow is also sensed by primary cilium that extend from the cell surface, whose deformation leads to the opening of ion channels resulting in the internalization or release of ions (50), though its exact role is debated (51). Other mechanisms include glycocalyx, and membrane-bound proteins such as connexions, or stretch-activated channels (52). It is yet to be ascertained whether detailed modelling of the cellular mechanisms that transduce the cell mechanical environment to the cell signals is even necessary; simply treating the region as a ‘black box’ while experimentally quantifying the inputs and outputs may be sufficient for tissue (re)modelling research, at least at this relatively early stage of computational prowess. Such computational biophysical simulations that explore and understand molecular dynamics are under development (53), however, incorporating such simulations into multiscale approaches in bone biomechanics would pose a challenge.

For now, one accessible building block could be the lacuna-canalicular system, which acts as a communication pathway, chemically, as shown by osteocyte calcium signalling correlations to dynamic loading magnitude (54) and frequency (55), and physically, via gap junctions. Ridha et al. (56) captured elements of these features by applying FEA to simulate rupturing of osteocyte cell connections, showing how the loss of connection leads to bone resorption, while Jahani et al. (57) used network simulations to model osteocyte apoptosis and its effect on bone lining cells, showing that only a 3% decrease in osteocytes was needed to have a significant reduction in peak signal to the bone lining cells. These types of studies begin to shed light on the interlinked, mechanosensitive biochemical relationship between osteocytes, osteoclasts and osteoblasts which collectively governs bone (re)modelling. The vast majority of these inter- and intra- cellular pathways, molecules and signals have been discovered in vitro, where creation of an artificial mechanical environment is relatively simple. Contrastingly, it is only in vivo, where the mechanical environment is inhomogeneous and substantially harder to measure, that such cell-specific information can be validated in the context of bone (re)modelling. Here, quantitative computational tools may be key to estimate and appreciate in vivo cell-scale loads and responses.

Towards Multiscale Approaches

Several approaches have attempted to aggregate the influence of mechanics over the range of scales required to investigate biological processes such as bone remodelling. Frost (58) proposed the concept of the Bone Multicellular Unit (BMU), a unit in which the relevant cell populations establish a localised mechanically driven homeostasis via (re)modelling. This concept allows the behaviour of this unit to be modelled without taking into account individualised cell behaviour, addressing the behaviour of cell populations within this BMU instead. Several authors (11, 38, 59) have adopted this approach and made use of a RVE of cortical bone to attempt to aggregate mechanics and capture the combined behaviour of the bone (re)modelling cells. The RVE approach claims to be large enough to account for all the microstructural heterogeneities, yet small enough to allow averaging of material behaviour over the region (60), hence predicting a relevant mechanical stimuli (11), especially if RVE convergence is considered (61). Further, the interconnectedness of the lacunar-canalicular network integrates extracellular matrix strain as well as fluid shear stress, and provides adequate connection between individual osteocytes that can sense mechanical stimuli on a larger scale, rather solely in the immediate dimensions surrounding a single cell (24). This results in the averaging of tissue level strain over a particular volume, and the conversion of these stimuli into a set of biochemical responses (38). Such approaches could argue that cellular stimuli can be captured by a volume substantially larger than an individual cell. Conversely, to sufficiently capture the microstructural heterogeneities of bone, such an RVE needs to be substantially smaller than the cell-scale; hence the appropriateness of the use of a RVE in trabecular bone is contested (62).

In contrast to the RVE approach, in vitro investigations have shown that osteocytes require substantially greater levels of strain to display a biological response than that measured in the tissue scale mechanical environment, established and termed as strain amplification (45). As known, complex interactions between solid and fluid states (43) and the microstructural geometries of the tissue (7, 21) lead to significant amplification factors. These can occur between the average tissue strain and the deformation of osteocytes, or the fluid shear stress either on the cell itself or on its processes (63). Currently, representative systems have begun to approach multiscale bridging. Whether full multiscale approaches, comprising of the organ to molecular scale, will provide insights that are more relevant over representative systems, is yet unclear.

Validation of Computational Approaches

While the use of computational bone-based biomechanical models consistently increases, validation of the mechanical signals used is in general very much lacking. Ascertaining whether mechanical signal inputs into (re)modelling models are truly representative of the in vivo mechanical signals is very difficult, with increasing ambiguity at smaller scales. At larger scales, the validation of models is somewhat achievable (61); historically, strain gauges have helped validate surface strains of finite element simulations (28). Other approaches, such as digital image correlation, have also been implemented as validation tools with varying degrees of success (64). A limitation of these techniques is that they are only appropriate for surface strains, they stiffen the bone surface, or only capture in plane movement of 2D sections (65).

Beyond the organ-scale, experimental in vivo validation of mechanical signals poses the greatest challenges. Cell amplification concepts, as discussed by Vaughan et al. (7), and Verbruggen et al. (21, 43), begin to address this with models that converge on results observed in experimental studies, generating results that align well with in vitro experimentation. Such indirect validation, with experimental observation within the mechanical local in vivo environment, has been performed with varying degrees of success. Several decades ago, Weinans et al. (66) proposed a feedback driven mechanical loading approach to bone remodelling, in which FEA calculated the mechanical environment, which was used as a remodelling stimulus in the simulation, leading to bone architecture changes. Over the years, more detailed and modern approaches have built on this. Recently, Schulte et al. (8) extended their own prior model (10), applying SED as a (re)modelling stimulus to predict local spatial patterns of formation and resorption. Here, an osteocyte density distribution of 1/10.5µm³ was combined with (re)modelling stimuli approximated by Gaussian smoothing of the mechanical environment. Using the same micro-FE methods (10), measured by SED value in the region, they could predict changes in bone volume fraction (BV/TV) with a maximum prediction error of 2.4%. However, this approach did not predict dynamics rates of bone formation/resorption effectively, with significant differences between the simulated data and experimental data. This approach was implemented by Levchuk et al. (67) in a large scale validation study of feedback controlled bone remodelling. The in silico model was used to predict bone (re)modelling behaviour in osteopenic mice under mechanical loading with treatments of bisphosphonates or parathyroid hormone. SED was once again used to describe the local mechanical environment and BV/TV was used as the assessment variable for simulation to experimental comparison. Similarly to Schulte et al. (8), overall errors for BV/TV prediction were low, ranging from 0.1% (combined mechanical loading and bisphosphonate treatment) to 4.5%, (control group), though again, they could not predict dynamic parameters well. Both these studies indicate the effectiveness of SED as a predictor of mechanical environment, primarily for static parameters. This “soft validation” approach of mechanical signals has provided an acceptable approach for assessing the local mechanical environment. Similar validation approaches have been used in other in silico models (6), such as model behaviour aligning to fundamental (re)modelling theories of bone. Despite the progress, what remains sorely lacking, is the in vivo validation by direct comparison of predicted (re)modelling patterns to in vivo outcomes. As computational methods gain complexity and incorporate multiple scales, the fundamental challenge of aligning and validating these models becomes even more demanding.

At the organ scale, material models are usually isotropic and purely elastic; inclusion of the viscous effects (68, 69) and anisotropic effects (70) found in bone could improve such models. This can be extended to bone marrow, where comparisons between highly viscous fluid, viscoelastic solid and soft elastic solid constitutive models display different results (36). Therefore, the correct choice of model is essential, and parameters require a comprehensive and application specific database. Of further benefit would be an ability to quantify the differences between mechanical environments determined under varying model parameters and solving approaches, i.e. linear versus non-linear solvers.

While tissue-averaged strain approaches have shown success in predicting (re)modelling, it is clear that strain and fluid stresses are amplified within the canaliculi-lacunae network, causing cells to receive stimulation in the range found to cause a biological response in in vitro experiments. Hence, multiscale models incorporating strains and fluid stresses on the cells themselves, based on tissues strains, could help explain the role of single cells on the (re)modelling process. These models would provide cell specific mechanical stimuli boundary conditions to inform experimental techniques heading towards single cell analysis. However, many challenges remain. Firstly, accurate mapping of the osteocyte lacunae system, or the location of osteoblasts or osteoclasts on the bone surface, is needed for (re)modelling experiments. Secondly, coupling detailed imaging techniques with in vivo experiments represents a significant challenge due to destructive doses of radiation, or long imaging times (22), and a lack of techniques linking the two realms. Regardless, validation of input signals, and the model themselves, appear the biggest hurdle towards accuracy and confidence.

Conclusion

Over the last few decades in bone systems biomechanics, substantial progress has begun to elucidate the mechanosensitive mechanisms of bone (re)modelling. Complete multiscale modelling of the mechanical environment has significant application towards understanding cellular mechanotransduction, and the resultant processes in bone. In particular, the knowledge of the exact forces and strain experiences by an individual cell, or small populations of cells can be leveraged by rapidly maturing experimental techniques. Techniques, such as laser capture microdissection, or imaging mass spectroscopy, that can gather molecular information from small populations of cells, can be coupled with inter- and intra-cellular downstream simulations converting the mechanical local in vivo environment to direct mechanical transduction within the cell. Combining multiscale models, from organ level to protein and molecular responses, with experimental data, will allow the establishment of a continuum of knowledge from organ-scale to protein expression. This will foster progress towards understanding of the exact effect mechanics have on bone tissue, allowing accurate characterisation of the molecular pathways and processes involved in (re)modelling, repair and growth.