New Deep Learning Methods for Protein Loop Modeling

Abstract

Computational protein structure prediction is a long-standing challenge in bioinformatics. In the process of predicting protein 3D structures, it is common that parts of an experimental structure are missing or parts of a predicted structure need to be remodeled. The process of predicting local protein structures of particular regions is called loop modeling. In this paper, five new loop modeling methods based on machine learning techniques, called NearLooper, ConLooper, ResLooper, HyLooper1 and HyLooper2 are proposed. NearLooper is based on the nearest neighbor technique; ConLooper applies deep convolutional neural networks to predict Ca atoms distance matrix as an orientation-independent representation of protein structure; ResLooper uses residual neural networks instead of deep convolutional neural networks; HyLooper1 combines the results of NearLooper and ConLooper while HyLooper2 combines NearLooper and ResLooper. Three commonly used benchmarks for loop modeling are used to compare the performance between these methods and existing state-of-the-art methods. The experiment results show promising performance in which our best method improves existing state-of-the-art methods by 28% and 54% of average RMSD on two datasets while being comparable on the other one.

1. Introduction

KNOWLEDGE of three-dimensional (3D) structure of a protein is critical for understanding its function, mutagenesis experiments and drug development. Some experimental methods such as the X-ray crystolography or Nuclear Magnetic Resonance (NMR) can determine a good 3D structure but they are very time consuming and expensive [1]. To address those limitations, many protein structure prediction methods have been developed. Due to its ability to predict protein structure fast and accurately, template-based protein structure prediction is being used in many biological applications [2–5]. This approach is mainly based on the idea of finding good template in the Protein Data Bank (PDB) [6] with a high level of sequence similarity of a query protein [7]. In many cases, parts of the protein structure cannot be predicted due to no alignment to known structures for these parts. Thus, it is necessary to predict the structure of these missing parts to complete the final protein structure prediction. This is called the loop modeling problem. In some experimental structures, loop modeling is also needed due to lack of structural information in certain parts of the protein.

Loop modeling methods can be divided into two main approaches: ab initio and template-based approaches. The ab initio approach is based on the idea of using biological and physical properties of the loop region in the protein to determine the best loop conformation. Some ab initio methods such as LOOPY [8], PLOP [9], and MODELLER [10] can predict the loops with short length (below seven) quite well [5]. On the other hand, the template-based approaches, such as LIP [11], NGK [12], Galaxy PS1 [13], or Galaxy PS2 [14] tries to derive some the loop structure candidates and possibly combine with some energy functions or selection methods to finish the loop modeling task.

The methods mentioned above are different from one another in details, but most of them still share a general framework that starts with sampling a large number of feasible conformations.

Ab initio methods mainly depend on the performance of two factors: the conformational search algorithm and the energy (scoring) function [45]. There are many computational search algorithms that have been proposed such as simulated annealing [46,47], genetic algorithm [48,49], random tweak [50,51] and many others [45]. Similarly, many energy functions have been used for loop modeling including OPLS [52], CHARMM [53], AMBER [54], etc.

Among ab initio methods, the LOOPY algorithm is based on the random tweak algorithm [15] and carries out loop closure while avoiding steric clashes. MODELLER constructs and samples loop conformations with a bond-scaling and relaxation method. Basically, it combines conjugate gradient minimization and molecular dynamics with simulated annealing [5]. On the other hand, PLOP uses a systematic dihedral angle based build-up process to sample conformation space.

Basically, the template-based methods try to extract loop structures from experimental structural databases such as the Protein Data Bank (PDB) first. Then, further sampling and optimization methods are applied on the extracted loop structures to come up with a good set of candidate structures. Finally, a ranking method such as energy or scoring function is employed to get the best loop structure [7].

Among template-based methods, NGK performs sampling for loop conformation based on the idea of combining intensification of torsion and parameter annealing strategies. Both Galaxy PS1 and Galaxy PS2 are loop refinement methods that starts with an inaccurate loop structure. The energy of Galaxy PS1 is optimized for application to the refinement of template-based models, while Galaxy PS2 is developed for higher performance for the nearnative models as well [13].

In this paper, five novel methods are proposed for loop modeling, called NearLooper, ConLooper, HyLooper1, ResLooper and HyLooper2. The NearLooper method is based on the idea of selecting loop templates with a similar structure of surrounding environment. ConLooper uses Convolutional Neural Networks (CNN) [29–33] to predict candidate loop template. By combining the results of NearLooper and ConLooper, the HyLooper1 method takes advantages of both methods. ResLooper uses Residual Networks to predict candidate loop template. And Hy-Looper2 method is the combination of NearLooper and ResLooper. ConLooper and ResLooper use distance matrix that contains pairwise distances between two residues’ C_a atoms in the model as an orientation-independent representation of protein 3D structure. Experiment results show that these methods achieve comparable results to other state-of-the-art methods and outperform them in some cases.

This paper is organized as follows. Section II introduces major techniques and methods that we used for loop modeling. Section III presents experimental results and discussion on experimented datasets. Finally, Section IV concludes the paper.

2. Methods

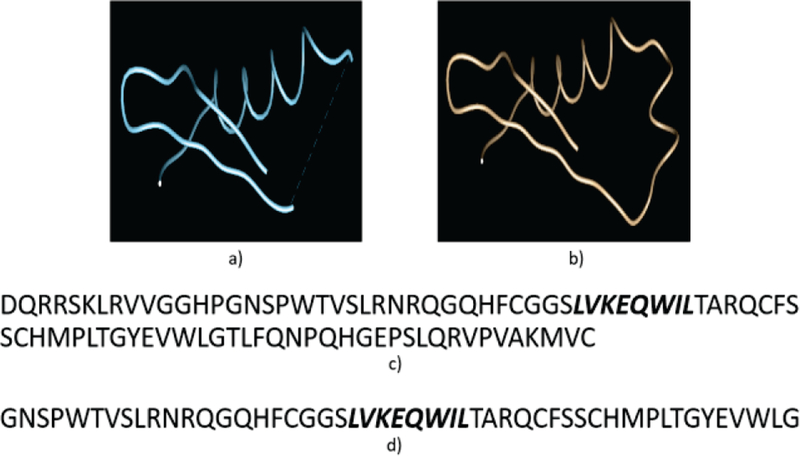
The loop modeling problem is formulated as a partial protein structure construction in this paper: given an incomplete protein structure that has a gap region (also called loop) with unknown structure coordinates inside, predict the conformation (structure coordinates) of the gap region. It is indeed the missing value problem in machine learning which can be defined as: given an input N-dimensional matrix with some areas of missing values, predict an ouput N-dimensional matrix so that the areas of missing values are filled in. Chao et. al. [41] is a good example of this. As an example, Figure 2(a) shows a protein structure with a gap in the middle and 2(b) shows the result of a complete structure with the gap region predicted.

Fig. 2.

An example of the loop modeling problem. a) A protein 3D structure with a gap region in the middle; b) The protein 3D structure with the gap region filled in; c) The original protein sequence with the gap region in the middle marked as bold and italic text; d) An extracted subsequence of length 50 from the original sequence that contains the gap region.

Let S = {s_i, 1≤ i ≤ n} be the amino acid sequence of a target protein of length n, and A = {a_i, 1 ≤ i ≤ n} be its incomplete 3D structure, where a_i represents the 3-D coordinates of the ith amino acid, that contains a gap region between two indices u and v, 1 < u ≤ i ≤ v < n. Suppose a predicted model of the gap region is M = {m_i, u ≤ i ≤ v} and the truth structure of the gap region is D= {d_i, u ≤ i ≤ v}, the goal is to find an M given A so that the root-mean-square deviation (RMSD) between M and D is minimized.

To calculate RMSD between M and D, which measures the structural similarity between two 3-D structures of the same length, M is first optimally superimposed over D. Then, the root-mean-square deviation (RMSD) is calculated using the coordinates of the corresponding main chain atoms (N, Cα, C and O) in the two structures as follows:

$$\text{RMSD}=\sqrt{\frac{1}{k}{\sum }_{i=1}^k{\left|\left|m_i-d_i\right|\right|}^2}$$ (1)

where k is the number of pairs of corresponding atoms.

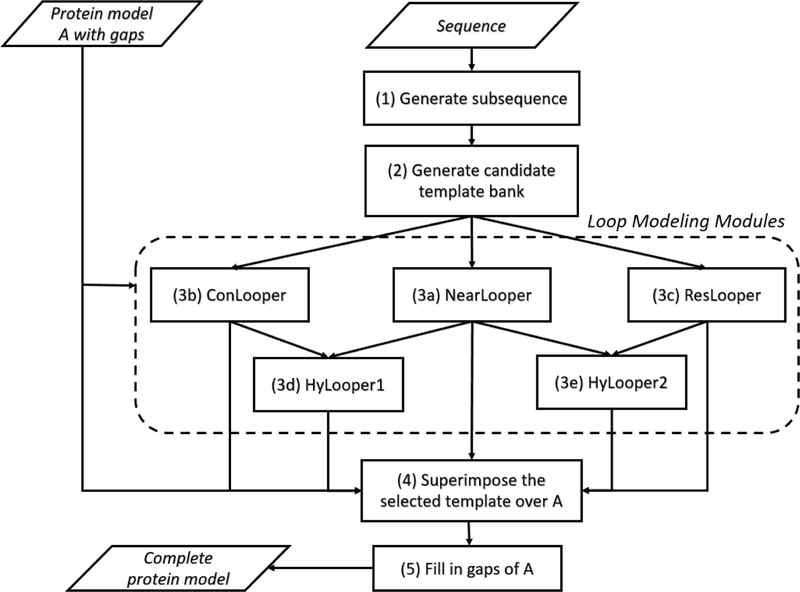
In this section, five new methods are presented for loop modeling, i.e., finding M. They are NearLooper, ConLooper, ResLooper, Hylooper1 and HyLooper2. Figure 1 shows the framework of the five methods that share the following common pre-processing and post-processing steps:

Fig. 1.

The framework of the five proposed loop modeling methods, NearLooper, ConLooper, HyLooper1, ResLooper and HyLooper2.

1. Generate subsequence. A subsequence of the target protein with a gap region is extracted from the original sequence. This subsequence is selected so that it is longer than the gap region and contains the gap region at the center. As an example, Figure 2(c) shows an input sequence with a gap region LVKEQWIL and 2(d) shows the selected subsequence of length 50 that contains the gap region in the middle.

2. Generate candidate template bank. Here, the term “template” is defined as a protein with complete 3D structure (including the loop region) that was found from alignment tools. A pool of templates (candidate 3D structures) for the selected subsequence are generated using sequence-based alignment tools on a protein structure database (e.g. PDB), such as PSI-BLAST [16] and HHSearch [17]. This pool of templates will be used later to train models.

3. Loop modeling. The five different methods generate loop models using the pool of templates in different ways.

4. Superimpose the generated loop model over the target protein structure based on their overlapping regions.

5. The gap region in the target protein structure is filled in with coordinates from the superimposed loop model. As an example, Figure 2(b) shows the result for input 2(a).

2.1. NearLooper, a nearest neighbor algorithm for loop modeling

NearLooper first finds a pool of templates for an extended loop region (the loop region extended on both sides) using sequence-based search from a protein structure database, and select from them a template whose structure optimally matches with the target structure (A) in their overlapping region. Then, the selected template is superimposed over the original incomplete structure A based on their overlapping region (on both sides of the gap region) and the coordinates of the template in the gap region is outputted as the predicted loop model M, which can be inserted into A to make A complete.

Following the framework in Figure 1, NearLooper uses the nearest neighbor idea to select one template from the template pool in step (3). To determine the similarity between different templates and the target structure, the RMSD value of the overlapping region between a template and the target protein is used as the selection metric: the template with the lowest RMSD is selected.

2.2. ConLooper, a novel deep learning method for loop modeling

In this method, a novel idea of applying CNN on the distance matrix representation of 3-D structures is employed for predicting loop conformation instead of using the 3-D coordinates of protein directly. A protein that is rotated in space will have many different sets of values of coordinates. That leads to difficulty for machine learning methods to “learn” the data. On the other hand, distance matrix is an orientation-independent representation of protein structure that eliminates the problems of rotated proteins.

To create the distance matrix of a protein structure, only coordinates of Cα atoms are kept. A 3D model with n Cα atoms can be converted into an n by n distance matrix B with the Euclidean distance of two points in a 3D space:

$$B_{ij}=\sqrt{{\left(U_x^i-U_x^j\right)}^2+{\left(U_y^i-U_y^j\right)}^2+{\left(U_z^i-U_z^j\right)}^2}$$ (2)

where$U_{x,y,z}^i$, $U_{x,y,z}^j$ are the 3D coordinates of points i and j, respectively.

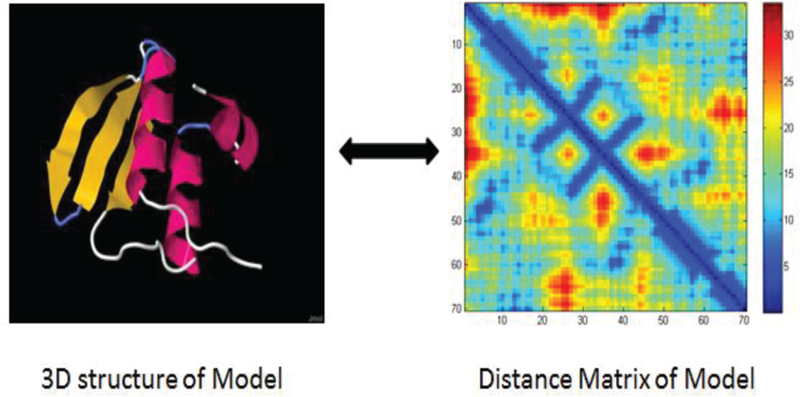
Given a distance matrix, a 3D model can be derived using multidimensional scaling [18]. Figure 3 shows an example of conversion between a 3D model and its distance matrix. The distance matrix is an orientation and translation independent representation of a 3D structure of protein structure. Since it is derived from protein structure which has constraints between one residue to other local surrounding residues, this type of distance matrix data does contain local relations information, which is suitable for applying the current CNN techniques to predict loop models [19].

Fig. 3.

The 3D structure and its corresponding distance matrix of a protein model.

In recently years, deep learning based on deep neural networks (DNN) has had a huge impact on computer science and achieved unprecedented performance on many machine learning problems. Deep-learning methods take raw data to automatically discover the multiple layers of representations needed for detection or classification. These layers of representation in deep learning are learned from input data. Deep convolutional neural networks (DCNN) have made breakthroughs in processing audio, image, video, and playing games. DCNNs are made up of neurons that have learnable weights and biases. Each neuron takes some inputs, perform some calculations and produce an output. DCNNs typically have layered structures including convolutional (CONV) layer, rectify linear units (RELU) layer [28], pooling (POOL) layer and fully connected (FC) layer [20,21].

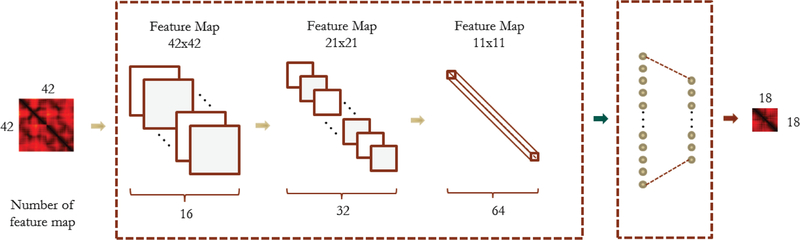
The DCNN architecture of the ConLooper method is shown in Figure 4: taking the input of a distance matrix representation of a 3-D structure, the network applies several convolutional layers followed by RELU layer alternatively and finally generates a predicted distance matrix as the output. The DCNN is trained to learn a network that can predict an output distance matrix from an input distance matrix.

Fig. 4.

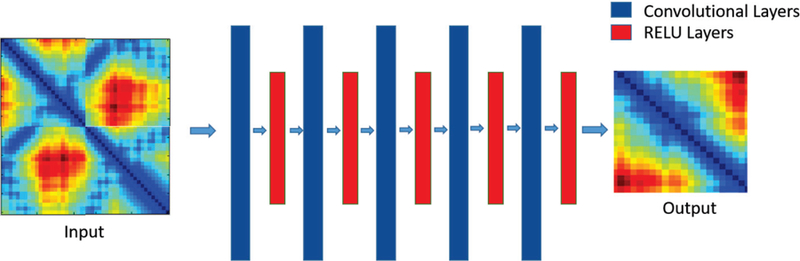
DCNN architecture of the ConLooper method.

In this network architecture, there are no pooling or dense layers used since the network is trying to do a regression task to map input distance matrix to output distance matrix instead of trying to do a classification prediction as in other classical DCNN models. If dense layers are used at the end of DCNN network, the output would be a vector of features instead of a 2D matrix as the expected output. Thus, the final layer of DCNN should be just a convolutional layer which represented by a 2D matrix as the expected output. The key operation of our DCNN model is Convolutional layers where it convolutes the input distance matrix to map it to another output distance matrix. This type of DCNN model has been shown that it can perform the regression task efficiently given the condition of input and output are 2D matrix. A reference of this can be found from the work of Oxford Visual Geometry Group [26].

First, ConLooper trains a DCNN using the pool of templates and then predict a loop model using the trained DCNN based on the partial structure of the target protein structure, as shown in Figure 1. As an example, Figure 5 shows the input, a distance matrix with a gap region, for a DCNN to predict the gap region’s 3-D structure.

Fig. 5.

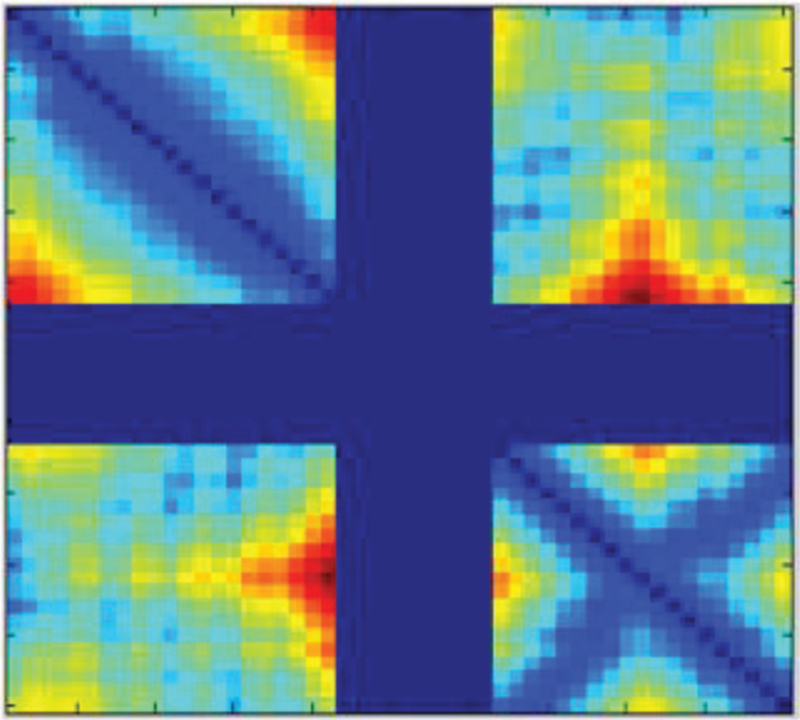
An example of the distance matrix of a protein structure containing a gap region in the middle (the blue bands), the Con-Looper method is used to predict the gap region’s 3-D structure.

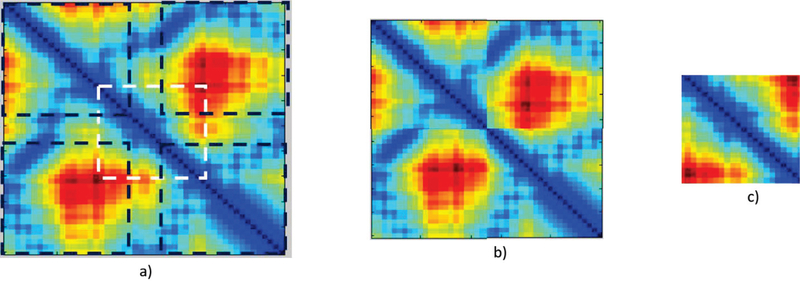
Figure 6 shows a training example of the DCNN. Given a template found by some 3rd party alignment tools, the input and output of the DCNN, both distance matrices, are derived from the template’s distance matrix. The goal is to learn the mapping from the context structure of the gap region to the structure of the gap region.

Fig. 6.

A training example of the DCNN in ConLooper. a) The distance matrix of a template found by a 3rd party alignment tool. b) Input distance matrix for DCNN. It is a combination of 4 corner squares marked as black boxes in a). The boundaries of these black boxes are derived from the gap position in the structure. c) Output distance matrix for CNN. It is created from the white box in a).

Details of ConLooper are as follow:

1. In training, the candidate templates are first converted into distance matrices using Equation (2) and normalized with zero mean and unit variance based on the training data. Then, each distance matrix generates a training example, a pair of input and output sub-distance matrix, in the way illustrated in Figure 6. Finally, a DCNN is trained using the train examples, i.e., learning its paramaters.

2. In prediction, coordinates of Cα atoms in the original target protein structure are extracted. Then, its sub-structure corresponding to the templates is cropped out. Note that just like the templates, this sub-structure contains the gap region, but are bigger. Next, the distance matrix of the sub-structure is calculated and normalized using the normalization parameter calculated in the training phase, while any distance involving an atom in the gap region is set to 0. Figure 5 shows an example.

   The area of non-gap region is used as the input to the trained DCNN. The output of the DCNN is a distance matrix for the extended gap region (the gap region with some extra amino acid on both sides), similar to the one in Figure 6(c). The output distance matrix is unnormalized and converted into a 3-D structure (Cα atoms only) using the multidimensional scaling method. Finally, Pulchra [27] is used to generate the full atom model from the predicted Cα model.

The full atom model of the extended gap region predicted by the DCNN will be used in the step 4 of the framework in Figure 1. The model is superimposed over the target protein structure based on their overlapping region.

2.3. Res Looper, another deep learning method for loop modeling

ResLooper uses the same idea as ConLooper to apply deep learning method for predicting loop conformation. Specifically, ResLooper uses Residualdue Neural Networks [35] to predict loop conformation instead of CNN as in ConLooper.

The Residual Neural Network (ResNet) was introduced recently in the ImageNet competition and the results were quite impressive. The basic structure of this network architecture is the building block, in which there are stacked activation layers and convolutional layers. If the input of a building block is X_l, then the output of this block is X_l + X_l+1 , in which X_l+1 is the non-linear transformation of X_l. We define a function $\mathcal{F}$ indicating the difference between the input and output of the building block, then $\mathcal{F}$ is called residual function. This feature of the network gives it the ability to learn something different from what the input has already encoded. Also, this network handles the vanishing gradient problem well.

In our network, the pre-activation [36] configuration of the building block was used, as shown in Figure 8. We have two activation layers and two convolutional layers together with ReLU as the activation function. In Figure 8, BN stands for Batch Normalization. BN is first proposed in the work of Ioffe et al. [44]. It can normalize the training mini-batch features in a layer in the neural network to zero mean and unit variance.

Fig. 8.

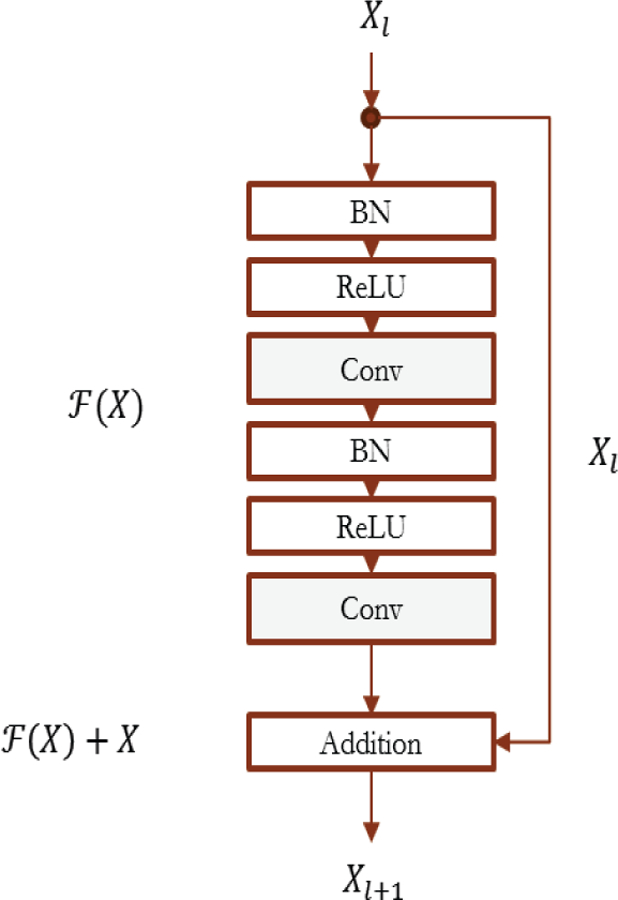
Configuration of the pre-activation building block in our residual neural network.

The ResLooper network architecture is shown in Figure 7. The input and output format of the ResLooper is the same as ConLooper, with the input as a 42 by 42 distance matrix and output as an 18 by 18 distance matrix. The network contains 9 residual blocks, plus the first initial convolutional layer and the last fully connected layer. There are 20 weighted layers totally in our network. The first initial convolutional layer has a kernel size of 3 and the number of filters is 16. Then there are 9 residual blocks and we divided them into 3 parts, each part has 3 residual blocks. Between each part, we use stride 2 to perform downsampling, wich results in the feature map sizes {42, 21, 11}, respectively. Then number of filters are {16, 32, 64}, respectively for each part. The kernel size is 3 for all convolutions. After the final fully connected layer, we reshape the output vector to a distance matrix.

Fig. 7.

ResNet architecture of the ResLooper method.

In the building block, for the shortcut connection, there are two cases. For the case that the depth dimension changes, we use 1 by 1 convolution to match the dimension. For the case that the depth dimension does not change, we use identity connection.

2.4. HyLooper1 and HyLooper2, hybrid methods for loop modeling

The HyLooper1 method combines the results of NearLooper and ConLooper as follows:

1. Run NearLooper to output one candidate model, T1.

2. Run ConLooper to output another candidate model, T2.

3. Select between T1 and T2 based on the RMSD value of the overlapping region between each and the target protein structure. The one with smaller RMSD is selected as the model for the extended gap region.

4. Continue steps 4 and 5 of the framework in Figure 1. Basically, HyLooper1 is a hybrid method, aiming to improve over the two individual methods NearLooper and ConLooper.

The HyLooper2 method is very similar to HyLooper1 method but it uses ResLooper instead of ConLooper together with NearLooper to solve the loop modeling problem. HyLooper2 also follows the 4 steps as HyLooper1 but the method ConLooper in step 2 is replaced by ResLooper.

3. Results and discussion

3.1. Dataset and experimental settings

Four datasets were used in our experiments: The first dataset, called Set CASP, is chosen from The Critical Assessment of protein Structure Prediction experiments year 2014 (CASP11) [34]. This is a biennial world-wide event in the protein structure prediction community to assess state-of-the-art protein structure prediction methods. More specifically, the protein sequence search program (HHSearch) is used to search for possible candidate templates of target protein sequences in CASP11. The tool is configured to remove native-like protein from its results. The top template with its known 3D structure from the Protein Data Bank (PDB) dataset will be added to the Set CASP dataset if it satisfies the following criteria: (1) has a gap of length between 5 and 12; and (2) both sides of the gap can be extended to have a total length of 50 residues. In total, 9 proteins were selected for this training dataset.

The two other datasets from public data of Park et al. [14] are common benchmark sets used in the loop modeling community for testing performance of loop modeling methods. It composed of two subsets of 20 8-residues loops and 20 12-residues, called Set 8Res and Set 12Res, respectively. To create these sets, the first 2-ns molecular dynamics (MD) simulations at 300 K was performed, starting from the energy-minimized crystal structures using the AMER12 package [22]. Then, the Generalized Born/Surface Area (GB/SA) implicit solvation model [24, 25] and the AMBER99SB force field [23] were used [14].

The last dataset is called TBM set. It is comprised of 22 proteins with loops in more inaccurate environment of template-based models with the loop length varies from 6–11 residues. This dataset is also derived directly from the publication of Park et. al. [14] which is the template-based model set with 23 proteins. One exception is that the protein 1DF6A is removed from this set since its length is shorter than 50 residues. It was created by running MODELLER 9.6 [37] with the templates and multiple sequence alignments taken from the SALIGN benchmark study [38,39] on the HOMSTRAD set [40]. All targets for which the template-based models have GDTTS smaller than 70 or greater than 90 are excluded. The model consensus method for detecting unreliable modeled regions were used to select the target loop regions [14].

Totally, there are 71 proteins from 4 sets of data that have been used in our experiments. The loop length varies from 6 to 12 residues. The first dataset CASP is used for model selection while the other 3 datasets including set 8Res, 12Res and TBM are used for testing.

The training and validation are done for each protein of loop modeling. That means given a protein that is needed to do loop modeling, first a set of candidate templates will be created from Protein Data Bank by using 2 alignment tools PSI-BLAST [11] and HHSearch [12] on the sequence of given protein. All native-like templates in this set of templates are removed to make sure that there is no ground-truth data included in the training phase. The number of templates varies from 250 minimum to 617 maximum and 415 on average. Each template could be seen as a candidate to fill in the loop region of the protein. Then a deep learning method will be applied to train on the template set. The training/validation ratio is 75/25 on DCNN model and 90/10 on ResNet model.

Root-mean-square deviation (RMSD) of the main chain atoms N, Cα , C and O is used as the metric to compare performances between different loop modeling methods. These atoms are used since they can be seen as the representative atoms of the protein and can be used to recover to full atom model. In our experiments, our methods are compared with existing state-of-the-art methods with the results published on Park et. al [14]. These results use N, alpha, C and O atoms for RMSD measurement. Hence, we use the same set of atoms to make it comparable between our methods and other existing methods. This set of atoms has been used widely in different publications [12,13,14] for loop modeling problems. Its formula is defined in Eq. (1).

There are 3 current state-of-the-art methods including NGK [12], Galaxy PS1 [13] and Galaxy PS2 [14] that have been used as the baseline to compare with our newly developed methods for loop modeling problem. Experimental results of NGK, Galaxy PS1 and Galaxy PS2 are acquired directly from the published results of Park et. al. [14].

The average computation time of ConLooper on each loop modeling task is 1 CPU hours on a desktop computer with Intel Core i7, memory 16GB, graphics card NVID-IA GeForce GTX 980. NearLooper takes 0.5 CPU hour while ResLooper takes 1.5 CPU hours. HyLooper1 and HyLooper2 take 1.75 CPU hours and 2 CPU hours respectively.

MatConvNet toolbox version 1.0-beta20 is used as the DCNN implementation [26]. ResNet is implemented based on Keras [42] with Tensorflow [43] backend. The length of subsequence that is used for alignment is set to 50 while the size of overlapping region is set to 5.

3.2. Determining the best configuration for ConLooper

In this experiment, Set CASP is used to find the best configuration for ConLooper method so that it can be used later on the other datasets. Specifically, ConLooper method is applied on Set CASP with different number of hidden layers and different number of epochs. For each setting of hidden layers and epochs, ConLooper ran 10 times with different random initizlization and the average RMSD and standard deviation on each of 9 proteins in Set CASP are reported.

Table 1 shows performance of ConLooper method on different number of hidden layers. Four different settings are tested including 2 layers, 6 layers, 10 layers and 14 layers. The result shows that the setting of 10 layers is the best, with average RMSD of the main chain atoms 2.87 and standard deviation 0.92. In this experiment, the number of epochs in training is set to 500.

TABLE 1.

ConLooper with different number of hidden layers on Set CASP

	2 Layers	6 Layers	10 Layers	14 Layers
Average RMSD	3.03	3.09	2.87	3.17
Std. dev.	1.18	0.85	0.92	1.14

Average RMSD and standard deviation are calculated on set CASP with different configurations.

Table 2 shows performance of ConLooper on different number of epochs with the number of hidden layers set as 10. Four different settings are tested, including 100 epochs, 500 epochs, 1000 epochs, 1500 epochs and 200 epochs. The result shows that the setting of 500 epochs is the best, with-average RMSD of the main chain atoms 2.87 and standard deviation 0.92. Other settings either underfit or overfit the training data. Increasing from 1500 epochs to 2000 epochs seems to improve the RMSD and further increasing number of epoch could help. But due to resource limitatin, the max number of epochs is set to 2000.

TABLE 2.

ConLooper with different number of epochs on Set CASP

	100 Epochs	500 Epochs	1000 Epochs	1500 Epochs	2000 Epochs
Average RMSD	3.16	2.87	3.12	3.22	3.04
Std. dev.	1.05	0.92	0.83	1.06	1.06

Average RMSD and standard deviation are calculated on set CASP with different configurations.

Table 3 shows the final configuration of CNN in ConLooper derived from the Set CASP with 9 proteins. The number of epochs is 500 while the number of hidden layers is 10. This configuration is used by ConLooper when compared with other loop modeling methods on other datasets.

TABLE 3.

Configuration of CNN in ConLooper method after training on Set CASP

Configuration	Value
Learning rate	0.002
Number of epochs	500
Number of hidden layers	10
Batch size	10
Training / Validation ratio	75% / 25%

3.3. Determining the best configuration for ResLooper

In this experiment, Set CASP is used to find the best configuration for ResLooper method so that it can be used later on the other test datasets. Specifically, ResLooper method is applied on Set CASP with different number of hidden layers and different number of epochs. For each setting of hidden layers and epochs, ResLooper ran 10 times with different random initizlization and the average RMSD and standard deviation on each of 9 proteins in Set CASP are reported.

Table 4 shows the performance of ResLooper method on different number of hidden layers. Four different settings are tested including 8 layers, 20 layers, 32 layers and 44 layers. The result shows that the setting of 20 layers is the best, with average RMSD of the main chain atoms 3.04 and standard deviation 1.27. In this experiment, the number of epochs in training is set to 500.

TABLE 4.

ResLooper with different number of hidden layers on Set CASP

	8 Layers	20 Layers	32 Layers	44 Layers
Average RMSD	3.13	3.04	3.11	3.07
Std. dev.	1.29	1.27	1.18	1.22

Average RMSD and standard deviation are calculated on set CASP with different configurations.

Table 5 shows performance of ResLooper on different number of epochs with the number of hidden layers set as 20. Four different settings are tested, including 100 epochs, 300 epochs, 500 epochs and 700 epochs. The result shows that the setting of 500 epochs is the best, withaverage RMSD of the main chain atoms 3.04 Å and standard deviation 1.27. Other settings either underfit or overfit the training data.

TABLE 5.

ResLooper with different number of epochs on Set CASP

	100 Epochs	300 Epochs	500 Epochs	700 Epochs
Average RMSD	3.13	3.09	3.04	3.1
Std. dev.	1.21	1.21	1.27	1.2

Average RMSD and standard deviation are calculated on set CASP with different configurations.

Table 6 shows the final configuration of ResNet in ResLooper derived from the Set CASP with 9 proteins. The number of epochs is 500 while the number of hidden layers is 20. This configuration is used by ResLooper when compared with other loop modeling methods on other test datasets.

TABLE 6.

Configuration of ResNet in ResLooper method after training on Set CASP

Configuration	Value
Learning rate	0.1 -> 0.01 (250 epochs) -> 0.001 (375 epochs)
Number of epochs	500
Number of hidden layers	20
Batch size	8
Training / Validation ratio	90% / 10%

3.4. Performance comparison of loop modeling methods

In this section, the new methods are compared with 3 state-of-the-art loop modeling methods, including Nextgeneration KIC (NGK), GalaxyLoop-PS1 (Galaxy PS1) and GalaxyLoop-PS2 (Galaxy PS2) on the Set 8Res, Set 12Res and Set TBM datasets. For each protein in those datasets, ConLooper and ResLooper runs 10 times to derive the average RMSD of the main chain atoms and standard deviation.

Table 7 shows the performances of the methods on 20 proteins in Set 8Res. Among the 3 existing methods, Galaxy PS2 achieves the best performance of average RMSD 2.02 Å and standard deviation 1.87. All five new methods achieve better results than the existing methods. HyLooper2 achieves the best performance with average RMSD 1.45 Å (28% improvement) and standard deviation 1.4. Individually, it outeperforms Galaxy PS2 in 65% (13/20 proteins) cases in this dataset.

TABLE 7.

Loop reconstruction results for the 8-Residue loop dataset Set 8Res

PDB	NGK	Galaxy PS1	Galaxy PS2	NearLooper	ConLooper	HyLooper1	ResLooper	HyLooper2
135l	3.9	3.7	4.3	0.6	1.5 (0.21)	0.6	1.7 (0.68)	0.6
1alc	1.3	1.4	1.4	0.2	0.4 (0.06)	0.2	0.9 (0.32)	0.2
1btl	0.4	1.3	0.9	0.2	1.4 (0.11)	0.2	0.5 (0.04)	0.2
1cex	2.1	2	1.8	3.3	3 (0.27)	3.3	3.3 (0.09)	3.3
1clc	0.4	0.4	0.3	4.5	4.3 (0.17)	4.5	4.6 (0.05)	4.5
1ddt	3.7	2	1.5	4.1	3.4 (0.24)	3.3	3.4 (0.23)	3.5
1ezm	4.3	4.2	3.8	0.9	1.7 (0.51)	0.9	0.7 (0.11)	0.9
1hfc	0.7	1	0.9	3.6	3.5 (0.26)	3.5	3.6 (0.07)	3.6
1iab	1	2.2	1.8	0.6	1.9 (0.19)	0.6	0.7 (0.09)	0.7
1ivd	2.7	3.6	2.2	0.5	1.5 (0.32)	0.5	1.1 (0.13)	0.5
1lst	1.2	1.1	1.1	0.3	1.5 (0.49)	0.3	1.5 (0.18)	0.3
1nar	1.4	2.1	1.8	2.4	2.9 (0.3)	2.4	2.8 (0.24)	2.4
1oyc	1.1	1.6	1.7	2.3	2.2 (0.1)	2.3	2.3 (0.02)	2.3
1prn	8.3	6.9	8.8	3	2.7 (0.16)	3	3.0 (0.13)	2.9
1sbp	0.9	0.8	0.8	1.4	1.6 (0.21)	1.4	1.0 (0.13)	0.9
1tml	1.1	1.1	0.6	0.2	2.3 (0.46)	0.2	0.5 (0.10)	0.2
2cmd	1.9	4	2.3	0.2	1.1 (0.38)	0.2	0.3 (0.13)	0.2
2exo	1.5	1	1.1	0.4	1.2 (0.46)	0.4	0.8 (0.10)	0.8
2sga	1.7	1.2	1.3	0.5	1.2 (0.42)	0.5	3.3 (0.12)	0.5
5p21	1.7	1.9	1.9	1.6	0.9 (0.1)	1	0.6 (0.05)	0.6
Average	2.07	2.18	2.02	1.54	2.01	1.47	1.83	1.45
Std. dev.	1.84	1.57	1.87	1.46	1.01	1.39	1.32	1.4

RMSD scores are used to compare performances among methods. For ConLooper and ResLooper, the experiment is executed 10 times to get the average RMSD and standard deviation for each protein. All the numbers are in Å.

Table 8 shows the performance of the methods on 20 proteins in Set 12Res. Similar to Table 7, among the 3 existing methods, Galaxy PS2 achieves the best performance of average RMSD 2.15 Å and standard deviation 1.4. It is also the best among all methods. Among the new methods, HyLooper1 is the best. Comparing with Galaxy PS2, HyLooper1 is comparable and outperforms Galaxy PS2 in 45% (9/20 proteins) cases in this dataset. Even though Galaxy PS2 achieves the best performance on Set 12Res, it has the disadvantage of needing initial loop information to do refinement while our methods can predict loop region directly without initial loop conformation.

TABLE 8.

Loop reconstruction results for the dataset Set 12Res

PDB	NGK	Galaxy PS1	Galaxy PS2	NearLooper	ConLooper	HyLooper1	ResLooper	HyLooper2
1a8d	3.7	4.5	3.1	2.8	2.6 (0.38)	2.8	2.8 (0.14)	2.8
1arb	1.7	2.1	1.9	0.4	1.2 (0.78)	0.4	1.1 (0.21)	0.4
1bhe	1.7	2.3	3.5	4.6	3.7 (0.28)	3.4	3.5 (0.71)	3.3
1bn8	1.1	4.3	1.1	4.8	4.4 (0.22)	4.8	5.7 (0.4)	4.8
1c5e	1.2	2.2	1.5	1.7	2 (0.71)	1.7	3.6 (0.22)	1.7
1cb0	0.9	5.7	0.9	6	5.8 (0.65)	6	5.9 (0.4)	5.9
1cnv	6.3	6.4	6.5	1.1	2.4 (0.9)	1.1	1.2 (0.16)	1.1
1cs6	1.1	1.7	1.6	2.3	2.3 (0.29)	2.3	2.4 (0.23)	2.3
1dqz	7.5	1.5	3.3	0.2	1.3 (0.94)	0.2	1.2 (0.23)	0.2
1exm	1.1	3	1.3	4.2	3.4 (0.25)	4.2	3.9 (0.3)	3.8
1f46	2.6	4.5	3.8	4.4	3.5 (0.59)	3	3.7 (0.75)	4.4
1i7p	1.9	2.8	1.7	4.3	3.4 (0.25)	4.3	4.3 (0.9)	4.3
1m3s	3.2	4.3	2.7	0.9	2.5 (0.54)	0.9	1.5 (0.33)	0.9
1ms9	1.8	1.8	1.8	5.2	4.7 (0.64)	5.2	5 (0.11)	5.2
1my7	0.9	2.4	1	0.5	1.6 (0.45)	0.5	0.7 (0.8)	0.7
1oth	0.8	1.1	0.9	1.6	2 (0.43)	1.6	1.4 (0.16)	1.4
1oyc	0.7	2.7	1.2	3.1	3 (0.27)	3.1	3 (0.3)	3.1
1qlw	6	2.5	2.9	4.2	5.1 (0.59)	4.2	5.1 (0.72)	4.2
1t1d	1.3	2.5	1.5	0.9	1.8 (0.64)	0.9	1.1 (0.21)	0.9
2pia	0.7	4.5	0.7	2.5	2.9 (0.3)	2.5	2.1 (0.45)	2.5
Average	2.31	3.14	2.15	2.79	2.98	2.65	3.01	2.69
Std. dev.	2.03	1.46	1.4	1.82	1.27	1.73	2.67	1.74

RMSD scores are used to compare performances among methods. For ConLooper and ResLooper, the experiment is executed 10 times to get the average RMSD and standard deviation for each protein. All the numbers are in Å.

Finally, Table 9 shows the results of loop modeling between different loop modeling methods. All five newly developed methods show good performance on this dataset over the best existing method Galaxy PS2 with average RMSD 3.73 Å and standard deviation 1.46. HyLooper2 achieves the best results with average RMSD 1.69 Å (54% improvement) and standard deviation 1.07. Individually, it outeperforms Galaxy PS2 in 77% (17/22 proteins) cases in this dataset.

TABLE 9.

Loop reconstruction results for the dataset Set TBM

PDB	NGK	Galaxy PS1	Galaxy PS2	NearLooper	ConLooper	HyLooper1	ResLooper	HyLooper2
1a49a_463–472	5	2.3	2.7	0.8	2.2 (0.43)	0.8	3.2 (0.7)	0.8
1a49a_86–94	4.6	3.8	4.2	0.5	1.8 (0.97)	0.5	1.2 (0.5)	0.5
1asza_313–322	2.9	2.3	1.9	0.3	2.3 (0.41)	0.3	0.7 (0.15)	0.3
1avk_20–29	1.2	1.2	1.5	2.9	3.4 (0.34)	2.9	3.4 (0.13)	2.9
1buca_61–68	5.3	3.9	3.2	4.5	3.3 (0.63)	3.3	3.2 (0.63)	3.2
1csn_216–223	6.5	8.8	6.1	2.1	1.7 (0.73)	1.8	1.5 (0.37)	1.3
1d2ka_349–354	1.9	4	5.7	1.2	2.4 (1.32)	1.2	2.5 (0.28)	1.2
1e0ca1_53–60	3.8	6.7	5.9	2	2.7 (0.27)	2	2.0 (0.45)	1.8
1esl_40–48	3	3.2	2.4	2.6	2.3 (0.23)	2.2	3.5 (0.16)	2.6
1esl_54–59	1.8	2.6	1.5	0.2	1.8 (0.57)	0.2	1.2 (0.76)	0.2
1f3g_123–131	4	3.5	3.3	2.6	2.4 (0.31)	2.6	2.7 (0.39)	2.6
1gpb_261–271	4.3	4.4	3	3.7	3.3 (0.66)	3.7	3.8 (0.66)	3.7
1iala_32–42	6.8	4.6	4	0.5	2.8 (0.51)	0.5	2.9 (0.16)	0.5
1kbt_26–31	3.9	3.4	3.5	2.1	2.7 (0.43)	2.8	2.2 (0.5)	2.1
1lxa_102–107	3.6	3.8	4.7	0.7	2.7 (0.53)	0.7	1.9 (0.5)	0.7
1qdlb_59–67	4.2	2.7	2.8	3.7	2 (1.67)	2.1	3.4 (0.21)	3.2
1qu9a_93–98	7	6.6	6.3	2.8	2.8 (0.27)	2.6	2.6 (0.2)	2.8
1rsy_74–79	4	3	3.1	1	2 (1.07)	1	0.5 (0.13)	0.5
1tml_45–50	5.4	4.7	5.1	2	2.3 (0.89)	2	2.2 (0.11)	2.2
2oata_347–353	2.7	3	5	1.4	2.5 (0.28)	1.4	2.1 (0.23)	1.4
2pola2_23–32	2.8	4.3	3.7	1.6	1.8 (0.96)	1.6	1.3 (0.42)	1.1
3fib_40–47	2.8	2.8	2.6	1.7	1.9 (0.52)	1.7	1.8 (0.1)	1.7
Average	3.97	3.89	3.73	1.85	2.41	1.72	2.26	1.69
Std. dev.	1.57	1.69	1.46	1.19	0.5	1	0.94	1.07

RMSD scores are used to compare performances among methods. For ConLooper and ResLooper, the experiment is executed 10 times to get the average RMSD and standard deviation for each protein. All the numbers are in Å.

Comparing performance on the loop modeling task between our five newly developed methods on test datasets, HyLooper2 is the best one in general. Between two deep learning methods, ResLooper is better than ConLooper which implies the better performance of ResNet over DCNN.

4. Conclusion

This paper presents five new loop modeling methods, in particular a new approach based on deep learning (DCNN, ResNet) and distance matrix representation of 3-D structures. From the rotation and translation independent representation of distance matrix, DCNN and ResNet are able to learn a mapping function to predict a loop model. To the best of our knowledge, this is the first attempt to combine deep learning and geometric information of distance matrix for loop modeling task.

Experiments using selected CASP models and common benchmark datasets have shown promising results. Compared to state-of-the-art loop modeling methods, our HyLooper2 achieves the best result on two test datasets and being comparable on the other test dataset. The ResNet in ResLooper is able to generate good loop candidates in many cases. The HyLooper2 method, which is the combination of ResLooper and NearLooper achieves good performance because both methods are complementary and have their own strengths.

Due to the limitation of computing power, experiments have been done on a limited sets of different network configurations. Exploring more network configurations can help improve the overall performance of loop modeling. This would be a good direction for future work.

Biography

Son Phong Nguyen received the M.S. degree in Computer Science in 2014 and the Ph.D. degree in Computer Science in 2017 from the University of Missouri, USA. His current research interests focus on machine learning, deep learning, big data analytics and bioinformatics.

Zhaoyu Li received the M.S. degree in Computer Science from the University of Missouri, USA in 2014. He is currently a Ph.D. candidate in Computer Science from University of Missouri, USA. His current research interests focus on machine learning, deep learning, and bioinformatics.

Dong Xu is James C. Dowell Professor of Computer Science Department, Director of Information Technology Program, with appointments in the Christopher S. Bond Life Sciences Center and the Informatics Institute at the University of Missouri-Columbia. He obtained his Ph.D. from the University of Illinois, Urbana-Champaign in 1995 and did two years of postdoctoral work at the US National Cancer Institute. He was a Staff Scientist at Oak Ridge National Laboratory until 2003 before joining the University of Missouri, where he served as Department Chair of Computer Science during 2007–2016. He has published nearly 300 papers. He is a Fellow of American Association for the Advancement of Science (AAAS).

Yi Shang is Professor, Associate Chair and Director of Graduate Studies, Department of Electrical Engineering and Computer Science, University of Missouri, Columbia, Missouri. He received Ph.D. in Computer Science from University of Illinois at Urbana-Champaign in 1997, M.S. from the Institute of Computing Technology, Chinese Academy of Sciences, Beijing, in 1991, and B.S. from University of Science and Technology of China, Hefei, in 1988. He has published over 160 refereed papers in the areas of nonlinear optimization, artificial intelligence, wireless sensor networks, mobile computing, and bioinformatics and was granted 6 patents. His research has been supported by NSF, NIH, Army, DARPA, Microsoft, and Raytheon. http://dslsrv1.rnet.missouri.edu/~shangy.