Dosimetric Effect of Rotational Setup Errors in Single-Isocenter Volumetric-Modulated Arc Therapy of Multiple Brain Metastases

Abstract

Aim:

The aim of this study is to investigate the dosimetric effects of rotational uncertainties in patient positioning on target coverage in stereotactic radiosurgery (SRS) of multiple brain metastases using single isocenter volumetric modulated arc therapy (VMAT).

Materials and Methods:

Ten SRS cases with multiple brain metastases (2-8) planned with single isocenter non-coplanar VMAT technique were investigated in this study. Pitch, yaw and roll displacements of 1, 3 and 5° were simulated about isocenter along each axes and nine plans were obtained for each case. Gross tumor volume (GTV) coverage obtained on simulated plans were compared with the original plan on four metrics of mean dose (Dmean), minimum dose to GTV (Dmin), dose to 95% of GTV (D95) and the volume covered by the 95% of the prescribed dose (V95).

Results:

At 1° rotation about 4% of the PTV had V95 and D95 values <95%. The minimum dose obtained across all PTV was 85.1% and there was not much change in the mean dose values obtained. The PTV volume which had V95 and D95 values <95% were in the range of 0.05 - 0.07cc and at a radial distance of 6.2 cm - 7.2 cm. At 3° rotation almost 50% of the PTV had V95 and D95 values <95%. The minimum dose obtained across all PTV was 48.3% and the mean dose reduced to as low as 78.8%. At 5° rotation almost 74% of the PTV had V₉₅ and D95 values <95%. The minimum dose obtained across all PTV was 21.2% and the mean dose reduced to as low as 49.2%.

Conclusion:

Our results indicate that correcting rotational uncertainties is critical in single-isocenter, multi-target SRS. For rotational deviations, radial distance of the target from isocenter along the respective axis has a strong influence on target coverage. For rotational setup deviation at a given radial distance larger targets tend to have lesser geometric miss compared to smaller targets. Mathematical model for spherical targets can be used to estimate V95 for given rotational errors.

INTRODUCTION

Stereotactic radiosurgery (SRS) is a nonsurgical radiation therapy used to treat functional abnormalities and small tumors of the brain. A stereotactic system uses x, y, z coordinates to stereotactically localize any point in a three-dimensional (3D) space to deliver a high dose of radiation to a small focused area. Brain metastases are one of the most common neurological complications of cancer. The incidence is 9%–17% based on various studies although the exact incidence is thought to be higher.[1] SRS achieves high rates of local progression-free survival of SRS-treated lesions, and its efficacy may be less influenced by histology or radiosensitivity than that of fractionated radiotherapy.[2] Several studies showed the superiority of SRS alone as initial treatment of 5–10 brain metastases compared with 2–4 brain metastases in terms of overall survival and most secondary endpoints.[3,4,5]

Conventionally, linear accelerator-based SRS for multiple brain metastases utilizes a multiple-isocenter approach, aligning each isocenter to the individual metastatic lesion and treating each lesion separately. This results in increased treatment time, where the treatment time increases proportionately to the number of lesions treated. With the increased number of metastases treated with SRS, it becomes inevitable to treat multiple metastases simultaneously with single isocenter. Volumetric-modulated arc therapy (VMAT) can achieve improved plan quality and high delivery efficiency with reduced treatment times. Several studies were performed comparing single-isocenter VMAT to more traditional methods of treatment such as intensity-modulated radiotherapy, dynamic conformal arc, and 3D conformal radiotherapy. These studies found that the plan quality of single-isocenter VMAT was equivalent or better than other treatments.[6,7,8,9] A comparative study for multiple target SRS reported that single-isocenter VMAT plan produced clinically equivalent conformity, dose fall off, 12 Gy isodose volume, and low dose spill and reduced treatment time compared to Gamma Knife.[10] Several studies reported that using a single-isocenter approach for treating multiple intracranial metastases can produce similar clinical outcomes compared with conventional radiosurgery.[11,12] One caveat of a single-isocenter, multi-target technique is its susceptibility to rotational setup deviations. If each target is separately planned, the isocenter is placed at the center of each target, thereby limiting the effect of rotational deviations. However, with single-isocenter, multi-target technique, the isocenter is usually placed at the geometric center of combined target volumes; this displaces the center of each target from the isocenter making it more vulnerable to rotational deviations. Previous studies on positioning accuracy have shown a wide range of rotational patient setup uncertainties in various immobilization systems and have reported rotational uncertainties greater than 5°.[13,14,15] It is therefore important to establish the positioning accuracy attainable with the immobilization system utilized for this single-isocenter, multi-target technique.

The purpose of this study is to evaluate the dosimetric effect of rotational setup errors in single-isocenter VMAT treatment of multiple brain lesions by simulating rotations of known degrees on the treatment planning system. Further mathematical analysis was done to estimate the impact of rotations on spherical targets located at various distances from isocenter.

MATERIALS AND METHODS

Ten SRS patients with multiple metastases were selected for this study. Each patient had two to eight intracranial lesions. In total, there were 38 lesions, and all lesions were planned to receive a dose of 20 Gy. Table 1 shows the physical tumor characteristics of the examined cases and the radial distance is measured from the geometric center of the lesion to the rotational axis passing through isocenter. For this study, no additional margin was given to gross tumor volume (GTV) and this target volume is the radiosurgery planning target volume (PTV).

Table 1.

Physical tumor characteristics of the examined cases and the radial distance measured from the geometric center of the lesion to the rotational axis passing through isocenter

Patient	PTV	Volume (cc)	Equivalent sphere diameter (cm)	Radial distance from the axis of rotation (cm)
				Pitch axis	Yaw axis	Roll axis
1	1	0.29	0.8	6	7.3	4.4
	2	0.37	0.9	6.9	3.15	7
	3	1.74	1.5	2.3	1.9	1.2
	4	6.15	2.3	3.1	2.4	3.3
	5	0.61	1	3.2	2.9	4
	6	0.1	0.5	4.7	2.5	5
	7	0.1	0.5	2.9	5.3	5.9
	8	0.42	0.9	4.8	3.3	4
2	1	7.5	2.4	1.9	2	2.6
	2	0.39	0.9	4.7	4.9	5.2
	3	0.13	0.6	7.1	2.4	7.3
	4	0.11	0.6	3.9	0.9	3.8
	5	0.11	0.6	3.2	5.9	5.1
3	1	0.04	0.4	0	5.4	5.4
	2	0.05	0.5	0	6.5	6.5
	3	0.05	0.5	7.2	0	7.2
	4	0.06	0.5	7	0	7
	5	0.07	0.5	7	7	0
	6	0.04	0.4	6.2	6.2	0
4	1	12.7	2.9	0.6	1.9	1.8
	2	0.8	1.2	2	2.7	2.5
5	1	7.33	2.4	2.5	1.1	2.5
	2	1.07	1.3	1.2	2.9	3
	3	0.44	0.9	3.8	2.5	4.1
	4	0.75	1.1	2	3	3.3
6	1	0.28	0.8	5.1	5.3	1.9
	2	0.58	1	4.9	0.9	5
	3	0.79	1.1	5.2	3.7	3.7
7	1	0.13	0.6	4.2	5	5.2
	2	5.96	2.2	2.7	2.6	3
	3	0.47	1	0.8	4	4
8	1	0.05	0.4	1.2	1.5	1.9
	2	0.13	0.6	4	1.9	4.1
	3	1.05	1.3	3.7	0.8	3.7
9	1	1.17	1.3	2.3	2	1.2
	2	7.34	2.4	1.3	1.1	0.5
10	1	8.14	2.5	1	3.8	3.9
	2	12.63	2.9	0.9	3.6	3.7

PTV: Planning target volume

Single-isocenter noncoplanar VMAT plans were created in eclipse treatment planning system version 13.6. The plan isocenter was positioned at the center of all targets to minimize the jaw size, midway between the maximum extending targets in the anterior and lateral beams eye view. Dose-limiting ring structures were created around the combined target volume and used along with the normal tissue objective function in optimization to restrict the dose spillage. Critical structures were restricted to clinically accepted dose levels. Plans were normalized such that at least 100% prescription dose covers 99% of the target volume. Further, plan quality metrics conformity and dose gradient were maximized with dose-control tuning structures surrounding individual targets and maximum dose was kept below 120% of the prescription dose. Dose was calculated on a 1 mm grid using the analytical anisotropic algorithm with heterogeneity corrections turned on.

The objective of this study is to determine the impact of rotational deviations on patient with multiple metastases in cranial radiotherapy. In this study, rotational errors were simulated about the plan isocenter by rotating the contours around the isocenter. Radial distances of PTV were recorded about isocenter along each cardinal plane. Rotations of 1°, 3°, and 5° were simulated for individual PTV, and new rotated contours were created about the three orthogonal planes. Simulation of rotations is achieved in image registration process by rotating the duplicated image along with contours about the isocenter and copying the rotated contours to the original computed tomography. In this way for each PTV, pitch, yaw, and roll deviations were simulated along individual planes and nine rotated PTVs were created. Figure 1 shows the radial distance from isocenter and PTV contour rotated through isocenter in different planes. PTV dose metrics such as dose to 95% of the PTV (D₉₅), volume of the PTV receiving 95% of the prescription dose (V₉₅), mean dose (D_mean), and minimum dose (D_min) were obtained.

Figure 1.

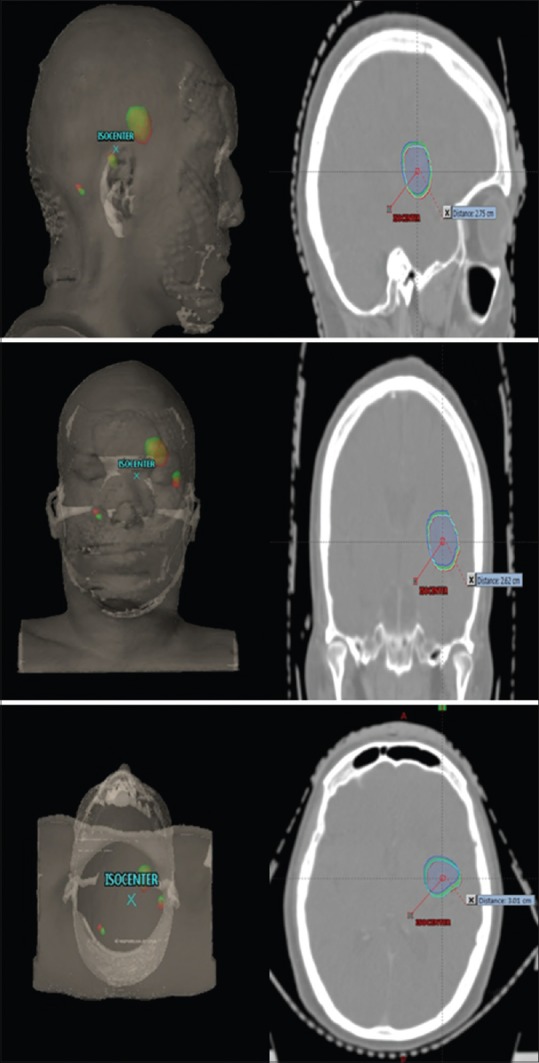
Three-dimensional view representing isocenter and planning target volume contour rotated through isocenter. Planning target volume (red - no rotation and green - 5° rotation). Planar view depicting one of the three planning target volume contour rotated through isocenter along planning target volume centroid. Planning target volume (red - no rotation, cyan - 1° rotation, green - 3° rotation, and blue - 5° rotation)

Mathematical estimation of volume covered by the 95% of the prescribed dose for spherical targets for given rotational setup error

Rotational drift of a point at a distance d from isocenter can be estimated with the equation (1).

R = dtanθ      (1)

where θ is the rotational error in degrees and R is rotational drift of a point.

Mathematically, volume of the spherical cap is given by

where H is the height of the spherical cap and D is the diameter of sphere.[16]

Diameter (D) of spherical volume V is given by

Figure 2 shows a spherical cap and rotational drift of a point at a distance d from isocenter.

Figure 2.

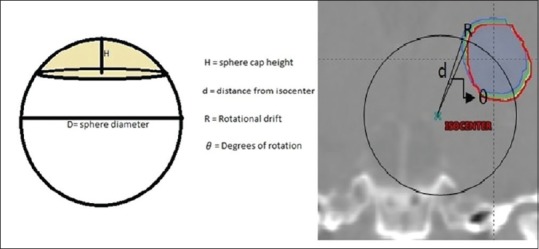
Spherical cap and rotational drift of a point at a distance d from isocenter

The rotational drift R is comparable to the spherical cap height H, by substituting the spherical cap height H with the rotational drift R.

Volume of PTV receiving 95% of the prescription dose is given by

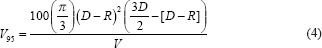
where V is the volume of the spherical PTV, D is the diameter of the sphere, and R is the rotational drift for a given rotation.

Chi-square goodness-of-fit test was employed to check whether the predicted V₉₅ matches the actual values.

RESULTS

Across the 10 cases and 38 lesions studied, the range and mean ± standard deviation in the PTV volumes were 0.04–12.63 cc and 2.11 ± 3.55 cc, respectively. Mean distances from the PTV centroid to the plan isocenter along lateral axis, vertical axis, and longitudinal axis were 3.46 ± 2.14, 3.16 ± 1.94, and 3.79 ± 1.94 cm, respectively. The maximum distance from PTV centroid to the plan isocenter was 7.2, 7.3, and 7.2 cm along the lateral axis, vertical axis, and longitudinal axis, respectively.

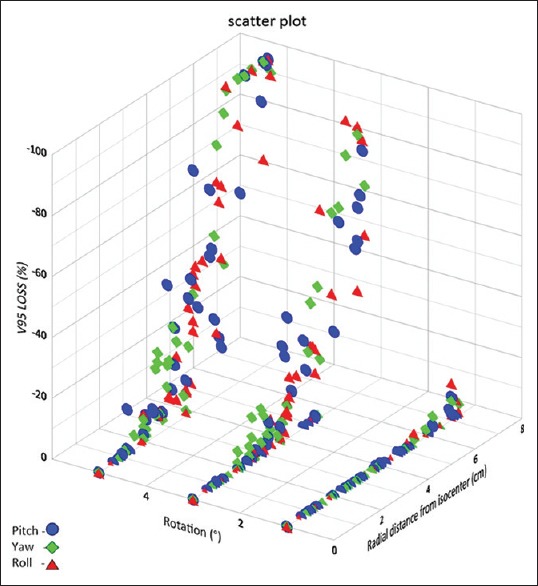
Rotationally induced uncertainties on target coverage at 1°, 3°, and 5° rotations along individual axis were obtained with V₉₅, D₉₅, D_mean, and D_min for each PTV. Obtained V₉₅, D₉₅, D_mean, and D_min values were plotted as a function of radial distance to isocenter along respective axis for simulated rotations and are shown in Figures 3–6, respectively.

Figure 3.

Loss in volume covered by 95% of the prescription dose (in %) as a function of radial distance from the rotational axis through isocenter for various rotational errors

Figure 6.

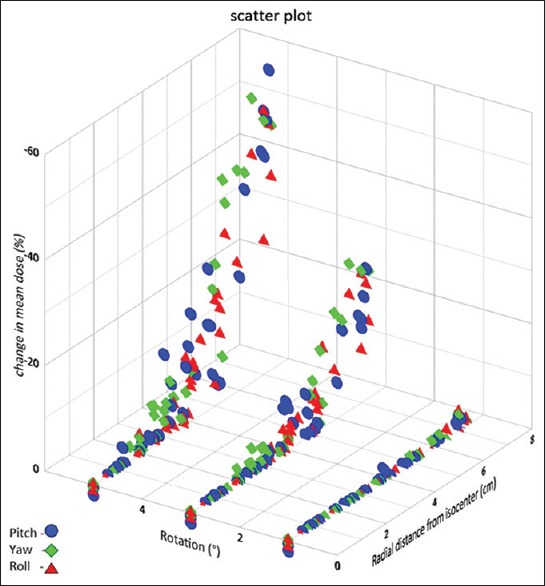
Change in mean dose values plotted as a function of radial distance from the rotational axis through isocenter for various rotational errors

Figure 3 shows the V₉₅ loss (%) values plotted as a function of radial distance to isocenter for simulated rotations of 1°, 3°, and 5°. At 1° rotation, about 4% of the PTV had V₉₅ <95% and all PTVs at a radial distance <6 cm had V₉₅ >95%. Volumes of the PTV in which V₉₅ reduced by more than 5% were in the range 0.05–0.07 cc and were at a radial distance of 6.2–7.2 cm. At 3° rotation, about 50% of the PTV had V₉₅ <95%, and all PTV^'s at a radial distance <2.5 cm had V₉₅ >95%. Volumes of the PTV in which V₉₅ reduced by more than 5% were in the range 0.04–8.14 cc and were at a radial distance of 2.5–7.3 cm. At 5° rotation, about 74% of the PTV had V₉₅ <95%, and all PTV^'s at a radial distance <1.2 cm had V₉₅ >95%. Volumes of the PTV in which V₉₅ reduced by more than 5% were in the range 0.04–12.63 cc and were at a radial distance of 1.2–7.3 cm. At a given radial distance for a given rotation, there is a marked variation in the V₉₅ for different targets, this is due to the varying sizes of target volumes, and smaller volumes suffer greater loss in V₉₅.

Figure 4 shows the D₉₅ loss (%) values plotted as a function of radial distance to isocenter for simulated rotations of 1°, 3°, and 5°. Mean D₉₅ values were 101.98%, 100.68%, 91.16%, and 79.58% of the prescription dose at 0°, 1°, 3°, and 5°, respectively. D₉₅ values reduced by more than 5% in 12%, 49%, and 75% of PTVs at 1°, 3°, and 5°, respectively. More variation of D₉₅ values was observed in smaller PTV volume or PTV at larger radial distance from isocenter or both.

Figure 4.

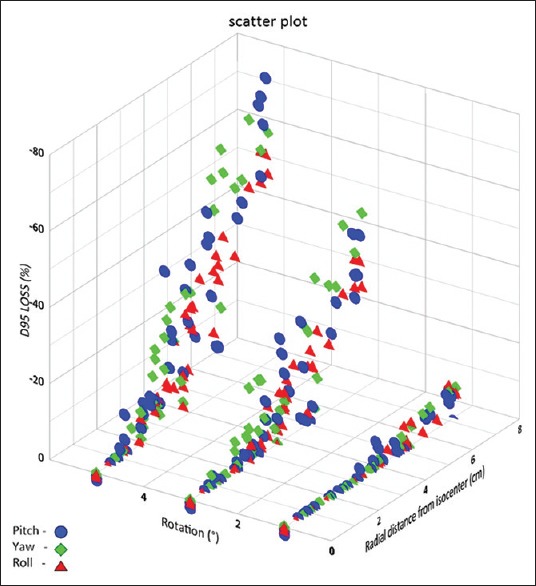
Decrease in dose to 95% of GTV (in %) as a function of radial distance from the rotational axis through isocenter for various rotational errors

Figure 5 shows the change in D_min values plotted as a function of radial distance to isocenter for simulated rotations of 1°, 3°, and 5°. The D_min obtained across all PTVs were 93.1%, 85.1%, 48.3%, and 21.2% at 0°, 1°, 3°, and 5° rotations. This represents the extent to which there can be a miss in the target volume coverage with various rotations and along with PTV volume and radial distance from isocenter, dose conformity, dose fall off, and distance between targets could have an impact on D_min. The mean D_min of the PTV was 97.4% of the prescribed dose for the original plans and decreased to 95%, 82.4%, and 68.8% at 1°, 3°, and 5° rotations, respectively.

Figure 5.

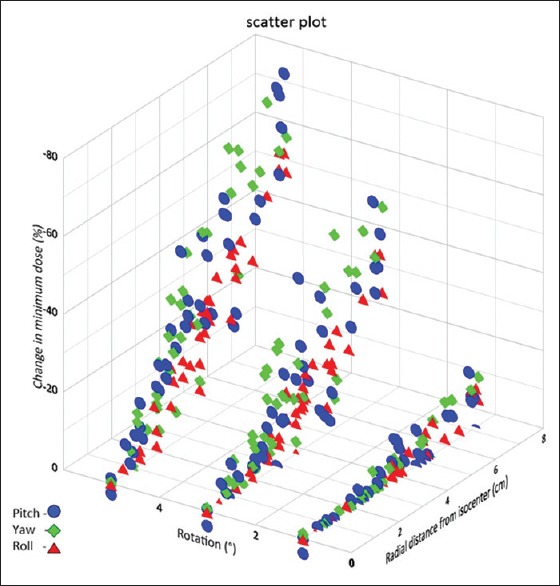
Change in minimum dose values plotted as a function of radial distance from the rotational axis through isocenter for various rotational errors

Figure 6 shows the change in D_mean values plotted as a function of radial distance to isocenter for simulated rotations. The average D_mean of the PTV was 106.5% of the prescribed dose for the original plans which reduced to 106.2, 101.8, and 94.4 for 1°, 3°, and 5° rotations, respectively. At 1° rotation, there was not significant change in the D_mean values obtained. At 3° rotation, nearly 7% of the PTVs had D_mean reduced to <90% of the prescription dose which had volumes in the range of 0.04–0.29 cc and at a radial distance of 6.2–7.3 cm, and at 5° rotation, nearly 23% of the PTVs had D_mean reduced to <90% of the prescription dose which had volumes in the range of 0.04–0.39 cc and at a radial distance of 5.0–7.3 cm.

Figure 7 shows the obtained V₉₅ values plotted as a function of PTV volume for various radial shift. Radial shifts of 0–0.49 mm, 0.5–1.49 mm, 1.5–2.49 mm, 2.5–3.49 mm, and 3.5–4.5 mm are grouped into 0, 1, 2, 3, and 4 mm, respectively. Figure 8 shows the estimated V₉₅ (%) for spherical targets of various volumes for a given radial shift.

Figure 7.

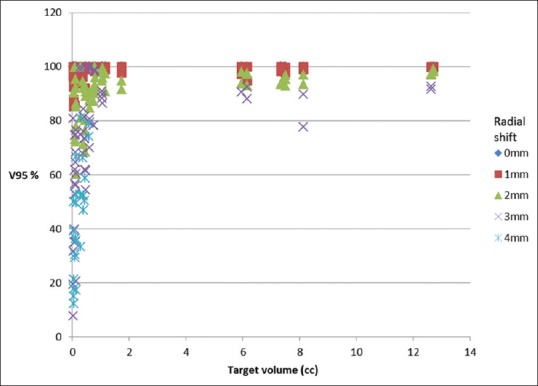
Drop in V95 (volume of PTV covered by 95% of prescription dose, expressed in %) as a function of PTV volume for various radial shifts

Figure 8.

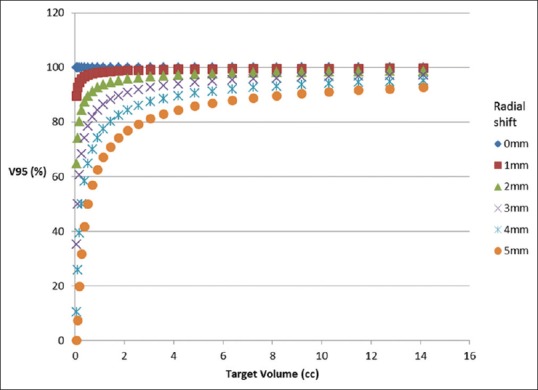
Estimated volume covered by the 95% of the prescribed dose (%) for spherical targets of various volume for a given radial shift

The V₉₅ values were estimated using equation (4) by substituting the radial distance from isocenter and volume of the PTV. At 1° rotation, the predicted V₉₅ values and that obtained by rotational simulation were matching within 5% for all volumes greater than 0.15 cc. Chi-square test returned a P = 1, indicating match between predicted and obtained values. At 3° rotation, Chi-square test returned a P = 0.33 for volumes greater than 0.1 cc which indicates that we could not reject the null hypothesis that the data came from the specified distribution. At 5° rotation, Chi-square test returned a P = 0, which is <0.05, indicating poor match between the values.

DISCUSSION

Pitch is the rotation around a transversal axis of the patient, yaw is the rotation around a vertical axis, and roll is the rotation around a longitudinal axis of the patient. All radiotherapy couches can correct for translational setup deviations, but not all couches are capable of correcting rotational setup deviations. Aligning the patient to isocenter by correcting for translational setup deviations only leaves rotational deviations uncorrected along the axes through isocenter. For single-isocenter multi-target patients treated with VMAT, our results indicate that the dosimetric uncertainties increase with increasing rotational setup deviations and increasing radial distance to isocenter in the respective axis. For a given rotational error and radial distance. PTVs having smaller volumes are more prone to dosimetric variation than the ones with relatively larger volumes.

Previous studies on multiple nonisocentric lesions have analyzed only two lesions with the isocenter placed at midway between the lesions. Furthermore, in all these studies, pitch, yaw, and roll rotational errors were simulated about all the axes simultaneously.[17,18,19] Another study reported the margin requirements based on target-isocenter separation.[20] Hence, the results are not specific along individual rotational axis.

For a given rotation, the dosimetric deviations in target are different for pitch, yaw, and roll; this is due to its varying radial distances in respective planes. Rotational deviations will yield anisotropic radial shift, i.e., the size of the shift will vary depending on the position with respect to the axis of rotation. At larger radial distance, the shift is more leading to greater coverage loss for targets. This attribute is utilized in estimating V₉₅ for spherical targets. Figure 8 shows the estimated V₉₅ (%) for spherical targets of various volumes for a given radial shift. It shows that smaller volumes suffer greater dosimetric loss than larger volumes. Assuming all the targets to be spherical, the estimated V₉₅ values were compared with the actual values obtained for various rotations. The Chi-square goodness-of-fit test was utilized to check the assumption. The test results indicated that the estimate was good up to 3° rotation for volumes greater than 0.15 cc. Discrepancies in smaller volumes can be attributed to larger conformity indices of these targets.[21] This estimate is simple requiring only two input values: target volume in cc and expected radial shift in cm. Few studies have favored the placement of isocenter closer to the smaller target volume, and the estimate would be able to assist in deciding how closer it has to be placed.

The critical size of the tumor that affects the dose deviation depends on multiple factors such as radial distance from isocenter and amount of rotational deviation expected. At a given radial distance, by knowing the expected rotational deviation, the expected rotational drift can be estimated with equation (1), and then, Figure 8 serves as a ready reference for identifying the critical volume. For V₉₅ to be within 95% threshold, the critical volume is 0.18 cc, 1.44 cc, 5.5 cc, and 12.8 cc at 1, 2, 3, and 4 mm rotational drift, respectively.

For targets treated nonisocentrically, the rotational deviation has a direct impact; similar to translational displacement, the displacement is given by two factors: distance from isocenter and degree of rotational deviation. Therefore, it is important to reduce this displacement of targets to acceptable thresholds. For a given target, the rotational displacement is not the same in all three axes owing to varying radial distance from isocenter at various axes and varying rotational deviations observed clinically. The rotational deviation is in addition to other discrepancies that exist such as translational deviations, image registration discrepancies while matching, fusion accuracy between multimodality images utilized in target delineation, and intrafractional deviation, so it is crucial to reduce the effect of this rotational deviation so as to keep the target coverage at maximum levels. Furthermore, if critical structures are in proximity to tumor, the effect could be adverse if rotational deviations are left uncorrected.

In our clinic, the observed maximum rotational deviation was 4.1° in dedicated stereotactic immobilization and 90% of deviations were within 2.5° while the observed maximum rotational deviation was 7° in a three-clamp head immobilization setup and only 65% of deviations were within 2.5°. Whenever larger rotational deviations are observed, we reposition the patient. We utilize ExacTrac 6D couch for correcting rotational deviations. In clinics without 6D couch, more rigid immobilization, repositioning, and, if feasible, additional PTV and PRV margins could be explored for managing rotational deviations.

CONCLUSION

The dosimetric effects of pitch, yaw, and roll on target coverage were analyzed along individual axis through isocenter. Our results indicate that correcting rotational errors is critical in single-isocenter, multi-target SRS. For rotational deviations, radial distance of the target from isocenter along the respective axis has a strong influence on target coverage. Smaller target volumes are more liable to rotational deviations compared to larger target volumes; V₉₅ estimate explains this with radial shift as compared to diameter of targets. Mathematical model for spherical targets can be used to estimate V₉₅ values for given rotational errors and was helpful in predicting and explaining the obtained results.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.