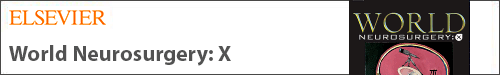Machine Learning Versus Logistic Regression Methods for 2-Year Mortality Prognostication in a Small, Heterogeneous Glioma Database

Abstract

Background

Machine learning (ML) is the application of specialized algorithms to datasets for trend delineation, categorization, or prediction. ML techniques have been traditionally applied to large, highly dimensional databases. Gliomas are a heterogeneous group of primary brain tumors, traditionally graded using histopathologic features. Recently, the World Health Organization proposed a novel grading system for gliomas incorporating molecular characteristics. We aimed to study whether ML could achieve accurate prognostication of 2-year mortality in a small, highly dimensional database of patients with glioma.

Methods

We applied 3 ML techniques (artificial neural networks [ANNs], decision trees [DTs], and support vector machines [SVMs]) and classical logistic regression (LR) to a dataset consisting of 76 patients with glioma of all grades. We compared the effect of applying the algorithms to the raw database versus a database where only statistically significant features were included into the algorithmic inputs (feature selection).

Results

Raw input consisted of 21 variables and achieved performance of accuracy/area (C.I.) under the curve of 70.7%/0.70 (49.9–88.5) for ANN, 68%/0.72 (53.4–90.4) for SVM, 66.7%/0.64 (43.6–85.0) for LR, and 65%/0.70 (51.6–89.5) for DT. Feature selected input consisted of 14 variables and achieved performance of 73.4%/0.75 (62.9–87.9) for ANN, 73.3%/0.74 (62.1–87.4) for SVM, 69.3%/0.73 (60.0–85.8) for LR, and 65.2%/0.63 (49.1–76.9) for DT.

Conclusions

We demonstrate that these techniques can also be applied to small, highly dimensional datasets. Our ML techniques achieved reasonable performance compared with similar studies in the literature. Although local databases may be small versus larger cancer repositories, we demonstrate that ML techniques can still be applied to their analysis; however, traditional statistical methods are of similar benefit.

Introduction

Gliomas are a heterogeneous class of tumors comprising approximately 30% of all brain malignancies.¹ Previously, the World Health Organization (WHO) grading system stratified them by histologic origin (i.e., astrocytoma, oligodendroglioma, mixed oligoastrocytoma, ependymoma), with additional grading (I–IV) according to pathologic features of aggression. In 2016, the WHO presented a novel classification system with incorporation of molecular biomarkers including isocitrate dehydrogenase (IDH1/IDH2) mutations,² O⁶-methylguanine-DNA methyltransferase (MGMT) methylation,³ p53 and phosphate and tensin homolog (PTEN) deletion,4, 5 epidermal growth factor receptor (EGFR) amplification,⁶ 1p/19q deletions,7, 8 9p(16q) deletions,⁹ and Ki67 index.¹⁰ The phenotypic expression of these markers by a glioma carries unique prognostic¹¹ and therapeutic implications.6, 7, 11, 12, 13, 14 Moreover, the prognostic implications of the relationship between a tumor possessing more than 1 molecular marker and a patients' baseline clinical and demographic status is not fully understood.15, 16 Existing prognostic systems separate patients into low-grade (i.e., WHO grades I and II) or high-grade (i.e., WHO grades III and IV) groups, and incorporate additional clinical features such as performance status, age, and tumor size13, 17, 18, 19, 20, 21 into their stratifications. Although some newer studies have incorporated limited molecular classification features,²² it is clear that older prognostic indices are likely to become obsolete in the molecular medicine era.

Machine learning (ML) is a subset of computer science, whereby a computer algorithm learns from prior experience. Using specified training data with known input and output values, the ML algorithm is able to devise a set of rules which can be used as predictors for novel data with similar input characteristics to the training data.²³ Previously, a human investigator would have to approach data collection and analysis using a set of a priori assumptions to prevent the burden of collecting data irrelevant to their hypothesis. The risk of this approach is that potentially meaningful trends caused by disregarded variables go unnoticed. ML lends itself naturally to trend delineation in large, unprocessed datasets.²⁴ It may also be used for clinical prediction using known inputs and desired outputs (e.g., mortality). Moreover, when implemented in a local database, ML-derived prognosticators may take into account unique features of the local population and treatment infrastructure, making them potentially more useful than evidence from noncontiguous populations. Local databases may however be considerably smaller than large-scale cancer repositories, limiting their academic study, but potentially providing the local clinician with meaningful clinical information.

Bearing these factors in mind, we aimed to apply a selection of ML algorithms to a database of 76 glioma cases to devise a 2-year mortality predictor. The complex histologic and molecular pathologic features of gliomas, combined with a series of clinical prognosticators, such as performance status, age, and treatment techniques,²⁵ make them an ideal multidimensional application for ML techniques. Additionally, because of our database characteristics, we aimed to compare the performance of ML algorithms using an unprocessed dataset with a dataset where only statistically significant variables had been preselected.

ML Methods

Logistic Regression

Logistic regression (LR) (Figure 1A) is a traditional statistical method used for binary classification and has been adopted as a basic ML model. It differs from linear regression (Figure 1B) because it uses a sinusoidal curve, delineating a boundary between 2 categories. Similar to linear regression, the logarithmic function is derived from weighted transformation of the categorical data points. The regression function therefore categorizes novel inputs into 1 of 2 categories based on what side of the line its coordinates fall on.

Figure 1.

Graphical representation of traditional statistical approaches to regression, with logistic (A) and linear regression (B) on the top row. The bottom row demonstrates machine learning approaches graphically, with support vector machine (C), artificial neural network (D), and decision tree (E) approaches.

Support Vector Machines

Support vector machines (SVMs) (Figure 1C) are based on the LR method and assign training examples to 1 of 2 categories, with a bisecting hyperplane separating the data points. Unlike LR, however, the optimal hyperplane bisects the points representing the largest separation between the 2 categories, and its shape may not be defined by a simple function. The algorithm is tasked with finding the data points (support vectors) defining the hyperplane and derivative line coefficients. The function can then categorize novel input values into groups falling on either side of the hyperplane, similar to LR.

Artificial Neural Networks

Artificial neural networks (ANNs) (Figure 1D) are so called because they are modelled after the layer-like histologic stratification of neurons. The input and output values represent the most superficial-but-opposing layers of the network, whereas the inner hidden layers consist of successive transformations of the input values. The algorithm therefore learns from the training set by progressive transformation of initial inputs. Values of these transformed inputs are then used by the model to predict output values.

Decision Trees

Decision tree (DT) (Figure 1E) algorithms split data into binary categories using progressive iterations. ML algorithms aim to find optimal features at which to perform data splitting, creating a branching tree–shaped diagram. Each node represents a point at which the data are split, and the leaves at the end of the tree are the output variables. Because the method involves binary classification, categorical data are preferred, whereas noncategorical data are preferably discretized prior to input.

Methods

Study Population

Our study population consisted of 76 patients (40 women and 36 men) with WHO grade I–IV gliomas, presenting to the neurosurgical oncology service at the University of Pittsburgh Medical Center from 2009 to 2017. At the end of the 2-year follow-up period, 52 patients were alive, whereas 24 had died. The mean age for the whole population at diagnosis was 47.3 ± 16.8 years. Interventions included total or subtotal resection (as stated by the operating surgeon), stereotactic biopsy, gamma knife therapy, or no intervention. Other information collected included radiologic maximum tumor diameter (centimeters); tumor location (lobe); pre- and postoperative Eastern Co-operative Oncology Group (ECOG) Performance Status score (0–5); whether the patient underwent subsequent chemotherapy, radiotherapy, or vaccine therapy; or had more than 1 surgical intervention. Surgical histopathology data included the presence of EGFR amplification, PTEN deletion, p53 mutation, 1p deletion, 19q deletion, 9p(p16) deletion, IDH1/IDH2 mutations, MGMT methylation, and Ki67 proliferation index.

Study Design

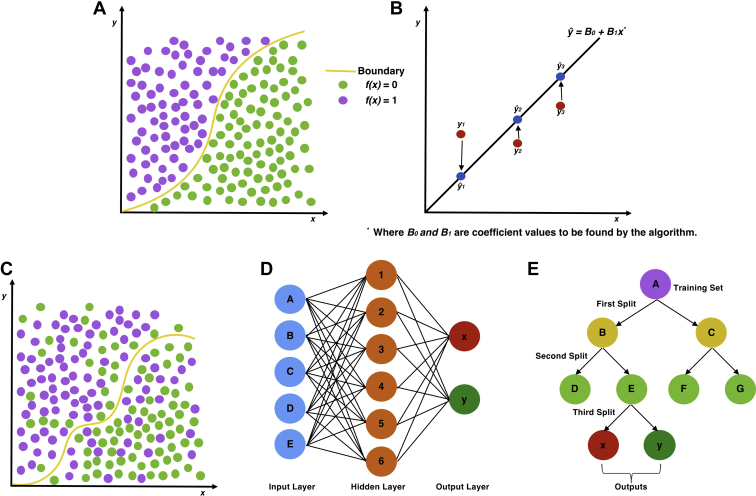
Because of the relatively small number of subjects in our database (N = 76), and the high dimensionality of the data, with 21 variables, we adopted 2 approaches to ML for this population (Figure 2). The first was to apply the algorithms to the raw dataset, for which input variables had not been preselected. The second was to apply χ² (for categorical variables) and independent samples t tests (for continuous variables) to the dataset, as outlined by Oermann et al.²⁶ to discern features with influence upon mortality (“feature selection”). As this involved a number of independent statistical tests, Bonferroni correction was subsequently applied. Fourteen variables were therefore identified for which there was a significant difference between subjects who survived 2 years and those who did not. Nonsignificant variables were excluded from the input (Table 1).

Figure 2.

Diagram of study design demonstrating both approaches to machine learning (ML). Left demonstrates the raw approach, and right demonstrates the initial statistical testing of variable significance prior to ML input (feature selection). Outputs (performance) were analyzed independently and then compared. ANN, artificial neural network; DT, decision tree; LR, logistic regression; SVM, support vector machine.

Table 1.

Demographic and Variable Features of the Population Categorized by 2-Year Survival

Variable	Total (N = 76)	Dead at 2 Years (n = 24)	Alive at 2 Years (n = 52)	Statistic∗	P Value†
Age (years)	47.29 ± 16.78	60.48 ± 14.03	43.10 ± 15.85	4.81	<0.05
Sex
Male	37	14	23	3.84	0.25
Female	39	10	29
Average diameter (cm)	3.41 ± 1.61	3.40	3.42	–0.06	0.95
Initial intervention				10.69	<0.05
Total resection	29	5	24
Subtotal resection	38	18	20
Biopsy only	6	0	6
Gamma knife	2	1	1
None	1	0	1
ECOG Performance Status
Preoperative score	1.70 ± 0.67	1.92	1.60	1.98	0.05
Postoperative score	1.55 ± 0.85	1.92	1.38	2.44	<0.05
Adjunctive treatment				0.06	0.97
Chemotherapy	51	18	33
Radiotherapy	48	18	30
Vaccine	3	1	2
Number of surgeries				0.22	0.64
1	51	17	34
>1	25	7	18
Lobe				10.16	0.12
Frontal	28	5	23
Temporal	22	11	11
Parietal	2	1	1
Occipital	2	0	2
Brainstem	2	0	2
Other	3	0	3
Multiple	17	7	10
WHO grade				16.73	<0.05
1	6	0	6
2	24	2	22
3	8	2	6
4	38	20	18
Molecular features (number unknown)				23.71	<0.05
EGFR amplification	21	12 (1)	9 (2)
PTEN deletion	30	16 (1)	14 (2)
p53 mutation	29	6 (1)	23 (2)
1p deletion	15	2 (1)	13 (2)
19q deletion	19	5 (1)	14 (2)
9p(p16) deletion	34	14 (1)	20 (2)
IDH1 mutation	24	3 (1)	21 (2)
IDH2 mutation	3	0 (1)	3 (2)
MGMT methylation	35	10 (1)	25 (2)
Ki67 index	18.80 ± 16.73	27.90	14.60	3.74	<0.05

Values are mean ± SD, number of patients, or as otherwise indicated.

WHO, World Health Organization; MGMT, O⁶-methylguanine-DNA methyltransferase; PTEN, phosphate and tensin homolog.

^∗Statistic is either χ² (categorical variables) or T statistic (continuous variables).

^†Because multiple independent statistical tests were performed, P values have been adjusted via application of Bonferroni correction.

Data Collection, Information Encoding, and Dataset Splitting

The raw data were collected using Microsoft Excel (Microsoft Corp., Redmond, Washington, USA). The data were parsed using Python 2.7 programming language (Python Software Foundation, Beaverton, OR, USA), using a custom written code. We used binary notation for ordinal variables (i.e., yes = 1, no = 0). Categorical and continuous variables were scaled (e.g., for the Ki67 index and age at diagnosis) to values between 0 and 1. Scaling was done using normalization (unit length vectors) and minimum-maximum scaling techniques, implemented in scikit-learn's²⁷ preprocessing libraries. The continuous variables were age, maximum tumor diameter, and Ki67 index. Categorical variables were total resection, ECOG Performance Status, lobe/area of brain affected, and WHO grade. There were 3 subjects whose surgical pathology results were unavailable. Instead of discarding these from analysis, we assigned a value of 0.5 for each variable (e.g., IDH1/IDH2, PTEN). This was done to reflect the common situation where clinical data is partly missing from records. All the features were then normalized using a normal vector. The dataset was partitioned using a 70/30 training/testing split, meaning that 53 subjects were used for training and 23 were used for testing for each cycle of each algorithm.

ML Algorithms

All ML and LR models were imported from the scikit-learn library. All models were run 15 times for each model, in an attempt to reduce the problem of overfitting due to small database size. Each cycle consisted of a training and testing stage, where the dataset was repetitively partitioned. Per cycle, the same subject was not used for both training and testing. The subjects used (and their characteristics) for training and testing varied between cycles and algorithms. The number of dead and alive participants in the training and testing sets did vary between cycles however. Metrics presented are averaged figures from the 15 testing cycles for each ML method.

ANN Method

Our ANN method used a single layer of neurons between the input and output layers. The intermediate layer contained 100 neurons, each with a mini-batch size of 5. The network was trained using 1000 epochs, using an Adam optimizer,²⁸ with a default 0.001 learning rate. Briefly, the Adam optimizer is an algorithm for first-order gradient-based optimization, which is an extension to stochastic gradient descent.

DT Method

The criteria used to split each node was determined by the Gini index,²⁹ a standard measure of information gain in DT applications.³⁰ This represents a more intuitive approach than randomly selecting criteria at which to split data. The minimum number of samples for each leaf was 1, whereas the minimum number of samples to split a node was 2.

SVM Method

Our SVM model used a radial basis function Kernel, with a C-penalty parameter of 100 and a gamma value of 0.1.

LR

LR was the benchmark, traditional statistical method we used for comparison with the performance of the ML algorithms. Nevertheless, it was also implemented using the same platform (scikit-learn) as the ML algorithms. The penalization parameter used was l2 norm. The C parameter was 150.0, and the optimization algorithm used was coordinate descent.

Data Processing

The averaged output values from the 15 cycles were then tabulated into standardized 4 × 4 confusion matrices. The sensitivity, specificity, positive likelihood ratio (PLR), negative likelihood ratio (NLR), positive predictive value (PPV), negative predictive value (NPV), and overall accuracy were calculated. All probabilities were calculated to 95% certainty. Receiver operating curves and the area under the receiver operating curves were additionally calculated and tabulated using the roc_curve model imported from the scikit-learn toolbox. To optimize comparison between accuracy (percentages) and area under the curve (AUC) (ratio), we multiplied AUC results by 100.

Results

Comparison of Diagnostic Performance

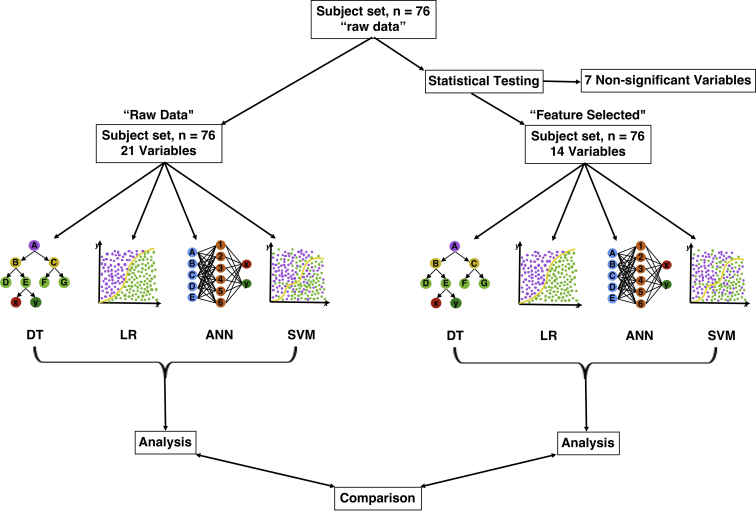
For raw data, the ANN method performed best in terms of sensitivity (81.54%), followed by the SVM (79.31%), LR (76.75%), and DT (73.65%) methods. Using a feature-selected dataset, sensitivity decreased for DT (68.93%), ANN (78.39%), and LR (74.26%), but increased slightly for SVM (80.54%). Using a feature-selected dataset, the specificity of all algorithms increased for all methods, with ANN performance showing the biggest increase (+11.62%) and DT showing the smallest (+7.56%). Using a feature-selected versus a raw dataset, all methods demonstrated a performance increase in terms of PPV (SVM = +7.69%; ANN = +7.08%; LR = +7.03%; DT = +5.87%), whereas all (DT = −6.21%; ANN = −3.79%; LR = −3.37%) but SVM (+0.54%) demonstrated a decrease in NPV performance. Likewise, ANN (+0.42), SVM (+0.36), LR (+0.28), and DT (+0.14) demonstrated an increase in PLR performance using a feature-selected dataset. In terms of NLR, all methods (SVM = −0.10; LR = −0.04; ANN = −0.02) aside from DT (+0.55) demonstrated a decrease in NLR prediction. All methods demonstrated an increase in accuracy using the feature-selected dataset (SVM = +5.38%; ANN = +2.71%; LR = +2.62%; DT = +0.17%). Finally, feature-selection increased overall performance, as represented by the AUC for all methods (LR = +8.58%; ANN = +6.21%; SVM = +2.83%) aside from DT, which demonstrated a decrease in the AUC (−7.54%) (Table 2; Figure 3).

Table 2.

Performance for All Machine Learning Categories

ANN: Raw Data			SVM: Raw Data			DT: Raw Data			LR: Raw Data
	Alive	Dead		Alive	Dead		Alive	Dead		Alive	Dead
Predicted alive	19.13	6.20	Predicted alive	18.67	6.67	Predicted alive	17.33	6.40	Predicted alive	18.06	6.53
Predicted dead	4.33	6.26	Predicted dead	4.87	5.80	Predicted dead	6.20	6.07	Predicted dead	5.47	5.93

Performance (ANN)	Value	95% CI		Performance (SVM)	Value	95% CI		Performance (DT)	Value	95% CI		Performance (LR)	Value	95% CI
		Lower	Upper			Lower	Upper			Lower	Upper			Lower	Upper
Sensitivity (%)	81.54	65.85	97.24	Sensitivity (%)	79.31	62.95	95.68	Sensitivity (%)	73.65	55.85	91.45	Sensitivity (%)	76.75	59.69	93.82
Specificity (%)	50.24	22.48	78.00	Specificity (%)	46.51	18.83	74.20	Specificity (%)	48.68	20.94	76.42	Specificity (%)	47.59	19.86	75.32
PLR	1.64	0.91	2.96	PLR	1.48	0.85	2.59	PLR	1.44	0.79	2.59	PLR	1.46	0.82	2.60
NLR	0.37	0.13	1.01	NLR	0.44	0.17	1.20	NLR	0.54	0.22	1.31	NLR	0.49	0.19	1.25
PPV (%)	75.52	58.78	92.27	PPV (%)	73.68	56.53	90.82	PPV (%)	73.03	55.17	90.89	PPV (%)	73.44	55.99	90.90
NPV (%)	59.11	29.50	88.72	NPV (%)	54.36	24.47	84.25	NPV (%)	49.47	21.50	77.45	NPV (%)	52.02	23.02	81.02
Accuracy (%)	70.68			Accuracy (%)	67.95			Accuracy (%)	65.00			Accuracy (%)	66.66

ANN: Feature Selected			SVM: Feature Selected			DT: Feature Selected			LR: Feature Selected
	Alive	Dead		Alive	Dead		Alive	Dead		Alive	Dead
Predicted alive	19.33	4.07	Predicted alive	20.40	4.67	Predicted alive	17.46	4.67	Predicted alive	18.67	4.53
Predicted dead	5.33	6.6	Predicted dead	4.93	6.00	Predicted dead	7.87	6.00	Predicted dead	6.47	6.13

Performance (ANN)	Value	95% CI		Performance (SVM)	Value	95% CI		Performance (DT)	Value	95% CI		Performance (LR)	Value	95% CI
		Lower	Upper			Lower	Upper			Lower	Upper			Lower	Upper
Sensitivity (%)	78.39	62.14	94.63	Sensitivity (%)	80.54	65.12	95.96	Sensitivity (%)	68.93	50.91	86.95	Sensitivity (%)	74.26	57.18	91.35
Specificity (%)	61.86	32.71	91.00	Specificity (%)	56.23	26.47	86.00	Specificity (%)	56.23	26.47	86.00	Specificity (%)	57.51	27.83	87.18
PLR	2.05	0.93	4.54	PLR	1.84	0.91	3.73	PLR	1.57	0.76	3.26	PLR	1.75	0.84	3.65
NLR	0.35	0.14	0.85	NLR	0.35	0.13	0.90	NLR	0.55	0.25	1.21	NLR	0.45	0.19	1.04
PPV (%)	82.61	67.25	97.97	PPV (%)	81.37	66.13	96.61	PPV (%)	78.90	61.90	95.90	PPV (%)	80.47	64.34	96.60
NPV (%)	55.32	27.11	83.53	NPV (%)	54.90	25.40	84.40	NPV (%)	43.26	17.19	69.33	NPV (%)	48.65	21.05	76.25
Accuracy (%)	73.39			Accuracy (%)	73.33			Accuracy (%)	65.17			Accuracy (%)	69.27

Smaller tables are 2 × 2 confusion matrices containing the averaged output variables of the 15 cycles of machine learning for each algorithm. Underneath each confusion matrix is the performance of each test, calculated from the matrix and given to 95% CI. The upper 2 rows of the tables are for the raw datasets, and the lower 2 rows of tables are for the feature selected datasets.

ANN, artificial neural network; SVM, support vector machine; DT, decision tree; LR, logistic regression; CI, confidence interval; PLR, positive likelihood ratio; NLR, negative likelihood ratio; PPV, positive predictive value; NPV, negative predictive value.

Figure 3.

A 4 × 3 array of figures demonstrating the algorithm performance using both raw data (far left column) and feature-selected (middle column) approaches. Change in performance between raw and feature-selected data is demonstrated in the far-right column. The first row shows sensitivity versus specificity performance; the second row shows positive predictive value versus negative predictive value performance; the third row shows positive likelihood ratio versus negative likelihood ratio performance; and the fourth row shows accuracy versus area under the curve performance. *Area under the curve metrics have been scaled to 100 to correlate with accuracy. ANN, artificial neural network; AUC, area under the curve; DT, decision tree; LR, logistic regression; NLR, negative likelihood ratio; NPV, negative predictive value; PLR, positive likelihood ratio; PPV, positive predictive value; SVM, support vector machine.

Receiver Operating Curves and Confidence Intervals

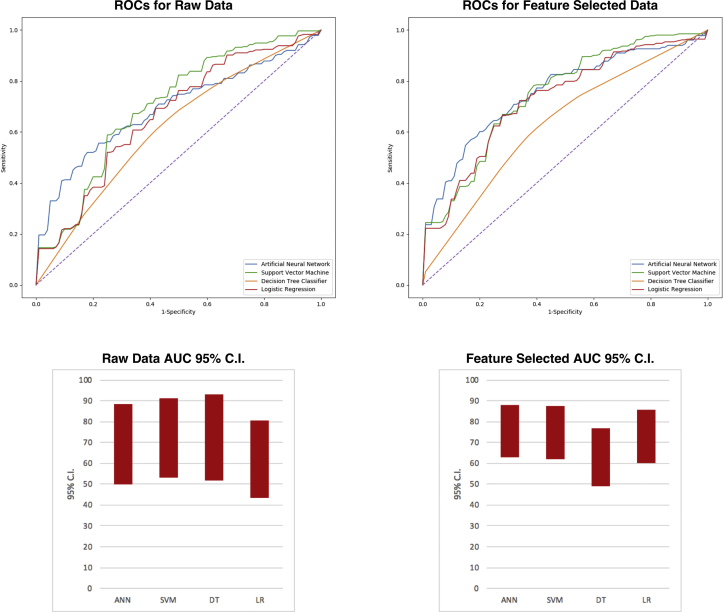
When comparing the receiver operating curves performance to that of y = x, with an area of 0.5 (50), the SVM (AUC = 71.88) demonstrated the best performance, followed by DT (AUC = 70.54), ANN (AUC = 69.19), and LR (AUC = 64.29). Although these were higher than 0.5, the 95% confidence intervals (CIs) for both the ANN (49.86–88.52) and LR (43.63–84.95) both included 50, indicating non-significance. Even though the SVM (53.40–90.36) and DT (51.62–89.46) algorithms had CI values more than 50, these were only marginally greater than 50. The feature-selected datasets provided a performance increase for all but the DT algorithms, which demonstrated a decrease in AUC value. The performance benefit was indicated by higher AUC values, with ANN (AUC = 75.40) performing best, followed by SVM (AUC = 74.71), LR (AUC = 72.87), and DT (AUC = 63.00). Using feature-selected data also yielded overall narrower 95% CIs, with all methods aside from DT demonstrating at least a 10-unit increase of lower CI boundary above 50, indicating significance over random guessing and use of raw data. Nevertheless, for both feature-selected and raw data, none of the ML methods demonstrated significant performance improvement versus LR, nor over one another (Table 3; Figure 4).

Table 3.

Receiver Operating Curve Characteristics for Uncensored and Censored Approaches

Uncensored					Feature Selected
Algorithm	AUC	SE	95% CI (Lower)	95% CI (Upper)	Algorithm	AUC	SE	95% CI (Lower)	95% CI (Upper)
ANN	69.19	9.86	49.86	88.52	ANN	75.40	6.40	62.90	87.90
SVM	71.88	9.43	53.40	90.36	SVM	74.71	6.50	62.10	87.40
DT	70.54	9.65	51.62	89.46	DT	63.00	7.10	49.10	76.90
LR	64.29	10.54	43.63	84.95	LR	72.87	6.60	60.00	85.80

Machine learning versus LR methods for 2-year mortality prognostication in a small, heterogeneous glioma database.

AUC, area under the curve; CI, confidence interval; ANN, artificial neural network; SVM, support vector machine; DT, decision tree; LR, logistic regression.

Figure 4.

Receiver operating curves for raw (left) and feature-selected (right) data. Lines are color coordinated using the figure legend in the bottom right corner of the graph. Perforated diagonal line is y = x, with an area under the curve of 0.5 (indicative of random guessing). The performance increase is discerned by the increased distance between all curves and that of y = x. The lower right column chart demonstrates the scaled 95% confidence intervals of the area under the curves calculated for each machine learning method. Artificial neural network and logistic regression methods were not statistically different from 0.5. Support vector machine and decision tree methods were better than random guessing; however, their statistical significance was weak. Performance of algorithms using raw datasets can be compared with the chart for the feature-selected dataset in the lower right corner. These are the 95% confidence intervals for all machine learning methods, and can be concluded to be not only further away from 0.5 but also narrower, indicating greater significance. ANN, artificial neural network; AUC, area under the curve; C.I., confidence interval; DT, decision tree; LR, logistic regression; ROC, receiver operating curve; SVM, support vector machine.

Discussion

We have successfully demonstrated the application of 3 ML techniques and a ML-implemented LR technique to a database of 76 patients with glioma of all stages, molecular phenotypes, and heterogeneous clinical characteristics. Relative to older, published prognostic studies, which do not incorporate molecular features, our study involves considerably fewer subjects. We accomplished our goal of applying ML techniques to this database with a relatively low subject number/variable ratio; furthermore, we demonstrate that ML can be applied with a reasonable level of confidence to make prognostic inferences from this data.

Comparison with Similar Studies

In the neuro-oncology literature, much focus of ML application has been directed toward discernment of magnetic resonance imaging characteristics of central nervous system tumors (subsequently discussed). Only 1 non–imaging-focused study has used ML for glioma outcome prediction,³¹ whereas the study by Oermann et al.²⁶ used a similar methodology for cerebral metastasis prognostication. The study by Malhotra et al.³¹ applied a novel data mining algorithm to extract relevant features pertaining to treatment and molecular patterns in a database of 300 newly diagnosed glioblastoma multiforme cases. The ML component of their study involved the extraction of relevant treatment and pathologic features, which were then classified and subjected to classical statistical methods for prognostication. This is in effect the opposite approach to our method of using feature-selected data, as the authors used data mining to extract relevant features which were subsequently subjected to statistical testing, whereas we conducted statistical tests of significance for feature-selection prior to ML implementation. They achieved maximal C values of 0.85 using LR and 0.84 using Cox multivariate regression. The study by Oermann et al.,²⁶ although pertaining to cerebral metastases rather than gliomas, used a similar methodology to our feature-selected approach to prognosticate 1-year survival in a total of 196 patients. In this study, the pooled voting results of 5 independent ANNs (AUC = 84%) significantly outperformed traditional LR methods (AUC = 75%). Further, they found that ML techniques were more accurate at predicting 1-year survival than 2 traditional prognostic indices. Because our study used data from gliomas of all stages, we did not compare our results to existing prognostic indices, which specifically differentiate patients into low- and high-grade categories. Using a feature-selected approach, our best performing algorithm (which was coincidentally also an ANN) achieved approximately 10-unit lower AUC metric than their ANN approach. We suspect that this is for 2 reasons. First, their training set consisted of 98 patients, which was over twice the size of our training set of 40, offering more examples to learn from. Second, their method only used 6 input variables, compared to 21 for our raw approach and 14 for our feature-selected approach. It is therefore likely that increased proportionality of subjects to variables in their dataset also enhanced predictive performance of the ML algorithm by providing a less-noisy dataset. From this, it is apparent that smaller datasets may require feature selection prior to ML application if predictive performance is to be maximized. We cannot conclude that for small, highly dimensional datasets, ML approaches including ANN, DT, or SVM offer any significant performance advantage over traditional LR methods. Nevertheless, we achieved reasonably good predictive metrics using feature selected data with all ML approaches.

Future Directions

ML algorithms have been intuitively applied to data-rich magnetic resonance imaging sequences in an effort to quantitatively discern characteristic imaging features of gliomas.32, 33, 34, 35, 36 These methods have yielded the ability to discern occult imaging features not detectable by humans and which indiate the presence of MGMT methylation,³⁵ IDH1 mutation,37, 38, 39 and 1p/19q co-deletion.³⁸ This approach may potentially allow for the noninvasive identification40, 41 and even prognostication41, 42 of gliomas using imaging characteristics alone. It is not unreasonable to suggest that the next generation of prognostic indices will be derived from a combination of clinical database mining techniques, such as our present study combined with novel techniques of image-based ML. This will represent a substantial step forward because previous prognostic systems relied on invasive methods for definitive diagnosis, prognostication, and treatment stratification. It may also permit clinicians to prognose the clinical course of low-grade tumors noninvasively and with greater accuracy by using information from local databases to guide clinical decision making, rather than relying upon data from non-contiguous populations, which may be subject to confounding (and potentially clinically-significant) genetic and environmental effects. Depending on the integrity and scale of the localized database, predictions can be made with reasonable accuracy, as we have demonstrated in the present study.

Limitations

Although we achieved acceptable predictive performance using feature-selected data, our study has highlighted potential difficulties of ML application to smaller, highly dimensional clinical databases. Feature selection of relevant data may optimize ML algorithms in studies using smaller subject sets; however, censoring of particular variables may result in weaker trends going unnoticed. We also anticipate that the predictive accuracy and AUC would improve by increasing the number of subjects included in the training set. Despite our study using a training set less than half the size of that of Oermann et al.,²⁶ we achieved only slightly weaker prognostic performance. Nevertheless, the relative success of our algorithms could also be attributed to the potential effect of including both low- and high-grade tumors, which have significantly different prognostic profiles and which may exert a skewing effect on the data. An alternative to the manual statistical testing of variables for feature selection is principal component analysis,⁴³ which is an entirely ML-based method of reducing dataset dimensionality, therefore reducing scope for human error or bias.

Another important concern with small datasets is overfitting of the data, which is when the models, having had few data to train with, cannot appropriately anticipate novel data with fundamentally different data parameters, or when outlier values in the data exert a substantial effect which is not realistic and which impose a penalty on the models' overall accuracy. We attempted to minimize this problem by running 15 cycles of each algorithm using the same split proportions and with different subjects used for training and testing in each cycle. Feature selection reduced the variability (and dimensionality) of data without reducing database size and improved algorithmic performance, which is another method of reducing the effect of data overfitting. Other methods to reduce the issue of overfitting include early stoppage of training (i.e., before accuracy decreases), ensembling (using multiple models in parallel),⁴⁴ and dropouts for neural networks.⁴⁵

When selecting variables to include for our data collection, we attempted to extract as much information as possible for each subject. Nevertheless, some of the features we included are considered unconventional from a traditional neurosurgical and oncologic standpoint (e.g., use of intraoperatively determined total or subtotal resection extent [which was not a significant effector of survivability and was therefore excluded during the process of feature selection anyway]). Nevertheless, the purpose of this paper was to demonstrate the potential of ML in the neurosurgical domain and provide a blueprint for neurosurgeons wishing to implement the methodology on their own datasets.

Conclusions

As clinical approaches to gliomas are beginning to adapt to the molecular-medicine era, the small size of a local database does not provide a barrier to the implementation of ML techniques for prognostication purposes. Although our study was purely academic, it demonstrates the potential for ML to provide meaningful insight into the diagnosis and treatment of these heterogeneous tumors at a local level.