Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Jun 18.
Published in final edited form as: Sci Total Environ. 2018 Nov 5;655:512–519. doi: 10.1016/j.scitotenv.2018.11.022

Modeling groundwater nitrate exposure in private wells of North Carolina for the Agricultural Health Study

Kyle P Messier 1,2,*,†, David C Wheeler 3,†, Abigail R Flory 4, Rena R Jones 5, Deven Patel 5, Bernard T Nolan 6, Mary H Ward 5
PMCID: PMC6581064  NIHMSID: NIHMS1016458  PMID: 30476830

Abstract

Unregulated private wells in the United States are susceptible to many groundwater contaminants. Ingestion of nitrate, the most common anthropogenic private well contaminant in the United States, can lead to the endogenous formation of N-nitroso-compounds, which are known human carcinogens. In this study, we expand upon previous efforts to model private well groundwater nitrate concentration in North Carolina by developing multiple machine learning models and testing against out-of-sample prediction. Our purpose was to develop exposure estimates in unmonitored areas for use in the Agricultural Health Study (AHS) cohort. Using approximately 22,000 private well nitrate measurements in North Carolina, we trained and tested continuous models including a censored maximum likelihood-based linear model, random forest, gradient boosted machine, support vector machine, neural networks, and kriging. Continuous nitrate models had low predictive performance (R2 < 0.33), so multiple random forest classification models were also trained and tested. The final classification approach predicted < 1 mg/L, 1 – 5 mg/L, and ≥5 mg/L using a random forest model with 58 variables and maximizing the Cohen’s kappa statistic. The final model had an overall accuracy of 0.75 and high specificity for the higher two categories and high sensitivity for the lowest category. The results will be used for the categorical prediction of private well nitrate for AHS cohort participants that reside in North Carolina.

1. Introduction

Nitrate (NO3-) is an essential plant nutrient, but it is also a widespread contaminant of groundwater and surface water across the United States. Important anthropogenic sources include nitrogen fertilizers, animal and human waste, and atmospheric deposition of nitrogen oxides from fossil fuel combustion(Katz et al., 2009; Messier et al., 2014; Nolan and Hitt, 2006). In the United States, two-thirds of U.S. coastal systems are moderately to severely impaired due to nutrient loading (Davidson et al., 2012). Ecological impacts include but are not limited to eutrophication of surface waters, reduction in biodiversity, and harmful algal blooms leading to hypoxic (low oxygen) waters and fish kills (Davidson et al., 2012).

When ingested, nitrate undergoes chemical transformations in the gastrointestinal tract that may result in the formation of harmful N-nitroso-compounds (NOC), many of which are potent animal carcinogens and teratogens (International Agency for Research on Cancer, 2010). In a review of the evidence for nitrate and nitrite ingestion and cancer, the International Agency for Research on Cancer (IARC) concluded that nitrate and nitrite are probable human carcinogens when ingested under conditions that increase the formation of NOC (International Agency for Research on Cancer, 2010). The U.S. Environmental Protection Agency (EPA) maximum contaminant level (MCL) for nitrate in public drinking water supplies is 10 mg/L NO3-nitrogen (N), which is similar to the World Health Organization (WHO) guideline of 50 mg/L as NO3 (equivalent to 11.3 mg/L NO3-N). These regulations were based on prevention of infant methemoglobinemia (blue baby syndrome), an acute and potentially fatal condition. Other health risks from drinking water nitrate ingestion including cancer and adverse reproductive outcomes (Ward et al., 2018) were not considered in the development of the regulatory limits.

It is estimated that 14 percent of the US population use private wells as their primary drinking water source, while approximately 35 percent of North Carolina residents utilize private wells as their household water source (Maupin et al., 2010). Of the US population with self-supplied private wells, 7 percent exceed the MCL for nitrate based on a national study (Dubrovsky et al., 2010). In agricultural areas across the US, about 22 percent of private wells exceed the nitrate MCL (Dubrovsky et al., 2010). Private wells are not regulated and measurement data are sparse; therefore, understanding the spatial extent of nitrate contamination through modeling approaches is pertinent to protecting the health of private well users.

The Agricultural Health Study (AHS) is a prospective cohort of approximately 90,000 licensed pesticide applicators (mostly farmers) and their spouses residing in Iowa and North Carolina. The AHS was initiated to study agricultural exposures and risk of multiple health outcomes including cancer, nonmalignant respiratory disease, thyroid disease, and other chronic health effects. About 60 percent of the cohort used private wells as their drinking water source at enrollment in 1993–1997. To evaluate the risk of cancer and other health effects in relation to nitrate concentrations in private wells, retrospective estimates of exposure are needed.

Messier et al. (2014) developed separate non-linear regression plus Bayesian Maximum Entropy (BME) models for both monitoring and private wells; however, predicting continuous nitrate concentration in private drinking water wells proved more difficult compared to monitoring wells, likely due to the high proportion of measurements that were below the detection limit. More recently, machine learning approaches have been used to predict environmental contaminants. In a study directly pertaining to the Agricultural Health Study, random forest models were used to predict nitrate levels in private drinking water wells among the Iowa participants (Wheeler et al., 2015). In groundwater, Ayotte et al. (2016) used boosted regression trees to predict the probability that arsenic exceeds the MCL and Tesoriero et al. (2017) used a random forest model to predict nitrate in private drinking water wells in Wisconsin. Gemitzi et al. (2009) used neural networks to predict groundwater nitrate in Greece with high fidelity.

In the current study, the aim was to extend the efforts of Messier et al. (2014) to develop a private well groundwater nitrate model in North Carolina for use in predicting drinking water nitrate exposures for the remaining AHS participants. This study is needed because additional machine learning modeling approaches and geographic covariate data may improve upon the previous study’s results thereby reducing the exposure misclassification. First, continuous models, including a suite of machine learning approaches (e.g. random forest), for private well groundwater nitrate were developed and assessed for their out-of-sample test set prediction. Next, classification prediction models were fitted to predict categories of nitrate concentrations in order to help improve prediction performance. This study demonstrates an approach applicable to many environmental exposure assessments in which a series of modeling methods are tested against independent, hold-out datasets in order to achieve the best possible predictions.

2. Methods

2.1. Nitrate Data

Groundwater nitrate measurements reported as nitrate-nitrogen (NO3-N) from private wells (N=22,059) were collected and maintained by the North Carolina Department of Health and Human Services (NC-DHHS). Data were obtained by Messier et al. (2014) and used here for the years 1990 through 2011. Geographic coordinates were determined through address geocoding using a multistage process described previously (Messier et al., 2012).

The private well data that we used were collected by the NC-DHHS as part of state requirements for private well testing for new home purchases, other real estate transactions, and voluntary testing by homeowners. Since routine ambient monitoring or research studies were not the purpose of compiling this dataset, the chemical analytical method used to quantify nitrate concentration had a high detection limit of 1 mg/L. Consequently, out of the 22,059 private well samples, 15,304 (69.4 percent) of the samples were below the detection limit. We estimated nitrate concentrations below the detection limit by imputing below detect observations from a log-normal distribution of uncensored nitrate data using Tobit regression models with no covariates (Lubin et al., 2004).

The hydrogeologic units in North Carolina are variable. The inner coastal plains region is generally characterized by sandy, sedimentary, shallow aquifers with high hydraulic conductivity, low organic carbon, and interspersed with small impermeable confining units (Kennedy and Genereux, 2007; Winner Jr. and Coble, 1996). The outer coastal plains have poorly drained soils and high organic carbon content (Tesoriero et al., 2004). Moreover, well depths in the coastal plains can vary substantially, which results in neighboring wells withdrawing water from different groundwater units, such as one well withdrawing from a surficial aquifer and one from a confined aquifer. In the Piedmont and Blue Ridge (mountains) regions of North Carolina, impermeable and fractured igneous and metamorphic rocks predominate, which contributes to additional heterogeneity and low water yields compared to the coastal plains (Daniel III and Dahlen, 2002).

2.2. Geographic Covariates

2.2.1. Kriging of Well Depths

A limitation of our dataset was that well depth information was not available for water quality measurements; however, a separate database (i.e., the U.S. Geological Survey, National Water Information System [NWIS]) containing private well construction information for data distributed across the entire state, was used to estimate well depths for sampled wells used in this study (U.S. Geological Survey, 2018). While well construction information is available from NWIS, a listing of specific wells is not presented here owing to their proprietary nature (i.e., private residential wells). Readers should contact B.T. Nolan for more information. The mean depth was 95 feet (ft; ~ 30 m) with a standard deviation of 109 ft (~ 33 m). Wheeler et al. ( 2015) and others (Nolan and Hitt, 2006; Ransom et al., 2017) found well depth to be an important predictor of groundwater nitrate concentrations, therefore the well construction database was used with ordinary kriging to predict well depth as a candidate geographic covariate in models described later.

The well depth kriging analysis was conducted using BMElib (Christakos et al., 2002; Serre and Christakos, 1999) software in MATLAB (MathWorks Inc., Natick, USA). Well depth was log-transformed for the covariance and kriging analysis, which reduced the skewness from 2.48 to −0.13. A two-component exponential model was fit to model the spatial covariance of well depth:

C(r)=C01exp⁡(−3ra1)+C02exp⁡(−3ra2), (1)

where r is the isotropic distance between well locations, C01 = 0.26 (log-meter)2 is the first component covariance, C02 = 0.33 (log-meter)2 is the second component covariance, a1 = 15 m is the first component spatial range, and a2 = 99 km is the second component spatial range. The components of the kriging model capture both the local heterogeneity from topographic, soil, geologic, and built-environment variations and regional trends from large hydrogeologic units. A 10-fold cross-validation of the ordinary kriging model resulted in a mean prediction R2 of 0.41 and root mean squared prediction error of 0.59 log-meters.

2.2.2. Covariate Descriptions

Geographic covariates representing sources, transport, and attenuation mechanisms of nitrate were constructed prior to model development (Messier et al., 2014; Nolan and Hitt, 2006; Wheeler et al., 2015). The candidate set included variables from Messier et al. (2014), plus additional variables calculated from the U.S. Department of Agriculture (USDA), Natural Resources Conservation Service (NRCS) State Soil Geographic (STATSGO) soil data, agricultural land cover, and improved nitrogen fertilizer estimates (see SI). All explanatory variables have an inherent spatial distance parameter such as circular buffer radius or exponential decay range. Each variable is calculated with multiple distance parameter values because optimal distance is unknown a priori. The distance parameter values tested include 1000, 2000, and 5000 m. The candidate set of covariates is summarized below, with details and data available in the SI.

National Landcover Database (NLCD) categories for 2006 were calculated as a percent of each landcover type within a circular buffer. NLCD 1992 agricultural landcover types (Pasture/Hay, Row Crops, Small Grains, Fallow, and Orchards/Vineyards/Other) were aggregated into a single category and calculated as a percent within a circular buffer. On-site wastewater treatment plant variables, septic density and average nitrate loading, were created following the methods of Pradhan et al. ( 2007). Point sources associated with nitrogen releases were calculated as the sum of exponentially decaying contributions (Messier et al., 2012). These included wastewater treatment plants, cattle farms, poultry farms, swine farms, swine lagoons, and waste treatment residual spray-fields. Mean slope in degrees and topographic wetness index (TWI) (Beven and Kirkby, 1979) were calculated within circular buffers. Population density was calculated within circular buffers from 2000 US Census block data assuming an even distribution of population per census block. Summed nitrate sources from 1992 annual farm and non-farm county fertilizer data (Mueller and Gronberg, 2013) were apportioned to 1992 NLCD agricultural lands and calculated as Kg of N within circular buffers. The low value for range in depth to seasonally high water table was obtained from the STATSGO database and calculated as mean depth (feet) within circular buffers (USDA NRCS, 1994).

2.3. Modeling Approach

Our goal was to develop a model with the best possible out-of-sample prediction ability for AHS cohort participants. First, we started with continuous models of nitrate because they provide the best precision. Once the results for continuous models were evaluated, we then made a posteriori choice to develop and evaluate categorical models. Prior to model development, the dataset was randomly divided into training (70 percent) and test (30 percent) sets. All subsequent models were developed on the training set while the test set remained independent and was used to quantify out-of-sample prediction accuracy.

2.4. Continuous Models

2.4.1. Censored Maximum Likelihood Regression

A censored maximum likelihood (ML) regression model was developed to test continuous out-of-sample prediction accuracy of groundwater nitrate while accounting for the large number of below detection observations. ML regression can directly account for the below detection values by modifying the likelihood equation, with the censored observations given by the cumulative distribution function (CDF) evaluated at the detection limit (Helsel, 2005). The ML equation is:

L(z|x;β,σ2)={∏zi|zi≥tif(zi|xi;β,σ2)}*{∏zi|zi≤tiF(ti|xi;β,σ2)} (1)

where f(zi|xi;β,σ2) denotes the conditional probability distribution function (PDF) of log-transformed (natural log) nitrate, zi, on the regression parameters β,σ2, and F(ti| xi;β,σ2) denotes the CDF of the distribution taken at the log of the detection limit ti, also conditional on the regression parameters. The parameters were estimated by minimizing the negative of the log-likelihood using MATLAB’s fmincon constrained minimization routine (MathWorks Inc., Natick, USA).

Model selection for the censored ML regression was conducted through a modified stepwise procedure (Messier et al., 2014; Raaschou-Nielsen et al., 2013), which adds variables while constraining physical significance (i.e. sources of nitrate are positive; attenuation of nitrate is negative), maintaining variance inflation (VIF) of variable in the model below 3, and selecting only one variable from a set of variables that differ only by their distance hyperparameter (i.e. buffer size; decay range). In the procedure, a null model was fit first and the sample-size-corrected Akaike information criterion (AICc) was calculated. Then, each candidate variable model was fit using a 5-fold validation procedure. The training set was divided into 5 approximately equal size sets. K-fold cross-validation was performed where the candidate model was fit on four folds and tested on the fifth and repeated until each K-fold was used as the testing exactly once. The mean AICc was calculated to determine the overall fit for the model with the given candidate variable. At each iteration, the candidate variable with the lowest mean AICc was added to the model. This procedure continues until none of the variables added decrease the AICc by 5.

2.4.2. Machine Learning Methods

Several machine learning methods were considered for predicting continuous nitrate concentration using the covariates described above. The imputed below detection limit data were used for the continuous machine learning approaches. First, ensembles of different methods were fitted using the R package SuperLearner. The first ensemble included bagging, random forest, gradient boosted machine (GBM), support vector machine (SVM), and a neural network. These are popular machine learning methods that are available in the R computing environment. In this ensemble, bagging, GBM, and the neural network received 0 weight. The random forest received most of the weight (0.91 out of a total of 1). In a subsequent ensemble of a random forest and SVM, the random forest again received most of the weight (0.87). The smaller ensemble predicted slightly better (R2= 0.181) compared with the large ensemble (0.180) in the testing set.

Given these results, we next focused on tuning the random forest model using the R package caret. We tuned through 5-fold cross-validation a random forest with 500 trees for the number of variables to consider at each node and the minimum number of observations per leaf. The best tuned random forest model had a better prediction score (R2 = 0.189) than the ensembles. As a comparison, we also tuned GBM and SVM models independently, which resulted in worse prediction scores for both GBM (0.168) and SVM (0.145). Due to the best overall predictive performance of the tuned random forest, we used it for the final predictions of continuous nitrate.

2.4.3. Kriging of Residuals

Geostatistical approaches such as kriging and Bayesian Maximum Entropy (BME) (Christakos et al., 2002; Christakos and Li, 1998; Messier et al., 2012) have been used extensively to model the residual spatial variation from a primary model such as a land use regression (de Hoogh et al., 2018; Messier et al., 2014; Reyes and Serre, 2014) and random forest (Guo et al., 2015; Li et al., 2011). Here, we utilized a common geostatistical model in which the concentration of nitrate at a given location is a function of a spatially explicit mean trend, a spatially correlated error term, and an independent and identically distributed error (i.e. noise) term. The classical geostatistical approach models the mean trend as a linear combination of geographic covariates; however, we took the approach that the mean may be modeled as the best continuous model from the previous sections such as the censored maximum likelihood regression, support vector machine, or random forest. In practice, this results in a multistep process. First, we subtracted the best continuous model from observed nitrate in the training set. Then we perform ordinary kriging (using the geoR package in R) on the residuals. We utilized an exponential model with a nugget effect, which accounts for the spatially explicit error term and the independent error term, respectively. Next, we used the fitted kriging model and the residual training set to predict at the test set location. Finally, we added back the best continuous model mean trend at the test location to obtain the final predictions.

2.5. Classification Models

Given the high proportion of below detection data and the low R2 in predicting continuous private well nitrate in the testing set, we explored classification models that transformed the nitrate classifications into categories. Classification models may improve out-of-sample prediction accuracy in cases where a high proportion of the continuous distribution is observed in a small range or single value by reducing the overall variability (Li et al., 2011; Stein et al., 1988). We classified the observed nitrate into three categories: <1, 1 – 5, and ≥5 mg/L and tuned random forest models with 500 trees for the number of variables to consider at each node using the R package caret. Due to the large proportion of observations falling into the first category and the propensity for classification models to overpredict for the first (lowest) category, we considered different agreement metrics and sampling strategies to achieve more balanced predictive performance across categories. We fitted models to maximize either overall accuracy or the Cohen’s kappa coefficient of agreement and tuned for the number of variables to consider at each node split. We used up-sampling and down-sampling in the caret package, and a hybrid up-sampling and down-sampling approach (SMOTE) in the R package DMwR to create more balanced datasets for model fitting (Chawla et al., 2002). Up-sampling randomly samples so that replacement from the smallest class is the same size as the largest class and down-sampling randomly samples a data set so that all categories have the same frequency as the smallest class. The SMOTE algorithm is a combination of over-sampling of the smallest class and under-sampling of the majority categories.

2.6. Model Fit Statistics

We compared the predictive models for continuous nitrate using R2 in the testing set. For categorical models, we compared the overall accuracy, Cohen’s kappa, sensitivity, and specificity for each category in the test set. Cohen’s kappa is a measure of classification accuracy that accounts for expected agreement based on random chance (Banerjee et al., 1999). We also calculated the variable importance scores for the random forest models to give a measure of relative importance of the variables in predicting continuous and categorical nitrate.

3. Results and Discussion

3.1. Summary Statistics

Observed private well groundwater nitrate concentration (including imputed values for below the detection limits) median (mean) for the training and test sets were 0.43 (1.51) mg/L and 0.44 (1.56) mg/L NO3-N, respectively. Additionally, for data observed above the detection limit, the medians (mean) were 2.56 (4.26) mg/L and 2.60 (4.30) mg/L NO3-N. In total, 2.4 percent of the data were observed above the EPA MCL of 10 mg/L of NO3-N.

3.2. Continuous Model Results

3.2.1. Censored ML Regression

The censored ML regression model was tested using both normal and log-normal as the assumed likelihood distributions and the results were comparable. With an assumed log-normal distribution, the test set prediction R2 was 0.08 indicating poor predictive performance. Despite the poor performance, the model selection procedure included geographic covariates that align with expectations such as swine waste lagoons with positive coefficients (i.e. nitrate source) and histosol soils with a negative coefficient (i.e. reducing nitrate via denitrification). The full model coefficients and standard errors are available in the supporting information (Table S1).

3.2.2. Random Forest

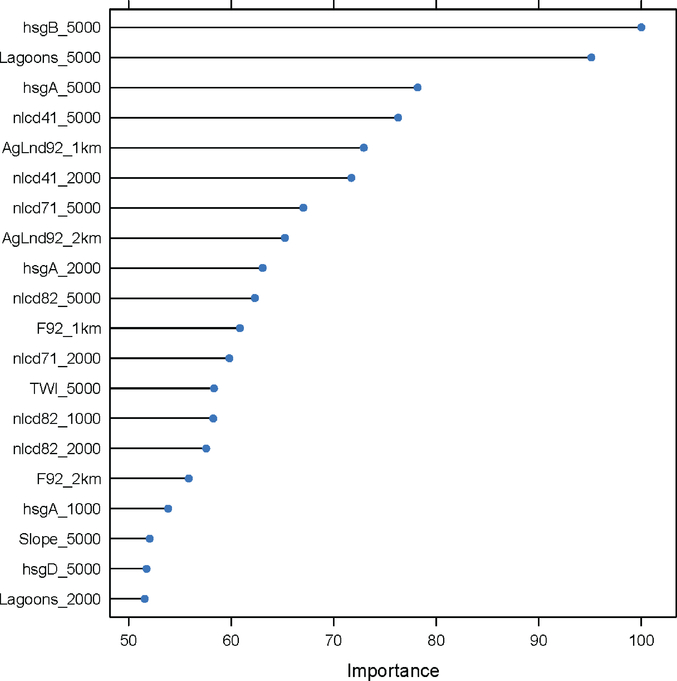
The best tuned random forest model had a test-set prediction R2 of 0.189. The most important variables in the model are plotted in Figure 1. The most important variables were all physically realistic and plausible representing sources, and transport and attenuation processes. The top 5 variables include percent hydrologic soil group B (i.e. moderately low runoff potential; between 50–90 percent sand and loamy sand) within a 5 km buffer, swine waste lagoons with an exponential decay range of 5 km, percent hydrologic soil group A (i.e. low runoff potential; typically, greater than 90 percent sand and gravel) within a 5 km buffer, percent agricultural land use within a 1km buffer, and percent deciduous forest (inversely related) within a 5km buffer.

Figure 1.

Figure 1.

Open in a new tab

Variable importance for top 20 most important variables in random forest continuous model for nitrate (all predictor variables are defined in the SI).

3.2.3. Kriging of Residuals

The best continuous model in terms of test-set prediction R2 was the random forest model. We integrated this model into an ordinary kriging model, which further increased the test-set R2 of the random forest model to 0.33.

3.2.4. Continuous Model Performance

Groundwater nitrate concentrations in private wells of North Carolina were found to be difficult to predict in independent test samples. Multiple natural and human-based factors contribute to the substantial heterogeneity observed in groundwater nitrate concentrations. In addition to the large anisotropic heterogeneity in North Carolina groundwater, private well depths also vary substantially. A major factor in well depth is the budgeted cost in well and casing construction. Confined aquifers generally contain older, less polluted groundwater, but drilling deeper and through confining layers to access confined aquifers is substantially more expensive. This highlights the importance of having measured well depths for predictions of groundwater contaminants such as nitrate. The lack of measured well depths associated with private well chemical measurements likely resulted in a substantial loss in predictive ability. Well depth is a useful proxy for redox conditions and groundwater age, two depth-related factors that strongly influence groundwater nitrate concentrations but are difficult to measure. Nitrate is less likely to occur in deeper groundwater because of reducing conditions and/or the predominance of older groundwater that predates the period of intensive N fertilizer use in the United States (1960s and later) (Tesoriero et al., 2005). Outputs from three-dimensional models of redox conditions and groundwater age improved prediction of groundwater nitrate in the Central Valley, California, when used as predictor variables in a gradient boosted model (GBM) (Ransom et al., 2017). Another major factor affecting the continuous nitrate prediction power was that private well nitrate measurements were derived from a chemical analytical technique with a minimum detection limit of 1 mg/L, substantially higher than the current best available methods (0.1 mg/L) and the methods used in Wheeler et al. (2015), which resulted in nearly 70 percent of the data observed below the detection limit.

Although the validation statistics are not directly comparable to Messier et al. (2014) (leave one out cross-validation compared to hold-out test set used here), we found that applying the new continuous model methods did not result in any substantial improvements. This finding highlights the difficulty in predicting continuous groundwater nitrate from a private well database, particularly without accompanying well depth measurements.

3.3. Categorical Model Results

The best tuned random forest for categories of nitrate considered 58 of the 120 variables at each node split. The fit statistics for the different modeling approaches are listed in Table 1. The max accuracy and max kappa approaches had similar performance, with slightly better accuracy and kappa found by maximizing kappa. Specificity was high for nitrate categories 1–5 mg/L (category 2) and ≥5 mg/L (category 3), but low for category <1 mg/L (category 1). The opposite pattern was observed for sensitivity. As expected, the down-sampling and up-sampling strategies produced sensitivity and specificity that were more balanced across categories of nitrate concentrations. Down-sampling produced more balance than up-sampling, but at the cost of substantially decreased overall accuracy. With SMOTE, the overall accuracy was between that of up-sampling and down-sampling, but it produced a low sensitivity for category 1–5 mg/L without increasing balance in specificity. Among the sampling approaches, up-sampling was the best at increasing balance among categories while minimizing the decrease in specificity of the highest exposure class and the decreases in sensitivity across categories.

Table 1.

Overall accuracy, kappa coefficient of agreement, and sensitivity and specificity for each of the three categories of nitrate (mg/L NO3-N) from the random forest in the testing set.

Sensitivity Specificity
Method Accuracy kappa < 1 mg/L 1 – 5 mg/L ≥5 mg/L < 1 mg/L 1 – 5 mg/L ≥5 mg/L
Max Accuracy 0.747 0.371 0.923 0.359 0.352 0.430 0.923 0.982
Max kappa 0.750 0.375 0.928 0.358 0.352 0.426 0.928 0.982
Down-sampling 0.576 0.268 0.584 0.543 0.611 0.772 0.721 0.849
Up-sampling 0.725 0.369 0.867 0.419 0.389 0.514 0.884 0.963
SMOTE 0.690 0.282 0.876 0.191 0.564 0.420 0.960 0.894
Open in a new tab

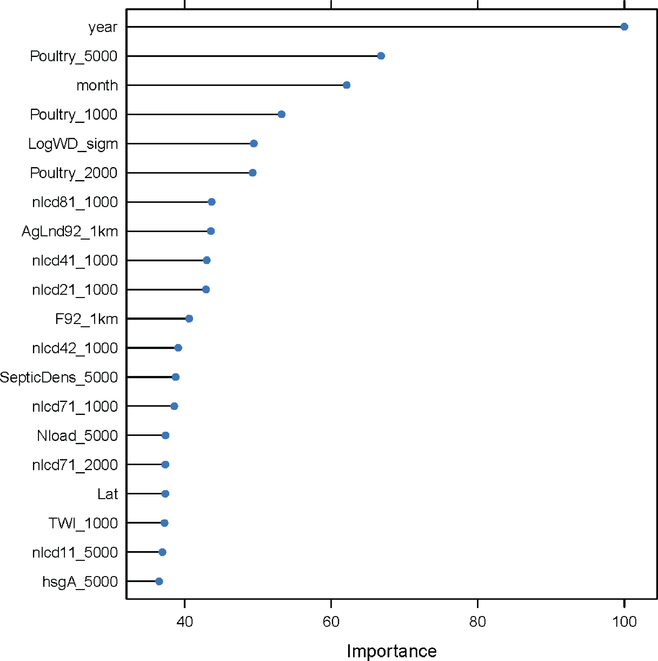
The variable importance scores for the top 20 most important variables in the max-kappa model are plotted in Figure 2. Year, poultry, well depth, and agricultural land covariates were most important for predicting nitrate categories. Partial dependence plots with respect to the year are shown in the supporting information (Figure S1-S3). The 5–10 mg/L class shows a sharp increase after the year 2008, which may be due to increased private well sampling following implementation of a North Carolina state law requiring new private wells to be tested for chemical analytes. Partial dependence plots with respect to poultry agricultural variables are also shown in the supporting information (Figure S4-S6). The 5–10 mg/L class also shows a sharp increase as this covariate increases. The observed and predicted nitrate categories are mapped in Figure 3. The maps show that the predictions generally describe the overall observed pattern but underestimate the medium and high categories of nitrate in some areas. The predictions successfully identify regional trends such as the area in the southeast, where Duplin County and Sampson County (filled areas in Figure 3) had the largest concentration of observed high values. This is likely driven by the models emphasizing key explanatory variables such as agricultural fertilizer, confined animal feeding operations (CAFO), and forested land cover.

Figure 2.

Figure 2.

Open in a new tab

Variable importance for the random forest classification model that maximized the kappa agreement for three categories of nitrate (all predictor variables are defined in the SI)

Figure 3.

Figure 3.

Open in a new tab

(Top) Max kappa classification model predictions from the tuned random forest model. (Bottom) Observed test set nitrate concentrations (mg/L NO3-N) in the three categories. The areas of Duplin County and Sampson County with high observed nitrate concentrations are highlighted with solid fill.

The under prediction of medium and high categories of nitrate is analogous to the under prediction of continuous nitrate concentrations for the private well model developed in Messier et al. (2014). They found the private well model was dominated by the below detection data, thus rarely predicted concentrations significantly above the detection limit. The regional low concentrations interspersed with fine-scale heterogeneity of high concentrations was also observed in previous studies of drinking water (Nolan and Hitt, 2006) and recently recharged aquifers (Gurdak and Qi, 2012). The southeastern coastal region of North Carolina generally contains soil and subsurface conditions favorable towards denitrification, which is a likely factor for many low observed nitrate concentrations despite a large density of nitrate sources. Moreover, as mentioned previously, the well depth varies substantially, which contributes to the heterogeneity in observed nitrate concentrations. Additionally, the lack of measured well depths likely hampered the accuracy of the models.

The results from the categorical models highlight a valuable lesson in environmental exposure assessment modeling. By reducing the variability of the nitrate data to three categories, we were able to reduce the difficulties of the high proportion of non-detections and obtain better accuracy in out-of-sample predictions. This improvement comes at the cost of reduced numerical precision in the predictions, which in many cases, such as epidemiological analyses, may be a worthwhile trade-off.

3.4. Comparison with Iowa groundwater nitrate model

There were key differences between the Iowa nitrate prediction model (Wheeler et al., 2015) and the North Carolina private well model presented here. The Iowa model used available well depth data as a covariate and it was identified as an important predictor. Additionally, the Iowa model included covariates, which are not available in many states including North Carolina, describing aquifer texture and flow characteristics at depth, such as thickness of fine-grained sediments above the well screen, the average and minimum thicknesses of fine-grained sediments near wells, and average horizontal and vertical hydraulic conductivities. In North Carolina, the private well data were not directly linked with well depth measurements in the well construction database. Moreover, the North Carolina private well database’s primary purpose was not for regulatory or ambient monitoring, therefore the chemical analytical method had a higher detection limit than other available methods.

The more homogeneous hydrogeologic units underlying Iowa likely contribute to less fine-scale nitrate variability and a greater ability to predict groundwater nitrate compared to North Carolina. North Carolina has 29 descriptive rock units with no formation except sedimentary rocks dominating in the coastal plains region (Schruben et al., 1994). Conversely, Iowa has 19 distinct rock units of which rocks of Middle to Upper Pennsylvanian and Upper Cretaceous ages dominate in overall coverage.

4. Conclusions

In this study, we developed and tested many different models for the prediction of private well nitrate in North Carolina with the goal of producing exposure estimates for the Agricultural Health Study cohort. The results were critical in assessing the out-of-sample prediction ability for private well nitrate concentrations since none of the AHS cohort have nitrate measurements. We will use the classification model based on maximizing kappa for the North Carolina AHS cohort participants since it has a high overall accuracy and overall agreement. The Iowa model developed by Wheeler et al. (Wheeler et al., 2015) may easily be converted to categorical responses for congruency with these results. Lastly, the categorical predictions of this study provide sufficient out-of-sample accuracy to provide an effective exposure assessment for the AHS cohort.

Supplementary Material

Supplemental Material

5. Acknowledgements

This research was partially funded by the intramural research program of the National Cancer Institute. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

References

  1. Ayotte JD, Nolan BT, Gronberg JA, 2016. Predicting Arsenic in Drinking Water Wells of the Central Valley, California. Environ. Sci. Technol 50, 7555–7563. 10.1021/acs.est.6b01914 [DOI] [PubMed] [Google Scholar]
  2. Banerjee M, Capozzoli M, Mcsweeney L, Sinha D, 1999. Beyond kappa : A review of interrater agreement measures. Can. J. Stat 27, 3–23. [Google Scholar]
  3. Beven KJ, Kirkby MJ, 1979. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci 24, 43–69. [Google Scholar]
  4. Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP, 2002. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res 16, 321–357. 10.1613/jair.953 [DOI] [Google Scholar]
  5. Christakos G, Bogaert P, Serre ML, 2002. Temporal GIS: Advanced Function for Field-Based Applications. Springer, New York, NY. [Google Scholar]
  6. Christakos G, Li X, 1998. Bayesian Maximum Entropy Analysis and Mapping : A Farewell to Kriging Estimators ? Math. Geol 30, 435–462. [Google Scholar]
  7. Daniel CC III, Dahlen PR, 2002. Preliminary Hydrogeologic Assessment and Study Plan for a Regional Ground-Water Resource Investigation of the Blue Ridge and Piedmont Provinces of North Carolina. U.S. Geol. Surv. Water-Resources Investig. Rep 02–4105. [Google Scholar]
  8. Davidson E. a, David MB, Galloway JN, Goodale CL, Haeuber R, Harrison J. a, Howarth RW, Jaynes DB, Lowrance RR, Nolan BT, Peel JL, Pinder RW, Porter E, Snyder CS, Townsend AR, Ward MH, 2012. Excess Nitrogen in the U.S. Environment: Trends, Risks, and Solutions. Issues Ecol. [Google Scholar]
  9. de Hoogh K, Chen J, Gulliver J, Hoffmann B, Hertel O, Ketzel M, Bauwelinck M, van Donkelaar A, Hvidtfeldt UA, Katsouyanni K, Klompmaker J, Martin RV, Samoli E, Schwartz PE, Stafoggia M, Bellander T, Strak M, Wolf K, Vienneau D, Brunekreef B, Hoek G, 2018. Spatial PM2.5, NO2, O3and BC models for Western Europe – Evaluation of spatiotemporal stability. Environ. Int 120, 81–92. 10.1016/j.envint.2018.07.036 [DOI] [PubMed] [Google Scholar]
  10. Dubrovsky NM, Burow KR, Clark GM, Gronberg JM, Hamilton PA, Hitt KJ, Mueller DK, Munn MD, Nolan BT, Puckett LJ, Rupert MG, Short TM, Spahr NE, Sprague LA, Wilber WG, 2010. The Quality of Our Nation’s Waters: Nutrients in the Nation’s Streams and Groundwater, 1992–2004. U.S. Geological Survey Circular 1350; Reston, Virginia. [Google Scholar]
  11. Gemitzi A, Petalas C, Pisinaras V, Tsihrintzis VA, 2009. Spatial prediction of nitrate pollution in groundwaters using neural networks and GIS: an application to South Rhodope aquifer (Thrace, Greece). Hydrol. Process 23, 372–383. 10.1002/hyp [DOI] [Google Scholar]
  12. Guo PT, Li MF, Luo W, Tang QF, Liu ZW, Lin ZM, 2015. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 237–238, 49–59. 10.1016/j.geoderma.2014.08.009 [DOI] [Google Scholar]
  13. Gurdak JJ, Qi SL, 2012. Vulnerability of Recently Recharged Groundwater in Principle Aquifers of the United States To Nitrate Contamination. Environ. Sci. Technol 46, 6004–6012. 10.1021/es300688b [DOI] [PubMed] [Google Scholar]
  14. Helsel DR, 2005. More Than Obvious: Better Methods for Interpreting Nondetect Data. Environ. Sci. Technol 39, 419A–423A. [DOI] [PubMed] [Google Scholar]
  15. International Agency for Research on Cancer, 2010. Ingested nitrate and nitrite, and cyanobacterial peptide toxins., IARC monographs on the evaluation of carcinogenic risks to humans. 10.1002/food.19940380335 [DOI] [PMC free article] [PubMed]
  16. Katz BG, Griffin DW, Davis JH, 2009. Groundwater quality impacts from the land application of treated municipal wastewater in a large karstic spring basin: chemical and microbiological indicators. Sci. Total Environ 407, 2872–86. 10.1016/j.scitotenv.2009.01.022 [DOI] [PubMed] [Google Scholar]
  17. Kennedy CD, Genereux DP, 2007. 14C groundwater age and the importance of chemical fluxes across aquifer boundaries in confined cretaceous aquifers of North Carolina, USA. Radiocarbon 49, 1181–1203. 10.1017/S0033822200043101 [DOI] [Google Scholar]
  18. Li J, Heap AD, Potter A, Daniell JJ, 2011. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw 26, 1647–1659. 10.1016/j.envsoft.2011.07.004 [DOI] [Google Scholar]
  19. Lubin JH, Colt JS, Camann D, Davis S, Cerhan JR, Severson RK, Bernstein L, Hartge P, 2004. Epidemiologic evaluation of measurement data in the presence of detection limits. Environ. Health Perspect 112, 1691–1696. 10.1289/ehp.7199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Maupin MA, Kenny JF, Hutson SS, Lovelace JK, Barber NL, Linsey KS, 2010. Estimated Use of Water in the United States in 2010 Circular 1405, US Geological Survey; [Google Scholar]
  21. Messier KP, Akita Y, Serre ML, 2012. Integrating address geocoding, land use regression, and spatiotemporal geostatistical estimation for groundwater tetrachloroethylene. Environ. Sci. Technol 46, 2772–80. 10.1021/es203152a [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Messier KP, Kane E, Bolich R, Serre ML, 2014. Nitrate Variability in Groundwater of North Carolina using Monitoring and Private Well Data Models. Environ. Sci. Technol 48, 10804–10812. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mueller DK, Gronberg JAM, 2013. County-level estimates of nitrogen and phosphorus from animal manure for the conterminous United States, 2002 1987–2006.
  24. Nolan BT, Hitt KJ, 2006. Vulnerability of shallow groundwater and drinking-water wells to nitrate in the United States. Environ. Sci. Technol 40, 7834–7840. [DOI] [PubMed] [Google Scholar]
  25. Pradhan SS, Hoover MT, Austin RE, Devine HA, 2007. Potential Nitrogen Contributions from On-site Wastewater Treatment Systems to North Carolina ‘ s River Basins and Sub-basins. North Carolina Agricultural Research Service Technical Bulletin 324; Raleigh, North Carolina. [Google Scholar]
  26. Raaschou-Nielsen O, Andersen ZJ, Beelen R, Samoli E, Stafoggia M, Weinmayr G, Hoffmann B, Fischer P, Nieuwenhuijsen MJ, Brunekreef B, Xun WW, Katsouyanni K, Dimakopoulou K, Sommar J, Forsberg B, Modig L, Oudin A, Oftedal B, Schwarze PE, Nafstad P, De Faire U, Pedersen NL, Ostenson C-G, Fratiglioni L, Penell J, Korek M, Pershagen G, Eriksen KT, Sørensen M, Tjønneland A, Ellermann T, Eeftens M, Peeters PH, Meliefste K, Wang M, Bueno-de-Mesquita B, Key TJ, de Hoogh K, Concin H, Nagel G, Vilier A, Grioni S, Krogh V, Tsai M-Y, Ricceri F, Sacerdote C, Galassi C, Migliore E, Ranzi A, Cesaroni G, Badaloni C, Forastiere F, Tamayo I, Amiano P, Dorronsoro M, Trichopoulou A, Bamia C, Vineis P, Hoek G, 2013. Air pollution and lung cancer incidence in 17 European cohorts: prospective analyses from the European Study of Cohorts for Air Pollution Effects (ESCAPE). Lancet. Oncol 14, 813–822. 10.1016/S1470-2045(13)70279-1 [DOI] [PubMed] [Google Scholar]
  27. Ransom KM, Nolan BT, Traum A, J., Faunt CC, Bell, Gronberg JAM, Wheeler DC, Rosecrans Z, C., Jurgens B, Schwarz GE, Belitz K, Eberts M, S., Kourakos G, Harter T, 2017. A hybrid machine learning model to predict and visualize nitrate concentration throughout the Central Valley aquifer, California, USA. Sci. Total Environ 601–602, 1160–1172. 10.1016/j.scitotenv.2017.05.192 [DOI] [PubMed] [Google Scholar]
  28. Reyes JM, Serre ML, 2014. An LUR/BME Framework to Estimate PM2.5 Explained by on Road Mobile and Stationary Sources. Environ. Sci. Technol 48, 1736–44. 10.1021/es4040528 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schruben PG, Arndt RE, Bawiec WJ, 1994. Geology of the Conterminous United States at 1:2,500,000 Scale -- A Digital Representation of the 1974 P.B. King and H.M. Beikman Map. U.S. Geol. Surv. Digit. Data Ser DDS-11. [Google Scholar]
  30. Serre ML, Christakos G, 1999. Modern geostatistics: computational BME analysis in the light of uncertain physical knowledge - the Equus Beds study. Stoch. Environ. Res. Risk Assess 13, 1–26. 10.1007/s004770050029 [DOI] [Google Scholar]
  31. Stein A, Hoogerwerf M, Bouma J, 1988. Use of Soil-Map Delineations to Improve (Co-) Kriging of Point Data on Moisture Deficits. Geoderma 43, 163–177. [Google Scholar]
  32. Tesoriero AJ, Spruill TB, Eimers JL, 2004. Geochemistry of shallow ground water in coastal plain environments in the southeastern United States: Implications for aquifer susceptibility. Appl. Geochemistry 19, 1471–1482. 10.1016/j.apgeochem.2004.01.021 [DOI] [Google Scholar]
  33. Tesoriero AJ, Spruill TB, Mew HE, Farrell KM, Harden SL, 2005. Nitrogen transport and transformations in a coastal plain watershed: Influence of geomorphology on flow paths and residence times. Water Resour. Res 41, 1–15. 10.1029/2003WR002953 [DOI] [Google Scholar]
  34. United States Department of Agriculture, Natural Resources Conservation Service, 1994. U.S. General Soil Map (STATSGO2).
  35. Ward MH, Jones RR, Brender JD, de Kok TM, Weyer PJ, Nolan BT, Villanueva CM, van Breda SG, 2018. Drinking water nitrate and human health: An updated review. Int. J. Environ. Res. Public Health 15, 1–31. 10.3390/ijerph15071557 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wheeler DC, Nolan BT, Flory AR, DellaValle CT, Ward MH, 2015. Modeling groundwater nitrate concentrations in private wells in Iowa. Sci. Total Environ 536, 481–488. 10.1016/j.scitotenv.2015.07.080 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Winner M Jr.., Coble RW, 1996. Hydrogeologic Framework of the North Carolina Coastal Plain. U.S. Geological Survey Professional Paper 1404-I; Washington D.C. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
NIHMS1016458-supplement-Supplemental_Material.doc (1.3MB, doc)

RESOURCES