Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jan 17;20(3):1217–1223. doi: 10.1021/acs.biomac.8b01606

Cooperation of Helix Insertion and Lateral Pressure to Remodel Membranes

Mohammad A A Fakhree 1, Sjoerd A J Engelbertink 1, Kirsten A van Leijenhorst-Groener 1, Christian Blum 1, Mireille M A E Claessens 1,*
PMCID: PMC6581421  PMID: 30653915

Abstract

graphic file with name bm-2018-01606m_0006.jpg

Nature has developed different protein mediated mechanisms to remodel cellular membranes. One of the proteins that is implicated in these processes is α-synuclein (αS). Here we investigate if besides αS’s membrane bound amphipathic helix the disordered, solvent exposed tail of the protein contributes to membrane reshaping. We produced αS variants with elongated or truncated disordered solvent exposed domains. We observe a transformation of opaque multi lamellar vesicle solutions into nonscattering solutions containing smaller structures upon addition of all αS variants. Experimental data combined with model calculations show that the cooperation of helix insertion and lateral pressure exerted by the disordered domain makes the full length protein decidedly more efficient in membrane remodeling than the truncated version. Using disordered domains may not only be cost-efficient, it may also add a new level of control over vesicle fusion/fission by expansion or compaction of the domain.

Introduction

α-Synuclein (αS) is a 140 amino acid long intrinsically disordered protein (IDP) that has been associated with membrane remodeling processes, vesicle trafficking, and synaptic transmission.1−3 αS has been observed to localize at the synaptic terminal where it binds to the surface of synaptic vesicles.4,5 At the synaptic terminal, vesicle bound αS is thought to mediate membrane fusion processes by acting as a nonconventional chaperone for the V-SNARE protein, synaptobrevin.6 The contribution of αS to membrane remodeling may, however, be much more direct. The IDP αS has been reported to bind net negatively charged model membranes.7,8 Upon binding membranes, the ∼90 amino acids at the N-terminal side of the protein undergo a disorder-to-order transition; in both in vitro experiments and in cells, they fold into an amphipathic α-helix.9,10

The insertion of amphipathic α-helices into one of the membrane leaflets is a well-known mechanism of generating curvature.11,12 The area difference between the inner and outer membrane leaflet that results from partial insertion of helices contributes to the curvature generating properties of proteins such as epsin13 and endophilin.14 Accordingly, the insertion of αS into lipid bilayers has been reported to stabilize a positive mean curvature15 and to convert flat membranes into highly curved vesicles and tubules.16

Besides the asymmetric insertion of membrane helices, the asymmetric grafting of polymers, including DNA, has been shown to generate spontaneous membrane curvature.17 Several membrane remodeling proteins that bind membranes via amphipathic α-helices contain additional, polymer-like, disordered domains. It has been argued that these long relatively bulky, disordered domains can contribute to the curvature generating mechanism of these proteins.18 At high surface concentrations, where the unstructured domains of the proteins start to overlap, non α-helical membrane bound αS has been suggested to generate curvature due to steric effects.19 However, also considerably below the overlap concentration, proteins have been observed to generate curvature. Here diffusion is thought to result in collisions between protruding solvent exposed parts of the membrane bound proteins, generating a lateral pressure that causes membranes to bend even in the absence of membrane-bound helices.20 The contribution of lateral pressure to curvature generation is, however, debated.11 The mechanism is nonspecific, any protruding part of a freely diffusing membrane-bound protein would contribute. However, compared to well-folded proteins of an equally long amino-acid chain, IDPs are relatively bulky and, therefore, thought to be particularly effective in creating lateral pressure. In this respect, the 568 and 431 amino acid long disordered adaptor domains of AP180 and epsin1, respectively, have been argued to efficiently drive membrane bending.18 The C-terminal disordered domain of membrane-bound αS is more than 10× shorter, but highly negatively charged. If the lateral pressure exerted by the relatively short disordered domain of membrane-bound αS at physiological surface densities is high enough to contribute to the curvature-generating mechanism is an open question. Here we address this question and show that both helix insertion and lateral pressure contribute to the membrane remodeling capacity of αS.

Materials and Methods

Preparation of α-Synuclein

αS1–108, wt-αS, and αS4xC were expressed in Escherichia coli strain BL21(DE3) using the pT7–7 expression plasmid, and wt-αS and αS4xC were purified as previously reported.21 The αS1–108 (NH4)2SO4 pellet was dissolved in 50 mM glycine buffer pH 3.3 and purified on a Resource S cation exchange column (GE healthcare Life Sciences, Little Chalfont, Buckinghamshire, U.K.). To quadrupulate amino acids 111–140 of the full length protein and create the αS4xC construct we made use of the ApoI restriction site that is present in the disordered C-terminal tail of the protein. The disordered C-terminal tail of αS was extended in two steps. First, amino acids 111–140 of wt-αS C-terminal tail were multiplied with PCR and Apol restriction sites were created. The PCR fragment was cut with ApoI and ligated into the pT7-wt-αS plasmid using the corresponding restriction site. This resulted in the αS2xC construct. The last of the now two ApoI restriction sites was subsequently removed by mutagenesis and the 2x 111–140 amino acid construct of αS2xC was multiplied by PCR and an ApoI restriction site was created. This PCR fragment was again cut with ApoI and ligated into the pT7- αS2xC plasmid using the corresponding restriction site.

Before doing the experiments, the freshly thawed αS solutions were spin-filtered using prewashed Pierce filter Spin-Cups (Thermoscietific, Rocford, IL, U.S.A.) at 3000g for 5 min at 4 °C (IEC MicroMax RF, Needham Heights, MA, U.S.A.). Next, the concentration of the filtered αS was determined using UV/vis absorption (Nanodrop ND-1000, Thermofisher Scientific Inc., U.S.A.) with known extinction coefficients of 5600, 1400, and 18200 M–1·cm–1 for wt-αS, αS1–108, and αS4xC at 276 nm, respectively. For clearing assays dilutions were done in HEPES buffer (20 mM HEPES, 10 mM NaCl, pH 7.4). For CD measurements, dilutions were done in modified PBS buffer (Na2HPO4 10 mM, KH2PO4 1.8 mM, NaCl 13.7 mM, KCl 2.7 mM, pH 7.4). In order to prevent nonspecific binding of αS to microtubes, which can alter the effective concentration, Protein LoBind tubes (Eppendorf, Germany) were used.

MLV and LUV Preparation

POPG (1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol)) was purchased from Avanti Polar Lipids Inc. (Alabaster, AL, U.S.A.), aliquots were prepared and dried under a nitrogen flow. For preparing POPG MLVs, the protocol from the producer was used. In short, 76 μL of 10 mg/mL chloroform solution of the lipid were added into 1 mL chloroform under nitrogen flow. By rotating the glass tube under nitrogen flow, the lipid solution was dried as an even layer on the inner wall of the glass tube. This resulted in 0.76 mg lipid films. In the next step for rehydration of the lipid films, 1 mL HEPES buffer for clearing assays, or 1 mL modified PBS buffer for CD measurements, were added to the dried lipid layers under nitrogen flow. Following the addition of the aqueous buffer, the cap of the glass tube was sealed and vortexed five times at maximum shaking power for 1 min using Vortex Genie 2 (Scientific Industries Inc., Bohemia, NY, U.S.A.). This resulted in a final concentration of 1 mM POPG MLVs for the clearing assays. For the CD experiments 4 mM POPG MLV solutions were prepared.

For preparation of 100 nm large unilamellar vesicles (LUVs), the content of the glass tube went through 10 freeze–thawing cycles. This made the suspension less turbid and more homogeneous. Next, extrusion was used to make the 100 nm LUVs. This was done by extruding the suspension of POPG vesicles through a polycarbonate NucleporeTM membrane filter (Whatman, GE Healthcare, U.S.A.) with pore size of 100 nm, with two drain discs as filter supports (Whatman, GE Healthcare, U.S.A.), located inside a manual extruder (Avanti Polar Lipids Inc., Alabaster, AL, U.S.A.). To make sure that the final size of the LUVs was homogeneous, the extrusion was repeated 21 times. The size distribution of the LUVs was checked by dynamic light scattering (Zetasizer Nano ZS, Malvern Panalytical Ltd., U.K.) and a narrow size distribution centered at 100 nm was found.

Clearing Assay

To a final concentration of 500 μM POPG MLVs, dilutions of αS were added, resulting in the concentrations indicated in the clearing curves. For the time-dependent experiments, immediately after addition of the protein, the mixture was transferred to a 1 cm path length, 60 μL quartz cuvette, and the optical density (OD) was measured at a wavelength of 500 nm using a UV–vis spectrophotometer (UV-2401PC, Shimadzu, Japan). A 1 nm slit size was used to collect the data. After measuring the OD values for the first 5 min, the sample was transferred back to the LoBind microtube and stored at 4 °C. Finally, after 24 h the OD values were measured as the end points of the clearing assays.

CD Measurements

A Jasco J-1500 Circular Dichroism Spectrometer (Jasco Inc., Easton, MD, U.S.A.) was used to perform the measurements. Spectra were measured in the wavelength range of 190 to 260 nm, step size of 1 nm, bandwidth of 1 nm, dwell time of 1 s/step, and averaging of 8 scans per sample with a 1 mm path length at 21 °C. Samples of αS (final concentrations of 25 μM) with 100 nm LUVs (final concentrations of 0, 6.5, 11.4, 20, 37, 65, 114, 200, 370, 650, 1140, and 2000 μM) in the modified PBS buffer were mixed and after 2 h the corresponding CD spectra were measured.

To obtain the apparent equilibrium dissociation constant KD, the fraction of vesicle bound protein XB as a function of the POPG concentration was determined from the measured ellipticities at 222 nm.

graphic file with name bm-2018-01606m_m001.jpg

In this expression the initial and final values refer to the plateau ellipticities at low and high lipid concentrations, respectively. Assuming that the equilibrium binding can be described with the following reaction:

graphic file with name bm-2018-01606m_m002.jpg

where αS represents the free αS concentration, L is the free lipid concentration, n is the number of lipids associated with a single protein, and [αSLbound] is the concentration of lipid bound protein, the fraction bound can be described in terms of the known total concentrations of lipid ([Ltotal]) and αS ([αStotal]) following the law of mass action. In this equation we assume that all lipid-binding sites are equivalent, we do not take into account any cooperativity in binding.22

graphic file with name bm-2018-01606m_m003.jpg

Fitting the measured XB([Ltotal]) to this equation gives KD and n.

Dithionite Experiment

Dithionite experiments were done as described elsewhere.23 In short, POPG MLVs were prepared with 1% (mol/mol) embedded NBD labeled PE (Avanti Polar Lipids Inc., Alabaster, AL, U.S.A.) and diluted to a final POPG concentration of 10 μM. Next, using a fluorescence spectrophotometer (FluoroMax-4, HORIBA Jobin Yvon, Edison, NJ, U.S.A.), the sample was excited at 470 nm and fluorescence was collected every second at 540 nm. After measuring the emission for a short time to see that fluorescence was not changing, dithionite was added to the sample to a final concentration of 10 mM. The drop in fluorescence was followed in time. Following reaching a steady fluorescence signal, Triton X-100 was added to the sample to a final concentration of 1.25% w/w, which resulted in complete dissolution of the lipid layers and, consequently, 100% quenching of the NBD dyes.

Calculations

To obtain an estimate for the radius of gyration of the highly negatively charged solvent exposed disordered domain of membrane bound αS we calculated the Flory radius of a sphere for a self-avoiding polymer chain in good solvent. With a diameter of 0.5 nm and a Kuhn length of 1 nm, the properties of this polymer chain aim to reflect the properties of the amino acid chain. We assumed that the disordered domain of membrane bound wt-αS comprises 48 amino acid residues24 while the construct with the elongated disordered domain was 139 amino acids in length. For the disordered domains of wt-αS and αS4xC this resulted in radii of 3.9 and 7.5 nm, respectively. These values are in good agreement with experimental observations for disordered amino-acid chains.25

The contribution of lateral pressure to the spontaneous curvature was calculated following the method reported by Stachowiak et al. with a small modification.20 Instead of assuming that lateral pressure resulted in the formation of membrane tubules, we argue for the formation of vesicles. The pressure exerted by the spherical disordered domain of αS is isotropic; hence, we adjusted the expression for the free energy to account for the appearance of vesicles. This results in the following expression for the radius of the vesicles:

graphic file with name bm-2018-01606m_m004.jpg

In this expression, R is the radius of the vesicles. The membrane’s bending rigidity, Kbend, was assumed to be 10 kBT, σ represents 2× the radius of gyration of the disordered domain, and p is the pressure obtained from the Carnahan–Starling equation.20

graphic file with name bm-2018-01606m_m005.jpg

Since p is a function of the fraction of the membrane area covered by proteins, η, this term contains the dependence of R on protein concentration.

To obtain an estimate for the (contribution of) helix insertion to the spontaneous curvature we took into account the area difference between the inner and outer membrane leaflet as a result of helix insertion. We determined the spontaneous curvature from the ratio between the inner and outer membrane area as a function of the protein concentration. In our calculations we did not account for the equilibrium dissociation constant (which was measured to be the same for all constructs used) but assumed that all proteins were membrane bound. To obtain the spontaneous curvature we estimated the area occupied by the helix to be 15 nm2.15 The POPG headgroup area and bilayer thickness were assumed to be 0.66 nm2 and 3.7 nm, respectively.26

Results and Discussion

To obtain insight into the contribution of the disordered domain of αS to the membrane remodeling capacity of αS, we compare the full length wild type αS (wt-αS) with a variant in which the disordered C-terminal tail is truncated (αS1–108; Figure 1). To differentiate the membrane reshaping capability of the proteins we used a phospholipid vesicle clearing assay.16 Nonextruded multilamellar phospholipid vesicle (MLV) solutions strongly scatter light because of their large size and multilamellarity, they hence appear opaque. The conversion of the large vesicles into highly curved smaller structures by interacting proteins, results in a decrease of scattering and clearing of the solution. The decrease in scattering by the formation of small, nonscattering structures, can be quantitatively followed using UV/vis spectroscopy and is visible as a decrease in optical density (OD; Figure 2a).

Figure 1.

Figure 1

Open in a new tab

Cartoon of the mechanisms that may contribute to generating curvature by binding of αS to membranes. Curvature can be induced by helix insertion (αS1–108) (left) and be further enhanced by lateral pressure exerted by the IDR of membrane bound αS (wt-αS) (right). The green circles indicate the volume occupied by the IDR.

Figure 2.

Figure 2

Open in a new tab

(a) POPG MLV clearing assay. Upon the addition of wt-αS (blue squares) and αS1–108 (red circles), a reduction in OD measured at a wavelength of 500 nm is visible as a result of remodeling into  small, nonscattering structures. The OD of the control, nontreated sample (black triangles) does not change significantly in 24 h. After addition of protein the OD was followed for 24 h. After 24 h, the OD remained constant. (b) The ellipticity at 222 nm observed by CD spectroscopy as a function of the phospholipid concentration due to αS binding to POPG LUVs. The CD spectra were obtained at a protein concentration of 25 μM, the POPG concentration in form of vesicles was varied. Symbols show experimentally determined ellipticity at 222 nm as readout for membrane bound wt-αS (blue squares) and αS1–108 (red circles). Presented data are average values of at least two independent sample preparations and measurements. Black line shows the global fit, for both proteins, to the data to determine the dissociation constant, KD.

αS preferentially binds net negatively charged phospholipid bilayers in the liquid disordered state. We therefore selected membranes composed of POPG as a model system. To test if the wt-αS and αS1–108 differ in their ability to clear the MLV solution, the POPG MLVs were aliquoted into three samples. To the first two samples, equimolar amounts of wt-αS and αS1–108 were added, respectively, while the third sample served as a control (Figure 2a). The change of scattering of these samples was recorded over time. While the control shows only a minor decrease in OD, the MLV solution shows an initial sharp decrease in OD in the presence of both wt-αS and αS1–108. This initial decrease is followed by a slower decrease in optical density. After 24 h, we do not observe changes in OD anymore. Although both wt-αS and αS1–108 are able to clear the solution, identical concentrations of wt-αS result in lower OD values. wt-αS seems to be more efficient in MLV clearing than αS1–108.

The higher clearing efficiency of wt-αS compared to αS1–108 could either result from the lateral pressure exerted by the disordered tails or may be the result of a higher membrane binding affinity, and thus a higher number density of wt-αS on the membrane surface. To test if there is a difference in membrane binding affinity for wt-αS and αS1–108, we obtained binding curves for both proteins from CD spectra. In these experiments, we kept the αS concentration constant and followed the formation of α-helical structure, representing the membrane bound state of the protein, by measuring CD spectra at increasing POPG vesicle concentration (Figure S1). From these CD spectra we obtained the ellipticity at 222 nm as a function of the POPG concentration. With increasing concentration of POPG vesicles we clearly observe the signature of α-helical structure at 222 nm evidencing αS binding to the membrane (Figure 2b). The data points for both wt-αS and αS1–108, presented in Figure 2b, show strong overlap and can be globally fitted with a single apparent equilibrium dissociation constant, KD of 0.4 μM, n = 25, with n being the number of lipids associated with one protein. Apparent KD values in the micromolar range are in good agreement with literature.27,28 We conclude that the observed difference in clearing efficiency does not primarily result from a difference in membrane binding affinity. Since the membrane binding affinity is identical, the protein number density on the membrane is identical for all protein concentrations and the clearing assays in the presence of either wt-αS or αS1–108 can be directly compared. Considering that the membrane binding α-helical domains are identical and intact in both wt-αS and αS1–108, this is not unexpected.

To further investigate the role of lateral pressure in membrane remodeling, we measured the OD of the MLV solution as a function of the αS concentration (Figure 3). For this purpose, the equilibrium OD values were recorded 24 h after addition of the protein. At low protein concentrations no clearing is observed. With increasing protein concentrations clearing sets in and levels to almost complete clearing. The OD versus protein concentration curves for wt-αS and αS1–108 are similar in shape but the wt-αS curve is shifted to lower concentrations. 50% clearing is reached at 1.8× lower concentrations for wt-αS compared to αS1–108. It is observed at 3.8 μM for wt-αS and at 6.8 μM for αS1–108. This shift to lower αS concentrations shows that the clearing capacity of wt-αS is decidedly higher.

Figure 3.

Figure 3

Open in a new tab

αS MLV clearing assay. Change in optical density (OD)at 500 μM POPG MLV solutions upon addition of wt-αS (blue squares) and αS1–108 (red circles). The OD was measured 24 h after protein addition at a wavelength of 500 nm. At low protein concentrations, no decrease in OD is observed, with increasing protein concentration clearing sets in. wt-αS is more efficient in clearing than αS1–108. Black lines serve as guide to the eye and the error bars represent the instrumental errors only. Additional errors resulting from sample preparations are not included.

Toward a more mechanistic understanding, we quantified the initial protein exposed membrane area in our clearing experiments. The clearing assays were performed on MLVs. The inner layers of MLVs are protected from binding protein by the outer layers, hence, only a fraction of the total membrane surface area is available for protein binding. To determine the fraction of solvent accessible membrane area at the start of the experiment, we prepared POPG vesicles labeled with NBD-PE. After measuring the initial fluorescence intensity of a solution of these vesicles, the fluorescence quencher dithionite was added. Dithionite cannot penetrate intact membranes; hence, only NBD at the outer solvent accessible surface is quenched. Upon adding dithionite, we observe a 13% decrease in fluorescence intensity corresponding to 13% protein accessible membrane area (Figure S2). The total concentration of lipid used and POPG headgroup area29 gives the total accessible surface area. The addition of the surfactant Triton-X100 results in micellization of the bilayer and a total loss of fluorescence.

At low protein concentrations the coverage of the accessible membrane surface area is low, hence no clearing of the MLV solution is observed. With increasing protein concentration the MLV surface facing the solution becomes covered with protein. Above a certain protein coverage vesicle clearing sets in. The protein concentrations at the onset of clearing are much too low to solubilize the membrane. The \accessible lipid to protein ratio at the onset concentrations for wt-αS is >300. For other membrane binding proteins, membrane solubilization and transitions to nonlamellar phases are typically observed at an order of magnitude lower lipid-to-protein ratios.30,31 This indicates that clearing results from the formation of small nonscattering bilayer structures. To verify the presentence of small vesicles we measured the diffusion coefficient of the structures formed just above the clearing onset concentration of wt-αS in a single particle tracking experiment (SI). We find a mean diffusion coefficient of 2.4 μm2 s–1 which corresponds to a vesicle diameter of ∼90 nm. We therefore conclude that at the clearing onset concentration the outer MLV bilayer breaks up into less or nonscattering small vesicles. This consumption of the outer layers results in a reduction in the observed optical density of the MLV solution and is visible as the onset of clearing. At the same time, new MLV surface becomes available for binding protein. Clearing will continue until the protein is depleted from the solution. At 13% protein exposed membrane area we estimate from our clearing assay for wt-αS the onset of clearing to be ∼0.22 μM, while for αS1–108, the onset is shifted to ∼0.43 μM. Using these concentrations, the apparent KD, and the exposed membrane surface area this results in an estimate for the lipid surface area per membrane bound αS at the onset of clearing of 195 nm2 for wt-αS and 100 nm2 for αS1–108.

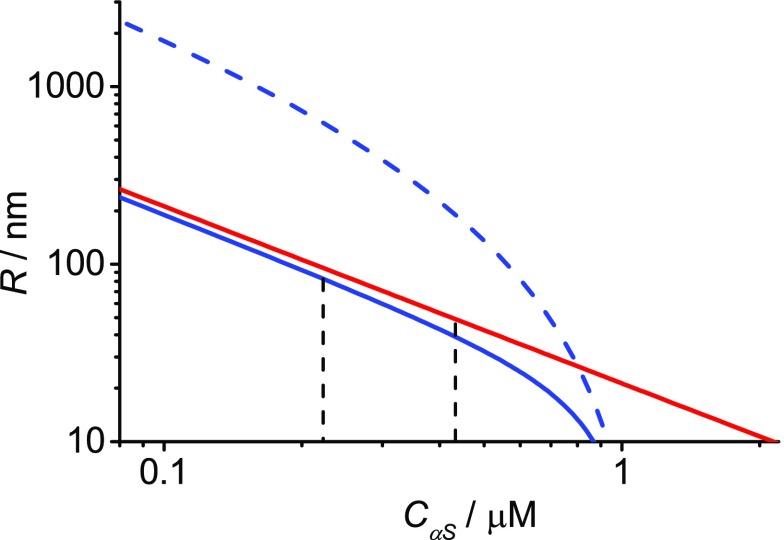
Using the measured protein exposed membrane areas and assuming that clearing follows the mechanism outlined above, we estimated the magnitude of the contributions of helix insertion and lateral pressure. We based our calculations on existing models (Materials and Methods) and used the size of the amphipathic α-helix and the solvent exposed disordered domain of αS as input (Materials and Methods). In our model we do not correct for the binding affinity; based on the KD determined and the concentrations used, we assume that all proteins bind to the membrane. From the calculations we obtain the radius of curvature as a function of the protein concentration. In Figure 4 we show the radius of curvature of the small vesicles induced by the α-helix alone, the disordered domain alone and the combined effect of helix insertion and lateral pressure. As expected, the modeling shows that at low concentrations insertion of amphipathic α-helices is much more efficient in generating curvature than lateral pressure. Only at high concentrations lateral pressure is more efficient. The combined effect of helix insertion and lateral pressure further decreases the radius of curvature.

Figure 4.

Figure 4

Open in a new tab

Calculated spontaneous membrane curvature radii. The red line denotes the curvature generated by helix insertion. It represents αS1–108 in our experiments. The dashed blue line gives the spontaneous curvature as a result of lateral pressure only, while the solid blue line represents the combined effect of helix insertion and lateral pressure. It represents wt-αS. The dashed vertical lines indicate the experimentally observed clearing onset concentrations.

At the concentrations at which we observe the onset of clearing, which for wt-αS is at approximately 0.22 μM, the curvature radius amounts to about 80 nm, according to the model we use. This agrees well with the mean hydrodynamic vesicle radius measured using single particle tracking experiments (Figure S3) and thus confirms the validity of the assumptions made in the calculations. Small vesicles of that size would not scatter and remodeling membranes into such vesicles would thus be visible as a decrease in OD. The correspondence in the radii found at the clearing onset concentrations of both wt-αS and αS1–108 confirms that modeling and experiment agree well. Both helix insertion and lateral pressure seem to contribute to curvature induction.

The model calculations predict that the clearing onset concentration depends on the available protein-exposed membrane surface area, as well as on the size of the disordered domain. To test these dependencies, we constructed an αS variant with a much larger disordered domain by quadruplicating the C-terminal 111–140 amino acids of the full length protein (αS4xC). After confirming that the presence of the larger disordered domain did not affect the membrane binding affinity of the protein (Figure S4), we performed clearing assays on MLV preparations with different protein exposed surface areas. We performed clearing assays with all three protein constructs for 32% and 50% protein exposed membrane area. As expected, the larger exposed area results in a shift of the clearing onset concentration to larger values, while the larger disordered coil results in a lower clearing onset concentration (Figure S5). All experimental data and model predictions are combined in Figure 5.

Figure 5.

Figure 5

Open in a new tab

Calculated protein concentration required to obtain vesicles with a radius between 50 and 100 nm for αS1–108 (red), wt-αS (blue), and αS4xC (green) as a function of the available membrane surface area. The same colored symbols are the experimentally observed clearing onset concentrations.

In Figure 5, we plot the calculated protein concentration required to obtain vesicles with a radius between 50 and 100 nm for the three protein constructs as a function of the available membrane surface area. To this graph, we added the experimentally observed clearing onset concentrations. For αS1–108 and wt-αS the clearing onset concentrations fall into the protein concentration range for which vesicles with a radius between 50 and 100 nm are predicted. Interestingly, the αS4xC clearing onset concentrations clearly fall outside this size range. The clearing onset is found at αS4xC concentrations for which our model predicts much larger vesicle radii than for the clearing onset concentrations of αS1–108 and wt-αS. This either indicates that larger vesicles are formed, or, it could mean that the disordered part of αS4xC does not behave as a self-avoiding random walk. Intrachain interactions could result in a nonspherical shape of the disordered domain and most likely exist within the C-terminal region of the protein.32 One can imagine that when the longest dimension of this disordered domain is preferentially oriented parallel to the membrane surface clearing will set in at lower concentrations than predicted by our much simplified model.

Translating our in vitro findings to the function of αS in vivo, we consider known interactions of αS with vesicles in cells. The synaptic and endocytic vesicles found in neurons have been shown to bind αS and have a radius between 20 and 40 nm. Our model calculations estimate the number of wt-αS protein molecules required to obtain vesicles of 30 nm to be 75. This number fits surprisingly well in the number distribution of αS-GFP on single vesicles in cells.33 At the same time the coverage is low enough (∼30%) to guarantee accessibility of other membrane proteins and functional interactions.

Conclusion

In summary, we conclude that helix insertion and lateral pressure together contribute to curvature induction. Considering that disordered protein domains occupy considerably larger volumes than folded proteins of the same length, the combined action of amphipathic α-helix insertion and lateral pressure may represent efficient use of material. Longer helices or a higher number of helices may generate the same effect as the disordered domains but, because of their compactness, require longer amino acid chains. The failure of our simplified model to include the behavior of αS4xC indicates that additional factors such as intramolecular interactions encoded in protein sequence may have to be accounted for. These encoded interactions may also add to the biological function of the protein. An external trigger may induce compaction or expansion of the disordered domain, thereby releasing lateral pressure thus assisting vesicle fusion/fission events.

Acknowledgments

We thank Nathalie Schilderink for cloning αS2xC, Robert Molenaar for performing the particle tracking experiments, and Ine Segers Nolten for critical reading of the manuscript and providing us with helpful suggestions.

Glossary

Abbreviations

αS

alpha-synuclein

αS1–108

C-terminally truncated αS

wt-αS

wild type αS

αS4xC

C-terminal-quadruplicated αS

CD

circular dichroism

IDP

intrinsically disordered protein

IDR

intrinsically disordered region

KD

dissociation equilibrium constant

LUV

large unilamellar vesicles

MLV

multilamellar vesicles

NBD

nitrobenzoxadiazole

OD

optical density;

PE

phosphatidylethanolamine

POPG

16:0–18:1 phosphatidylglycerol

V-SNARE

vesicle associated SNARE.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biomac.8b01606.

  • Supplementary figures cited throughout the text are presented separately (PDF).

Author Contributions

M.A.A.F.: data acquisition, data analysis, and manuscript writing; S.E.: data acquisition and data analysis; K.A.L.G.: Cloning and protein purification; C.B.: experiment design, data analysis, and manuscript writing; M.M.A.E.C.: funding acquisition, experiment design, data analysis, and manuscript writing.

The authors declare no competing financial interest.

Supplementary Material

bm8b01606_si_001.pdf (811.4KB, pdf)

References

  1. Nemani V. M.; Lu W.; Berge V.; Nakamura K.; Onoa B.; Lee M. K.; Chaudhry F. A.; Nicoll R. A.; Edwards R. H. Increased Expression of alpha-Synuclein Reduces Neurotransmitter Release by Inhibiting Synaptic Vesicle Reclustering after Endocytosis. Neuron 2010, 65 (1), 66–79. 10.1016/j.neuron.2009.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Snead D.; Eliezer D. Alpha-synuclein function and dysfunction on cellular membranes. Experimental neurobiology 2014, 23 (4), 292–313. 10.5607/en.2014.23.4.292. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Murphy D. D.; Rueter S. M.; Trojanowski J. Q.; Lee V. M. Y. Synucleins are developmentally expressed, and alpha-synuclein regulates the size of the presynaptic vesicular pool in primary hippocampal neurons. J. Neurosci. 2000, 20 (9), 3214–3220. 10.1523/JNEUROSCI.20-09-03214.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Maroteaux L.; Campanelli J. T.; Scheller R. H. Synuclein - a neuron-specific protein localized to the nucleus and presynaptic nerve-terminal. J. Neurosci. 1988, 8 (8), 2804–2815. 10.1523/JNEUROSCI.08-08-02804.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Jensen P. H.; Nielsen M. S.; Jakes R.; Dotti G.; Goedert M. Binding of alpha-synuclein to brain vesicles is abolished by familial Parkinson’s disease mutation. J. Biol. Chem. 1998, 273 (41), 26292–26294. 10.1074/jbc.273.41.26292. [DOI] [PubMed] [Google Scholar]
  6. Burre J.; Sharma M.; Tsetsenis T.; Buchman V.; Etherton M. R.; Sudhof T. C. alpha-Synuclein Promotes SNARE-Complex Assembly in Vivo and in Vitro. Science 2010, 329 (5999), 1663–1667. 10.1126/science.1195227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Rhoades E.; Ramlall T. F.; Webb W. W.; Eliezer D. Quantification of alpha-synuclein binding to lipid vesicles using fluorescence correlation spectroscopy. Biophys. J. 2006, 90 (12), 4692–4700. 10.1529/biophysj.105.079251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Stoeckl M.; Fischer P.; Wanker E.; Herrmann A. alpha-Synuclein selectively binds to anionic phospholipids embedded in liquid-disordered domains. J. Mol. Biol. 2008, 375 (5), 1394–1404. 10.1016/j.jmb.2007.11.051. [DOI] [PubMed] [Google Scholar]
  9. Eliezer D.; Kutluay E.; Bussell R.; Browne G. Conformational properties of alpha-synuclein in its free and lipid-associated states. J. Mol. Biol. 2001, 307 (4), 1061–1073. 10.1006/jmbi.2001.4538. [DOI] [PubMed] [Google Scholar]
  10. Fakhree M. A. A.; Segers-Nolten I.; Blum C.; Claessenes M. M. A. E. Different conformational subsensembles of the intrinsically disorderd protein alpha-synuclein in cells. J. Phys. Chem. Lett. 2018, 9, 1249–1253. 10.1021/acs.jpclett.8b00092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Campelo F.; McMahon H. T.; Kozlov M. M. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 2008, 95 (5), 2325–2339. 10.1529/biophysj.108.133173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kozlov M. M.; Campelo F.; Liska N.; Chernomordik L. V.; Marrink S. J.; McMahon H. T. Mechanisms shaping cell membranes. Curr. Opin. Cell Biol. 2014, 29, 53–60. 10.1016/j.ceb.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ford M. G. J.; Mills I. G.; Peter B. J.; Vallis Y.; Praefcke G. J. K.; Evans P. R.; McMahon H. T. Curvature of clathrin-coated pits driven by epsin. Nature 2002, 419 (6905), 361–366. 10.1038/nature01020. [DOI] [PubMed] [Google Scholar]
  14. Isas J. M.; Ambroso M. R.; Hegde P. B.; Langen J.; Langen R. Tubulation by Amphiphysin Requires Concentration-Dependent Switching from Wedging to Scaffolding. Structure 2015, 23 (5), 873–881. 10.1016/j.str.2015.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Braun A. R.; Sevcsik E.; Chin P.; Rhoades E.; Tristram-Nagle S.; Sachs J. N. alpha-Synuclein Induces Both Positive Mean Curvature and Negative Gaussian Curvature in Membranes. J. Am. Chem. Soc. 2012, 134 (5), 2613–2620. 10.1021/ja208316h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Varkey J.; Isas J. M.; Mizuno N.; Jensen M. B.; Bhatia V. K.; Jao C. C.; Petrlova J.; Voss J. C.; Stamou D. G.; Steven A. C.; Langen R. Membrane Curvature Induction and Tubulation Are Common Features of Synucleins and Apolipoproteins. J. Biol. Chem. 2010, 285 (42), 32486–32493. 10.1074/jbc.M110.139576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Nikolov V.; Lipowsky R.; Dimova R. Behavior of giant vesicles with anchored DNA molecules. Biophys. J. 2007, 92 (12), 4356–4368. 10.1529/biophysj.106.100032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Busch D. J.; Houser J. R.; Hayden C. C.; Sherman M. B.; Lafer E. M.; Stachowiak J. C. Intrinsically disordered proteins drive membrane curvature. Nat. Commun. 2015, 6, na. 10.1038/ncomms8875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jiang Z. P.; de Messieres M.; Lee J. C. Membrane Remodeling by alpha-Synuclein and Effects on Amyloid Formation. J. Am. Chem. Soc. 2013, 135 (43), 15970–15973. 10.1021/ja405993r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Stachowiak J. C.; Schmid E. M.; Ryan C. J.; Ann H. S.; Sasaki D. Y.; Sherman M. B.; Geissler P. L.; Fletcher D. A.; Hayden C. C. Membrane bending by protein-protein crowding. Nat. Cell Biol. 2012, 14 (9), 944. 10.1038/ncb2561. [DOI] [PubMed] [Google Scholar]
  21. van Raaij M. E.; Segers-Nolten I. M. J.; Subramaniam V. Quantitative morphological analysis reveals ultrastructural diversity of amyloid fibrils from alpha-synuclein mutants. Biophys. J. 2006, 91 (11), L96–L98. 10.1529/biophysj.106.090449. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Iyer A.; Petersen N. O.; Claessens M. M. A. E.; Subramaniam V. Amyloids of Alpha-Synuclein Affect the Structure and Dynamics of Supported Lipid Bilayers. Biophys. J. 2014, 106 (12), 2585–2594. 10.1016/j.bpj.2014.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. McIntyre J. C.; Sleight R. G. Fluorescence assay for phospholipid membrane asymmetry. Biochemistry 1991, 30 (51), 11819–11827. 10.1021/bi00115a012. [DOI] [PubMed] [Google Scholar]
  24. Ulmer T. S.; Bax A.; Cole N. B.; Nussbaum R. L. Structure and dynamics of micelle-bound human alpha-synuclein. J. Biol. Chem. 2005, 280 (10), 9595–9603. 10.1074/jbc.M411805200. [DOI] [PubMed] [Google Scholar]
  25. Grupi A.; Haas E. Segmental Conformational Disorder and Dynamics in the Intrinsically Disordered Protein alpha-Synuclein and Its Chain Length Dependence. J. Mol. Biol. 2011, 405 (5), 1267–1283. 10.1016/j.jmb.2010.11.011. [DOI] [PubMed] [Google Scholar]
  26. Kucerka N.; Holland B. W.; Gray C. G.; Tomberli B.; Katsaras J. Scattering Density Profile Model of POPG Bilayers As Determined by Molecular Dynamics Simulations and Small-Angle Neutron and X-ray Scattering Experiments. J. Phys. Chem. B 2012, 116 (1), 232–239. 10.1021/jp208920h. [DOI] [PubMed] [Google Scholar]
  27. Shvadchak V. V.; Falomir-Lockhart L. J.; Yushchenko D. A.; Jovin T. M. Specificity and Kinetics of alpha-Synuclein Binding to Model Membranes Determined with Fluorescent Excited State Intramolecular Proton Transfer (ESIPT) Probe. J. Biol. Chem. 2011, 286 (15), 13023–13032. 10.1074/jbc.M110.204776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Braun A. R.; Lacy M. M.; Ducas V. C.; Rhoades E.; Sachs J. N. alpha-Synuclein-Induced Membrane Remodeling Is Driven by Binding Affinity, Partition Depth, and Interleaflet Order Asymmetry. J. Am. Chem. Soc. 2014, 136 (28), 9962–9972. 10.1021/ja5016958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Dickey A.; Faller R. Examining the contributions of lipid shape and headgroup charge on bilayer behavior. Biophys. J. 2008, 95 (6), 2636–2646. 10.1529/biophysj.107.128074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Killian J. A.; Salemink I.; dePlanque M. R. R.; Lindblom G.; Koeppe R. E.; Greathouse D. V. Induction of nonbilayer structures in diacylphosphatidylcholine model membranes by transmembrane alpha-helical peptides: Importance of hydrophobic mismatch and proposed role of tryptophans. Biochemistry 1996, 35 (3), 1037–1045. 10.1021/bi9519258. [DOI] [PubMed] [Google Scholar]
  31. Eichmann C.; Campioni S.; Kowal J.; Maslennikov I.; Gerez J.; Liu X. X.; Verasdonck J.; Nespovitaya N.; Choe S.; Meier B. H.; Picotti P.; Rizo J.; Stahlberg H.; Riek R. Preparation and Characterization of Stable -Synuclein Lipoprotein Particles. J. Biol. Chem. 2016, 291 (16), 8516–8527. 10.1074/jbc.M115.707968. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Dedmon M. M.; Lindorff-Larsen K.; Christodoulou J.; Vendruscolo M.; Dobson C. M. Mapping long-range interactions in alpha-synuclein using spin-label NMR and ensemble molecular dynamics simulations. J. Am. Chem. Soc. 2005, 127 (2), 476–477. 10.1021/ja044834j. [DOI] [PubMed] [Google Scholar]
  33. Fakhree M. A. A.; Zijlstra N.; Raiss C. C.; Siero C. J.; Grabmayr H.; Bausch A. R.; Blum C.; Claessens M. M. A. E. The number of α-synuclein proteins per vesicle gives insights into its physiological function. Sci. Rep. 2016, 6, 30658. 10.1038/srep30658. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

bm8b01606_si_001.pdf (811.4KB, pdf)

Articles from Biomacromolecules are provided here courtesy of American Chemical Society

RESOURCES