Heavy-tailed prior distributions for sequence count data: removing the noise and preserving large differences

Abstract

Motivation

In RNA-seq differential expression analysis, investigators aim to detect those genes with changes in expression level across conditions, despite technical and biological variability in the observations. A common task is to accurately estimate the effect size, often in terms of a logarithmic fold change (LFC).

Results

When the read counts are low or highly variable, the maximum likelihood estimates for the LFCs has high variance, leading to large estimates not representative of true differences, and poor ranking of genes by effect size. One approach is to introduce filtering thresholds and pseudocounts to exclude or moderate estimated LFCs. Filtering may result in a loss of genes from the analysis with true differences in expression, while pseudocounts provide a limited solution that must be adapted per dataset. Here, we propose the use of a heavy-tailed Cauchy prior distribution for effect sizes, which avoids the use of filter thresholds or pseudocounts. The proposed method, Approximate Posterior Estimation for generalized linear model, apeglm, has lower bias than previously proposed shrinkage estimators, while still reducing variance for those genes with little information for statistical inference.

Availability and implementation

The apeglm package is available as an R/Bioconductor package at https://bioconductor.org/packages/apeglm, and the methods can be called from within the DESeq2 software.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

RNA sequencing (RNA-seq) is a widely used assay for measuring the expression of transcripts from the genome. One common goal is to identify which genes are differentially expressed (DE) between experimental conditions, and to estimate the strength of the difference. The difference is usually defined in terms of the logarithmic fold change (LFC) between average expression levels of different conditions. The expression level of a gene in an RNA-Seq experiment is proportional across samples to a scaled count, representing the number of observed single- or paired-end reads that could be assigned to a given gene at a given library size. Scaling for the library size of the experiment is necessary, and other scaling factors can be included as well (Leek, 2014; Risso et al., 2014; Soneson et al., 2015). Many variations on the standard RNA-seq protocol exist, as well as other sequencing-based assays such as chromatin immunoprecipitation followed by sequencing (ChIP-seq), and to the degree that these other experiments assess differences in scaled counts using estimated LFCs, the methods described here are generally applicable to these other assays as well.

Many statistical methods have been developed for DE analysis of RNA-seq (Anders and Huber, 2010; Hardcastle and Kelly, 2010; Law et al., 2014; Leng et al., 2013; Li and Tibshirani, 2013; Love et al., 2014; McCarthy et al., 2012; Robinson et al., 2010; Trapnell et al., 2012; van de Wiel et al., 2013). Their common approach in detecting DE genes is to find sets of genes such that the null hypothesis of no difference in expression between conditions can be rejected, usually targeting the false discovery rate (FDR) for the set. However, a gene can be found significantly different, and the null rejected, even if the size of difference is very small (Love et al., 2014). For further research interests, rather than only considering the order of genes according to adjusted or unadjusted P-values, it is also of interest to order genes by the estimated effect size itself (the LFC).

It is challenging to accurately estimate the LFCs for genes with low expression levels, or genes with a high coefficient of variation. Due to experimental costs and time, RNA-seq experiments designed for hypothesis generation typically have a small number of biological replicates (n of 3–5) for each condition group (McCarthy et al., 2012). When the counts of sequenced reads are small or have a high coefficient of variation in one or a subset of the conditions, the estimated LFCs will have high variance, leading to some large estimated LFCs, which do not represent true large differences in expression. One approach that reduces the problem of these noisy LFC estimates is to filter out low count genes. Filtering also has the benefit of removing genes that may not have enough power for detecting DE, and so reducing the multiple test correction burden. Setting the threshold requires careful consideration of which genes may be lost. The authors of edgeR (McCarthy et al., 2012) and limma-voom (Law et al., 2014) suggest using a filtering rule that removes genes with low scaled counts before statistical analysis (Chen et al., 2016). Other methods take a Bayesian modeling approach, including ShrinkBayes (van de Wiel et al., 2013) and DESeq2 (Love et al., 2014). DESeq2 applies an adaptive Normally distributed prior, to produce a shrinkage estimator for the LFC for each gene. However, in our analysis, we found that filtering or application of Normal priors each can have drawbacks, either leading to loss of genes with sufficient signal, or overly aggressive shrinkage of true, large LFCs.

In this article, we present an empirical Bayes procedure that stabilizes the estimator of LFCs, without overly shrinking large LFCs, and uses the posterior distribution for point estimates and posterior probabilities, such as the aggregated s-value (Stephens, 2017) and the false-sign-or-smaller (FSOS) rate. We extend the basic framework of DESeq2, a Negative Binomial (NB) generalized linear model (GLM) (McCullagh and Nelder, 1989) with moderated dispersion parameter, by exchanging the Normal distribution as a prior on LFCs with a heavy-tailed Cauchy distribution (a t distribution with 1 degree of freedom). We use various approximation techniques to provide Approximate Posterior Estimation for the GLM (apeglm). We compare apeglm to four existing methods on two benchmarking RNA-seq datasets. We demonstrate the advantages of apeglm’s shrunken estimates in reducing variance while preserving the true large effect sizes. We also show that apeglm shrunken estimates improve gene rankings by LFCs, relative to methods which do not apply Bayesian shrinkage on the LFCs. apeglm is available as an open-source R package on Bioconductor, and can be easily called from within the DESeq2 software.

2 Materials and methods

2.1 NB model for RNA-seq counts

We start with summarized measures of gene expression for the experiment, represented by a matrix of read or fragment counts. The rows of the matrix represents genes, $(g=1,\dots ,G)$, and columns represent samples, $(i=1,\dots ,m)$. Let Y_gi denote the count of RNA-seq fragments assigned to gene g in sample i. We assume that Y_gi follows a NB distribution with mean μ_gi and dispersion α_g, such that $\text{Var}(Y_{gi})={\mu }_{gi}+{\alpha }_g{\mu }_{gi}^2$. The mean μ_gi is a product of a scaling factor s_gi and a quantity q_gi that is proportional to the expression level of the gene g. We follow the methods of Love et al. (2014) to estimate α_g and s_gi sharing information across G genes, and consider estimates as fixed for the following. We fit a GLM to the count Y_gi for gene g and sample i,

$$\begin{array}{l}{Y}_{gi}\sim \text{NB}({\mu }_{gi},{\alpha }_g)\\ {\mu }_{gi}=s_{gi}{q}_{gi}\\ \hspace{0.17em}\text{log}\hspace{0.17em}{q}_{gi}=X_{i,*}{\beta }_g\end{array}$$ (1)

where X is the standard design matrix and β_g is the vector of regression coefficients specific to gene g. Usually X has one intercept column, and columns for covariates, e.g. indicators of the experimental conditions other than the reference condition, continuous covariates, or interaction terms. We consider design matrices where the first element of β_g is the intercept. For clarity, we partition the β_g into ${\beta }_g=({\beta }_{g0},{\beta }_{g1},\dots ,{\beta }_{gK})$, where ${\beta }_{g0}$ is the intercept and β_gk, $k=1,\dots ,K$ is for kth covariate. The scaling factor s_gi accounts for the differences in library sizes, gene length (Soneson et al., 2015) or sample-specific experimental biases (Patro et al., 2017) between samples, and is used as an offset in our model.

In the GLM, we use the logarithmic link function. In the apeglm software, the estimated coefficients and corresponding SD estimates are reported on the same $\text{natural\hspace{0.17em}log}\hspace{0.17em}$ scale. The apeglm method can be easily called from DESeq2’s lfcShrink function, which provides LFC estimates on the ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2$ scale. The apeglm method and software is generic for GLMs and can be used with other likelihoods. For example, it can be used for the Beta Binomial or zero-inflated NB model, as long as estimates for the additional parameters, e.g. dispersion or the zero component parameters, are provided. An example of apeglm applied to Beta Binomial counts, as could be used to detect differential allele-specific expression, is provided in the software package vignette.

2.2 Adaptive shrinkage estimator for β_gk

We shrink coefficients representing differences between groups, continuous covariates, or interaction terms, but not the intercept. We propose a Cauchy distribution as the prior for the coefficients that the user wants to shrink. Therefore β_gk in the model (1) has the prior

$${\beta }_{gk}\sim \text{Cauchy}(0,S_k)$$ (2)

where the first parameter of the Cauchy gives the location and the second parameter is the scale, S_k. For simplicity, as apeglm shrinks only a single coefficient at a time, we will write S in place S_k. A similar default prior for coefficients associated with non-intercept covariates has been proposed by Gelman et al. (2008) in the bayesglm R package, which uses a zero-centered Cauchy distribution with a scale of 2.5. The proposed prior distribution assumes that the distribution of LFCs across genes is unimodal and symmetric. We assessed robustness to violations of this assumption and found apeglm still performed well (detailed in a later section). However, if most of the genes are differentially expressed in the same direction, the global normalization method used by all methods discussed here would break down, thus affecting any effect size estimation. This situation can be detected by histogram, MA-plot or more rigorously with quantro (Hicks and Irizarry, 2015).

For setting the scale of the prior S, we use the maximum likelihood estimates (MLEs) ${\widehat{\beta }}_{gk}$ and their standard errors e_gk. When making use of the set of MLEs for a coefficient, we shrink only a single coefficient at a time, and adapt the scale of the prior to the MLE by solving the following equation for $S^2=A$ (Efron and Morris, 1975).

$$A={\sum }_{g=1}^G({\widehat{\beta }}_{gk}^2-e_{gk}^2)I_g(A)/{\sum }_{g=1}^G{I}_g(A)$$ (3)

$$I_g(a)\equiv 1/[2{(a+e_{gk}^2)}^2]$$ (4)

This equation is motivated by assuming that the MLE ${\widehat{\beta }}_{gk}$ follows a Normal distribution around the true value β_gk with variance $e_{gk}^2$, and that the β_gk themselves follow a Normal distribution with mean zero. A is an empirical Bayes estimate of the variance of the generating Normal distribution, and $S=\sqrt{A}$ gives the scale. Although we use a Cauchy prior in apeglm in order to accommodate large effect sizes from potentially only a few genes, we found that setting the scale of the prior by assuming the β_gk follow a zero-centered Normal distribution performed well in practice. The equations above for estimating A are given by Efron and Morris (1975), as a generalization of empirical Bayes estimators for the situation of many parameters each distributed with unequal variances. Equation (3) is solved for A using Brent’s line search implemented in R (Brent, 1972).

Although the method above for estimating A proposed by Efron and Morris (1975) requires that the e_gk be known, here we have instead substituted an estimated quantity, the standard errors. We assessed the practical consequence of this substitution when the standard errors are unstable because the counts were very low. We found that the resulting estimate of A is only slightly biased, even when counts are very low (Supplementary Fig. S1).

If the MLEs of the coefficients are not supplied, we use a scale S = 1 for all non-intercept coefficients. The unscaled posterior for β_gk is the product of the prior density and the NB likelihood. We use the posterior mode, or maximum a posteriori (MAP), as the shrinkage estimator for the coefficient. The posterior mode is found using the L-BFGS algorithm (Nocedal, 1980) implemented in C++ using the RcppNumerical and L-BFGS++ libraries. Running apeglm is efficient: for the simulation dataset modeled on the Pickrell data (10 000 genes and 5 versus 5 samples), running DESeq2 to obtain dispersion estimates and MLE coefficients takes 4.7 s on a laptop with one core, running LFC shrinkage with the DESeq2 Normal prior takes 2.9 s, and running LFC shrinkage with the apeglm Cauchy prior takes 4.1 s. Running apeglm to only produce the MAP estimates (without calculating the posterior SD) takes 0.5 s.

We derive the posterior distribution for β_gk using the Laplace approximation: we estimate the covariance of the posterior distribution as the negative inverse of the Hessian matrix obtained from numeric optimization of the log posterior. We also attempted an alternate method for approximating the posterior by integrating the un-normalized posterior over a fine grid, but we found the Laplace approximation was consistently more accurate. Using the approximate posterior, we compute local false sign rate (FSR) and credible intervals. Following Stephens (2017), the local FSR is defined as the posterior probability that the posterior mode (MAP) is of the false sign, that is for gene g,

$${\text{lfsr}}_g=\{\begin{array}{ll}p({\beta }_{gk}<0)\hfill & \hspace{1em}\text{MAP} \text{of} {\beta }_{gk}\ge 0\hfill \\ p({\beta }_{gk}\ge 0)\hfill & \hspace{1em}\text{MAP} \text{of} {\beta }_{gk}<0.\hfill \end{array}$$

We also provide the local FSOS rate, relative to a given $\theta >0$ representing a biologically significant effect size,

$${\text{lfsosr}}_g^{\theta }=\{\begin{array}{ll}p({\beta }_{gk}<\theta )\hfill & \hspace{1em}\text{MAP} \text{of} {\beta }_{gk}\ge 0\hfill \\ p({\beta }_{gk}>-\theta )\hfill & \hspace{1em}\text{MAP} \text{of} {\beta }_{gk}<0.\hfill \end{array}$$

Analogous to the q-value (Storey, 2003), the s-value (Stephens, 2017) provides a statistic for thresholding, in order to produce a gene list satisfying a certain bound in expectation. The s-value can be computed as

$$s_g=\frac{1}{|\Gamma |}{\sum }_{j\in \Gamma }{\text{lfsr}}_j,\hspace{1em}\Gamma =\{j:{\text{lfsr}}_j\le {\text{lfsr}}_g\},$$

and likewise for the local FSOS rate. Other methods that have suggested using the cumulative average or the cumulative maximum of posterior probabilities for defining the set of interesting features in high-throughput experiments include Choi et al. (2008), Kall et al. (2008) and Leng et al. (2013).

3 Results

3.1 Strong filtering thresholds may result in loss of DE genes

It is difficult to accurately estimate the LFCs for genes with low read count; MLEs of LFCs for genes with low read count have high variance due to the dominance of sampling variance over any detectable biological differences. The MLEs of LFCs for these genes may not reflect the true biological difference of gene expression between conditions, and thus are not reliable for plotting or ranking genes by effect size (Love et al., 2014). Chen et al. (2016) suggested to remove from analysis the genes that have low scaled counts across samples. They define a scaled quantity, the counts per million (CPM), which is the counts Y_gi divided by a robust estimator for the library size, multiplied by one million. The filtering rule is to keep only those genes with n or more samples with CPM greater than the CPM value for a raw count of 10 for the least sequenced sample. The suggested value for n is the sample size of the smallest group. CPM filtering occurs prior to any statistical analysis. Other data-independent thresholds, such as requiring a CPM of 0.5 or 1 from n or more samples can be even more aggressive at removing genes with potential signal when the sequencing depth is high.

We illustrate how filtering can lead to loss of DE genes using the dataset by Bottomly et al. (2011), which contains 10 and 11 samples of RNA-seq data for mouses from two strains, C57BL/6J(B6) and DBA/2J(D2), respectively. We repeatedly randomly picked three samples from each strain, balancing across the three experimental batches. We then applied a CPM filtering rule to each random subset, repeating the process 100 times. For all genes in the full dataset, we used DESeq2 (Love et al., 2014) to test for DE across strains controlling for batch, defining a set of genes with a nominal FDR threshold of 5%. Supplementary Figure S2 shows four example genes that were removed >50% of the time across random subsets, but were reported as differentially expressed by DESeq2 on the full dataset. There were 207 such genes, which are shown in Supplementary Figure S3. These genes did have information to contribute: for example, they had on average the same sign of estimated LFCs 99% of the time when comparing to the LFCs from the full dataset. These genes, despite having low gene expression, may still be biologically relevant, so we considered statistical methods that produce LFC estimates with low variance for relatively low count genes as well. To be clear, we do not argue against any filtering, only against strong filtering for the purposes of obtaining precise LFCs which may discard genes with a relevant signal.

Besides filtering, an additional approach to produce precise effect sizes is to use scaled pseudocounts, or prior counts, to obtain shrinkage estimates of LFCs. The prior count approach is employed by edgeR and limma-voom. However, setting a prior count does not make use of the statistical information contained in the data for estimating the LFCs, such that the optimal prior count needs to be adapted per dataset. For example, as the sample size increases, the optimal prior count should go to zero, and so a fixed prior count may be sub-optimal. Furthermore, the prior count approach, while helping with high LFC variance from genes with low counts, helps less for high variance genes. Finally, we note that the prior count approach does not provide a posterior distribution for effect sizes, which may be useful for certain analyses discussed below.

3.2 Overview of the apeglm method

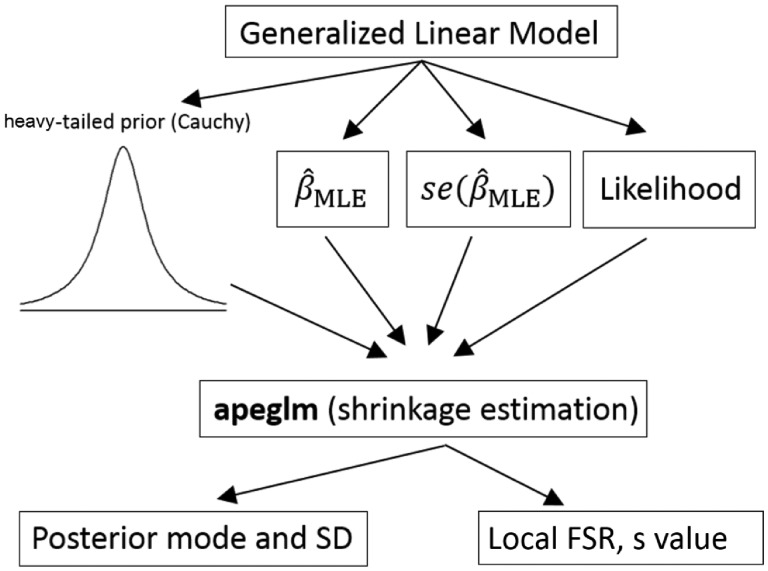
Following the basic framework of GLMs, we propose an adaptive Bayesian shrinkage estimator (Fig. 1). We employed a heavy-tailed prior distribution on the effect sizes, where the shape of the prior distribution is fixed, and the scale is adapted to the distribution of observed MLE of effect size for all genes (see Section 2). For each gene, the method uses a Laplace approximation to provide the mode of the posterior distribution as a shrinkage estimate, the posterior SD as a measure of uncertainty, and posterior probabilities of interest described below. Our method obviates the need for filtering rules or prior counts, and takes advantage of the statistical information in the data for estimating the effect size. The method is general for various likelihoods, but here we apply it to RNA-seq using a NB GLM, where the effect size is a particular LFC (log fold change between groups or an interaction term in a complex design). For genes that have low counts or high variance, this method shrinks the LFCs towards zero thus alleviating the problem of unreliably large LFC estimates.

Fig. 1.

An overview of the method. apeglm takes the MLE estimates and corresponding standard errors of a GLM model as input. In apeglm we provide a heavy-tailed prior distribution on the coefficients, and compute the shrinkage estimators and corresponding SDs. Users can also define a likelihood function that describes the data and feed to apeglm. apeglm also provides the local FSRs and s-values (Stephens, 2017) as part of the output

The local FSR (Stephens, 2017) is defined as the posterior probability for a gene that the sign of the estimated effect size is wrong. Similar to the FSR, we also make use of a local FSOS rate: the posterior probability of having mis-estimated the sign of an effect size, or the effect size being smaller than a pre-specified value. For the FSR and FSOS rates, apeglm provides an aggregate quantity, the s-value proposed by Stephens (2017), which can be used for generating lists of genes. The s-value for a gene is defined as the average of local FSR over the set of genes that have smaller local FSR than this one (likewise for FSOS, see Section 2).

3.3 An adaptive prior controls the FSR

We performed an initial assessment of our approach on simulated data, to confirm that the adaptive prior would control the aggregate FSR, when thresholding on s-values, for datasets with varying spread of true LFCs. Using a fixed, non-adaptive prior scale leads to loss of control of FSR when the true LFCs were drawn from a Normal distribution with small variance; matching the scale of the prior to the scale of the true distribution of LFCs regained control of FSR (Supplementary Fig. S4). Although a prior smaller in scale than the true distribution of LFCs also controlled the FSR, it lead to an increase in the relative error of point estimates (Supplementary Figs S5 and S6). Therefore we chose to set the scale of the prior to the estimated scale of the true LFCs using the MLEs and their standard error (Section 2).

3.4 Evaluation on highly replicated yeast dataset

To investigate the precision of various estimates of LFCs, we used a highly replicated RNA-seq dataset designed for benchmarking (Schurch et al., 2016). This dataset consists of RNA-seq data of Saccharomyces cerevisiae from two experimental conditions: 42 replicates in wild-type and 44 replicates in a $\Delta$snf2 mutant. We randomly picked three samples from each experimental condition to form a test dataset, and applied differential gene expression methods to estimate the LFCs. We compared the LFCs estimates against the ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2$ ratio of mean scaled counts in the full dataset, which was taken as ‘gold standard’ LFCs. We repeated the random sampling 100 times. We also performed this same experiment using a sample size of 5 versus 5. For this evaluation and all others, we minimized the influence of genes with no signal for estimating the LFCs, by only evaluating the methods over genes with an average of more than one scaled count per sample. This minimal filtering does not advantage apeglm.

We compared the performance of apeglm with four other methods for estimation of effect size in RNA-seq, DESeq2, edgeR, limma-voom, as well as ashr (Stephens, 2017). In comparing to DESeq2, we compared apeglm to the LFC shrinkage estimator produced using a Normal prior, as described in Love et al. (2014). ashr provides generic methods for adaptive shrinkage estimation, taking as input a vector of estimated β_g i.e. ${\widehat{\beta }}_g$, and the corresponding estimates of standard errors. For the Bayesian shrinkage estimation methods that we compared, the unimodal assumption of the true LFCs was checked for all the examples we considered below, and the assumption was met in all the examples (Supplementary Fig. S7). We also found that the Bayesian methods were robust to some degree of violation of the unimodal assumption, discussed in a later section. For ashr, we input ${\widehat{\beta }}_g$ and corresponding standard error using the MLE from DESeq2 (‘ashr DESeq2 input’), and the estimated coefficient from limma-voom, plus a standard error calculated using the moderated variance estimate (‘ashr limma input’). We also included edgeR with a prior count of 5, which helps to moderate the variance of the estimated LFCs from genes with low counts, (edgeR-PC5).

Stratifying genes by the absolute value of true LFCs allows us to see where the different methods excel and fall short systematically, across 100 iterations of sub-sampling (Fig. 2a and c). limma and edgeR had the lowest mean absolute error (MAE) for both sample sizes. DESeq2 had the highest error for the largest bin of true LFCs, meaning that DESeq2’s Normal prior could not accommodate the top 0.5% of effect sizes for this dataset and resulted in too much shrinkage. The other shrinkage estimators apeglm and ashr (with either input) maintained a middle range of MAE. edgeR-PC5 had low error for the small true LFCs, but then increased to higher error for the largest bin of true LFCs, especially when the sample size increased to 5 versus 5, where the bias approaches that of DESeq2.

Fig. 2.

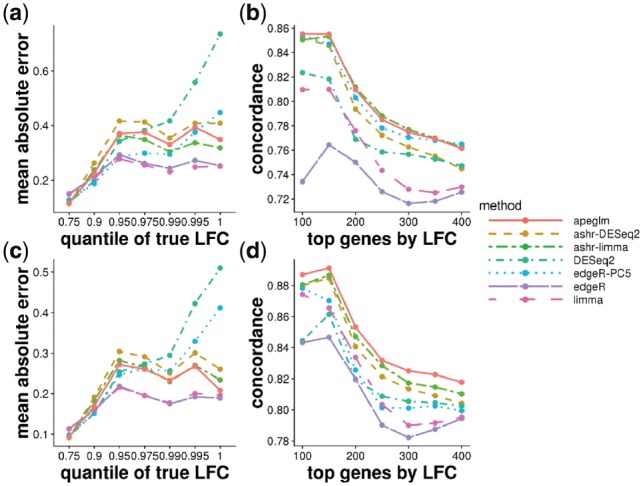
(a) MAE of estimates for 3 versus 3 samples, defined as the mean of the absolute value of the differences between the estimated and reference LFCs, stratified by absolute value of reference LFCs. The mean of MAE over 100 iterations is plotted for each method. The x-axis label gives the upper bound of the bin on absolute value of LFCs. (b) Concordance At the Top (CAT) plot (Irizarry et al., 2005) comparing ranked gene lists from each method against the reference ranked gene list for 3 versus 3 samples. Number of top genes ranked by the absolute value of the LFCs is on the x-axis, and the proportion of concordance between the two rankings is on the y-axis. For example, if the ranked gene list from apeglm estimated and reference LFCs share 85 of top 100 genes, then the apeglm point would fall at (100, 0.85). (c) MAE plot of estimates for 5 versus 5 samples. (d) CAT plot for 5 versus 5 samples

Ranking genes by estimated LFCs can assist with further investigation into the genes most affected in their expression by changes in condition. We compared the concordance of the top ranked genes by absolute LFC estimates (Fig. 2b and d). We examined, for the top w genes ranked by absolute value of estimated LFCs, the proportion which were among the top w genes by absolute value of reference LFCs ($w\in \{100,150,200,\dots ,400\}$). Although limma and edgeR had lowest MAE when binning by quantile of the true LFC, they meanwhile had the lowest concordance when ranking genes by LFC, while the shrinkage estimators tended to perform better (always the case past w = 250 genes). apeglm, ashr (with either input), and edgeR-PC5 had the highest concordance of top ranked genes by absolute LFC overall, for 3 versus 3. apeglm and ashr (with either input) had the highest concordance for the 5 versus 5 sub-sampling experiment. DESeq2 had relatively low concordance among the shrinkage estimators for the smallest w, due to over-shrinkage of the very largest effect size genes.

In one iteration of random sampling, much of the behavior that was seen systematically over all iterations can be observed (Supplementary Fig. S8). apeglm, ashr with DESeq2 or limma input, and edgeR-PC5 did well in estimating LFCs, with LFC estimates close to reference LFCs for most of the genes. DESeq2 and edgeR-PC5 had similar performance to apeglm, but were too aggressive in shrinking LFC for genes with large reference LFCs, for example ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2$ fold change near 4. We show the counts of such example genes in Supplementary Figure S9, where DESeq2 or edgeR-PC5 give small LFC estimates to genes with large reference LFC, while the apeglm method allows for large estimated LFCs. edgeR and limma returned large estimated LFCs for some genes with reference LFCs around zero, which is problematic for ranking genes by effect size without first applying some form of count filtering.

In summary, considering both aggregate error (Fig. 2a and c) and concordance in ranking of genes by effect size (Fig. 2b and d), apeglm, ashr and edgeR-PC5 were top performers for the 3 versus 3 experiment, and apeglm and ashr were top performers for the 5 versus 5 experiment. limma and edgeR were low performers for ranking genes by effect size, and DESeq2 and edgeR-PC5 had high error for the top effect size genes (DESeq2 for both experiments, while edgeR-PC5 only for the 5 versus 5 experiment). We therefore conclude that shrinkage estimation is useful for ranking genes by effect size, and does not necessarily come at the expense of much bias, depending on the design of the shrinkage method. Among the methods using shrinkage estimation, an advantage of apeglm is that it preserves true, large differences across conditions in the estimated LFCs. To demonstrate this, we calculated the average estimated LFCs for the methods that perform shrinkage (apeglm, DESeq2, ashr and edgeR-PC5), averaging over the 100 iterations. Comparing the average estimated LFCs to the reference LFCs demonstrates the extent of bias of the estimators, where it is expected that shrinkage estimators would have bias toward zero. We then constructed an MA plot, as typically used to visualize DE gene expression results, but where overshrinkage across many iterations i.e. biased estimation, is highlighted (Supplementary Fig. S10). All of the methods exhibited shrinkage of LFCs more than 0.5 for many genes with mean scaled counts <10, but apeglm preserved the most large LFCs for genes with larger mean scaled counts. DESeq2 and ashr with limma input tended to shrink the LFCs by >0.5 for genes with mean expression levels >10, including genes with absolute value of reference LFCs >2, thus representing large differences across condition.

3.5 Rank comparison with P-values

Many RNA-seq workflows use adjusted P-values from a statistical test of the null hypothesis of no difference in expression in order to rank the genes by importance. limma by default ranks by log odds of DE. However, adjusted P-values or log odds do not capture the magnitude of LFCs, unless the standard null of $\text{LFC}=0$ is replaced by a threshold test (Love et al., 2014; McCarthy and Smyth, 2009), wherein a positive threshold of biological importance is specified by the analyst. Using Bayesian methods, we can directly rank genes by their effect size, as unreliable LFCs from genes with low counts or high variability are moderated toward zero. We assessed whether our ranking by apeglm effect size provided substantially different output than a typical ranking of genes by P-values or Independent Hypothesis Weighting (IHW) adjusted P-values (Ignatiadis et al., 2016). We compared against the ranking of genes by the reference LFC—while making an important caveat that P-values are not designed to provide reliably rankings by effect size (Fig. 3). Comparing the percentage of concordance at top with the rank by reference LFCs, the ranking from apeglm estimated LFCs had over 80% concordance, while the ranking from DESeq2 P-values and IHW adjusted P-values had about 60% concordance. Furthermore, some of the genes with low rank (top of the gene list) from IHW adjusted P-values had high rank by apeglm, potentially indicating that the effect size was significantly different than zero but nevertheless small. This comparison revealed that apeglm does in fact give substantially different output in terms of gene lists, and the previous analysis reveals that the apeglm output is accurate on a highly replicated RNA-seq dataset.

Fig. 3.

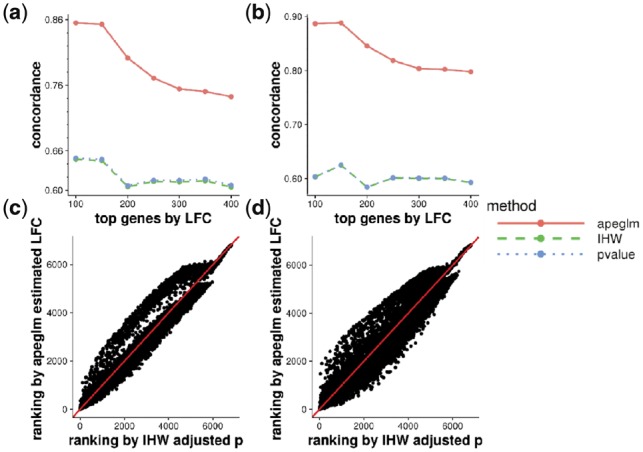
(a) CAT plot comparing ranked gene lists from apeglm estimated LFCs, DESeq2 p values and IHW adjusted P values for 3 versus 3 samples. (b) CAT plot comparing ranked gene lists from apeglm estimated LFCs, DESeq2 P values and IHW adjusted P values for 5 versus 5 samples. (c) Rank plot comparing the ranks of genes from apeglm estimated LFCs and IHW adjusted P values for 3 versus 3 samples. (d) Rank plot comparing the ranks of genes from apeglm estimated LFCs and IHW adjusted p values for 5 versus 5 samples

3.6 Evaluation on simulation modeled on experimental data

We also checked whether apeglm provides accurate estimates of LFCs in simulated data modeled on experimental datasets. We generated the ‘true’ LFCs from a mixture of zero-centered Normal distributions. The mean counts and NB dispersion estimates were drawn from the joint distribution of the estimated parameters over the Bottomly et al. (2011) and Pickrell et al. (2010) datasets, as was performed in Love et al. (2014). We simulated 10 000 genes with a sample size of 5 versus 5, and repeated the whole simulation 10 times per experimental dataset. We also doubled the sample size to 10 versus 10 to see if the methods provided consistent relative performance at higher sample size. For the Pickrell dataset, which has higher within-group variation, we used a mixture of Normal distributions with SDs of 1, 2, 3 (with mixing proportions 90, 5 and 5%, respectively). The Bottomly dataset has lower within-group variation, and so to make the simulation equally challenging, we used SDs of 0.25, 0.5 and 1 (90, 5 and 5%). We constructed the simulation such that the expected count for all simulated samples was always >10, to avoid overemphasizing the smallest count genes (this simulation choice does not advantage apeglm).

The simulation results for the Pickrell dataset (Fig. 4) and the Bottomly dataset (Supplementary Fig. S11) were mostly consistent with the previous result on the highly replicated yeast dataset. limma, edgeR, edgeR-PC5 and apeglm tended to have the lowest error when stratifying by true LFCs, although limma and edgeR had the lowest concordance when ranking genes by LFCs. The methods which do not shrink tended to produce large estimates for genes where the true LFCs are near 0 (Supplementary Figs S12 and S13). With one iteration of random sampling, we showed two genes that had true LFCs near zero for Pickrell dataset, for which edgeR and limma greatly overestimated the LFCs, but apeglm provided LFCs near 0 (Supplementary Fig. S14). As in the yeast dataset, as the sample size increased, apeglm had lower error compared with edgeR-PC5 for the largest LFCs. DESeq2 had the highest error for the largest LFCs, as was expected. Unlike the results from the highly replicated yeast dataset, here ashr with both inputs had higher error for the middle range of LFCs. With one iteration of random sampling, we showed two genes with middle range of LFCs for the Bottomly dataset, for which ashr estimated LFCs were much smaller than the true LFCs, while apeglm gave more accurate, large LFCs (Supplementary Fig. S15). We note that we simulated NB counts, and so the methods apeglm, DESeq2 and edgeR which assume the NB likelihood, are potentially at an advantage. apeglm was a top performer in the simulation for small and larger sample sizes, having consistently low error and also high concordance.

Fig. 4.

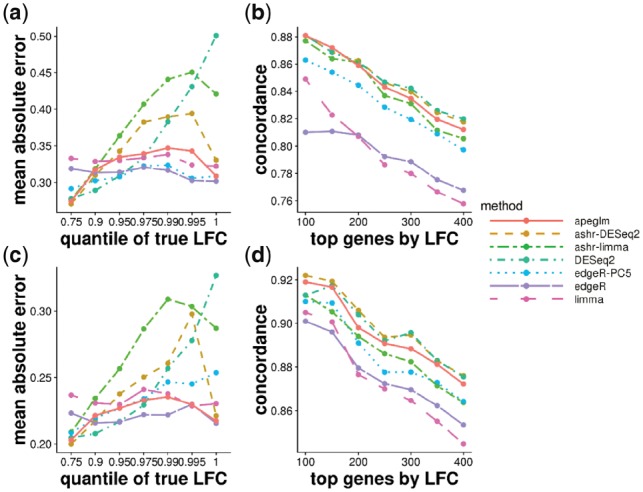
Simulation dataset (top row, 5 versus 5, and bottom row, 10 versus 10) modeled on estimated parameters from the Pickrell et al. (2010) dataset. Each point represents the average over 10 repeated simulations

The shrinkage estimators apeglm, DESeq2 and ashr tended to have low MAE across the range of counts (Supplementary Fig. S16). limma and edgeR had high MAE for low counts, as expected. The MAE for edgeR-PC5 when binning genes by counts was low for the sample size of 5 versus 5, but higher when the sample size was increased to 10 versus 10.

Finally, we considered whether the methods which produce s-values (ashr and apeglm) were able to achieve their FSR bounds. We also generated s-values for DESeq2 using the DESeq2 posterior mode estimate and the associated uncertainty. We generated plots using the iCOBRA package (Soneson and Robinson, 2016), showing the number of genes at various achieved FSR values (Supplementary Fig. S17). This analysis indicated that apeglm and ashr with DESeq2 input tended to hit the target of 1% and 5% FSR, while DESeq2 and ashr with limma input were just slightly above their nominal FSR. The iCOBRA data objects for four iterations of the simulation can be accessed at https://github.com/mikelove/apeglmPaper, and explored interactively using the iCOBRA Shiny app.

3.7 Evaluation of robustness, extensibility and consistency

To examine the robustness of apeglm and other Bayesian shrinkage methods to violations of the unimodal assumption, we modified the simulation such that the true LFCs no longer are generated from a unimodal distribution, but instead a mixture of a zero-centered and a non-zero-centered distribution. We first assessed how the addition of a non-zero-centered component affected the estimation of the scale of the prior in apeglm. We found that the estimated scale of the prior tracked with the variance of the mixture of distribution and not with the zero-centered component alone, as was expected (Supplementary Fig. S18). To assess performance of apeglm relative to other methods in LFC estimation, we simulated a mixture of $N(0,0.5)$ and N(3, 2) for the Pickrell dataset and a mixture of $N(0,0.125)$ and $N(0.75,0.5)$ for the Bottomly dataset, thus producing a bimodal distribution when the non-zero component was included at a high enough proportion. We considered the proportion of genes coming from the non-zero-centered component to be in the range {5, 10 and 20%}. apeglm was the top performing method, taking into account accuracy and concordance of ranking genes by effect size for the 5% case (Supplementary Figs S19 and S20 for Pickrell and Bottomly datasets, respectively). The differences were more moderate for a 10% non-zero component for the Pickrell dataset (Supplementary Fig. S21), where apeglm performed similarly to limma and edgeR which had decent concordance at ranking genes. However, apeglm outperformed those two methods in terms of ranking genes on the Bottomly dataset with 10% of genes from the non-zero component (Supplementary Fig. S22). Finally, the differences were more moderate at the extreme of 20% of genes coming from a non-zero, large positive LFC component (Supplementary Figs S23 and S24). Overall, we showed that apeglm still performed well with violation of the unimodal distribution assumption, with mean error close to limma and edgeR while having high concordance in ranking genes by effect size.

apeglm was developed in a general manner such that it can be extended to generic likelihoods, in addition to the NB likelihood that has been used so far. We considered using apeglm with Zero Inflated NB (ZINB) generated data and likelihood. We used the splatter Bioconductor package (Zappia et al., 2017) to simulate datasets with additional zeros beyond what would be expected with a NB distribution. We simulated 100 cells in the following partitions: (20, 20, 60), (30, 30, 40) or (50, 50). We focused the evaluation on the comparison of the first two groups which have the same sample size. We considered the proportions of genes that are differentially expressed across all three groups in the range 1, 5 or 10%. The estimation of the zero component was performed upstream of apeglm using the methods described in Van den Berge et al. (2018) and the zinbwave Bioconductor package (Risso et al., 2018), and was either used to define zero weights or as input to a ZINB likelihood. The zero weights can be used to isolate the contribution to the counts from the NB component; and therefore, potentially remove bias due to ‘technical zeros’. We compared performance of the following approaches: the simple ratio of average scaled count after adding a pseudocount of 0.1, a ratio of weighted average scaled counts after adding a pseudocount of 0.1, the MLE from DESeq2 taking into account the zero weights, usage of the Normal prior in DESeq2 with a weighted NB likelihood, apeglm with weighted NB likelihood, and apeglm with a ZINB likelihood. We assessed the Pearson correlation of estimates to truth, the MAE for the top 30 genes as ranked by the method, and the MAE for all genes (Supplementary Figs S25–S33). apeglm with both weighted NB likelihood function and ZINB likelihood function consistently had the smallest MAE (whether total or for the top 30 genes ranked by the method) across all the combinations of differentially expressed proportions and sample sizes. The two variations were equivalent, while the weighted NB likelihood approach was much faster, taking advantage of optimized C++ code for the NB likelihood in apeglm. The two apeglm variations outperformed the use of a Normal prior in DESeq2 in terms of MAE of the top 30 genes, when the percent of DE genes was 1 or 5%. The improvement in MAE from using Bayesian shrinkage was greatest for sample size 20 versus 20, moderate for 30 versus 30, and apeglm was comparable to weighted pseudocount and MLE approaches at 50 versus 50.

We finally assessed the consistency of the apeglm estimator, by considering bulk RNA-seq simulated datasets with large sample sizes (30 versus 30 and 50 versus 50). Here we expect that the relative advantage of Bayesian shrinkage for ranking genes will be reduced, as the posterior estimators converge to the MLE. We again produced simulated bulk RNA-seq data modeled on the Pickrell dataset (Fig. 5) and the Bottomly dataset (Supplementary Fig. S34). Across all methods, the MAE becomes much lower, and the concordance of gene ranks much higher. As seen previously, apeglm is one of the top performing methods, although the advantage over non-shrinkage based methods, limma and edgeR is reduced. This convergence is expected, and the large sample size analysis is mostly useful for assessment that the apeglm estimator is consistent—that it converges to the true, simulated value as the sample size increases. edgeR-PC5 performs worst in these large sample size cases than previously, as the large prior count is no longer necessary to stabilize the non-shrinkage estimators. Supplementary Figure S35 provides the MAE over the mean of counts for the large sample size simulations.

Fig. 5.

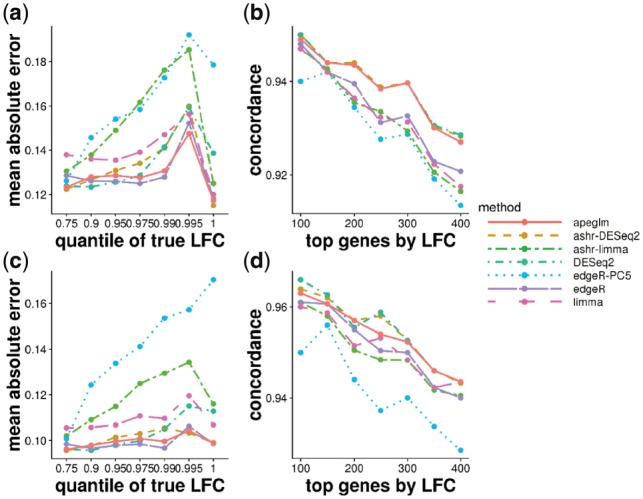
MAE plot over LFCs (left) and CAT plots (right) of simulation dataset (top row, 30 versus 30 and bottom row, 50 versus 50) modeled on estimated parameters from the Pickrell et al. (2010) dataset. Each point represents the average over 10 repeated simulations

The simulations in this article allowed an exploration of performance of various LFC estimators across sample size and for the case of relatively large dispersion values (Pickrell dataset) and relatively small dispersion values (Bottomly dataset). Across all simulated datasets, apeglm was the top performing method in balancing low MAE with high concordance when ranking genes by their true, simulated effect size. By process of elimination, DESeq2 and ashr in some cases had high error for medium to large effect sizes, limma and edgeR had low concordance in ranking genes, and edgeR-PC5 had high error for the large sample size cases, while apeglm demonstrated reliable estimation of LFCs throughout.

3.8 Evaluation on cell line mixture experiment

We additionally evaluated the relative performance of apeglm using a cell line mixture RNA-seq dataset designed for benchmarking (Holik et al., 2017). In this study, the investigators chose two cell lines from the same type of lung cancer, and grew the cell lines (NCI-H1975 and HCC827) as three biological replicates, then mixed the RNA concentrations from each of these replicates at five pre-specified proportions (100:0, 75:25, 50:50, 25:75, 0:100%). Following the notation of their paper, we use 100, 075, 050, 025 and 000 to represent the proportions. We used for evaluation the 15 normally processed samples prepared with Illumina’s TruSeq poly-A mRNA kit. We compared two groups of mixtures, each with three independent replicates: 075 versus 025 and 050 versus 025. We found the 100 versus 000 and 000 versus 100 mixtures were highly influenced by the 100 and 000 samples, which would be used both for estimation and for evaluation. We computed the estimation error as in Holik et al. (2017) as the difference between the LFCs estimated by each method using two groups of samples and the LFCs predicted by a non-linear model fit to all 15 samples, using the fitmixture function in the limma package.

The distribution of true LFCs for the 075 versus 025 and 050 versus 025 are bounded by $[{\hspace{0.17em}\text{log}\hspace{0.17em}}_2(1/3),{\hspace{0.17em}\text{log}\hspace{0.17em}}_2(3)]$ and $[{\hspace{0.17em}\text{log}\hspace{0.17em}}_2(2/3),{\hspace{0.17em}\text{log}\hspace{0.17em}}_2(2)]$, respectively, and so instead of considering the top ranked genes, we considered two plots to assess the accuracy of LFC estimation: once binning by true LFCs and once binning by estimated LFCs (Fig. 6). ashr with DESeq2 input and apeglm had higher MAE when binning by true LFCs, but had the lowest MAE when binning by estimated LFCs, which reveals that shrinkage did induce a bias, but protected against outputting large and unreliable LFCs. limma and edgeR had the opposite performance: low MAE when binning by true LFCs, but high MAE when binning by estimated LFCs. DESeq2 and ashr with limma input had mixed performance. In this experiment, edgeR-PC5 tended to have consistently low MAE, though we note that the sample size for the cell line mixture experiment was three per group, and we found that the relative bias of the prior count approach increased with sample size (Fig. 5).

Fig. 6.

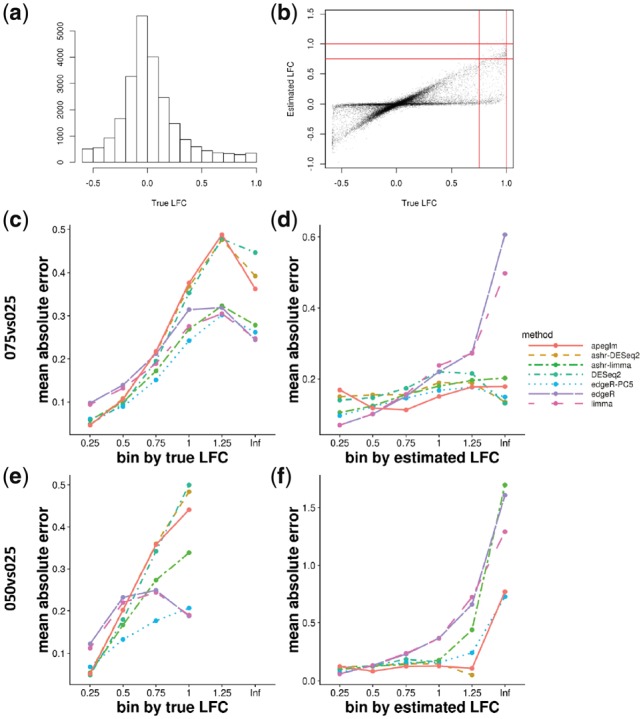
(a) The distribution of the true LFCs for comparison 050 versus 025, where the true LFCs is predicted with the fitted non-linear model. (b) Scatter plot of estimated LFCs from apeglm over true LFCs for comparison 050 versus 025. The vertical and horizontal lines indicate the two type of bins that were used for stratifying estimation error. (c and d) MAE plot binned by true LFCs and by estimated LFCs for comparison 075 versus 025 (e and f) MAE plot binned by true LFCs and by estimated LFCs for comparison 050 versus 025

4 Discussion

Here we compared various shrinkage estimators for LFCs in DE analysis of RNA-seq counts. RNA-seq experiments often have limited number of biological replicates in each condition group, typically in the range of 3–5. It is particularly difficult to estimate LFCs for genes with low counts or high coefficient of variation with such a small number of replicates. We examined methods for mitigating this problem of LFC estimation, and find that common filtering rules may lead to loss of DE genes. On the other hand, we found that existing methods for shrinking LFC estimates, such as DESeq2, may overly shrink those genes with very large LFCs, although the ranking was not greatly impaired. To reduce the shrinkage of large effect sizes that occurred using a Normal prior, we substituted an adaptive Cauchy prior, which has sufficient probability density in the tails of the distribution to allow for very large effects. The resulting estimator both reduced the variance associated with LFC estimates across the range from low to high counts, and also preserved true large LFCs.

We have shown the utility in an adaptive, heavy-tailed prior for high-throughput experiments in which an effect size is estimated over tens of thousands of features. The results presented here have focused on the task of estimating the LFCs in RNA-seq experiments, using an NB likelihood, but the software and methods are written in a general way, and in general, the use of the adaptive Cauchy prior may be adapted to other likelihoods and settings. The apeglm method accepts arbitrary likelihoods, as long as additional parameters are pre-specified, such as the dispersion. apeglm can therefore also be extended for use on other types of data, as long as it can be modeled by a GLM. For example, our method can be applied to allele-specific expression count data using a beta-binomial likelihood, as shown in the apeglm package vignette.

Providing low variance posterior mode effect sizes and their posterior SD allows for various downstream uses, for example, plotting LFC estimates from two experiments against each other in a scatter plot, without having to make arbitrary filtering decisions that would have to apply to both datasets. In another context, the effect sizes of genetic variants across many different traits can be systematically correlated to one another to suggest potential relationships between the traits (Pickrell et al., 2016). Such an analysis could benefit from shrunken estimates of effect size, to avoid hard filtering rules and to not have the correlations overly influenced by imprecise estimates.

The computation of the approximate posterior provides useful aggregate statistics, such as the FSR and s-value proposed by Stephens (2017), and the FSOS rate, which allows the user to define a range of effect sizes of biological significance. We note that, while the use of specific prior counts works well for providing point estimates of effect size for certain sample sizes and mean-variance relationships, it is difficult to choose a value that will work well for all datasets. For example, if one considers unique molecular identifiers (Kivioja et al., 2012) and the counts produced following de-duplication in such an experiment, the information content of a low count can be much higher than in standard RNA-seq experiments without de-duplication, and so filtering rules and prior counts would need to be re-considered and manually adjusted for such a dataset. A Bayesian procedure for shrinkage of effect sizes, which takes statistical information into account, is desirable across different types of high-throughput datasets.

5 Availability

apeglm is implemented as an R package and is available as part of the Bioconductor project (Huber et al., 2015), at the following address: http://bioconductor.org/packages/apeglm. A single function apeglm is used to estimate the LFCs in the package, which takes a data matrix, a design matrix and a user-defined likelihood function as input. The function will return a list of estimated LFCs and corresponding posterior SDs, interval estimates, and arbitrary tail areas of the posterior. The apeglm package comes with a detailed vignette that demonstrates the functions in the package on a real RNA-seq dataset. The apeglm shrinkage estimator for RNA-seq can also be easily accessed from the DESeq2 package, using the lfcShrink function. The R code used in this paper for evaluating methods is available at the following repository: https://github.com/mikelove/apeglmPaper

6 Software versions

The following versions of software were used: REBayes 1.3, DESeq2 1.20.0, edgeR 3.22.3, limma 3.36.1, ashr 2.2-7 and apeglm 1.2.1.

7 Accession numbers

The datasets analyzed during this study are available in the ENA, GEO, or SRA repositories: Schurch et al. (2016)https://www.ebi.ac.uk/ena/data/view/PRJEB5348, Holik et al. (2017)https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi? acc=GSE86337, Pickrell et al. (2010)https://trace.ncbi.nlm.nih.gov/Traces/sra/? study=SRP001540, Bottomly et al. (2011)https://trace.ncbi.nlm.nih.gov/Traces/sra/? study=SRP004777.