Neuronal Correlates of Tactile Working Memory in Prefrontal and Vibrissal Somatosensory Cortex

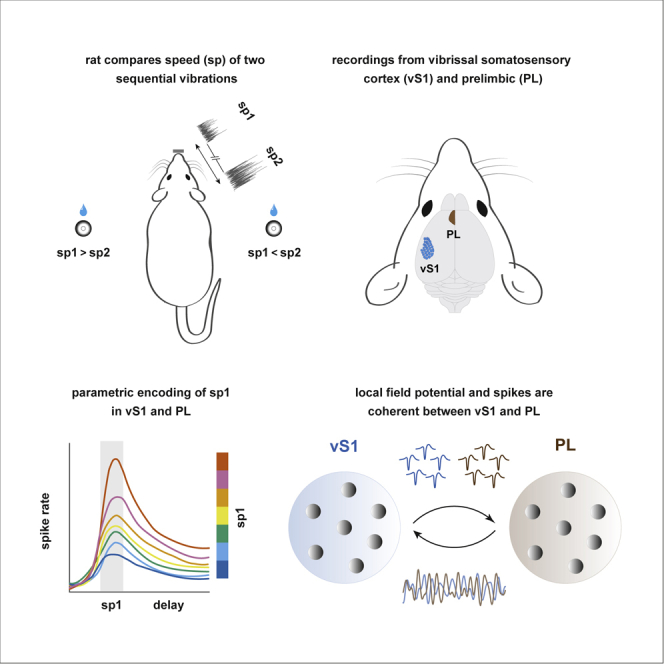
Summary

Tactile working memory engages a broad network of cortical regions in primates. To assess whether the conclusions drawn from primates apply to rodents, we examined the vibrissal primary somatosensory cortex (vS1) and the prelimbic cortex (PL) in a delayed comparison task. Rats compared the speeds of two vibrissal vibrations, stimulus1 and stimulus2, separated by a delay of 2 s. Neuronal firing rates in vS1 and PL encode both stimuli in real time. Across the delay, the stimulus1 representation declines more precipitously in vS1 than in PL. Theta-band local field potential (LFP) coherence between vS1 and PL peaks at trial onset and remains elevated during the interstimulus interval; simultaneously, vS1 spikes become phase locked to PL LFP. Phase locking is stronger on correct (versus error) trials. Tactile working memory in rats appears to be mediated by a posterior (vS1) to anterior (PL) flow of information, with performance facilitated through coherent LFP oscillation.

Graphical Abstract

Highlights

• •Rats compared the speeds of two sequential vibrissal vibrations, separated by 2 s
• •Neurons in the primary somatosensory (vS1) and prelimbic (PL) cortex coded the stimuli
• •Theta local field potential coherence between vS1 and PL peaked at trial onset
• •Intracortical coherent oscillations may play a role in rat tactile working memory

Esmaeili and Diamond show that tactile working memory in rats engages neuronal firing in the primary somatosensory cortex (vS1) and prelimbic cortex (PL), both in real-time stimulus coding and in the short-term memory trace. Theta-band local field potential oscillations become coherent between vS1 and PL at trial onset.

Introduction

Working memory (WM), the storage of information across a limited time interval in order to guide behavior, is a cognitive operation executed countless times each day, yet the precise neuronal mechanisms underlying this operation are not fully understood. In the case of parametric sensory WM, the stored information is graded along some continuous scale; the stimuli are not defined by category or distinct identity. Pioneering studies of parametric sensory WM, in which monkeys compared the frequencies of two fingertip vibrations separated with a delay (denoted stimulus1 and stimulus2), revealed the involvement of a network of regions ranging across primary somatosensory cortex (S1), secondary somatosensory cortex (S2), dorsolateral prefrontal cortex (dlPFC), premotor cortex (PC), and motor cortex (M1) (Hernández et al., 2000, Hernández et al., 2002, Romo et al., 1999, Romo et al., 2002). Neurons in S1 were involved in the real-time processing of stimuli, showing only a negligible memory trace of stimulus1. S2 neurons showed a brief trace of the just-concluded stimulus1, and neurons in dlPFC and PC showed a pronounced role in WM and in the comparison of stimulus1 and 2 during the second stimulus (Romo and Salinas, 2003).

In this study, we use a paradigm similar to the primate vibrotactile discrimination adapted to rats to investigate the neuronal correlates of parametric sensory WM. Although rats are the preferred models for a vast array of neuroscientific issues, they are particularly “expert” in the vibrissal tactile modality. The whisker sensorimotor system is an active, information-seeking system (Diamond and Arabzadeh, 2013, Zuo et al., 2011). Rats, in the “receptive mode”—where they suppress whisking and place their immobile whiskers on an object—can detect deflections as small as 3 μm (Lee et al., 2016). In the paradigm used here, rats operate in this receptive mode, and their WM capacity and acuity in stimulus discrimination overlaps the performance demonstrated by humans (Fassihi et al., 2014, Fassihi et al., 2017).

As candidate regions for participation in tactile WM, we have targeted the vibrissal primary somatosensory cortex (vS1) and the prelimbic area (PL). Rat PL has been implicated in cognitive processes such as WM, and may be homologous with primate dlPFC (Eichenbaum et al., 1983, Gabbott et al., 2003, Kolb, 1990, Preuss, 1995, Uylings et al., 2003, Vertes, 2004, Vertes, 2006). PL lesions produce pronounced deficits in delayed response tasks (Brito and Brito, 1990, Delatour and Gisquet-Verrier, 1996, Delatour and Gisquet-Verrier, 1999, Delatour and Gisquet-Verrier, 2000, Floresco et al., 1997, Ragozzino et al., 1998, Seamans et al., 1995), similar to those seen with lesions of the dlPFC in primates (Barbas, 1995, Barbas, 2000, Goldman-Rakic, 1994, Groenewegen and Uylings, 2000, Kolb, 1984). If PL is homologous with primate dlPFC, we would expect to find neurons that encode stimulus1 and store relevant information during the interstimulus delay period.

We confirm the participation of vS1 and PL in tactile WM using multi-electrode extracellular recordings and then ask an additional question: how do these distant brain regions communicate? Local field potential (LFP) coherence has been hypothesized to be an important mechanism for optimizing the efficiency of communication between connected brain areas (Engel et al., 2001, Fries, 2005, Grion et al., 2016, Varela et al., 2001). Thus, we examine the evidence for coherence between the two regions in simultaneously recorded LFPs.

Results

Tactile Working Memory Task

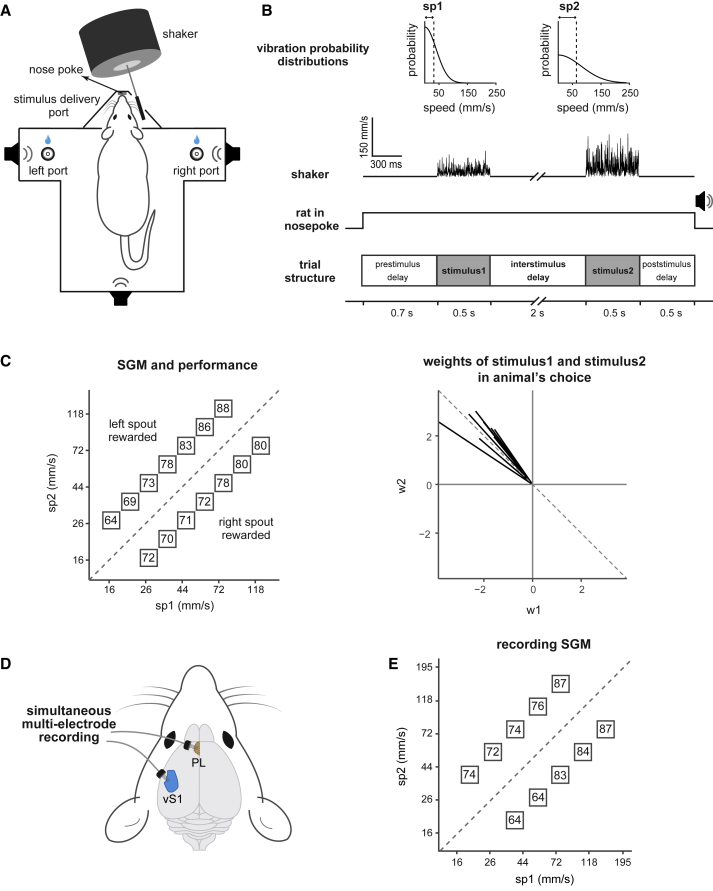
We trained eight rats to perform a tactile working memory task (Fassihi et al., 2014, Fassihi et al., 2017) and then correlated their working memory performance with activity in vS1 and PL. The rat placed its snout in a nose poke to initiate a trial (Figure 1A). After a prestimulus delay (0.7 s), two sequential tactile stimuli (each of 0.5-s duration), separated by an interstimulus delay (2 s), were delivered to the whiskers on the right side of the snout (Figure 1B). The two vibrations, stimulus1 and stimulus2, were sequences of speed values sampled from a half-Gaussian distribution. A single vibration is thus defined by its nominal mean speed, denoted as sp. The rat withdrew upon presentation of an auditory go cue after stimulus2. It selected one of the two spouts, with reward location determined by the relative mean speeds, sp2 > sp1 or else sp2 < sp1.

Figure 1.

Vibration Discrimination Task and Working Memory Performance

(A) Schematic of the behavioral setup.

(B) Speed probability distributions of stimulus1 and stimulus2 (top); dashed lines show sp1 and sp2. Timeline of vibration discrimination task (bottom).

(C) Stimulus generalization matrix and working memory performance. (Left) The [sp1, sp2] in each trial was taken from one box. On each box, average performance across 8 rats for that stimulus pair is shown. Sessions from last month of training before electrode implantation are included in this plot. (Right) Weights of stimulus1 and stimulus2 regressors in animal choice are represented by w1 and w2. Each (w1, w2) vector represents data from one rat.

(D) Schematic showing the simultaneous recordings from vS1 and PL.

(E) SGM set used during the recording sessions with reduced difficulty compared to training set (normalized speed difference = 0.33 as compared to 0.25 for training set in [C]). On each box, average performance across the same rats of (C) during the recording session is shown.

See also Figure S1.

To encourage rats to generalize the comparison rule, rather than developing alternative strategies, such as attending to just one of the two stimuli, they were trained with a stimulus generalization matrix (SGM). The SGM consisted of [sp1, sp2] pairs covering a wide range of speed values (Figure 1C) such that any strategy alternative to stimulus1 versus stimulus2 comparison would lead to performance approaching the chance level. Figure 1C shows the performance for each stimulus pair, as percent correct, averaged across all rats. On average, rats performed well in all SGM pairs with a tendency to perform better for higher-speed stimuli. This could be due to a phenomenon known as “contraction bias,” where the memory trace of stimulus1 shifts toward the prior of previous stimuli (Akrami et al., 2018). Weak stimuli might be below the threshold for many sensory neurons and thus would be encoded by a smaller population than strong stimuli. Thus, a less robust signal is put into short-term storage, allowing the bias from previous stimulus history to have a stronger effect.

As a further control to show that rats truly performed a sensory delayed comparison task, we weighed the contributions of each of the two stimuli to the rats’ decision by computing w1 and w2 regressors that best quantified the relative weight of stimulus1 and stimulus2, respectively, in the rat’s choice (see STAR Methods). w1 and w2 regressors for all rats are illustrated in Figure 1C, right panel. An ideal performer—one who precisely encodes both stimuli and then accurately judges the difference between them—would yield w1 = −w2, corresponding to the dashed line. All the (w1, w2) vectors lie close to the dashed line, indicating that all rats gave nearly equal (but opposite) weights to stimulus1 and stimulus2.

Representation of the Ongoing Stimulus in vS1 and PL

Rats’ performance relied on a sequence of operations: encoding stimulus1; storing the stimulus1 memory; encoding stimulus2; comparing it to the stimulus1 memory; and executing an action according to the reward rule. How do sensory and frontal cortexes contribute to these operations? After rats were well-trained, we recorded the activity of neurons in vS1 and, simultaneously, PL (Figure S1). Microwire arrays comprising 16 or 32 electrodes were implanted in the brain of each animal (one array per area; Figure 1D). In the recording sessions, we used a stimulus set with reduced difficulty (normalized speed difference = 0.33, compared to 0.25 outside of recording sessions). Performance was similar to that observed prior to electrode implantation (Figure 1E).

To examine the representations in vS1 and PL of stimulus1 and stimulus2 during real-time stimulus processing, we first grouped the trials based on the sp1 (from trial start until the end of interstimulus delay) and then based on sp2 (from stimulus2 onset until trial ending). We computed time-dependent firing rates for each stimulus condition (see STAR Methods). For the initial analysis, only trials with correct choice were included.

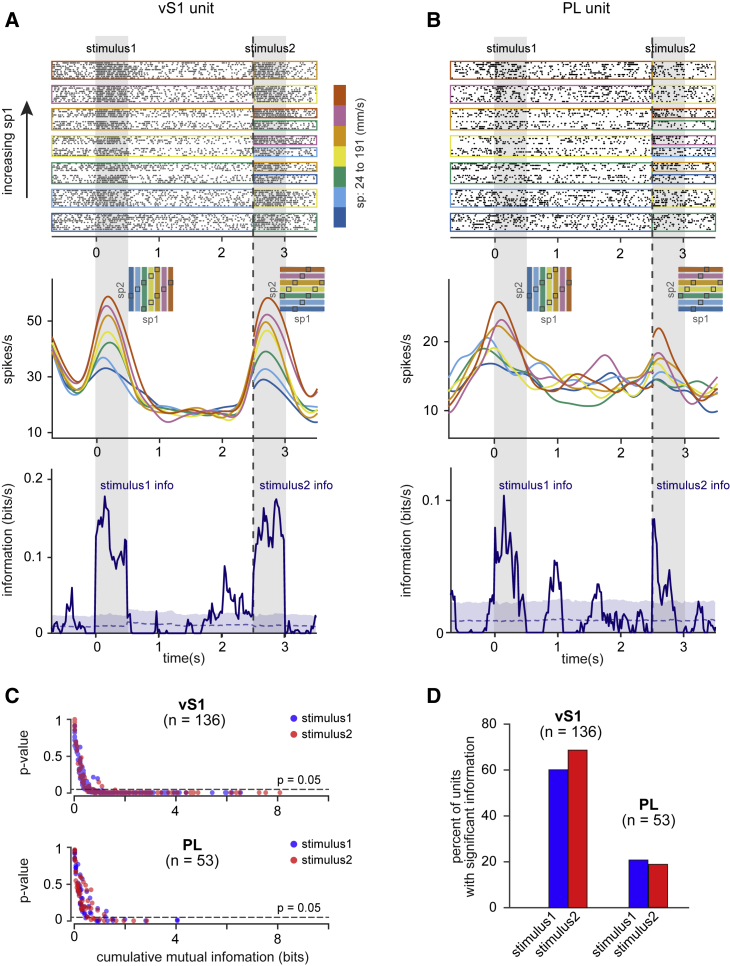
Figure 2A illustrates the raster plot (top panel) and firing rate (middle panel) of an example unit in vS1 whose discharge rate was positively correlated with the values of sp1 and sp2 during stimulus1 and stimulus2 epochs, respectively, but was uncorrelated during the interstimulus delay.

Figure 2.

Encoding of Ongoing Stimuli

All plots aligned to the beginning of the first stimulus (t = 0). Gray vertical bars mark stimulus1 and stimulus2 vibrations.

(A) (Top) Example raster plot of a vS1 unit. Trials are sorted and grouped by stimulus1. Color boxes demonstrate the trials with same sp1 until the termination of the delay (vertical dashed line); thereafter, they depict sp2 equal trials. (Middle) Mean firing rate of the neuron for each stimulus condition is plotted across time. The insets illustrate the grouping of the trials on the SGM. (Bottom) For the same neuron, time course of conditional MI between the firing rate of the neuron and stimulus is shown. From the beginning of the trial until the end of interstimulus delay period (vertical dotted line), information about stimulus1, MI(sp₁;fr|ch), is depicted; thereafter, information about stimulus2, MI(sp₂;fr|ch), is plotted. Blue dotted curve and blue band show mean ± SD information resulted from the shuffled distribution.

(B) Similar to (A) but for an example PL unit.

(C) Scatter plot of cumulative stimulus information in vS1 and PL neurons during the presentation of each stimulus versus p values for the test of significance of information. Significance of information during stimulus1 and stimulus2 for each unit is examined by comparing the observed cumulative information to shuffled distribution.

(D) Percentage of units with significant cumulative information (p < 0.05) about the ongoing stimuli in each cortical region. In 7 out of 8 rats, the recordings were performed simultaneously from both regions; units come from one recording session per rat in vS1 (n = 7 rats) and PL (n = 8 rats). The same data are used in Figures 3, 4, and 5.

See also Figure S2.

In addition, we calculated the mutual information (MI) between the trial-by-trial firing rate of each neuron and sp1 or sp2. Because firing might depend not only on the stimulus but also on the choice, we quantified pure stimulus-dependent information by making the measure conditional on the rat’s choice. Specifically, to measure MI between firing rate and stimulus1, we compared neuronal responses to different values of sp1 for a given choice (ch) at the conclusion of the trial, i.e., MI(fr, sp1|ch). For stimulus2, in a similar manner, we computed MI(fr, sp2|ch). The example vS1 unit in Figure 2A carried significant information (bottom panel) during all epochs of stimulus1 and stimulus2 (non-parametric permutation tests; p < 0.05). At the end of the delay interval, neuronal firing rate was briefly anticorrelated with sp1 (higher firing rate for lower sp), carrying significant information for about 300 ms. Stimulus coding during the delay is detailed later.

Figure 2B shows the raster plot, time-dependent firing rate, and MI for an example PL unit. This neuron also encoded the ongoing stimuli in its firing rate, especially during the early phases of stimulus1 and stimulus2.

We defined cumulative MI values as the sum of all the MI values within a given epoch and used non-parametric tests to assess whether cumulative MI was significant. Figure 2C shows the cumulative MI values for all the units in vS1 (top) and PL (bottom) and the p values of the significance test; Figure 2D shows that 60% of vS1 units carried significant MI in their mean firing rate during stimulus1 and 69% during stimulus2 (n = 136; non-parametric permutation test; p < 0.05). In PL, 21% of units carried significant stimulus1 MI and 19% stimulus2 MI (n = 53; non-parametric permutation test; p < 0.05), indicating the presence of a robust sensory representation in this frontal cortical region.

Memory of Stimulus1

As seen above, vS1 and PL both carried signals about the vibrissal vibrations in real time. To assess their contributions to the storage of the memory of stimulus1 during the retention interval, we quantified the stimulus-related activity of neurons during the delay period using the same method applied to real-time activity.

Figure 3 illustrates two example neurons, one in vS1 and one in PL, that represented stimulus1 both during stimulus presentation and during some parts of the delay period. The vS1 neuron (Figure 3A) encoded the first stimulus in real time in a graded manner, firing at a higher rate for larger values of sp1 (top and middle panels). Memory of sp1 was present in this unit’s firing rate, but the sign of coding was reversed: the unit fired at a higher rate for smaller sp1 during the “early delay” (labeled ED, from offset of stimulus1 until 500 ms into the delay period), “mid delay” (labeled MD, from 750 ms to 1,250 ms into the delay period), and “late delay” (labeled LD, from 1,500 ms after stimulus1 to end of the delay period), leading to significant values of MI during each of the three delay epochs (bottom panel). The neuron also robustly encoded stimulus2. The PL neuron (Figure 3B) reliably encoded stimulus1 through a positive correlation between sp1 and firing rate (top and middle panels) in real time and during the ED and MD epochs of retention interval. The neuron also robustly encoded stimulus2. The positive correlations between sp and firing rate were evident in values of MI across the trial (bottom panel).

Figure 3.

Memory of Stimulus during Interstimulus Delay

(A) Example raster plot (top), time-dependent firing rate (middle), and stimulus information plot (bottom) of a vS1 unit encoding the memory of stimulus1 in parts of the delay period. Plots are in the same format as Figures 2A and 2B. Colored bars mark early delay (ED) (first 500 ms of interstimulus delay), mid-delay (MD) (middle 500 ms of interstimulus delay), and late delay (LD) (last 500 ms of interstimulus delay) epochs as well as the post-stimulus2 (500-ms window following stimulus2).

(B) Same as (A) but for an example PL memory unit.

(C) Scatter plot showing the cumulative stimulus information versus p value of the test of significance of information. Significance of information is examined by comparing the observed cumulative information during each epoch to shuffled distribution for individual units.

(D) Percentage of memory-encoding units in each cortical region during different epochs of the interstimulus delay period and post stimulus2.

See also Figure S2.

We calculated the percentage of stimulus1 memory-encoding units during the three 500-ms interstimulus delay windows defined above—early, mid, and late delay. Figure 3C shows the cumulative MI values for all the units in vS1 and PL during each of the 3 windows and the p values of the significance test. In vS1, 32% of units encoded stimulus1 in the ED compared to 17% percent in PL (n = 136 units in vS1; n = 53 units in PL; non-parametric permutation test; p < 0.05; Figure 3D). During the MD period, 10% of units in vS1 and 9% of units in PL held the memory of stimulus1 in their firing rates. Finally, in the LD period, only 12% of units in vS1 and 8% of units in PL stored the stimulus1 memory. We further assessed the degree of retention of sensory signals during the delay relative to real-time encoding of stimulus. In vS1, the degree of retention was 54%, 17%, and 20% during early, mid, and late delay, respectively, and in PL, the degree of retention was 81%, 43%, and 38% across the same three periods. The degree of retention of sp2 in the post-stimulus2 window in both vS1 and PL was slightly lower compared to ED period (49% and 70%, respectively); the potential significance of stimulus2 memory will be considered in the Discussion. Interestingly, PL neurons during the delay period carried quantities of MI about stimulus1 similar to those found during real-time encoding of the stimulus, and vS1 MI values were typically higher during real-time stimulus 1 encoding (Figures S2C and S2D).

Next, we asked whether single neurons tended to carry the same form of signal consistently throughout the trial or whether neurons carried signals only during specific epochs. We quantified the percentage of neurons carrying significant information either during stimulus1 only, the interstimulus delay only, stimulus2 only, or in multiple epochs. In vS1, 69% of neurons (among those with significant signal at any time) showed significant MI in more than one window. In contrast, in PL, 32% of neurons (among those with significant signal at any time) had significant MI in more than one window (Figures S2A and S2B). These results suggest that, in vS1, overlapping populations of neurons encoded the stimuli at different epochs—there is a high degree of coding consistency—and in PL, different population of neurons encoded the stimuli in distinct epochs, suggesting that their functions might be tuned for specific operations comprising task.

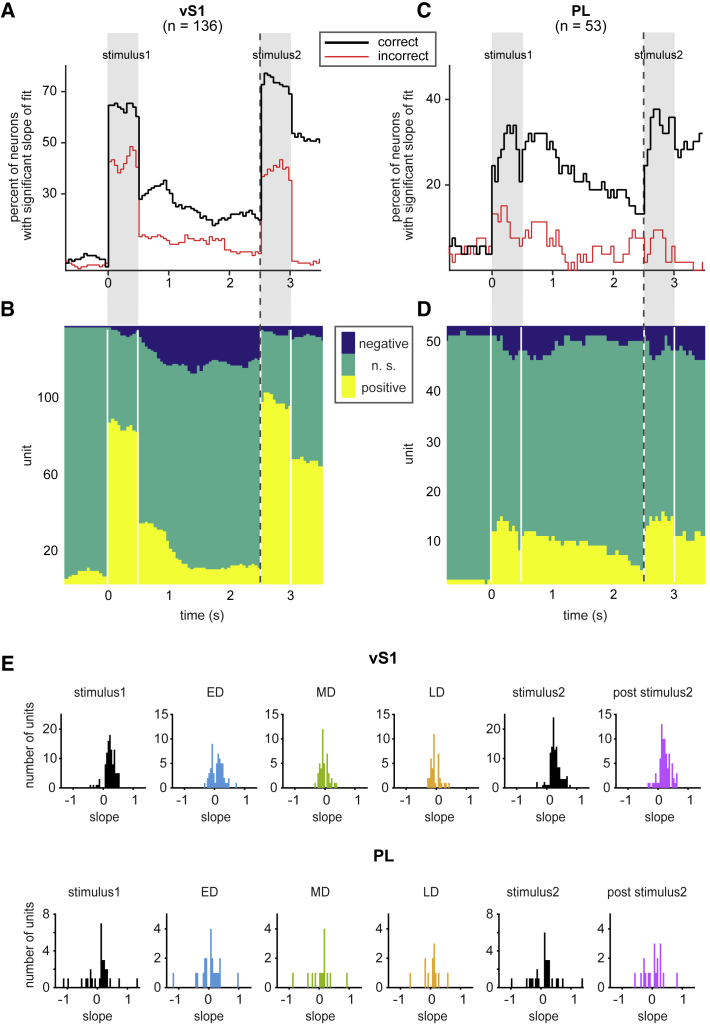
Parametric Coding of the Stimulus

Next, we investigated what proportion of vS1 and PL neurons, on correct trials, exhibited a parametric sp coding, that is, progressive steps in firing rate associated with progressive steps in sp. We employed a generalized linear model (GLM) to quantify the time-dependent correlation between the firing rate of vS1 and PL units and sp in a sliding window (see STAR Methods and Figure S3). Figure 4A, black trace, illustrates the percentage of neurons in vS1 with significant slopes of fit across time. During stimulus1 and stimulus2, 64% and 74% of neurons, respectively, had a significant slope of the fit. Figure 4B shows that most of these neurons encoded the ongoing stimulus by a significantly increased discharge rate for larger values of sp1 (96% of neurons with significant slope); a negligible proportion had a significantly decreased discharge rate for larger values of sp1 (4% of neurons with significant slope). We refer to the two forms of correlation as positive and negative coding, respectively.

Figure 4.

Correct versus Incorrect Trials and Monotonic Coding of Stimuli

(A) Fraction of units in vS1 with significant linear encoding of stimulus. The black curve shows the percentage of stimulus encoding neurons during correct trials. The red curve shows the percent significant during incorrect trials.

(B) Number of units that positively (yellow) or negatively (blue) encoded stimulus in vS1. Units with no significant linear encoding are shown in green.

(C) Same as (A) but for PL units.

(D) Same as (B) but for PL units.

(E) Histogram of distribution of mean slope of the fit at different trial epochs for vS1 (top) and PL (bottom) units. Only units with significant slope of the fit are included.

See also Figure S3.

Using a similar experimental design in monkeys, only a negligible proportion of primary somatosensory cortex neurons carried signals about stimulus1 during the delay (Hernández et al., 2000). If vS1 function were fully homologous to primate somatosensory cortex, one would expect no significant trace of the first stimulus in vS1 during the delay. On the contrary, we found that, in the ED, firing rate for 32% of neurons showed parametric stimulus coding (Figure 4A). This percentage decreased gradually and reached 22% at the end of the delay period. The predominance of positive coding in vS1 decreased across the delay (Figures 4B and 4E). Early in the delay, 68% of neurons with significant slope showed positive coding, although at the end of the delay, negative coding was more common (67%).

In PL, 28% of neurons showed real-time parametric coding on correct trials (Figure 4C, black trace). 73% of these showed positive coding during stimulus1 (Figure 4D). Thus, PL did not exhibit the preponderance of positively stimulus-speed-correlated neurons found in vS1.

At the beginning of the delay, 31% of PL neurons showed significant slopes, indicating that similar numbers of neurons represented the ongoing stimulus and kept the memory trace, at least in some parts of delay period. This percentage decayed gradually to 16% at the end of the delay interval. The ratio of neurons with positive versus negative slope did not vary systematically across the delay period. vS1 units had larger slopes during stimulus1, stimulus2, and ED epochs compared to PL units, while slopes were comparable during MD and LD (Figure 4E).

If vS1 and PL are part of the network supporting this working memory task, then erroneous choice should be associated with the incorrect encoding of stimulus1, incorrect storage of stimulus1, or incorrect encoding of stimulus2. To test this prediction, we used a sliding window to quantify across time the fraction of units in each area that exhibited a parametric encoding of stimulus speed on incorrect trials (see Figure S3 for more details). In vS1 on incorrect trials (Figure 4A, red trace), a diminished proportion of units exhibited parametric coding during stimulus1 and stimulus2. During the delay, the fraction of neurons began at about 13% and declined to 5%–10%. In PL on incorrect trials (Figure 4C, red trace), as in vS1, a diminished proportion of units exhibited parametric coding during stimulus1 and stimulus2. During the delay, the fraction of neurons fluctuated near the chance level of 5%, suggesting that PL neurons carried a negligible stimulus1 memory on incorrect trials. In sum, the findings are consistent with the proposal that the rats’ errors might originate, at least in part, by absence—during stimulus presentation and/or during memory—of the graded stimulus representation present in correct trials.

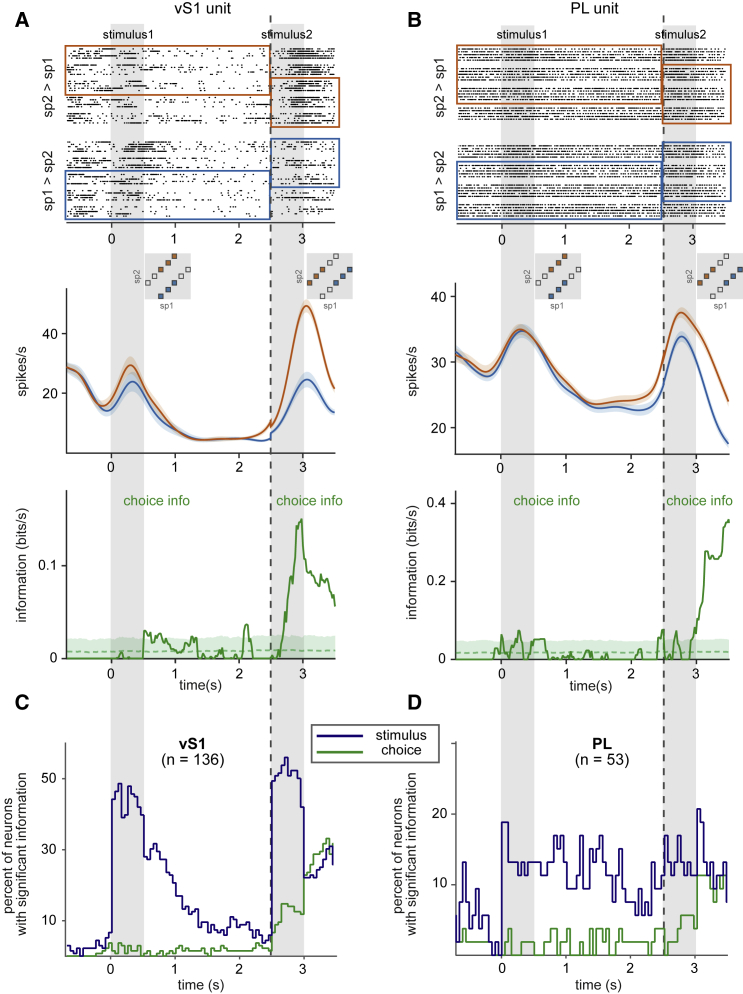
Representation of Choice

The final step in the task was to compare sp1 versus sp2 and to convert the stimulus relationship into a choice and action. We explored choice correlates in neuronal activity on correct trials (Figure 5). The SGM allowed us to dissociate choice from stimulus encoding information by considering distinct combinations during different epochs of the trial. Specifically, until the onset of stimulus2 (left side of dashed line), only trials in which the stimulus1 value could be followed by two different values of stimulus2 (and consequently two different actions) were considered; therefore, any information about choice in this period could not be explained by the value of stimulus1. After the onset of stimulus2, only trials in which the stimulus2 value could be preceded by two different values of stimulus1 were considered. Among the set of trials with a single value of stimulus2, differences in firing rate associated with choice could not be due to encoding of stimulus2 alone.

Figure 5.

Choice Encoding

(A) (Top) Example raster plot of a vS1 unit. Trials are grouped according to rat’s choice; only correct trials are included. Colored boxes demonstrate the parts of SGM that are included in the analysis (as also shown in the insets below the raster plots). Until the second stimulus, only trials with a stimulus1 that could be followed by two different stimulus2 values are considered; thereafter, trials with a stimulus2 that could be preceded by a smaller or larger stimulus1 are included. (Middle) Mean firing rate of the vS1 example unit for trials with sp2>sp1 is plotted in red and for trials with sp1 > sp2 is plotted in blue. Error bars show SEM. (Bottom) Time course of information for the same neuron is shown. Conditional MI between the firing rate of the neuron and rat’s choice is plotted. The green dotted curve and green band show mean ± SD resulted from the shuffled distribution.

(B) Similar to (A) but for a PL example unit.

(C) Percentage of vS1 units with significant information about animal choice (green) and stimulus sp (blue). Only correct trials are included.

(D) Similar to (C) but for PL units.

Raster plots and firing rates separated by the rat’s choice are illustrated for a vS1 neuron (Figure 5A) and a PL neuron (Figure 5B). The colored border in the raster plots (upper panel) groups together the trials from the stimulus pairs denoted by the same color in the SGM below; that is, the trials are sorted according to final choice. During and after stimulus2, the firing rates of these neurons (Figures 5A and 5B, middle panel) were modulated as a function of the rat’s choice.

To quantify these signals, we measured the conditional MI between neuronal firing rate and choice (Figures 5A and 5B, lower panel; see STAR Methods). From the start of the trial until the end of the delay period, we computed MI(fr,ch|sp1); from stimulus2 onward, we computed MI(fr,ch|sp2). Using this method, we could exclude spurious information caused by the inherent correlations between choice and stimulus1 and stimulus2 in the extreme pairs of the SGM. The two example neurons showed a rise in choice information during the occurrence of stimulus2, a signal which remained as the rat awaited the “go” cue.

Considering all neurons together on correct trials only (Figures 5C and 5D), in neither vS1 nor PL was there a significant choice-related signal (green traces) before the presentation of stimulus2, indicating no choice bias within this neuronal population. By contrast, many neurons carried sp information (blue traces) during stimulus1, the interstimulus delay, and during stimulus2. In vS1, a small but significant proportion of neurons carried information about choice soon after stimulus2 presentation began. The percentage increased during the post-stimulus delay and reached over 30% before the go cue was sounded. This suggests that vS1 in rats, similar to secondary somatosensory in primates, might participate in comparing stimulus1 and stimulus2 and the decision-making process.

Neurons in PL represented the animal choice mainly after the termination of the second stimulus. Around 10% of these neurons had choice information before the go cue was presented.

Phase Synchronization between vS1 LFP and PL LFP

How these spatially distant cortical areas, vS1 and PL, communicate with each other remains unclear. It has been proposed that coherent oscillation is one possible mechanism for mediating long-distance interaction (Fries, 2005, Grion et al., 2016). For instance, there are coherent oscillations between parietal and frontal cortices during the decision-making period in a vibration-delayed comparison task in primates (Nácher et al., 2013).

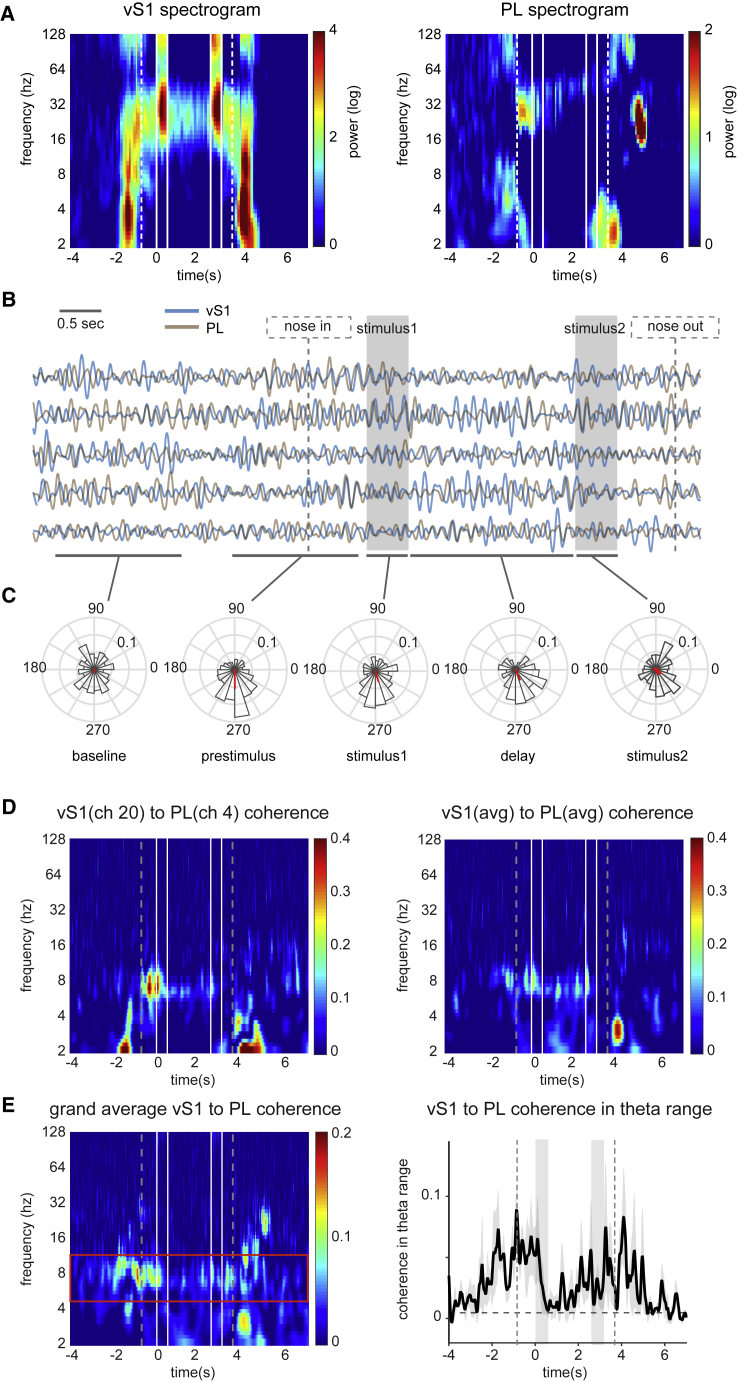
We first quantified LFP power from each area during the performance of the working memory task (Figure 6A). LFP power in vS1 increased in a wide frequency range, from 2 to 32 Hz, as the rat approached the nose poke, beginning almost 2 s before stimulus1 onset. In this period, PL LFP power also increased but was restricted largely to the theta range (5–12 Hz) and, just before stimulus1 onset, to a band around 30 Hz. In vS1, stimulus presentation was characterized by a sharp power increase in the range of 20–35 Hz, with weaker signals in the same range across the interstimulus delay. In PL, LFP did not exhibit prominent power during stimulus presentation or across the interstimulus delay. At the conclusion of stimulus2, LFP in vS1 again showed power in a wide range, resembling that before stimulus onset. In this period in PL, there was substantial LFP power at low frequencies, up to about 6 Hz.

Figure 6.

LFP Power Modulation and vS1-PL LFP Coherence

Data are aligned (t = 0) to the onset of the first stimulus. Dashed lines represent entry into the nose poke and go cue onset; solid lines (or gray shading in B and right of E) show onset and offset of stimuli.

(A) Average time-frequency maps of power modulation for vS1 (left) and PL (right) LFPs (n = 3 rats).

(B) Single-trial LFP traces (filtered in the theta range) of PL (brown) and vS1 (blue) overlaid.

(C) Histograms of the phase difference across different trials for the data in (B). Red vector shows amplitude and angle of the average phase shift across all trials. Phase difference at prestimulus period, during stimulus1, and during the interstimulus delay is significantly clustered in a consistent direction across trials, but not in the baseline period (p < 0.01; Rayleigh test of uniformity).

(D) (Left) Example time-frequency map of WPLI measure for two simultaneously recorded vS1 and PL channels. (Right) Average time-frequency WPLI map for the same animal across all vS1 and PL channels is shown.

(E) (Left) Grand average time-frequency WPLI map across animals (n = 3 rats). Red horizontal lines show theta band. (Right) Grand average coherence in the theta range (5–12 Hz) is shown.

Simultaneous recordings from vS1 and PL enabled us to investigate phase relationships between the LFP signals of the two regions. Selecting the theta frequency range, where LFPs in both regions were task modulated, we filtered the two LFP signals from multiple example trials and overlaid them (Figure 6B). In the baseline period (defined as 4.2–2.2 s before stimulus1 onset) the signals did not have any preferred phase relationship. The two signals became synchronized in the “prestimulus” period (defined as a 2-s window preceding stimulus1).

We quantified the phase relationship between the two LFPs in different behavioral epochs (Figure 6C). There was a consistent phase difference in the delay period immediately preceding stimulus1, during presentation of stimulus1, and during the interstimulus interval. In all these periods, PL led vS1 with a phase shift of about π/2. That the downstream region (PL) preceded the primary sensory cortical region (vS1) suggests that top-down, not stimulus-evoked, modulations might underlie the phase synchronization between the two areas.

We further quantified the phase synchronization between the two areas using a debiased weighted phase lag index, WPLI (Vinck et al., 2011). We measured coherence across the pair of LFP signals all over the time-frequency plane (Figures 6D and 6E). Figure 6D shows vS1 to PL coherence time-frequency map of one representative rat. Figure 6E shows that grand average coherence between the two LFP signals was most robust in the theta range. If coherence were a mechanism limited to facilitating the transfer of real-time information from sensory to prefrontal cortex, we would expect it to be highest during the presentation of stimuli, when relevant task-related information is present. Unexpectedly, theta coherence peaked during the prestimulus delay period as the rat anticipated stimulus1. Theta coherence also ramped up toward the end of the interstimulus period, just prior to stimulus 2 (Figure 6E). We interpret the high degrees of theta coherence in the prestimulus periods as reflecting preparatory or expectation mechanisms.

Phase Locking of vS1 and PL Spikes to LFP

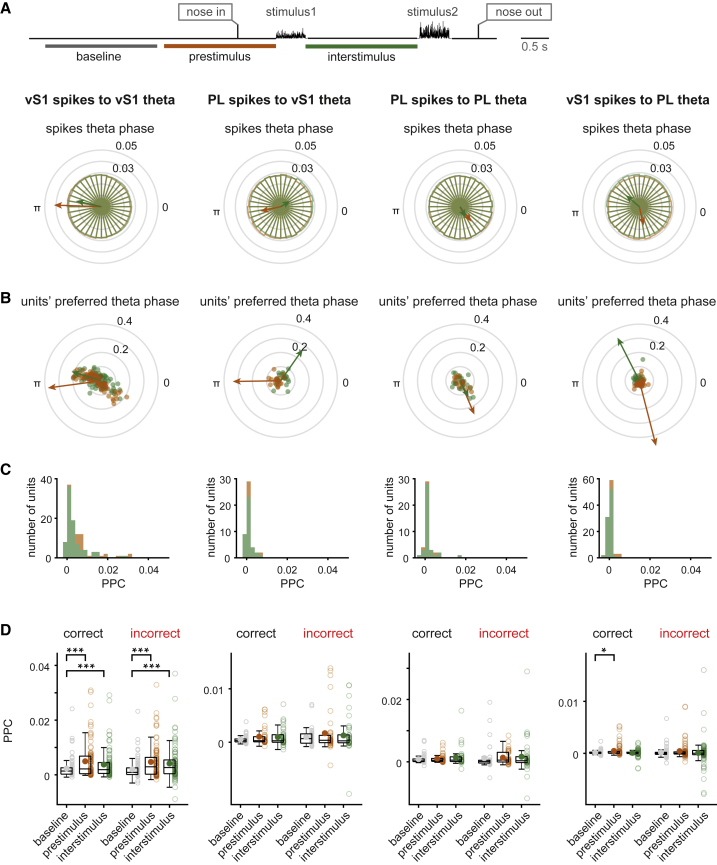
We then asked whether the enhanced theta coherence between the LFPs of vS1 and PL modulated spiking activity and consequently task performance. To address this question, we quantified intra- and inter-areal phase locking between spikes and theta by focusing specifically on the prestimulus and interstimulus delay periods. We defined prestimulus as a 2-s window immediately preceding stimulus1, covering the epochs of high LFP-LFP coherence. We examined phase locking of each unit to theta oscillation by testing the non-uniformity of phase distribution of spikes (during prestimulus and interstimulus windows) relative to the LFP theta (Rayleigh test; p < 0.05).

Within each window, entrainment of spiking activity with respect to theta from the same area or theta from the other area was tested in 3 ways. We first pooled spikes from all the significantly phase-locked units. Figure 7A shows the phase distribution of spikes relative to theta in bins of 10 degrees in brown and green for prestimulus and interstimulus windows, respectively. The preferred phase of all spikes is quantified as the circular mean of all angles, depicted with an arrow. Arrow length is proportional to the concentration parameter (κ) of the von Mises distribution (see STAR Methods). Overall, modulation of spikes was stronger in the prestimulus compared to the interstimulus window. Relevant κ values are in Table 1. The main finding is that, in both windows, vS1 and PL spikes were significantly modulated relative to vS1 theta (Figure 7A, first and second columns, respectively; p < 0.001; Rayleigh test), with vS1 spikes more concentrated around the preferred phase compared to PL spikes. PL and vS1 spikes were also modulated by PL LFP (Figure 7A, third and fourth columns, respectively; p < 0.001; Rayleigh test), but in contrast to vS1 LFP, the inter-areal concentration parameter was larger. This indicates that vS1 spikes in both windows were more concentrated around the mean preferred phase of PL theta than were PL spikes. All corresponding shuffled phase distributions were uniform (p > 0.05; Rayleigh test).

Figure 7.

Intra- and Inter-areal Spike-Theta Phase Locking

Coherence between spikes and theta during the prestimulus (−2 to 0 s from stimulus1) and interstimulus windows for each of the four pairwise vS1 versus PL comparisons (n = 3 rats).

(A) Polar plot of the distribution of spike phase relative to theta for vS1 spikes relative to vS1 theta (left panel), PL spikes relative to vS1 theta (second from left panel), PL spikes relative to PL theta (second from right panel), and vS1 spikes relative to PL theta (right panel). Spikes of all significantly phase-locked units during the prestimulus (brown) and interstimulus (green) windows are pooled. Only correct trials are included. The arrows indicate the mean preferred phase; length of the arrows is proportional to concentration of spikes around the mean direction.

(B) Mean preferred phase of significantly phase-locked units during prestimulus (brown) and interstimulus (green) windows for all 4 conditions. Arrows show the mean preferred angle across significantly modulated units for each window.

(C) The pairwise phase consistency (PPC) measure for all units for the same windows.

(D) Boxplots of PPC values comparing baseline (−4.2 to −2.2 s from stimulus1) to prestimulus and interstimulus for correct and incorrect trials. Circles show mean PPC value for each group. Asterisks represent significant difference (^∗ shows p < 0.05 and ^∗∗∗ shows p < 0.001; Wilcoxon signed rank test).

Table 1.

Prestimulus and Interstimulus Concentration Parameter (κ) and PPC

	vS1 Spikes to vS1 Theta	PL Spikes to vS1 Theta	PL Spikes to PL Theta	vS1 Spikes to PL Theta
κ for Spikes’ Phase Relative to Theta around the Mean Phase of All Spikes Pooled
Prestimulus	0.084	0.036	0.033	0.034
Interstimulus	0.046	0.020	0.021	0.031
κ for Units’ Preferred Phase Relative to Mean across All Significantly Modulated Units
Prestimulus	1.08	0.93	0.68	1.60
Interstimulus	0.57	0.72	0.33	0.94
Pairwise Phase Consistency (PPC)
Prestimulus	0.005 ± 0.007	0.001 ± 0.002	0.001 ± 0.001	0.000 ± 0.001
Interstimulus	0.004 ± 0.005	0.001 ± 0.002	0.001 ± 0.003	0.000 ± 0.001

As the second approach to quantifying spike-LFP coherence, we considered the preferred phase of each unit relative to theta. Figure 7B shows the significantly modulated units (Rayleigh test; p < 0.05) during prestimulus as brown dots and during interstimulus delay as green dots; the angle indicates units’ preferred phase, and the distance from center corresponds to κ. The grand average preferred direction among all units is shown by arrows. The resulting grand average among significantly modulated units, for all conditions, was consistent with the results obtained previously by pooling all spikes (Figures 7A and 7B). The lengths of arrows indicate the concentration of single units’ preferred phases around the average direction (proportional to κ). The vS1 units’ preferred phase relative to PL theta was more concentrated around the mean direction compared to other pairwise vS1 versus PL combinations reflected in the Figure 7B by the length of arrows (Table 1).

As the third approach, we quantified spike-LFP coherence by means of pairwise phase consistency (PPC), which is, unlike other measures of phase locking, unbiased by the number of spikes (Vinck et al., 2010). Figure 7C demonstrates the distribution of PPC values during the interstimulus period for all units in each of the 4 conditions. vS1 to vS1 PPC values surpassed those of all other comparisons, consistent with larger single units’ κ parameter represented as the distance from center for the dots in Figure 7B (Table 1).

Finally, by comparing the PPC values during the prestimulus and interstimulus periods to a baseline period of same length (from 4.2 to 2.2 before stimulus1), we asked whether the observed coherence varied according to performance. We tested coherence for each of the four pairwise vS1 versus PL comparisons labeled at the top of panel A, on both correct and incorrect trials (Figure 7D). PPC values for vS1 spikes to vS1 LFP were significantly modulated in the both prestimulus and interstimulus windows compared to baseline in correct and incorrect trials (p < 0.001; Wilcoxon signed rank test). PPC values for PL spikes to vS1 LFP and for PL spikes to PL LFP were not significantly higher than baseline in the two tested windows, either in correct or incorrect trials (p > 0.05; Wilcoxon signed rank test), indicating that these relationships did not influence performance.

On the other hand, PPC values for vS1 spikes to PL LFP during the prestimulus period increased significantly compared to baseline in correct (p < 0.05; Wilcoxon signed rank test), but not incorrect (p > 0.05; Wilcoxon signed rank test) trials, suggesting that synchronization of vS1 spikes to PL theta oscillations during the prestimulus window enhanced the performance of the upcoming trial. During the interstimulus delay, vS1 to PL PPC was not different from baseline (p > 0.05; Wilcoxon signed rank test). Together, these analyses show that vS1 spiking activity aligned with PL theta in specific epochs in a performance-related manner.

Discussion

Cortical Networks in Real-Time Stimulus Coding and Working Memory

Delay interval activity has been reported in V1 in visual working memory tasks (Supèr et al., 2001), arguing that early cortical processing areas have a role in sensory memories (Harris et al., 2001b). In pioneering studies reporting delay activity in primate S1 (e.g., Zhou and Fuster, 1996), the object manipulation task did not fully control for tactile and proprioceptive cues during the delay; neuronal firing was specific to selected contacted objects and was not graded across the stimulus set. In later studies, vibrations with parametrically varying values of frequency were introduced as a more controlled stimulus set, and a long inquiry into the cortical networks involved in tactile perception and decision making in primates ensued (Romo and Salinas, 2003). The recent discovery of similar perceptual and working memory capacities in rats has sparked the search for the underlying networks in the more accessible rodent cerebral cortex (Fassihi et al., 2014, Fassihi et al., 2017). In the present study, during presentation of stimulus1, a large fraction of neurons in vS1 (63%) and a smaller fraction of neurons in PL (28%) encoded the speed of the stimulus in a graded manner (Figure 4A). Similar fractions of neurons in vS1 and PL carried signals about stimulus1 during the interstimulus delay period—about 30% at the outset of the delay and about 20% at the conclusion (vS1 results are similar to the findings of Fassihi et al., 2017). The exact quantity of signal, of course, depends on the metric: by measures of MI, just over 10% of vS1 neurons and just under 10% of PL neurons carried stimulus1 signals late in the delay period (Figure 3D).

A previous study uncovered potential contributions of human S1 to a working memory task where subjects compared the frequencies of two sequential vibrations applied to a fingertip (Harris et al., 2002). Performance was disrupted when a transcranial magnetic stimulation pulse (TMS) was delivered to the contralateral S1 early (300 or 600 ms) in the retention interval. TMS did not affect tactile working memory if delivered to contralateral S1 late in the retention interval (at 900 or 1,200 ms), nor did TMS affect performance if delivered to the ipsilateral S1 at any time point. Human S1 thus might act not only as a center for real-time sensory processing but also as a transient storage site for information that contributes to working memory. If the neurophysiology of human S1 resembles that seen in vS1 in the current study, the information carried in S1 about the just-concluded stimulus1 would be consistent with its transient memory function.

In monkeys, the activity of populations of neurons in S2, the prefrontal cortex, and premotor cortical areas differentially encodes the frequency of the first vibration, and the populations sustain this differential activity across the retention interval. However, sustained activity is not observed among neurons in S1 (Salinas et al., 2000), leading to the conclusion that monkey S1 does not participate in maintaining the vibrotactile working memory trace, at odds with evidence from humans and rats. This discrepancy as to the role of S1 in working memory may form procedural differences. The monkeys were given several months of training on the task; during the course of extensive training, there may evolve a faster or more efficient transfer of information to “later” cortical areas. The reverse hierarchy theory of perceptual learning (Ahissar and Hochstein, 2004) posits that cognitive tasks are delegated to the highest level of processing that can accomplish the task. It might be that, although trained monkeys delegate working memory to S2 and frontal cortical regions, naive humans (Harris et al., 2002) and well-trained rats (current work) employ S1 for transient memory storage.

Forms of Neuronal Coding

During real-time representation of the vibration, nearly all vS1 neurons whose firing rate varied with stimulus speed showed positive coding—increasing firing rate with increasing speed. During the interstimulus delay, vS1 neurons showed mixed positive and negative coding. Around 70% of PL neurons showed positive coding, and the proportion was consistent across epochs of the trial. Positive versus negative monotonic coding is of interest because earlier work has found that S1 neurons in monkeys show only positive coding of vibration sinusoidal frequency, and mixed positive and negative coding first appears in S2 (Romo and Salinas, 2003). Theoretical work argues that negative coding is an outcome of higher-order processing of purely positive-coding neurons (Chow et al., 2009).

Here, we tested the neuronal bases of tactile WM in the form of persistent activity (Constantinidis et al., 2018). It has been suggested that memory traces can be held with other candidate mechanisms (Lundqvist et al., 2018a) such as transient activation of different neurons during the delay period (Harvey et al., 2012) and gamma-band bursting (Lundqvist et al., 2018b). An additional proposed WM mechanism is by calcium-mediated synaptic facilitation in the recurrent connections of neocortical networks (Mongillo et al., 2008); however, it is difficult to acquire experimental evidence to evaluate this hypothesis.

Representation of Choice and Stimulus2 in vS1 and PL

The post-stimulus delay period allowed us to assess choice information while the rat remained in the nose poke. In vS1, 30% of the neurons represented the choice of the animal at the end of this period and just before the go cue was sounded (Figure 5C). Indeed, choice signals already appeared during stimulus2. This suggests that vS1 in rats, similar to S2 in primates, might participate in the decision-making process (Romo et al., 2002). An alternative account is that rats began to move their head or whiskers as evidence for the comparison between stimulus2 and 1 accumulated, and choice-related movement was manifested in vS1. After the animal left the nose poke to report its decision, a high percentage of neurons in vS1 showed a firing rate correlation with choice, probably due to differential engagement of whiskers when turning left versus right.

In PL, around 10% of neurons represented the rat’s action, mainly after the termination of stimulus2 (Figure 5D). Presumably, areas involved in preparation of directional movements like anterior vM1 and anterior lateral motor cortex (ALM), which were not tested in this study, might be more involved in this part of the task (Chen et al., 2017, Erlich et al., 2011).

A novel finding is that the degree of retention of sp2 in firing rate after the termination of stimulus2 was similar to that found for stimulus1 in the early delay period, both in vS1 and in PL (Figure 3D). Memory of stimulus2 might seem superfluous and inefficient. However, neuronal populations may possess intrinsic properties that cause them to hold previous signals, independently of the phase of the task. That stored information may be used for upcoming operations or may be discarded downstream, according to the behavioral exigencies. On the other hand, there may be some functional role for stimulus2 memory even after a decision is made: the rat may interrogate its memory of both stimuli, confirming the task rule on rewarded trials and re-assessing the task rule on error trials. Future inactivation experiments during different behavioral epochs could address this question.

Top-Down Modulation through Coherent Low-Frequency Oscillations

LFP phase coherence between vS1 and PL was highest as the animal entered the nose poke and awaited the first stimulus (Figures 6C–6E). vS1 spikes were phase locked to PL theta in this period, and this entrainment improved task performance (Figure 7). Coherence remained high during various epochs of the two stimuli and across the interstimulus interval. In an auditory rule selection task in rats, there is anticipatory activity in PL up to 2.5 s before trial initiation (Rodgers and DeWeese, 2014). In primates, low-frequency synchrony between frontal and parietal areas has been observed during top-down attention (Buschman and Miller, 2007). As in the above studies that require deployment of attentional resources, the high degrees of coherence in the prestimulus period might reflect preparatory and expectation mechanisms.

The phase difference between vS1 and PL in the theta range showed that PL consistently led vS1 by an angle of π/2 (Figure 6), suggesting a top-down mechanism as opposed to bottom-up gating of the flow of information between these areas. With the greatest theta power at about 8 Hz, the phase difference can be approximated as 30 ms. The hypothesis that PL exerts an influence on vS1 that conditions communication through LFP could be tested in future experiments through directed measures of information transfer between different areas.

Parametric stimulus coding, both in real time and during a retention delay, has been documented in primate dorsolateral prefrontal cortex (dlPFC) (Romo et al., 1999) and, from the present work, can be extended to what may be the homologous region in rats. Our finding of a robust tactile reperesentaion in PL is consistent with the fast whisker-evoked responses in PL of mice performing a whisker detection task (Le Merre et al., 2018). Other cellular imaging studies show evoked neuronal activity in PL of trained mice but negligible or no evoked response in naive mice (Otis et al., 2017) or in response to non-relevant non-rewarded stimuli (Pinto and Dan, 2015), suggesting that sensory responses in PL might develop during learning of goal-directed behavior.

The anatomical connection between vS1 and PL has not yet been mapped. In future studies, it will be important to determine the pathways for transmission of sensory information to PL and synaptic and circuit mechanisms underlying the task-related sensory coding in this area. It is also important to assess how different populations of neurons in PL with different downstream targets contribute to the encoding and storage of sensory information in a working memory task (Otis et al., 2017).

Sources of Errors

In both vS1 and PL, the robustness of stimulus encoding was lower throughout all phases of the task on trials that ended with incorrect choice (Figure 4). The diminished strength of coding was particularly notable in PL, where neurons showed only negligible stimulus-dependent firing rate variation throughout error trials. These findings support the argument that the selected neuronal firing measures were a robust measure of the mechanisms underlying behavior and that errors originated from a degraded stimulus representation during the stimuli and/or during memory, especially in PL. Although unreliable stimulus encoding could even occur at the input level of the sensory pathway (for instance, due to incomplete placement of the whiskers on the plate), there is reason to believe that higher-order functions could play a role. PPC values for vS1 spikes to PL LFP increased significantly during the prestimulus period compared to baseline in correct, but not incorrect, trials, suggesting that failure to synchronize vS1 spikes to PL theta oscillations during the prestimulus window might diminish the performance on the upcoming trial. In a visual working memory short-term memory, the strength of theta-band phase locking between LFPs and single units in V4 and prefrontal cortex predicted the likelihood of correct or incorrect response (Liebe et al., 2012).

Overall, these analyses indicate that, although vS1 is particularly connected to the representation of the stimulus in real time, it also carries a non-negligible stimulus1 signal during the interstimulus interval, available to downstream centers as a potential memory trace. The signal carried by PL is more evenly balanced between real-time and memory encoding. These results should enable optogenetic manipulations of cortical regions, including vibrissal motor cortex (Fassihi et al., 2017), starting from basic knowledge of their functional properties.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Isoflurane	Merial	AP/DRUGS/220/96
Epigel	Ceva	N/A
Atropine	ATI	AIC no. 101948014
Antibiotic (Baytril)	Bayer	AIC no. 100155062
Analgesic (Rimadyl)	Zoetis	AIC no. 102191119
Topic antibiotic	Dechra	AIC no. 102881012
Local anesthetic (lidocaine)	Molteni Farmaceutici	AIC no. 005638010
Paraformaldehyde	Sigma-Aldrich	158127
Cresyl Violet	Sigma-Aldrich	C5042
Experimental Models: Organisms/Strains
Wistar rats	Harlan - Envigo	16808M
Software and Algorithms
LabView 2014	National Instruments	http://www.ni.com/download/labview-development-system-2014/4735/en/
OpenEx	Tucker-Davis Technologies (TDT)	SCR_016230
MATLAB v 2015a	MathWorks	https://www.mathworks.com/products/matlab.html
Wave-Clus for spike sorting	Quiroga et al., 2004	https://www2.le.ac.uk/centres/csn/research-2/spike-sorting
Information breakdown toolbox	Magri et al., 2009	N/A
Fieldtrip toolbox	Oostenveld et al., 2011	SCR_004849
Other
Digital TDT recording system	Tucker-Davis Technologies (TDT)	model: RZ2 BioAmp Processor
16/32 channel ZIF-Clip® microwire arrays	Tucker-Davis Technologies (TDT)	16-ch ZIF2010 & 32-ch ZIF2010

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Mathew E. Diamond (diamond@sissa.it).

Experimental Model and Subject Details

Eight Wistar male rats (Harlan, San Pietro al Natisone, Italy) were housed in pairs or individually and maintained on a 14/10-h light/dark cycle. All experiments were conducted during the dark phase. Rats were water-restricted and collected all necessary liquid during and immediately after the behavioral session, when they had access to water ad libitum for 10 min. Food was provided ad libitum in the home cage throughout the experiment. At the start of the experiment, rats were 6–8 weeks old and weighed 225–250 g; they gained weight steadily throughout the study, following the normal Wistar weight gain curve, demonstrating that water restriction did not influence overall intake. They were examined weekly by a veterinarian. Protocols conformed to international norms and were approved by the Ethics Committee of SISSA and the Italian Health Ministry (license numbers 569/2015-PR and 570/2015-PR).

Method Details

Behavioral Task

Experiments were controlled using LabVIEW software (National Instruments, Austin, Texas). The rat started each trial by entering the stimulus delivery port and positioning its snout in the nose poke (Figure 1A). While in the nose poke, the rat positioned the whiskers of the right side of the snout on a metal plate connected to a shaker (type 4808, Bruel & Kjaer). The plate was covered with adhesive tape to ensure stable contact with the whiskers. Activating the nose poke sensor triggered a brief delay (0.7 s), followed by stimulus1 (duration 0.5 s), characterized by nominal mean speed, sp1. After a delay of 2 s, stimulus2 (duration 0.5 s and nominal mean speed sp2) was presented (Figure 1B). Stimuli were irregular “noisy” vibrations, consisting of changes in the plate position in the rostral/caudal direction. The sequence of velocity values (v_t) was taken from a normal distribution at 10,000 samples/s. Converting v_t to its absolute value, sp_t, the distribution takes the form of a folded, half-Gaussian (Figure 1B).

The rat remained in the nose poke for the post stimulus delay of 0.5 s and withdrew when the “go” cue sounded. The rat then selected the left or right reward spout depending on the relative values of sp1 and sp2. Only correct responses were rewarded. Early withdrawal trials (when animal left the nose poke before the go cue) were aborted and were not rewarded.

To ensure that rats learned the delayed comparison task as opposed to shortcut strategies (e.g., applying a constant threshold to sp1 or sp2 alone), we used a stimulus generalization matrix (SGM; Figure 1C). The SGM spanned a wide range of sp pairs, with each pair characterized by normalized speed difference, (sp2 - sp1)/(sp2 + sp2), of 0.25. The arrangement of the SGM signifies that neither stimulus alone could provide sufficient knowledge to solve the task, so the rat was required to execute a direct comparison between the two stimuli on every trial (Fassihi et al., 2014).

Rats were implanted with electrode arrays once they reached stable performance, verified by two criteria: (i) more than 75% of trials correct in strings of at least 3 consecutive sessions, and (ii) statistical proof of working memory through a linear model (see next section) that ascertained whether choices were the outcome of a comparison between sp1 and sp2 (Fassihi et al., 2014). During recording sessions, the normalized speed difference of the SGM was increased slightly (to 0.33) to enhance motivation, and the number of stimulus pairs was reduced in order to increase the number of trials per condition for statistically sounder neuronal analyses (Figure 1E).

Weights of sp1 and sp2 in the animal’s choices

To weight the contributions of sp1 and sp2 to the animal’s choice we fit the animal’s choice using a generalized linear model (Fassihi et al., 2014). This model posits that a linear combination of sp1 and sp2 is mapped nonlinearly through a logistic link function, onto the animal’s choice, giving as output the percent of trials in which the rat judged sp2 > sp1:

$$Percentoftrialsjudgedsp2>sp1=\frac{1}{1+e^{-\left(c+w1\log sp1+w2\log sp2\right)}}$$

where w1 is the sp1 regressor, w2 is the sp2 regressor, and C captures the overall bias of the subject in calling sp2 > sp1 (for instance, a bias toward turning to the left reward spout regardless of the relation between sp1 and sp2).

The coefficients w1, w2, and C were computed using a least-squares algorithm implemented in MATLAB. The w1 and w2 regressors quantify the strength of the relationship between sp1 and sp2, respectively, and the animal’s choice. If the regressors are plotted in Cartesian coordinates (Figure 1C, right panel), the critical issue becomes the direction of the vector formed by w1 and w2. Any possible bias C is independent of stimulus weighting and would not affect the angle.

Electrode implantation

Once rats reached a stable performance in the behavioral task, they underwent surgery for electrode implantation. They were anesthetized with Isoflurane (2.5% for induction and craniotomy, 1.5% for maintenance) delivered through a snout mask. Three small screws were fixed in the skull to support the dental cement. One of the screws was advanced until it contacted the dura, where it served as the reference and ground electrode (reference and ground were shorted). Two craniotomies were made, one over vS1, centered at 2.5 mm posterior to bregma and 6 mm lateral to the midline, the other over medial prefrontal cortex, centered at 3.2 mm anterior to bregma and 0.6 mm lateral to the midline (Figure 1D). To minimize brain dimpling, the following steps were performed. First, dura mater was removed over the entire craniotomy using the hooked tip of small syringe needle. Then a drop of sterile ointment in the middle of the craniotomy and the surgical cyanoacrylate adhesive (Histoacryl, B.Braun) were applied directly to the pial surface bordering the edge of the cranial opening. This procedure fastened the pia mater to the overlying bone and the resulting surface tension prevented the brain from depressing under the advancing electrodes. The microwire arrays (Tucker-Davis Technologies) were then inserted into each area by slowly advancing a Narashige micromanipulator. Once at the intended depth, the remaining exposed cortex was covered with biocompatible silicon (KwikSil, World Precision Instruments). The array was then attached to the skull by dental cement (SEcure Starter Kit, Sun Medical).

One h after the beginning of the anesthesia, atropine (2 mg/kg) was injected (s.c.) to reduce secretions in the respiratory tract and maintain a stable heart rate. Rats were given the antibiotic (Baytril; 5 mg/kg; i.p.) and analgesic (Rimadyl; 2.5 mg/kg; i.m.) one h before conclusion of the operation. After surgery, a local antibiotic (Isaderm) was applied around the wound to speed the healing. In addition, both the antibiotic and the analgesic were delivered through the water bottle for 24 hr after completion of surgery. During this recovery time, rats had unlimited access to water and food. Recording sessions in the apparatus began thereafter. At the end of recording sessions rats were perfused and the electrode locations were verified in histological slices (Figure S1).

Electrophysiological recordings

The microwire array (Tucker-Davis Technologies) was comprised of 16 or 32 polyimide-insulated tungsten wires of 50 μm diameter, 250 μm electrode spacing and 375 μm row spacing. The impedance of each wire was 20 kΩ at 1 kHz, measured in saline, and around 150-200 kΩ when measured in vivo (Prasad and Sanchez, 2012). While lowering the arrays, the quality of raw signals was monitored and the detected spikes were clustered and sorted online (only for visualization purposes) using the OpenEx toolbox (Tucker-Davis Technologies). The vS1 array was fixed at a depth of around 900 μm, where it became possible to distinguish action potential waveforms evoked by manual whisker deflections. The depth of the final recording sites, together with the small receptive fields, is consistent with an electrode tip position in layers 4-5. However, our analyses and conclusions do not depend on the precise laminar localization of the neurons. The PL array was custom-designed with wires of two different lengths interleaved in each row. This resulted in half of the electrodes positioned 600 μm deeper than the others. The final depths were around 2800 μm for shorter wires and 3400 μm for the longer.

After passing through a unity-gain headstage, signals were transmitted through a cable to the PZ2 preamplifier (Tucker-Davis Technologies). Signals were then digitized at a sampling rate of 24 kHz and sent through an optical fiber to the RZ2 amplifier (Tucker-Davis Technologies), after which they were stored. Data were analyzed offline using custom-built MATLAB codes (MathWorks). To remove the common artifact and improve signal to noise ratio, local referencing was performed on each array. This was achieved by bandpass filtering of one min of data from all channels in the spiking range (300 Hz – 3 kHz) and selecting the channel with the lowest number of threshold crossing events to serve as reference for all the channels on that array.

Spike detection and sorting were then performed using Wave-Clus clustering algorithms (Quiroga et al., 2004). Only well separated units with stable waveform and firing rate over the course of a session and small refractory period violations (< 10, Hill et al., 2011) were included in the analysis. In total we recorded 136 single units in vS1 and 53 in medial prefrontal cortex of 8 rats.

Spike density functions

In the analysis of neuronal responses, we carried out a continuous-time data analysis approach. We first convolved the spike train of each neuron (with 1 ms resolution) with Gaussian kernels to obtain spike density functions. For visual presentation of PSTHs, we filtered the data continuously to avoid sharp discontinuities (Gaussian kernel with σ = 150 ms). For the quantification of information and monotonic encoding, stimulus periods were convolved separately from other periods (Gaussian kernel with σ = 300 ms) and the kernels were corrected for the edge effect. This has the advantage of avoiding any leakage of data from one period to another, and thus enabling us to quantify pure-sensory and pure-memory information. However, our approach in separately filtering data within different periods creates sharp transitions at the edges. The time-dependent spike density functions, which give an estimate of the instantaneous firing rate, were used for the rest of the analysis, as explained below.

Information theoretic analysis

To quantify the encoding of relevant task parameters in neuronal firing, we computed Shannon’s Mutual Information (Shannon, 1948), hereafter referred to simply as MI. To build the temporal profile of MI we measured the information by sampling from the spike density function of the neuron every 20 ms (50 ms in Figures 5C and 5D). The convolution of this kernel with the spike train of the neuron results in an estimate of instantaneous firing rate. Thus, we investigated the MI afforded by the “rate” code only. Additional signals, not captured by rate, may be present in the precise timing of spikes of neurons in each area (Panzeri and Schultz, 2001, Panzeri et al., 2001, Petersen et al., 2001, Pica et al., 2017, Zuo et al., 2015).

When estimating the MI in the neuronal response, we were concerned about spurious values caused by the inherent correlations between task parameters. This correlation comes from extreme [sp1, sp2] pairs of the SGM, where the value of a single stimulus (the smallest sp1 or largest sp2) specifies the other stimulus and the correct choice. In that case, a neuron carrying a signal about sp1 will necessarily carry a signal about sp2 and about the choice, and vice versa. To eliminate the possibility of such corollary signals, we used conditional MI, thus disentangling the signal about stimulus from the potential signal about the rat’s future choice:

$$\text{I}\left(\mathit{sp1;}\mathit{fr}|\mathit{ch}\right)=\text{I}\left(\mathit{sp1;}\left\{\mathit{fr,ch}\right\}\right)-\text{I}\left(\mathit{sp1;ch}\right)=\text{I}\left(\mathit{fr,}\left\{sp\mathit{1,ch}\right\}\right)-\text{I}\left(\mathit{fr,ch}\right)=\text{I}\left(\mathit{fr,}\left\{sp\mathit{1,sp2}\right\}\right)-\text{I}\left(\mathit{fr,ch}\right)$$

$$\text{I}\left(\mathit{sp2;}\mathit{fr}|\mathit{ch}\right)=\text{I}\left(\mathit{sp2;}\left\{\mathit{fr,}\mathit{ch}\right\}\right)-\text{I}\left(\mathit{sp2;}\mathit{ch}\right)=\text{I}\left(\mathit{fr,}\left\{sp\mathit{2,}\mathit{ch}\right\}\right)-\text{I}\left(\mathit{fr,}\mathit{ch}\right)=\text{I}\left(\mathit{fr,}\left\{sp\mathit{1,sp2}\right\}\right)-\text{I}\left(\mathit{fr,}\mathit{ch}\right)$$

where sp1 and sp2 are the stimulus1 and stimulus2 mean speeds, fr is the neuron’s firing rate and ch is the binary choice of animal, right or left, in each trial. This formulation is equivalent to a measure of how much the MI in the response of a neuron about stimulus1 exceeds the MI that could be extracted merely by knowing the rat’s choice. In other words, for a given choice, we measured whether there remained statistical dependence between firing rate and sp1. In the particular case of the SGM, this is equivalent to measuring MI about sp1 across the [sp1, sp2] pairs of SGM that correspond to the same choice, i.e., lying below (or above) the diagonal (Figure 1E). Note that the last equality in the formula above is due to the fact that knowing sp1 and choice on correct trials is equivalent to knowing sp1 and sp2. By the same method, we could compute the MI about sp2.

To obtain the neuronal signal about the rat’s choice, we computed the conditional MI given sp1 or sp2:

$$\text{I}\left(ch;fr|sp\mathit{1}\right)=\text{I}\left(ch;\left\{fr,sp\mathit{1}\right\}\right)-\text{I}\left(\mathit{ch;}sp\mathit{1}\right)=\text{I}\left(fr;\left\{ch,sp\mathit{1}\right\}\right)-\text{I}\left(fr;sp\mathit{1}\right)=\text{I}\left(fr\text{;}\left\{sp\mathit{1,}sp\mathit{1}\right\}\right)-\text{I}\left(fr;sp\mathit{1}\right),$$

$$\text{I}\left(ch;fr|sp2\right)=\text{I}\left(ch;\left\{fr,sp2\right\}\right)-\text{I}\left(\mathit{ch;}sp2\right)=\text{I}\left(fr;\left\{ch,sp2\right\}\right)-\text{I}\left(fr;sp2\right)=\text{I}\left(fr\text{;}\left\{sp\mathit{1,}sp2\right\}\right)-\text{I}\left(fr;sp2\right),$$

These equations quantify the MI about the rat’s choice in the firing rate across the [sp1, sp2] pairs of SGM with equal sp1, such that a given value of sp1 was associated with two different values of sp2 (Figure 5A, middle panel, left legend), and equal sp2 which could be proceeded by two different values of sp1 (Figure 5A, middle panel, right legend) respectively.

The probabilities in the equations mentioned above are not known a priori and must be estimated empirically from a limited number, N, of experimental trials for each unique task parameter and neuronal response. For some sessions in our dataset, N could be as low as 20. To obtain unbiased estimates of MI we reduced the dimensionality of the response space by grouping the firing rates into 3-4 classes. All of the MI values were computed using Information Breakdown Toolbox (Magri et al., 2009).

The degree of retention of sensory signals during the delay relative to real-time encoding of stimulus was quantified as the percent of neurons carrying the memory of stimulus1 in relation to the percent that encoded the stimulus in real time.

Generalized Linear Model

Mutual information measures whether a neuron’s response could provide knowledge to a decoder about the presented stimulus, but does not specify the nature of the neuronal code. To look for a systematic coding motif, we examined the linear relation between the stimulus mean speed and neuronal responses. The response of the neuron at each point in time was defined as its instantaneous firing rate taken from the spike density function. Employing a standard linear regression was not appropriate because it uses a squared-error loss function, and assumes that the noise (residual of the fit) is Gaussian distributed, which is not true for neuronal activity. Instead, we fitted a generalized linear model (Nelder and Wedderburn, 1972) to linearly map the stimulus mean speed to the response of the neuron through a Poisson link function which better captures the statistics of neuronal firing. We used glmfit in MATLAB (MathWorks) to estimate the optimal slope parameter of the linear fit with a maximum likelihood-based iteratively reweighted least-squares method.

Local field potential acquisition and analysis

We performed time-frequency analysis using the Fieldtrip toolbox (Oostenveld et al., 2011) and custom-built MATLAB codes. We obtained local field potentials (LFPs) offline by filtering the raw signal between 1-300 Hz and downsampling to 1000 Hz. Then we divided continuously recorded data into trials starting 5 s before nose poke until 5 s after the go cue.

The power spectrum of the LFP was estimated using a continuous wavelet transform using complex Morlet wavelets of 4 cycles length. This results in shorter wavelet duration for larger frequency values. To avoid redundancy in measuring power, we considered a logarithmic set of frequencies, starting at 2 Hz and increasing by 2¼ Hz. Time-frequency power maps were log-transformed and averaged across trials and then normalized by the mean power during the least active period during the behavioral task which we refer to as baseline (2.2-4.2 s before the nose poke).

To quantify the phase synchronization between the LFPs recorded from separate electrodes in vS1 and prefrontal cortex, we computed the Weighted Phase Lag Index (WPLI) (Vinck et al., 2011). The WPLI is a measure of phase coherence based exclusively on the imaginary component of the cross-spectrum, and is not spuriously affected by volume conduction from a single source’s activity to two separate sensors, or by a common reference. The WPLI has greater robustness to noise compared to other measures that are based on the imaginary component of the cross-spectrum (Nolte et al., 2004, Stam et al., 2007). A direct estimator of the WPLI can be biased by sample size. Therefore, we estimated the squared WPLI by using the debiased WPLI estimator (Vinck et al., 2011), ranging from zero (no phase coupling) to one (maximum coherence). The debiased WPLI has no sample size bias if the asymptotic WPLI value equals zero, hence does not spuriously indicate interactions

In order to analyze for a possible directional influence of activity from one area to the other, we calculated the phase difference between areas across the frequency range of interest (5-12 Hz). We estimated the instantaneous phase of each signal using a Hilbert transform and computing at each time the phase difference between pairs of electrodes in vS1 and PL. The significance of the phase shift difference from zero was tested using a Rayleigh test.

Phase-locking analysis of spikes was performed by first filtering the LFP in the theta range (5-12 Hz). The phase component was calculated using Hilbert transform and a corresponding phase was assigned to each spike. The data was tested against a von Mises distribution, a unimodal distribution with probability density function of:

$$f\left(\varphi |\mathrm{\theta },\text{k}\right)=\frac{e^{\text{kcos}\left(\varphi -\theta \right)}}{2\pi 1_0\left(\text{k}\right)}$$

Where κ is the concentration parameter, θ represents the mean angle and I₀ is modified Bessel function. The function has maximum value at Φ = θ. Parameters θ and κ are analogous to the mean and variance in the linear normal distribution. For κ = 0 the von Mises distribution takes the form of a uniform distribution; the larger the κ the more the distribution is concentrated around the mean angle, θ. To test data against the uniform distribution we applied the Rayleigh test. As the final approach we used pairwise phase consistency (PPC) method to quantify spike phase locking which is suggested to be bias-free to the number of spikes (Vinck et al., 2010). Nevertheless, to ensure a robust estimate of the spike phase we only included units with > 1000 spikes during the window of interest.

Quantification and Statistical Analysis

Test of significance of mutual information

We built a non-parametric permutation test to determine the epochs of the behavioral trial in which the recorded neurons had values of MI significantly greater than zero. This was achieved using a bootstrap procedure that consisted of randomly pairing stimuli and responses, thus destroying the real MI that the responses carried and providing an estimate of the MI expected by chance. We repeated this procedure 1000 times and compared the original response against the bootstrapped distribution. A neuron was considered significantly informative in one epoch if the true MI value exceeded the 95% percentile of the bootstrapped MI distribution (p < 0.05).

Test of significance of Generalized Linear Model

We performed a non-parametric test to evaluate whether the slope of the fit was significantly different from zero. To estimate the reliability of the GLM parameter, we first built a bootstrapped distribution of slopes by resampling (with replacement) 1000 times from different observations (trials) and fitting a GLM model. To obtain a baseline comparison, we then shuffled the stimulus tag across trials 1000 times and estimated the slope of the GLM fit in each iteration, resulting in a distribution of slopes expected if there were no real relationship between stimulus speed and neuronal response magnitude. We then computed the distribution of differences (observations-shuffled) and calculated the proportion of differences greater or smaller than zero, to identify positive or negative slopes respectively. This provided us with a p value for the statistical test on slope (taken as significant for p < 0.05). To build the temporal profile of the GLM weights, we sampled from the spike density function of the neuron every 50 ms.

LFP phase-locking tests

All the phase-locking significance tests for spikes and LFPs were implemented using CircStat toolbox in MATLAB (Batschelet, 1981, Berens, 2009).

Published: June 11, 2019

Supporting Citations

The following reference appears in the Supplemental Information: Paxinos and Watson (2007).