Abstract
Background
Prediction of polycyclic aromatic hydrocarbons (PAHs) desorption from soil to estimate available fraction regarding to initial concentration of the contaminant is of great important in soil pollution management, which has poorly been understood until now. In the present study estimation of fast desorption fraction which is considered as available fraction was conducted by evaluating desorption kinetics of phenanthrene (a three ring PAH) from artificially contaminated soils through the mathematical models.
Methods
Desorption rate of phenanthrene (PHE) was investigated by using the nonionic surfactant Tween80 in a series of batch experiments. The effects of reaction time from 5 to 1440 min and initial PHE concentration in the range of 100–1600 mg/kg were studied.
Results
Available fractions of the contaminant were achieved within the first hour of desorption process as the system reached to equilibrium conditions. Experimental data were examined by using kinetic models including pseudo-first-order, pseudo-second-order in four linearized forms, and fractional power. Among the models tested, experimental data were well described by pseudo-second-order model type (III) and (IV) and fractional power equation. Fast desorption rates, as Available fractions were determined 79%, 46%, 40%, 39%, and 35% for initial PHE concentrations of 100, 400, 800, 1200, and 1600 mg/kg respectively. Among the evaluated isotherm models, including Freundlich, Langmuir in four linearized forms, and Temkin, the equilibrium data were well fitted by the first one.
Conclusion
Applying the nonionic surfactant Tween80 is a useful method to determine available fraction of the contaminant. This method will provide the management of contaminated sites by choosing a proper technique for remediation and predicting achievable treatment efficiency.
Keywords: Phenanthrene, Desorption, Tween 80, Kinetic, Isotherm
Background
Industrial activities such as petroleum refinement, coal and gas production, incomplete combustion of fossil fuels, and leakages have led to the extensive discharge of polycyclic aromatic hydrocarbons (PAHs) into the soil and water resources [1, 2]. Thanks to their low volatility, hydrophobic nature and high octanol–water partition coefficients (Kow), these ubiquitous compounds are severely adsorbed onto the soil grains being very recalcitrant to degradation [1, 3]. Therefore, PAHs-contaminated sites are potentially serious threats to both environmental resources and human health, duo to their bioaccumulation potential and extreme toxicity, mutagenicity and carcinogenicity impacts, posing the remediation of contaminated soils as a principal challenge [4, 5]. In the last few decades, some environmental clean-up technologies including bioremediation, advanced chemical oxidation, electrochemical treatment, soil flushing, and soil washing have been applied for the remediation of PAHs-contaminated soils [6–12]. Nevertheless, removal efficieny of these technologies depends on the ability of the contaminat to be desorbed and transfer from soil to the liquid phase, which is defined as availability [13].
The methode for availability determination is based on the extraction of the contaminant [14]. Surfactants are amphiphilic compounds, having both hydrophilic head and hydrophobic tail that enhance the solubility and desorption of PAHs in soil/solution systems [15, 16]. At their low concentrations, surfactants are present as monomers. Increasing surfactant concentration leads to monomers aggregation in the solution to form micelles. The concentration at which first micelle is formed is known as critical micelle concentration (CMC) [15]. Therefore, solubilization of hydrophobic organic compounds (HOCs) increases by decreasing the surface and interfacial tension between pollutant and water by monomers at low surfactant concentration which accumulate them into the hydrophobic cores of surfactant micelles at concentrations more than CMC, consequently desorption rate and availability enhance in the system [16, 17]. Polyoxyethylene-20-sorbitan monooleate (Tween80), an environmentally-friendly nonionic surfactant, has been reported as the most perfect extractor agent with a great solubilization capacity for PAHs among other synthetic surfactants accompany with the less toxicity effects [3, 18–20]. Fastly desorbing fraction is considered as the available amount of the contaminant. This fraction is determined by evaluating desorption kinetics through mathematical models. Study of desorption kinetics models provide valuable information related to PAHs behavior in the system and rate of desorption to predict their transportation between different media [21].
The present study was carried out to examine desorption kinetics of PAH from artificially contaminated soil by using Tween80 to evaluate the availability of the contaminant. To our knowledge, desorption kinetics of PAHs for this purpose by using nonionic surfactants with high surfactant concentration and at high liquid/soil ratio has been rarely stuied [13]. The objectives of the study are (1) to investigate desorption rate of PAH from contaminated soil with different initial concentration in batch experiments, (2) evaluating desorption kinetic models to optimize desorption process and finding the most proper for estimation of fast desorption fraction, and (3) to examine equilibrium data by using isotherm models to select the best fitted one. Phenanthrene (PHE), a three ring PAH which is listed among priority pollutants of US EPA was selectected as a representative of PAHs.
Materials and methods
Chemicals
PHE with high purity >98%, acetone, sodium chloride (NaCl) and High-performance liquid chromatography (HPLC) grade acetonitrile (99.9%) were purchased from Merck Company, Germany. Tween80 and Mercuric chloride were also obtained from Fluka and BDH, respectively. In addition, all reagents were of analytical grade and all solutions were prepared using distilled water.
Preparation of PHE contaminated soil
Clean soil was collected from a depth of 10–20 cm below the ground surface, Tehran, Iran. Then, the soil samples were air-dried at room temperature (25 ± 2 °C) and passed through a 2-mm steel sieve. The physicochemical properties of the soil are presented in Table 1. Two grams of dry soil were placed into each 250 mL Erlenmeyer flask as non-continuous reactors which followed by spiking with an appropriate volume of PHE in acetone stock solution. Then, the reactors were placed on a reciprocating shaker (Heidolph, ProMax2020 model) at room temperature and at 180 rpm for 24 h in dark condition to be mixed thoroughly and evaporate the acetone to have the final PHE concentrations of 100, 400, 800, 1200 and 1600 ± 5 mg/kg.
Table 1.
Physicochemical properties of soil
| Parameter | Value |
|---|---|
| Sand (%) | 60 |
| Clay and silt (%) | 27 |
| Gravel (%) | 13 |
| Organic matter content (%) | 4.2 |
| pH | 8 |
| electrical conductivity (mmhos/cm) | 2.174 |
Batch desorption experiments
Desorption isotherms and kinetics studies of PHE were carried out through duplicate batch experiments. Tween80 solution with concentration of 2750 mg/L at liquid/soil ratio of 30v/w (mL/g) was added to every flask containing PHE-contaminated soil. All the aqueous solutions were included 0.01 M NaCl to keep the ionic strength constant and 0.001 M HgCl2 as an inhibitor for bacterial growth. In addition, the pH of solutions was set at 7 ± 0.2 using 0.5 M HCL and 0.5 M NaOH solutions. Afterwards, the samples were shaken (180 rpm, 20 ± 2 °C) for 5, 10, 15, 30, 45, 60, 120, 480, and 1440 min and subsequently centrifuged at 5000 rpm for 20 min to separate the solutions from solid phase completely. Then, the supernatants were sampled and filtered through 0.45 μm PTFE syringe filter and followed by injection to HPLC (Cecil 7400) for determination of PHE concentrations [13, 22].
Data analysis
Evaluation of the batch kinetic data
The amount of desorbed PHE from soil for each reaction time, qt (mg/kg) was calculated by the following equation:
| 1 |
Where, qt (mg/kg) is the amount of desorbed PHE from soil at time t (min), Ct (mg/L) is the concentration of PHE in the aqueous phase at various reaction times, V (L) is the volume of the liquid phase and W (kg) is the mass of adsorbent.
Evaluation of the batch equilibrium data
The amount of desorbed PHE from soil at equilibrium state (qe) (mg/kg) was calculated by the following equation:
| 2 |
Where, Ce (mg/L) is the concentration of PHE in the aqueous medium at equilibrium time. The retained PHE concentrations in soil were also determined as follows:
| 3 |
Analytical method
Analysis of PHE concentration was conducted by a HPLC instrument (CECIL Company) using a C18 column (5 μm pore size, 250 mm length and 4.6 mm internal diameter) with a photodiode array detector (Cecil CE 4200, En). Acetonitrile (90%) and deionized water (10%) were also used as the mobile phase isocratically, at a flow rate of 1.0 mL/min. The retention time of PHE was 10.0 min at a wavelength of 220 nm.
Results and discussion
Effect of contact time and study of PHE desorption kinetics in the presence of Tween80
Our previous studies on PHE desorption from the contaminated soils containing 500 mg PHE/kg dry soil indicated that PHE desorption rate (%) had a direct relationship with surfactant concentration when it was increased remarkably from 1% at Tween80 concentration of 500 mg/L to 70.39% at concentration of 5000 mg/L [25]. Although the least applied concentration of Tween80 is higher than the CMC of this surfactant (16 mg/L) [1], no significant desorption was observed. The reason for this occurrence is that in the soil surfactant solution system, due to the sorption of surfactant onto the soil particles, CMC would be greater than that of the liquid system, which is called effective CMC (CMCeff) [5, 15, 23]. By increasing the surfactant concentration beyond the CMCeff, the sorbed amount of the surfactant reaches the stationary level and surfactant micelles begin to form in the aqueous phase, resulting in partitioning of PHE molecules within hydrophobic cores of the surfactant micelles [24]. Effective CMC of Tween80 has been estimated between 500 to more than 1000 mg/L in the literature [15, 23].
However our investigation on the growth rate of bacterial consortium isolated from a petroleum-contaminated soil revealed the toxicity of Tween80 at the concentration of 5000 mg/L, due to the reduction of microbial population [25]. Therefore, for investigation of PHE desorption in the present work that can be considered as the bioavailability of the contaminant in the bioremediation projects, the Tween80 solution with concentration of 2750 mg/L was selected. Our results also showed the considerable raise in PHE desorptionrate as a result of increasing liquid/soil ratio from 10 to 30 v/w (mL/g) [25]. In the soil surfactant solution system, at concentrations gteater than the CMCeff, the sorption of surfactant onto the soil has been saturated; therefore increasing the volume of surfactant solution results in rising desorption and removal efficiency [26]. Therefore, the subsequent experiments were carried out at liquid/soil ratio of 30 v/w (mL/g).
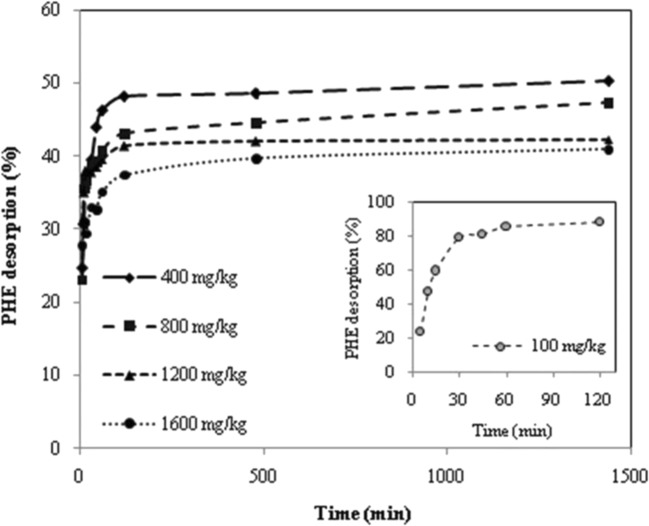
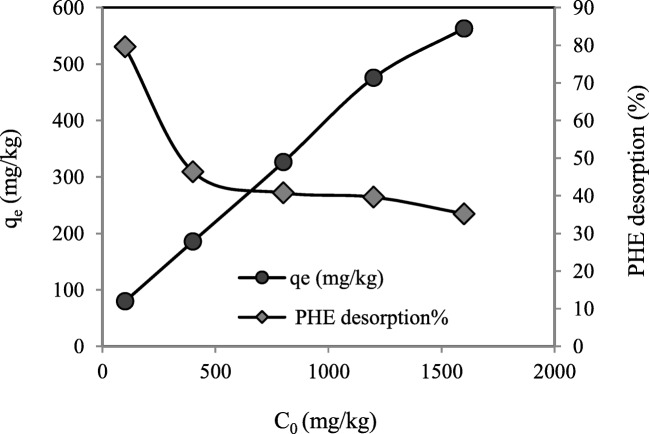
The percentages of PHE desorption at different initial PHE concentrations as a function of the reaction time is presented in Fig. 1. As observed, at initial PHE concentrations of 400–1600 mg/kg, PHE desorption rate (%) increased intensively within 60 min and then followed by equilibrium conditions that demonstrate significant decline in desorption velocity. The adsorbed contaminant in the surface layer with lower adsorption energy can readily and quickly be desorbed, but when the adsorption intensity is high, there is mass transfer limitation that causes the contaminant to resist against desorption [13]. A previous study reported higher equilibrium time of around 8 h with similar trend [13]. This dissimilarity can be due to the different properties of soil including coexistence of hevy metals with high concentration; however, the difference between liquid/soil ratio and the concentration of the surfactant solution may possibly have participated [13, 27]. Studies have demonstrated that the presense of metals in the soil influence on polar part of organic matter and create more hydrophobic sites for PAHs sorption, resulting in sever persistence of these compounds in soil and consequently decrease in mobility of them [27]. Our findings are consistent with those of previous studies in which stable conditions were observed after the first hour of desorption process [1, 23]. In the system with initial PHE concentration of 100 mg/kg in the current study, desorption rate increased rapidly with passage of the time within 30 min up to around 80% and then reached to a stationary state. This result is supported by those of Zhao et al. (2005) who indicated sharp increase in desorption rate during the first 30 min [28]. Results of analysis of variance (ANOVA) also revealed that the impact of reaction time on PHE desorption process was positively significant (P > 0.0001). According to Viglianti et al. (2006), dissolution of the pollutants is the principal feasible mechanism for extraction of PAHs from soil to the aqueous phase [29]. Chang and Wong (2006), who achieved PAHs desorption equilibrium within an hour after addition of surfactant, pointed out that half an hour should be adequate as a reaction time to form surfactant micelle [22]. Therefore in the present study based on the equilibrium time of the desorption kinetics, fast desorption fractions which is in general considered as available fractions [14], were determined 79%, 46%, 40%, 39%, and 35% for initial PHE concentration of 100, 400, 800, 1200, and 1600 mg/kg respectively.
Fig. 1.
Effect of contact time on PHE desorption% at initial PHE concentrations of 100, 400, 800, 1200, and 1600 mg/kg
In the present work, we evaluated the PHE desorption experimental data with three kinetic models of pseudo-first-order, pseudo-second-order and fractional power to discover the best fitted model for PHE desorption process. The pseudo-first-order model is defined as following equation [30, 31]:
| 4 |
The pseudo-second-order kinetic model is expressed through equation below [31]:
| 5 |
This model can be presented by at least four different linear types as follows [31]:
| 6 |
| 7 |
| 8 |
| 9 |
Fractional power kinetic model is given as equation below [13, 31]:
| 10 |
Where, qe and qt (mg/kg) are desorbed amount of PHE at equilibrium and time t (min). k1 (1/min), k2 (kg/mg.min) and k (mg/kg.min) are the pseudo-first-order, pseudo-second-order and fractional power rate constants of desorption, respectively, and v is the constant of the fractional power function [13, 30, 31]. The associated parameters of pseudo-first-order, pseudo-second-order type (I), type (II), type (III), and type (IV) and fractional power kinetic equation were obtained by plotting ln(qe − qt)vs. t, t/qtvs.t, 1/qtvs.1/t, qtvs. qt/t, qt/t vs. qt, and ln qtvs.lnt, respectively [31]. The correlation coefficient values and the related parameters of kinetic models at initial PHE concentrations of 400, 800, 1200, and 1600 mg/kg are presented in Table 2. Furthermore, selection of the best-fitted kinetic model was carried out by considering the correlation coefficient (R2) and comparison between the values of calculated qe and the experimental one [32].
Table 2.
Kinetic models parameters and correlation coefficients (R2) for desorption of PHE at various initial PHE concentration
| Kinetic models | Kinetic parameters | Initial PHE concentration,C0(mg kg−1) | |||
|---|---|---|---|---|---|
| 400 | 800 | 1200 | 1600 | ||
| qe, exp(mg kg−1) | 185.49 | 326.1 | 475.77 | 563.1 | |
| Pseudo-first order | k1 (min−1) | 0.073 | 0.072 | 0.067 | 0.071 |
| qe (mg kg−1) | 149.306 | 134.29 | 113.295 | 222.516 | |
| R2 | 0.928 | 0.896 | 0.841 | 0.767 | |
| Pseudo-second order | |||||
| Type (I) | k2p (kg mg−1 min−1) | 8.06 × 10−4 | 0.0005 | 0.0013 | 3.33 × 10−4 |
| qe(mg kg−1) | 200 | 500 | 500 | 1000 | |
| R2 | 0.997 | 0.998 | 0.999 | 0.996 | |
| Type (II) | k2p(kg mg−1 min−1) | 0.001 | 0.000333 | 0.002 | 0.0005 |
| qe (mg kg−1) | 200 | 500 | 500 | 1000 | |
| R2 | 0.977 | 0.917 | 0.962 | 0.770 | |
| Type (III) | k2p(kg mg−1 min−1) | 1.036 × 10−3 | 0.000791 | 0.00149 | 0.001554 |
| qe (mg kg−1) | 192.4 | 350.4 | 482.88 | 545.9 | |
| R2 | 0.952 | 0.794 | 0.942 | 0.727 | |
| Type (IV) | k2p(kg mg−1 min −1) | 9.759 × 10−4 | 0.000599 | 0.00139 | 0.001096 |
| qe (mg kg−1) | 194.68 | 376.5 | 485.524 | 562.013 | |
| R2 | 0.952 | 0.794 | 0.942 | 0.727 | |
| Fractional power | k (mg kg−1 min -v) | 69.13 | 159.6526 | 342.0647 | 393.8618 |
| v | 0.24 | 0.189 | 0.083 | 0.082 | |
| R2 | 0.980 | 0.727 | 0.839 | 0.853 | |
Correlation coefficient (R2) of pseudo-first-order model for desorption of PHE by Tween80 is significant (0.928) at initial PHE concentration of 400 mg/kg; however, they varied in the range of 0.782–0.896 at initial PHE concentrations of 800–1600 mg/kg, which are relatively good. Furthermore, the calculated qe obtained by this model at all initial concentrations are beyond the experimental values, showing that this is not the model that can describe the desorption of PHE from the soil.
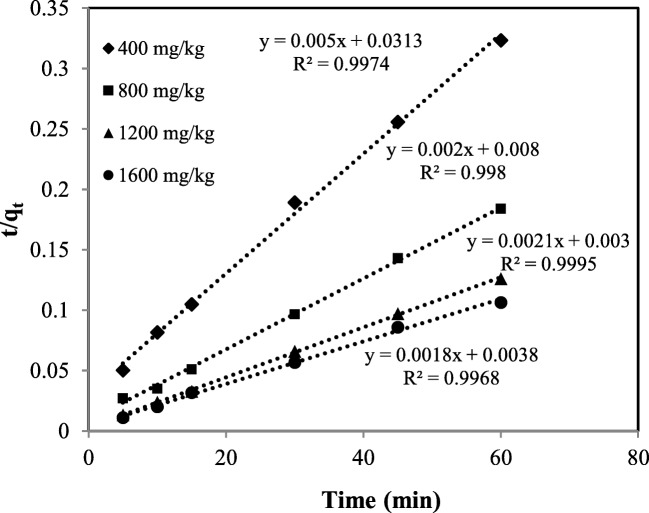
Linear plots of pseudo-second-order equation type (I) (t/qtvs.t) at initial concentrations of 400, 800, 1200, 1600 mg/kg are shown in Fig. 2. It can be seen that the linear regression is extremely reliable at all initial PHE concentrations. In addition, having a closer look to Table 2, the values of correlation coefficients obtained from the equation are the highest, compared to other equations at all the initial PHE concentrations. There is good compatibility between the calculated qe obtained by the equation and the experimental values at initial concentrations of 400 and 1200 mg/kg, but they disagree at initial concentrations of 800 and 1600 mg/kg.
Fig. 2.
Pseudo-second order kinetic model (type (I)) for desorption of PHE from soil by using Tween 80
The values of correlation coefficient of pseudo-second-order equation type (II) (1/qtvs.1/t) are high (0.917–0.977), except at initial PHE concentration of 1600 mg/kg which is moderate (0.770). As the equation type (I), the values of experimental and calculated qe are consistent at initial concentrations of 400 and 1200 mg/kg; however, these values are not close to each other at initial concentrations of 800 and 1600 mg/kg.
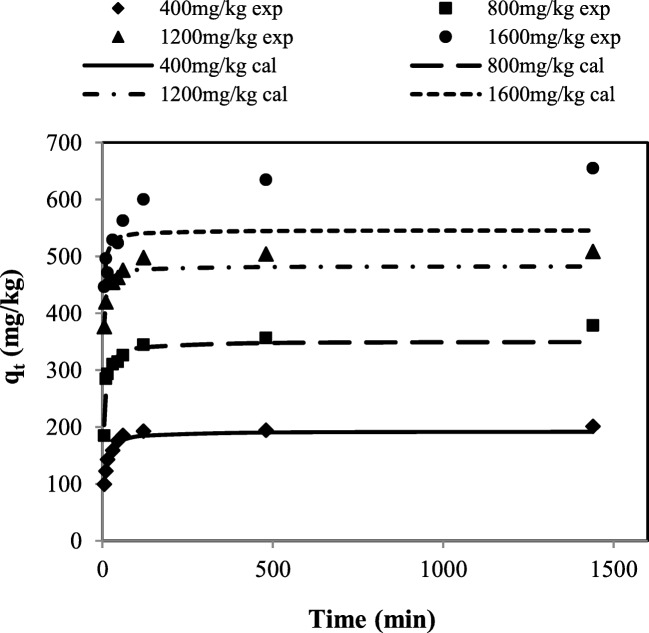
The values of correlation coefficients (R2) obtained from type (III) (qtvs. qt/t) and (IV) (qt/t vs. qt) of pseudo-second-order model linearized form were in the range of 0.727–0.952 for initial PHE concentrations of 400–1600 mg/kg. However, the calculated qe values by these equations are in good agreement with experimental values, demonstrating that these equations are appropriate to predict the values of qe. In Fig. 3, the calculated values of desorbed amount of PHE from the equation type (III) of pseudo-second-order model and the experimental values are plotted next to each other as a function of the reaction time. As can be seen, the calculated values are consistent with the experimental amounts of desorbed PHE at each initial PHE concentration. In previous studies, pseudo-second-order model was also reported as a suitable model to describe PHE desorption from soil [13, 30].
Fig. 3.
Desorbed amount of PHE as a function of time (experimental results (markers) and the calculated values (lines) obtained by equation type (III) of pseudo-second-order model) at initial PHE concentrations of 400, 800, 1200 and 1600 mg/kg
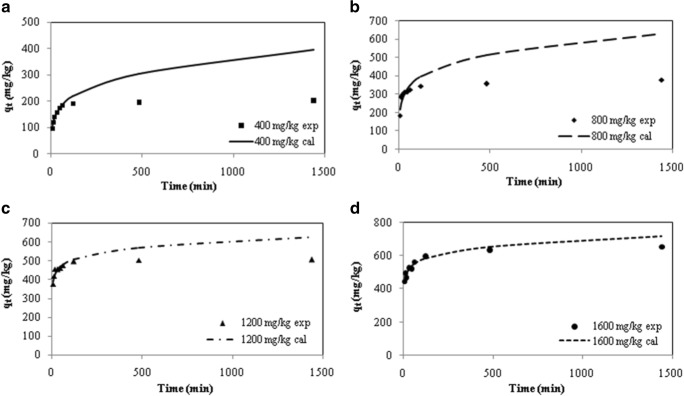
We also determined the amount of desorbed PHE by fractional power equation. The results are shown in Fig. 4a–d. It can be observed that the calculated values of PHE desorption quite agree with experimental data at various initial concentration up to the equilibrium time (60 min). In accordance with the present findings, Fonseca et al. (2010) found that the experimental values of desorbed PHE were well-fitted by empirical power function model [13]. However, in this study, it was observed that the experimental and calculated values did not match well in the times out of equilibrium. As seen in the Fig. 4a–d, this observation is more apparent at lower initial PHE concentrations and by increasing initial concentration, experimental data are being more consistent with calculated values. The values of qe obtained from fractional power equation at initial PHE concentration of 400, 800, 1200, 1600 mg/kg were 184.68, 346.13, 480.5, and 551 mg/kg respectively, which are considerably, close to the experimental values. It can be concluded that this model can estimate the values of qe accurately at every initial concentration.
Fig. 4.
Desorbed amount of PHE versus time (experimental results (markers) and the calculated values (lines) obtained by fractional power equation) at initial PHE concentrations of (a) 400, b 800, c 1200, and d 1600 mg/kg
Effect of initial PHE concentration and study of PHE desorption isotherms in the presence of Tween80
Initial concentration of PHE is among the critical parameters that influences on the effectiveness of PAHs desorption by using different surfactants. In the present study, based on the results obtained from ANOVA statistical test, initial PHE concentrations had also a significant effect on the desorbed amount of PHE and PHE desorption rate% as well (P > 0.0001). Figure 5 shows the amount of desorbed PHE and the percentage of PHE desorption versus different initial PHE concentrations. It can be seen that with increasing initial PHE concentration, a sharp decrease was happened in the PHE desorption% from 100 to 400 mg/kg which was followed by a slight reduction in the desorption percentage of PHE from 400 to 1600 mg/kg. However, as observed in Fig. 5 the raise in initial PHE concentration from 100 to 1600 mg/kg resulted in increment of the desorbed amount of PHE from 79.56 to 563.1 mg/kg. The reason of this phenomenon would be the higher solubilization capacity of Tween80 at its available concentration in the soil slurry system than the amounts of PHE in the soil in the present work. As mentioned before in the soil surfactant solution system, due to sorption of the surfactant onto the soil particles, CMC would be greater than that of the liquid system, which is called CMCeff [33]. The values of this parameter is 10 mg surfactant/g soil, based on our previous study, regarding to liquid/soil ratio of 30 v/w (mL/g) in the present study, it would be about 350 mg/L, implying that the available Tween80 concentration in the system is 2400 mg/L. On the basis of our previous research, solubilization capacity of Tween80 solution with this concentration for PHE is about 77 mg/L, that is higher than the maximum content of PHE in the soil in present work in case total amount of the PAH to be transferred and solubilized in liquid medium (~53 mg/L). Nevertheless, the sorption of the hydrophobic contaminant onto the soil and sorption of the surfactant that causes severe sorption of the PAH onto the soil particles hinder 100% desorption of PHE.
Fig. 5.
Desorbed amount of PHE and PHE desorption rate% as a function of initial PHE concentration, C0
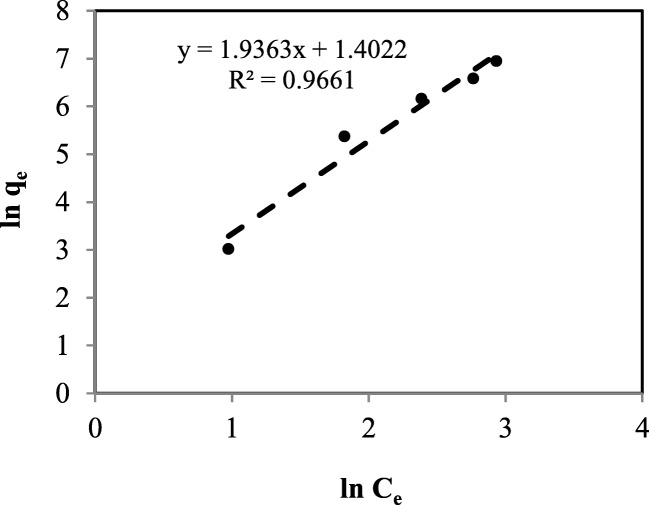
In the present study, the experimental data were examined by using linear form of three isotherm models including Freundlich, Langmuir, and Temkin. Freundlich isotherm equation is defined as follows [31]:
| 11 |
Langmuir isotherm model is given as following [31]:
| 12 |
This model can be existed as at least four linear equations which are [31]:
| 13 |
| 14 |
| 15 |
| 16 |
Temkin isotherm is described as following equation [31]:
| 17 |
Where, KF ((mg/kg) (L/mg)1/n) is Freundlich constant and can be described as the distribution coefficient and n is the Freundlich exponent. KL (L/mg) is the Langmuir constant, qm is the maximum desorption capacity (mg/g) and KT (L/mg) of Temkin isotherm constant [31, 34]. The related parameters of Freundlich, four linear forms of Langmuir and Temkin isotherm models can be obtained by plotting ln qe vs. lnCe, Ce/qe vs. Ce, 1/qe vs. 1/Ce, qe vs. qe/Ce, qe/Ce vs. qe, and qe vs. ln Ce, respectively [31]. The values of correlation coefficients and the parameters of isotherm models are given in Table 3. Choosing among the fitted isotherm equations to describe desorption process is conducted based on the correlation coefficient [32].
Table 3.
Isotherms parameters and correlation coefficients (R2) for the desorption of PHE
| Isotherms | Parameters | Values |
|---|---|---|
| Freundlich | KF (mg/kg) (L/mg)1/n | 4.063318 |
| n | 0.516529 | |
| R2 | 0.966 | |
| Langmuir | ||
| Type(I) | KL (L/mg) | −0.04902 |
| qm (mg/kg) | 200 | |
| R2 | 0.553 | |
| Type(II) | KL (L/mg) | −0.06667 |
| qm (mg/kg) | 100 | |
| R2 | 0.937 | |
| Type(III) | KL (L/mg) | −0.05 |
| qm (mg/kg) | 253.6 | |
| R2 | 0.808 | |
| Type(IV) | KL (L/mg) | −0.040 |
| qm (mg/kg) | 435.5 | |
| R2 | 0.808 | |
| Temkin | KT (L/mg) | 0.318916 |
| qm (mg/kg) | 478.2 | |
| R2 | 0.889 | |
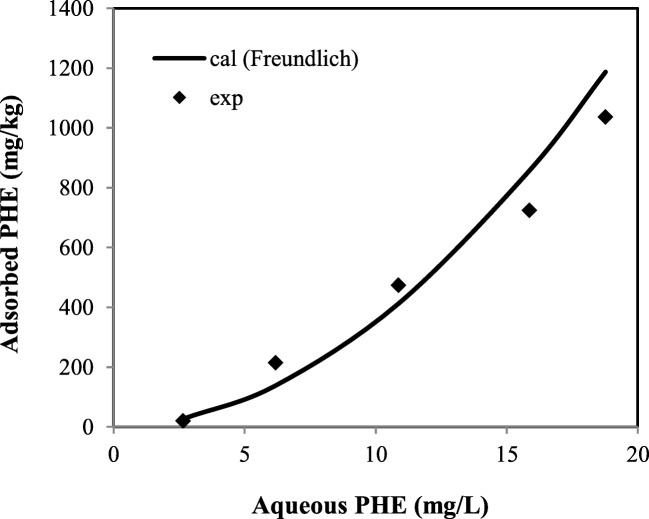
As presented in Table 3, Freundlich equation has the highest amount of correlation coefficient compared to the other applied models, indicating that it is the best-fitted model for description of PHE desorption process. Linear regression of this model is also depicted in Fig. 6. Calculated values of adsorbed (retained) PHE (mg/kg) obtained by Freundlich model beside experimental values as a function of the equilibrium aqueous PHE (mg/L) are shown in Fig. 7. As illustrated, the experimental data are quite well fitted with the obtained amounts of adsorbed PHE (mg/kg) by Freundlich model. However, the experimental values of adsorbed PHE (mg/kg) relatively disagreed with the calculated values obtained by the rest of the equations applied in the present study. This finding is in agreement with the obtained results of Yu et al. (2011) who reported the reliability of Freundlich isotherm model to fit the experimental data of PHE and PYR desorption by using DOM and biosurfactants [34].
Fig. 6.
Freundlich isotherm model for desorption of PHE from soil in the presence of Tween 80
Fig. 7.
Adsorbed PHE (experimental values and calculated values obtained by Freundlich model) versus to equilibrium aqueous PHE
Conclusion
PHE desorption rate from contaminated soil is highly affected by the nonionic surfactant Tween80. Therefore, this method is a useful method to determine available fraction of the contaminant. Results of the present study revealed that PHE desorption% increased sharply within the first hour of the reaction and then reached to the equilibrium conditions. Desorption equilibrium time is introduced to estimate the rapid desorption fraction, is considered to be the available fraction. In the current study this fraction decreased from 79% to 35% by increasing initial PHE concentration from 100 to 1600 mg/kg. Availability assessment provides the management of contaminated sites by choosing a proper option for remediation and predicting achievable treatment efficiency.
Experimental data were well described by equations type (III) and (IV) of pseudo-second-order model linearized form. In addition, more agreement was observed between the calculated values of desorption obtained by fractional power equation and the experimental data with increasing initial PHE concentrations. It can be concluded that the PHE desorption process from soil with high initial PHE concentration can be described by fractional power kinetic model. Finally, the obtained results of equilibrium studies showed that equilibrium data of Tween80 enhanced PHE desorption process were best fitted by Freundlich isotherm model.
Acknowledgements
This research has been supported by Tehran University of Medical Sciences & health Services [grant number 93-02-61-25084].
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.López-Vizcaíno R, Sáez C, Cañizares P, Rodrigo MA. The use of a combined process of surfactant-aided soil washing and coagulation for PAH-contaminated soils treatment. Sep Purif Technol. 2012;88:46–51. [Google Scholar]
- 2.Ravanipour M, Kalantary R, Mohseni-Bandpi A, Esrafili A, Farzadkia M, Hashemi-Najafabadi S. Experimental design approach to the optimization of PAHs bioremediation from artificially contaminated soil: application of variables screening development. J Environ Health Sci Eng. 2015;13(1):1–10. doi: 10.1186/s40201-015-0178-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aryal M, Liakopoulou-Kyriakides M. Biodegradation and kinetics of phenanthrene and pyrene in the presence of nonionic surfactants by Arthrobacter strain Sphe3. Water Air Soil Pollut. 2013;224(2):1–10. [Google Scholar]
- 4.Rezaei Kalantari R, Badkoubi A, Mohseni-bandpi A, Esrafili A, Jorfi S, Dehghanifard E. Modification of PAHs biodegradation with humic compounds. Soil Sediment Contam. 2013;22(2):185–198. [Google Scholar]
- 5.Portet-Koltalo F, Ammami MT, Benamar A, Wang H, Le Derf F, Duclairoir-Poc C. Investigation of the release of PAHs from artificially contaminated sediments using cyclolipopeptidic biosurfactants. J Hazard Mater. 2013;261:593–601. doi: 10.1016/j.jhazmat.2013.07.062. [DOI] [PubMed] [Google Scholar]
- 6.Mao J, Luo Y, Teng Y, Li Z. Bioremediation of polycyclic aromatic hydrocarbon-contaminated soil by a bacterial consortium and associated microbial community changes. Int Biodeterior Biodegrad 2012;70(0):141–147. 10.1016/j.ibiod.2012.03.002.
- 7.Kalantary RR, Mohseni-Bandpi A, Esrafili A, Nasseri S, Ashmagh FR, Jorfi S, et al. Effectiveness of biostimulation through nutrient content on the bioremediation of phenanthrene contaminated soil. J Environ Health Sci Eng. 2014;12(1):143. doi: 10.1186/s40201-014-0143-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yap CL, Gan S, Ng HK. Ethyl lactate-Fenton treatment of soil highly contaminated with polycyclic aromatic hydrocarbons (PAHs) Chem Eng J. 2012;200–202:247–256. [Google Scholar]
- 9.Saberi N, Aghababaei M, Ostovar M, Mehrnahad H. Simultaneous removal of polycyclic aromatic hydrocarbon and heavy metals from an artificial clayey soil by enhanced electrokinetic method. J Environ Manag. 2018;217:897–905. doi: 10.1016/j.jenvman.2018.03.125. [DOI] [PubMed] [Google Scholar]
- 10.Falciglia PP, Malarbì D, Greco V, Vagliasindi FGA. Surfactant and MGDA enhanced – Electrokinetic treatment for the simultaneous removal of mercury and PAHs from marine sediments. Sep Purif Technol. 2017;175:330–339. [Google Scholar]
- 11.Zhou W, Zhu L. Enhanced soil flushing of phenanthrene by anionic–nonionic mixed surfactant. Water Res. 2008;42(1–2):101–108. doi: 10.1016/j.watres.2007.07.021. [DOI] [PubMed] [Google Scholar]
- 12.Mousset E, Huguenot D, van Hullebusch ED, Oturan N, Guibaud G, Esposito G, Oturan MA. Impact of electrochemical treatment of soil washing solution on PAH degradation efficiency and soil respirometry. Environ Pollut. 2016;211:354–362. doi: 10.1016/j.envpol.2016.01.021. [DOI] [PubMed] [Google Scholar]
- 13.Fonseca B, Pazos M, Figueiredo H, Tavares T, Sanromán MA. Desorption kinetics of phenanthrene and lead from historically contaminated soil. Chem Eng J. 2011;167(1):84–90. [Google Scholar]
- 14.Barnier C, Ouvrard S, Robin C, Morel JL. Desorption kinetics of PAHs from aged industrial soils for availability assessment. Sci Total Environ. 2014;470-471:639–645. doi: 10.1016/j.scitotenv.2013.10.032. [DOI] [PubMed] [Google Scholar]
- 15.Mouton J, Mercier G, Blais J-F. Amphoteric surfactants for PAH and lead polluted-soil treatment using flotation. Water Air Soil Pollut. 2009;197(1–4):381–393. [Google Scholar]
- 16.Ahn CK, Kim YM, Woo SH, Park JM. Soil washing using various nonionic surfactants and their recovery by selective adsorption with activated carbon. J Hazard Mater 2008;154(1–3):153–60. 10.1016/j.jhazmat.2007.10.006, 153. [DOI] [PubMed]
- 17.Wei Y, Liang X, Lin W, Guo C, Dang Z. Clay mineral dependent desorption of pyrene from soils by single and mixed anionic–nonionic surfactants. Chem Eng J. 2015;264:807–814. [Google Scholar]
- 18.Zhu L, Zhou W. Partitioning of polycyclic aromatic hydrocarbons to solid-sorbed nonionic surfactants. Environ Pollut. 2008;152(1):130–137. doi: 10.1016/j.envpol.2007.05.001. [DOI] [PubMed] [Google Scholar]
- 19.Alcántara MT, Gómez J, Pazos M, Sanromán MA. PAHs soil decontamination in two steps: desorption and electrochemical treatment. J Hazard Mater. 2009;166(1):462–468. doi: 10.1016/j.jhazmat.2008.11.050. [DOI] [PubMed] [Google Scholar]
- 20.Jin D, Jiang X, Jing X, Ou Z. Effects of concentration, head group, and structure of surfactants on the degradation of phenanthrene. J Hazard Mater. 2007;144(1–2):215–221. doi: 10.1016/j.jhazmat.2006.10.012. [DOI] [PubMed] [Google Scholar]
- 21.Haddadi SH, Niri VH, Pawliszyn J. Study of desorption kinetics of polycyclic aromatic hydrocarbons (PAHs) from solid matrices using internally cooled coated fiber. Anal Chim Acta. 2009;652(1–2):224–230. doi: 10.1016/j.aca.2009.05.026. [DOI] [PubMed] [Google Scholar]
- 22.Cheng KY, Wong JWC. Combined effect of nonionic surfactant tween 80 and DOM on the behaviors of PAHs in soil–water system. Chemosphere. 2006;62(11):1907–1916. doi: 10.1016/j.chemosphere.2005.07.028. [DOI] [PubMed] [Google Scholar]
- 23.Peng S, Wu W, Chen J. Removal of PAHs with surfactant-enhanced soil washing: influencing factors and removal effectiveness. Chemosphere. 2011;82(8):1173–1177. doi: 10.1016/j.chemosphere.2010.11.076. [DOI] [PubMed] [Google Scholar]
- 24.Zhou W, Zhu L. Efficiency of surfactant-enhanced desorption for contaminated soils depending on the component characteristics of soil-surfactant–PAHs system. Environ Pollut. 2007;147(1):66–73. doi: 10.1016/j.envpol.2006.08.018. [DOI] [PubMed] [Google Scholar]
- 25.Gharibzadeh F, Rezaei Kalantary R, Nasseri S, Esrafili A, Azari A. Reuse of polycyclic aromatic hydrocarbons (PAHs) contaminated soil washing effluent by bioaugmentation/biostimulation process. Sep Purif Technol. 2016;168:248–256. [Google Scholar]
- 26.Laha S, Tansel B, Ussawarujikulchai A. Surfactant–soil interactions during surfactant-amended remediation of contaminated soils by hydrophobic organic compounds: a review. J Environ Manag. 2009;90(1):95–100. doi: 10.1016/j.jenvman.2008.08.006. [DOI] [PubMed] [Google Scholar]
- 27.Saeedi M, Li LY, Grace JR. Desorption and mobility mechanisms of co-existing polycyclic aromatic hydrocarbons and heavy metals in clays and clay minerals. J Environ Manag. 2018;214:204–214. doi: 10.1016/j.jenvman.2018.02.065. [DOI] [PubMed] [Google Scholar]
- 28.Zhao B, Zhu L, Gao Y. A novel solubilization of phenanthrene using Winsor I microemulsion-based sodium castor oil sulfate. J Hazard Mater. 2005;119(1):205–211. doi: 10.1016/j.jhazmat.2004.12.009. [DOI] [PubMed] [Google Scholar]
- 29.Viglianti C, Hanna K, de Brauer C, Germain P. Removal of polycyclic aromatic hydrocarbons from aged-contaminated soil using cyclodextrins: experimental study. Environ Pollut. 2006;140(3):427–435. doi: 10.1016/j.envpol.2005.08.002. [DOI] [PubMed] [Google Scholar]
- 30.Wang G, Zhou Y, Wang X, Chai X, Huang L, Deng N. Simultaneous removal of phenanthrene and lead from artificially contaminated soils with glycine-β-cyclodextrin. J Hazard Mater. 2010;184(1–3):690–695. doi: 10.1016/j.jhazmat.2010.08.094. [DOI] [PubMed] [Google Scholar]
- 31.Behnamfard A, Salarirad MM. Equilibrium and kinetic studies on free cyanide adsorption from aqueous solution by activated carbon. J Hazard Mater. 2009;170(1):127–133. doi: 10.1016/j.jhazmat.2009.04.124. [DOI] [PubMed] [Google Scholar]
- 32.Ahmadi M, Hazrati Niari M, Kakavandi B. Development of maghemite nanoparticles supported on cross-linked chitosan (γ-Fe2O3@CS) as a recoverable mesoporous magnetic composite for effective heavy metals removal. J Mol Liq. 2017;248:184–196. [Google Scholar]
- 33.Zhou W, Wang X, Chen C, Zhu L. Enhanced soil washing of phenanthrene by a plant-derived natural biosurfactant, Sapindus saponin. Colloids Surf A Physicochem Eng Asp. 2013;425(0):122–128. [Google Scholar]
- 34.Yu H, Huang G-h, An C-j, Wei J. Combined effects of DOM extracted from site soil/compost and biosurfactant on the sorption and desorption of PAHs in a soil–water system. J Hazard Mater. 2011;190(1–3):883–890. doi: 10.1016/j.jhazmat.2011.04.026. [DOI] [PubMed] [Google Scholar]