Comparative study of cell mechanics methods

Abstract

Cell mechanics controls important cellular and subcellular functions, including cell adhesion, migration, polarization, and differentiation, as well as organelle organization, and trafficking inside the cytoplasm. Yet, reported values of cell stiffness and viscosity vary strongly, suggesting disagreements in how results of different methods are obtained or analyzed. To address this issue and illustrate the complementarity of different instruments, we present, analyze, and critically compare measurements conducted by some of the most widely used methods of cell mechanics: atomic force microscopy, magnetic twisting cytometry, particle-tracking microrheology, parallel-plates rheometry, cell monolayer rheology, and the optical stretcher. These measurements highlight that elastic and viscous moduli of MCF-7 breast cancer cells can vary 1,000 fold and 100 fold, respectively. We discuss the sources of these variations, including the level of applied mechanical stress and rate of deformation, the geometry of the probe, the location probed in the cell, and the extracellular microenvironment.

Introduction

Cells in vivo are continuously subjected to mechanical forces, including shear, compressive, and extensional forces (terms highlighted in bold are defined in supplementary note 1; Fig. 1). The ability of cells to deform and actively respond to mechanical forces is critical to the proper embryonic development and the homeostasis of adult tissues and organs. Cell mechanics is the factor that defines cell response to the mechanical forces exercised by the cell microenvironment, including other cells and the extracellular matrix ¹. This cellular response can be viscous, elastic, or viscoelastic, as well as passive or active. Cell mechanics controls important cellular and subcellular functions, including cell adhesion, migration, polarization, and differentiation, as well as organelle organization, trafficking inside the cytoplasm, and activity. The recent development of tools to measure cell mechanics has revealed that changes in cell and nuclear mechanics are hallmarks of many human diseases, particularly metastatic cancer, cardiovascular disease, inflammation, laminopathies, host-microbe interactions in infectious diseases, and frailty in aging ^2–6. Values of cell elasticity (which measures the stretchiness of cells) and viscosity (which measures viscous dissipation) reported in the literature vary strongly even when different groups use the same instruments. A contribution to these variations is often attributed to differences in cell culture conditions (e.g., sometimes subtle differences in temperature, pH, cell passage number, etc.), which prevent direct comparisons among datasets and may have slowed down the translation of cell-mechanics instruments for clinical applications.

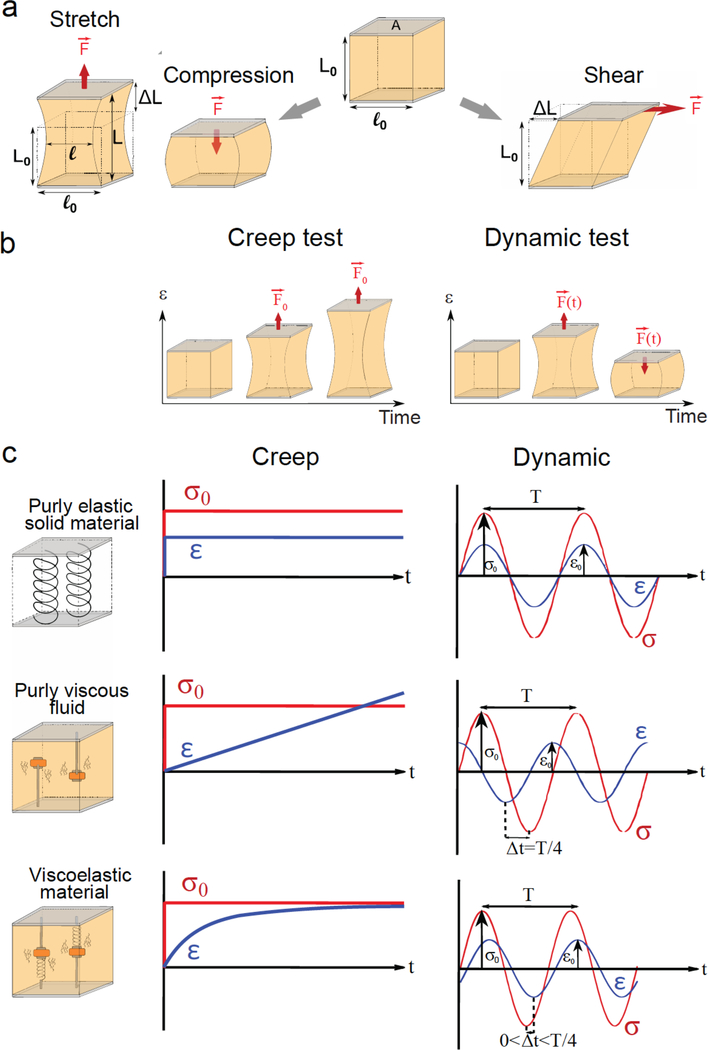
Figure 1: Description of rheological tests.

(a) Different geometries of deformation. To test the mechanical properties of a material, one can either stretch/compress it (left), or apply a mechanical shear stress (right). While stretching, deformation of the material results from applying a pulling force F perpendicular to the surface of the sample. For a surface of area A, the applied (normal) stress is given by σ = F/A, and the deformation (or strain) in the direction of the applied force is ε = ΔL/L_o, and ΔL = L-L₀ is the sample elongation along the direction of stretching. Similarly, compression corresponds to a deformation (shortening) that results from applying a pushing force perpendicular to the surface area. In contrast, a shear test implies deformations that occur when the applied force is parallel (tangential) to the surface of the sample. (b) Constant or oscillating applied stress: A creep test consists in applying a constant stress F₀/A overtime and recording the resulting deformation ε(t) of the sample (left). For a dynamic test, the applied force oscillates resulting in an oscillatory deformation of the sample (right). (c) Viscoelasticity: The mechanical response of any material can be described a combination of two ideal behaviors, those of an elastic solid and a viscous liquid. Purely elastic solids, like springs, deform instantaneously and in proportion to the applied force. In creep, the strain sets instantaneously to its equilibrium value ε_f. In dynamic tests, the deformation follows the oscillating applied stress, meaning that there is no phase shift between ε(t) and σ(t) signals. In both tests, the ratio between stress and strain is constant and corresponds to the elastic modulus E = σ/ε, which is expressed in Pascals (Pa),. E quantifies the rigidity of the material. Like springs, solids with high E are harder to deform. Purely viscous fluids, like water, will flow indefinitely when subjected to a creep test. The rate dε/dt at which the liquid flows under a given stress σ₀ depends on its viscosity η, δε/δτ = σ₀/η. In dynamic tests, the oscillating deformation is delayed compared to the applied oscillating stress, and the phase shift between ε(t) and σ(t) signals is Δt = T/4, where T is the period of the oscillations. The amplitudes of stress and strain are then related by σ = (2πfη)ε, where f = 1/T is the frequency of the oscillations. Thus (2πfη) has the dimension of a modulus, and quantifies the viscous response depending on the frequency of the test. Most materials are viscoelastic and share characteristics of both elastic solids and viscous liquids. Depending on the time scale (or, equivalently, on the frequency), the elastic or viscous-like behavior may dominate the response of such material. In dynamic tests, the phase shift between ε(t) and σ(t) will be between 0 and T/4. The response of the viscoelastic sample is then quantified through a complex modulus E* = E’ + i E”, allowing one to decouple the elastic-like contribution E’ (the in-phase component of the response) from the viscous-like component E” (phase shift Δt = T/4). In the particular example of the figure, E’ = E the elastic modulus of springs, and E”= 2πfη, where η is the viscosity of the surrounding liquid and f the frequency of the oscillations. Thus, at high frequency (short times) E” > E’ and the viscous behavior dominates, while at low frequency (long times) E’ > E” and the behavior is dominantly elastic, as observed from a creep test.

To address these issues and illustrate the great complementarity of different instruments, we present, analyze, and critically compare measurements conducted by different research groups using different instruments, applied to the same commonly used MCF-7 human breast cancer cells cultured in the same environmental conditions in vitro. The instruments tested include some of the most widely used methods of cell mechanics: atomic force microscopy (AFM), magnetic twisting cytometry (MTC), particle-tracking microrheology (PTM), parallel-plates rheometry, cell monolayer rheology (CMR), and optical stretching (OS).

Overall, although the underlying mechanical principles remain the same, our measurements highlight how cell mechanics depends exquisitely on the level of mechanical stress and rate of deformation to which the cell is subjected, the geometry of the mechanical probe used in the experiments, the probe-cell contact area, the probed location in the cell (e.g., cell cortex, nucleus, lamella, cytoplasm), and the extracellular context (e.g. monolayer of cells vs. single cells, adherent vs. free-floating cells, etc.). These results also highlight how mechanical properties of cells can vary by orders of magnitude, depending on the length scale at which cell viscoelasticity is probed, from tens of nanometers (e.g., the diameter of an actin fiber) to several microns (the size of a whole cell).

Results

To ensure consistency, the measurements presented below were conducted in different laboratories on MCF-7 cells from the same lot, cultured in medium from the same lot, all directly provided by ATCC. The mechanical properties of these cells were measured by a total of eight laboratories using AFM, MTC, PTM, parallel-plates rheometry, CMR and OS. Details of the techniques used by the participating laboratories can be found in Supplementary Table 1. Different moduli were measured by different methods, and a detailed description of moduli and their inter-relationship can be found in the supplemental information. Among the methods tested in this study, AFM, parallel plates, and OS, all provide measurements of Young’s modulus (E), while MTC, CMR, and PTM all provide measurements of the shear modulus (G).

AFM

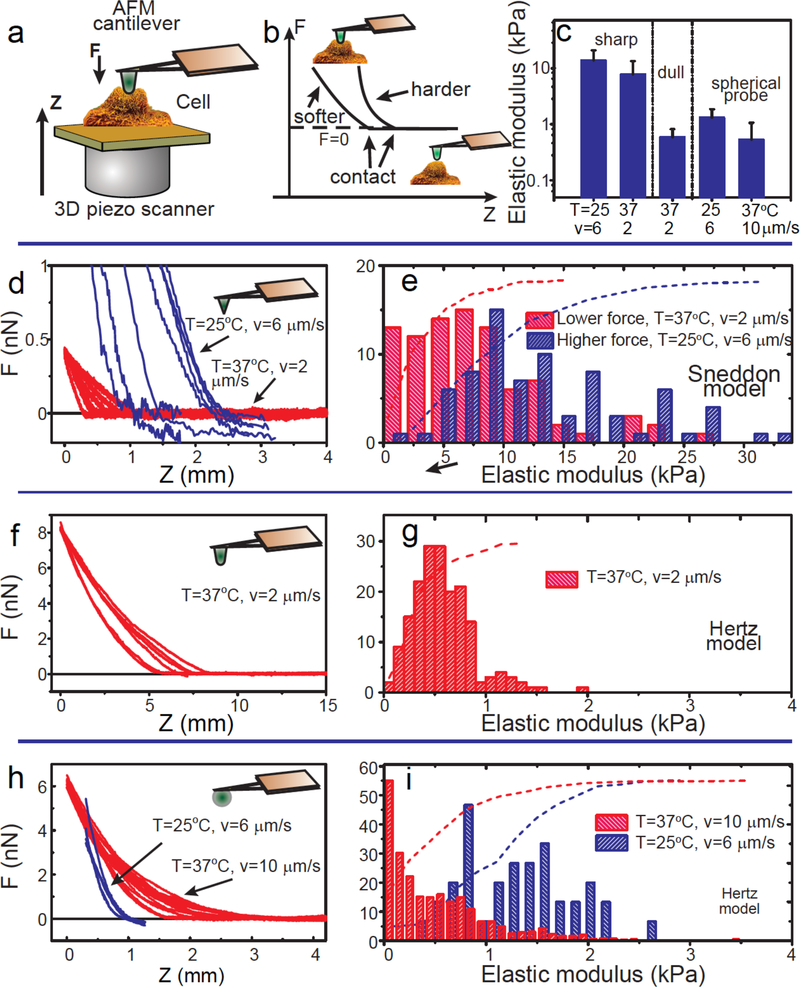
AFM-based indentation is a commonly used technique to quantify the mechanical properties of adherent cells with subcellular resolution. An AFM consists of a cantilever of calibrated stiffness applying a preset force or deformation at a defined speed onto an adherent cell or tissue and, through laser deflection and detection by a photodetector (Fig. 2a), measures the corresponding resisting force from the deformation of the cell (Fig. 2b). A 3D piezo scanner allows for x, y, and z displacements of the cantilever relative to the underlying cell (Fig. 2a). Here, MCF7 cells were indented by either nanoscale pyramidal probes (radius of the probe apex ~10 nm), mesoscale spheroconical probes (~750 nm) or microscale spherical probes (~ 5 μm) (Fig. 2c).

Figure 2. AFM measurements.

The measurements were conducted using sharp conical AFM probes, conospherical probes of radius 750nm, and spherical probes of radius 2500nm. (a) Schematics of the measurements of the cell mechanics. An AFM probe of well-defined geometry indents a cell along the vertical z-axis. (b) Force curves collected with AFM. Force F vs. vertical position z of the cell. Typical force curves for mechanically soft and hard samples are shown. (c) Average elastic moduli obtained with various AFM probes under different conditions (vertical indenting speed v and surrounding temperature T) are shown. The error bar indicates one standard deviation. (d, f, h) Raw AFM force data (F versus z) obtained with the sharp conical probes (d), the dull conospherical probe (semi-vertical angle ~22.5°) (f), and the spherical probes (h). (e, g, i) Corresponding histograms and cumulative probabilities of the elastic modulus obtained for indentation depths of 0–300nm. The appropriate models were used for each type of the AFM probes: the Sneddon model for the sharp conical probes (e), the Hertz model for the dull conospherical probe (g), and the spherical probes (i). Sample temperatures and indenting speeds are shown in the histograms. AFM measurements and measured cell sample size are summarized in Supplementary Table 2.

The elastic (effective Young’s) modulus of the cells is quantified by fitting the curves of the measured force as a function of the vertical position of the cantilever using so-called elastic contact models that account for the geometry of indentation (see supplementary information). When measured with a nanoscale AFM probe, the mechanical properties of cells are highly heterogeneous and display large cell-to-cell variations (Fig. 2, d and e). For indentations of ~1 μm produced at a speed of 2 μm/s with a sharp tip – which are both typical – the average static effective Young elastic modulus of MCF-7 cells over the central nuclear region was 5.5 ± 0.8 kPa (kiloPascal) and 3.8 ± 0.5 kPa over flat regions of the cell body, between the nucleus and the cell edge. Measurements at a higher indentation speed resulted in higher elastic moduli of 10.5 ± 0.5 kPa (Fig. 2, c–e).

By indenting cells with a larger probe (Fig. 2, f, g), AFM measurements are less sensitive to local cell heterogeneities, and the elastic modulus is significantly lower. Probes with an intermediate apex radius (~0.75 μm) which transitions to an axisymmetric cone to indent the nuclear region applied at a speed of 2 μm/s yielded an elastic modulus of 0.58 ± 0.23 kPa when computed using the “blunted indenter” contact model ^7,8. Applying the Hertz model of indentation ⁹, 5-μm diameter glass beads attached to tipless cantilevers (Fig. 2, h,i) and indentation depth of ~ 300 nm yielded elastic moduli of 0.53 ± 0.52 kPa for an indentation speed of 10 μm/s at 37° C and 0.81 ± 0.06 kPa for 6 μm/s at room temperature.

Whole-cell deformation measurements

Once MCF7 cells are detached from their underlying substrates, they round up (similarly to cancer cells in blood vessels after intravasation) and can be kept alive in suspension for a few hours. To measure the viscoelastic properties of cells in suspension, methods that preserve this suspended state are required, including the parallel-plates rheometer and the OS:

Parallel-plates rheometer

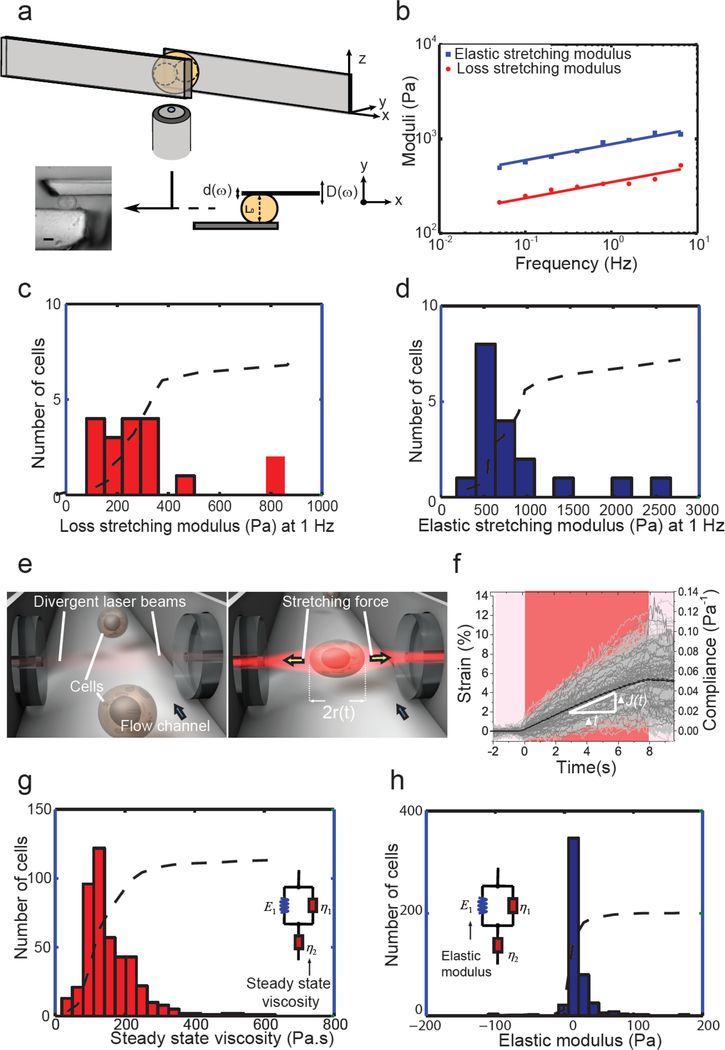
The parallel-plates rheometer extracts the Young (extensional) modulus and deformability (i.e., compliance) at the global cellular scale ¹⁰. A single cell is placed between a rigid plate and a flexible plate of calibrated stiffness k used as a force probe and stretched through constant or oscillatory displacements (Fig. 3a). For oscillatory displacements of the plates of frequency ω (Fig. 1), the elastic (storage) and viscous (loss) moduli, E’(ω) and E”(ω), were observed to be weak power laws of the frequency, E’(ω) ~ E”(ω) ~ ω^α with α<<1 (Fig. 3b). The exponent α of this power law estimates the balance between dissipative and elastic behaviors: A higher exponent signifies higher viscous dissipation; in particular, α = 0 for a purely elastic solid (e.g. rubber), while α = 1 for a viscous liquid (e.g. water). The viscous modulus of MCF-7 cells at a frequency of 1 Hz was E₀” = 340 ± 40 Pa, the elastic modulus was E₀’ = 950 ± 150 Pa (Fig. 3, c and d), and α = 0.18 ± 0.01, indicating a predominantly elastic response.

Figure 3. Whole-cell deformation measurements.

(a-d): cells between surfaces. (a) Schematic of the parallel-plates rheometer. An oscillating displacement D(ω) is applied at the basis of the flexible microplate and the resulting displacement d(ω) at the tip of this microplate is recorded. The force applied to the cell is proportional to the flexible plate deflection δ: F = kδ. The picture represents a side view of an MCF7 cell between the microplates. Scale bar, 10 μm. (b) Elastic (E’, blue squares) and viscous (E”, red circles) extensional moduli as a function of frequency for a single MCF-7 cell in a log-log graph showing weak power-law behavior. (c and d) Distributions of viscous (c) and elastic (d) moduli (n = 18 cells). The mean values for viscous and elastic moduli were 340 ± 50 Pa and 950 ± 140 Pa, respectively. (e) Schematic of the OS: two diverging, counter-propagating laser beams emanating from single-mode optical fibers trap cells at low powers as they are being flowed into the trapping region using a microfluidic channel (left) and stretch them at higher powers (right). (f). Strain and compliance profiles for each cell measured in the OS. Cells (n = 514 cells) were trapped for 2 s at 0.2 W per fiber and stretched for 8 s (red portion of graph) at 0.75 W per fiber. The black curve shows average strain and compliance for the entire population. The average peak strain (at t = 8 s) was 5.16 ± 0.11%; the average peak compliance was 0.053 ± 0.001 Pa⁻¹. The white triangle indicates a linear increase of strain, suggesting a dominant viscous behavior. (g) Distribution of steady-state viscosity obtained by fitting the compliance results for each cell to the so-called standard linear liquid model. The average steady-state viscosity was 158 ± 84 Pa.s. (h) Distribution of elastic moduli obtained from the standard linear liquid model fitting, where the average elastic modulus obtained was 18 ± 24 Pa. Dotted lines represent cumulative distributions.

The parallel-plates rheometer also measures the relaxation and creep functions of individual cells, i.e. the stress evolution under constant strain and the deformation under constant stress, respectively. MCF-7 cells showed a weak power-law behavior with an extensional modulus $E_0=\sqrt{E_0^{\prime 2}+E_0^{\prime \prime 2}}=1020\pm 150$ Pa at 1 Hz (Supplementary Fig. 1). Moreover, when applying static cell elongations and measuring the corresponding lateral cell deformations, we found a Poisson’s ratio ν = 0.33. The shear modulus could be estimated to be G₀ = E₀ /2(1+ ν) = 380 Pa at 1 Hz.

Optical stretcher (OS)

The OS consists of a dual-beam optical trap capable of inducing well-defined mechanical stresses on whole cells in suspension, to measure the creep compliance and modulus of single cells ^2,11,12. The forces that trap and deform the cell outwardly (Fig. 3e) arise from the change in the refractive index, RI, at the cell-medium interface and the ensuing transfer of momentum from the light to the cell ¹². The average RI = 1.374 ± 0.002 of MCF7 cells was measured by digital holographic microscopy ¹³ (Supplementary Fig. 2). The stress on the cells is computed using an electromagnetic wave model ¹⁴. For convenient delivery of the cells into the trapping region, the OS is integrated into a microfluidic system (Fig. 3e), which enables measurement rates > 100 cells/h.

In this study, MCF7 cells were analyzed after each cell was trapped for 2 s at a power of 0.2 W per fiber and stretched for 8 s at 0.75 W per fiber. We obtained an average peak strain (at t = 8 s) of 5.16 ± 0.11% (Fig. 3f.) and the average peak compliance (i.e. deformability) was 0.053 ± 0.001 Pa⁻¹ (Fig. 3f). The creep compliance profile reveals the composite viscous and elastic properties of cells. The white triangle (Fig. 3f) indicated a clear linear increase of strain (i.e. deformation) with time, demonstrating a dominant viscous behavior when cells are in suspension. The inverse of the slope enables a first estimation of steady-state viscosity, which we found to be about 180 Pa.s. Fitting using finer models ² yields a viscosity of 158 ± 84 Pa.s (Fig. 3g). We note here that this overwhelming dominance of viscosity over elasticity is not a feature of all cell types as measured in the OS. Elastic moduli obtained from the standard linear liquid model fitting were 18 ± 24 Pa (Fig. 3h). Even with MCF7 cells, stretching at higher laser powers produced creep curves with more pronounced elastic components (see Supplementary Fig. 2d).

Multicellular measurements

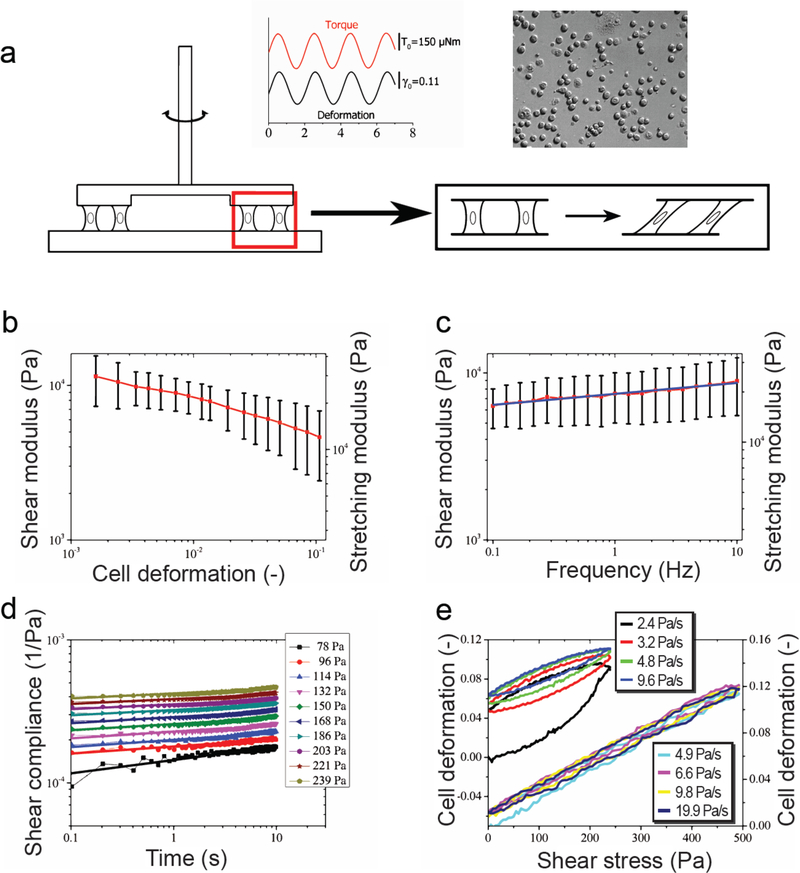
Cell monolayer rheology (CMR) consists of cells placed between two plates of a commercial rotational rheometer with a glass sensor of plate-ring geometry ¹⁵. Fibronectin coating (2 μg/cm²) of the plates enhances cell adhesion; cells form a sparse monolayer observed through a microscope during measurements (Fig. 4a). The ring rotates around its symmetry axis, which leads to the simultaneous shear deformation of the cells by about the same amount. At an oscillation frequency of 0.5 Hz, MCF7 cells exhibit a decrease in shear modulus with increasing amplitude of the imposed shear deformation. The cell shear modulus G at a relative deformation of 0.1 is G = 4.6 ± 2.2 kPa. The cell elastic (stretching) modulus was E = 12 ± 5.7 kPa, assuming a Poisson ratio of 0.3. We extracted elastic and viscous contributions to the cell shear modulus from the phase shift between excitation and cell response, G’ = 4.5 ± 2.2 kPa and G” = 1.1 ± 0.5 kPa, corresponding to elastic and viscous stretching moduli Y’ = 12 ± 5.7 kPa and Y” = 3.9 ± 2.9 kPa (Fig. 4). At a constant relative deformation of 0.02, the cell shear modulus increased with increasing oscillation frequency to fit a power law with an exponent β=0.065. Under constant load, single-cell creep compliances followed a power law in time with an exponent that decreased with increasing stress from approximately 0.1 to 0.01 (see supplementary information).

Figure 4: Cell monolayer rheology.

(a) Schematic of the experimental setup. (b) Deformation-controlled amplitude sweep: the Young’s modulus exhibits a decrease in cell stiffness with increasing oscillation amplitude at a constant frequency of 0.5 Hz. (c) Frequency sweep: cell shear modulus increases with increasing frequency at a constant shear deformation of 0.02 as a power law with exponent β=0.065 (n = 8). Error bar represents standard deviation. (d) Creep experiments at different applied stress (insert). The creep compliances follow power laws. Exponents decrease with increasing stress from ~0.1 to 0.01 (data not shown). (e) Deformation-stress curves obtained from cyclic stress ramp experiments. We apply different rates of stress increase (insert). For low rates, the deformation-stress curves exhibit nonlinear hysteresis (left x-axis, upper curve), which vanishes at high rates (right x-axis, lower curve).

Bead-based measurements

The magnetic twisting cytometer (MTC)

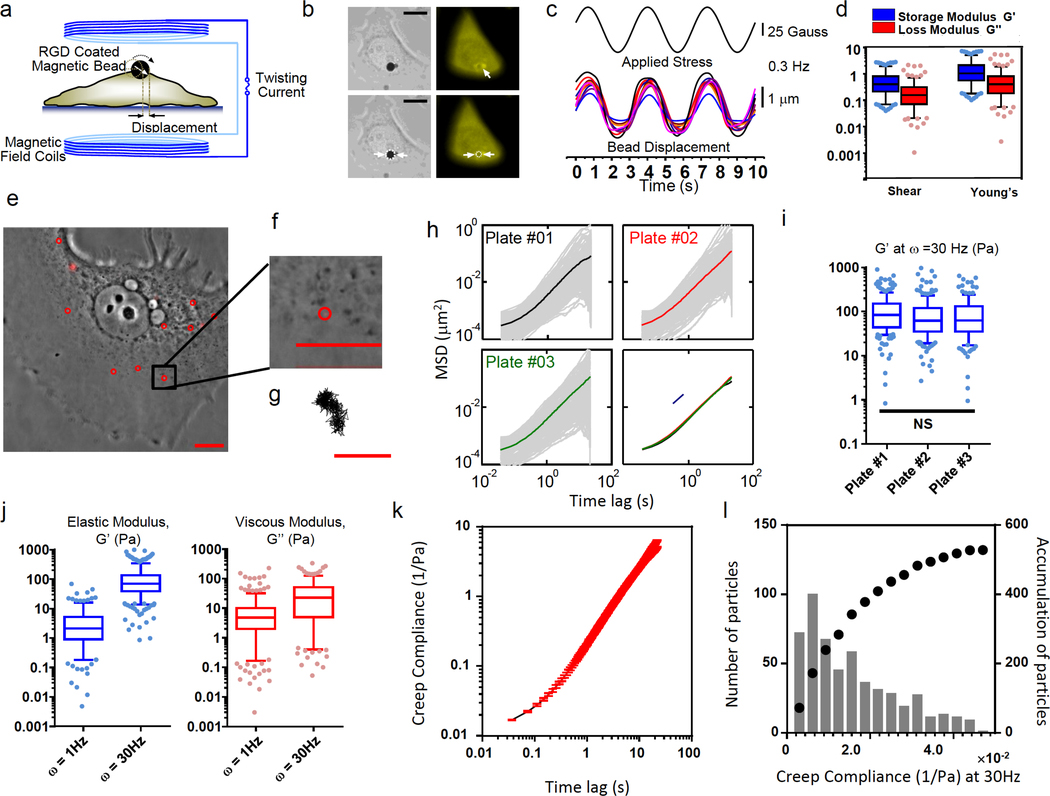
The MTC utilizes an RGD-coated ferromagnetic magnetic bead bound to the apical surface of the MCF-7 cell (Fig 5a) ¹², ¹³. A controlled homogeneous magnetic field is then applied to the cell via magnetic coils, causing the bead to displace and rotate. Based on the magnitude of the bead-cell area of contact (Fig 5b), the magnetic field applied (Fig 5c), and the displacement of the magnetic bead (Fig 5c), the MCF-7 cell stiffness is quantified ^{14, 15}. The shear modulus of MCF-7 cells was $G_0=\sqrt{G_0^{\prime 2}+G_0^{\prime \prime 2}}=0.69\pm 0.05$ kPa; the elastic modulus was G’ = 0.62 ± 0.04 kPa and the viscous modulus was G” = 0.25 ± 0.02 kPa. Assuming a Poisson’s ratio of 0.3, the Young modulus of MCF-7 cells was E₀=1.78 ± 0.12 kPa, the elastic modulus was E’=1.62 ± 0.11 kPa, and the viscous modulus was E”= 0.66 ± 0.06 kPa (Fig 5d).

Figure 5. Bead-based measurements.

(a-d) Magnetic twisting cytometry (MTC). (a) Schematic of the MTC. Dashed line denotes the position of the bead before twisting; white arrow indicates the direction of the bead magnetic moment. (b) Quantification of magnetic bead embedment in MCF7 cells. The bead embedment (~30%) was estimated by measuring the actin ring diameter from the fluorescent image and comparing it to the bead diameter from the brightfield image (double arrows). Scale bar, 10 μm. (c) Continuous magnetic field of 50 Gauss with a stress modulation (17.5 Pa peak stress) and displacements of the magnetic beads as a function of cyclic forces (0.3 Hz). For visual clarity, only data from 10 representative beads out of a total of 193 beads are shown. (d) The box-and-whisker plot shows the elasticity of MCF-7 cell measured using MTC. (e-l) Particle tracking microrheology (PTM). (e) Representative MCF-7 phase contrast image with fluorescent beads after recovery. Scale bar, 15 μm. (f). Zoom-in image of a fluorescent bead (diameter, 100 nm) inside a cell. (g) Trajectory corresponding to the bead shown in panel f. Scale bar, 200 nm. (h) PTM is reproducible: 20 cells (>100 beads) were measured from each plate. Ensemble-averaged MSDs from three different cell-culture plates were identical (bottom right). (i) Two-sided Student t-test was applied on elastic modulus at 30 Hz measured from three different plates and showed there was no significant difference (p > 0.05). (j) The box-and-whisker plot shows distribution of elastic moduli of MCF-7 cells. (k) Creep compliance of MCF-7 cells calculated from the bead MSDs. l. Distribution of creep compliance (bars) and its cumulative distribution (dotted line). For box-and-whisker plots, center lines show the median values, edges of boxes is defined by 25 and 75 percentile value, whiskers show 5 and 95 percentile value, and dots show data points below or above 5 and 95 percentile value.

Particle-tracking microrheology (PTM)

In PTM, sub-micron fluorescent beads are ballistically injected into the cytoplasm or nucleus; the cells are then allowed to recover in fresh medium overnight ¹⁶. The spontaneous movements of the beads inside the cells are recorded with ~5 nm spatial resolution, typically at video rate for 20 s ^16–18. The mean square displacements (MSDs) of beads were computed from the bead trajectories (Fig 5e–g). The ensemble-averaged MSDs from three different cell-culture plates were identical (Fig 5h). Student t-test showed that there was no significant difference in elastic modulus from three different plates measured at 30 Hz, suggesting consistent and reproducible results (Fig 5i). At 1 Hz, the elastic modulus was G’ = 4.5 ± 0.4 Pa and the viscous modulus was G” = 10.1 ± 0.9 Pa (Fig 5j). The creep compliance of the cytoplasm of MCF-7 could also be calculated from the MSDs of the beads (Fig 5k). The peak incidence of creep compliance from beads is ~ 7 × 10⁻³ (1/Pa) (Fig 5i).

Discussion

Mechanical forces are increasingly recognized as major regulators of cell phenotypes and tissue and organ formation and organization. The modulus of a cell - its viscoelastic properties - is a key factor in how cells sense these forces and interact with other cells and the extracellular matrix. In this study, the mechanical properties of a cell are here measured by different methods, including AFM, PTM, OS, CMR, MTC, and parallel-plates rheometry. In principle, different types of rheological measurements should be related to each other if certain assumptions about the materials being measured are valid, yet the average values of moduli vary by at least two orders of magnitude (Table 1). In general, the results presented in table 1 can be divided into three categories by the values of the obtained modulus: small (OS, PTM), intermediate (AFM with dull probes, parallel-plates rheometry, MTC), and high (AFM with a sharp probe, CMR). This range demonstrates the complex mechanical behavior of cells in response to forces and highlights the importance of choosing the correct technique depending on the biological question being addressed (Supplementary Table 1). These methods differ widely in how the measurements are collected and what area of the cell is probed (Supplementary Table 1) which in part explain the huge differences. Below, we discuss the reasons for similarities and variations among different measurements.

Table 1.

Overview of measurements

Technique	Results Elastic/storage modulus (kPa)*	Location of the measurement	Throughput
AFM (tip size, temperature, loading rate)
conical probe, 25 °C, 6 pm/s	13.5 ± 7.0
conical probe, 37 °C, 2 pm/s	5.5 ± 0.8
750 nm, 37 °C, 2 pm/s	0.58 ± 0.23	At the cell surface	1 – 20 cells/h
2500 nm, 25 °C, 6 pm/s	1.31 ± 0.54
2500 nm, 37 °C, 10 pm/s	0.53 ± 0.52
Whole-cell measurements
Optical stretcher	0.018 ± 0.024	Whole suspended cell	60 – 300 cells/h
Parallel plates (1 Hz)	0.95 ± 0.15	Whole adherent cell	6 cells/h
Cell monolayer measurements
Cell monolayer rheology	4.5 ± 2.2	Monolayer of cells	5–6 h/monolayer
Bead-based measurements
Particle tracking microrheology (1 Hz)	0.0045 ± 0.0004	Intracellular	30 cells/h
Particle tracking microrheology (30 Hz)	0.111 ±.002
Magnetic twisting cytometry	1.62 ± 0.11	At the cell surface	2000 cells/h

^*Elastic moduli derived from AFM represent effective Young’s modulus.

Comparison between different methods

Methods that produce intermediate modulus (AFM with dull probe, MTC, and parallel-plate rheometry) share physical similarities in the measurements and it has been shown it is possible to derive the elastic modulus of the cell body by AFM¹⁹. Smaller values derived from the AFM measurements can be explained by examining the difference in the physics of the probe-cell contact in these methods. The modulus derived from MTC data is about ~60% higher than the one derived from parallel-plates rheometry. The difference could be explained by the additional contact between the beads and microscopic roughness of the pericellular membrane (microvilli and microridges). While forces are applied to the cell directly due to physical contact in AFM, the parallel plates apply forces through molecular links developed between the plates and the cell body. In CMR, the measured elastic modulus is about an order of magnitude higher than the ones obtained from other contact probe-based methods, and this can presumably be explained by the increased level of a tensile pre-stress²⁰. Cells in CMR can apply high tensile forces in between plates due to the coating fibronectin ^10,21,22. It is also consistent with the observations of substantially higher modulus in AFM experiments when using the sharp conical AFM probe. Such probe produces much higher stresses compared to the use of dull probes. As a result, the cell presumably becomes overstretched and becomes stiffer, and this is similar to what was observed in other soft materials and viscoelastic polymer solutions ²³. In this study, MTC and CMR employ an “active” mechanical measurement where specific ligands are used. Mechanical measurements can then propagate deeply into the cell through prestress and stiff actin bundles that guide the propagation of forces over long distances ²⁴. This “active” mechanical measurement can be achieved with AFM and Parallel-plates^10,21,22.

The elasticity of MCF-7 cells measured by OS was more than two orders of magnitude smaller than the elasticity measured by AFM or MTC. The difference is likely because OS measures free-floating cells whereas the other methods measure cells adhered to a rigid glass substrate. Since it was shown that weakly adherent MCF-7 cells do not significantly change their modulus ²⁵, complete detachment of cells from the surface may require to mechanically “relax” cells. Location of probes relative to cell can also affect the mechanical measurement and it has been shown that cell nucleus is typically harder than cell periphery ^8,25–29. Elastic moduli measured by PTM are the one of the lowest among all other techniques. It is likely due to the low pre-stress in PTM measurement as well as it probes mechanical properties of cytosol ³⁰.

For further comparison of the various measurement methods, physical models are used and with these, certain assumptions are introduced such as linear elasticity for AFM or viscoelastic behavior for the other methods. The second assumption underlying most mechanical measurements of cells is that the Poisson’s ratio is close to 0.5, or at least is a constant. However, recent work indicates that the cytoplasm of living cells can behave as a poroelastic material³¹. Furthermore, Young’s and shear moduli during macroscopic measurements of biopolymer networks such as collagen networks ^32,33 and intact biological tissues ^34,35 become uncoupled from each other at deformations as small as a few percent. Consequently, error can be introduced in transforming the primary data into the material properties.

Other mechanical measurement methods

The current study does not cover the whole spectrum of cellular mechanic measurement methods. Several new techniques have recently been developed to measure cell mechanical properties at high speed (10 – 10,000 cells/sec) such as microfluidic-based methods ^36–39 and optics-based non-invasive Brillouin microscopy method^40,41. These methods potentially provide new avenues to extend cellular mechanical studies to clinically relevant samples. However, most of these techniques do not provide a direct measurement of Young’s modulus, which makes inter-comparison between techniques difficult.

Limitation of the results

Though the goal of this work is to directly compare different cell mechanical methods by probing the same type of cells with minimal biological variations, systematic errors may arise from the different instrumentations setups, which could also contribute to the observed wide spectrum of results. For example, distinct from other methods presented here, sample temporal heating while probing is one of the primary sources of systematic error for OS⁴². Cells measured with OS at different temperatures (e.g., induced by the stretching laser) leads to a shortening of the time-scales at which the cells respond. The potential source of systematic error has been discussed in the literature, for PTM ^43,44, AFM ^23,33,34, MTC ^45,46, and parallel plates ⁴⁷. Importantly, the reported systematic relative error is, in general, < 20%, while the observed difference in measured elastic moduli from these different methods can be more than three orders. The results from AFM and PTM of the present study (~1,000 fold difference) were in the same range as shown in a previous study in which mechanical properties of non-tumorigenic breast epithelial MCF-10A and tumorigenic breast cancer cell MDA-MB-231 ⁴⁸. Therefore, the measurement spread between different cell mechanical assays is less likely to be due to method-dependent systematic errors, and more likely to be due to the reasons discussed above.

Online Methods

Cell Culture

MCF-7 Cell lines (American type cell culture, Manassas, VA) were cultured at 37⁰C and 5% CO₂ in the culture medium of DMEM supplemented with 10% fetal bovine serum and Penicillin-streptomycin. Cell lines were passed every 3 to 4 days, based on their growing conditions.

Viscoelastic materials

Viscoelastic moduli are commonly used to describe both static and dynamic measurements of mechanical properties of materials. The methods considered in this paper allow us to measure either static or dynamic moduli, or both. Three primary moduli of elasticity are typically used by experts: the Young’s modulus (compression/extension), the shear modulus, and the bulk modulus. The Young’s modulus (usually denoted E) is generally measured by applying a uniaxial stress perpendicular to one of the surfaces of the sample to deform it either in compression or extension. The modulus is then measured as a function of the force per unit area (stress) and as a function of the relative change in length of the sample (strain). An important feature of Young’s moduli measurements, especially for hydrated samples, is that the volume of the sample is not necessarily conserved during such deformations. The extent to which a sample changes its volume, or equivalently the relationship between changes in vertical dimension and in the two orthogonal dimensions, is quantified by the Poisson’s ratio. If the sample maintains a constant volume, the Poisson’s ratio is 0.5. If the sample loses volume in compression or gains it in extension, then the Poisson’s ratio is < 0.5. The shear modulus (usually denoted G) is measured by applying a force parallel to the surface of the sample. An important feature of shear deformations is that they maintain the volume during application of the force, regardless of what the Poisson’s ratio is. Finally, the bulk modulus (usually denoted K) is measured by applying forces on all surfaces of the sample and determining the volume change as a function of applied force per unit area, it corresponds to the inverse of the compressibility. For biological samples that are mostly water, true bulk moduli are almost never measured since water is nearly incompressible.

Parallel Plates

Each MCF-7 cell was submitted, successively, to three different protocols: dynamic moduli measurements, then a relaxation experiment, and eventually a creep experiment. Each measurement was separated by a lag time of 1 min; the whole protocol lasted just 6 min to limit the evolution of cell behavior in response to mechanical solicitations. We applied stress values of about 80 Pa and strains of around 10% in amplitude to ensure linear mechanical behavior of the cells (when the mechanical stress induced by the applied strain increases linearly with strain amplitude) ^47,49. In dynamic rheometry, single cells were deformed sinusoidally and the storage and loss moduli were retrieved as functions of the frequency f (obtained from the measurements of the ratio |δ|/|D| and the phase lag between δ(t) and D(t) for 0.01Hz < f < 10 Hz, where δ (t) and D(t) were the instantaneous deflection of the flexible plate and the rigid plate displacement, respectively). In relaxation experiments, cells were submitted to a constant strain (constant applied D) and we measured δ(t). In creep experiments, single cells were stretched under constant applied stress. We thus applied a constant deflection δ on the flexible plate and measured the displacement D(t) of the rigid plate which was proportional to cell elongation. These three different protocols are detailed in Desprat et al ⁵⁰.

Optical stretching

During a typical OS experiment, cells were introduced into a microfluidic delivery system, serially trapped and then stretched along the laser beam axis (Fig. 3e). The elongation of the cell body along the laser beam axis was recorded by a CCD camera. The time-dependent strain was extracted from the video camera images, normalized by the applied peak stress and a geometric factor ⁵¹, to obtain the creep compliance for each cell. For each passage, the number of cells per OS experiment was n ≥ 55. Compliance data are presented as mean ± SEM. Overall, the number of individual cells analyzed was 514. Curve-fitting of the average compliance was performed using the curve-fitting tool box in MATLAB (Mathworks, Natick, MA). To fit the compliance of individual cells, a custom code was written to implement non-linear least squares fitting based on the Matlab function fminsearch (Nelder-Mead algorithm).

Monolayer Rheology

To characterize the rheology of MCF7 breast cancer cells, we used standard protocols that probe different aspects of cell mechanics. We imposed either strain or stress and measured the other.

1. Amplitude sweep: An oscillatory excitation at a fixed frequency with stepwise increasing amplitude of either strain or stress (Fig 4b). This protocol probes the amplitude-dependence of the mechanical properties of MCF7 cells. Here we oscillated at a frequency of 0.5 Hz and probed a strain γ between 0.001–0.1, which corresponds to 0.015μm-0.5μm in displacement of the rheometer-plates (gap between plates, 15μm). First we performed strain-controlled measurements. We then selected stress values as a function of the results from strain-controlled measurements for stress-controlled measurements. This way the cell strain remained within reasonable linear bounds.

2. Frequency sweep: The amplitude of oscillation was kept constant (at a value of 0.02 for strain-controlled measurements, or at the corresponding stress value (Fig. 4c)). We increased the oscillation frequency gradually, from 0.1 to 10 Hz.

3. Creep experiments: The strain was recorded as a function of time, while a constant stress was applied. The stress was increased in a stepwise manner every 10s. The cell compliance was analyzed as described in Fig 4d. Here, we applied ten stress steps with increasing amplitude, each 10s long.

4. Stress ramp: The applied stress was increased at a constant rate until it reached a maximum stress, then it was decreased with the same rate, back to zero (Fig 4e). The time course of the resulting strain was recorded. This was performed again 3 times, each time with an increased rate.

Magnetic Twisting Cytometry (MTC)

Ferromagnetic beads (Fe₃O₄, ~4.5 μm in diameter) were coated with the Arg-Gly-Asp (RGD) peptide using a previously described protocol ^52,53. Coating density was 50 μg of RGD peptide per milligram of magnetic beads. Beads were first added to the cell culture dish and incubated for 10 min prior to the experiment. Beads were then magnetized with a strong magnetic impulse (~1000G, <100 μs), giving rise to the bead’s magnetic moment. A sinusoidal varying magnetic field (0.3 Hz) perpendicular to that of the bead’s magnetic moment was then applied to rotate the bead. The MTC technique of measuring cell stiffness ^52–56 was used to exert an oscillatory force on the cells with a peak stress of 17.5 Pa by varying the magnetic twisting field between 0 and 50 Gauss. By quantifying the magnetic bead displacements, the cell stiffness in units of Pa/nm, and the bead embedded area, the cell complex modulus was then estimated ^54,57.

The complex modulus (G) is defined as

$$G=G^{\prime }+i{G}^{\prime \prime }$$

where the real part (G′) is the storage modulus, the imaginary part (G″) is the loss modulus, and i is the unit imaginary number $\sqrt{-1}$. The component of the bead displacement that is in phase with the applied magnetic torque corresponds to G′ and it is a measure of stiffness. G′ is proportional to the stored mechanical energy. The component of the bead displacement that is out of phase with the magnetic torque corresponds to $G^{\prime \prime }$ and it is a measure of friction. $G^{\prime \prime }$ may be taken as the dissipated mechanical energy. Since the MTC applies a rotational shear stress, the Young’s modulus is calculated with the assumption that the cell is incompressible and it is 3 times that of the shear modulus. Details on stiffness calculations have been previously described ^{7, 10}

Ballistic Injection Nanorheology

MCF-7 cells were plated on a 35-mm dish (Corning) and reached ~90% confluence before ballistic injection. 100-nm diameter fluorescent polystyrene nanoparticles (Invitrogen) were ballistically injected into the cells with a Biolistic PDS-1000/HE particle delivery system (Bio-Rad, Richmond, CA). Nanoparticles were coated on microcarriers (Bio-Rad) and allowed to dry for 6h before injection. 1,100 psi rupture disks (Bio-Rad) were used to apply the pressure to accelerate nanoparticles. Cells were repeatedly washed with Hanks’ balanced salt solution (HBSS) (GIBCO) after ballistic bombardment to eliminate excess nanoparticles, thus reducing endocytosis of nanoparticles. Cells were allowed to recover in fresh growth medium overnight before embedded nanoparticles were tracked with a high magnification objective (60x Plan Apo lens, N.A. 1.4, Nikon Melville, NY). We verified that none of the probed nanoparticles underwent directed motion. An optimized region of interest (ROI) was generated using NIS-Element software. Movies of the Brownian motion of the fluorescent nanoparticles were captured at 30 frames per second for 20 seconds with an electron-multiplying charge-coupled device (EMCCD) camera (Andor Technology, Belfast, Ireland) mounted on a Nikon TE2000 microscope. Particle trajectories were tracked and analyzed with customized Matlab software (MathWorks, Natick, MA, USA). At least 200 different nanoparticles were tracked per condition. Three biological repeats were conducted. Detailed protocol was described in a previous publication ⁵⁸.

After injection and recover overnight, nanoparticles were uniformly dispersed throughout the entire cytoplasm in cells. Since neither the perinuclear nor lamellar region is overrepresented in each nanoparticle population, the differences detected represent global changes in cytoskeletal stiffness as opposed to location-specific cytoskeletal changes. The mean-squared displacements (MSDs) of individual nanoparticles are calculated from 20 s-long streams of the time-dependent coordinates of the center of each nanoparticle. The mean elasticity of the cytoplasm is calculated from the ensemble-averaged MSD, as described by Mason et. al.59. Briefly, the ensemble-averaged MSD of the nanoparticles is related to the complex viscoelastic modulus using the after equation ⁶⁰,

$$G^{\mathrm{*}}\left(\omega \right)=\frac{k_{B}T}{\pi ai\omega {\mathfrak{I}}_u\left\{〈\mathrm{\Delta }{r}^2\left(\tau \right)〉\right\}}$$

where k_B is Boltzmann’s constant, T is the absolute temperature of the cell (in Kelvin), a is the radius of the nanoparticles, $\omega =1/\tau ,\tau$ is the time lag, and ${\mathfrak{I}}_u\left\{〈\mathrm{\Delta }{r}^2\left(\tau \right)〉\right\}$ is the Fourier transform of $〈\mathrm{\Delta }{r}^2\left(\tau \right)〉$, the time-lag dependent, ensemble-averaged MSD. The above equation can be solved analytically ⁶¹, allowing the frequency-dependent elastic modulus to be calculated algebraically using the relationship

$$G\mathrm{\prime }\left(\omega \right)=\left|G^{\mathrm{*}}\left(\omega \right)\right|cos\left(\frac{\pi a\left(\omega \right)}{2}\right)$$

where

$$\left|G^{\mathrm{*}}\left(\omega \right)\right|=\frac{2k_{B}T}{3\pi a〈\mathrm{\Delta }{r}^2\left(1/\omega \right)〉\mathrm{\Gamma }\left(1+\alpha \left(\omega \right)\right)}$$

Where $\alpha$ is the local logarithmic slope of $〈\mathrm{\Delta }{r}^2\left(1/\omega \right)〉$ at the frequency of interest and $\mathrm{\Gamma }$ is the $\gamma$-function. The elastic modulus, $G\text{'}$, describes the propensity of a complex fluid to store energy.

Atomic Force Microscopy

Conical Tip

AFM was conducted with a DAFM-2X Bioscope (Veeco, Woodbury, NY) mounted on an Axiovert 100 microscope (Zeiss, Thornwood, NY) using a triangular silicon nitride cantilevers with a conical tip (Veeco, model: DNP-10) for indentation over the cell lamella (as opposed to cell nucleus). The indentation was carried out at a 1 Hz loading rate and a ramp size of 3 μm. The spring constant of the cantilever, calibrated by resonance measurements, was typically 0.06 N/m. To quantify cellular stiffness, ~80 force–distance curves from 18 cells in four different samples were collected and analyzed according to the Hertz model modified for a conical probe.

Sharp Tip

The cells were plated on a 50-mm optical dish 48 h prior to experiments (Fluorodish, World Precision Instruments, Sarasota, FL). AFM nanoindentation was performed by a MFP3D-BIO AFM (Asylum Research, Santa Barbara, CA) mounted on an IX-71 inverted optical microscope (Olympus America, Center Valley, PA) equipped with an iXon⁺ EMCCD camera (Andor Technology, Belfast, Northern Ireland). We indented the cells with an MLCT probe (Bruker, Santa Barbara, CA) that has a soft (nominal spring constant k = 0.01 N/m) Si_xN_y cantilever with a sharp (nominal radius r = 10 nm) Si_xN_y tip. Measurements were performed in the growth medium at 37°C. Each cell was indented at two locations: one location over the nuclear region, and one location over the cytoplasm (lamella). These locations were selected to insure that the region was relatively flat and not too close to any neighboring cells. At each location, the cell was indented 10 times, with 1 min between each indentation. The loading rate was 2 μm/s and the trigger force (the applied force at which the probe is retracted) was 600 pN.

The same experiment was conducted using an intermediate sized LRCH-750 probe (Nanoscience Instruments, Phoenix, AZ) (r = 680 nm, k = 0.214 N/m) wherein cells were indented 3–4 times over only the nuclear region. The loading rate was 2 μm/s and the trigger force (the applied force at which the probe is retracted) was 8.5 nN.

Data processing method

For all force-indentation curves, the virtual deflection was corrected by fitting a line through the non-contact region and subtracting the force value of the fit line from the force value of the curve at every (F, d) coordinate. Contact points were determined and any pathological curves were filtered by visual inspection. The contact region of each curve is separated into 100 nm segments starting at the contact point. Each segment is then fit separately to the contact model to get the effective modulus at the corresponding depth. The geometry of the contact determines the power law exponent and prefactors relating the (F, d) data to the elastic modulus. Segments are linearized to the model and then least-squares linear regression is performed to find the best value of the modulus. For the conical indenter model,

$$F=\frac{2}{\pi }\frac{E{d}^2\tan \theta }{\left(1-{\nu }^2\right)}$$

where F is the indentation force, d is the indentation distance, θ is the half angle of the cone, ν is the Poisson’s ratio of the sample, and E is the Young’s modulus of the sample. The intermediate sized LRCH-750 tips are fit with a blunted cone model introduced by Briscoe et. al.,

$$F=\frac{2E}{\left(1-{\nu }^2\right)}\left\{ad-\frac{a^2}{2\tan \theta }\left[\frac{\pi }{2}-{\sin }^{-1}\left(\frac{R\cos \theta }{a}\right)\right]-\frac{a^3}{3R}+{\left(a^2-{R\cos \theta }^2\right)}^{1/2}\left(\frac{R\cos \theta }{2\tan \theta }+\frac{a^2-{R\cos \theta }^2}{3R}\right)\right\}$$

$$d+\frac{a}{R}\left[{\left(a^2-{R\cos \theta }^2\right)}^{1/2}-a\right]-\frac{a}{\tan \theta }\left[\frac{\pi }{2}-{\sin }^{-1}\left(\frac{R\cos \theta }{a}\right)\right]=0$$

where R is the apex radius of the tip and a is the contact radius the probe forms with the sample. The latter equation is numerically solved for a given d, and the former is approximated by a power law equation over the defined segment. The segment is linearized by the approximate power law and fit in the same manner as the conical indenter model.

Spherical Probe

Bioscope catalyst (Bruker/Veeco, Inc., CA) AFM placed on Nikon U2000 confocal Eclipse C1 microscope was used. A standard cantilever holder cell for operation in liquids was employed. To record force curves over the cell surface and simultaneously record cell topography, the force-volume mode of operation was utilized. This is important because the mechanical (Hertz) models to derive the elastic (Young’s) modulus have been developed for an indenter deforming a surface of known (spherical) geometry. Thus, we processed force curves collected only near the top of the cell (which can typically be approximated as a spherical surface). The force curves were collected with the vertical ramp size within 5–6 μm to ensure that the AFM probe detaches from the cell after each retraction. The AFM probe moves up and down during the force collection with a frequency of 1Hz to reasonably minimize viscoelastic effects while keeping the total measurement time relatively short. It is impossible to avoid the viscoelastic effects completely, and to be consistent, we performed all measurements with the same ramping speed. The force-volume images of cells were collected with the resolution of 16×16 pixels (typically within 50 × 50 μm² area). A relatively flat (as described above; <10–15^o of inclination angle with respect to the cell topmost point) area around the top (nucleus region of the cell) was identified. It gave about 10 force curves per cell. The global position of the AFM probe at the beginning of the scanning was controlled by the optical microscope. The measurement methodology described in detail can be found in Sokolov et. at. ^62,63.

A NPoint close-loop scanner (200 μm × 200 μm × 30 μm, XYZ) was used in this study. A large vertical close-loop Z-range was particularly important because the cell height was >10 μm. Close loop is important for quantitative description of the force curves with such extended scan range.

AFM probe: spherical indenter

A V-shaped standard narrow 200 μm AFM tipless cantilever (Veeco, Santa Barbara, CA) was used throughout the study. A 4.5–5 μm diameter silica ball (Bangs Labs, Inc.) was glued to the cantilever as described in ⁶⁴. The radius of the probe was measured by imaging the inverse grid (TGT1 by NT-NGT, Russia). The cantilever spring constant was measured using the thermal tuning method before gluing the spherical probe.

Data processing method

The force curves were processed through the cell – brush model ^63,65. Briefly, the cell is considered in this model as a homogeneous isotropic medium covered with entropic brush ⁶⁶. Consequently, when deforming, the AFM probe squeezes the brush which in turn deforms the cell body. Both mechanical deformation on the substrate and long-range force cause the deflection of the cantilever d. The load force F can then simply be found from the Hooke’s law: F=kd, where k is the spring constant of the cantilever. Z is the vertical position of the cantilever. It is typically assigned Z=0 for the maximum allowable deflection d_max(which is assigned by the AFM user). Z=Z₀ is non-deformed position of the sample and p is the deformation of the substrate at the point of contact, respectively; h is the separation between the substrate and AFM probe. The presented geometry implies the following relation between the parameters:

$$h=Z-Z_0+i+d$$ (1)

AFM allows users to directly collect parameters Z and d (so-called raw data). For the case of an AFM probe of well-defined geometry, e.g., a spherical probe and homogeneous isotropic material, we can use a particular case of the Hertzian model ⁵¹, which implies

$$i={\left[\frac{9}{16}\frac{kd}{E}\sqrt{\frac{R+R_s}{R{R}_s}}\right]}^{2/3},$$ (2)

where is the radius of curvature of the substrate at the point of contact (the Poisson ratio was chosen to be equal to 0.5 for simplicity).

Using eqs. (2) and (3), one can write the following formula for each specific point of contact i,

$$h=Z-Z+{\left[\frac{9}{16}\frac{kd}{E}\sqrt{\frac{R+R_s}{R{R}_s}}\right]}^{2/3}+d.$$ (3)

This approach allows us to unambiguously derive the brush forces due to the adsorbed molecules as well as the Young’s modulus of the substrate. Specifically, it is done in two steps. First, the Young’s modulus of the substrate is found assuming h=0 at the moment of maximum load. Using Equation (5), one can arrive at

$$E=\frac{9}{16}k\sqrt{\frac{R+R_s}{R{R}_s}}{\left(\frac{d_{\max }^{2/3}-d^{2/3}}{Z-d_{\max }+d}\right)}^{3/2}\approx \frac{3}{8}\sqrt{\frac{2}{3}}k{d}_{\max }^{-1/2}\sqrt{\frac{R+R_s}{R{R}_s}}{\left(\frac{d_{\max }-d}{Z-d_{\max }+d}\right)}^{3/2}{|}_{d\to d_{\max }}.$$ (4)

After that, one can find the force due to brush of the adsorbed molecules by the following equation

$$h(d)=Z-{\left[\frac{9}{16}\frac{k}{E}\sqrt{\frac{R+R_s}{R{R}_s}}\right]}^{2/3}\left({d_{\max }}^{2/3}-d^{2/3}\right)-\left(d_{\max }-d\right),\text{where}F=kd.$$ (5)

By modeling the force on the adsorbed molecules with the help with the entropic brush formula, one can find the length of the molecular brush L and grafting density N as follows ⁶⁶:

$$F_{steric}\approx 50k_{B}T\frac{R{R}_s}{R+R_s}{N}^{3/2}\exp (-2\pi h/L)L.$$ (6)

Here we assumed finite radius of the surface asperity R_s. As previously, this formula is a good approximation for 0.2 < h/L < 0.8. A nonlinear curve fitting of equations (4–6), allow deriving both the Young’s modulus of the cell body and parameters of the brush (length and grafting density).

Statistics

For AFM measurement, 20 and 60 cells were measured with conical probe at 25^oC 6um/s and 37^oC 2um/s. With sphere probe, 30, 10 and 20 cells were measured at R750nm 37^oC 2um/s, at R2500nm 25^oC 6um/s and at R2500nm 37^oC 10um/s. For parallel plates, 18 different cells were measured. For OS, 514 cells were measured. For cell monolayer rheology, the results were derived from 8 different cell monolayers. For MTC, 193 cells were measured. For PTM, the results were derived from three different cell culture plates and in each plate at least 20 cells were measured (with total of ~100 beads). In figure 5i, two-tailed student t-test was used with p-value of 0.05 used as threshold for significance.

Code availability

Custom code used in this study are available from the corresponding author upon reasonable request.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.