Atlas-based algorithm for automatic anatomical measurements in the knee

Abstract.

We present an algorithm for automatic anatomical measurements in tomographic datasets of the knee. The algorithm uses a set of atlases, each consisting of a knee image, surface segmentations of the bones, and locations of landmarks required by the anatomical metrics. A multistage volume-to-volume and surface-to-volume registration is performed to transfer the landmarks from the atlases to the target volume. Manual segmentation of the target volume is not required in this approach. Metrics were computed from the transferred landmarks of a best-matching atlas member (different for each bone), identified based on a mutual information criterion. Leave-one-out validation of the algorithm was performed on 24 scans of the knee obtained using extremity cone-beam computed tomography. Intraclass correlation (ICC) between the algorithm and the expert who generated atlas landmarks was above 0.95 for all metrics. This compares favorably to inter-reader ICC, which varied from 0.19 to 0.95, depending on the metric. Absolute agreement with the expert was also good, with median errors below 0.25 deg for measurements of tibial slope and static alignment, and below 0.2 mm for tibial tuberosity-trochlear groove distance and medial tibial depth. The automatic approach is anticipated to improve measurement workflow and mitigate the effects of operator experience and training on reliability of the metrics.

1. Introduction

Orthopedic diagnosis and surgical planning rely on a variety of anatomical measurements obtained from imaging data.¹ In the knee, various metrics of tibial slope (TS) are used in osteotomies, ligament repair, and arthroplasty.^1–3 Assessment and correction of patellar instability involve measurements of trochlear groove and position of the patella relative to other bones.^1,4–6 Anatomical metrics might also provide risk stratification in anterior cruciate ligament injury.^3,7–9 However, the repeatability and reliability of anatomical measurements are often challenged by factors associated with operator training and measurement techniques,^1,10–12 diminishing their potential as quantitative biomarkers.^3,9 The need to mitigate the effects of operator and technique variability stimulates the development of semi-automated and fully automated measurement algorithms.^10,11,13,14

The anatomical metrics of the knee are conventionally defined as distances and angles between landmarks associated with distinct morphological features. The measurements had been typically performed using two-dimensional (2-D) radiographs, but recent years have seen an increasing shift toward computed tomography (CT) and magnetic resonance imaging (MRI).^2,9,10 The use of tomographic modalities mitigates errors due to anatomic superposition and patient positioning, but places additional burden on the reader, who now needs to interrogate complex volumetric datasets. This further underscores the need for automated measurement algorithms. Our approach achieves this goal for cone-beam computed tomography (CBCT) of the knee by automating the identification of anatomical landmarks. The metrics are then computed using their traditional definitions, enabling interpretation consistent with current clinical practice. (An alternative approach, not considered here, could involve redefinition of anatomical measurements using features more readily tractable by image analysis than morphological landmarks.¹⁵)

The anatomical measurements considered in this work are based on landmarks placed on bone surfaces. Several categories of algorithms for automatic localization of skeletal landmarks have been proposed. One general approach involves detection of geometric features, typically associated with local curvature, that match the shape properties of the landmark.^10,16 Alternatively, machine learning algorithms can be used to detect landmarks based on distinctive image features identified through training on annotated data.^17,18 Our proposed algorithm also uses a set of annotated datasets (atlases), but belongs to a family of methods that utilize image registration to transfer expert landmarks from the atlases to the new image. To simplify the registration step in such algorithms, the atlas volumes are typically first segmented to yield a set of bone surface meshes. Ehrhardt et al.¹⁹ and Phan et al.²⁰ proposed methods that use only one atlas image combined with multistage local registrations conducted separately in regions surrounding each landmark. For cases where multiple atlases are available, registration and transfer of landmarks are achieved with active shape models^11,21 or by using individual registrations of each atlas followed by a voting stage to select the best-matching registered atlas for landmark transfer.²² Our approach, first proposed in Ref. 14, also involves using multiple atlases that are individually registered to the new subject. In a crucial contrast to Ref. 22, we do not require a prior surface segmentation of the subject volume. Instead, we have developed a multistage volume-to-volume and mesh-to-volume registration framework to transfer the landmarks from the atlases to the new volume. The time-consuming segmentation is thus only required to generate the atlases, which are then directly applied to the new image dataset without any additional preprocessing.

The paper presents the details of the multistage registration and landmark identification framework. The algorithm is evaluated against expert users in seven metrics of the tibio-femoral and patello-femoral alignment that utilize 27 distinct anatomical landmarks. Compared to our initial conference report,¹⁴ we have expanded the number of metrics considered in the study, implemented numerous refinements to the algorithm, and conducted a more thorough validation in leave-one-out experiments. Among the most significant enhancements to the workflow is improved surface-to-volume registration utilizing gradient vector flow (GVF) of the target volume.

The proposed algorithm is applied to data of 24 subject volunteers acquired with a specialized extremity CBCT scanner.²³ Extremity CBCT systems provide the unique capability for weight-bearing three-dimensional (3-D) imaging of the knee^4,15,24 and foot.^15,24,25 Development of diagnostic applications of this new modality will benefit from improvements in the workflow, repeatability, and reliability of anatomical measurements that are anticipated with the automatic algorithm.

2. Materials and Methods

Development and validation of the proposed automated measurement algorithm involve patient knee scans acquired on an extremity CBCT scanner. Section 2.1 provides details on the patient dataset. Expert readers obtained common anatomical measurements of the knee in the reconstructed volumes; the anatomical metrics are detailed in Sec. 2.2. Section 2.3 introduces the automated algorithm, which relies on an atlas set generated from the CBCT volumes and the expert landmarks. Validation of the algorithm in leave-one-out experiments is described in Sec. 2.4.

2.1. Patient Dataset and Manual Measurements of Anatomical Metrics

Following Institutional Review Board approval, $N=24$ healthy male volunteers were imaged using a weight-bearing extremities CBCT system.²³ Age of the subjects ranged from 18 to 33 (mean 20.2) years. No patient had any previous injury of the tibiofemoral or patellofemoral joint or any hardware present in the knee region.

The CBCT scanner uses a flat-panel detector and a compact fixed anode $x$-ray source. The design allows the patient to straddle the gantry in a natural standing stance, with only one extremity placed inside the imaging bore. Deformable cushions are placed in the bore to minimize leg motion. The scans cover a $20\times 20\times 20{\mathrm{cm}}^3$ field of view (FOV) centered on the tibiofemoral joint space of the dominant leg. A standard “standing knee” clinical acquisition protocol is used, involving 90-kVp tube voltage, 72-mAs total exposure, and $\sim 12\text{-}\mathrm{mGy}$ patient dose. The reconstructed volumes consisted of $384\times 384\times 576$ isotropic voxels measuring $0.56\times 0.56\times 0.56{\mathrm{mm}}^3$ each.

The morphological metrics were first measured by three experts using an in-house-developed software package, the Joint Morphology Analysis Toolkit.¹⁴ The software provided multiplanar rendering of the reconstructed volume and implemented a database of common anatomical metrics. The user identified the appropriate anatomical landmarks in the volume and the software computed the metrics (typically angle or distance) based on the landmarks. The three experts who performed the measurements differed in the level of expertise and training. “Reader 1” was a musculoskeletal radiology research fellow with 4+ years of experience, “reader 2” was a biomechanics researcher trained by reader 1, and “reader 3” was a sports medicine fellowship-trained orthopedic surgeon with 7 years of experience. The landmarks identified by reader 1 were used in construction of the atlas set for the automated algorithm (Sec. 2.3).

2.2. Anatomical Metrics of the Knee

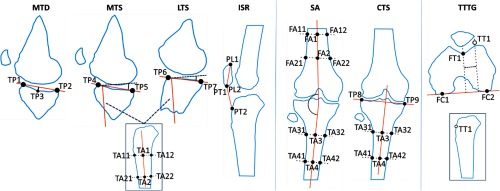
Definitions of the anatomical measurements were based on Refs. ¹ and ². The metrics and their associated landmarks are described below and illustrated in Fig. 1:

Fig. 1.

Schematic illustration of the anatomical metrics. MTD, MTS, LTS, and ISR are computed in a sagittal plane and SA and CTS are obtained in a coronal plane. Landmarks for TTTG are selected in axial and sagittal views and are then projected onto a common axial plane for the measurement. In total, 27 distinct landmarks have been used.

• •Medial tibial depth (MTD) was the distance between the deepest point of the medial tibial plateau and a line connecting the peak anterior and posterior points of the plateau in a sagittal plane that contained the deepest point.
• •Medial and lateral tibial slopes (MTS and LTS, respectively) measured the angle between a line connecting the peak anterior and posterior points in the medial (lateral) tibial plateau and the anatomical axis of the tibia. The peak points for the measurements were located in the sagittal midplane of the medial (lateral) aspect of the tibial plateau. Anatomical axis was established as the line connecting the midpoints of two pairs of anterior–posterior landmarks placed on the cortex of the tibial shaft. Midsagittal plane of the tibia was used to select those landmarks.
• •Coronal Tibial Slope (CTS) was analogous to MTS and LTS, but the measurement was performed in the midcoronal plane of the tibial plateau. Peak medial and lateral points on the plateau were used, together with the midcoronal anatomical axis of the tibia.
• •SA was a measurement of the angle between the anatomical axes of tibia and femur in their midcoronal planes.
• •Insall–Salvati ratio (ISR) was the ratio of the distance between the inferior-most and superior-most poles of the patella to the distance between the inferior-most pole of the patella and the attachment point of the patellar tendon on the tibial tuberosity. The landmarks were selected in the midsagittal plane of the tibia.
• •Tibial tuberosity trochlear groove distance (TTTG) was the distance between the deepest point of the trochlea and the tibial tuberosity, measured along the line connecting the posterior-most points on the epicondyles. The measurement was performed after projecting all landmarks onto a common axial plane.

In total, 27 distinct landmarks were used. The peak points of the medial tibial plateau were shared between MTD and MTS. The landmarks defining the midcoronal axis were shared between CTS and SA and midsagittal axes of the tibia were shared between MTS and LTS.

As indicated in the descriptions above and in Fig. 1, the users did not interrogate the whole volume to place each landmark, but rather used a small set of viewing planes, each shared by a group of landmarks. The volumetric landmarks were then perpendicularly projected onto a common reference plane (see Fig. 1) to perform the measurement. The use of a reference plane follows the methodology of Ref. 2 for translating definitions of anatomical metrics from 2-D radiography to 3-D tomographic datasets. Among the measurements described above, all except for TTTG originate from radiography.

2.3. Algorithm for Automated Anatomical Measurements

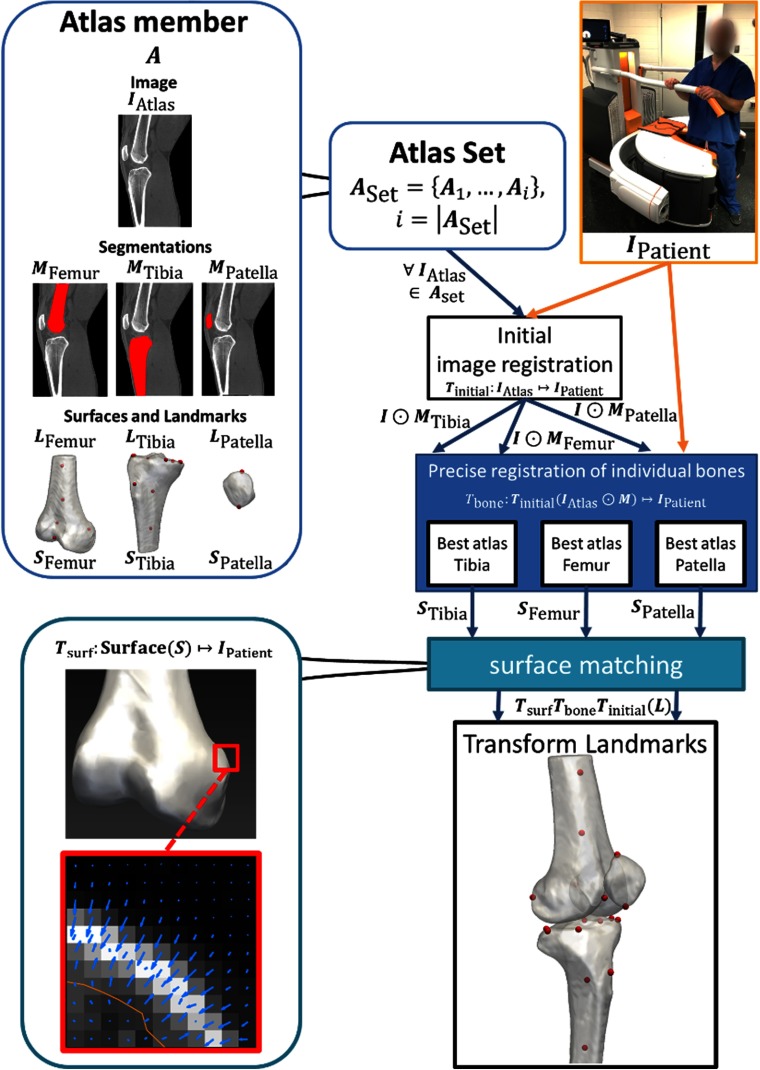
The general workflow of the algorithm is depicted in Fig. 2. The proposed approach relies on an atlas set (${\mathit{A}}_{\text{Set}}$) built from patient images that have been annotated by an expert with anatomical landmarks. Each of the atlas members (${\mathit{A}}_{\mathit{i}}$, $\mathit{i}=|{\mathit{A}}_{\text{Set}}|$) consists of a normalized grayscale image (${\mathit{I}}_{\text{Atlas}}$), the expert-selected landmarks ($L_{\text{bone}}=\{L_{\text{Tibia}},L_{\text{Femur}},L_{\text{Patella}}\}$), and manual segmentations of each bone of the knee (volumetric masks ${\mathit{M}}_{\text{bone}}=\{{\mathit{M}}_{\text{Tibia}},{\mathit{M}}_{\text{Femur}}{\mathit{M}}_{\text{Patella}}\}$ and tessellated bone surfaces ${\mathit{S}}_{\text{bone}}=\{{\mathit{S}}_{\text{Tibia}},{\mathit{S}}_{\text{Femur}}\text{and}{\mathit{S}}_{\text{Patella}}\}$). The algorithm utilizes a series of image-based registrations and a final surface deformation step to transfer the landmarks $L$ from the best-matching atlas member to a newly acquired patient scan (${\mathit{I}}_{\text{Patient}}$). The image-to-image (also denoted as volume-to-volume) registration steps involve the grayscale images of the atlas members, whereas the surface-to-image (surface-to-volume) registrations use the tessellated bone surfaces of the atlas set. First, each ${\mathit{I}}_{\text{Atlas}}$ is rigidly aligned with ${\mathit{I}}_{\text{Patient}}$ (Sec. 2.3.1). Next, the individual bone volumes from the atlas are precisely registered to the patient volume using a similarity transformation (Sec. 2.3.2). The final surface deformation and landmark transformation are only performed using the atlas members (different member for each bone) that best match ${\mathit{I}}_{\text{Patient}}$ after the initial image-based registrations. Anatomical measurements on ${\mathit{I}}_{\text{Patient}}$ are then obtained using the transformed landmarks (Secs. 2.3.3 and 2.3.4).

Fig. 2.

Flowchart illustrating the algorithmic pipeline. First, the patient image is rigidly registered to all atlas member images. This yields a coarse initial alignment of the volumes to serve as an input to the next step. The individual bones (tibia, femur, and patella) from all atlas members are then individually registered to the patient image using a similarity transformation. Finally, a deformation is applied to the (previously segmented) surfaces of the best-matching registered atlas bones and atlas landmarks are transformed using the composite transformation from all registration steps. Metrics are computed from the transformed landmarks.

The processing pipeline is explained in detail in the following sections. The method is implemented in MATLAB (R2018a, The Mathworks, Natick, Massachusetts) and C++. Global and individual bone registrations are performed using the elastix toolkit.²⁶

2.3.1. Global registration

The first step is a rigid registration of each of the atlas member images to the patient image, yielding a set of transformations: ${\mathit{T}}_{\text{initial}}:{\mathit{I}}_{\text{Atlas}}\mapsto {\mathit{I}}_{\text{Patient}}$ (atlas member index $i$ has been omitted for brevity). This global registration of the two volumes achieves an initial coarse alignment between corresponding bones in ${\mathit{I}}_{\text{Patient}}$ and each ${\mathit{I}}_{\text{Atlas}}$.

We used the mean squared difference as the registration metric and adaptive gradient descent for optimization. Mean squared difference was chosen because it provided a fast and relatively simple metric that was sufficient for the initial coarse volume-to-volume alignment. Since this step of the pipeline involved global registration of the entire volume, rigid registration without scaling was used. Intersubject size differences were better addressed at the level of individual bones (e.g., two subjects might present similar-sized tibia, but different-sized patellae) and thus adjustment of scale was deferred to the subsequent stage, individual bone registration.

The patient volume was the moving image; the registration metric was computed over a region given by a union of dilated segmentations of the atlas member bone segmentations $[\text{dilate}({\mathit{M}}_{\text{Tibia}})\cup \text{dilate}({\mathit{M}}_{\text{Femur}})\cup \text{dilate}({\mathit{M}}_{\text{Patella}})]$. The dilating element was a sphere with a radius of two voxels. Both images were $4\times$ downsampled to decrease computation time. There were only a few tunable parameters in the first stage of the pipeline (size of the dilating element and downsampling factor during registration); both were selected through manual experimentation and visual inspection of the registration result using a small set of test cases.

2.3.2. Individual bone registration

Next, we perform individual similarity-transform registrations of each bone in the atlas set. This step compensates for rotations, translations, and scaling differences that could not be addressed by the initial rigid global alignment. As mentioned in Sec. 2.3.1, intersubject differences in bone size become a potentially significant source of mismatch at the individual bone level, justifying the use of similarity transform in this stage of the pipeline.

First, we separate the tibia, femur, and patella in each atlas member by applying their respective segmentation masks (${\mathit{I}}_{\text{Atlas}}\odot {\mathit{M}}_{\text{bone}}$). Next, the global transformation ${\mathit{T}}_{\text{initial}}$ is applied to the bone volumes. Finally, another registration is performed to find a similarity transform between the transformed bone volume and the patient image, denoted as ${\mathit{T}}_{\text{bone}}:{\mathit{T}}_{\text{initial}}({\mathit{I}}_{\text{Atlas}}\odot {\mathit{M}}_{\text{bone}})\mapsto {\mathit{I}}_{\text{Patient}}$. We use covariance matrix adaptation evolution strategy (CMA-ES) as the optimizer, with mutual information (MI) as the registration metric. Gaussian scale space multiresolution smoothing is applied (two resolutions: $\sigma =2$ and original).

The choice of MI was made based on the observation that once the bones were separated by masking, their local density distributions could provide additional information to improve the alignment of the two volumes. MI was better suited at this stage than in the previous global registration step, where similar patterns of local density might be present in different bones, misleading the registration. Initial experiments showed that MI indeed improved the alignment in the individual bone registration stage compared to, e.g., the mean squared difference used in the previous step.

Similar to Sec. 2.3.1, the tunable parameters of the CMA-ES optimizer and the MI metric (chiefly the settings of the multiresolution smoothing) were established through simple manual experimentation on a small set of test cases.

2.3.3. Atlas member selection

The proposed method uses a multimember atlas set to capture anatomical variability of landmark locations. To obtain the anatomical measurement for a new patient image, the data from all atlas members need to be reduced to a single set of landmarks.

To this end, the atlas member with the highest value of MI after the individual bone registration of Sec. 2.3.2 is identified for each bone. In the remainder of the paper, this dataset is referred to as the “best-matching” atlas member for a given bone and target image. The best-matching atlas might be different for each bone. Alternative approaches include multi-atlas methods similar to those proposed for label transfer in segmentation, such as those reported by Heckemann et al.²⁷ for brain MRI segmentation, by Langerak et al.²⁸ for label fusion with simultaneous performance estimation in prostate cancer images, and others.^29–33 Next steps of the pipeline (surface deformation and landmark transformation) are only performed on the bone surface ${\mathit{S}}_{\text{bone}}$ and landmark locations ${\mathit{L}}_{\text{bone}}$ of the best-matching atlas member for that bone.

2.3.4. Surface deformation and landmark transformation

To account for individual anatomical variations, the surface meshes ${\mathit{S}}_{\text{bone}}$ of the best-matching atlas members (one for each bone) are deformed to match the bone surfaces in the patient image. Transformations ${\mathit{T}}_{\text{initial}}$ and ${\mathit{T}}_{\text{bone}}$ are first applied to the best-matching ${\mathit{S}}_{\text{bone}}$. The GVF³⁴ of the patient image is then used to guide the deformation of ${\mathit{T}}_{\text{bone}}[{\mathit{T}}_{\text{initial}}({\mathit{S}}_{\text{bone}})]$. For each mesh vertex, the local direction of GVF is searched over a distance of 4  mm to find a local maximum of the magnitude of image gradient. The vertex is then displaced to that point and the process is repeated until reaching a location where the GVF changes its direction by $>90\mathrm{deg}$.

The proposed approach deforms the surface along the direction of GVF, instead of using the somewhat more common³⁵ approach of deforming along surface normals. The latter method is employed in the preliminary implementation of the automated measurement algorithm,¹⁴ but was later found to lead to self-intersections and other degeneracies for certain topologies of bone surface (in particular when concavities were present).

In the final step of the algorithm, the composite of ${\mathit{T}}_{\text{initial}}$, ${\mathit{T}}_{\text{bone}}$, and surface deformation is applied to the landmarks of each bone (${\mathit{L}}_{\text{bone}}$) in the best-matching atlas member for that bone. The anatomical metrics are computed for the transformed landmarks following the definitions in Sec. 2.2. Analogously to manual measurements, the automatically identified landmarks are perpendicularly projected onto a common reference plane. This approach does not imply that the measurements cannot be performed directly in the 3-D space. Rather, it has been chosen here for the purpose of consistency with expert reader results and with conventional definitions of the metrics.

2.4. Evaluation of the Automated Algorithm

The automated algorithm was validated in a series of leave-one-out experiments using 24 volunteer CBCT images of Sec. 2.1. Each subject ($s$) was used as a test case once. For each $s$, we built an atlas set ${\mathit{A}}_{\mathit{s}}$ consisting of the remaining 23 subjects. As explained previously, the atlas set included (i) CBCT images, (ii) manual segmentations of bone surfaces, and (iii) landmarks identified by expert reader 1. The automated algorithm using ${\mathit{A}}_{\mathit{s}}$ was then applied to obtain landmarks and anatomical measurement for test subject $s$. The procedure was repeated for all subjects.

For each landmark and each metric, results were evaluated in terms of landmark distance error (LDE) and absolute metric error (AME)

$$\mathrm{LDE}(s)=\Vert \overrightarrow{l_{\text{auto}}}(s;{\mathit{A}}_{\mathit{s}})-\overrightarrow{l_{\text{expert}}}(s)\Vert ,$$ (1a)

$$\mathrm{AME}(s)=|m_{\text{auto}}(s;{\mathit{A}}_{\mathit{s}})-m_{\text{expert}}(s)|.$$ (1b)

In the above equations, $\overrightarrow{l_{\text{auto}}}(s;{\mathit{A}}_{\mathit{s}})$ and $m_{\text{auto}}(s;{\mathit{A}}_{\mathit{s}})$ are, respectively, the landmark location and anatomical metric value estimated by the automated algorithm for subject $s$ based on leave-one-out atlas ${\mathit{A}}_{\mathit{s}}$. Expert reader landmark location and metric value are denoted by $\overrightarrow{l_{\text{expert}}}(s)$ and $m_{\text{expert}}(s)$; $\Vert ·\Vert$ is the Euclidean norm; and $|·|$ is the absolute value. LDE and AME are computed against the expert Reader 1, who annotated the atlases. The LDE is equivalent to target registration error (TRE) at the location of the landmark. LDE, thus, measures both the accuracy of the automated landmark identification and the local error of the registration between subject $s$ and the best-matching atlas for this subject. Since the focus of this work is not on registration in itself, but on landmark localization for the purpose of anatomical measurement, the analysis below is performed primarily in terms of the LDE of individual landmarks. However, a global assessment of registration accuracy in the areas used for anatomical measurement is also provided in terms of the mean LDE of all landmarks on a given bone, averaged across all leave-one-out experiments.

In the next section, the distribution of LDE and AME in the 24 leave-one-out experiments is analyzed using descriptive statistics (median and maximal error) and box plots.

In addition to AME, we used absolute agreement intraclass correlation coefficients (ICCs) under a two-way mixed effects model [ICC(A,1) in notation of McGraw³⁶] to assess the consistency of anatomical measurements obtained by the automated algorithm and the three human readers. The automatic metric values in the calculation of ICCs were the same as in the error study above, i.e., the measurement for each subject $s$ was computed based on the corresponding leave-one-out atlas set ${\mathit{A}}_{\mathit{s}}$.

3. Results

The proposed algorithm has an average total computation time of 2 min per image ($384\times 384\times 576\text{voxels}$) using a GPU implementation and an atlas set of 20 images. The test system is equipped with an Intel Xeon CPU (E5-2620), 64 GB of RAM, and two Nvidia GeForce GTX Titan X GPUs. Within this computation time, the method produces landmark locations for all seven metrics discussed in the paper. For comparison, manual processing using software for computer-assisted measurements described in Ref. 14 takes about 5 min for annotation of all seven metrics (average time of two experts).

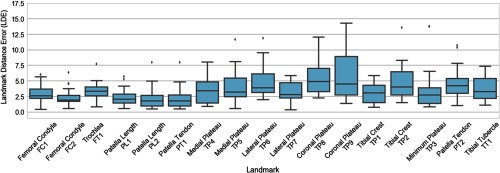
Figure 3 summarizes the LDE Eq. (1a) of the automatic algorithm compared to a ground-truth reader 1, which is equivalent to the TRE. Each bar graph shows the distribution of distance errors of target landmarks for the 24 leave-one-out test images. Median LDE remains below 5 mm (9 to 10 voxels) for all 17 landmarks shown in the plot. The highest value of the median error is found for peak lateral and medial points of the tibial plateau (TP8 and TP9, with median error of 4.9 and 4.5 mm, respectively), located at steep crests of the articular surface. Those landmarks are also the only ones for which maximum LDE in the sample of 24 leave-one-out experiments (excluding outliers) exceeded 10 mm. Other landmarks exhibiting relatively broad distribution of LDE and relatively large maximal errors ($>\sim 7\mathrm{mm}$) are also typically located on the sharp curvatures of the tibial plateau (e.g., TP2, TP4, TP5, and TP6). In comparison, the errors for femoral and patellar landmarks are generally smaller and less variable among study subjects, with median LDE of $\sim 2.5\mathrm{mm}$ or less and maximal LDE (excluding outliers) of $\sim 5\mathrm{mm}$ or less.

Fig. 3.

LDEs [Eq. (1a)] of the automatic algorithm compared to expert Reader 1. Each box plot shows the distribution of LDE for a given landmark (see Fig. 1, for definitions) obtained in leave-one-out validation on 24 CBCT test images. The boxes represent the interquartile range (IQR), the vertical line is the median, the whiskers extend to the extreme data points within $\pm 1.5$ IQR of the median, and the dots are outliers.

Figure 3 omits the anterior–posterior and medial–lateral cortical landmarks used for estimating the tibial and femoral axes (landmarks TA11–TA44 and FA11–FA22 in Fig. 1). These points are excluded from error analysis because they are not associated with any specific anatomical features. Rather, the expert readers could set them anywhere along the shaft to yield two pairs of landmarks on the opposing cortical boundaries of the bone. The landmarks transferred by the algorithm from the best-matching atlas might thus correspond to a different location along the shaft than the expert landmarks in the test image. In this case, LDE is not an appropriate metric and the performance should be evaluated primarily in terms of anatomical metrics that rely on tibial and femoral axes, in particular SA. Average error of individual bones per atlas for all landmarks of this bone is 4.2 mm for tibia, 2.9 mm for femur, and 2.2 mm for patella.

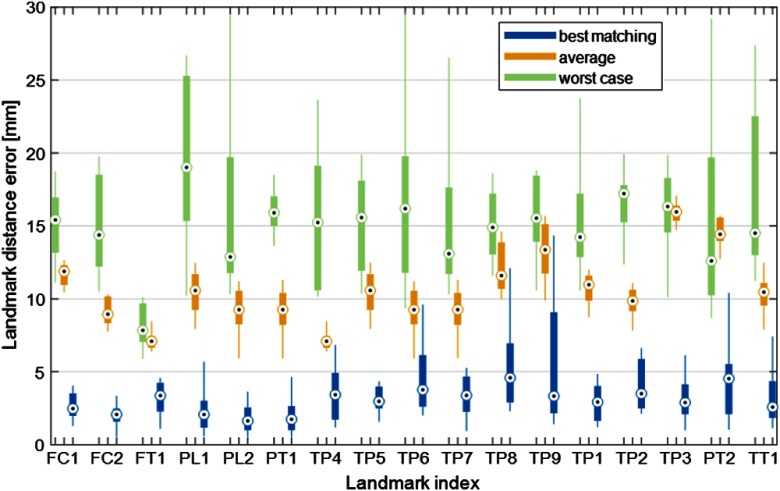
Selection of best-matching atlas reduces the average error by $\sim 7\mathrm{mm}$ (see Fig. 4), compared to the average error of all available atlas members. Figure 4 provides evidence that using the best-matching atlas member in the final registration step is indeed a reasonable strategy to ensure accurate landmark localization. Distributions of LDEs across all target images in the study sample (all leave-one-out experiments) are shown as box-and-whisker plots for different methods of atlas member selection and different landmarks. Results for the default approach of employing the best-matching dataset are illustrated in blue. The plots in yellow have been generated as follows: for each target image, all atlas members are propagated through the final surface-to-volume deformable registration step and are used as the landmark localization template. The mean of the LDEs of all those registrations is computed for each target image and the distribution of the mean LDE across the target image set is summarized in the box-and-whisker plots. These data can be thought of as representing the average performance of an algorithm that selects the atlas member at random. Finally, the distribution of errors when using the worst-matching atlas member as the landmark localization template is shown in green. There might be some target images for which better landmark accuracy could be achieved by using a different template than the best-matching dataset. However, the latter strategy appears to yield LDEs at the lower end of those achievable using this atlas set, since the LDEs obtained with the best-matching image are generally lower than the average LDE of all atlas members. The median LDE is 4 to 12 mm smaller using the best-matching atlas compared to the average LDE of all members, and 4 to 18 mm smaller compared to using the worst-matching atlas.

Fig. 4.

Distribution of LDEs across all target images is analyzed in the leave-one-out experiments. Blue box-and-whiskers represent errors for the default workflow of the algorithm, which uses registration of the best-matching atlas member to propagate the landmarks. Yellow box-and-whiskers show the distribution of the mean of the landmark errors obtained by registering the target image to each of the atlas members (no atlas selection step). The case of using the worst-matching atlas for each target image is shown in green.

The results above were primarily concerned with landmark identification accuracy. To augment this analysis, the mean LDE of all landmarks on a given bone provided insight into the global error of the final deformable registration between the best-matching atlas member and the target image. The mean LDE of all tibial landmarks (averaged over all leave-one-out experiments) was 4.2 mm, femoral mean LDE was 2.9 mm, and patellar mean LDE was 2.2 mm; the mean errors were again computed excluding the tibial and femoral axes landmarks. The relatively large mean LDE of the tibia was likely due to the fairly complex shape of the tibial plateau that challenged the final deformable surface-to-volume registration in the area where the majority of tibial landmarks was located.

Figure 5 presents a visual assessment of landmark localization accuracy on the tibial plateau. Three subjects are shown, selected based on the mean LDE of all tibial landmarks discussed above. The case in Fig. 5(a) is a subject who exhibits the highest mean tibial LDE (3.83 mm) among all leave-one out experiments. The differences in the location of the automated and expert landmarks (magenta and yellow spheres, respectively) appear to be dominated by sliding along the edge of the tibial plateau, reflecting perhaps a slight rotational mismatch between the deformed atlas and the target image. Similar error pattern is apparent in Fig. 5(b), which shows a subject who achieved mean tibial LDE close to the average tibial LDE of all leave-one-out experiments (2.69 mm). The subject in Fig. 5(c) has the lowest tibial LDE across all analyzed cases (0.9 mm), as confirmed by the substantial overlap of the automated and expert landmarks.

Fig. 5.

Tibial surfaces of three example subjects showing the landmarks set by an expert (magenta) compared to the result of the proposed method (yellow). (a) Subject with highest mean tibial LDE among all leave-one-out experiments. (b) Subject with a mean tibial LDE that is close to the average tibial LDE for the study sample. (c) Subject with the lowest mean tibial LDE achieved in the leave-one-out experiments.

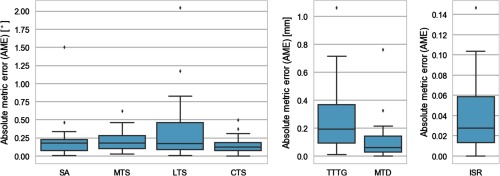
Performance of the proposed algorithm in anatomical measurements is summarized in Fig. 6 in terms of AME Eq. (1b), and in Fig. 7 and in Table 1 in terms of ICC. Similar to Fig. 3, the figures of merit in Figs. 6 and 7 are computed against reader 1. The median AME is below 0.18 deg for tibial slopes and SA, below 0.2 mm for distance-based metrics of TTTG and MTD, and 0.028 for the relative distance metric of ISR. Excluding outliers, the maximal AME in the leave-one-out experiments never exceeds 1 deg for SA and tibial slopes, 0.8 mm for TTTG and MTD, and 0.11 for ISR. Anatomical metrics obtained with the algorithm show generally better agreement with reader 1 than the automatic landmarks on which they are based. The primary reason for this discrepancy is that most of the measurements have been performed in 2-D, after the landmarks has been projected onto a common plane. Consequently, landmark localization errors in planes other than the measurement plane did not affect the anatomical metric.

Fig. 6.

Distribution of errors [AME, Eq. (1b)] of automatic anatomical measurements compared to expert reader 1. For each metric, the plots summarize data from 24 leave-one-out experiments (see Fig. 1, for metric definitions). The same box plot conventions are used as in Fig. 3.

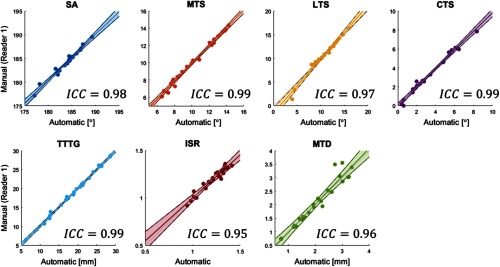
Fig. 7.

Linear regression (including 95% confidence intervals) and ICCs between the automatic method and expert reader 1. Data points represent automatic and manual measurements of 24 test subjects.

Table 1.

ICCs of anatomical measurements obtained by expert readers and by the proposed automatic approach (auto). Not all measurements have been performed by all readers. Reader 1 has generated anatomical landmarks for the atlases by using the automatic algorithm. The algorithm has performed the measurements according to a leave-one-out paradigm, i.e., each test subject has been processed using an atlas set that excluded that subject.

	MTS		LTS		CTS		TTTG
	Auto	Reader 1	Auto	Reader 1	Auto	Reader 1	Auto	Reader 1
Auto	—	0.99	—	0.97	—	0.99	—	0.99
Reader 1	0.99	—	0.97	—	0.99	—	0.99	—
Reader 2	0.91	0.91	0.71	0.75	0.95	0.94	0.38	0.19
Reader 3	0.71	0.72	0.63	0.66	0.70	0.67	0.95	0.95
		SA		ISR		MTD
		Auto	Reader 1	Auto	Reader 1	Auto	Reader 1
	Auto	—	0.98	—	0.95	—	0.96
	Reader 1	0.98	—	0.95	—	0.96	—
	Reader 2	0.74	0.77	0.61	0.61	0.83	0.82

The AMEs are small compared to typical metric magnitudes, as evidenced in scatter plots of automated measurements versus reader 1 shown in Fig. 7. The data points in Fig. 7 are narrowly distributed around the identity line, indicating good agreement between the proposed algorithm and the expert. The resulting ICC is good to excellent, with values above 0.95 for all metrics.

Table 1 extended the analysis to include comparisons with experts other than Reader 1. The inter-reader ICC varied from 0.19 (for TTTG and reader 1 versus reader 2) to 0.95 (for TTTG and reader 1 versus reader 3), with ICC of $\sim 0.7$ for the majority of metrics and inter-reader correlations. The automatic approach achieved better agreement with reader 1, who generated atlas landmarks, than the agreement between that expert and other readers. The reason was most likely in varying levels of experience among the readers and their differing interpretations of landmark definitions. The ICC between the algorithm and readers 2 and 3 was comparable to the ICC between reader 1 and those experts, as expected from the good agreement between the automatic approach and measurements of reader 1.

4. Discussion and Conclusion

We have presented and validated an algorithm for automatic anatomical measurements in 3-D tomographic scans of the knee. The proposed approach utilizes a set of atlas images annotated with landmarks. A sequence of rigid image-to-image registrations followed by a deformable surface-to-image registration is used to transform the landmarks from the best-matching atlas member (one for each bone) onto the target volume. The method does not require a prior segmentation of the target image. The metrics are then computed from the transformed landmarks following their standard definitions.

The algorithm was validated in leave-one-out studies using extremity CBCT scans of 24 volunteers. The automatic method agreed well with an expert reader. The median errors across all leave-one-out tests were $<0.2\mathrm{deg}$ for angular measurements and $<0.2\mathrm{mm}$ for distance measurements. Excellent correlation with the expert was achieved, with ICC of 0.95 or more for all metrics. The errors and correlations stated here were computed against the expert who generated atlas landmarks, but since the leave-one-out paradigm was used, the measurements for each test case were performed using a different atlas set built from the remaining 23 cases. The results demonstrate that it is feasible to use a modestly sized sample of previous measurements of the expert to replicate (“predict”) their measurements on a new subject.

The ICCs between the algorithm and the expert who annotated the atlas set are generally better than ICCs between that reader and other experts, indicating that training and experience level have a measurable effect on inter-reader reliability of the metrics. We note that the inter-reader correlations reported here are consistent with previous studies of 3-D anatomical measurements.² The automatic method might be useful in improving the reliability since it consistently applies the landmark localization methodology of a single expert (or a consensus of multiple readers) who annotated the atlas set.

A similar approach for atlas-based landmark identification has been proposed in Ref. 22. Our method is potentially advantageous in that it does not require prior surface segmentation of the target volume. Considering corresponding points on the tibia (MPB in Ref. 22 corresponds to LM23, LPB↔LM24, and CMTP↔LM25) and femur (LPC↔LM03, MPC↔LM04, and AWL↔LM05), the average localization error in Ref. 22 is 4.36 mm for tibial landmarks and 5.39 mm for femoral landmarks, compared to 3.88 and 2.9 mm with our approach. This suggests that landmark localization accuracy of the two methods is likely similar.

To our knowledge, the algorithm introduced in Ref. 22 is the most closely related to the proposed method among recently published work, both in terms of the multi-atlas methodology and in the scope of the anatomical landmarks that have been evaluated. As mentioned in Sec. 1, other atlas-based landmark identification methods for musculoskeletal applications have been published, either using a single atlas^19,20 or an active shape model.^11,21 References 20 and 21 have reported landmark localization errors compared to expert readers for a variety of femoral and hip locations. The tibia and patella have not been considered in those studies. The average errors ranges from $\sim 1.5$ to $\sim 4.5\mathrm{mm}$ (depending in the landmark) in Ref. 20, and from $\sim 2.5$ to $\sim 6\mathrm{mm}$ in Ref. 21. Reference ¹¹ had been concerned with planar radiography. Overall, our method yields a LDE of $\sim 2.5\mathrm{mm}$ to $\sim 5\mathrm{mm}$, which is comparable to the performance of previously reported algorithms for musculoskeletal applications. A direct comparison among various automated landmark identification approaches and anatomical measurements is best performed using a common dataset of the same anatomical region. While such an investigation is beyond the scope of this feasibility study, future collaboration and/or a challenge initiative could facilitate the requisite algorithm implementation, training, and optimization to ensure fair comparison.

The localization accuracy might be improved by developing new criteria to select the best-matching atlas members for the final landmark transformation. Currently, we use mutual information between the target image and the atlases, computed separately for each bone after rigid registration of individual bones (Sec. 2.3.3). One possible alternative could be to advance all atlases to the deformable registration stage (Sec. 2.3.4) and to transfer the landmarks of the atlas that require the least amount of deformation to align with the target image. Another strategy could involve combining the landmark information from multiple deformably registered atlases using some form of a voting scheme, similar to multi-atlas segmentation (MAS).³⁷ For example, each landmark could be transferred from the atlas that has achieved the best match with the target image in the vicinity of that landmark, or a weighted average of landmark locations from multiple atlases could be used in a manner somewhat resembling locally weighted label propagation in MAS.³⁸ However, all these approaches would likely be challenged by longer processing times, because deformable registration would need to be performed for each bone in each atlas. This processing overhead could be addressed by incorporating some of the atlas ranking and selection methods developed in MAS.³⁷ Development of such atlas-matching criteria is an important topic of future work. The current approach, based on choosing the atlas with the lowest MI after initial rigid registration, has been found to be sufficient to achieve submillimeter/subdegree agreement for anatomical metrics considered in this feasibility study.

Further enhancements of the proposed methodology could involve alternative registration strategies. For example, the surface-to-volume alignment in the final stage of the algorithm could be replaced with a deformable volume-to-volume registration, such as a B-spline transformation³⁹ or the Demons algorithm.⁴⁰ In initial tests with an unoptimized B-spline registration using elastix,³⁹ we found almost twofold increase in processing time compared to our approach ($\sim 5\min$ per volume pair using B-splines compared to $\sim 2\min$ for the surface-to-volume alignment). An optimized implementation might reduce this speed penalty, but it is likely that a volume-to-volume deformable registration will still contend with somewhat higher computational cost than a surface mesh method. Furthermore, the current surface-based methodology has the advantage that it can be naturally extended to support development of active shape models (which typically rely on surface meshes). Such models provide an attractive paradigm for combined segmentation, landmark identification, and population studies of bone morphology.

Recognizing that other registration, atlas selection, and landmark training strategies might improve the performance of the proposed methodology, the results achieved with the current implementation, nonetheless, illustrate the feasibility of automated anatomical measurements in the 3-D images of the knee. Optimization of the automatic pipeline using some of the approaches outlined in the preceding paragraphs is the subject of ongoing research.

A potential limitation of our study involves the relatively homogeneous population of study volunteers in terms of age and health status. In particular, no significant pathological deformations such as bone erosions are present in the sample. Such unique morphological variants may challenge any atlas-based approach, since they might not be captured in the atlas set. Our method includes a deformable registration step to address individual variability that is not adequately represented in the training data. While this deformable alignment may not be able to resolve particularly severe pathologies of the joint surface, such as advanced erosions, it is likely that manual identification of landmarks would be equally challenging in such cases. Furthermore, the metrics considered in this work are primarily concerned with joint alignment and are thus often performed on patients who exhibit relatively normal joint surfaces, but abnormal biomechanics. The study sample is thus reasonably representative of populations (e.g., athletes or military personnel) whose diagnostic evaluation may involve anatomical measurements.

Another potential limitation of this investigation involves the definition of ground truth for landmark locations and anatomical measurements. We have used the annotations of a single expert reader to train the algorithm. Error analysis is also performed with respect to individual readers. The study thereby includes potential error or bias associated with a single expert in defining landmark locations. An alternative approach could establish consensus landmarks of a group of readers. This could be achieved using a methodology similar to simultaneous truth and performance level estimation (STAPLE⁴¹), initially proposed for performance evaluation of segmentation algorithms. An analogous expectation-maximization framework could be developed to estimate a probabilistic consensus of expert landmarks accounting for relative performance the raters. Once such consensus is formed for each of the atlas members, it could then be propagated onto new images using our automated approach. Since the STAPLE framework produces performance-level estimates for each rater as part of the consensus estimation, it could also be used to validate the algorithm. This could be done by running the STAPLE-based algorithm on a rater group which includes the output of the algorithm in addition to all experts. Overall, generation of consensus-based ground truth for bony landmarks of the knee represents a promising future extension of the current investigation.

The proposed method can be generalized to other joints and 3-D imaging modalities. Another potential extension involves using an active shape model³⁵ instead of the current atlas set comprising individual subject scans. Such an approach will likely still require a final deformable registration step to achieve a precise match with the target image but might be overall more accurate when sufficiently large atlas set is used to build the underlying statistical shape model. It is likely that such an atlas set would need to be larger than the $\sim 20$ subjects used by our method. We are currently investigating performance of an automatic measurement algorithm for foot and ankle that combines the landmark-transfer principle outlined in this paper with an active shape model of the ankle complex.⁴²

In summary, we presented an atlas-based method for automatic anatomical measurements in volumetric imaging datasets. A feasibility study in extremity CBCT scans of the knee showed that the algorithm correlated well with expert readers. The improved workflow and consistency of measurements made possible by the automated approach are likely to benefit development and proliferation of quantitative diagnostic methodologies in orthopedics.

Biography

Biographies of the authors are not available.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.