Abstract
Introduction
Inertial measurement units have been proposed for automated pose estimation and exercise monitoring in clinical settings. However, many existing methods assume an extensive calibration procedure, which may not be realizable in clinical practice. In this study, an inertial measurement unit-based pose estimation method using extended Kalman filter and kinematic chain modeling is adapted for lower body pose estimation during clinical mobility tests such as the single leg squat, and the sensitivity to parameter calibration is investigated.
Methods
The sensitivity of pose estimation accuracy to each of the kinematic model and sensor placement parameters was analyzed. Sensitivity analysis results suggested that accurate extraction of inertial measurement unit orientation on the body is a key factor in improving the accuracy. Hence, a simple calibration protocol was proposed to reach a better approximation for inertial measurement unit orientation.
Results
After applying the protocol, the ankle, knee, and hip joint angle errors improved to , and , without the need for any other calibration.
Conclusions
Only a small subset of kinematic and sensor parameters contribute significantly to pose estimation accuracy when using body worn inertial sensors. A simple calibration procedure identifying the inertial measurement unit orientation on the body can provide good pose estimation performance.
Keywords: Inertial measurement unit, human pose estimation, joint angle, forward kinematics, extended Kalman filter, calibration, sensitivity analysis, misorientation, clinical application
Introduction
Current clinical assessment protocols in rehabilitation, orthopedic surgery and sports medicine rely on visual observation of patient performance of mobility tests such as squats, hops, lunges, etc.1 Visual assessment is subjective, relies on clinician expertise, and is limited to visually observable parameters.2,3 Developing a reliable automatic human motion tracking system for sports medicine or rehabilitation applications can provide objective measurements of the motion, reduce issues of inter-rater variability, and provide long-term analyzable data. A sensor platform is needed for automated pose estimation; researchers have proposed marker-based systems,4 Microsoft Kinect5 or inertial measurement units (IMUs)6,7 for this purpose.
IMUs are well suited for motion measurement in clinical settings, as they are small, wearable, capable of long-term data recording and have low cost and low power consumption.8 In order for an IMU-based pose estimation method to be suitable for clinical applications, it should provide a direct estimate of joint angles in three-dimensional space, the accuracy should be comparable to or better than visual estimation, and the system should be fast to set up and easy to use.
Accurate estimation of joint angles from IMU measurements is challenging due to gyroscope drift, sensor to segment misalignment, and motion artifacts. Several methods have been proposed7 to recover joint angle data from IMU measures. The majority use strap-down integration of angular velocity to estimate the orientation of the limb to which the IMU is attached with respect to a world frame and extract joint angles from relative orientations of the two adjacent limbs.9–11 However, IMU sensor readings are noisy and may have bias. When position is estimated by integrating angular velocity, even a small amount of bias will grow over time and cause considerable errors in estimation.12 To correct gyroscope drift, the common approach is to fuse accelerometer and gyroscope data. Examples include applying the complimentary13 or Kalman filters10,12,14 for data fusion. A comparison between different filtering techniques for sensor fusion and drift removal was conducted by Ohberg et al.15 Drift can lead to physically unrealizable joint angle estimates. To avoid this, some studies also introduced kinematic constraints to their estimation model.12,16,17 Applying a kinematic model can help with three-dimensional multiple joint angle estimation and reduce drift, but the drawback is that it requires additional parameters to be known, such as the position of the sensors and limb (kinematic link) lengths.
Another major issue with IMUs is their sensitivity to misalignment.11 Joint angles should be measured in the anatomical joint coordinate system; any misalignment between the sensor local frame and the anatomical joint frame may lead to error. An exact positioning of the sensor or a calibration procedure is needed for best results. Calibration techniques include pose or functional calibration or a combination of both.18 In pose calibration, the subject is asked to stand in a known posture, while in functional calibration, the sensor alignment is found using limb movements.15,18–22 Although these methods can improve accuracy, they are time consuming and the precision depends on the accuracy of the movements/pose executed by the subject. Moreover, some of these methods may require prescribed motions to be performed, which might not be possible for patients with limited range of motion (ROM). Seel et al.11 have proposed a functional calibration method which works based on arbitrary movements; however, their method requires at least two IMUs around the target joint, and the arbitrary motions have to excite all degrees of freedom (DoF).
The most accurate systems reported in the literature to date can achieve joint positioning accuracy within for the knee joint angle,9,11,23 within for hip joint angles, and within for ankle joint angles.23–25 However, this degree of accuracy relies on a detailed calibration procedure which requires the subject to accurately perform the calibration movement,9,24 requires additional tools,25 or is only achievable for limited joints.11
Clinicians usually have a busy appointment schedule, which does not allow time for extensive sensor calibration or accurate measurement of the required parameters for pose estimation. One solution is to only measure those parameters whose variation affects the pose estimation accuracy and to use anthropometric data26,27 for less sensitive parameters. Therefore, a sensitivity analysis is required to identify the parameters most sensitive to sensor mispositioning. While several studies have mentioned the importance of sensor positioning and suggested methods for more accurate estimation of the sensor orientation,11,19,22 very few studies have investigated the effect of sensor placement errors on the pose estimation quantitatively.
Trojaniello et al.28 investigated the sensitivity of four different single IMU-based gait initial contact estimation methods to IMU misplacement. The lower back IMU was virtually rotated around the medio-lateral axis within a range of . Two methods had acceptable performance only in a limited range of IMU orientation change. One method was quite insensitive but also had poor accuracy. Only one method showed acceptable performance in terms of a compromise between good accuracy and least sensitivity.
Leardini et al.29 compared a magnetic IMU-based rehabilitation assistive system to the optical motion capture (Mocap) analysis gold standard using a 3 IMU system applied to the thorax, thigh and shank to estimate hip, knee and thorax inclination angles. The sensitivity of the hip adduction/abduction (Add/Abd) angles to frontal plane misorientation of the thigh IMU within ±15° of the optimal orientation and the sensitivity of the hip flexion/extension (Flex/Ext) angles to mispositioning of the thigh IMU within ±7 cm in the mediolateral direction of the correct position was analyzed. Their results showed more error due to mediolateral displacement than due to frontal plane misorientation and concluded that overall error due to introduced misplacement was less than 5°, which they deemed acceptable. However, misconfigurations were limited to two scenarios tested on one of the sensors, and the effect was investigated on hip angle estimation in the sagittal plane only.
The main research focus of the aforementioned studies was pose estimation, and sensitivity analysis was only investigated as a secondary component. To the authors’ best knowledge, no study to date has addressed the influence of IMU positioning errors on pose estimation as a primary research focus. For a pose estimation system to be usable in clinical settings, the robustness of system accuracy to variations in sensor placement must be systematically assessed. In this study, an IMU-based pose estimation method is applied to estimate lower body pose during the single leg squat (SLS) mobility test. The sensitivity of the pose estimation to the variations resulting from inaccurate sensor placement is quantified, and a practical protocol for the estimation of the sensitive parameters in clinical settings is proposed.
The rest of the article is organized as follows: The proposed approach section describes the approach for IMU-based pose estimation using approximated parameters, and the sensitivity analysis of the pose estimation accuracy to each of the parameters. Experiments section describes the experimental setting for the data collection. Calibration protocol for IMU orientation estimation section proposes a calibration protocol for fast approximation of the sensitive parameters, and provides joint angle errors after applying the calibration. Results and discussion sections discuss the results, and conclusions and future work section concludes the paper.
Proposed approach
IMU-based pose estimation
In this study, three IMU sensors are used to estimate ankle, knee, and hip joint angles during the SLS. The SLS is a mobility test often used to assess knee function in orthopedics, sports medicine and rehabilitation.30 The SLS test aids in the identification of individuals at risk of knee injury.31 Crucial to the clinical utility of this test is the evaluation of the dynamic knee valgus motion, which is a combined motion of thigh adduction occurring in the coronal plane and thigh internal rotation moving in the transverse plane. Therefore, estimates of the hip and ankle internal/external and adduction/abduction angles are required, so a pose estimation method capable of only sagittal plane estimates is not sufficient for dynamic knee valgus assessment.
Since the IMU data are noisy and can suffer from drift, a kinematic model of the lower leg similar to Lin and Kulíc17 was applied to predict the angular velocity and linear acceleration at each time step. The kinematic model predictions and sensor measurements are fused via an extended Kalman filter (EKF). The algorithm proposed in Lin and Kuli'c17 is modified to incorporate a seven DoF leg model and further minimizes drift by introducing a virtual yaw sensor at the hip.
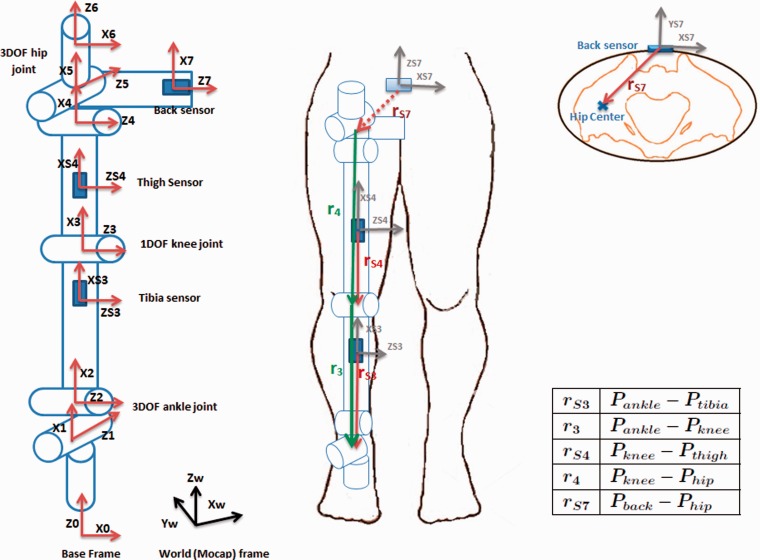
The developed kinematic model for the human leg is composed of a three DoF ankle joint, one DoF knee joint, and three DoF hip joint. Frame assignment is carried out according to the Denavit Hartenberg (DH) convention32 as depicted in Figure 1 (left). Frames 0, 1, and 2 correspond to ankle internal/external rotation (IR/ER), Add/Abd and Flex/Ext, respectively, followed by the tibia link. Frame 3 corresponds to knee Flex/Ext, followed by the thigh link. Frames 4, 5, 6 correspond to hip Flex/Ext, Add/Abd, and IR/ER, respectively, followed by the pelvis link. Frame 7 is the final frame located at the back sensor. Frame 0 is the inertial frame, as it is stationary during the SLS motion. To estimate linear acceleration at sensor locations, information of the sensor positions on the kinematic chain is required, which is incorporated into the model through displacement vectors .17 The model and the displacement vectors are shown in Figure 1. For hip center estimation, Harrington et al.’s33 method was applied, which estimates the hip center location based on leg length (LL), pelvic depth (PD), and pelvic width (PW).
Figure 1.
Seven DoF kinematic model of the right leg showing sensor positions, frame assignments, and displacement vectors. and refer to joint center position vectors and and refer to IMU position vectors.
The estimates of the angular velocity and linear acceleration from the kinematic model and the IMU measurements of these parameters are fused into an EKF to recover the joint angles.17 The position, velocity, and acceleration of each DoF are defined as the states to be estimated by the EKF.
For rotation angles parallel to gravity, drift due to gyroscope bias cannot be compensated by the accelerometer and can result in large IR/ER angle errors. The drift problem is most prevalent in the hip IR/ER due to accumulation of error from previous states. To alleviate this issue, similar to Joukov et al.,34 a virtual yaw sensor was assumed at the hip location to measure hip internal rotation only.
A separate EKF is assigned to each sensor. The three filters are run sequentially, so that the estimate of the ankle joint’s states is used as input to the knee estimate, and the ankle and knee estimates are used as inputs to the hip EKF estimator. Ankle joint states are estimated using the tibia sensor EKF, knee joint states are estimated using the thigh sensor EKF, and hip joint states are estimated using the back sensor EKF.
The measurement noise covariance (R) and the process noise covariance (Q) are determined via optimization, by minimizing the root mean square (RMS) error between joint angle estimates obtained with motion capture35 and from the algorithm. The optimization problem was solved by global search optimization implemented using the MatlabR2016a optimization toolbox.
Pose estimation using approximated parameters
Since the IMU-based pose estimation algorithm is to be applied in the absence of marker information, an estimation method for the sensor orientation, displacement vectors, and kinematic link lengths has to be defined.
To obtain displacement vectors and kinematic link lengths, we assume sensor positions and replace person-specific body parameters by values from anthropometric tables.
Assuming that sensors are placed exactly in the middle of the tibia and thigh and that the knee and ankle centers are aligned, the displacement vectors with respect to the sensor frame can be approximated according to Table 1. In addition, if the leg is assumed to have a conical or cylindrical shape, the Y component of and is equal to the radius of the leg at the sensor location.
Table 1.
Sensor displacement vectors approximated based on thigh and tibia lengths, sensor vertical distance to previous joint center and leg radius at sensor location.
| Vector | X | Y | Z |
|---|---|---|---|
| 0 | |||
| 0 | 0 | ||
| 0 | |||
| 0 | 0 |
Ltibia: Tibia length Lthigh: Thigh length : Tibia radius at tibia sensor location CTib: Tibia circumference at tibia sensor location CThi: Thigh circumference at thigh sensor location : Thigh radius at thigh sensor location : Vertical distance from middle of the tibia sensor to the knee center : Vertical distance from middle of the thigh sensor to the knee center
and distances are specified during sensor placement and assumed to have a fixed value for all subjects.
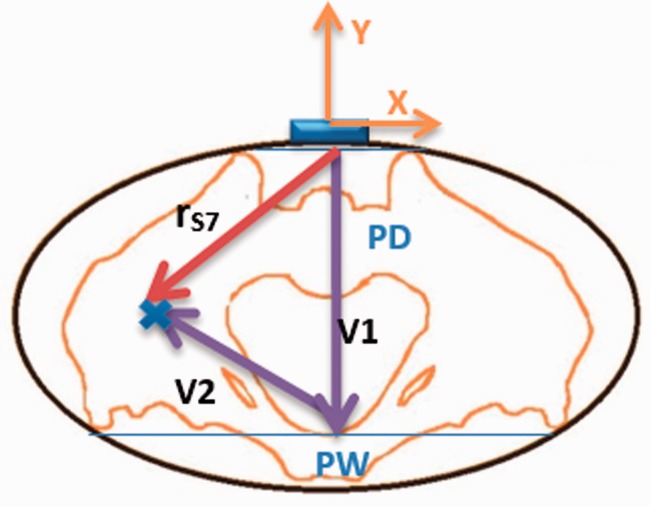
The vector can be estimated using PD, PW, and LL33 as depicted in Figure 2. Given that the back sensor is placed at the midpoint between the right and left anterior superior iliac spine (ASIS), the Z and X components of are assumed to be zero and the Y component is equal to PD with negative sign (according to the back sensor frame shown in the Figure 1), fully defining . was estimated using PD, PW, and LL according to the Harrington et al.33 instructions.
Figure 2.
The vector can be estimated as the summation of vectors and , where is estimable using PD, PW and LL. is assumed to have only Y component equal to PD.
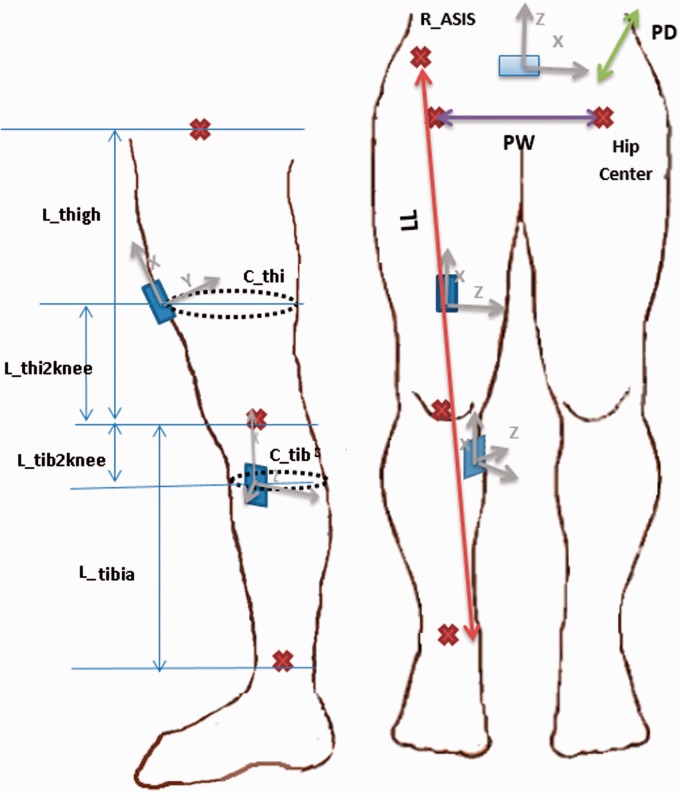
Using the abovementioned assumptions, the required measurements are: LL, PD, PW, tibia length (Ltibia), thigh length (Lthigh), tibia and thigh circumference at sensor locations (CTib, CThi), and the tibia and thigh sensor distances to the knee (), all shown in Figure 3. To avoid manual measurement of these values, the pelvic width, tibia and thigh lengths were estimated as a fraction of participant height following Winter.36 The circumference of the thigh and tibia at sensor locations was estimated as the “MidThigh Circumference” and “Maximal Calf Circumference” values from McDowell et al.26 For the four remaining values (pelvic depth, leg length, and the tibia and thigh sensor distances to the knee), the average value of all participants was used for analysis.
Figure 3.
Required parameters for pose estimation including PW, PD, LL, Ltibia, Lthigh, CTib, CThi, . Red cross signs correspond to the anatomical locations of the ankle, knee, and hip centers within the body. The back sensor is also made visible in the front view to show that it is placed at the same height as ASIS and PSIS bony landmarks above the hip center.
IMU orientations
We assume that the back and thigh sensors are perfectly aligned with the sagittal plane, and that the tibia sensor, placed on the flat part of the tibia, is rotated by about the roll axis.
Sensitivity analysis
To find out how pose estimation is impacted by variations in the kinematic parameters and sensor alignment, a sensitivity analysis is performed. The needed parameters for the forward kinematics (described in Table 1 and Section 2.2 and depicted in Figure 3) include:
There are a total of 24 parameters, which can be obtained from marker data if available, or must be approximated. The set of parameters obtained from markers are called Pm1. These parameters were changed one-by-one by ± 5% of their nominal value, called Pm2, and used to calculate the one-at-a-time sensitivity analysis.37
Sensitivity analysis is performed based on the resulting joint angle errors of the IMU-based method described in Section 2.1 using Pm1 and Pm2 and according to the following formula
| (1) |
Pm1 is the accurate parameter values obtained from markers, Pm2 is the modified parameter values equal to , Err1 is the error between Mocap and IMU-based joint angle estimates when Pm1 values are used in the forward kinematic model, and Err2 is the error between the Mocap and IMU joint angle estimates when Pm2 values are used in the forward kinematic model.
Experiments
To evaluate the accuracy of pose estimation, SLS data were collected with marker-based motion capture and IMUs simultaneously. Ten participants (five men, five women, mean age: 28.5 ± 6.37) were recruited. Inclusion criteria were adults without any lower back or leg injuries within the past six months. The experiment was approved by the University of Waterloo Research Ethics Board (approval number: 20728), and all participants signed a consent form prior to the start of data collection. Data from three participants were excluded from the analysis due to corruption of the IMU data.
Data collection
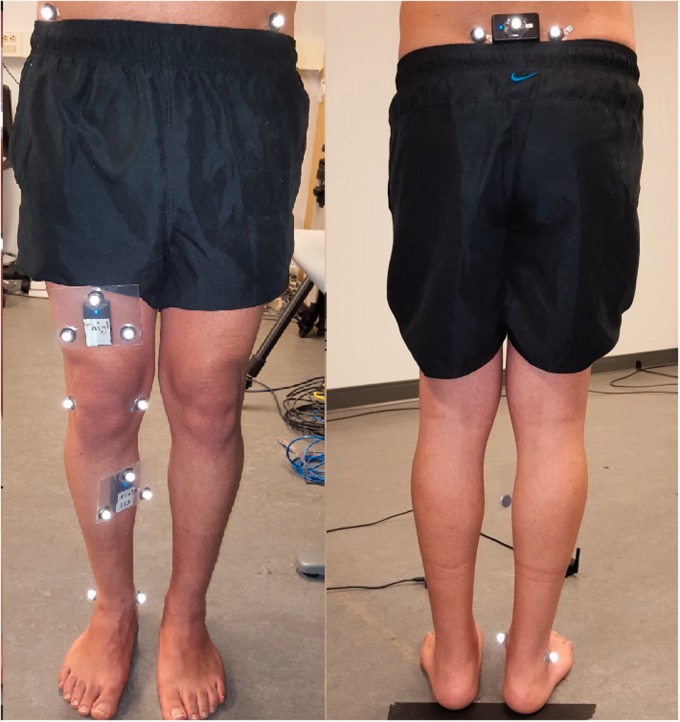
Three IMUs38 were affixed to the participants using hypoallergenic tape, one at the back at the level of the first sacral vertebra, the second at the anterior thigh 10 cm above the patella aligned with the sagittal plane, and the third at the flat surface of the tibia at the level of the tibial tuberosity. Sensor placement locations are illustrated in Figure 4. Data were communicated to a nearby computer via Wifi with an average sampling rate of 90 ± 10 Hz. Data were interpolated and resampled to the same rate of 200 Hz (equal to the Mocap camera frame rate) before subsequent analysis.
Figure 4.
Sensor and marker placement for the single leg squat experiment in the Motion Capture Lab.
At the same time, eight reflective markers were attached to bony landmarks including: right and left ASIS, right and left posterior superior iliac spine (PSIS), medial and lateral femoral condyles, and medial and lateral malleoli of the squatting leg. Moreover, three markers were attached to the thigh and tibia sensors to enable sensor orientation recovery from the marker data. Due to the vicinity of the back sensor to the right and left PSIS markers, attaching three markers on the back sensor resulted in marker swapping; hence, only one marker was attached to the back sensor. Mocap data collection was performed with eight Eagle cameras and Motion Analysis Cortex software for data collecting and post-processing.
Participants were instructed to remove their shoes and perform five continuous cycles of SLS with their toes pointing forward and arms crossed in front of the body. They were asked to perform SLS with their dominant leg (defined as the leg they would use to kick a ball) without moving the foot or lifting the heel. In instances where subjects lost their balance, their legs contacted each other, or the non-weight bearing leg touched the ground, the trial was deemed unsuccessful and all cycles were repeated.
Before starting the SLS movement, subjects were asked to lift their squatting leg up and back down and then stay for a few seconds in a rest position. This additional motion was used for synchronization of the IMUs and Mocap and was not included in the data analysis.
Calibration protocol for IMU orientation estimation
According to the sensitivity analysis results (discussed in Section 5), the sensor orientations are a key factor for accurate pose estimation. To extract full sensor orientations without requiring patients/subjects to perform any calibration movement or posture, we developed a simple and easy to use calibration protocol.
For short duration movements, orientation can be estimated by gyroscope measurement integration. Sensor orientations can therefore be retrieved from gyroscope data under specific considerations for sensor placement. For this purpose, a protocol for sensor placement was developed as follows:
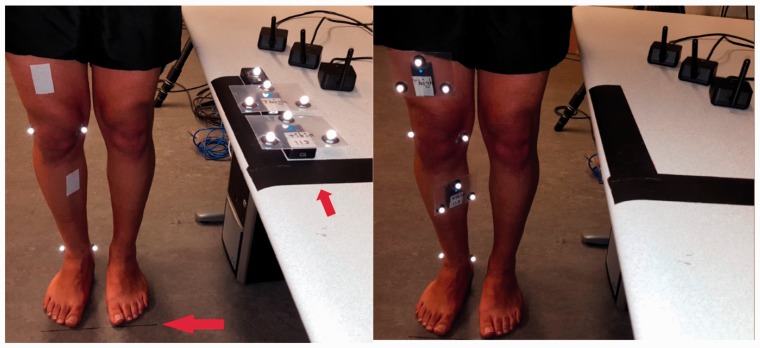
All sensors were placed on the table in the same known orientation (Figure 5, left).
Sensor locations were marked on the thigh and tibia using a double-sided tape attached to the desired sensor location.
The outer side of the tape was removed, and the participant was asked to stand still in a defined frontal orientation with respect to the table as depicted in Figure 5.
Data collection was started, and sensors were moved to the defined locations one by one (Figure 5, right).
After a few seconds at the final defined locations, data collection was stopped. This process took less than 1 min which is reasonable to avoid gyroscope drift.
Figure 5.
Different steps of performing the calibration protocol. In the left picture, the red arrow on the floor emphasizes the black guide line which is to make sure participants are standing in a correct frontal orientation. The red arrow on the table emphasizes that the sensors’ initial orientation (along the direction of the arrow) is to be parallel to participant’s sagittal plane. The two arrows are orthogonal.
Please note that the calibration protocol does not require any marker information. However, since we were simultaneously collecting IMU and Mocap data for validation, there are both markers and sensors on the body in Figure 5. The markers are used only for ground truth data collection and are not required during clinical use.
In the next step, the Rodrigues method39 was applied to gyroscope data to calculate rotation matrices from the start to the final position for each sensor according to equations (3) to (5). is the rotation matrix between the initial position on the table and the sensor at time t. To get the final orientation, we averaged the last 200 samples, which is equal to the last second of data collection when all sensors were in their assigned position on the body.
| (2) |
| (3) |
| (4) |
| (5) |
Here, refer to the X, Y, Z components of the angular velocity at time t, respectively. ω is the magnitude of angular velocity. S and I are the skew-symmetric and identity matrices, and δt is the sampling interval.
Results
Sensitivity values were calculated for both increase and decrease of ±5% of the nominal value of each parameter and for each participant. The average value for both decrease and increase, and over all participants was then calculated for the ankle, knee, and hip joints and reported as an overall sensitivity value of the pose estimation accuracy to each of the defined parameters in Tables 2 and 3.
Table 2.
Sensitivity analysis results for the ankle and knee joints.
| Sensitivity % | |||||
|---|---|---|---|---|---|
| Parameter | Ankle IR/ER | Ankle Abd/Add | Ankle Flex/Ext | Knee Flex/Ext | Ankle average |
| 3.4 | 15.1 | 5.8 | 3.1 | 8.3 | |
| CTib | 2.9 | 2.5 | 2.8 | 2.3 | 2.7 |
| 6.1 | 10 | 1.1 | 1 | 5.7 | |
| Ltibia | 10.7 | 43.6 | 16.3 | 9.5 | 23.5 |
| 0 | 0 | 0 | 1.4 | 0 | |
| 0 | 0 | 0 | 0.1 | 0 | |
| 0 | 0 | 0 | 8.5 | 0 | |
| CThi | 0 | 0 | 0 | 4.4 | 0 |
| 0 | 0 | 0 | 0.1 | 0 | |
| Lthigh | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | |
| PW | 0 | 0 | 0 | 0 | 0 |
| PD | 0 | 0 | 0 | 0 | 0 |
| LL | 0 | 0 | 0 | 0 | 0 |
| 47.7 | 309.5 | 28.5 | 38.9 | 128.6 | |
| 24.6 | 107.8 | 2.2 | 3.7 | 44.9 | |
| 4 | 1.3 | 113.5 | 51.4 | 39.6 | |
| 0 | 0 | 0 | 8.3 | 0 | |
| 0 | 0 | 0 | 1.6 | 0 | |
| 0 | 0 | 0 | 67.5 | 0 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | |
| Average | 4.2 | 20.4 | 7.1 | 8.4 | 10.6 |
Sensitivity values above 30% as well as average sensitivities for each joint are shown in bold.
Table 3.
Sensitivity analysis results for the hip joint.
| Sensitivity % | ||||
|---|---|---|---|---|
| Parameter | Hip Flex/Ext | Hip Abd/Add | Hip IR/ER | Hip average |
| 2.7 | 12.9 | 30.8 | 15.5 | |
| CTib | 0.8 | 13.4 | 21.2 | 11.8 |
| 1.8 | 7.8 | 10.6 | 6.7 | |
| Ltibia | 2.3 | 22.8 | 37.9 | 21 |
| 0.6 | 3.8 | 9 | 4.5 | |
| 0.7 | 2.7 | 3.7 | 2.4 | |
| 4.2 | 18.1 | 50.6 | 24.3 | |
| CThi | 4.1 | 4.2 | 8.3 | 5.5 |
| 0.2 | 2.9 | 2.5 | 1.9 | |
| Lthigh | 12.3 | 14.1 | 28.7 | 18.4 |
| 0.3 | 0.9 | 2 | 1.1 | |
| 0.2 | 1.1 | 2.2 | 1.2 | |
| PW | 1.5 | 5.6 | 20.6 | 9.2 |
| PD | 3.5 | 18.1 | 30.4 | 17.3 |
| LL | 1.1 | 5.4 | 4.9 | 3.8 |
| 7.7 | 167.5 | 55.8 | 77 | |
| 1.2 | 44.8 | 12.3 | 19.4 | |
| 1.2 | 3.1 | 3.3 | 2.5 | |
| 7.6 | 7.9 | 13.5 | 9.6 | |
| 0.8 | 0.2 | 1 | 0.7 | |
| 89.4 | 2.5 | 7.6 | 33.2 | |
| 92.5 | 33.4 | 26.6 | 50.8 | |
| 6.3 | 36.5 | 4.7 | 15.9 | |
| 1.8 | 23.4 | 5.5 | 10.2 | |
| Average | 10.2 | 18.9 | 16.4 | 15.2 |
Sensitivity values above 30% as well as average sensitivities for each joint are shown in bold.
According to Tables 2 and 3, the most sensitive parameters for ankle joint estimation are the tibia sensor orientation parameters, specifically the tibia roll angle. The most sensitive joints include the hip and ankle, with the ankle and hip Abd/Add and hip IR/ER most affected.
The knee joint angle estimation is sensitive to the tibia sensor roll and yaw angles as well as the thigh sensor yaw angle.
The most sensitive parameters for the hip joint are the tibia and back sensor roll angles as well as the thigh sensor yaw angle.
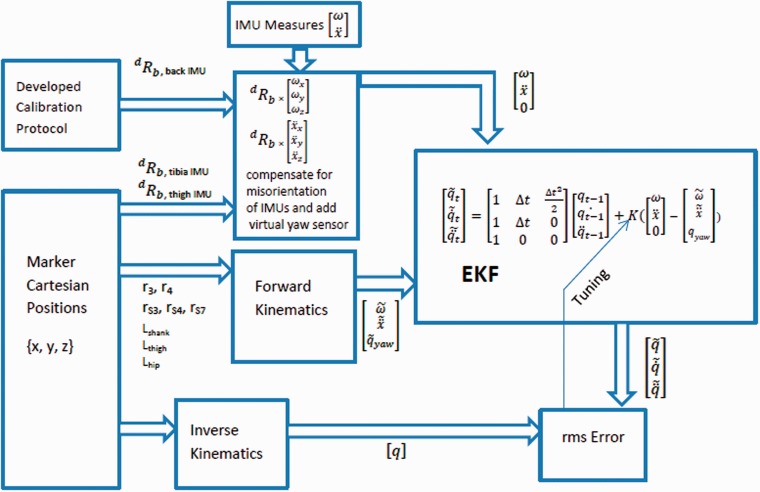
Table 4 reports RMS errors between Mocap and joint angles estimated by the algorithm, when using different approaches for kinematic parameter estimation. In the first column, labeled “Marker-calib.”, all required parameters including displacement vectors and link lengths as well as thigh and tibia sensor orientations were extracted from the marker data. Due to the lack of three markers on the back sensor, marker-based extraction of the back sensor orientation was not possible. For this reason, we used the estimated orientation of the back sensor from the calibration approach described in Section 4. Figure 6 summarizes the workflow of the pose estimation algorithm used to generate the results shown in the first column of Table 4.
Table 4.
The first three columns report the RMS error and standard deviation between IMU and Mocap estimated joint angles (in degrees), averaged over all participants. The last two columns report the average error difference between the marker-calibrated and fixed offset joint angle estimates, and the fixed offset and calibration-protocol joint angle estimates, respectively.
| Method | Marker-calib. | Fixed-offset | Calib. Prot. | Error difference between marker Calib. and fixed-offset | Error difference between calib. prot. and fixed-offset |
|---|---|---|---|---|---|
| Ankle IR/ER | 3.3° ± 1.4 | 5.0° ± 2.8 | 3.8° ± 1.8 | 1.7° | 1.2° |
| Ankle Abd/Add | 2.3° ± 1.1 | 6.4° ± 4.8 | 3.6° ± 1.3 | 4.1° | 2.8° |
| Ankle Flex/Ext | 3.9° ± 1.0 | 6.8° ± 4.8 | 5.1° ± 2.1 | 2.9° | 1.7° |
| Knee Flex/Ext | 5.5° ± 1.8 | 12.8° ± 3.9 | 6.3° ± 3.2 | 7.3° | 6.5° |
| Hip Flex/Ext | 10.9° ± 3.9 | 12.5° ± 8.4 | 11.6° ± 4.8 | 1.6° | 0.9° |
| Hip Abd/Add | 4.5° ± 2.0 | 8.3° ± 2.7 | 5.3° ± 1.8 | 3.8° | 3° |
| Hip IR/ER | 5.5° ± 2.5 | 9.1° ± 4.2 | 8.0° ± 3.1 | 3.6° | 1.1° |
| Average error/ error difference | 5.1° ± 1.1 | 8.7° ± 1.6 | 6.2° ± 1.4 | 3.6° | 2.5° |
Figure 6.
Pose estimation algorithm overview. is the rotation matrix from the body orientation to the desired orientation on the kinematic chain. ω and are measured and estimated values for angular velocity. and are measured and estimated values for linear acceleration. q and correspond to marker-based and estimated values for joint angle. and are estimated values for joint velocity and acceleration.
Using kinematic parameters estimated from the markers, the average estimated errors for the ankle (average of 3 DoFs), knee, and hip (average of 3 DoFs) joints are , and , respectively. The total estimated error averaged over all participants and all angles is , which is comparable to similar IMU-based pose estimation studies.10,12,40
The second column in Table 4, labeled “fixed-offset,” shows the RMS error for the pose estimation when approximated parameters described in Section 2.2 are used in the pose estimation algorithm. Referring to Figure 6, we have removed the marker information block as well as the calibration block and approximated the kinematic model lengths, the sensor displacement vectors, and orientations instead.
The third column of Table 4, labeled “Calib. prot.”(calibration protocol), shows the RMS error of pose estimation when approximated values are used for displacement vectors and sensor orientations are extracted from the calibration protocol.
The fourth column in Table 4, labeled “Error Difference between Marker Calib. and Fixed-offset,” shows that the error increased in all joint angle estimates when using approximated values, as expected. The most affected angle is knee Flex/Ext, with an increase in error, while the ankle IR/ER and hip Flex/Ext are less affected, with and increases, respectively. The overall increase in error, averaged over all joints and all participants, is .
The last column of Table 4, labeled “Error Difference between Calib. Prot. and Fixed-offset,” compares the results of using Calib.Prot. with the results of using fixed parameters, indicating significant improvements in accuracy for the ankle and hip Add/Abd angles ( and ) and the knee flexion angle (). The results improved for all participants and the overall improvement is .
Discussion
Presently, standard clinical tools used to assess joint motion, such as visual estimation, goniometers and inclinometers, limit clinicians to static position measurements of ROM.41 They do not provide practitioners with the ability to confidently assess higher order kinematics, such as velocity and acceleration. Moreover, due to the subjective nature of visual assessment or goniometry, reliability of these measurements can be an issue.41 Specifically related to the visual clinical evaluation of the SLS, significant differences in inter-rater reliability have been reported between experienced and inexperienced clinicians, which limit the broad clinical use of the data generated from these types of assessments.3
The proposed method in this study offers significant benefits to clinicians as it provides objective and reliable pose measurements during dynamic coordinated multiple joint movements. This enables not only estimation of ROM but also the assessment of higher order kinematics, such as velocity and acceleration, which has been shown to have clinical discriminative utility.42
However, in order to utilize a sensor-based measurement system in a clinical setting, a fast and easy to use calibration method is required. Our sensitivity analysis demonstrated that the joint angle estimates are most sensitive to the sensor orientations. Therefore, having a good estimation of the sensors’ orientation can improve joint angle estimation results considerably.
This analysis also reveals that for most of the lower body joints, approximations using the population-average leg circumference and assuming alignment between joint centers will not impact the estimation results considerably. Therefore, parameters such as limb lengths can be, for the most part, approximated using anthropometric tables without greatly affecting accuracy. One exception is the hip joint. Errors at the hip, especially in the IR/ER direction, were higher because the hip is at the end of the kinematic chain. If hip IR/ER angle is of great interest, it is recommended that anthropometrics of each patient be carefully measured.
Previous investigations have been conducted on visual estimation errors of joint motion. Reported mean errors of visual assessment in Rachkidi et al. are up to for hip Add/rotation angles and up to in hip flexion angles. Edwards et al.43 have reported visual knee flexion visual estimation error of . Allington et al.44 also reported error for ankle Flex/Ext visual assessment. Shetty et al.45 investigated visual estimation errors from 400 orthopedic surgeons who were asked to place a knee into static knee flexion angles, and their accuracy was compared to a surgical computer navigation system. They found that the errors of visually estimating knee flexion angles ranged from to , with 44% of surgeons deviating more than and 4.7% deviating by more than . Our results revealed RMS error of for ankle Flex/Ext, for hip Add/IR, for knee Flex, and for hip flexion. In comparison to previous work, the ankle error is better than visual assessment due to less variance, knee flex and hip Add/IR errors are similar, but hip Flex is higher than the reported values for human visual assessment capabilities. Overall, estimated flexion angle errors are higher because the motion is mainly performed in the sagittal plane, and flexion angles have the largest ROM in the SLS movement. Also, knee flexion has higher error than ankle flexion because of the larger ROM.
The highest errors correspond to hip joint angles and particularly hip flexion. Examining hip Flex/Ext and Hip Abd/Add estimates of all subjects revealed that a large portion of this error is due to a fixed offset because the exact estimation of back sensor orientation from markers was not possible. Moreover, since the hip center location is not directly measurable, approximation of the hip center based on other estimated parameters such as the pelvic depth, width, and LL also contribute to decreased accuracy. However, if an absolute joint angle value is not required but ROM is desired (which is the case in many clinical applications), offset is not an issue and a more accurate estimation for ROM may be attainable with our method. It should be noted that in our study, active pose measurements were conducted. Given that studies evaluating visual estimation errors are often conducted on static measurements of ROM, our results are promising. In fact, visual estimation and goniometric measurements of dynamic movement are difficult to conduct; therefore, an IMU system that can provide pose estimation for dynamic movements can better assist clinicians in assessing active movement when evaluating their patients.
There are several IMU-based pose estimation methods with more accurate results than the applied method.9,11,23–25 However, the key advantage in using the proposed method is that it provides three-dimensional estimates of the ankle, knee, and hip joints simultaneously and directly, is robust to drift, and takes into account joint kinematic constraints, which are the key requirements in clinical applications. In this paper, we showed that it is not necessary to provide the method with exact body measures; anthropometric table estimates and population averages can be used instead. The proposed calibration protocol for sensor orientation is simple and can be easily implemented in clinical settings.
Conclusions and future work
This paper analyzed the sensitivity of an IMU-based lower body pose estimation method to inaccuracies in sensor placement. The results revealed that pose estimation is mostly sensitive to sensor orientations. An easy to use calibration protocol was proposed to extract the sensor orientation on the body and improve pose estimation accuracy.
Future work can evaluate the clinical utility of this system for injury risk screenings, for the evaluation of lower limb pathology, and for its potential to track a patient’s response to interventions over the course of care.
Acknowledgements
We thank the study participants for contributing their time to the study.
Declaration of conflicting interests
The author(s) declared the following potential conflicts of interest with respect to the research, authorship, and/or publication of this article: AL and SR are employees of MSK Metrics. DK has received grants from MSK Metrics and the Natural Sciences and Engineering Research Council of Canada.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Natural Sciences and Engineering Research Council of Canada IPS Scholarship and MSK Metrics.
Guarantor
RK.
Contributorship
RK was the primary author and conducted the experiments. VJ contributed to the algorithm design. AL contributed to the study design and article preparation. SR contributed to the study design, experiments and manuscript preparation. DK was the principal investigator and contributed to study design and article preparation.
References
- 1.Hattam P, Smeatham A. Special tests in musculoskeletal examination: an evidence-based guide for clinicians, London, UK: Elsevier Health Sciences, 2010. [Google Scholar]
- 2.DiMattia MA, Livengood AL, Uhl TL, et al. What are the validity of the single-leg-squat test and its relationship to hip-abduction strength? J Sport Rehab 2005; 14: 108–123. [Google Scholar]
- 3.Weeks BK, Carty CP, Horan SA. Kinematic predictors of single-leg squat performance. A comparison of experienced physiotherapists and student physiotherapists. BMC Musculoskel Disord 2012; 13: 207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aristidou A, Lasenby J. Real-time marker prediction and COR estimation in optical motion capture. Visual Comput 2013; 29: 7–26. [Google Scholar]
- 5.Chien-Yen Chang, Lange B, Mi Zhang, et al. Towards pervasive physical rehabilitation using Microsoft Kinect. In: 6th International conference on pervasive computing technologies for healthcare (PervasiveHealth), San Diego, CA, USA, 2012. pp. 159–162. IEEE.
- 6.Lam AWK, Varona-Marin D, Li Y, et al. Automated rehabilitation system: movement measurement and feedback for patients and physiotherapists in the rehabilitation clinic. Human Comput Interact 2016; 31: 294–334. [Google Scholar]
- 7.Wang Q, Chen W and Markopoulos P. Literature review on wearable systems in upper extremity rehabilitation. In: IEEE-EMBS international conference on biomedical and health informatics (BHI), Valencia, Spain, 2014, pp.551–555. IEEE.
- 8.Fong DTP, Chan YY. The use of wearable inertial motion sensors in human lower limb biomechanics studies: a systematic review. Sensors 2010; 10: 11556–11565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Favre J, Jolles BM, Aissaoui R, et al. Ambulatory measurement of 3D knee joint angle. J Biomech 2008; 41: 1029–1035. [DOI] [PubMed] [Google Scholar]
- 10.Daponte P, De Vito L, Riccio M, et al. Design and validation of a motion-tracking system for rom measurements in home rehabilitation. Measurement 2014; 55: 82–96. [Google Scholar]
- 11.Seel T, Raisch J, Schauer T. IMU-based joint angle measurement for gait analysis. Sensors 2014; 14: 6891–6909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Šlajpah S, Kamnik R, Munih M. Kinematics based sensory fusion for wearable motion assessment in human walking. Comput Meth Progr Biomed 2014; 116: 131–144. [DOI] [PubMed] [Google Scholar]
- 13.Boonstra MC, Van Der Slikke RMA, Keijsers NLW, et al. The accuracy of measuring the kinematics of rising from a chair with accelerometers and gyroscopes. J Biomech 2006; 39: 354–358. [DOI] [PubMed] [Google Scholar]
- 14.Luinge HJ, Veltink PH. Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Med Biol Eng Comput 2005; 43: 273–282. [DOI] [PubMed] [Google Scholar]
- 15.Ohberg F, Lundström R, Grip H. Comparative analysis of different adaptive filters for tracking lower segments of a human body using inertial motion sensors. Measur Sci Technol 2013; 24: 85703. [Google Scholar]
- 16.Bonnet V, Mazzà C, Fraisse P, et al. A least-squares identification algorithm for estimating squat exercise mechanics using a single inertial measurement unit. J Biomech 2012; 45: 1472–1477. [DOI] [PubMed] [Google Scholar]
- 17.Lin JFS, Kulić D. Human pose recovery using wireless inertial measurement units. Physiol Measur 2012; 33: 2099–115. [DOI] [PubMed] [Google Scholar]
- 18.Morton L, Baillie L and Ramirez-Iniguez R. Pose calibrations for inertial sensors in rehabilitation applications. In: 9th international conference on wireless and mobile computing, networking and communications (WiMobi), Lyon, France, 2013, pp. 204–211. IEEE.
- 19.Favre J, Aissaoui R, Jolles BM, et al. Functional calibration procedure for 3D knee joint angle description using inertial sensors. J Biomech 2009; 42: 2330–2335. [DOI] [PubMed] [Google Scholar]
- 20.Luinge HJ, Veltink PH, Baten CTM. Ambulatory measurement of arm orientation. J Biomech 2007; 40: 78–85. [DOI] [PubMed] [Google Scholar]
- 21.Salehi S, Bleser G, Reiss A, et al. Body-IMU autocalibration for inertial hip and knee joint tracking. In: Proceedings of the 10th EAI international conference on body area networks (Bodynets-2015) 2015. pp: 51–57. ICST (Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering).
- 22.Li Q, Zhang JT. Post-trial anatomical frame alignment procedure for comparison of 3D joint angle measurement from magnetic/inertial measurement units and camera-based systems. Physiol Measur 2014; 35: 2255–2268. [DOI] [PubMed] [Google Scholar]
- 23.Filippeschi A, Schmitz N, Miezal M, et al. Survey of motion tracking methods based on inertial sensors: a focus on upper limb human motion. Sensors 2017; 17: 1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Palermo E, Rossi S, Marini F, et al. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis. Measurement 2014; 52: 145–155. [Google Scholar]
- 25.Picerno P, Cereatti A, Cappozzo A. Joint kinematics estimate using wearable inertial and magnetic sensing modules. Gait Posture 2008; 28: 588–595. [DOI] [PubMed] [Google Scholar]
- 26.McDowell MA, Fryar CD, Ogden CL, et al. Anthropometric reference data for children and adults: United States, 2003–2006. Natl Health Stat Rep 2008; 10: 1–48. [PubMed] [Google Scholar]
- 27.Fryar CD, Gu Q, Ogden CL. Anthropometric reference data for children and adults: United states, 2007–2010. Vital Health Stat 2012; 11: 1–40. [PubMed] [Google Scholar]
- 28.Trojaniello D, Cao S, Cereatti A, et al. Single IMU gait event detection methods: sensitivity to IMU positioning. Gait Posture 2013; 37: S24. [Google Scholar]
- 29.Leardini A, Lullini G, Giannini S, et al. Validation of the angular measurements of a new inertial-measurement-unit based rehabilitation system: comparison with state-of-the-art gait analysis. J NeuroEng Rehab 2014; 11: 136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bailey R, Selfe J, Richards J. The single leg squat test in the assessment of musculoskeletal function: a review. Physiother Pract Res 2011; 31: 18–23. [Google Scholar]
- 31.Padua DA, Bell DR, Clark MA. Neuromuscular characteristics of individuals displaying excessive medial knee displacement. J Athlet Train 2012; 47: 525–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Uicker J, Denavit J, Hartenberg R. An iterative method for the displacement analysis of spatial mechanisms. J Appl Mech 1964; 31: 309–314. [Google Scholar]
- 33.Harrington ME, Zavatsky AB, Lawson SEM, et al. Prediction of the hip joint centre in adults, children, and patients with cerebral palsy based on magnetic resonance imaging. J Biomech 2007; 40: 595–602. [DOI] [PubMed] [Google Scholar]
- 34.Joukov V, Bonnet V, Karg M, et al. Rhythmic EKF for pose estimation during gait. In: IEEE-RAS 15th international conference on humanoid robots (Humanoids), Seoul, South Korea, 2015, pp.1167–1172. IEEE.
- 35.Joukov V. Pose estimation and segmentation for rehabilitation. Master’s Thesis, University of Waterloo, Canada, 2015.
- 36.Winter DA. Biomechanics and motor control of human movement, Hoboken, New Jersey, USA: John Wiley & Sons, 2009. [Google Scholar]
- 37.Hamby D. A review of techniques for parameter sensitivity analysis of environmental models. Environ Monitor Assess 1994; 32: 135–154. [DOI] [PubMed] [Google Scholar]
- 38.Yei 3-space sensors, YOST engineering, Portsmouth, OH, http://yostlabs.com/ (2018, accessed 11 November 2018).
- 39.Rodrigues O. Des lois géométriques qui régissent les déplacements d’un système solide dans l’espace: et de la variation des cordonnées provenant de ces déplacements considérés indépendamment des causes qui peuvent les produire. J Mathematiques Pures Appliquees 1840; 5: 380–440.
- 40.El-Gohary M, McNames J. Human joint angle estimation with inertial sensors and validation with a robot arm. IEEE Trans Biomed Eng 2015; 62: 1759–1767. [DOI] [PubMed] [Google Scholar]
- 41.Norkin CC, White DJ. Measurement of joint motion: a guide to goniometry, Philadelphia, USA: FA Davis, 2016. [Google Scholar]
- 42.Kianifar R, Lee A, Raina S, et al. Automated assessment of dynamic knee valgus and risk of knee injury during the single leg squat. IEEE J Transl Eng Health Med 2017; 5: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Edwards JZ, Greene KA, Davis RS, et al. Measuring flexion in knee arthroplasty patients. J Arthroplasty 2004; 19: 369–372. [DOI] [PubMed] [Google Scholar]
- 44.Allington NJ, Leroy N, Doneux C. Ankle joint range of motion measurements in spastic cerebral palsy children: intraobserver and interobserver reliability and reproducibility of goniometry and visual estimation. J Pediatr Orthopaed B 2002; 11: 236–239. [DOI] [PubMed] [Google Scholar]
- 45.Shetty GM, Mullaji A, Lingaraju AP, et al. How accurate are orthopaedic surgeons in visually estimating lower limb alignment? Acta Orthopæd Belgica 2011; 77: 638. [PubMed] [Google Scholar]