Limits in accuracy and a strategy of RNA structure prediction using experimental information

Abstract

RNA structural complexity and flexibility present a challenge for computational modeling efforts. Experimental information and bioinformatics data can be used as restraints to improve the accuracy of RNA tertiary structure prediction. Regarding utilization of restraints, the fundamental questions are: (i) What is the limit in prediction accuracy that one can achieve with arbitrary number of restraints? (ii) Is there a strategy for selection of the minimal number of restraints that would result in the best structural model? We address the first question by testing the limits in prediction accuracy using native contacts as restraints. To address the second question, we develop an algorithm based on the distance variation allowed by secondary structure (DVASS), which ranks restraints according to their importance to RNA tertiary structure prediction. We find that due to kinetic traps, the greatest improvement in the structure prediction accuracy is achieved when we utilize only 40–60% of the total number of native contacts as restraints. When the restraints are sorted by DVASS algorithm, using only the first 20% ranked restraints can greatly improve the prediction accuracy. Our findings suggest that only a limited number of strategically selected distance restraints can significantly assist in RNA structure modeling.

INTRODUCTION

Biological functions of RNA molecules rely on a variety of complex 3D conformations, such as pseudoknots and non-canonical base pairs. Over the past few decades, high-resolution structures (1–3) of these complex conformations have significantly advanced our understanding of RNA structure and function. However, the gap between high-resolution RNA tertiary structures solved experimentally and newly discovered functional RNAs is immense due to lack of efficient structural biology tools for solving RNA tertiary structures. Although computer-based methods have progressed substantially in the past decade for RNA structure modeling (4–21), based on the results of an RNA tertiary structure prediction competition, RNA-Puzzles (9–11), these methods are not yet adequate to model large RNA structures with complex architectures. Predicting structures of large RNA molecules with non-canonical interactions has become increasingly difficult due to the longer time scales needed to sample vast conformational landscapes. Nonetheless, the efficiency and accuracy of secondary (22–24) and tertiary structure prediction algorithms (4–11,14–21,25) can be substantially improved by combining with structural restraints derived from either sequence co-evolution analysis data (12,26,27) or chemical detection data (e.g. SHAPE-MaP (28) and RING-MaP (29)) or hydroxyl radical detection (30) or mutation and mapping methods (31). In this process, researchers have efficiently developed advanced methodologies for RNA structure prediction or modeling by amalgamating experimental and computational techniques (4,12,27,30,32). SimRNA (15,33) supports user-designated distance restraints that represent any type of pairwise interaction as long as it can be defined in terms of any pair of the five atoms (P, C4′ and N1, C2, C4 for pyrimidines or N9, C2, C6 for purines) or a virtual point at the middle of the base. FARFAR (20,34) integrates NMR ¹H chemical shift data with Rosetta de novo modeling to consistently produce high-resolution RNA structures. 3dRNA (12,35) utilizes sequence coevolution analysis results to guide the structure optimization procedure after an initial fragment assembly procedure. NAST (36) supports known or predicted tertiary contacts and additionally, it can use residue-resolution experimental data such as hydroxyl radical to filter the generated decoy structures. Vfold (6) is a statistical mechanics-based RNA folding model that can predict both RNA 2D and 3D structures. RNAComposer (16) is a knowledge-based RNA modeling method employing fully automated fragment assembly. ModeRNA (17) is a comparative RNA modeling method capable of handling 115 different nucleotide modifications. We have previously developed a platform iFoldRNA (http://iFoldRNA.DokhLab.org) (5,14) for RNA tertiary structure modeling using physical force field combined with different types of experimental data, including those obtained from NMR (4) or FRET (37).

While the incorporation of restraints could efficiently improve the prediction accuracy, additional restraints impose significant burden on computational cost, especially when the number of restraints is extremely large. Furthermore, unlike protein modeling (38), the incorporation of restraints in RNA structure prediction may not always lead to an increase of the prediction accuracy due to kinetic traps in over-constrained models. There is currently no strategy available for selecting suitable restraints that contribute to improving the accuracy of RNA structure prediction. Such strategy would have significantly reduced experimental burden for structural characterization of RNA molecules by focusing on determining experimental information that would result in most accurate RNA structures. Here, we ask two critical questions: (i) What is the limit in accuracy that one can achieve with arbitrary number of pair-wise distance restraints? (ii) Is there a strategy for selection of the minimal number of restraints that would result in the best structural model of RNA?

We utilize the Gō model (39) to mimic pair-wise distance restraints. In Gō model, two nucleotides attract or repel each other if they are or not in proximity in the native state. Gō potential effectively biases formation of native contacts and disfavors non-native ones, thus allowing proteins (38,40-50) and RNA molecules (4,30,51,52) to navigate the energy landscape (53–56) to their native state by reducing frustrations in the free energy landscape (57). Utilization of the Gō model in simulations ensures consistency of the modeled RNA molecules with their native structures without any specific force field biases. We have found that (4,30,51,58–61) RNA native structures can be reproduced with high fidelity using experimental-derived restraints through Gō model in discrete molecular dynamics (DMD) simulations. Using a fraction of native contacts as restraints in Gō model allows us to directly interrogate prediction accuracy as a function of the fraction of utilized restraints, and address the first question.

To address the second question, we develop a restraints-sorting algorithm based on distance variation allowed by secondary structure (DVASS), which ranks restraints by the distance variation between two residues when the given secondary structure is formed. Using the distance variation metric, we measure the importance of restraints on RNA tertiary structure prediction, that is, how much a constraint would improve the prediction accuracy. The DVASS algorithm is based on purely geometrical considerations and does not rely on molecular dynamics simulations, allowing rapid evaluation of restraints’ importance. Our results show that DVASS can effectively rank all restraints, and the high-ranking restraints could greatly improve the structure prediction, while the low-ranking restraints result in insignificant accuracy improvement. Without using DVASS, approximately 40–60% of all the restraints are needed to maximally improve the prediction accuracy. After sorting the restraints by DVASS, if merely the 20% top ranked sorted restraints are employed, the improvement of the prediction accuracy is comparable to the improvement of the prediction accuracy obtained by using 60% unsorted restraints. Our findings suggest that due to the rugged free energy landscape of RNA, constraining the molecule in simulations beyond 60% of the total number of restraints is not beneficial for accurate structure prediction. Our new algorithm reduces the burden of determining pair-wise distance restraints to 20%, thus offering a strategy for integration of experimental and computational workflows for RNA structure modeling. The implementation of DVASS algorithm could be downloaded from http://dokhlab.org/dokhlab/download/dvass.tar.gz or https://bitbucket.org/dokhlab/dvass.

MATERIALS AND METHODS

iFoldRNA

iFoldRNA utilizes a coarse-grained three-bead RNA model (5), in which each bead represents a phosphate, sugar or nucleobase. The prediction is based on the discrete molecular dynamics (DMD) (51,60,62) engine implemented in Dokholyan Lab. Base-pairing information is incorporated in the simulation as an additional potential. A collection of RNA molecules are subject to replication exchange molecular dynamics at different temperatures to enhance conformation sampling (63). After the DMD simulation, the 100 lowest energy structures are selected and clustered according to the RMSD between the selected pair of structures. The centroid of the resulting cluster is preserved for all-atom reconstruction. If hydroxyl radical reactivity probing (30) or NMR data (4) are available, an additional force field is applied to effectively bias the RNA to the native structure. The reconstruction of an all-atom model from the coarse grained model is performed by replacing each of the three-bead nucleotides with a rotamer of the corresponding nucleotide selected at random from all-atom structures available in Protein Data Bank (64).

Restraints definition

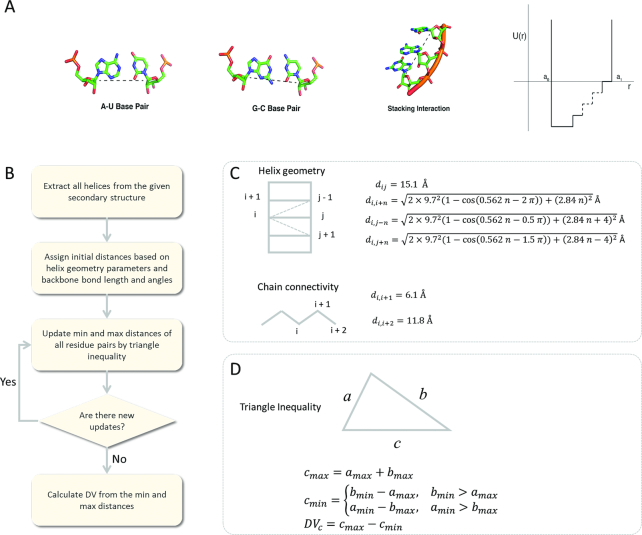
Base pairs between nucleotides in the form of Watson–Crick interactions are the general form of restraints used in RNA structure prediction approaches. Additional interactions exist such as base stacking and non-canonical base pairs such as reverse base pair interactions and Hoogsteen base pairs (65). These interactions together form the basis for the contacts defining RNA tertiary structures. We measure various canonical and non-canonical interactions seen in published RNA structures in the Protein Data Bank (64) to define a native contact reaction coordinate for our DMD simulations (Figure 1A). We find that the optimal definition for a native contact in RNA is between any distance less than or equal to 15 Å between C1′ atoms in any two nucleotides. The C1′ atom, located in the sugar ring, is between the nucleobase and phosphate group and provides a central and consistent marker for defining contacts of various canonical and non-canonical RNA interactions. We can then use this distance measurement to implement Gō restraints that reinforce native contacts with an energy bonus defined by a step function (Figure 1A).

Figure 1.

Design of RNA Native Contacts, Gō Potential Restraints and the DVASS Algorithm. (A) Distances between C1′ atoms in RNA fall under 15 Å for many common base interactions such as A-U Watson–Crick base pairs (10.2 Å) and G-C Watson–Crick base pairs (10.7 Å) or stacking interactions with adjacent nucleotides (5.4–10.7 Å). Native restraints are modeled using a step-wise function in DMD simulations. Potential energy values for the well reach −1.0 kcal/mol/K and the walls of the restraints span from 3.75 to 15 Å. (B) The workflow of DVASS algorithm. (C) The helix geometry parameters and the chain connectivity parameters. (D) The triangle inequality.

Implementation of RNA Gō potential

The potential is designed as step functions constraining distances between beads of the iFoldRNA three bead model. Both attractive and repulsive restraints are tested and implemented to either limit beads within or outside of the 3.75–15 Å range. The restraints are only applied to pairs of nucleotides with sequence numbers i and j ≥ i + 2. The energy well for inter-unit interactions is assumed to be identical for all interacting pairs and is assigned a value of 1.0 kcal/mol/K. The step-function also contains a single well over the distance range allowing for flexibility within the system during folding simulations.

Computational modeling using Gō restraints

We perform RNA coarse-grained DMD simulations, consisting of three pseudo-atoms per nucleotide representing base, sugar and phosphate groups. The native contacts and Gō restraints are generated using a custom Python script that analyzes the atom distances within a model from X-ray crystal structures or the lowest energy model from NMR ensembles downloaded from the Protein Data Bank. We incorporate the native contacts into the DMD simulations as attractive potentials and base pair (A•U, G•C Watson–Crick pairs and G•U wobble base pairs) restraints into the state file before running replica exchange DMD simulations for 500 000 time units (∼25 ns) at temperatures of 0.2, 0.225, 0.25, 0.27, 0.3, 0.333, 0.367 and 0.4 kcal/mol•kB. We perform a clustering analysis on the lowest energy models that satisfy the native contacts from the coarse-grained trajectories. Clustering analysis is performed using an RMSD-based hierarchical clustering algorithm, OC (66), to select the final structural model.

Thermodynamic study of the DMD simulation

We derive the potential of mean force (PMF) as follows:

where E is the iFoldRNA energy, k_b is the Boltzmann constant, T is the temperature (K), W is a function that defines the probability of a given pair of RMSD and the iFoldRNA energy, and the constant C sets the lowest PMF value at any given temperature to be zero.

The DVASS algorithm

Using only the secondary structure as the input, the DVASS algorithm estimates and outputs distance variation values for all pairs of residues (or the given residue pairs list provided by the user). Distance variation of two residues is the difference between the maximum and minimum distances between the two residues among all possible structures in the conformational space. By forming the secondary structure, the distance between any two residues in helix regions is supposed to be nearly fixed because helices in RNA structures ordinarily possess similar structures without significant disparity. Based on distances between C1′ atoms in residues, we compiled a set of parameters (Figure 1C) depicting characteristic local structures, such as helix, generally assuming a canonical double-helical form, and backbone bond, typically featuring fixed values of both bond length and bond angle. The distance between two successive residues in the backbone, calculated by the distance between C1′ atoms in the two residues, is around 6.1 Å. The distance between two residues in the backbone separated by one residue is ∼11.2 Å. Based on this distance information derived from the secondary structure, we could infer the maximum and minimum distances of all other residue pairs by conducting the steps in the workflow in Figure 1B. A distance variation is then defined as the difference between the minimum possible distance and the maximum possible distance. The algorithm is implemented by iteratively applying the triangle inequality (Figure 1D). If we know the minimum and the maximum distances between residue a and residue b, and the minimum and maximum distances between residue b and residue c, then we could infer the minimum and maximum distances between residue a and residue c.

We show in Supplementary Figure S1 an example of the calculation of distance variations given an artificial secondary structure: ‘((((….((((…))))..(((())))..))))’. Initially, we construct a matrix (N × N), where N is the number of residues. Entries in the upper triangle of the matrix are all assigned 999 (Å) and entries in the lower triangle are assigned 6.1 (Å), which is the distance between C4′ atoms in two adjacent residues in RNA. The pair-wise distances in the chain and the three helix regions (Supplementary Figure S1F) are determined based on the formula in Figure 1C and 1D, and they are then assigned to the corresponding positions in the matrix (Supplementary Figure S1A). The triangle inequality is then iteratively applied in the matrix. In each step, all entries in the matrix are updated by applying triangle inequality to all possible ternary tuples. The procedure is converged after five steps when there are no changes in the matrix (Supplementary Figure S1B, C and D). The distance variations are then calculated by subtracting the lower triangle from the upper triangle (Supplementary Figure S1E).

Once we attain all distance variations, the next step is to cluster them since we observed that certain distance variations are inter-correlated. Suppose residue a and residue b have a fairly large distance variation, while residue a and residue c have an extremely small distance variation, then the distance variation between residue c and residue b is likely to be large. The clustering algorithm is based on such a straightforward observation described above. Initially, each of the distance variations is allotted to a distinct cluster, then we randomly pick out a distance variation and then assign the distance of the corresponding residue pair a definite value, which renders the selected distance variation to be 0. We then merge this distance variation and those distance variations that undergo drastic change (larger than a customized cut-off) into one single cluster. By iteratively conducting this procedure, we cluster all the distance variations. The selection of the cut-off is crucial to the resulted number of clusters. A small cut-off may result in a plethora of clusters, while a large cut-off will only engender a smattering of clusters.

Prediction of the number of contacts

We extend the DVASS algorithm to predict the number of contacts given the secondary structure. First, we likewise assign some initial distances by the knowledge of RNA helix geometry parameter and backbone conformation (Figure 1C). We then iteratively utilize the triangle inequality (Figure 1D) to deduce the distance variations of all the residue pairs. We traverse all the distance variations to find out the one that has the largest value and then assign a definite value to the distance between the two residues pertaining to the corresponded distance variation. Thus, the new distance variation of this residue pair is 0. We then again iteratively utilize the triangle inequality to update all the distance variations. We repeat this process 50 times and then count the number of residue pairs that have the minimum distance <15.2 Å, which is trained in a 22 RNAs dataset (Supplementary Table S1) and slightly larger than the aforementioned cut-off value 15 Å. This number serves as the final predicted number of contacts.

RESULTS

Dataset generation

We perform simulations of RNA folding using native contact restraints in coarse-grained DMD simulations (iFoldRNA) to evaluate the relationship between the prediction accuracy and the number of restraints imposed. We select 22 RNAs (Supplementary Table S1) from PDB database as the test set. We choose RNA structures from PDB database in such a way that the lengths of the 22 RNAs vary from 22 to 233 nt, and they have various types of loops, including hairpin loops (3OVA, 2ZY6), internal loops (2PXV, 4QVI), junction loops (2N3R, 3RG5) and pseudo-knots (2M8K, 3L1V). Subsequently, we extract all contacts from their native structures. The contacts between two nucleotides are defined by a distance less than or equal to 15 Å between corresponding C1′ atoms. This definition covers commonly occurring native contacts, such as Watson–Crick base pairs, and non-canonical interactions crucial for proper modeling of complex RNA. Each of the contacts could be used in the structure prediction as a constraint.

Correlation between the number of restraints and the prediction accuracy

To test how the prediction accuracy changes with the number of restraints, we vary percentages (0%, 5%, 10%, 20%, 40%, 60%, 80% and 100%) of the total native contacts restraints used in simulation to determine the tertiary structures of the 22 RNAs. For each set of restraints, we randomly select a corresponding subset of restraints and perform 20 different simulation attempts. The restraints in different simulation attempts are different. For each of the RNAs, we calculate the average RMSD and the corresponding standard deviation of each of the constraint sets.

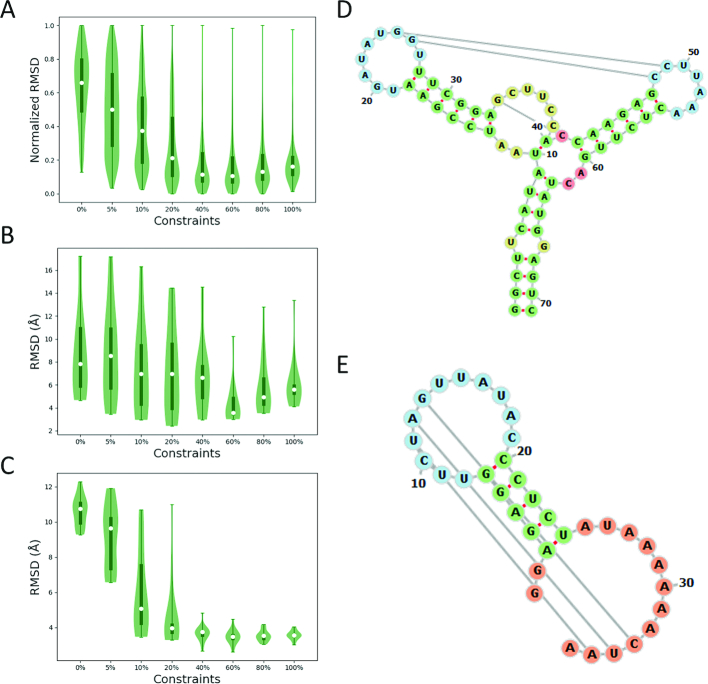
From our simulations, we find that the RMSD decreases steadily with the rise in the percentage of restraints from 0 to 40% (Figure 2A). The RMSD shows no noticeable decrease when the restraints percentage increases from 40% to 60% (Figure 2A). The RMSD increases when more than 60% restraints are imposed on the RNA model, suggesting that the molecule becomes kinetically trapped in local minima. Using 100% native contacts restraints to model RNA results in a slightly higher RMSD of the predicted structure than that using 60% restraints (Figure 2A) for some but not all studied RNA. For some of the RNAs (such as 2L1V, Figure 2C), using 100% restraints results in an RMSD as low as that of 60% restraints, while for other RNAs (such as 3LA5, Figure 2B), 100% restraints result in a much higher RMSD than that of 60% restraints. Kinetic traps associated with RNA folding are likely related to the complexity of RNA structure. For example, the secondary structure of 3LA5 is a complex three-way junction (Figure 2D); correspondingly, the RMSD of the predicted native structure significantly increases when more than 60% restraints are imposed (Figure 2B). The secondary structure of 2L1V is relatively simple since it contains only two short helices (Figure 2E), although it is a pseudo-knot structure; correspondingly, the RMSD of the predicted native structure does not increase when more than 60% restraints are imposed (Figure 2C).

Figure 2.

Relationship between the normalized RMSD and the percentage of imposed restraints. (A) The average normalized RMSD of the 22 RNAs when using 0%, 5%, 10%, 20%, 40%, 60%, 80% and 100% restraints, respectively. (B) The RMSD of 3LA5 when using different fractions of restraints. (C) The RMSD of 2L1V when using different fractions of restraints. (D) The secondary structure of 3LA5. (E) The secondary structure of 2L1V.

The folding landscape by using Gō model

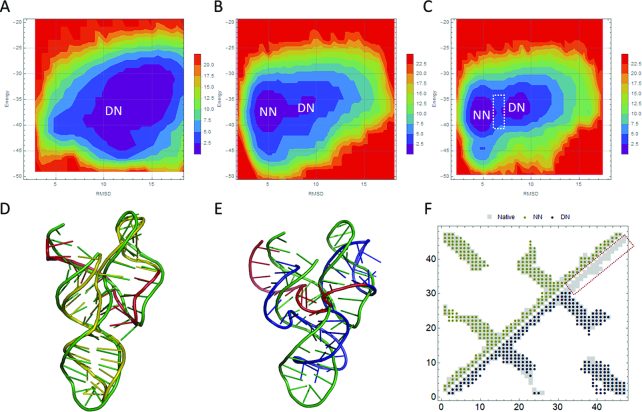
We select a three-way junction from the Varkud Satellite Ribozyme (67) (PDB ID: 2MTJ) as a case to interrogate how a Gō model constrains the folding landscape during simulations. The simulations with no restraints show a single free energy minimum (Figure 3A), which is referred to as a distal-native state (DN). The simulations with 40% restraints (Figure 3B) show both a DN state and a near-native state (NN), suggesting that the imposed restraints are capable of shifting the sampling space of the simulations toward the NN states. The RMSD of the NN state is ∼3.37 Å (Figure 3D), and that of the DN state is ∼9.96 Å (Figure 3E). Almost no energy barrier exists between the two states, suggesting that the DN and NN states could be inter-converted readily. The simulations with 80% restraints (Figure 3C) show separated NN state and DN state, indicating that the two states are hard to inter-convert due to the kinetic barriers formed by the additional restraints. Once the structure situates in one state, it is prone to being trapped due to the higher free energy barrier (white dashed box in Figure 3C). The dissection of the contacts in the native structure, the NN and the DN structures (Figure 3F) suggests that a portion of the contacts (red dashed box in Figure 3F) do not readily form even though they are imposed as restraints. The existence of the free energy barrier hinders the conversion of the structure to a near-native state, in which all contacts are formed.

Figure 3.

Thermodynamic analyses of a three-way junction in Varkud Satellite Ribozyme. (A, B and C) The free energy landscapes of 2MTJ obtained by imposing no restraints (A), 40% restraints (B) and 80% restraints (C), respectively. NN refers to the near-native structure, and DN refers to the distal-native structure. The white box refers to a free energy barrier that impedes the inter-conversion of the NN and DN states. The landscapes are derived from the potential of mean force of RMSD and iFoldRNA energies. The color bar represents the relative Helmholtz free energy in kcal/mol. (D) Overlap of the crystal structure (green) of 2MTJ and the NN structure (olive) with an RMSD of 3.37 Å. The red color refers to the red boxed region in (F). (E) Overlap of the crystal structure (green) of 2MTJ and the DN structure (blue) with an RMSD of 9.96 Å. The red color refers to the red boxed region in (F). (F) The comparison of the contacts in the native structure (grey square), the NN structure (olive circle) and the DN structure (blue circle) of 2MTJ.

DVASS strategy for restraints selection

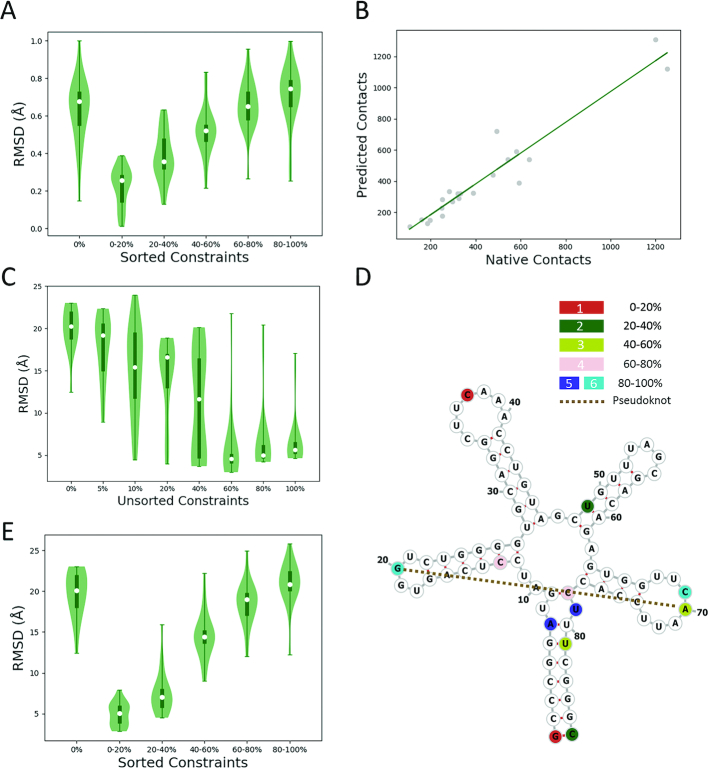
We have demonstrated that the usage of ∼40–60% restraints yields optimum structures in RNA structure prediction. We will utilize the DVASS algorithm to further reduce the minimum required number of restraints. We hypothesize that the extent of distance variation is directly correlated with its ability to improve the prediction accuracy of RNA tertiary structure. We test our hypothesis and subsequently the potency of DVASS using the same dataset of 22 RNAs. Initially, we extract all native contacts from these RNAs as restraints, calculate distance variation between every two bases by using DVASS and sort all the restraints according to distance variation. The larger the distance variation, the higher the corresponding constraint is ranked. Subsequently, we divide the ranked restraints into five groups, where each group consists of the top 20%, 20–40%, 40–60%, 60–80% and 80–100% restraints, respectively. In addition, we consider a control group with no restraints. We perform 20 predicting attempts for each of the groups, and the average RMSDs are shown in Figure 4A. The average normalized RMSD reaches a minimum when the top 20% ranked restraints are employed, and RMSD gradually increases when low ranked restraints are used (Figure 4A). The positive correlation (Figure 4A) between the average normalized RMSD, standing for the prediction accuracy, and the rank of restraints, standing for the extent of distance variation, attests to our hypothesis that the extent of distance variation is correlated with its ability to improve the prediction accuracy. The RMSDs of 3RG5 (Figure 4E) generated by using different groups of restraints present the same trend as the overall average normalized RMSD. It is intriguing to find that by using only the top 20% ranked restraints, we could achieve an RMSD as low as that obtained by using 60% unsorted restraints (Figure 4C and E).

Figure 4.

DVASS Algorithm Test Results in the 22 RNAs Dataset. (A) The average normalized RMSD of the 22 RNAs when using 0%, 0–20%, 20–40%, 40–60%, 60–80% and 80–100% top ranked restraints. (B) Predicted number of contacts versus the number of native contacts. The green line refers to the linear regression of the correlation between the predicted and native contacts, which is: N_predicted = 0.989 × N_native − 13.9, where N_predicted is the predicted number of contacts and N_native is the genuine number of contacts. The Pearson Correlation Coefficient is 0.962. The P-value is 3.54 × 10⁻¹². (C) The RMSD of 3RG5 obtained by imposing 0%, 5%, 10%, 20%, 40%, 60%, 80% and 100% unsorted restraints. (D) The secondary structure of 3RG5. Restraints in residue pairs colored by red, green, light green, pink, blue and cyan are predicted to be located in top 0–20%, 20–40%, 40–60%, 60–80%, 80–100% and 80–100% ranked area, respectively. The brown dashed line refers to the pseudoknot. (E) The average RMSD of 3RG5 obtained by imposing 0%, 0–20%, 20–40%, 40–60%, 60–80% and 80–100% top ranked restraints.

We use 3RG5 as an example to demonstrate how differently ranked restraints are typically distributed in the RNA structure. The secondary structure of 3RG5 (Figure 4D) is a 5-way junction encompassing a pseudo-knot between residue 20 and 70. Six different residue pairs are colored by red, green, light green, pink, blue and cyan, respectively. The red residue pair [1, 37] is predicted to have the largest distance variation. Residues 1 and 37 are located at the very end of the two longest stems in the junction. The blue [7, 79] and cyan [20, 69] residue pairs are predicted to have the lowest distance variations. Residues 7 and 79 are spaced by only one residue, which makes sense of having a low distance variation. Although the location of residue 20 and residue 69 is similar to that of residues 1 and 37, which are also located at the very end of two stems, the existence of the pseudo-knot [20, 70] makes the two residues spatially close to each other. Apparently, a high-ranked restraint such as the one in residue pair [1, 37] affects the spatial arrangement of the two longest stems, while a low-ranked restraint in residue pair [7, 79] or [20, 69] only affects local structures, and restraints in other residue pairs colored in Figure 4D affect the structure of 3RG5 to various extent.

Predict the number of native contacts

Although using 20% top ranked restraints is demonstrated to be sufficient to obtain a satisfactory prediction accuracy, the percentage is relative to the total number of native contacts. In most cases we lack a priori knowledge of the tertiary structure, thus we cannot calculate the total number of native contacts to further derive the minimum needed number of restraints for optimum prediction accuracy. Hence, it is necessary to estimate the number of native contacts given only the sequence and the secondary structure. Therefore, we extend the DVASS algorithm further (see ‘Materials and Methods’ section) to predict the number of contacts from RNA secondary structure. We test our prediction ability in 22 RNAs based on their secondary structural data. Our analyses provide a direct correlation between the predicted number of contacts and the number of native contacts (Figure 4B), thereby validating our methodology.

DISCUSSION

We find that the reduction in the number of restraints does not negatively influence the prediction accuracy, while utilization of 100% restraints does not necessarily improve the accuracy of RNA tertiary predictions. Hence, we can choose only a fraction of the restraints (40–60%) to reduce the overhead caused by restraints. The application of DVASS algorithm can further reduce the number of restraints to be imposed by outlining crucial restraints for structure prediction. Through our analyses, we observed that a portion of restraints does not play a significant role in improving the prediction accuracy (Figures 3D and 4A). In even worse cases (Figure 4E), imposing the lowest ranked (80–100%) restraints result in higher RMSD than that produced by not using any constraint. This finding sheds light on the phenomenon that imposing 100% restraints does not necessarily lead to better prediction accuracy, because some restraints play negligible or even negative role on improving the prediction accuracy. Hence, we can safely ignore such restraints to unload computational burden and to improve the speed of calculation. Therefore, using only a subset of all possible restraints that are beneficial for structure prediction is a rational strategy to reduce the time overhead and improve the prediction accuracy.

We observe a strong correlation between distance variation and the capacity of restraints to improve the prediction accuracy (Figure 4A), which could be rationalized from a conformational space perspective. Suppose all distances between all residues are given definite fixed values, the conformational space would thus contain only one structure. If the distance between two certain residues is no longer fixed, rather it varies in a range, the conformational space then extends to some allowed volume. The larger is the distance variation, the larger is the allowed conformational space, the smaller is the probability of finding the native structure upon sampling, the more likely the prediction accuracy will be low. Therefore, large distance variations strongly affect prediction accuracy compared to that of small distance variations.

The DVASS algorithm, described in the ‘Materials and Methods’ section, is not limited to RNA. We initially extract all the helices from the 22 RNA structures and subsequently obtain inter-residue distances from the helices (Figure 1C). In addition, based on the chain connectivity of RNA strands, we acquire distance information between adjacent residues. Then, we employ DVASS to derive the maximum and minimum distances between other residues in the RNA structure. Thus, the DVASS algorithm is essentially utilized to deduce other distance restraints from a given set of distance restraints. Hence, it is apparent that the DVASS algorithm can be not only used to predict the importance of RNA restraints, but also technically used to derive the importance of restraints used in protein structure prediction.

Gō model was initially proposed in protein folding research (68). While Gō model is computationally efficient, its application has been limited by several known shortcomings. First, the details of the computational folding kinetics mechanisms are not always exactly the same as experiments (69–72). Second, the simulated folding temperature in the Gō model appears to show a strong dependence on the number of native contacts and the number of residues (53). The utilization of Gō model in our work is not aimed at studying the details of RNA folding kinetics mechanisms, but rather on the thermodynamic outcomes—the prediction of the native structural ensemble of RNAs. Hence, these shortcomings of Gō model have no ramification on our work. Interestingly, the formation of kinetic traps for some RNAs (Figure 3) may, in some cases, be attributed to Gō model artifacts. Kinetic traps might be the reason behind the anti-correlation between larger than optimal number of restraints and the extent of the improvement of RNA tertiary structure prediction accuracy. The utilization of DVASS algorithm circumvents this shortcoming to some extent by significantly reducing the number of restraints to decrease the odds of forming kinetic traps. Hence, amalgamating Gō model and DVASS algorithm provides an avenue of efficiently and accurately predicting RNA tertiary structure. In the future, we plan to propose more sophisticated strategies to more confidently subdue the shortcomings of Gō model. For example, an ostensibly reasonable and viable method is to tune the order in which the restraints are applied in the simulation. It is well known that the assembly of ribosomal RNA (rRNA) is a complex process with multiple assembly steps at different locations within the cell (73,74). If we can determine how the order of the formation of contacts affects the folding of rRNA, we may be able to computationally mimic the folding process or even predict the structure of ribosomal RNA efficiently, which is not currently feasible.

DATA AVAILABILITY

The DVASS algorithm, the 22 RNAs dataset and the distance variations of the 22 RNAs can be downloaded from: http://dokhlab.org/dokhlab/download/dvass.tar.gz or https://bitbucket.org/dokhlab/dvass

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

We gratefully acknowledge the G. Thomas Passananti endowment and U.S. National Institutes of Health [R01 GM123238–01, R01 GM064803–12]. Funding for open access charge: National Institutes of Health [R01 GM123238–01, R01 GM064803–12].

Conflict of interest statement. None declared.