Integrating Structural Information to Study the Dynamics of Protein-Protein Interactions in Cells

SUMMARY

The information of how two proteins interact is embedded in the atomic details of their binding interfaces. These interactions, spatial-temporally coordinating each other as a network in a variable cytoplasmic environment, dominate almost all biological functions. A feasible and reliable computational model is highly demanded to realistically simulate these cellular processes and unravel the complexities beneath them. We therefore present a multiscale framework that integrates simulations on two different scales. The higher-resolution model incorporates structural information of proteins and energetics of their binding, while the lower-resolution model uses a highly simplified representation of proteins to capture the long-time-scale dynamics of a system with multiple proteins. Through a systematic benchmark test and two practical applications of biomolecular systems with specific cellular functions, we demonstrated that this method could be a powerful approach to understand molecular mechanisms of dynamic interactions between biomolecules and their functional impacts with high computational efficiency.

Graphical Abstract

INTRODUCTION

Proteins in highly crowded cellular environments rarely act alone (MacPherson et al., 2013; Pawson and Nash, 2000). Their biological functions are closely associated to the knowledge of their interactions with each other. For this reason, genome-wide databases of direct protein-protein interaction (PPI) (Janin and Chothia, 1990; Plewczynski and Ginalski, 2009) have been constructed for many species with the technological advances in high-throughput screening techniques such as yeast 2-hybrid (Y2H) (Joung et al., 2000). The large-scale networks in these PPI databases serve as an important overview of physical connections between proteins (De Las Rivas and Fontanillo, 2010). A cellular process, however, often involves coordinated dynamics of several proteins that interact in a temporally ordered and environment-dependent manner (Barabasi and Oltvai, 2004). These fundamental aspects of cellular functions cannot be interpreted by the static maps of PPI, but rather require modeling of PPI in more dynamic details. In order to model the dynamics of protein interactions, one needs to understand the binding properties between each specific pairs of interacting proteins in a network, which are rooted in the structural features at the interfaces of two molecules (Agius et al., 2013). Traditionally, atomic structures of protein complexes can be determined by x-ray crystallography (Marsh and Teichmann, 2015), while dynamic parameters of interactions between proteins are measured by Isothermal Titration Calorimetry (ITC) (Ghirlando, 2011) or surface plasma resonance (SPR) (Daghestani and Day, 2010). Unfortunately, large-scale automation of these experimental techniques can be a time-consuming and resource-intensive endeavor. Although efforts have been made to integrate protein structures with PPI networks on a systematic level (Aloy and Russell, 2006; Beltrao et al., 2007; Devos and Russell, 2007) and template-based modeling of protein complexes has hastened a more comprehensive picture of the networks (Szilagyi and Zhang, 2014; Zhang et al., 2012), there is still a missing link in characterizing dynamic features from these structural models. Furthermore, all these in vitro or in silico approaches are limited by the fact that they isolate protein interactions from their in situ biological surroundings. In brief, it is highly demanding to study dynamics of protein-protein interactions in the context of variable physiological conditions, while how to integrate atomic-level binding properties of protein complexes into systems-level PPI networks is still a big challenge.

Computational modeling offers an efficient alternative to detect protein interactions with dynamic details that may currently be difficult to attain in laboratory. Simulation methods such as MCell (Stiles and Bartol, 2001) and Smoldyn (Andrews and Bray, 2004) provide a realistic treatment of protein reaction networks in specific cellular environments. However, they cannot explicitly resolve particle collisions, due to the fact that the excluded volumes of particles are ignored in these models. Recently, the physical sizes of molecules were considered by several more advanced simulation techniques. Unfortunately, these highly simplified models are still not able to include structural details and energetic feature of interacting molecules (Frazier and Alber, 2012; Ridgway et al., 2008). On the other hand, atom-based Brownian dynamic (BD) simulations are widely used to reproduce the kinetics of protein association (Ermakova, 2005; Haddadian and Gross, 2006; Wieczorek and Zielenkiewicz, 2008). The current applications of BD simulations are mainly focused on calculating the association rate between two individual proteins, leaving aside the impacts of their cellular environments in which they might interact with multiple binding partners. Despite recent progresses in computational capacity which have enabled BD simulations to start reproducing crowded cytoplasmic environments (Ando and Skolnick, 2010; Frembgen-Kesner and Elcock, 2013; Yu et al., 2016), only the effects of cellular crowding on diffusions, folding, and pairwise binding were evaluated. The intensive computational consumption of these structural-based simulations has still prohibited them from being applied to more complicated dynamic processes (Im et al., 2016), such as assembly of protein oligomers. Multiscale modeling is becoming a promising technique to overcome the limitations in computational models of different scales. Most of the current multiscale models belong to two different categories. In one category, models are built by coarse-graining atomic structure of biomolecules to study their dynamics and functions (Ayton et al., 2007; Noid et al., 2008; Sherwood et al., 2008), while in the other, lower resolution models are used to study biological processes from subcellular to cellular level (Chakrabarti et al., 2012; Krobath et al., 2009; Ramis-Conde et al., 2008). Very few models have been developed to bridges the gap between molecule-level and cell-level models (Stein et al., 2007).

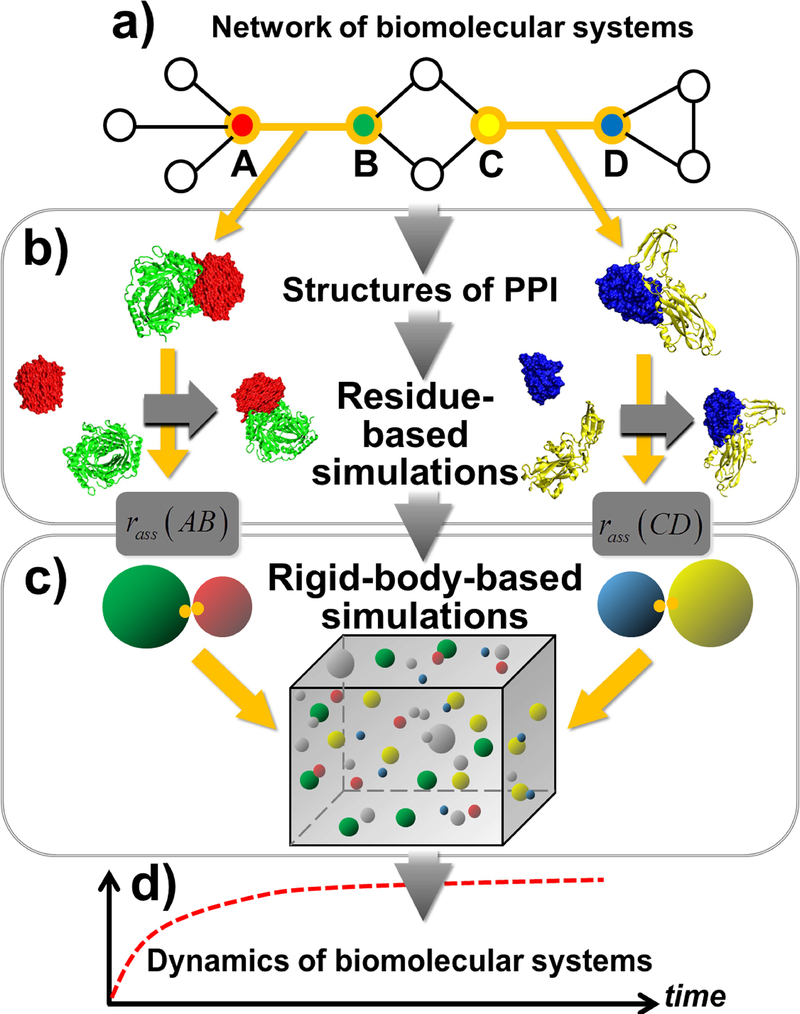
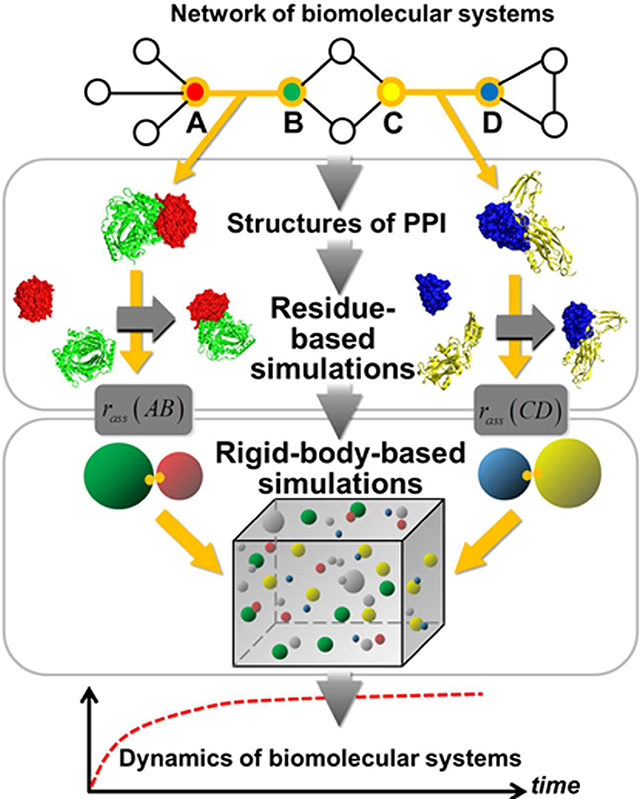
In order to fill in the blank and access the dynamics of protein interactions in cells with both long time-scale and high structural-resolution, here we present a framework of multiscale simulation methods. The framework consists of simulations on two different scales to study any biomolecular system which can be represented by a network model (Figure 1a). The higher-resolution model incorporates the information of protein structures to estimate the binding rates between each pair of interacting proteins in the network (Figure 1b). The lower-resolution model uses a rigid body (RB) based representation for proteins to simulate the dynamic details of the system (Figure 1c). By feeding the binding rates calculated from the structural-based simulations into the RB-based simulations, two levels of models are integrated together so that any dynamic process of a biological system can be studied with both molecular detail and cellular context (Figure 1d). After calibrating the model accuracy by a benchmark of two-body protein association, the feasibility of the method on more complicated problems has been tested by two specific examples of many-body protein interactions, which are commonly occurred in cells. Our study demonstrated that this multiscale framework serves as a powerful approach to study the complicated dynamics of biomolecular interactions in cellular environments with high computational efficiency.

Figure 1:

The outline of our multiscale modeling framework is illustrated as follows. Given a biomolecular system which can be represented by a network model (a), the framework combines simulations on two different scales. For a pair of interacting proteins in the network, the binding rate is first estimated by the higher-resolution residue-based simulation model which incorporates the information of their structures (b). Afterwards, the lower-resolution rigid-body-based model is applied to simulate the binding process of all interacting proteins by feeding their binding rates that are calculated from the residue-based simulations (c). Through the integration of these two levels of models, the long-time-scale dynamics of the system can be studied with both molecular detail and cellular context (d).

RESULTS

Calibrate the multiscale modeling framework by binary protein interactions

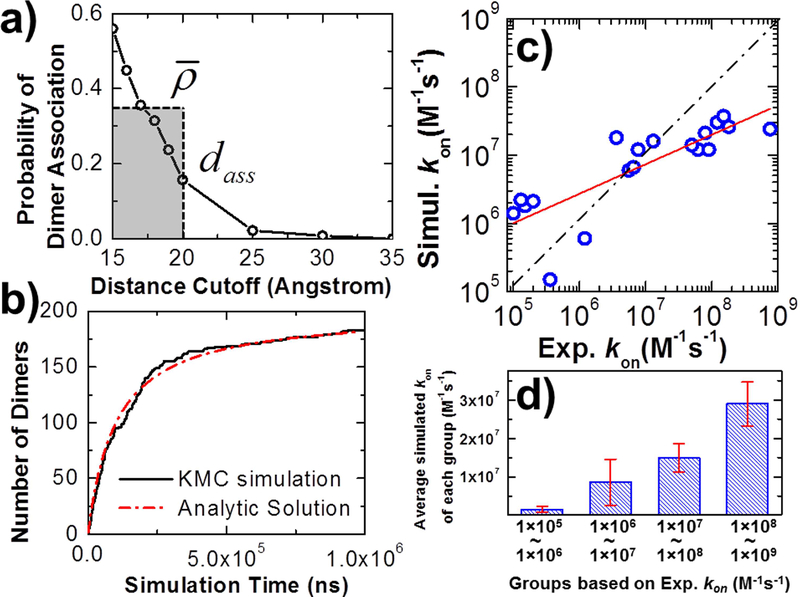
The accuracy of the multiscale modeling framework was verified by simple processes of protein dimerization. We started our tests from a well-studied system, the barnase/barstar complex (PDB id 1BRS). The complex consists of a bacterial protein barnase with its inhibitor barstar. In order to estimate the effective rate of association r_ass and effective distance of association d_ass for this protein complex in the RB simulations, 10³ trajectories of residue-based simulations were generated. In the initial conformation of each trajectory, barnase and barstar were placed with a random position relative to each other in which the distance between their binding interfaces is fallen within the cutoff d_c. Each trajectory contained the maximal length of 10³ simulation steps, with a time step of 0.01 ns, so that the total length of each trajectory is 10 ns that is equivalent to a time step in RB simulation. Based on the simulation results collected from all the trajectories, we counted how frequently an encounter complex was formed given a specific value of d_c. We further tested different values of d_c, ranging from 15Å to 30Å. The relation between d_c and ρ is plotted in Figure 2a. The figure shows that probabilities of dimer association drop when increasing the distance cutoff, suggesting that dimers are more difficult to form when two molecules are more extensively separated in the beginning. From these calculated probabilities, we attained the values of r_ass and d_ass. As shown in Figure 2a, the effective distance of association d_ass equals 20Å, where the probability of dimer association falls below 30% of the highest value based on the definition in the third section of STAR METHODS. The average value of probabilities $\overline{\rho }$ for all distance cutoffs below d_ass equals 0.35. Consequently, the effective rate of association r_ass equals 0.35 10ns = 0.035ns⁻¹.

Figure 2:

The effective rate and distance of association are derived after we calculate the probability of dimer association along with distance cutoff (a). Feeding the effective rate and distance of association into the RB simulations and assuming the binding affinity infinitely strong, the number of dimers formed in the system can be plotted along with the simulation time and directly compared with the analytic solution (b). A benchmark set for protein dimerization was constructed. The correlation between the logarithmic values for our calculated values and their corresponding experimental data is plotted in (c). The red line is from the linear regression fit between calculations and experiments, while the dashed line indicates the perfect fit. The benchmark set was further classified into 4 groups based on the experimental k_ons. We calculated the averaged values of simulated k_ons for each group and plot the histogram in (d).

The derived r_ass and d_ass were fed into the RB simulations, in which 200 rigid bodies of barnase and 200 rigid bodies of barstar were randomly distributed in a 3-dimensional cubic box with volume of 10⁶ nm³. Diffusion constants and molecular sizes of two proteins were set the same values as in the residue-based simulations. For simplification, the binding affinity between barnase and barstar was assigned to be infinitely strong. Therefore, the dissociation rate in the simulation k_off equals 0s⁻¹. As shown by black curve in Figure 2b, with the inputs of all these simulation parameters, the number of dimers formed in the system increases along with the simulation time, but the rate of growth becomes slower after the system approach to the equilibrium. If we assume there is no dissociation in the system and the initial concentrations of two proteins are equal, the growth of dimers can be solved analytically using the equation $A_t=M_0^2\cdot k_{on}t/\left(M_0{k}_{on}t+1\right)$ (Xie et al., 2014), in which A_t is the concentration of dimers at time t, M₀ is the concentrations of monomers in the beginning, and k_on is the on rate between two proteins. Given the initial concentration of barnase and barstar in the system, we fitted our simulation data with this equation, which is shown by the red dashed curve in Figure 2b. The good agreement between the analytic solution and our numerical results indicates that our simulations qualitatively capture the kinetic feature of protein dimerization. Moreover, the on rate derived from the fitted curve equals 3.0×10⁷ M⁻¹s⁻¹. This value, which is close to the experimental measurement (1.2×10⁸ M⁻¹s⁻¹) at the ionic strength of 103 mM(Alsallaq and Zhou, 2007), suggests that the association between two proteins can be quantitatively reproduced by our multiscale modeling framework in this specific system.

We also simulated the association of the barnase/barstar complex at different ionic strengths, as well as tested the effect of mutations on the calculated association rates. The tested results can be found in the Supplemental Testing Results and Figure S1. We further constructed a benchmark set for protein dimerization to test the generality of our modeling framework. The benchmark was selected from a large-scale data set in our previous study which consists of 59 protein complexes(Xie et al., 2017). The selection of this subset is based on the following criteria. First, the experimentally measured rate constants are restricted between 1.0×10⁵ and 1.0×10⁹ M⁻¹s⁻¹. Second, only dimeric complexes were considered in the benchmark, while proteins in the complexes should contain more than 50 residues to ensure that they are in globular shape, and less than 500 residues due to computational feasibility. The complexes that show large gaps or unresolved fragments at their binding interface were excluded from the benchmark. Finally, the experimental data for complexes in the benchmark, such as atomic coordinates of complex structures, association rate constants, and ionic strength need to be all well documented. Consequently, a test set including 19 protein dimers was generated. Detailed information about this benchmark set can be found in the Table S1.

For each protein complex in the benchmark with its corresponding ionic strength, 10³ trajectories of residue-based simulations were carried out under different values of distance cutoff. The simulations followed the same procedure as described in the complex of barnase/barstar. The blue circles in Figure 2c show the correlation between the logarithmic values for our calculated k_ons and their corresponding experimental values for all 19 dimer complexes, with a Pearson’s correlation coefficient of 0.82. The red line in the figure is from linear regression fit between simulations and experiments, while the dashed line indicates the perfect fit. We further divided the 19 protein complexes into 4 groups based on their experimental k_ons. As shown by the histogram in Figure 2d, we calculated the averaged values of simulated k_ons for each group. Comparing with experiments, the results suggest that our simulations generally overestimated slow protein associations, and underestimated fast protein associations. However, the strong correlation between simulation and experimental data as shown in Figure 2c and Figure 2d indicates that our method is able to distinguish between fast and slow kinetics for different types of protein dimers with a wide range of association rates.

Overall, our tests on protein dimerization demonstrate the effectiveness of multiscale framework in reflecting binding kinetics between proteins. In the next two sections, we will apply the framework to the systems with more complicated dynamic properties and cannot be approached by conventional methods on the atomic level.

Simulate competitive binding of the NK cell receptor with different ligands

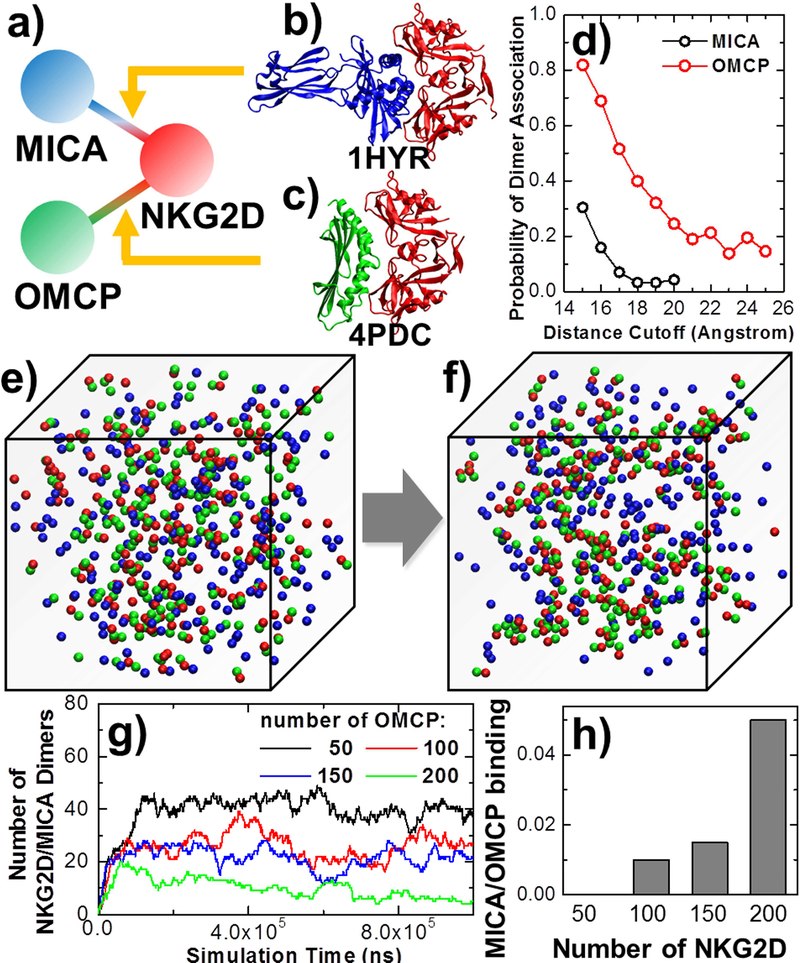
In PPI network, there are a relatively small number of proteins having multiple binding partners, which are called “hubs” of the network (Agarwal et al., 2010). In some cases, binding partners of a protein share the same interface, so that they will compete with each other for binding to the target protein when they coexist in the same system. This target protein corresponds to the concept of “date hubs” in PPI network(Kim et al., 2006). A well-known example of “date hubs” is ligand recognition of cell surface receptors in the immune system. The spatial-temporal regulations of immune response are triggered by the receptors on surfaces of immune cells through their binding with various extracellular ligands. One specific case is natural-killer cell receptor NKG2D (natural-killer group 2, member D). At least two ligands that bind to NKG2D are documented. One is a human cell-surface protein called MICA (Li et al., 2001), while the other is encoded by the Cowpox Virus and called OMCP (Lazear et al., 2013). Structural studies show that different ligands bind to relatively equal surface areas on the same region of the receptor, indicating that ligands can compete with each other for receptor binding. This relationship of protein interactions corresponds to the simple network motif that contains a subnet of three nodes, in which NKG2D is the “date hub” (Figure 3a). Moreover, binding experiments suggest that significant differences in binding rates and affinities of these ligands may have functional implications (Li and Mariuzza, 2014).

Figure 3:

We simulated the competitive binding between the receptor NKG2D and two of its ligands, MICA and OMCP (a). The atomic coordinates of these two ligand-receptor interactions are taken from the Protein Data Bank with PDB id 1HYR for NKG2D/MICA complex (b) and 4PDC for NKG2D/OMCP complex (c). Using residue-based simulations, we first compared the receptor association probability with two ligands under various distance cutoff values (d). RB simulations were then applied to simulate the system when both ligands coexist and bind to receptors with the overlapping interface. Starting from an initial configuration (e), we found that most receptors (red) form complexes with ligands OMCP (green) instead of MICA (blue) at the end of the simulation (f). While changing the concentration of ligand OMCP to different values and keeping the number of receptor and ligand MICA in the system, less NKG2D/MICA complexes are observed for the systems containing more OMCP ligands (g). On the other hand, when we kept the number of both ligands and changed the concentration of receptors, the ratio between NKG2D/MICA versus NKG2D/OMCP complexes increased for the systems with more receptors (h).

In practice, residue-based simulations were first performed to test the binding of the receptor with the human ligand MICA, as well as with the viral ligand OMCP. The atomic coordinates of protein complex containing NKG2D receptor and MICA are taken from the PDB id 1HYR (Figure 3b), while the atomic coordinates of NKG2D/OMCP complex are taken from the PDB id 4PDC (Figure 3c). Figure 3d compares the dimer association probability of ligand MICA with ligand OMCP along with various distance cutoff values. The figure shows that at the same distance cutoff, much higher probabilities of association were observed for ligand OMCP than ligand MICA. Based on the distributions of these probabilities, we derived the r_ass and d_ass for association of the receptor with both ligands. For MICA, d_ass equals 16Å and r_ass equals 0.015ns⁻¹, while for OMCP, d_ass equals 24Å and r_ass equals 0.05ns⁻¹. The on rates of binding between NKG2D and two ligands were further calculated by RB simulations using their corresponding values of r_ass and d_ass. In each system of RB simulations, 200 rigid bodies of receptors and 200 rigid bodies of ligands were randomly distributed in a 3-dimensional cubic box with volume of 10⁶ nm³. The binding affinities were assigned to be infinitely strong. By fitting the RB simulation results with analytic solutions, we attained that the k_on between receptor NKG2D and ligand MICA equals 9.6×10⁶ M⁻¹s⁻¹, while the k_on between receptor NKG2D and ligand OMCP equals 6.6×10⁷ M⁻¹s⁻¹. Our simulation results therefore suggest that the binding between receptor and viral ligand is much faster than the binding between receptor and human ligand. This is consistent with the previous experimental test (Li and Mariuzza, 2014).

If both ligands coexist in the same system, they will bind to receptors with overlapping interfaces. As a result, each receptor can simultaneously bind to only one type of these two ligands. In another word, there is competition between these two ligand types for receptor binding.. In order to understand the detailed mechanism of this competitive binding, we added both types of ligands into the RB simulations. Specifically, in a 3-dimensional cubic box with volume of 10⁶ nm³, we randomly placed different numbers of receptor NKG2D, as well as ligand MICA and OMCP in the rigid body representation as an initial configuration. The rates of association between receptor and two types of ligands were adopted from their corresponding values of r_ass and d_ass that were calculated from above simulations. In order to estimate the rates of dissociation between receptor and ligands, we further used DCOMPLEX(Liu et al., 2004) to evaluate the stability of NKG2D/MICA and NKG2S/OMCP complexes. The calculated binding free energy of NKG2D/MICA is −15.35Kcal/mol, while the calculated binding free energy of NKG2D/OMCP is −17.16Kcal/mol, indicating that the binding between receptor and viral ligand is stronger than human ligand. These binding free energies and our previously derived k_ons gave the dissociation rates for NKG2D/MICA complex (10⁻⁵s⁻¹) and NKG2D/OMCP complex (10⁻⁶s⁻¹). Using these values as reference, we accelerated dissociation in our simulations by tuning down both calculated k_off s with the same amount, to assure that the kinetics of the whole process remains qualitatively unchanged but can be computationally accessible to simulate. As a result, the value of k_off for NKG2D/MICA complex dissociation in the simulation is set to 10⁻⁵ns⁻¹, while the value of k_off for NKG2D/OMCP complex dissociation is set to 10⁻⁶ns⁻¹.

Using the association and dissociation parameters, Figure 3e gives an example of the initial configuration which contains 200 rigid bodies of receptors with red spherical representation, as well as 200 rigid bodies of ligand MICA and OMCP with blue and green spherical representation, respectively. At the end of the simulation, it is found that most receptors form complexes with ligands OMCP, indicating by the dimers between red and green rigid bodies shown in Figure 3f. More quantitative results are plotted in Figure 3g, in which we keep the number of receptor and ligand MICA (200) and change the concentration of ligand OMCP to different values. The figure shows that less NKG2D/MICA complexes are observed when the systems contain more OMCP ligands. In another set of experiments, we keep the number of both ligands (200) in the simulation box and change the concentration of receptors to different values. Figure 3h plots the histogram of ratio between NKG2D/MICA and NKG2D/OMCP dimers observed under different receptor concentrations. The figure shows that the ratio of NKG2D/MICA versus NKG2D/OMCP binding increases when there are larger numbers of receptors in the system. This result suggests that if there is limited number of receptor available, competition will be biased towards the ligand that has stronger relation to the receptor, while the other ligand will face higher pressure of competition. Overall, the general biological implication underlying our study suggests that the viral ligand, based on our structural based simulation, can bind to the receptor NKG2D more rapidly and stably than the human ligand. During virus infection, these viral ligands will be exposed to the receptors expressed on surfaces of immune cells. As a result, the original ligands of the receptors in human will lose their binding by competing with the viral ligands, as illustrating by our RB simulations. The newly formed receptor–ligand interactions will trigger the signaling pathways in the immune cells and leads to the cytotoxic lysis of the cells that are infected by virus. Therefore, through the example of natural killer cell receptor, both basic dynamic mechanism and pathological significance of this simple network motif were manifested by our multiscale simulations.

The structures of NKG2D/MICA and NKG2D/OMCP dimers show differences of side-chain packing between the interfaces of two protein complexes. For instance, LYS 150 is one of the polar residues at the binding interface of receptor NKG2D. Figure 4a shows that LYS 150 is closely packed against the residues on the surfaces of ligand OMCP. It forms salt bridges with two residues (ASP 129 and ASP 132) from OMCP at the binding interface. In contrast, the interface between NKG2D and ligand MICA is not as well-packed as the NKG2D/OMCP complex. There is no effective interaction between LYS 150 and any positively charged residues on the surface of ligand MICA, as highlighted in Figure 4b. Given the insight of this difference, we propose a point mutation by replacing the side-chain of LYS 150 with alanine. In order to test the effect of this mutant (K150A), we truncated the coordinates of the original side chain atoms in LYS 150 except its Cβ atom, which became the new representative center of sidechain for the mutated alanine and the charge of the side chain was neutralized. We first applied residue-based simulation to generate 10³ trajectories under different distance cutoff values for this mutant in both NKG2D/MICA and NKG2D/OMCP complexes. The probabilities of dimer association were calculated (red dots) and compared with the wild-type complexes (black circles) in Figure 4c for NKG2D/OMCP complexes, and in Figure 4d for NKG2D/MICA complexes. The figures show that the mutant remarkably reduces the association rate of NKG2D/OMCP dimer, while it slightly affects the association of NKG2D/MICA dimer in the opposite direction. These results indicate that mutation of a single residue in the receptor can bring distinctive impacts on its binding with different ligands.

Figure 4:

Differences of side-chain packing are shown when we compared the interfaces of two protein complexes. For instance, LYS 150, one of the polar residues at the binding interface of receptor NKG2D, forms salt bridges with two residues (ASP 129 and ASP 132) on the surfaces of ligand OMCP (a). In contrast, there is no effective interaction between LYS 150 and any positively charged residues on the surface of ligand MICA (b). We therefore propose a point mutation by replacing the side-chain of LYS 150 with alanine. Using residue-based simulations, the association probabilities were calculated for this mutant (red dots) and compared with the wild-type (black circles) for NKG2D/OMCP complex (c) and NKG2D/MICA complex (d). The following RB simulations suggest that the K150A mutant in the receptor NKG2D greatly shifts the balance of ligand competition (e).

Based on the distributions of these probabilities, we derived the r_ass and d_ass for association of two mutated complexes and integrated these parameters into the rigid-body-based simulations. DCOMPLEX further gave the calculated binding free energy of mutated NKG2D/MICA complex (−15.1Kcal/mol) and mutated NKG2D/OMCP complex (−16.18Kcal/mol). As a result, the dissociation rates for both mutant complexes are set to 10⁻⁵ns⁻¹. Figure 4e shows the results from the rigid-body simulations in which 200 rigid bodies of the receptor, as well as 200 rigid bodies of ligand MICA and OMCP are included in a simulation cubic box with volume of 10⁶ nm³. The black curve is the number of dimers formed between mutated receptor and ligand MICA along the simulation, while the red curve is the number of dimers formed between mutated receptor and ligand OMCP. In contrast, the black and red dashed curves are the number of dimers formed between wild-type receptor and the corresponding ligands. In the original wild-type system, ligand OMCP dominates the competition. It forms more than 150 dimers with the receptor, while only less than 10 dimers are attained for ligand MICA. However, Figure 4e indicates that the K150A mutant in the receptor NKG2D greatly shifts the balance of this competition. In the mutant, less than half of dimers are formed for ligand OMCP, while the number of dimers for ligand MICA is doubled. Therefore, our simulation results suggest that this specific mutant will lower the binding specificity of receptor NKG2D to the viral ligand. Consequently, we speculates that individuals whose DNA sequences carry this mutant are less sensitive to the invasion of Cowpox Virus, and thus are more likely to get infection.

Understand the assembling mechanism of a heterogeneous signaling complex

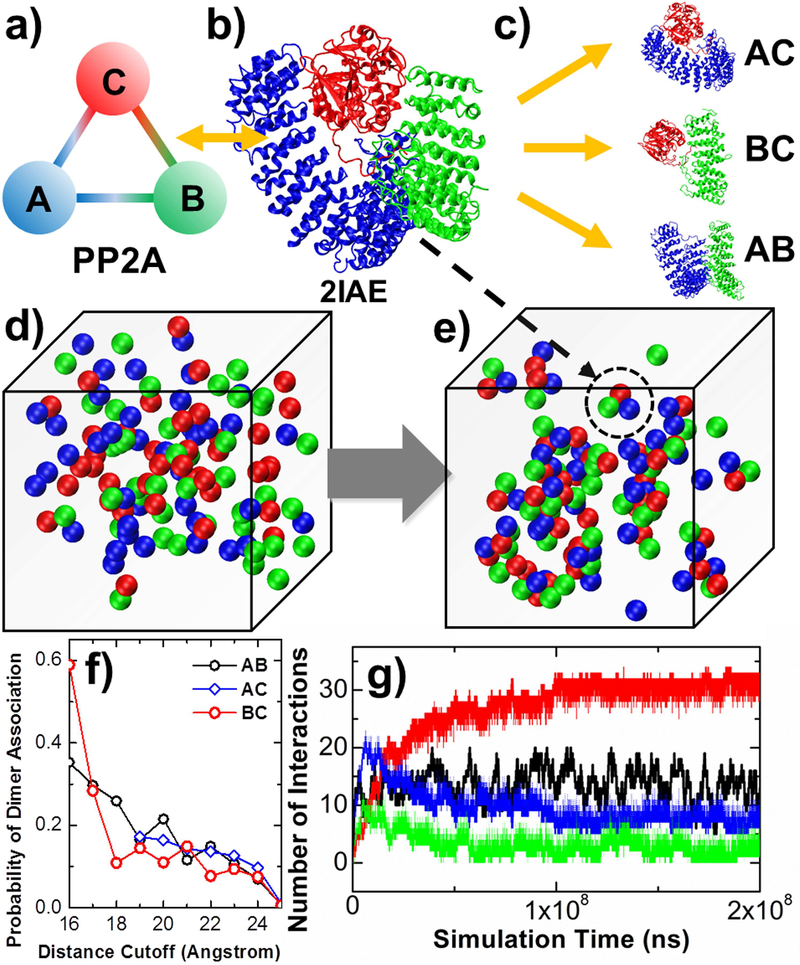
In graph theory, a clique is defined as a subset of nodes in a network such that every two distinct nodes in the clique are connected (Alba, 1973). In PPI networks, this corresponds to a cluster of proteins that interact closely with each other and have fewer interactions with proteins outside the cluster. Proteins in a clique share highly similar expression levels in different cell lines, and thus they are deemed to coordinate single functions in cells. One typical example of cliques in PPI networks is protein complexes consisting of different subunits that form close interactions with each other. In order to understand the dynamics of protein complex assembly and their functional implication, we applied the multiscale simulation framework to the simplest system of protein complexes, a trimer that contains three subunits. This corresponds to a three-node clique in which all nodes are connected with each other (Figure 5a).

Figure 5:

We studied the assembling kinetics of a heterotrimeric holoenzyme, protein phosphatase 2A (PP2A) (a). The atomic coordinates of the entire protein complex are taken from the PDB id 2IAE (b). Residue-based simulations were first performed to three systems to test the binding between all pairs of subunits in the complex (c). In RB simulations, there are 120 rigid bodies in the system. Each rigid body belongs to one of the three types of subunits, as indicated in red, green and blue (d). Hetero-trimers that share the same quaternary arrangement as the crystal structure are found at the end of the simulation (e), one of which is highlighted in the dashed circle. The association probabilities between three pairs of subunits calculated from residue-based simulations are plotted in (f), under different values of distance cutoff. Finally, the RB simulation results are plotted in (g), with the number of trimeric complexes (red curve); the number of A-C dimers (blue curve); the number of B-C dimers (green curve) formed along simulation; and the number of B-C dimers (black curve) formed in a control simulation in which only rigid bodies of subunit B and C were included in the system.

Specifically, a heterotrimeric holoenzyme, protein phosphatase 2A (PP2A) is used as a test system. Dynamic phosphorylation and de-phosphorylation of proteins are essential mechanism in cell signaling pathways, as well as regulation of most other cellular activities. The family of PP2A protein complexes consist of a scaffolding A subunit, a catalytic C subunit, and a regulatory B subunit. All three subunits form pairwise interactions with each other, as a classic network motif of three-node clique. The substrate specificity of PP2A is regulated by the binding of one of at least 18 different B subunits to the core enzyme formed by subunits A and C. Therefore, the assembling dynamics of the complex directly control its biological function in cells.

The atomic coordinates of the entire protein complex are taken from the PDB id 2IAE (Figure 5b) (Cho and Xu, 2007). Residue-based simulations were first performed to test the binding between all pairs of subunits in the complex. In practical, three systems were built to test: 1) the binding between subunits A and C; 2) the binding between subunits B and C; as well as 3) the binding between subunits A and B, respectively (Figure 5c). Figure 5f plots the association probabilities between different pairs of subunits along with various distance cutoff values. The association between subunits A and C can only be detected when their initial distance is larger than 19Å. The figure shows that under small distance cutoff, higher probabilities of association were obtained between subunits B and C than the other two pairs. Previous studies indicated that the regulatory B subunit control the substrate specificities of catalytic C subunit (Seshacharyulu et al., 2013). Therefore, the fast association between these two subunits can facilitate the biological function of the complex. We further derived the r_ass and d_ass for association between different pairs of subunits. For association between A and C, d_ass equals 24Å and r_ass equals 0.015ns⁻¹. For association between B and C, d_ass equals 17Å and r_ass equals 0.04ns⁻¹. Finally, for association between A and B, d_ass equals 23Å and r_ass equals 0.025ns⁻¹.

With all these association parameters, we placed all three types of subunits in rigid-body-based simulations to investigate the detailed assembling mechanism of the complex. In the RB model, all three subunits are represented by rigid bodies with a radius of 5nm. Because each subunit forms interactions with the other two subunits in the complex, as shown in the crystal structure, two binding sites are assigned on the surface of each rigid body. These two sites form a packing angle of 60° with the center of the corresponding rigid body, so that the three rigid bodies in a trimeric complex form an equilateral triangle. Three binding interfaces are found in the complex, corresponding to the interface between subunits A and B, the interface between B and C, as well as the interface between A and C. Given the geometrical representation, we generated an initial configuration for RB simulations in which 120 rigid bodies were randomly distributed in a 3-dimensional cubic box with volume of 10⁶ nm³. Each rigid body belongs to one of the three types of subunits, as indicated by red, green and blue in Figure 5d. Following the initial conformation, the system was evolved by the diffusion-reaction algorithm. We further used DCOMPLEX to estimate the rates of dissociation between subunits. The calculated binding free energy between subunit A and B is −11.4Kcal/mol, the calculated binding free energy between subunit B and C is −14.9Kcal/mol, while the calculated binding free energy between subunit A and C is −19.0Kcal/mol. These calculations suggest that the binding between subunit A and C is the most stable. This is consistent with experimental studies, which show that the core enzyme consisting of subunit A and C is a physiologically more than just an intermediate state during the process of complex formation (Shi, 2009). Given association parameters and binding free energies, we determined the approximate values of dissociation rate constants for all pairs of subunits in the complex. Specifically, the k_off between subunit A and B is 10⁻⁵ns⁻¹. The k_off between subunit A and C is 10⁻⁸ns⁻¹. The k_off between subunit B and C is 10⁻⁶ns⁻¹.

Using the association and dissociation parameters, the dynamics of complex assembly was simulated. Figure 5e shows a snapshot taken from the simulation trajectory. Hetero-trimers that share the same quaternary arrangement as the crystal structure were formed along the simulations. One of these trimers is highlighted with the same color index in the dashed circle of the figure. More quantitative information about assembly kinetics was further provided in Figure 5g. In the figure, the number of trimeric complexes was plotted as red curve along simulation time. In parallel, the number of dimers between subunit A and C is plotted as blue curve, while the number of dimers between subunit B and C is plotted as green curve. The figure indicates that dimers, as partially assembled complexes, are formed at the beginning of the simulations. Their numbers, however, decrease to a much lower level as simulations continue. In the meanwhile, the number of trimers monotonically increases with a much slower rate of growth. At the end of the simulation, more than 30 trimers are found in the system. These results suggest that complexes are assembled through a two-step process. Different subunits are first associated into dimers, which serve as transient intermediates. This relatively rapid kinetics is followed by a second step in which trimers are finally formed by adding additional subunits to the corresponding dimers.

In order to further explore the functional significance about why trimeric complex is needed for PP2A, a control simulation was carried out, in which only rigid bodies of subunit B and C were included in the system. The same number of rigid bodies for both these two types of subunits was generated in a cubic box with the same size as in the previous simulation. All the other relevant diffusion and reaction parameters in both systems are the same. Without the scaffold subunits A, the catalytic C subunit and the regulatory B subunit can still form dimers with active functions. The kinetic profile of dimerization between subunit B and C is plotted as black curve in Figure 5g. The figure suggests that approximately 15 dimers can be formed between these two subunits in the system without subunit A. When subunit A is presented, however, this number is doubled, as illustrated by red curve of the figure. This result indicates that trimeric complex of the enzyme is thermodynamically more stable. It also emphasizes the functional importance of the scaffold subunit in the holoenzyme. Although this subunit is not directly involved in the catalytic activity, we demonstrated that it acts as a structural basis to escort the catalytic C subunit and facilitate its interaction with the regulatory B subunit.

Moreover, we found that the time scale of trimeric complex assembly was much slower than that of direct dimerization between subunit B and C. The system reached equilibrium before 1×10⁷ns in dimerization. However, the system of trimeric complex assembly did not reached equilibrium until after 1×10⁸ns. Despite the slower kinetics, the curve of trimer assembly shows much smaller fluctuations than dimerization, indicating that the system of trimer assembly is more resistant to external noises. Altogether, these kinetic features reveal following biological insights. Although the multistep kinetics leads to a slower process of complex assembly, the intrinsic cooperativity between subunits makes the final complex more stable than the binary interactions. Additionally, the biological noises can be effectively reduced through the spatial assembly of high-order protein complexes. These properties assure that a protein complex could exhibit an all-or-none threshold-like response only to a persistent and high dose of external stimulation, which is biologically important for cells to remain functional in a stochastic environment (Qian, 2012).

The multiscale simulation framework further provides us the possibility to test how the structural variations at the interfaces between different subunits affect the kinetic balance of complex assembly. Previous studies show that in melanoma cancer patients, an R418W mutation in subunit A can disrupt the interaction between subunit A and C (Ruediger et al., 2001). Another mutation at the neighboring residue K416E was also reported to abolish the A-C interaction (Turowski et al., 1997). In the crystal structure of PP2A complex, it is found that both residues K416 and R418 are located at the interface between A and C subunits (Figure 6a). They form specific hydrogen bonds with subunit C. In order to test the effect of these two mutants on complex assembly, we first applied the software SCRWL4 (Krivov et al., 2009) to reconstruct the sidechains of mutated residues at A-C binding interface (Figure 6b). Residue-based simulation was then used to generate 10³ trajectories under different distance cutoff values for this double mutation system. The probabilities of A-C association were calculated (red circles) and compared with the wild-type (black circles) in Figure 6c. Much to our surprise, the figure shows that the double mutants almost totally prevent the association between subunit A and C. This indicates that only a small number of residues can thoroughly change the energetic features of a binding interface. In another word, the association between two proteins is dominated by a limited number of so-called “hot spot” residues at binding interfaces.

Figure 6:

In the wild-type complex, both residues K416 and R418 are located at the interface between A and C subunits and form specific hydrogen bonds with sidechains of residues in subunit C (a). We reconstructed the sidechains of mutated residues R418W and K416E at the interface between A subunits and C (b). Residue-based simulation shows that the double mutants almost totally prevent the association between subunit A and C (c). Furthermore, RB simulations suggest that comparing with the wild-type, the B-C interactions in the mutant dramatically decrease and their fluctuations are distinctively enhanced, although the mutations at subunit A do not directly interfere with the binding interface between subunit B and C (d).

The r_ass and d_ass for association between subunit C and mutated subunit A were derived based on the probability distributions in Figure 6c. DCOMPLEX was further used to calculate the A-C binding free energy from the structure in which residues K416 and R418 are mutated (−9Kcal/mol). As a result, the rate for dissociation between subunit C and mutated subunit A is set to 10⁻³ns⁻¹. Using these binding parameters to model the mutated A-C interface, together with all the other original parameters for A-B and B-C interfaces, RB simulations were carried out to illustrate the impacts of this double mutants on complex assembly. Figure 6d shows the simulation results in which a number of mutated subunit A, together with wild-type subunit B and C were included in a 3-dimensional cubic box with volume of 10⁶ nm³. The total number of three types of subunits is 120. Comparing with the wild-type complex assembly, all the other relevant simulation parameters remain unchanged as well. The black curve in the figure is the number of interactions formed between subunit C and mutated subunit A along the simulation, while the red curve is the number of interactions formed between subunit B and C in the system of mutant. On the other hand, the black and red dashed curves are the number of A-C and B-C interactions formed in the system of wild-type. The figure shows that, firstly, the number of A-C interactions almost vanishes in the mutant, due to the energetic variation at the interface between these two subunits. Interestingly, although the mutations at subunit A do not change the binding interface between subunit B and C, our simulation results show that B-C interactions in the mutant dramatically decrease and the fluctuations of these interactions are distinctively higher than the wild-type. Our simulation therefore suggests that the mutations not only disrupt the interaction between subunit A and C, but also largely affect the biological function of the entire enzyme complex by reducing the effective binding of the catalytic C subunit with its regulatory B subunit. This loss of enzymatic function finally leads to the pathological consequence such as melanoma cancer.

DISCUSSION

In summary, the multiscale simulation method presented in this paper can be improved to overcome its current limitations in the following aspects. For instance, the intramolecular degrees of freedom of each protein were fixed in both residue-based and RB-level simulations. In other words, the effects of protein conformational changes on the dynamics of their interactions were not considered. We applied a proof-of-concept analysis by integrating the elastic network model (ENM) into the residue-based simulation, and found that in some cases conformational fluctuation due to high structural flexibility can impede protein association(Xie et al., 2017). In the future, the method of conformational modeling will further be sophisticated and integrated into current multiscale framework. Additionally, each protein in the RB-based simulation of current multiscale model is represented by a spherical rigid body. It is over-simplified to study systems including proteins with irregular shape or with more than one globular domain. Each structure of these proteins can be coarse-grained into multiple rigid bodies in an advanced version of RB-based simulation, which also includes information of conformational fluctuations between rigid bodies in a specific protein. Another limitation of current method is that it can only be applied to simulate the dynamics of protein-protein interactions with known complex structures. Since the structures for a large fraction of interacting proteins have not been determined in current PPI network, future improvement needs to be made to extend the current method to model the situations where only the fact of binding is known. One possibility if this extension is to apply the template-based modeling method (Szilagyi and Zhang, 2014) on top of the current simulation framework to computationally build the structure of a protein complex before simulating its dynamics of interaction.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Yinghao Wu (yinghao.wu@einstein.yu.edu).

METHOD DETAILS

Simulate multi-protein systems by a RB-based diffusion-reaction algorithm

In a crowded cytoplasmic environment, any cellular process involves systems that contain a large number of biomolecules. In order to simulate these biological systems with a long time-scale, each molecule in a specific system is represented by a spherical rigid body with a given radius (Figure 1c) (Xie et al., 2014), so that simulations can be greatly accelerated by eliminating the intramolecular degrees of freedom. Because a protein molecule might contain one or more binding interfaces while interacting with others, either single or multiple binding sites are assigned on the surface of each rigid body. Binding occurs when the corresponding sites of two rigid bodies are closer than a pre-calculated distance cutoff, called the effective distance of association d_ass. The spatial assignment of each binding site depends on the quaternary arrangement of a specific complex that is formed by different proteins under study.

Given the geometric representation for each type of protein in a specific biological system, a large number of copies are generated and randomly distributed in a 3D simulation box for all types of proteins (Figure 1c). The copy number of each protein type and the size of box determine the concentrations and the stoichiometry of the protein system under study. Due to the lack of experimental data for concentrations of the proteins that are studied in this work, the values of these parameters in simulations were adopted from the similar scales that were used in our previous studies (Chen et al., 2017; Xie et al., 2014). These values were chosen within the typical range of protein concentrations in cells (Milo, 2013), and assure that the sizes of the systems are feasible for computational simulations. After set-up of this initial configuration, simulations proceed with a diffusion-reaction algorithm. Within each simulation time step, the system undergoes a two-step process. The diffusion scenario is implemented in the first step, while the reaction scenario is implemented sequentially in the second. In the diffusion scenario, molecules are randomly moved along their three translational and three rotational degrees of freedom by our previously designed algorithm(Xie et al., 2014). The amplitude of movements for each molecule is determined by its corresponding diffusion coefficients. If a complex is formed by two or more proteins along simulations, all molecules in the complex move together with a predefined diffusion coefficient of smaller value.

Diffusions are followed by the reaction scenario which is to simulate the binding kinetics of protein molecules in the system. Association between any specific pair of proteins will be triggered with the probability P_on = r_ass ×Δt_RB, if the distance between the binding sites of these two molecules is smaller than d_ass. The value of Δt_RB is given by the length of time step in the RB simulations, while the effective rate of association r_ass and effective distance of association d_ass depend on the specific structures of interacting proteins and will be calculated by residue-based simulations. On the other hand, any protein complex will have the probability to break into separate molecules within each simulation time step, which is calculated by P_off = k_off×Δt_RB. The value of dissociation rate k_off for a specific protein complex can be derived either by our calculation or by previous experimental studies in the literature. After dissociation, all proteins from the original complex diffuse separately until they encounter with any other binding partners in the following simulation steps. When both scenarios are completed within a corresponding time step, the new configuration is updated. Finally, as the above process is iterated, the kinetics of the system evolves in both Cartesian and compositional spaces.

Estimate pairwise association between proteins by residue-based Monte-Carlo

For a given pair of interacting proteins, the rate of association can be calculated based on a previously developed kinetic Monte-Carlo (KMC) simulation algorithm (Xie et al., 2017). The simulation starts from an initial conformation, in which two proteins are placed randomly and their binding interfaces are within a given distance cutoff d_c. Following the initial conformation, both proteins undergo random diffusions within each simulation step. The diffusions of each protein consist of a random translational movement and a random rotation along three Euler angles. The simulation steps are iterated until two originally separated proteins either form an encounter complex (Figure 1b) or fail within a given time limit. A scoring function in this algorithm is used to evaluate the energy between two proteins along simulation and guide their diffusions. The scoring function contains three different terms, the electrostatic interactions, the hydrophobic interactions, and the excluded volume effect. In order to implement these interactions, each residue in a protein is coarse-grained into two points, one is represented by the Cα atom and the other is the representative center of a side-chain selected based on the specific properties of a given amino acid. In detail, the inter-molecular energy between two proteins can be written as follows:

$$E_{TOT}=\sum _{i,j}{q}_i{q}_j/\left(4\pi {\epsilon }_0{D}_{eff}{r}_{ij}\right)+\omega \sum _{i,j}\left[H{P}_i+H{P}_j\right]+\sum _{i,j}{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_0}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_0}{r_{ij}}\right)}^6\right]$$ (1)

The first term is the electrostatic interaction between the i^th residue in one protein and the j^th residue in the other, where q_i is the charge of residue i. At pH 7, q_i equals +e for Lys and Arg, −e for Asp and Glu, and +0.5e for His (e is the elementary charge). The charge was assigned to the representative center of the side-chain of each corresponding residue, and ε₀ is the vacuum electric permittivity. An effective dielectric coefficient, D_eff = D_s exp(r_ij/ξ), is used to reflect the shielding effect between two residues in which the representative centers of the side-chain are separated by a distance of r_ij, and ξ is the Coulomb Debye length used to mimic the screening effect at different ion strength.

The second term in Equation (1) is the hydrophobic interactions. The score is the summation of all contact residue pairs, in which the value of hydrophobicity for each residue type HP_i was taken from a previous study by Kyte and Doolittle. The weight constant w (w=0.04) is used to re-scale the weights of energy terms and determines the relative contributions between hydrophobic and electrostatic interactions. Finally, in the excluded volume effect, the depth of the potentials ε_ij equals 5kT if the distance between two atom r_ij is smaller than σ. Otherwise, if the distance between two atom r_ij is larger than σ, the value of ε_ij equals 0. The value of σ defines the finite distance at which the potential between two atoms is zero. It equals 3.8 Å between two Cα atoms, 2.8 Å between a Cα atom and a side-chain representative center, and 2.2 Å between two sidechain representative centers.

The total intermolecular energy between two proteins is calculated by equation (1) after each step of diffusions. The probability to accept the diffusions is calculated by Metropolis criterion. At the end of each simulation step, if at least three native-like contacts are found between two proteins, an encounter complex is formed and the current simulation trajectory was terminated. Otherwise, the simulation continues until it reached the maximal time duration. A native-like contact between the representative centers of two residues is counted if the difference of their distance is less than 2 Å from the original distance in the native complex.

In order to estimate the effective rate of association between a given pair of interacting proteins, KMC simulations need to be performed under different values of distance cutoff. For a specific distance cutoff d_c, multiple trajectories are carried out. Each trajectory starts from a different initial conformation, but the initial distance between the binding interfaces of two proteins in these conformations are all below this d_c. Dimers are successfully formed at the end of some trajectories. On the other hand, two proteins diffuse far away from each other at the end of other trajectories. Consequently, the value for the effective rate of association r_ass and effective distance of association d_ass can be derived from the statistical analysis of these trajectories. These effective rate and distance are used as input parameters in the following RG-based simulations, as introduced in the next section.

Link residue-based to RB-based models by a multiscale modeling framework

A multiscale framework was constructed to incorporate the results from the residue-based KMC simulations into the RB-based diffusion-reaction model, so that a dynamic system with multiple types of protein interactions can be studied with both structural details and long temporal information (Xie et al., 2016). As illustrated in Figure 1a, different classes of proteins and their interactions form a network with specific functions. The kinetic features of each PPI pair in the network provide the basis to understand the global dynamics of this biomolecular system. Therefore, we start the multiscale modeling from evaluating the association rate for each type of protein interactions in the system by residue-based KMC simulations (Figure 1b). Detailed algorithm of KMC simulations has been described in the last section (Estimate pairwise association between proteins by residue-based Monte-Carlo). In particular, the purpose of residue-based simulation is to estimate the effective rate of association r_ass and effective distance of association d_ass for RB-based simulation. The parameter d_ass gives the range of which two proteins can effectively form an encounter complex, while r_ass in residue-based simulations reflects the likelihood of complex formation within the maximal time duration. On the other hand, based on the definition of r_ass in the RB model, the probability of their association within each time step Δt_RB is r_ass ×Δt_RB, if binding sites of two proteins are closer to each other than d_ass. In order to connect residue-based simulations with RB-based simulations under the same time-scale, the maximal time duration of each trajectory to terminate residue-based simulations is fixed to Δt_RB. In another word, each trajectory of residue-based simulation consists of n steps, so that the total length of simulation time for each trajectory satisfies Δt_RB = n×Δt_res, in which Δt_res is the simulation time step for residue-based model. In this study, the simulation time step of residue-based model Δt_res is set as 0.01ns, while the simulation time step of residue-based model Δt_RB is set as 10ns. Therefore, each trajectory of residue-based simulations contains 10³ steps.

In order to estimate r_ass and d_ass, KMC simulations are carried out with different trails of distance cutoff. For each specific distance cutoff d_c, we generate a large number (10³) of simulation trajectories in parallel. We count how many protein complexes are successfully formed after all simulation trajectories are completed. The probability of dimer association ρ for this distance cutoff is then calculated by dividing the number of success with the total number of trajectories. As shown in the Results, the probabilities are different from different cutoff values. In general, the highest value of probability is normally the one with the smallest distance cutoff, while larger distance cutoff leads to lowerer probability of dimer association. The final value of r_ass and d_ass are derived based on the following criterion. The value of d_ass is the distance where the probability of dimer association falls below 30% of the highest value. The parameter d_ass (30%) was adopted purely based on empirical estimation to assure that the curve between ρ and d_c can be transferred to a step function in which the average of association probability equals half of the highest value, as shown in Figure 2a. Accordingly, the effective rate of association r_ass equals $\overline{\rho }/\Delta t_{RB}$, in which $\overline{\rho }$ is the average value of probabilities for all distance cutoffs below d_ass. It is worth of mentioning that in order to improve the accuracy of KMC simulations in the future, the parameters can be further adjusted by fitting the experimental k_ons in a predetermined training set.

The derived r_ass and d_ass for each type of protein interactions in the system are then integrated together to guide the RB-based simulation (Figure 1c). Other simulation parameters such as the size and concentration of each interacting protein in the system, their rates of dissociation and diffusion constants, are determined either based on calculations or by previous experimental studies in the literature. Detailed diffusion-reaction algorithm of RB-based simulations has been described in the first part of methods. In particular, after each step of diffusions, we enumerate all possible pairs of rigid bodies in the simulation box. For a specific pair, if the proteins that represent these two rigid bodies can bind to each other, we further calculate the distance between their binding sites. A complex is able to form when the distance is below the corresponding value of d_ass. The probability of association is determined by the corresponding r_ass. The values of r_ass and d_ass depend on specific types of protein interactions, which are all derived from residue-based simulations. As a result, the functional dynamics of a biomolecular system can be quantified from the simulations results of RB-based model (Figure 1d).

QUANTIFICATION AND STATISTICAL ANALYSIS

In order to estimate r_ass and d_ass in residue-based method, simulations were carried out under different trails of distance cutoff. For each specific distance cutoff d_c, 10³ simulation trajectories were carried out in parallel. Each trajectory contained the maximal length of 10³ simulation steps, with a time step of 0.01 ns, so that the total length of each trajectory is 10 ns that is equivalent to a time step in RB simulation. After all simulations were completed, we count how many protein complexes are successfully formed after all simulation trajectories are completed, as described in the METHOD DETAILS.

DATA AND SOFTWARE AVAILABILITY

Source codes and trajectories for multiscale simulations of barnase/barstar complex association are available at: https://zenodo.org/record/1319599#.W1XkJNgzWUk.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
VMD	Humphrey et al., 1996	www.ks.uiuc.edu/Research/vmd/
Deposited Data
Source codes and trajectories for multiscale simulations of barnase/barstar complex association	This paper	https://zenodo.org/record/1319599#.W1XkJNgzWUk

• We can distinguish between fast and slow protein-protein associations.

• We can design mutants at interfaces of proteins to affect their binding kinetics.

• The dynamics of a date hub is under kinetic control.

• The assembly dynamics of protein complexes are closely related to their functions.

Biography

Wang et al. developed a multiscale modeling framework that is able to realistically simulate the complicated dynamics of a protein network. They demonstrated that this multiscale framework serves as a powerful approach to understand the molecular mechanisms of protein-protein interactions and their functional impacts with high computational efficiency.