Personalized Models for Injected Activity Levels in SPECT Myocardial Perfusion Imaging

Abstract

We propose a patient-specific ("personalized") approach for tailoring the injected activities to individual patients in order to achieve dose reduction in SPECT-myocardial perfusion imaging (MPI). First, we develop a strategy to determine the minimum dose levels required for each patient in a large set of clinical acquisitions (857 subjects) such that the reconstructed images are sufficiently similar to that obtained at conventional clinical dose. We then apply machine learning models to predict the required dose levels on an individual basis based on a set of patient attributes which include body measurements and various clinical variables. We demonstrate the personalized dose models for two commonly used reconstruction methods in clinical SPECT-MPI: 1) conventional filtered backprojection (FBP) with post-filtering, and 2) ordered-subsets expectation-maximization (OS-EM) with corrections for attenuation, scatter and resolution, and evaluate their performance in perfusion-defect detection by using the clinical Quantitative Perfusion SPECT (QPS) software package. The results indicate that the achieved dose reduction can vary greatly among individuals from their conventional clinical dose, and that the personalized dose models can achieve further reduction on average compared to a global (non-patient specific) dose reduction approach. In particular, the average personalized dose level can be reduced to 58% and 54% of the full clinical dose, respectively, for FBP and OS-EM reconstruction, while without deteriorating the accuracy in perfusion-defect detection. Furthermore, with the average personalized dose further reduced to only 16% of full dose, OS-EM can still achieve a detection accuracy level comparable to that of FBP with full dose.

I. Introduction

REDUCTION of the amount of injected radionuclide in patients is critically important in myocardial perfusion imaging (MPI) with single-photon emission computed tomography (SPECT)[1-4]. SPECT-MPI provides important findings for the detection and evaluation of coronary artery disease [5] and is a frequently ordered test in nuclear medicine, affecting a large number of patients.

There have been vigorous efforts in the field of emission tomography focused on improving the image quality through advanced image reconstruction algorithms [6-12]. For example, it was demonstrated in [6] that iterative reconstruction methods such as ordered-subsets expectation-maximization (OS-EM) [7], in conjunction with correction for common imaging artifacts [8], could improve the diagnostic accuracy over conventional filtered backprojection (FBP) image reconstruction. In addition, reconstruction methods including correction for cardiac and respiratory motion [13-17] were also shown to improve the image accuracy in gated SPECT.

Recently, there have been a number of studies demonstrating that the improvements in image reconstruction can be used to preserve the image quality while lowering the injected dose [18-25]. For example, the effect of halving the imaging dose via iterative reconstruction with resolution recovery was studied in [18]. In [18-21], methods for reduction of imaging time instead of injected dose were evaluated. In [25], we quantified the extent to which the dose could be reduced for SPECT-MPI, and demonstrated that studies reconstructed by OS-EM with resolution recovery (RC), attenuation correction (AC) and scatter correction (SC) could be reduced down to 25% of the original administered dose while maintaining the perfusion-defect detectability above that achieved by FBP with 100% dose.

Although these studies have demonstrated the potential for dose reduction in SPECT-MPI, the majority of them, if not all, have been focused on reducing the administered activity level uniformly across patients. However, the level of required dose may differ from patient to patient in order to achieve a consistent diagnostic accuracy across patients [26-29]. Some studies have shown that the amount of dose reduction should be different for obese and normal-weight patients [26], and that injected dose should depend on patient weight or body mass index (BMI) so that the acquired count statistics is maintained [30-32]. The American Society of Nuclear Cardiology (ASNC) noted that “a one-size-fits-all to imaging is no longer acceptable”, urging that decisions regarding imaging should be carefully tailored to each individual patient [29].

In this paper we propose a patient-specific ("personalized") approach for dose reduction, in which we aim to determine the minimum dose level needed to obtain consistent diagnostic performance for each individual patient. We apply machine learning algorithms to determine the extent to which tailoring the injected dose can lead to further dose reduction based on the clinical characteristics of individual patients.

First, we develop a strategy to determine the administered activity levels required on an individual basis from a large set of clinical SPECT-MPI acquisitions (857 subjects). The personalized dose is defined as the minimum dose level at which the reconstructed image is sufficiently similar to that obtained at conventional clinical dose for a given patient. This is to serve the following two purposes: 1) To demonstrate that the achievable dose reduction from the clinical dose can vary largely from patient to patient, hence the need for an individualized approach, and 2) To provide data samples for subsequently developing machine learning algorithms toward personalized dose prediction.

We then develop predictive models to be used in a clinical setting for pre-determining the personalized dose level for a given patient prior to the SPECT-MPI procedure. The input to these models is formed by a set of patient attributes such as body measurements and patient’s medical conditions. Currently, the administered dose in the clinic is typically adjusted for the body mass index (BMI) or weight of a patient. However, many other variables relating to patient’s size and shape (affecting attenuation), and variables relating to disease and physiology (which can impact uptake parameters) can affect the image quality, and thus impact the diagnostic accuracy [27]. Therefore, these variables are also considered in our predictive models.

In the paper, we develop our personalized dose approach with two commonly used reconstruction methods in clinical SPECT-MPI: 1) conventional FBP with post-filtering, and 2) OS-EM with corrections for attenuation, scatter and resolution (AC-SC-RC). Both reconstruction methods were studied previously for optimizing dose reduction [25] and by others on clinical dose reductions [18-24]. However, it is noted that the proposed approach is general and can be easily applied for other reconstruction methods; moreover, the proposed approach should be applicable to other imaging modalities such as PET or CT as well.

The rest of the paper is organized as follows. In Section II, we describe how to determine patient-specific dose levels based on two strategies and present a validation procedure for the task of perfusion-defect detection. In Section III, we present the personalized dose prediction models and their implementation details. In Section IV, we describe the methods using clinical data for evaluation of the personalized dose models. Finally, we present the results in Section V and conclusions in Section VI.

II. Determining Patient-Specific Dose Levels

The approach used to determine patient-specific (“personalized”) dose levels is as follows: Given the acquisition data of a patient with conventional full dose, we obtain a set of reconstructed images of the patient by successively reducing the acquired count levels (which correspond to reduced dose levels). Specifically, let f_l denote the image obtained at dose level d_l, l = 1,…, L, where L is the number of reduced dose levels considered. For example, d_l can be 75% of the full dose administered. Our goal is to determine the smallest dose level:

$$y=\underset{l}{\min }{d}_l,l=1,\dots ,L$$ (1)

at which the reconstructed image f_i remains to be sufficiently similar to the image f_100% obtained at full dose. Below we consider two strategies for determining the similarity between reduced dose and full dose.

A. Image similarity based strategy

In the first strategy, we aim to maintain the image difference between f_l and f_100% to be sufficiently small. For this purpose, we use the Pearson correlation coefficient, denoted by ρ_l, to quantify the image similarity between f_l and f_100%. This correlation measure is equivalent to measuring the mean-squared-error difference of the reduced dose from the full dose; however, given the differing count levels between the two, we use the correlation measure instead. Moreover, since we are mainly interested in the accuracy of the reconstructed myocardium, the correlation measure is computed for a fixed bounded box containing the entire left-ventricular volume for all patients.

Thus, for a given patient, the personalized dose is determined according to (1) as:

$$y=\underset{l}{\min }{d}_l,l=1,\dots ,L,\text{subject to}{\rho }_l\ge {\rho }_0$$ (2)

where ρ₀ represents a specified lower bound on the image similarity between personalized dose and full dose.

B. Perfusion based strategy

In the second strategy, we aim to maintain the reduced dose image f_l to be sufficiently similar in myocardial perfusion to the full dose [32]. For this purpose, we use the total perfusion deficit (TPD) score, provided by the clinically validated commercial package Quantitative Perfusion SPECT (QPS) [33], to quantify the image perfusion. The TPD score is a measure of the non-uniformity of myocardial perfusion with respect to a reference database of normal studies [33].

For a given patient, let s_l denote the TPD score obtained at reduced dose level d_l. The personalized dose for the patient is determined as:

$$y=\underset{l}{\min }{d}_l,l=1,\dots ,L,\text{subject to}\mid s_l-s_{100\%}\mid \le \delta$$ (3)

where s_100% denotes the TPD score at full dose for the patient and δ is the allowance parameter controlling the amount of deviation in TPD score from the full dose.

C. Reconstruction methods

The perfusion-defect detectability in clinical patients can be greatly affected by the image reconstruction methods used, as was demonstrated in our previous study [25]. As noted in the introduction, in this study we consider both FBP and OS-EM with AC-SC-RC. Both were previously optimized for various dose levels (100%, 50%, 25% and 12.5% of full clinical dose) [25]. These optimized settings are also used for this study (Section IV.C).

D. Validation of personalized doses using ROC study

To validate the personalized doses determined from the two strategies above, we perform a receiver operating characteristics (ROC) study for the task of perfusion-defect detection and compare the detection performance with that obtained at full dose. The study is performed using a set of “hybrid studies” which are clinical studies with realistic simulated perfusion defects as in [25]. To quantify the presence of perfusion defects, we compute the TPD scores for the personalized dose and full dose data. We then obtain the perfusion-defect detectability by using the area under the ROC curve (AUC).

Note that the parameters ρ₀ and δ in the two strategies above are used to control the level of deviation in image similarity of the personalized dose from the full dose. A higher ρ₀ (or lower δ) value corresponds to a smaller difference between the reduced dose and full dose images for a given patient, and vice versa. In the experiments, we varied these parameters and evaluated their impact on perfusion-defect detectability in the ROC study.

III. Machine-Learning Models For Prediction of Personalized Doses

A. Personalized dose prediction

With the personalized doses determined from the strategies explained in the previous section, we next utilize them to train a prediction model to determine these dose levels based on the characteristics of the patients. This prediction model will allow us to pre-determine the activity to be administered for a patient prior to the SPECT-MPI procedure in a clinical setting.

Specifically, let vector x = (x₁, …., x_J)^T denote a set of J features describing the attributes of a patient, and y denote the corresponding personalized dose level. Then, the prediction model is to estimate y from x as:

$$y=f(\mathbf{x})$$ (4)

where f (x) is a regression function to be determined with machine learning from a set of training patients.

Assuming N patients available for training, we obtain the following training dataset of input-output pairs:

$$\{({\mathbf{x}}_i,y_i),i=1,\dots ,N\}$$ (5)

where x_i denotes the attributes of patient i, and y_i the corresponding personalized dose for the patient. our goal is then to determine the function f(x) in (4) based on the training set in (5).

In this study, we consider several prediction models with differing complexity in order to identify the best performance [34]. These models include linear regression as well as non-linear regression. For practical purposes, a linear model can be easier to interpret in how different attributes may contribute to the personalized dose level. Thus, we considered two linear models, ridge regression [35] and least-absolute shrinkage and selection operator (LASSO) [36]; these models have built-in regularization and feature selection, which is desirable given the many patient attributes involved (Section V). on the other hand, the relationship between the personalized dose level and patient characteristics is expected to be rather complex (highly non-linear), and thus, a non-linear model could be a better fit. Therefore, we also considered two non-linear regression models: Random Forest [37] and epsilon-Support Vector Regression (ε- SVR) with radial basis functions (RBF) [38].

B. Patient attributes

There are many attributes that can potentially affect the acquired data counts from a patient, and thus impact diagnostic accuracy [27, 29, 30]. Therefore, we decide to include a wide set of variables, some of which directly affect image quality while others may have less impact. The purpose is to apply feature selection so that the machine learning models automatically identify the most relevant variables.

The variables to be considered fall in two groups: 1) patient size/shape/gender: height, weight, chest, waist, hips, torso measurements, age and gender; and 2) patient condition/disease status: pharmacologic/exercise stress, blood pressure values, lipid panel values (such as total cholesterol, LDL (low density lipoprotein), HDL (high density lipoprotein) and triglycerides), exercise capacity and medical conditions (such as hypertension, dyslipidemia, family history of CAD, and previous events such as myocardial infarction, percutaneous coronary intervention, coronary artery bypass graft, etc.).

All the patient size measurements were in inches. Chest measurements 1-3 correspond to the circumferences above, around and below the breast (the rib cage), respectively. Hips, waist and torso length (from the armpit to the hip) were also measured. Shoulder measurement was the width of the shoulders (i.e. the distance from the right to the left shoulder). BMI is based on the patient height and weight (weight/height², in kg/m²). The units are mg/dL (milligrams per deciliter) for LDL and HDL. Systolic and diastolic pressure values were measured in millimeters of mercury (mmHg). Ejection Fraction (EF) was determined by the blood volume at end systole vs. end diastole.

Among the variables used, some are categorical, e.g., gender (male or female), type of stress scan (pharmacological or exercise induced), exercise capacity (low, average, high), and medical conditions (patient has or not), while other variable are continuous, e.g., blood pressure values, heart rate and lipid panel values. All the continuous variables were normalized to be within the range of [0,1].

C. Personalized dose models based on reconstruction methods

As noted earlier, given that the perfusion-defect detectability is dependent on the image reconstruction methods used, we develop our personalized dose models based on two reconstruction algorithms commonly used in clinical SPECT-MPI. Specifically, we consider the following personalized predictive models:

1. Model 1 for providing personalized dose for FBP reconstruction to achieve the same perfusion-defect detectability as FBP at full clinical dose;

2. Model 2 for providing personalized dose for OS-EM reconstruction with AC-SC-RC to achieve the same perfusion-defect detectability as OS-EM with AC-SC-RC at full clinical dose; and

3. Model 3 for providing personalized dose for OS-EM reconstruction with AC-SC-RC to achieve the same perfusion-defect detectability as FBP at full clinical dose.

Note that the first two models aim to achieve the same performance with personalized dose as with full clinical dose for each reconstruction algorithm. The third model aims to achieve further dose reduction while maintaining the diagnostic accuracy of FBP at full dose, which is still commonly used in the clinic.

D. Model training and testing

For training the machine-learning models described earlier in Section III.A, we adopted a 3-fold stratified cross validation procedure for determining the associated model parameters from the training data (Section IV) [39]. Afterward, the trained models were tested on a separate set of data unseen during training (evaluation dataset).

To measure the error level in predicted dose by different models, we computed the average normalized prediction error between the predicted personalized dose values and their target values. Specifically, for M patients, the relative error in predicted dose is measured as

$$e_p=\sum _{i=1}^M\frac{\mid {\widehat{y}}_i-y_i\mid }{y_i}$$ (6)

where y_i and ${\widehat{y}}_i$ denote the target and the predicted dose values of patient i, respectively. In addition, we also computed the average personalized dose levels by the different models and compared to the full dose. Finally, we also conducted an ROC study to validate the performance of the personalized dose models for perfusion-defect detection studies (Section IV).

IV. Evaluation Study

A. Clinical SPECT-MPI data

We made use of data acquired from a total of 857 consecutive patients under Institutional Review Board (IRB) approved written consent. These studies were stress imaging acquired on a Philips BrightView SPECT/CT system in list-mode with Tc-99m sestamibi from 2013 to 2016 at the University of Massachusetts Medical School. Clinical acquisitions in this study were based on ASNC recommendations [40] in which injected activities were adjusted based on patients’ BMI. The SPECT/CT system was configured with two camera heads at 90° apart and 64 projection angles over 180° were used. The list-mode data were framed in 128×128×64 projection matrices with pixel size equal to 0.466 cm for image reconstruction. In addition, attenuation maps from cone-beam CT imaging prior to emission imaging were obtained for use in attenuation correction (AC) during image reconstruction [41-44]. The cone-beam acquisitions were acquired in 0.83-degree steps over 360°.

The characteristics of the 857 patients were as follows: 408/449 male/female, BMI: 31.7 ± 5.8 kg·m⁻², age: 62.3 ± 11.1 years. Among them, 395 were read as having normal scans, 272 as having either perfusion or motion abnormalities, while the rest were read as somewhat normal.

The 857 patients also included the set of 190 patients used in the previous study for uniform dose reduction optimization in [25]. For the ease of comparison, in this study this same set of 190 patients (denoted as Subset A hereafter) was reserved for testing the personalized dose models (to be detailed in Section IV.D), while the other 667 patients (denoted as Subset B) were used to develop the personalized dose strategies (described in Section II).

For personalized dose studies, reduced dose data were obtained by statistical subsampling of the full dose list-mode data as in [25]. To determine the personalized dose levels (Section II), the acquired counts were successively decreased from 100% of the full dose counts in steps of 1/16 at a time.

B. Extracting data samples for personalized dose models

For determining the personalized dose, we first extracted the effective dose injected at full dose level for each patient. To obtain the effective amount of injected activity at the time of the scan, the injected activity was corrected for both the time decay and the residue activity left in the syringe after injection. This corrected activity (in units of mCi) was then used to obtain the personalized dose level y_i for each patient i in the dataset.

For determining the personalized dose prediction models, we extracted the patient features (described in Section III.B) from the patient medical records. In particular, for those features related to the patient condition/disease status, the diagnostic codes (ICD-9 and ICD-10) [45] of the patients were used. These diagnostic codes were considered in groups as follows: E_code (diabetes group), F_code (nicotine dependence), I_code (circulatory system disease), J_code (respiratory system disease), R_code (abnormal lab findings), V_code (external case of morbidity), Z_code (factors influencing health status and/or contract with health services), 272_code (disorders of lipoid metabolism), 4**_code (heart complications), 5**_code (chronic glomerulonephritis) and 7**_code (general symptom). Each group was treated as a categorical variable (present or absent) in the dataset.

C. Reconstruction of clinical data for personalized dose

As described earlier in Section II.C, the following two reconstruction methods were applied in this study: FBP with post-smoothing and OS-EM with AC-SC-RC. Both methods were optimized at 100%, 50%, 25%, and 12.5% of standard clinical dose in our previous study [25]. Specifically, for FBP, the optimal bandwidth values of the Butterworth filter were 0.22, 0.2, 0.19, and 0.18 cycles/pixel for these four respective dose levels. For OS-EM, the optimum values for (Gaussian width parameter [voxels], number of iterations) were (1.2, 12), (1.2, 8), (1.2, 4), (1.4, 4), respectively; the number of subsets was fixed at 16. As the personalized dose levels decreased from 100% of the full dose in steps of 1/16, the values of the reconstruction parameters at each dose level were obtained by interpolation from the optimal values at the four dose levels above.

D. Validation of predictive dose models in perfusion-defect detectability

We conducted ROC studies to evaluate the performance in perfusion-defect detection based on dose levels prescribed by the predictive models. For this purpose, we made use of the patients in Subset A in the same way as in [25]. Specifically, the 190 patients were divided as follows: 1) 60 patients (30 male and 30 female) for use as reference database by the QPS observer, 2) 130 patients in the ROC study, of which 58 patients were to serve as normal and 72 patients to create hybrid studies [46] in which perfusion defects were introduced with varying vascular locations, sizes and contrast levels as described in [25].

The 60 reference cases were used by QPS to derive the normal limits for computing the total perfusion deficit (TPD) scores of other study cases. They were set aside in order to avoid being reused as study patients in the ROC study. This also enabled us to use a common library for determining the personalized dose level in the TPD strategy (Section II.C). That is, the library cases were never used as study subjects either in personalized dose training or in the ROC study.

For each personalized dose model (Models 1-3 in Section III.C), we reconstructed the images at the personalized doses for the study patients and computed their TPD scores, based on which we performed the ROC analysis to obtain the AUC value.

It is noted that when computing the TPD scores, the 60 cases in the reference database were reconstructed in the same way as the study cases in order to match the image characteristics (algorithm parameter values, patient gender, etc.)[25]. For example, when determining the personalized dose for a patent (Section II), if the personalized dose level was 50% of the full dose, then the cases in the reference database were also reconstructed at 50% dose. Similarly, for each of the personalized dose models, the reference database was also reconstructed accordingly with personalized doses applied for the 60 subjects.

V. Results and Discussions

A. Determining personalized dose levels

The perfusion-defect detection results obtained with personalized doses determined using image similarity based strategy are given in Fig. 1. In the figure, the x-axis represents the fraction of personalized dose (in percentage) relative to the full dose averaged over the test subjects, whereas the y-axis represents the AUC values obtained at different dose levels with FBP or Os-EM reconstruction. The different dose levels were controlled by varying the image similarity parameter ρ₀ (as indicated on each curve). For example, with ρ₀ = 0.9975, the AUC obtained with FBP is 0.754, compared to 0.755 for the full dose; the corresponding personalized dose fraction is 69% on average (or 22.3 mCi). Similarly, for OS-EM, the AUC obtained with personalized dose is 0.799, compared to 0.801 for the full dose; the corresponding personalized dose fraction is 60% on average (or 19.4 mCi). It is noted that with smaller values of ρ₀, the average personalized dose is further reduced in both FBP and OS-EM, but the AUC values also begin to decrease.

Fig. 1.

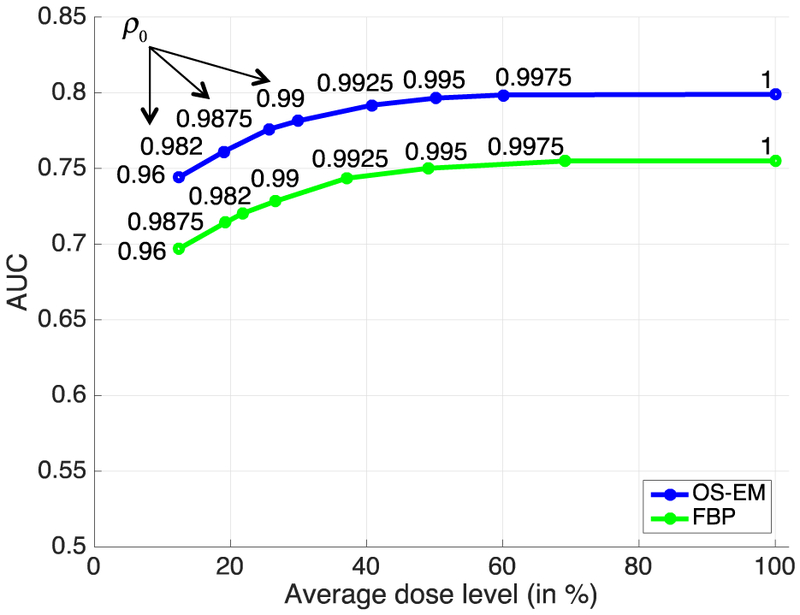
Perfusion-detect detection results (measured in AUC) obtained with personalized doses determined using image similarity-based strategy. The personalized dose levels were controlled by varying the image similarity parameter ρ₀.

The perfusion-defect detection results obtained with personalized doses determined using perfusion based strategy are shown in Figure 2. In this strategy, the different dose levels were controlled by varying the allowance parameter δ on the deviation of TPD score from the full dose (average 32.3 mCi), as indicated on each curve. In particular, with δ = 0.25, the AUC obtained with FBP is 0.753 (average personalized dose fraction = 68%, or 22.0 mCi); similarly, for OS-EM, the AUC obtained with personalized dose is 0.797 (average dose fraction = 67%, or 21.7 mCi). With larger allowance values of δ, the average personalized dose is further reduced in both FBP and OS-EM, but the AUC values also decrease accordingly.

Fig. 2.

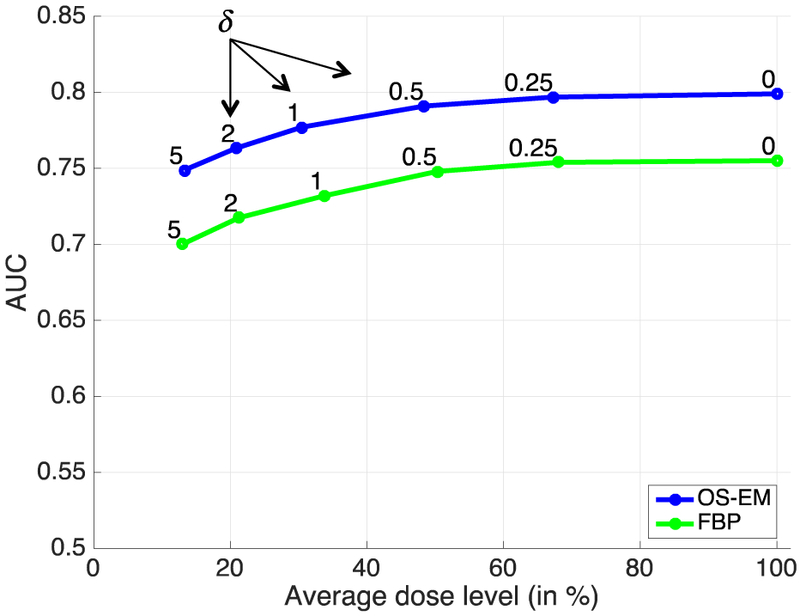
Perfusion-detect detection results (measured in AUC) obtained with personalized doses determined using perfusion-based strategy. The personalized dose levels were controlled by varying the TPD allowance parameter δ.

These results indicate that with either image similarity based strategy (ρ₀ = 0.9975) or perfusion strategy (δ = 0.25), the personalized dose can yield essentially identical perfusion-defect detection performance to the clinical full dose. Furthermore, by relaxing the similarity parameter ρ₀ (or the allowance parameter δ), one can obtain further dose reduction. For example, with the setting of ρ₀ = 0.982 (Fig. 1), the personalized dose level with OS-EM reconstruction on average is only 19% of the full dose (or 6.15 mCi); at this level, the personalized doses with OS-EM yielded AUC=0.760, comparable to the AUC=0.755 obtained at full dose by FBP.

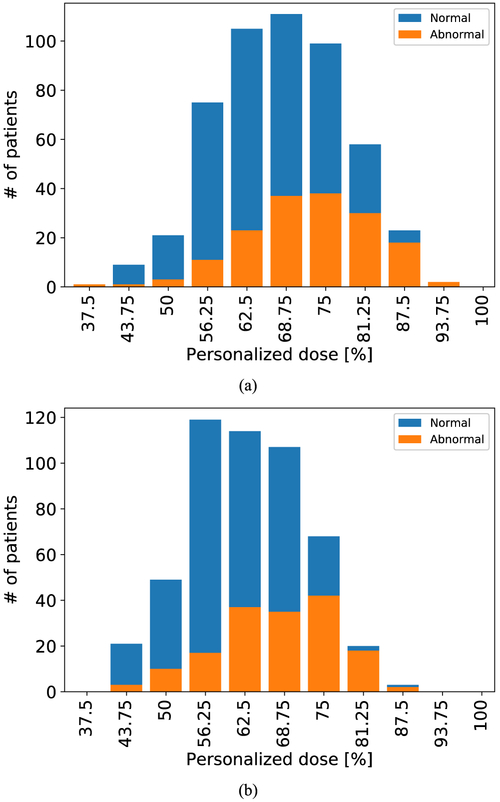
The above results reveal that the personalized dose level on average is notably lower than the full dose. To demonstrate this, in Fig. 3 we show a distribution of the personalized dose levels (relative to full dose) among the 667 patients in Subset B obtained using the image similarity based strategy with ρ₀ = 0.9975 for FBP reconstruction (Fig. 3(a)) or OS-EM reconstruction (Fig. 3(b)). Note that the personalized dose levels vary greatly among the individual subjects, ranging from 37.5% to 93.75% for FBP and from 43.75% to 87.5% for OS-EM. This indicates that dose reduction can be more effective on an individual basis rather than a uniform reduction among all patients. Moreover, the results in Fig. 3 indicate that the personalized dose can achieve on average more reduction in patients with normal perfusion than those with abnormal perfusion readings.

Fig. 3.

Distribution of personalized dose levels (relative to full dose) among 667 patients determined with similarity-based strategy (ρ₀ = 0.9975) for: (a) FBP (Model 1), and (b) OS-EM (Model 2).

In addition, from the results in Fig. 1 and 2, it is observed the image similarity-based strategy generally achieved lower personalized dose levels on average than the perfusion based strategy for a given AUC level. For example, at AUC=0.796 with OS-EM reconstruction, the average personalized dose fraction is 50% for the image similarity-based strategy and 68% for the perfusion based strategy. In addition, the image similarity-based strategy is also much easier to apply (e.g., no need of a reference normal database). Based on these considerations, we focus on results obtained with this strategy in the rest of the study.

B. Personalize dose prediction models

Below we provide results obtained with each of the following three personalized dose prediction models (described in Section III.C): Model 1 for personalized doses with OS-EM reconstruction (ρ₀ = 0.9975), Model 2 for personalized doses with FBP reconstruction (ρ₀ = 0.9975), and Model 3 for further dose reduction with OS-EM reconstruction (ρ₀ = 0.982).

As noted in Section III.C, Model 1 (or 2) was aimed to achieve the same perfusion detect detectability as full clinical dose when FBP (or OS-EM) reconstruction was used. To be conservative, we used ρ₀ = 0.9975 as the threshold for Model 1 and Model 2; as noted in the results in Section V.A above, with this threshold, the AUC value of personalized dose is almost identical to that of full dose (Model 1: 0.754 vs. 0.755; Model 2: 0.799 vs. 0.801). Of course, one may also pick a lower threshold (e.g., (ρ₀ = 0.995), which would allow for even lower dose levels, albeit at the expense of only a slightly lower AUC value than the full dose; at ρ₀ = 0.995, no statistically significant difference was found between the two (p-value > 0.05 for both Model 1 and Model 2). In contrast, Model 3 was chosen to demonstrate how much personalized dose can be further reduced by varying the similarity threshold (ρ₀ = 0.982, AUC=0.760) while still achieving a performance level above that of FBP reconstruction at full clinical dose (AUC=0.755).

Figure 4 shows the results of the relative error in predicted dose, defined earlier in equation (6), for the different personalized dose models (Models 1-3). For each model, the results are shown for two linear regression algorithms (ridge and LASSO), and two non-linear regression algorithms (Random Forest and SVR-RBF). These results were obtained on the 667 patients in Subset B using 3-fold cross-validation (Section III.D). Observe that the non-linear algorithms obtained smaller errors than the linear ones in all three models; moreover, LASSO (linear) achieved smaller errors than ridge (linear) (p-value<0.05 in Models 1 and 2; paired t-test), and Random Forest (non-linear) achieved smaller errors than SVR-RBF (non-linear) (p-value<0.05 in Models 1 and 2). Based on these results, we choose LASSO as the linear algorithm and Random Forest as the non-linear algorithm for the three personalized models in the results below.

Fig. 4.

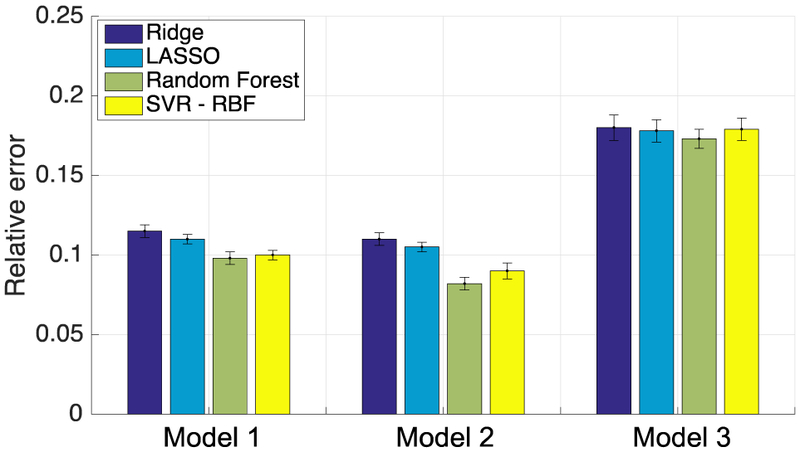
Relative error in predicted dose obtained by various learning algorithms in the three personalized dose models using 3-fold cross validation on Subset B.

Figure 5 shows the relative error in predicted dose obtained on the 190 test patients in Subset A by LASSO and Random Forest for the three personalized dose models. Consistent with the results in Figure 4, Random Forest (non-linear) achieved smaller error than LASSO (linear) in all three models.

Fig. 5.

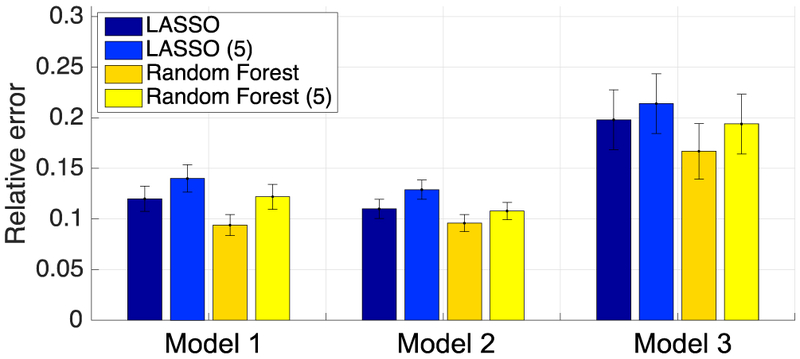
Relative error in predicted dose obtained by various learning algorithms in the three personalized dose models on the test subjects in Subset A. LASSO (5) and Random Forest (5) denote results obtained when only BMI, Chest measurement 2, Age, LDL and Height were used.

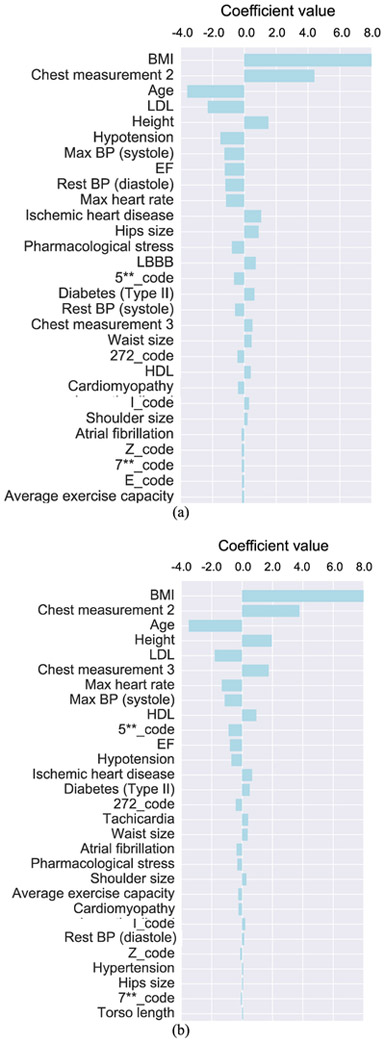
In Fig. 6 we show the relevant patient features selected by the LASSO learning algorithm in personalized Model 1 (Fig. 6(a)) and Model 2 (Fig. 6(b)). Note that BMI, Chest measurement 2, Age, LDL and Height were among the top five contributing features in both models, followed by Hypotension, Max BP (systole), EF, Rest BP (diastole), Max heart rate, etc. These variables were quantitative features directly related to the body size/shape of a patient (which can affect photon attenuation) or physiological features related to the blood perfusion in the myocardium. It is also noted that the variables in the form of diagnostic codes appear to have less influence in both models. We believe a possible reason for this is that these variables are likely correlated with other variables such as blood pressure, LDL and BMI, etc.

Fig. 6.

A list of patient features in personalized dose Model 1 (a) and Model 2 (b) using the LASSO algorithm. The individual features are ordered by the magnitude of their linear coefficients in the model. Abbreviation terms: BMI: body mass index; LDL: low density lipoprotein; BP: blood pressure, EF: ejection fraction, LBBB: left bundle branch block, HDL: high density lipoprotein.

A similar set of features was also obtained in personalized dose Model 3, but not shown here for brevity. In addition, these features were also selected similarly when the non-linear Random Forest regression algorithm was used (Models 1-3); however, lipid values such as cholesterol-to-HDL ratio and triglycerides were also selected as important features. This may be an indicative of a non-linear relationship among the various patient features (and personalized dose levels).

The results in Fig. 6 indicate that there can be a rather large number of patient features that are relevant to determining the personalized dose. However, in practice a simplified model with fewer patient parameters can be easier to implement. For this purpose, we also re-trained the prediction models by using only the top five features in Fig. 6 (i.e., BMI, Chest measurement 2, LDL, Age and Height). The corresponding relative error obtained with these five features is also shown Fig. 5 for both LASSO (LASSO (5)) and Random Forest (Random Forest (5)) in each of the personalized dose models. Note that the relative error in predicted dose gets significantly larger than using the full set of features in both LASSO and Random Forest for each model (p-value<0.05; paired t-test).

C. Perfusion-defect detection performances using predicted personalized doses from trained models.

Figure 7 shows the perfusion-defect detection performance results (measured by AUC in the ROC study) obtained by using the predicted personalized doses for the subjects in the test set (Subset A). In the figure, the results are shown separately for each of the three personalized dose prediction models (Models 1-3). Within each model, the results are given for both the LASSO and Random Forest algorithms.

Fig. 7.

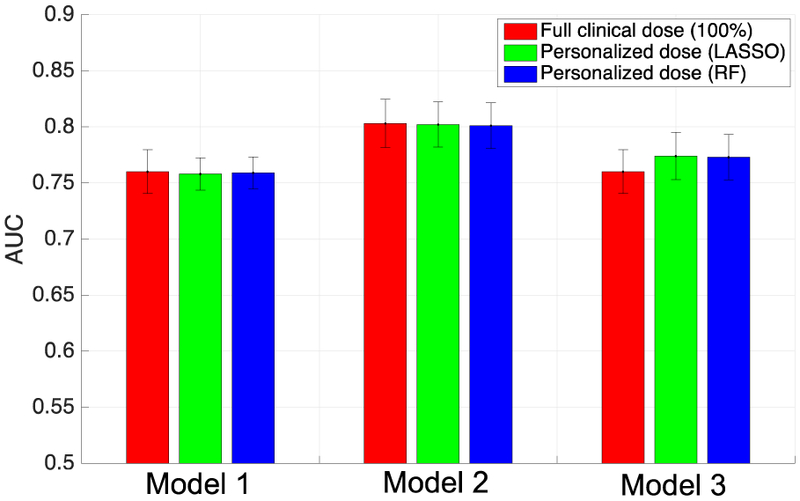
Perfusion-defect detection performance (measured by AUC) obtained with personalized dose models. For reference, the full dose results are also included for each model. Note that FBP reconstruction was used in Model 1, and OS-EM was used in Model 2. In Model 3, OS-EM was used for personalized dose, and FBP was used for the reference full dose.

As reference, the AUC values are also given in Fig. 7 for Models 1 and 2 when the full clinical doses were used. Recall that these two models were designed to achieve the level of performance of the full dose; indeed, in both models, the AUC values obtained by LASSO and Random Forest are noted to be virtually identical to that of the full dose (p-values all larger than 0.5). For Model 3, the AUC is also shown for FBP with full dose; recall that Model 3 was intended to achieve lower personalized dose by using OS-EM reconstruction while maintaining the detection performance of full clinical dose with FBP reconstruction.

It is observed that the personalized doses yielded essentially identical perfusion-defect detection performance to that of the full dose. In terms of dose levels, when LASSO was used, the average personalized dose levels were 19.4, 17.9 and 5.4 mCi for Models 1-3, respectively; when Random Forest was used, the average dose levels were 18.8, 17.6 and 5.3 mCi for Models 1-3, respectively. Note that the average full dose level was 32.3 mCi. We can see that Random Forest achieved further dose reduction in all three models in comparison with LASSO. In particular, the average personalized dose level achieved with Model 3 (Random Forest) was only 16% of full dose, which yielded AUC=0.773; in comparison, from the results previously obtained on uniform dose reduction [25], at 25% of the full dose, OS-EM achieved AUC=0.764.

These results indicate that the personalized dose models can accurately determine the dose levels needed for individual patients prior to the SPECT-MPI procedure. They can effectively reduce the injected activity on average while maintaining the detection performance of perfusion defects that would be obtained if the patients were imaged at clinical full dose levels.

D. Reconstruction examples with personalized dose models

In Fig. 8 we show the reconstructed images (in short-axis slices and polar maps) of a female subject (BMI=31.5, age=65). The subject was interpreted to have normal perfusion. For comparison, the images are shown for both the full dose and personalized dose data of Models 1-3 (Random Forest). Specifically, the top panel in Fig. 8 shows the FBP reconstruction from the full dose data (31.5 mCi) and the personalized dose at 20.7 mCi (Model 1); similarly, the middle panel shows the OS-EM reconstruction from the full dose data and the personalized dose at 19.4 mCi (Model 2). It is observed that in both cases the images obtained from the personalized dose are almost identical to that obtained from the full dose. In addition, the bottom panel in Fig. 8 shows the OS-EM reconstruction from the personalized dose at merely 6.2 mCi (Model 3; a 80% reduction). While these images may not appear visually identical to the FBP with full dose, the wall resolution and noise level are similar between the two; the ROC results above indicated that the personalized dose Model 3 achieved slightly better perfusion-defect detection performance than the full clinical dose with FBP reconstruction.

Fig. 8.

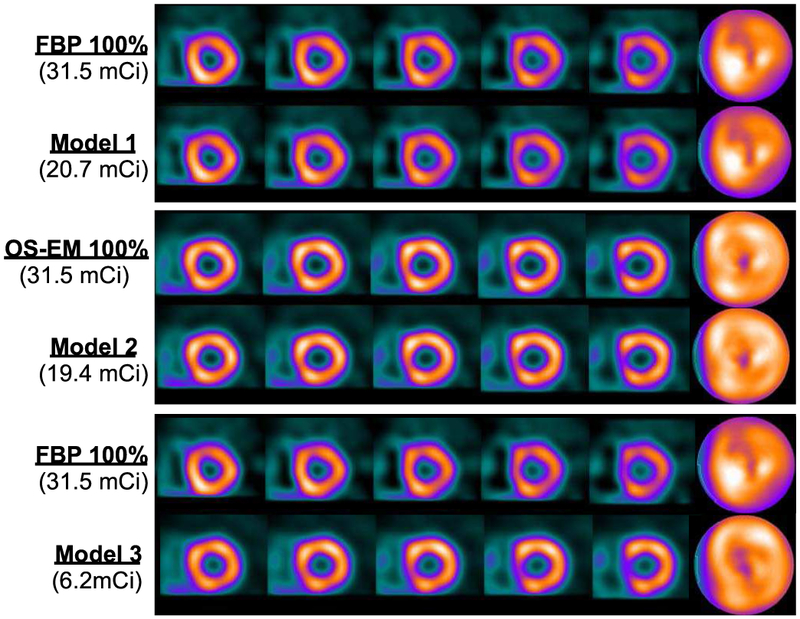
Reconstructed images with personalized dose and full dose data for Subject #1 (female, BMI=31.5, age=65). Top panel: FBP reconstruction with full dose (first row) and with personalized dose (second row). Middle panel: OS-EM reconstruction with full dose (first row) and with personalized dose (second row). Bottom panel: FBP reconstruction with full dose (first row), and OS-EM reconstruction with personalized dose (second row).

Similarly, Fig. 9 shows the reconstructed images for a male subject (BMI=25.8, age=48). This subject had a moderate sized defect introduced in the left circumflex artery (LCX) territory. The full dose level was 35 mCi, while the personalized dose levels were 16.7, 16.2 and 4.9 mCi for Model 1 (top panel), Model 2 (middle panel) and Model 3 (bottom panel), respectively. As in Fig. 8, the personalized dose images of Models 1 and 2 appear virtually no different from their counterparts with full dose. Even with personalized dose reduced to 4.9 mCi (a 86% reduction), the extent and contrast of the defect in the reconstructed images remain to be similar to that of full dose (bottom panel).

Fig. 9.

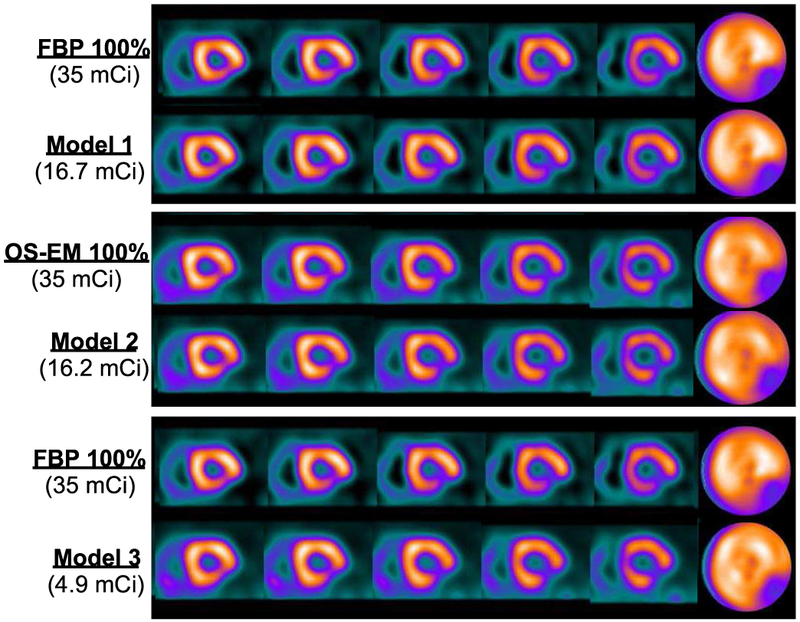
Reconstructed images with personalized dose and full dose data for Subject #2 (male, BMI=25.8, age=48). There was a moderate sized perfusion defect introduced in the left circumflex artery (LCX) territory. Top panel: FBP reconstruction with full dose (first row) and with personalized dose (second row). Middle panel: OS-EM reconstruction with full dose (first row) and with personalized dose (second row). Bottom panel: FBP reconstruction with full dose (first row), and OS-EM reconstruction with personalized dose (second row).

Finally, it is noted in Figs. 8 and 9 that the polar maps appear to be different between FBP and OS-EM. This is largely due to the fact that attenuation correction was applied in OS-EM, but not in FBP. This difference is particularly more pronounced in Figure 8 (an obese female patient); without attenuation correction, the polar map of FBP becomes notably less uniform than that of OS-EM. In the clinic an experienced clinician can compensate for this artifact in their read based on the patient profile. In the model observer QPS, this is compensated for by using separate reference databases for male and female subjects and for different reconstruction algorithms.

E. Discussion

Due to its high prevalence and large installation base in clinics, myocardial perfusion imaging (MPI) with SPECT has become the number two contributing source of increased radiation risk to the public (only after CT) in medical imaging [47]. In an effort to reduce this risk, the recent guidelines of American Society of Nuclear Cardiology (ASNC) mandate reducing the injected imaging dose to patients [48]. However, it is also pointed out [48] that while reducing the dose is important, the image quality must not be sacrificed. The focus of this work is to present a strategy to determine the optimal dose level needed for each patient, and apply machine learning to predict this dose level based on the patient’s attributes. Our results indicate that the effective imaging dose needed can vary greatly from patient to patient (Fig. 3), and that with our personalized approach the injected imaging dose can be reduced on average by as much as 41.8% (Model 1) to 84% (Model 3). Such reduction is expected to lead to great benefit in cutting the radiation risk not only to the individual patients themselves but also others around them in the clinic (e.g. technologists).

In this study, we resorted to using ROC studies to determine the relationship between the perfusion detection performance and the image similarity threshold ρ₀ρ₀ or δ in developing the personalized dose models. This allowed us to directly optimize the threshold value for the clinical task of perfusion detection. Alternatively, it can be more desirable to seek an analytical approach to determine a priorithe image similarity threshold. However, such relationship is expected to be highly non-linear and can be complicated by the high variability in patient characteristics observed clinically. Thus, some simplifying assumptions likely would have to be made in order for the problem to become mathematically tractable.

It is noted that the resulting model from a machine-learning algorithm is used to describe only how well the target variable (i.e., the dose) can be predicted by other variables such as BMI and age. But this model does not necessarily reveal a causal (biological) relationship among the variables. That is, two variables can be highly correlated, but there may not be a causal relationship between them. In the personalized dose prediction models, age was shown to have a negative correlation with the predicted dose. We believe that this may simply reflect that patients who live longer are more likely to have a healthier heart; indeed, the distribution in Fig. 3 indicates that patients with normal perfusion tend to have more reduction in personalized dose than those with abnormal perfusion. Interestingly, age is indeed a factor used for calculating the pretest probability of CAD of a patient in the clinic. In addition, some of the variables can be related in a highly nonlinear fashion. Indeed, the results above (Section V.B) show that the nonlinear model Random Forest can yield a significantly lower relative error in predicted dose than its linear counterparts.

In Fig. 5, we considered the case of using only five most relevant features to illustrate that the relative error would increase when the relevant features selected by the prediction models were trimmed down. While the mean relative error may not seem to be increased by a large amount (albeit statistically significant), it is also somewhat not surprising because only the most dominant features were used in the reduced models. However, the error level is expected to only further increase if the number of features is further reduced (i.e., down to only two), because the coefficient values of the third and fourth features (Figure 6) are rather comparable to that of the second feature. This increased error is expected to eventually affect adversely the quality of resulting images, and thus diagnostic accuracy, for certain patients.

As noted earlier in Section V.B, a simplified model (with fewer variables) may be more desirable in a clinic. However, it should be noted that, once a prediction model is trained, it becomes fixed and the calculation of personalized dose is rather straightforward (and can be implemented via a simple web interface). It can even be automated as patient records are now increasingly becoming electronic in clinics. In such a case, there should be little difference between using two or five variables as far as calculation is concerned. When electronic records are not available, one may elect to use a model with fewer variables in order to reduce the amount of manual work involved in obtaining these variables (e.g., searching through paper records).

We acknowledge that dosing errors are inevitable in clinical practice (due to tracer decay and difficulties with administering doses). Nevertheless, it is always beneficial to keep the model prediction error as small as possible, as it will further contribute to the overall error (in an additive way), which can adversely affect the image quality in patients. It might be interesting in a future study to further investigate how the dosing error may affect the diagnostic accuracy.

It is important to note that, for computing the similarity metric in the personalized dose models, we used only one noise realization per patient, and relied on the large number of patients to improve the model training in the experiments. Alternatively, one could apply multiple noise realizations to improve the accuracy of the estimated image similarity metric, which in turn can provide a more accurate target for training the dose prediction model. Of course, this would also greatly increase the computational complexity especially when iterative reconstruction is used. In the experiments, we also computed the similarity metric ρ from 100 noise realizations for three randomly selected patients at 50% of full dose using FBP reconstruction. The obtained values for the three patients are: ρ = 0.9956±3.4×10⁻⁴, 0.9947±3.3×10⁻⁴, 0.9950±3.1×10⁻⁴, respectively. Note that the standard-deviation values are very small compared to the mean values in all three patients. We believe the reason for this is that the similarity metric was computed over the entire 3D heart volume. Thus, the high noise variations among the individual voxels from multiple noise realizations were averaged out over the volume.

VI. Conclusions

We developed predictive models to determine patient-specific administered activities for SPECT-MPI based on patient attributes. The predictive models based on non-linear regression were demonstrated to achieve better relative error in predicted dose and yield lower dose levels on average when compared to linear models. The determined features in these personalized dose models via machine learning consisted of body measurements (such as BMI and chest size), and physiological variables (e.g., LDL and blood pressure) as well as medical conditions (diabetes, cardiac conditions, etc.). Our results indicate that the achieved dose reduction can vary greatly among individuals from their conventional clinical dose. The personalized dose models can also achieve further reduction on average compared to a global (non-patient specific) dose reduction approach studied previously. We note that the clinical protocol used in this study (i.e., full dose data) was based on ASNC recommendations [40], in which the injected dose was adjusted according to the BMI of the subject.

In the study we validated the personalized dose models on perfusion-defect detection using the clinically validated observer QPS. Encouraged by these results, in the future we plan to conduct a reader study using clinical readers to further evaluate the personalized dose models in potential clinical use.